the Creative Commons Attribution 3.0 License.
the Creative Commons Attribution 3.0 License.
Insights into Atlantic multidecadal variability using the Last Millennium Reanalysis framework
Hansi K. A. Singh
Gregory J. Hakim
Robert Tardif
Julien Emile-Geay
David C. Noone
The Last Millennium Reanalysis (LMR) employs a data assimilation approach to reconstruct climate fields from annually resolved proxy data over years 0–2000 CE. We use the LMR to examine Atlantic multidecadal variability (AMV) over the last 2 millennia and find several robust thermodynamic features associated with a positive Atlantic Multidecadal Oscillation (AMO) index that reveal a dynamically consistent pattern of variability: the Atlantic and most continents warm; sea ice thins over the Arctic and retreats over the Greenland, Iceland, and Norwegian seas; and equatorial precipitation shifts northward. The latter is consistent with anomalous southward energy transport mediated by the atmosphere. Net downward shortwave radiation increases at both the top of the atmosphere and the surface, indicating a decrease in planetary albedo, likely due to a decrease in low clouds. Heat is absorbed by the climate system and the oceans warm. Wavelet analysis of the AMO time series shows a reddening of the frequency spectrum on the 50- to 100-year timescale, but no evidence of a distinct multidecadal or centennial spectral peak. This latter result is insensitive to both the choice of prior model and the calibration dataset used in the data assimilation algorithm, suggesting that the lack of a distinct multidecadal spectral peak is a robust result.
- Article
(10808 KB) - Full-text XML
-
Supplement
(1533 KB) - BibTeX
- EndNote
Modeling and observational studies have shown that North Atlantic sea surface temperatures (SSTs) covary with the following: precipitation over the African Sahel (Zhang and Delworth, 2006), Eurasia (Lu et al., 2006; Zhang and Delworth, 2006), and North America (Enfield et al., 2001); hurricane development and intensity over the Atlantic (Zhang and Delworth, 2006); drought over the North American interior (McCabe et al., 2004; Nigam et al., 2011); summer temperatures over Europe and the Americas (Sutton and Hodson, 2005); sea ice thickness and extent over the Arctic (Miles et al., 2014); climate variability over the Pacific (Dong et al., 2006); and marine primary productivity (Henson et al., 2009). Improved prediction of global climate perturbations likely depends on a better understanding of North Atlantic variability.
Kushnir (1994), following the earlier hypotheses of Bjerknes (1964), shows that North Atlantic sea surface temperatures (SSTs) appear to vary on both interannual and interdecadal timescales and that variability on these different timescales is substantively different. While wind and surface pressure appear to covary with North Atlantic SSTs on short timescales, longer-timescale variability appears to be uncorrelated with these fields. Kushnir (1994) concludes that these different timescales constitute different phenomena and suggests that the longer-timescale portion of the variability could be driven by ocean–atmosphere coupling. This longer-timescale variability is known today as Atlantic multidecadal variability (AMV), with the unforced, internally driven component referred to as the Atlantic Multidecadal Oscillation (AMO).
Studies of the observational and paleoproxy records provide evidence of multidecadal variability centered over the Atlantic. The Central England Temperature record, the longest observational temperature time series, suggests a 65-year timescale of variability over the last 350 years (Tung and Zhou, 2013). Evidence of multidecadal Atlantic variability (with timescales anywhere between 20 and 80 years) has also been found in proxy tree ring records (Delworth and Mann, 2000; Gray et al., 2004), annually resolved ice cores (Chylek et al., 2011), and coral isotope records (Hetzinger et al., 2008). Lengthy proxy records extending over the last 8000 years also show multidecadal spectral power, though this power is not stationary over space or time (Knudsen et al., 2011).
Many studies have explored ocean–atmosphere interactions as driving factors for AMV, with changes in SSTs in the North Atlantic controlled by natural (unforced) fluctuations in the Atlantic meridional overturning circulation (AMOC) (see, e.g., Delworth et al., 1993; Polyakov et al., 2005; Zhang et al., 2007). Several dynamical studies using both ocean-only and fully coupled models have suggested that zonal and meridional oscillations in the AMOC on multidecadal timescales may drive changes in North Atlantic SSTs (for a description of the dynamical mechanism, see Raa and Dijkstra, 2002; Dijkstra et al., 2006, 2008). While long-term observational records of the AMOC state are unavailable, observational evidence of sea surface height appears to support the idea that North Atlantic SSTs covary with changes in sea surface height along the eastern seaboard of the United States, which is consistent with changes in the AMOC (McCarthy et al., 2015).
Nevertheless, there remains disagreement regarding the role of AMOC changes in driving North Atlantic SST variability over multidecadal timescales. Tandon and Kushner (2015) show that the relationship between AMV and the AMOC may not be stationary between the preindustrial and industrial periods: while AMOC fluctuations appeared to lead changes in North Atlantic SSTs over the preindustrial period in models, this lead–lag relationship reversed during the industrial era with strong anthropogenic forcing of the climate system (though there was substantial variations in the lead–lag relationship between models). Recently, Clement et al. (2015) have shown that stochastic coupling between the atmosphere and oceanic mixed layer is sufficient to recover the AMV found in most climate models, calling into question the role of the oceanic MOC as a driver of the AMO. Indeed, only some state-of-the-art global climate models (GCMs) simulate multidecadal variability in Atlantic SSTs (Clement et al., 2015), while one older GCM has been shown to display spurious multidecadal variability due to poor parameterization of ocean mixing processes (see Danabasoglu, 2008). Hakkinen et al. (2011) suggest that changes in the strength of the North Atlantic subpolar and subtropical gyres may be more closely linked to the AMO than variations in the AMOC; such multidecadal shifts in the gyres alter atmospheric blocking patterns which may, in turn, perturb SSTs over the entire Atlantic basin.
The role of aerosols and other forcings as external drivers of North Atlantic SST variability has also been debated. Aerosol release by volcanic eruptions has been suggested to act as an external driver of AMV in the preindustrial period (Ottera et al., 2010; Knudsen et al., 2014), contrary to other studies that suggest that AMV is internally driven by ocean–atmosphere interactions. Over the industrial period, the role of anthropogenic aerosols in driving AMV also remains an open question. Booth et al. (2012) argue that aerosol direct and indirect effects over the modern era (post-1850) have strongly impacted multidecadal SST variability over the North Atlantic, resulting in an evolution of North Atlantic SSTs that mimics an internally driven oscillation. This argument, however, has been challenged by Zhang et al. (2013), who suggest that the GCM used in Booth et al. (2012) incorrectly modeled aerosol effects and show that improved representation of these effects reveals that 20th century surface temperature variations cannot be explained in full by changes in anthropogenic aerosol emissions. Nevertheless, more recent work by Murphy et al. (2017) and Bellucci et al. (2017) further challenges the premise that North Atlantic SST variability over the industrial period is unaffected by anthropogenic forcings.
Given major disagreements between climate models in AMO representation, it is clear that the study of AMO dynamics would benefit from using observational data from the real Earth system. However, the detailed study of the AMO has been severely limited by the brevity of the instrumental record, which is less than 2 centuries long. Furthermore, these observations are from a time period characterized by intense anthropogenic forcing of the climate system through greenhouse gases, aerosols, land use changes, ozone-depleting substances, and others. While the instrumental record is short and likely biased towards a forced response, the proxy record does not suffer from this shortcoming. Indeed, annually resolved proxies for temperature from tree rings, corals, ice cores, and others exist at annual resolution over the last several millennia. Although proxy records exist over much longer periods than observations, an objective procedure for assimilating these proxies into coherent spatial fields remains an ongoing challenge.
The Last Millennium Reanalysis (LMR) provides a robust framework for such objective assimilation of proxies for the reconstruction of spatial fields (Hakim et al., 2016). In this study, we use climate field reconstructions made possible by the LMR to analyze the climate dynamics of the AMO. By assimilating temperature-dependent information from proxy records, we consider what thermodynamic features characterize the AMO over the last 2000 years and whether these features have changed with time, particularly between the preindustrial (years 0 to 1850) and modern (years 1850 to 2000) eras. Since the data assimilation procedure used in the LMR relies on the use of a prior dataset (as described in Steiger et al., 2014; Hakim et al., 2016), we will also note what additional information the assimilation of proxies yields beyond that found in this prior dataset. Finally, we will use the LMR to consider what, if any, robust timescales characterize the AMO over the last 2 millennia and how these timescales computed from the assimilation of the observations compare to those found in previous studies.
The remainder of this paper is organized as follows. We describe the LMR proxy assimilation and climate field reconstruction procedure, along with details of our regression and timescale analysis methodologies, in Sect. 2. In Sect. 3.1, we consider the AMO index over the last 2000 years, as inferred from the LMR, and in Sect. 3.2, we describe the basic climate state that corresponds to a positive AMO index. We highlight the energetics associated with a positive AMO index in Sect. 3.3, particularly top-of-atmosphere and surface fluxes, the implied meridional energy transports, and flux imbalances. In Sect. 3.4, we consider timescales of the AMO using wavelet analysis. We conclude by discussing our findings, their implications, and caveats of our approach in Sect. 4.
The climate field reconstruction methodology used in the LMR is described in detail by Steiger et al. (2014) and is validated for temperature reconstructions over the modern era (years 1850 to 2000 CE) in Hakim et al. (2016).
The LMR uses a novel ensemble data assimilation procedure in which information from a prior expectation of the climate derived from a climate model is weighted against information in proxy records. Weights are determined from the relative error in these two estimates of the climate, as defined by the update equation in the Kalman filter, which is optimal if the errors are Gaussian distributed. We proceed with an overview explanation of the Kalman update equation, before describing the solution method for this equation.
In brief, the data assimilation procedure updates the state of the prior, xp, to some new state xa using information from the proxies y that is weighted using a Kalman gain matrix K:
Here, ℋ is the observation model that converts the prior state to its proxy equivalent, ℋ(xp). The innovation, y−ℋ(xp), contains new information from the observations that is not already present in the prior. The Kalman gain matrix K, which weights the innovation and maps from proxy space to physical space, is
where B is the error covariance matrix for the prior data, H is the linearization of the observation model ℋ about the prior mean, and R is the error covariance matrix for the proxies (described further below). The numerator of matrix K, BHT, is the covariance expectation between the prior and the prior estimated observations and acts to spread information from proxy locales into the physical space.
The solution to Eqs. (1) and (2) is fully described in Steiger et al. (2014) and Hakim et al. (2016), and a summary of the essential elements follows. First, we describe our method for estimating the proxies from the prior data (i.e., H) and the associated errors (i.e., R). Second, we describe our method for creating the prior and the associated errors (i.e., xp and B) using an ensemble sampling technique. This ensemble technique relates directly to the solution method for Eqs. (1) and (2).
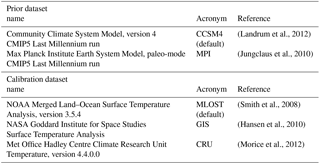
The observation model H, a forward model that maps from physical space to the proxy space, is constructed using a calibration dataset and assumes a linear relationship between the proxy state and temperature over the calibration period:
where T′ is the annual mean 2 m air temperature anomaly from the calibration dataset, β0 is the intercept, β1 is the slope, and ϵ is a Gaussian random variable with zero mean and a variance of σ2. The calibration temperature T′ for a given proxy record is chosen from the grid point closest to the proxy location at concurrent time periods, and parameters β0, β1, and σ are computed using a linear least-squares fit against the NOAA Merged Land–Ocean Surface Temperature Analysis (MLOST; Smith et al., 2008) during the time period 1900–2000. The diagonal elements of R, the error covariance matrix for the proxies, are the variance of the regression residuals, σ2. In principle, other sources of error contribute to R, such as instrumental (laboratory) error and representativeness error (the climate model grid cell resolves spatial averages rather than the points that are observed), but the errors in Eq. (3) are large by comparison and so we approximate R accordingly.
In operational weather data assimilation, prior data are determined by a short-term forecast that is initialized from an analysis derived at an earlier time. Because the forecast applies to a short time interval (1–12 h), it provides an accurate estimate of the observations at the future time; that is, it is a well-informed prior. In contrast, climate model forecasts on proxy timescales (yearly for the proxies used here) contain little forecast skill and are expensive to compute. Consequently, model simulations on annual timescales are nearly agnostic of the initial state and are thus statistically nearly the same as forecasts drawn randomly from the climate of the model. This fact motivates an “offline” approach to the prior and data assimilation method in which prior data are defined using an ensemble sampling strategy. Here we randomly draw an ensemble of 100 annual mean samples from an existing climate model simulation. Specifically, we use the Community Climate System Model version 4 (CCSM4) Last Millennium run (from Phase 5 of the Climate Model Intercomparison Project) for the prior and use the same 100-member sample from this simulation as the prior for each year in the reconstruction. The mean value of this sample serves as xp in Eq. (1).
We use an ensemble square-root solution method to Eqs. (1) and (2), including serial observation processing (Whitaker and Hamill, 2002), so that proxies are assimilated one at a time for each year of the reconstruction. In this approach, the matrix inverse in Eq. (2) becomes a trivial scalar inverse, and the covariance matrix B, which can be enormous, is never explicitly formed; rather, only the ensemble-estimated covariance between the proxy and the reconstructed field at each point is needed (see Steiger et al., 2014, for further details). Proxy estimates ℋ(xp) are computed in advance and updated each year along with the reconstructed fields with the assimilation of each proxy.
Using this method, we reconstruct annual mean fields between 0 and 2000 CE. The proxies used are a total of 465 time series from the PAGES2K dataset (Consortium, 2013; Hakim et al., 2016), which includes lake sediment calcium to phosphorus ratios, ice core water isotopes (both oxygen and hydrogen), coral oxygen isotopes, tree rings (width and density), and speleothem water isotopes. As described in Hakim et al. (2016), the LMR reconstructions of temperature and 500 hPa geopotential height have been validated over the instrumental period. Moreover, the results have also been validated against independent proxies (not assimilated) before and during the instrumental period and to ensure that the error in the ensemble mean is statistically equivalent to the predicted error in the ensemble variance as expected from theory. Though the reanalysis results obtained when using different prior and observation–model calibration datasets are quantitatively distinct (see Fig. 12 in Hakim et al., 2016), they all yield qualitatively similar results. Therefore, much of the ensuing analysis, apart from the calculation of timescales (see below), is performed using this single reanalysis, hereafter referred to as MLOST-CCSM4.
We note that because the prior is the same for every year, all temporal variability is determined by the proxies. As a result, the weighting in Eq. (1) involves a temporally invariant prior and temporally variable proxies so that, for any given proxy, reduced temporal variability may be expected. However, since the time series at any point in the reconstruction depends on the prior and many proxies all having different errors, the variability at a proxy location may in fact be larger or smaller than that of a given proxy at that point.
Following Clement et al. (2015) and others, we quantify AMV using the AMO index, which is computed annually as the average of the area-weighted SSTs from 60∘ N to the Equator and 80∘ W to the prime meridian. Links between climate variables and the AMO are defined by regression onto the AMO index and computing the value of the variable at two SDs of the AMO index. In order to isolate multidecadal (and longer) timescale variability, both the AMO index and variable fields are filtered using a 20-year low-pass Lanczos filter with 31 filter weights prior to computing the regressions (unless otherwise noted; see Duchon, 1979, for a full description of the Lanczos filter). The AMO index and climate variable fields are detrended before regression. Regression results from the LMR are computed for three time periods to highlight potential nonstationarity in the AMO: years 0 to 1850 (the preindustrial era), 1200 to 1850 (the part of the preindustrial era when proxy coverage is substantial), and 1850 to 2000 (the industrial era). These results are compared to similar results from the CCSM4 prior.
AMO index timescale analysis was performed with wavelets using the methodology described by Torrence and Compo (1998). The Paul wavelet is used with a scale spacing of 0.25 and a total of 52 scales spanning 2 to 1000 years. Significance is computed at p<0.05 using a one-step autoregression (AR(1); i.e., red noise) process as the null hypothesis; significance results were found to be insensitive to the choice of the mother wavelet. Wavelet analysis was performed on six different AMO index reconstructions using two different priors and three different calibration datasets (see Table 1).
Landrum et al. (2012)Jungclaus et al. (2010)Smith et al. (2008)Hansen et al. (2010)Morice et al. (2012)3.1 The AMO index in the LMR
Over the last 2000 years, the AMO index reconstructed from the LMR resembles the global mean surface temperature (GMST) time series (Fig. 1a and b; r=0.97 at lag 0). Like the GMST, the AMO has the least variability over the first 1000 years of the reanalysis, possibly due to the lack of globally distributed proxy records over this early period of the reanalysis. Over the latter portion of the reanalysis (year 900 CE forward), a cooling trend is evident in both the AMO and GMST, which is punctuated by a warmer period centered at year 1500 CE. A warming trend is evident in both the AMO and GMST time series following year 1900 CE.
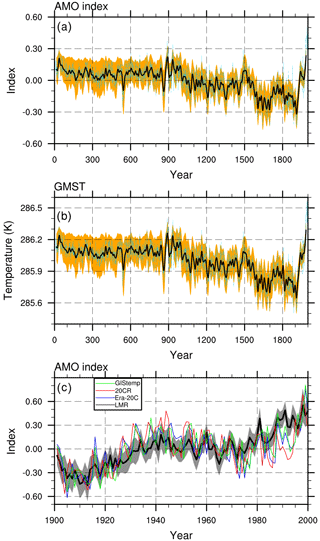
Figure 1(a) Atlantic Multidecadal Oscillation (AMO) index time series and (b) global mean surface temperature (GMST) time series computed from the LMR over the last 2000 years, with the yearly time series (light blue, dotted) and 20-year low-pass time series (black; 95 % confidence interval shown in orange). (c) AMO index over the last 100 years (bottom) as computed from the LMR (black; 95 % confidence interval shown in grey), the 20th Century Reanalysis (20CR, red), the ERA-20C reanalysis (Era-20C, blue), and the NASA GIStemp reanalysis (GIStemp).
In Fig. 1c, we show the LMR reconstruction of the AMO index over years 1900 to 2000 CE, along with three different reanalysis datasets: NASA's GIStemp, ERA-20C, and the 20CR. Comparison with these other reanalyses suggests that the LMR MLOST-CCSM4 reconstruction reasonably recreates the North Atlantic SST record over the last century: as expected, the LMR and the three reanalyses all show an upward trend in the AMO index over this time period and all reveal intermittent periods of rapid and slower temperature rise ( between the LMR MLOST-CCSM4 AMO index reconstruction and the GIStemp, ERA-20C, and 20CR AMO indices, respectively), suggesting a multidecadal oscillation. The LMR displays slightly weaker amplitude in this multidecadal timescale than the other reanalyses. We return to this question of timescales in Sect. 3.4.
3.2 Thermodynamics of the AMO in the LMR
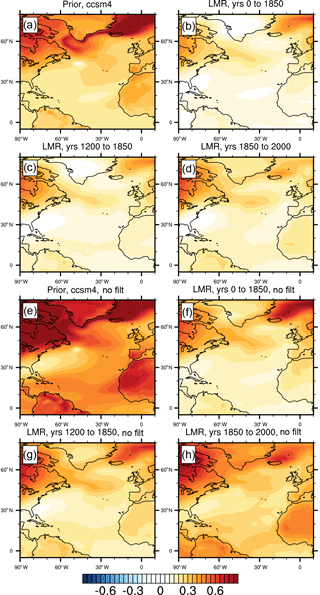
Globally, the temperature field associated with a positive AMO index is characterized by warming over the continents and especially strong warming over the far northern reaches of the Atlantic and Arctic (Fig. 2). Warming is greater over the Northern Hemisphere (NH) than the Southern Hemisphere (SH) over all time periods, and the magnitude of warming is strongest over all regions in the CCSM4 prior compared to that in the LMR. Over both the CCSM4 prior and the LMR, there is warming over the Arctic, though the location of maximum warming is different: in the CCSM4 prior, warming is greatest over the Greenland, Iceland, and Norwegian (GIN) seas, while warming is greatest in the LMR over the Barents Sea. In the LMR, variability is relatively stationary over all time periods (r=0.92 between the regression over years 0 to 1850 and r=0.73 over years 1200 to 1850 and years 1850 to 2000), though differences in warming over the high northern latitudes are apparent; in the preindustrial period (pre-1850), warming over northern Eurasia is most prominent, while warming over boreal North America and central Asia dominates in the industrial period.
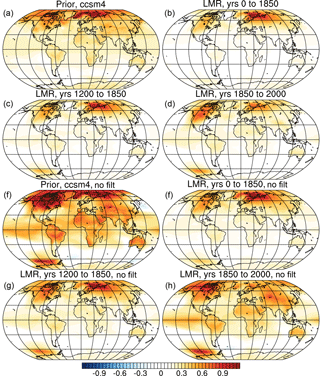
Figure 2Low-pass-filtered regression of the AMO index on surface temperature (in K) in (a) the CCSM4 prior, (b) the LMR from years 0 to 1850, (c) the LMR from years 1200 to 1850, and (d) the LMR from years 1850 to 2000. Panels (e) through (h) are similar to (a) through (d), but show the unfiltered regression.
Comparison of the 20-year low-pass-filtered regression of the AMO index on temperature (Fig. 2a to d) with the unfiltered regression (Fig. 2e to h) reveals that the temperature response associated with the AMO is stronger on the shorter timescales that dominate the unfiltered regression.
Over all time periods in the LMR (years 0 to 1850, years 1200 to 1850, and years 1850 to 2000), warming is not uniform over the North Atlantic basin: maxima in warming are evident at 50 and 5∘ N (Fig. 3a to d). Over shorter timescales than those explored in the remainder of this study, however, the two-lobed pattern becomes a horseshoe with the tropical and midlatitude warming maxima linked by warming over the eastern Atlantic (compare Fig. 3a–d to Fig. 3e–h). This distinct horseshoe pattern of warming over the midlatitudes and tropics that characterizes North Atlantic SST variability on shorter timescales has been noted by others and is the leading mode of variability found with empirical orthogonal functional decomposition analysis over this region (see, e.g., Hartmann, 1994). Because our focus is on longer-timescale variability, we will utilize 20-year low-pass filtering for the rest of our analysis (except for time series analysis of the AMO index; Sect. 3.4).
During the positive phase of the AMO, the LMR shows that warming over the high-latitude North Atlantic is linked to the retreat of sea ice from the GIN and Barents seas (Fig. 4, contours), with strong spatial agreement between the LMR over all time periods (r=0.89 between the regression over years 0 to 1850 and r=0.69 over years 1200 to 1850 and years 1850 to 2000). In contrast, the CCSM4 prior shows a much more sharply defined spatial pattern of sea ice retreat than the LMR, though the general regions of retreat are the same. Sea ice also thins over much of the Arctic (Fig. 4, colors) in both the LMR and CCSM4 prior; in the CCSM4, sea ice thins over the entire Arctic, while in the LMR, there is a small region of sea ice thickening centered about the Beaufort Sea. This thickening of ice in the Beaufort sea is linked to a low pressure center over the Arctic in the LMR, which is not present in the CCSM4 prior (or in other reanalyses of the instrumental period). Sea ice retreat coincident with the positive phase of the AMO has also been shown in model-based studies (see, e.g., Miles et al., 2014). Such retreat and thinning of sea ice is also consistent with increased ocean heat transport into the North Atlantic, possibly due to strengthening of the AMOC during the positive phase of the AMO (considered further in Sect. 3.3).
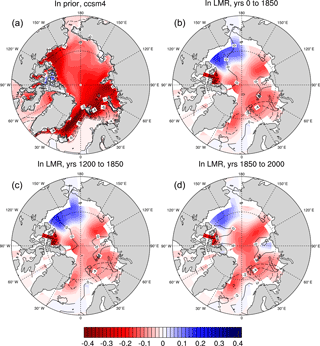
Figure 4As for Fig. 2 panels (a) to (d), but for the low-pass-filtered regression of the AMO index on sea ice thickness (colors, in millimeters) and on sea ice concentration (contours, %).
While warming associated with the positive phase of the AMO is strongest over the high northern latitudes, associated precipitation changes are most prominent at the Equator over all basins (Fig. 5). Surprisingly, the magnitude of these changes is larger in the LMR (years 1200 to 1850 and years 1850 to 2000) than in the CCSM4 prior, though temperature increases associated with the AMO are largest in the latter (recall Fig. 2). On the other hand, the magnitude of these changes is very small over years 0 to 1850 CE in the LMR, possibly due to poor proxy coverage during the earlier part of this period. Most changes in precipitation are colocated in the CCSM4 prior and the LMR ( between the CCSM4 and the LMR over years 0 to 1850, 1200 to 1850, and 1850 to 2000, respectively), though the LMR predicts stronger AMO-linked drying over the maritime continent than found in the CCSM4 prior. In general, the magnitude of the increase in precipitation is greatest in the NH, and a northward shift in the equatorial precipitation maximum (the Intertropical Convergence Zone, i.e., the ITCZ) is particularly evident over the Atlantic basin (see also Knight et al., 2006). We also note that the double ITCZ apparent in the CCSM4 prior is consolidated into a single precipitation maximum in the LMR.
3.3 Energetics
The energetics associated with a positive AMO index differ significantly between the LMR and the CCSM4 prior. While surface and TOA fluxes and their imbalances are qualitatively similar between the LMR and the CCSM4 prior, we find that the energy transports implied by these fluxes differ between the LMR and CCSM4 prior. Overall, the energetics and implied dynamics in both the LMR and CCSM4 prior are consistent with most findings from previous studies (see Knight et al., 2006), though there are some discrepancies. We describe these findings in detail below.
In the LMR, a positive AMO index is linked to net top-of-atmosphere (TOA) radiative flux (positive upward) anomalies that are negative in the NH and positive in the SH over all time periods (Fig. 6a). While the anomaly in the TOA incoming shortwave (SW) flux is nearly zero (Fig. 6b), large compensating changes in the outgoing SW flux and outgoing longwave (LW) flux mostly determine the net TOA radiative flux (Fig. 6c and d, respectively). The outgoing SW flux anomaly is negative nearly everywhere (i.e., the outgoing SW flux decreases), with the LMR showing the strongest anomalies north of the Equator. These anomalies are consistent with either an increase in atmospheric SW absorption by water vapor in the warmer hemisphere or a decrease in reflected SW due to fewer clouds in the warmer hemisphere. The outgoing LW flux increases nearly globally, commensurate with increased temperatures at the effective radiating level associated with warming during the positive phase of the AMO. This increase in outgoing LW radiation dominates in the SH, while the decrease in outgoing SW radiation dominates in the NH, implying a net southward meridional energy transport in the LMR (see Fig. 8a and accompanying text). At the Equator, there is an increase in the outgoing SW radiation, which is balanced by a decrease in the outgoing LW radiation; both are consistent with greater cloudiness in the deep tropics and strengthening of the equatorial precipitation noted earlier (Fig. 5).
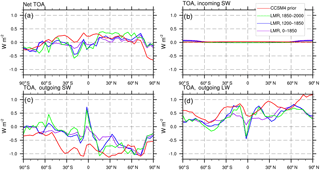
Figure 6Low-pass-filtered regression of the AMO index on top-of-atmosphere (TOA) energy fluxes (in W m−2) in the LMR (from years 0 to 1850, 1200 to 1850, and 1850 to 2000) and the CCSM4 prior: (a) net (incoming) flux, (b) incoming shortwave (SW) flux, (c) outgoing SW flux, and (d) outgoing longwave (LW) flux.
In the CCSM4 prior, the TOA radiative fluxes suggest a very different picture. While the outgoing SW flux decreases (Fig. 6c) and the outgoing LW flux increases (Fig. 6d) as in the LMR, the sum of these, the net upward TOA flux (Fig. 6a), is positive in the high latitudes in both hemispheres and negative in the lower and midlatitudes; as a result, the implied meridional total energy transport in the CCSM4 prior is polewards in both hemispheres.
At the surface, both the LMR and the CCSM4 prior have net fluxes associated with a positive AMO index that are downwards in the tropics, upwards in the subtropics and midlatitudes, and downwards in the NH high latitudes (Fig. 7a). This pattern is most pronounced in the CCSM4 prior, but is also evident over all time periods in the LMR. Globally, we find that this spatial pattern results from decreases in both the net (upward) surface SW radiation (i.e., an increase in SW coming down at the surface; Fig. 7b) and the net (upward) surface LW radiation (i.e., an increase in the LW coming down at the surface; Fig. 7c); these increased surface SW and LW radiative fluxes are mostly balanced by an increase in the surface latent heat flux (Fig. 7e), which renders the net surface flux small over most latitudes. At the Equator, an increase in the net (upward) surface SW radiation and a decrease in the net (upward) surface LW radiation is consistent with greater cloud cover. Sensible heat flux anomalies at the surface are small everywhere (Fig. 7d).
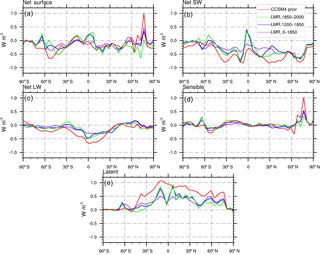
Figure 7Low-pass-filtered regression of the AMO index on surface energy fluxes (in W m−2) in the LMR (from years 0 to 1850, 1200 to 1850, and 1850 to 2000) and the CCSM4 prior: (a) net (downward) surface flux, (b) net (upward) SW flux, (c) net (upward) LW flux, (d) sensible heat flux, and (e) latent heat flux.
These results from the LMR suggest that the positive phase of the AMO is associated with greater atmospheric water vapor, likely a result of Clausius–Clapeyron scaling of atmospheric moisture with temperature. These findings, together with the TOA fluxes described earlier, also suggest that the positive phase of the AMO is associated with fewer (reflective) low clouds in the extratropics and more clouds near the Equator; the latter is in agreement with positive precipitation anomalies in the deep tropics (recall Fig. 5).
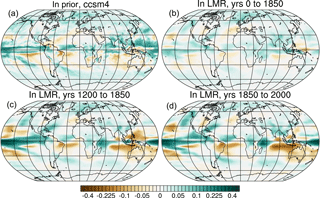
As alluded to earlier, differences in the net TOA radiative fluxes between the LMR and the CCSM4 prior imply very different total energy transport anomalies. The total implied meridional energy transport, TET, at latitude ϕ0 can be computed using the zonally averaged net TOA fluxes RTOA(ϕ) as
where ϕ and θ are the latitude and longitude coordinates, respectively, rearth is the radius of Earth, and Rstorage(ϕ) is the heat storage tendency of the climate system at latitude ϕ (Peixoto and Oort, 1992). We find that the TET is anomalously southward north of 20∘ S and northward south of 20∘ S for the LMR over later time periods (1200 to 1850 and 1850 to 2000) and is particularly large between 10∘ S and 20∘ N (Fig. 8a). In the CCSM4 prior, on the other hand, the TET is anomalously southward south of 10∘ N and anomalously northward north of 10∘ N.
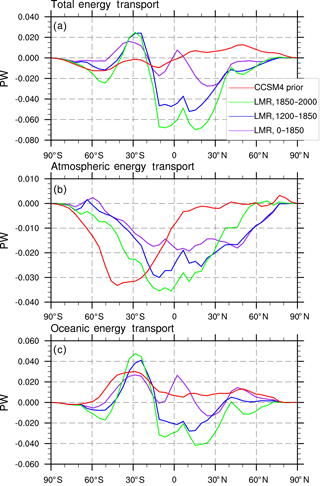
Figure 8Low-pass-filtered regression of the AMO index on energy transport (in PW) in the LMR: (a) total energy transport, (b) atmospheric energy transport, and (c) oceanic energy transport for the LMR from years 0 to 1850 (purple lines), the LMR from years 1200 to 1850 (blue lines), the LMR from years 1850 to 2000 (green lines), and CCSM4 prior (red).
The atmospheric energy transport, AET, at latitude ϕ0 is computed using the difference between RTOA(ϕ) and net surface flux RSfc(ϕ) as
The AET anomaly associated with a positive AMO is southwards at most latitudes in both the LMR (over all time periods) and in the CCSM4 prior (Fig. 8b). The maximum southward AET is further northward in the LMR compared to the CCSM4 prior (close to the Equator in the former, while in the southern midlatitudes in the latter). The increase in southward cross-equatorial energy transport in the LMR is consistent with the northward shift of the ITCZ noted previously (recall Fig. 5). The increase in southward cross-equatorial energy transport is also consistent with an increase in the interhemispheric temperature difference associated with the AMO that preferentially warms the NH over the SH (recall Fig. 2; also see Friedman et al., 2013), which arises from a strengthening of the Hadley circulation in the cooler hemisphere. On the other hand, the increase seen in the CCSM4 prior occurs most prominently in the midlatitudes, suggesting a strengthening of poleward energy transport by midlatitude eddies in the SH rather than an adjustment of the tropical circulation.
The oceanic energy transport OET(ϕ0) is computed as a residual from the TET and AET:
From Fig. 8c, it is clear that, aside from the subtropical SH, the LMR and CCSM4 prior differ significantly in anomalous OET associated with the positive phase of the AMO. In the LMR (over 1200 to 1850 and 1850 to 2000), energy transport by the ocean is anomalously southward in the NH and northward in the SH, with a significant southward cross-equatorial component; much of the anomalous transport is confined to the subtropics. These anomalies are larger over the 1850–2000 time period and are consistent with a decrease in oceanic energy transport by the wind-driven subtropical gyres and subtropical cells when the AMO is in its positive phase. A large southward cross-equatorial component to the OET anomaly suggests a decrease in northward cross-equatorial energy transport by the AMOC. In the CCSM4 prior, on the other hand, the OET response is anomalously positive at all latitudes, suggesting that an increase in northward energy transport by the AMOC corresponds to a positive AMO index.
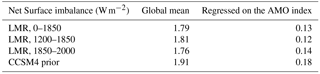
In both the LMR and CCSM4 prior, we find that the average net TOA flux over the last 2000 years is positive, indicating that energy is being removed from the Earth system; when the AMO index is positive, however, the net TOA flux decreases such that energy is being anomalously added to the Earth system relative to the mean state (Table 2). The extent to which this occurs is similar between the CCSM4 prior and the LMR over all time periods, suggesting that this aspect of the AMO has been stationary over the last 2000 years.
Table 2Net top-of-atmosphere (TOA) flux imbalances in the LMR (from years 0–1850, 1200–1850, and 1850–2000) and the CCSM4 prior shown for the global mean and regressed on the AMO index. Fluxes out of the Earth system (i.e., upward) are positive.
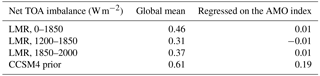
Surface flux imbalances in the LMR (Table 3) are also qualitatively similar to the TOA flux imbalances, with positive surface flux anomalies characterizing the mean state over all time periods (i.e., energy is leaving the oceans), which is consistent with millennial-scale cooling. When the AMO is in its positive phase, on the other hand, the surface flux anomaly decreases, indicating that energy is being anomalously absorbed by the oceans relative to the mean state. This is consistent with the TOA flux imbalance linked to a positive AMO index, which also decreases relative to the mean. The results from the CCSM4, however, are more energetically consistent in the magnitude of the energy uptake by the climate system when the AMO is in its positive phase (0.19 and 0.18 W m−2 for the TOA and surface flux imbalances, respectively) compared to the LMR (e.g., 0.01 and 0.13 W m−2 for the TOA and surface flux imbalances, respectively, in the LMR over the years 0 to 1850 CE).
3.4 Timescales of variability
We now consider what timescales characterize the AMO index. Tung and Zhou (2013) show a distinct 50- to 80-year peak in the Central England Temperature record (HadCET; see Parker et al., 1992) and suggest that this variability may be related to coherent variability in North Atlantic SSTs. Other studies have synthesized proxy records from the North Atlantic basin over the last 500 years to infer the existence of such a multidecadal oscillation over the last millennium (see Delworth and Mann, 2000; Gray et al., 2004). Furthermore, Knudsen et al. (2011) suggest that multidecadal variability that is nonstationary and possibly linked to North Atlantic SSTs is evident in global ice core and sedimentary records over a span of the last 8000 years.
Motivated by previous research, we now analyze what timescales are evident in the LMR reconstruction of North Atlantic SSTs. The LMR uses records from proxies over the last 2 millennia weighted heterogeneously relative to the prior and includes the proxy data used by Delworth and Mann (2000), Gray et al. (2004), and others; these records are processed here using the data assimilation algorithm described herein (see Sect. 2; Hakim et al., 2016). If the timescales present in individual proxy record time series are indicative of variability over the large-scale North Atlantic in general, these timescales should also be present in the reconstructed AMO index.
Wavelet analysis of the AMO index is performed on six different LMR reconstructions that use three distinct calibration datasets (MLOST, GIS, and CRU; see Table 1) and two different model priors (CCSM4 and MPI; see Table 1). The reconstructions reveal statistically significant power over different time periods on several different timescales, and the details vary with the reconstruction (Fig. 9). For all reconstructions, longer-timescale variability (>40 years) is only evident over the latter portion of the record (mostly after year 800 CE). The MLOST-MPI reconstruction, in particular, shows very little of this longer-timescale variability, while the CRU-CCSM4 reconstruction displays it prominently. None of the reconstructions show longer-timescale variability in the early portion of the record, though several of the reconstructions reveal an event at year 500; this may reflect either a lack of proxy records over this period or nonstationarity in the climate system over the preindustrial period.
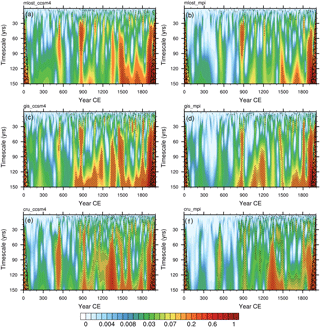
Figure 9Wavelet analysis of AMO time series from six different LMR reconstructions (in units of variance of the AMO index, K2): (a) MLOST-CCSM4, (b) MLOST-MPI, (c) GIStemp-CCSM4, (d) GIStemp-MPI, (e) CRU-CCSM4, and (f) CRU-MPI. All analyses are performed using the Paul wavelet. Stippled areas are statistically significant at p<0.05, and the hatched region demarcates the cone of influence.
We assess the significance of variability on these different timescales using the global wavelet power spectrum, which is an average of the coincident wavelet power on each timescale over the entire record. These global power spectra, shown in Fig. 10a, suggest that there is no distinct multidecadal spectral peak in the AMO index. Many of the reconstructions suggest reddening of the spectrum near the 50- to 60-year timescale, particularly those reconstructions using the GIS and MLOST calibration datasets, though none of these are statistically significant at p<0.05. Furthermore, reconstructions using the CRU calibration dataset show that longer-timescale (≥90 year) variability cannot be explained by a simple AR(1) process. However, our results appear to rule out the presence of distinct multidecadal oscillations in North Atlantic SSTs over the last 2 millennia. We find that this result is insensitive to the wavelet type and is not affected if a shorter time period is used for the analysis (e.g., years 1200 to 2000 CE). Furthermore, we find that the global power spectrum is very quantitatively similar when the same analysis is performed using a fixed-proxy network for the reconstruction (i.e., one in which all proxy records are continuous for the entire time period of the analysis), further suggesting that these results are insensitive to the choice of proxy network used. In addition, multitaper spectra (Thomson, 1982) confirm that none of our AMO reconstructions exhibit any spectral power on multidecadal timescales above that expected from red noise (see the Supplement), which is consistent with results gleaned from the global wavelet power spectrum (Fig. 10a).
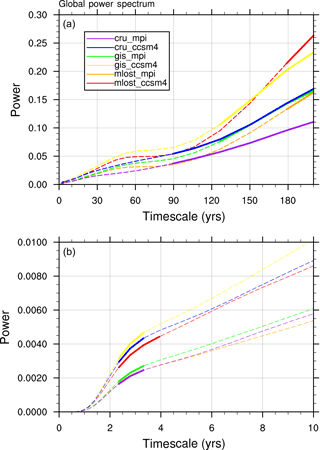
Figure 10Global wavelet spectra of reconstructions shown in Fig. 9 (a) for timescales between 0 and 200 years and (b) zoomed in to show timescales between 2 and 10 years. Timescales that are statistically significant over the red noise background (at p<0.05) are shown as solid lines, while timescales that are not statistically significant are shown as dotted lines. In units of variance of the AMO index, K2.
While we do not find a statistically significant multidecadal spectral peak in the AMO index, we do find a significant 3- to 4-year spectral peak (Fig. 10b). We suggest that this peak may be a result of teleconnections with the tropical Pacific and El Niño–Southern Oscillation (ENSO) variability therein, which has a similar timescale (see, e.g., Dong et al., 2006). We reserve study of connections between tropical Pacific and Atlantic variability for future work.
3.5 Limitations of LMR investigation of the AMO and other variability
While we have been able to show that the LMR captures thermodynamic aspects of the AMO, there are factors that limit its utility in investigating the dynamics of the AMO. While proxy records synthesize information about temperature and precipitation, their utility for reconstructing fields that are relatively invariant to temperature remains uncertain. We find that dynamic spatial fields like surface pressure and winds are not well reconstructed by the LMR (not shown); therefore, we have not included such reconstructions in this analysis. The limitations of paleoclimate reanalyses using proxies that record primarily thermodynamic variables, rather than dynamic ones, remains an open question that will be considered in future work.
We have considered the thermodynamics of the AMO over the last 2000 years using the LMR, a paleoclimate reanalysis method that objectively assimilates information from paleoclimate records. Several aspects of our findings regarding the AMO agree with previous model-based and observational studies of North Atlantic SST evolution. We find that a positive AMO index coincides with warmer continents, a two-lobed pattern of warming over the Atlantic, and a warmer Arctic (Kushnir, 1994; Delworth and Mann, 2000; Chylek et al., 2009). In the Arctic, sea ice retreats from the Greenland, Iceland, and Nordic seas and thins over much of the Arctic Ocean (Miles et al., 2014). Globally, precipitation increases and the ITCZ strengthens and shifts northward (Knight et al., 2006).
With the LMR, we also find several elements of the AMO that have not been reported in the literature. When the AMO is in its positive phase, southward cross-equatorial energy transport increases, mostly mediated by the atmosphere (the northward shift in the equatorial precipitation); these latter changes are consistent with energy balance requirements as necessitated by stronger warming in the NH than the SH during the positive phase of the AMO, i.e., an effect of the increase in the interhemispheric temperature anomaly (see Friedman et al., 2013). The LMR also shows that when the AMO is in its positive phase, the Earth system loses less (net) energy to space, with much of this excess energy absorbed by the oceans. TOA and surface flux anomalies are consistent with an increase in atmospheric specific humidity and a decrease in low (reflective) clouds.
Our study of the AMO using the LMR demonstrates that climate field reconstruction methods, which assimilate information from the proxy record, can provide valuable information on climate variability in the Earth system. While correlations between North Atlantic SSTs and various thermodynamic fields (temperature, precipitation, and sea ice) are similar in the LMR and the CCSM4 prior, the LMR provides a temporal reconstruction of the AMO index that informs our understanding of North Atlantic SST variability beyond that from the model prior. First, energetic changes associated with the AMO are distinct in the LMR and CCSM4 prior, with the LMR predicting consistent changes in the cross-equatorial energy transport, tropical circulation, and extratropical cloud cover that are not found in the CCSM4 prior. Second, the LMR helps resolve the dominant timescales that characterize the AMO. Since there is little agreement between various GCMs regarding the dominant timescales that characterize the AMO (see Clement et al., 2015), LMR reconstruction of the AMO index is invaluable. Our results suggest that the proxy observations over the last 2000 years, when objectively assimilated, do not exhibit a multidecadal timescale.
The lack of a distinct multidecadal spectral peak in the LMR reconstruction of the AMO is in contrast to other studies that have found such variability in individual observational records (see, e.g., Tung and Zhou, 2013) or limited collections of proxies (see, e.g., Delworth and Mann, 2000; Gray et al., 2004). We point out that such a significant spectral peak in an individual record or collection of records does not necessarily translate into a coherent mode of basin-scale multidecadal variability. While certain records may display oscillations, a basin-scale oscillation requires both spatial coherence and matching timescales in these records over certain regions. The objective assimilation procedure used in the LMR climate field reconstruction utilizes the information provided by the proxy records investigated in these previous studies; the results of this objective assimilation suggest that there is no distinct multidecadal or centennial spectral peak in the AMO index, though there is reddening of the spectra. These results support the null hypothesis presented by Clement et al. (2015) and suggest that there may be little need to consider longer-timescale processes when studying the mechanism of the AMO over the late Holocene, particularly the preindustrial period.
In our reconstructions, multidecadal spectral power is evident only over the latter portion of the LMR, year 1500 CE forward, and is particularly pronounced following year 1900 CE. While there has been much hypothesized regarding these oscillations in the instrumental record and whether they are a result of internal climate variability or a result of external forcing (see, e.g., Booth et al., 2012; Zhang et al., 2013; Murphy et al., 2017; Bellucci et al., 2017, and others), we point out two important characteristics of the instrumental period that render it a poor era for studying multidecadal variability in the climate system. First, the instrumental record is very short; as a result, there is very little that can be said about multidecadal timescale variability over this time period that carries any statistical weight (see, e.g., Wunsch, 1999; Vincze and Janosi, 2011). Second, the instrumental period is one in which the climate system has been strongly anthropogenically forced, suggesting that any variability observed over this period may differ significantly from variability from the preindustrial era when anthropogenic forcing was much smaller. Indeed, Tandon and Kushner (2015) show that in models, the lead–lag relationships between North Atlantic SSTs and the AMOC are very different between the preindustrial and modern periods, suggesting a shift in the mechanism underlying AMV between these two time periods. Both of these limitations suggest that caution must be exercised in extrapolating characteristics of multidecadal variability in the Earth system from the instrumental record.
We also point out that our objective data assimilation approach cannot completely rule out a distinct multidecadal spectral peak in North Atlantic SSTs. While we have shown that objective data assimilation of the proxy record to reconstruct the surface temperature field over the last 2 millennia does not yield any evidence of multidecadal variability, it is likely that further improvements in the proxy network, the proxy system models, or the data assimilation procedure will improve the reconstruction in such a way as to modify our current conclusions. From this study, however, we can say that the surface temperatures reconstructed over the last 2000 years, which are obtained from assimilating the existing network of proxies using today's state-of-the-art methods, do not provide compelling evidence for multidecadal oscillations over the North Atlantic.
We conclude by pointing out some important limitations of studies of climate variability using the LMR. First, the data assimilation approach itself is Gaussian, which may limit its utility in regimes very different from that of the base climate state. Second, LMR reconstructions depend on the climate models, proxies, and observation models that are used to create them. These components, in turn, are being continually tuned and refined. Third, it is unknown what effects the limitations in the size and distribution of the proxy network have on the reconstruction made possible by the LMR. In particular, we note that the more limited network from the early portion of the instrumental record (pre-1200 CE) may affect the reconstruction and its variability. Further study will be required to assess sensitivity to the sparsity of the proxy network. Finally, we note that there are other ways to improve paleoclimate reanalyses using proxy records, including the incorporation of linear inverse modeling into the reconstruction methodology to achieve online data assimilation (see Perkins and Hakim, 2016). In the future, such refinement of reconstruction methods will help to further the study of the Earth system over its long and varied climatic history.
The data assimilation software for the LMR project will be publicly released on BitBucket and GitHub at the end of the project in 2018.
Datasets used in this study are publicly available on the Zenodo data archiving service: https://doi.org/10.5281/zenodo.1162342 (Singh, 2018).
The supplement related to this article is available online at: https://doi.org/10.5194/cp-14-157-2018-supplement.
The authors declare that they have no conflict of interest.
Hansi K. A. Singh thanks Andre Perkins for informative discussions and
technical help. All authors acknowledge funding support from the
following sponsors to the University of Washington: the National Science
Foundation (awards AGS-1304263 and AGS-1602223) and the National Oceanic
and Atmospheric Administration (award NA14OAR4310176). All authors
also acknowledge the World Climate Research Program's Working Group
on Coupled Modeling, which is responsible for CMIP, and thank the
climate modeling groups (CCSM4 and MPI, listed in Table 1) for
producing and making available their model output. For CMIP the
US Department of Energy's Program for Climate Model Diagnosis and
Intercomparison provides coordinating support and led the development of
software infrastructure in partnership with the Global Organization
for Earth System Science Portals.
Edited by: André Paul
Reviewed by: Javier García-Pintado and one anonymous referee
Bellucci, A., Mariotti, A., and Gualdi, S.: The role of forcings in the 20th century North Atlantic Multidecadal Variability: the 1940–1975 North Atlantic cooling case study, J. Climate, 16, 7317–7337, 2017. a, b
Bjerknes, J.: Atlantic air–sea interaction, Adv. Geophys., 10, 1–82, 1964. a
Booth, B., Dunstone, N., Halloran, P., Andrews, T., and Bellouin, N.: Aerosol implicated as a prime driver of twentieth-century North American climate variability, Nature, 484, 228–232, 2012. a, b, c
Chylek, P., Folland, C., Lesins, G., Dubey, M., and Wang, M.: Arctic air temperature change amplification and the Atlantic Multidecadal Oscillation, Geophys. Res. Lett., 36, L14801, https://doi.org/10.1029/2009GL038777, 2009. a
Chylek, P., Folland, C., Dijkstra, H., Lesins, G., and Dubey, M.: Ice-core data evidence for a prominent near 20 year time-scale of the Atlantic Multidecadal Oscillation, Geophys. Res. Lett., 3, L13704, https://doi.org/10.1029/2011GL047501, 2011. a
Clement, A., Bellomo, K., Murphy, L., Cane, M., Mauritsen, T., Radel, G., and Stevens, B.: The Atlantic Multidecadal Oscillation without a role for ocean circulation, Science, 350, 320–324, 2015. a, b, c, d, e
Consortium, P.: Continental-scale temperature variability during the past two millennia, Nat. Geosci., 6, 339–346, 2013. a
Danabasoglu, G.: On multidecadal variability of the Atlantic multidecadal overturning circulation in the community climate system model version 3, J. Climate, 21, 5524–5544, 2008. a
Delworth, T. and Mann, M.: Observed and simulated multidecadal variability in the Northern Hemisphere, Clim. Dynam., 16, 661–676, 2000. a, b, c, d
Delworth, T., Manabe, S., and Stouffer, R.: Interdecadal variations of the thermohaline circulation in a coupled ocean-atmosphere model, J. Climate, 6, 1993–2011, 1993. a
Dijkstra, H., te Raa, L., Schmeits, M., and Gerrits, J.: On the Physics of the Atlantic Multidecadal Oscillation, Ocean Dynam., 56 , 36–50, https://doi.org/10.1007/s10236-005-0043-0, 2006. a
Dijkstra, H., Frankcombe, L., and von der Heydt, A.: A stochastic dynamical systems view of the Atlantic Multidecadal Oscillation, Philos. T. R. Soc. A, 366, 2545–2560, 2008. a
Dong, B., Sutton, R., and Scaife, A.: Multidecadal modulation of El Nino-Southern Oscillation (ENSO) variance by Atlantic Ocean sea surface temperatures, Geophys. Res. Lett., 33, L08705, https://doi.org/10.1029/2006GL025766, 2006. a, b
Duchon, C.: Lanczos filtering in one and two dimensions, J. Appl. Meteorol., 18, 1016–1022, 1979. a
Enfield, D., Mestas-Nunez, A., and Trimble, P.: The Atlantic multidecadal oscillation and its relation to rainfall and river flows in the continental U. S., Geophys. Res. Lett., 28, 2077–2080, 2001. a
Friedman, A., Hwang, Y.-T., Chiang, J., and Frierson, D.: Interhemispheric temperature asymmetry over the twentieth century and in future projections, J. Climate, 26, 5419–5433, 2013. a, b
Gray, S., Graumlich, L., Betancourt, J., and Pederson, G.: A tree-ring based reconsruction of the Atlantic Multidecadal Oscillation since 1567 AD, Geophys. Res. Lett., 31, L12205, https://doi.org/10.1029/2004GL019932, 2004. a, b, c
Hakim, G., Emile-Geay, J., Steig, E., Noone, D., Anderson, D., Tardif, R., Steiger, N., and Perkins, W.: The last millennium climate reanalysis project: framework and first results, J. Geophys. Res.-Atmos., 121, 6745–6764, 2016. a, b, c, d, e, f, g, h
Hakkinen, S., Rhines, P., and Worthen, D.: Atmospheric blocking and Atlantic multidecadal ocean variability, Science, 334, 655–659, 2011. a
Hansen, J., Ruedy, R., Sato, M., and Lo, K.: Global surface temperature change, Rev. Geophys., 48, RG4004, https://doi.org/10.1029/2010RG000345, 2010. a
Hartmann, D.: Global Physical Climatology, International Geophysics, 56, Academic Press, San Diego, CA, USA, 1994. a
Henson, S., Dunne, J., and Sarmiento, J.: Decadal variability in North Atlantic phytoplankton blooms, J. Geophys. Res., 114, C04013, https://doi.org/10.1029/2008JC005139, 2009. a
Hetzinger, S., Pfeiffer, M., Dullo, W.-C., Keenlyside, N., Latif, M., and Zinke, J.: Caribben coral tracks Atlantic Multidecadal Oscillation and past hurricane activity, Geology, 36, 11–14, 2008. a
Jungclaus, J. H., Lorenz, S. J., Timmreck, C., Reick, C. H., Brovkin, V., Six, K., Segschneider, J., Giorgetta, M. A., Crowley, T. J., Pongratz, J., Krivova, N. A., Vieira, L. E., Solanki, S. K., Klocke, D., Botzet, M., Esch, M., Gayler, V., Haak, H., Raddatz, T. J., Roeckner, E., Schnur, R., Widmann, H., Claussen, M., Stevens, B., and Marotzke, J.: Climate and carbon-cycle variability over the last millennium, Clim. Past, 6, 723–737, https://doi.org/10.5194/cp-6-723-2010, 2010. a
Knight, J., Folland, C., and Scaife, A.: Climate impacts of the Atlantic Multidecadal Oscillation, Geophys. Res. Lett., 33, L17706, https://doi.org/10.1029/2006GL026242, 2006. a, b, c
Knudsen, M., Seidenkrantz, M.-S., Jacobsen, B., and Kuijpers, A.: Tracking the Atlantic Multidecadal Oscillation through the last 8000 years, Nat. Commun., 2, 178, https://doi.org/10.1038/ncomms1186, 2011. a, b
Knudsen, M., Jacobsen, B., Seidenkrantz, M.-S., and Olsen, J.: Evidence for external forcing of the Atlantic Multidecadal Oscillation since termination of the Little Ice Age, Nat. Commun., 5, 3323, https://doi.org/10.1038/ncomms4323, 2014. a
Kushnir, Y.: Interdecadal variations in North Atlantic sea surface temperature and associated atmospheric conditions, J. Climate, 7, 141–157, 1994. a, b, c
Landrum, L., Otto-Bliesner, B., Wahl, E., Conley, A., Lawrence, P., Rosenbloom, N., and Teng, H.: Last Millennium Climate and its Variability in CCSM4, J. Climate, 26, 1085–1111, 2012. a
Lu, R., Dong, B., and Ding, H.: Impact of the Atlantic multidecadal oscillation on the Asian summer monsoon, Geophys. Res. Lett., 33, L24701, https://doi.org/10.1029/2006GL027655, 2006. a
McCabe, G., Palecki, M., and Betancourt, J.: Pacific and Atlantic Ocean influences on multidecadal drought frequency in the United States, P. Natl. Acad. Sci. USA, 101, 4136–4141, 2004. a
McCarthy, G., Haigh, I., Hirschi, J.-M., Grist, J., and Smeed, D.: Ocean impact on decadal Atlantic climate variability revealed by sea-level observations, Nature, 521, 508–510, 2015. a
Miles, M., Furevik, D. D. T., Jansen, E., Moros, M., and Ogilvie, A.: A signal of persistent Atlantic Multidecadal Variability in Arctic sea ice, Geophys. Res. Lett., 41, 463–469, 2014. a, b, c
Morice, C., Kennedy, J., Rayner, N., and Jones, P.: Quantifying uncertainties in global and regional temperature change using an ensemble of observational estimates: the HadCRUT4 dataset, J. Geophys. Res.-Atmos., 117, D08101, https://doi.org/10.1029/2011JD017187, 2012. a
Murphy, L., Bellomo, K., Cane, M., and Clement, A.: The role of historical forcings in simulating the observed atlantic multidecadal oscillation, Geophys. Res. Lett., 44, 2472–2480, 2017. a, b
Nigam, S., Guan, B., and Ruiz-Barradas, A.: Key role of the Atlantic multidecadal oscillation in 20th century drought and wet periods over the Great Plains, Geophys. Res. Lett., 38, https://doi.org/10.1029/2011GL048650, 2011. a
Ottera, O., Bentsen, M., Drange, H., and Suo, L.: External forcing as a metronome for Atlantic Multidecadal Variability, Nat. Geosci., 3, 688–694, https://doi.org/10.1038/ngeo955, 2010. a
Parker, D., Legg, T., and Folland, C.: A new daily Central England temperature series, Int. J. Climatol., 12, 317–342, 1992. a
Peixoto, J. and Oort, A.: Physics of Climate, American Institute of Physics, New York, NY, USA, 1992. a
Perkins, W. A. and Hakim, G. J.: Reconstructing paleoclimate fields using online data assimilation with a linear inverse model, Clim. Past, 13, 421–436, https://doi.org/10.5194/cp-13-421-2017, 2017. a
Polyakov, I., Bhatt, U., Simmons, H., Walsh, D., Walsh, J., and Zhang, X.: Multidecadal variability of north Atlantic temperature and salinity during the twentieth century, J. Climate, 18, 4562–4581, 2005. a
Raa, L. T. and Dijkstra, H.: Instability of the Thermohaline Ocean Circulation on Interdecadal Timescales, J. Phys. Oceanogr., 32, 138–160, 2002. a
Singh, H.: Datasets for “Insights into Atlantic multidecadal variability using the Last Millennium Reanalysis framework”, available at: https://doi.org/10.5281/zenodo.1162342, last access: 29 January 2018.
Smith, T., Reynolds, R., Peterson, T., and Lawrimore, J.: Improvements to NOAA's historical merged land-ocean surface temperature analysis (1880–2006), J. Climate, 21, 2283–2296, 2008. a, b
Steiger, N., Hakim, G., Steig, E., Battisti, D., and Roe, G.: Assimilation of time-averaged pseudoproxies for climate reconstruction, J. Climate, 27, 426–441, 2014. a, b, c, d
Sutton, R. and Hodson, D.: Atlantic Ocean forcing of North American and European summer climate, Science, 309, 115–118, 2005. a
Tandon, N. and Kushner, P.: Does external forcing interfere with the AMOC's influence on North Atlantic sea surface temperature, J. Climate, 28, 6309–6323, 2015. a, b
Thomson, D.: Spectrum Estimation and Harmonic Analysis, Proc. IEEE, 70, 1055–1096, 1982. a
Torrence, C. and Compo, G.: A Practical Guide to Wavelet Analysis, B. Am. Meteorol. Soc., 79, 61–78, 1998. a
Tung, K. and Zhou, J.: Using data to attribute episodes of warming and cooling in instrumental records, P. Natl. Acad. Sci. USA, 110, 2058–2063, 2013. a, b, c
Vincze, M. and Jánosi, I. M.: Is the Atlantic Multidecadal Oscillation (AMO) a statistical phantom?, Nonlin. Processes Geophys., 18, 469–475, https://doi.org/10.5194/npg-18-469-2011, 2011. a
Whitaker, J. and Hamill, T.: Ensemble data assimilation without perturbed observations, Mon. Weather Rev., 130, 1913–1924, 2002. a
Wunsch, C.: The Interpretation of Short Climate Records, with Comments on the North Atlantic and Southern Oscillations, B. Am. Meteorol. Soc., 80, 245–255, 1999. a
Zhang, R. and Delworth, T.: Impact of Atlantic multidecadal oscillations on India/Sahel rainfall and Atlantic Hurricanes, Geophys. Res. Lett., 33, L17712, https://doi.org/10.1029/2006GL026267, 2006. a, b, c
Zhang, R., Delworth, T., and Held, I.: Can the Atlantic Ocean drive the observed multidecadal variability in Northern Hemisphere mean temperature, Geophys. Res. Lett., 34, L02709, https://doi.org/10.1029/2006GL028683, 2007. a
Zhang, R., Delworth, T., Sutton, R., Hodson, D., Dixon, K., Held, I., Kushnir, Y., Marshall, J., Ming, Y., Msadek, R., Robson, J., Rosati, A., Ting, M., and Vecchi, G.: Have aerosols caused the observed Atlantic Multidecadal Variability, J. Climate, 70, 1135–1144, 2013. a, b