SCUBIDO: a Bayesian modelling approach to reconstruct palaeoclimate from multivariate lake sediment data

Quantification of proxy records obtained from geological archives is key for extending the observational record to estimate the rate, strength, and impact of past climate changes but also for validating climate model simulations, improving future climate predictions. SCUBIDO (Simulating Climate Using Bayesian Inference with proxy Data Observations) is a new statistical model for reconstructing palaeoclimate variability and its uncertainty using Bayesian inference on multivariate non-biological proxy data. We have developed the model for annually laminated (varved) lake sediments, as they provide a high temporal resolution to reconstructions with precise chronologies. This model uses non-destructive X-ray fluorescence core scanning (XRF-CS) data (chemical elemental composition of the sediments) because it can provide multivariate proxy information at a near-continuous, sub-millimetre resolution, and, when applied to annually laminated (varved) lake sediments or sediments with high accumulation rates, the reconstructions can be of an annual resolution. Whilst this model has been built for this proxy type, its flexibility means that the model could be applied to other multivariate proxy datasets.

SCUBIDO uses a calibration period of instrumental climate data and overlapping µXRF-CS data to learn about the direct relationship between each geochemical element (reflecting different depositional processes) and climate but also the covariant response between the elements and climate. The understanding of these relationships is then applied to the rest of the record to transform the proxy values into a posterior distribution of palaeoclimate with quantified uncertainties. In this paper, we describe the mathematical details of this Bayesian approach and show detailed walk-through examples that reconstruct Holocene annual mean temperature from two varved lake records from central England and southern Finland. We choose to use varved sediments to demonstrate this approach, as SCUBIDO does not include a chronological module; thus the tight chronology associated with varved sediments is important. The out-of-sample validation for both sites shows a good agreement between the reconstructed and instrumental temperatures, emphasising the validity of this approach. The mathematical details and code have been synthesised into the R package, SCUBIDO, for simplification and to encourage others to use this modelling approach and produce their own reconstructions. Whilst the model has been designed and tested on varved sediments, µXRF-CS data from other types of sediment records that record a climate signal could also benefit from this approach.

1 Introduction

Anthropogenic climate change over the most recent decades has heightened the need to look beyond the instrumental period to find common patterns in both today's climate and future climate projections (IPCC, 2023; Kaufman and McKay, 2022). This calls for chronologically constrained, climate-sensitive proxy records to extend the understanding of climate variability before the instrumental period. These reconstructions can be used to contextualise present changes observed in the climate system, to identify recurrent trends which are unable to be observed in the short instrumental record (e.g. decadal–centennial variability), and as potential analogues for future climate scenarios (Bova et al., 2021; Liu et al., 2020; Snyder, 2010). In addition, quantitative reconstructions provide the opportunity to perform climate sensitivity experiments between proxy reconstructions and climate model simulations, strengthening climate projections for the future (Kageyama et al., 2018; Burls and Sagoo, 2022; Zhu et al., 2022).

The Holocene epoch (11 700 years to present, where present is 1950 CE) has been the focus of many proxy and modelling investigations (e.g. Liu et al., 2014; Bader et al., 2020; Kaufman et al., 2020a; Bova et al., 2021; Erb et al., 2022). This time period experienced temperatures which were similar to those of today, and the availability of proxy records makes the Holocene a favourable interglacial to investigate climate variability across multi-millennial timescales. Recently, there have been a number of new reconstructions of global temperature which are based on large proxy dataset compilations (Kaufman et al., 2020a, b; Osman et al., 2021; Erb et al., 2022). These synthesise different marine (Osman et al., 2021), or a combination of terrestrial and marine (Kaufman et al., 2020b), proxy records and either use statistical approaches (Kaufman et al., 2020a) or combine these with data assimilation (Osman et al., 2021; Erb et al., 2022) to reconstruct climate both spatially and temporally. These have provided great insight into climate variability across large spatial scales, which is not possible when looking at individual site records. However, they all have a common limitation, which is the temporal resolution of their reconstructions. Due to the nature of the proxies included in the large datasets (e.g. pollen, isotopes, foraminifera), the proxy signal is often non-continuous, creating a median reconstruction resolution of ca. 100–200 years (Kaufman et al., 2020b). Whilst this temporal resolution is acceptable for looking at spatially extensive and long-term climate variability across centennial to millennial timescales (Cartapanis et al., 2022), higher-frequency variability, such as the multi-decadal climate system, is unable to be investigated, even though it is key to improving climate predictions within this century (Cassou et al., 2018). Erb et al. (2022) produced a global temperature reconstruction at a decadal resolution. However, they used the Temp12k dataset, in which only 11 out of the 1276 records have a decadal or higher temporal resolution and some records have a resolution of up to 700 years (Kaufman et al., 2020b; Erb et al., 2022). This means that, in order for them to achieve a decadal reconstruction, they had to leverage from transient climate simulations in a data assimilation approach to upscale their temporal resolution to decadal. Whilst a lot can be learnt from their reconstruction, using the transient simulations means that much of the decadal climate variability observed in this reconstruction would be forced by the model, rather than by the proxy data alone.

Reconstructions of climate from a proxy record, whether for a single site or a compilation of multiple sites, require a transformation from the qualitative climate information derived from proxy values to a quantified climate parameter with physical units of measurements (i.e. °C, mm of precipitation) (Chevalier et al., 2020). A number of statistical or mechanistic methods can be used, each with varying levels of complexity, uncertainty, and functionality (Tingley et al., 2012). Each method requires a calibration stage or training set relying on modern observations of the relationship between the proxy and climate which is then projected onto the proxy data (Juggins and Birks, 2012). Quantitative approaches have matured from rather simplistic methods, including linear regression (e.g. Imbrie and Kipp, 1971), to methods of increased complexity, such as weighted averaging regression (e.g. ter Braak and Juggins, 1993; Liu et al., 2020), composite plus scaling (e.g. Jones et al., 2009; Kaufman et al., 2020a), modern analogue techniques (e.g. Jiang et al., 2010), and artificial neural networks (e.g. Wegmann and Juame-Santero, 2023), which are summarised well in Chevalier et al. (2020). Interpreting the palaeoclimate record and reconstructing climate can be complex and is often faced with several challenges, including uncertain chronologies, assumptions on proxy formation and preservation, and non-stationary relationships between the climate system and proxy response through time (Sweeney et al., 2018; Cahill et al., 2023). This is especially true when the archives used to reconstruct climate have faced significant alterations due to rising anthropogenic activity over the last several thousand years, questioning the stationarity of proxy–climate relationships. Each of these complexities has led to a greater reliance on hierarchical statistical approaches, such as Bayesian statistics to reconstruct climate through time (Tingley et al., 2012).

Bayesian statistics is an approach based on Bayes' theorem and can be summarised as applying prior knowledge to update the probability of a hypothesis when new data become available (van de Schoot et al., 2021). It has been used to answer many statistical problems, including the reconstruction of palaeoclimate (e.g. Haslett et al., 2006; Parnell et al., 2015; Tierney et al., 2019; Cahill et al., 2023). Many frequentist (non-Bayesian) approaches to reconstruct climate mentioned previously often struggle to capture the complex relationships inherent between climate and proxy data. This occurs when the learnt relationship in the calibration interval or training data is fixed and then applied directly onto the palaeodata, resulting in the assumption of a stationary relationship through time and fixed uncertainty estimates (Birks et al., 2012; Sweeney et al., 2018; Zander et al., 2024). However, we argue that climate often exhibits non-stationary behaviour and that this needs to be captured in the chosen model. By contrast, a Bayesian approach allows a continued update about the belief of the relationship between the proxy, the climate, and associated parameters (Chu and Zhao, 2011). In addition, Bayesian analysis can holistically account for different sources of uncertainty influencing a reconstruction (Birks et al., 2012; Sweeney et al., 2018). Bayesian methods can consider the uncertainties at all stages of the modelling process and model these as joint probability distributions producing properly quantified uncertainties with credible intervals (Tingley and Huybers, 2010; Sweeney et al., 2018; Cahill et al., 2023).

A rising number of studies have used a Bayesian framework in their climate reconstructions (e.g. Haslett et al., 2006; Holmström et al., 2015; Parnell et al., 2015; Tierney et al., 2019; Hernández et al., 2020; Cahill et al., 2023). However, they provide low temporal resolutions, as they are based on non-continuously sampled proxies, resulting in reconstructions of climate across multi-decadal to centennial timescales. This calls for a greater number of quantified climate reconstructions using hierarchical modelling from records with refined chronologies and proxies sampled at a high resolution.

Micro-X-ray fluorescence core scanning (µXRF-CS hereafter) is a non-destructive approach which provides multivariate information about the geochemical composition of marine and lacustrine sediment cores (Davies et al., 2015). The geochemical information produced by µXRF-CS provides relative changes in the element abundance (Bertrand et al., 2024). Unlike alternative geochemical proxies (e.g. stable isotopes) or biological proxies (e.g. pollen, foraminifera), which require discrete sampling, the µXRF-CS approach scans sediment sequences, continuously enabling the proxy data to be produced at very high sampling resolutions (up to 0.2 mm). When this approach is applied on sediment sequences with either sufficient sedimentation rates ($>\mathrm{0.5}\mathrm{mm}{\mathrm{yr}}^{-\mathrm{1}}$) or annual laminations (varves) (Zolitschka et al., 2015), it can provide proxy information at a seasonal to decadal timescale. µXRF-CS has mostly been used to qualitatively reconstruct palaeoenvironments, as the relative changes in the geochemical composition of sediments are a direct response to the changing climatic and environmental conditions in the lake catchment system (Peti and Augustinus, 2022).

Our main goal here is to combine the advantages of using Bayesian inference in climate reconstructions with the palaeoclimate value of varved records. In this methods-based paper, we aim to (i) present a Bayesian approach to transform multivariate µXRF-CS data into a quantitative palaeoclimate dataset; (ii) demonstrate the applicability of this approach on two varved lake records from Europe; (iii) compare the output of the Bayesian model to previously published reconstructions to test the climatic reliability; and (iv) promote its use through the user-friendly R package, SCUBIDO (Simulating Climate Using Bayesian Inference with proxy Data Observations).

2 Methods

2.1 Proxy data

The modelling approach has been built for the use of µXRF-CS data as the chosen proxy. Raw µXRF-CS data originate in the form of element intensities, which are often non-linear to the concentration of elements in the sediment and can also be affected by the sediment's physical properties, measurement time, and sample geometry; therefore we use a centred log ratio (clr hereafter) to mitigate against these problems (Aitchison, 1986; Tjallingii et al., 2007; Weltje and Tjallingii, 2008; Weltje et al., 2015; Dunlea et al., 2020). Transforming raw elements to clr elements requires a dataset with minimal low or null counts (Bertrand et al., 2024). Therefore, elements with excessive null values should be removed before the transformation is performed. Following this, this approach does not assume that any element has a stronger relationship with climate; thus, we pass all elements which were able to be clr-transformed to the model.

2.2 Bayesian framework

For our quantitative reconstruction of climate given the µXRF-CS proxy data, we use Bayesian inference and base our framework on the modelling approach described in Parnell et al. (2015) and Hernández et al. (2020). Below we outline the notation used throughout:

• C is used to represent the value of the climate variable at each time point.

• We use XRF_ij to indicate the centred-log-transformed µXRF-CS data at each depth of the sediment core (i), where $i=\mathrm{1},\mathrm{\dots },n$ depths. As the µXRF-CS data are multivariate, j reflects the number of different centred-log-ratio-transformed elements ($j=\mathrm{1},\mathrm{\dots },n$ elements).

• t_i denotes the calibrated age (t) of each depth (i) in cal yr BP (before present, where present refers to 1950). It is important to note that SCUBIDO does not contain a geochronological module; thus age uncertainty is not considered in this modelling approach.

• θ is used to represent the parameters ($\mathit{\mu },{\mathit{\beta }}_{\mathrm{0}},{\mathit{\beta }}_{\mathrm{1}},{\mathit{\beta }}_{\mathrm{2}}$) which govern the relationship between each of the µXRF-CS elements at each time point and the climate variable. These are subscripted with j to denote the element to which they refer.

• σ_c is used to represent the standard deviation of climate per unit of time for our random walk model detailed in this paper.

• A superscripted m and f are applied to each of the variables when referring to the modern and fossil datasets, respectively. For example, C^m equates to the modern climate, and XRF^f refers to the fossil µXRF-CS data.

More definitions of variables and model parameters used in the model framework are presented in Table S1 in the Supplement.

The Bayesian posterior distribution we aim to estimate is outlined below:

$$\begin{array}{}\text{(1)}& \begin{array}{l}p\left(C^{\mathrm{f}},\mathit{\theta },{\mathit{\sigma }}_{\mathrm{c}}|{\text{XRF}}^{\mathrm{f}},C^{\mathrm{m}},{\text{XRF}}^{\mathrm{m}}\right)\\ \propto p\left({\text{XRF}}^{\mathrm{m}}\right|C^{\mathrm{m}},\mathit{\theta })\cdot p\left(C^{\mathrm{f}},C^{\mathrm{m}}|{\mathit{\sigma }}_{\mathrm{c}}\right)p({\mathit{\sigma }}_{\mathrm{c}}\left)p\right(\mathit{\theta }).\end{array}\end{array}$$

The posterior distribution on the left side of the equation, $p(C^{\mathrm{f}},\mathit{\theta },{\mathit{\sigma }}_{\mathrm{c}}|{\text{XRF}}^{\mathrm{f}},C^{\mathrm{m}},{\text{XRF}}^{\mathrm{m}})$, represents the probability distribution of the fossil climate given fossil and modern µXRF-CS data and modern climate. We use the likelihood expression $p\left({\text{XRF}}^{\mathrm{m}}\right|C^{\mathrm{m}},\mathit{\theta })$ to represent the calibration period, where we learn about the relationship between the µXRF-CS data and climate variable, discussed in more detail in Sect. 2.3.2. $p\left({\text{XRF}}^{\mathrm{f}}\right|C^{\mathrm{f}},\mathit{\theta }$) then represents the likelihood of the fossil data given the climate, and, finally, $(C^{\mathrm{f}},C^{\mathrm{m}}|{\mathit{\sigma }}_{\mathrm{c}})$ represents the prior distribution associated with the fossil climate and its dynamics over time.

2.2.1 Model fitting

To fit the above model, we follow the computational shortcut of Parnell et al. (2015), which assumes that all the information about the calibration parameters (θ) comes from the modern data. This means that the model is fitted in two parts, with the first part being the estimation of θ within a calibration period and the second part estimating the fossil climate (C^f) and σ_c. Thus, the resulting model becomes

$$\begin{array}{}\text{(2)}& \begin{array}{l}p\left(C^{\mathrm{f}},\mathit{\theta },{\mathit{\sigma }}_{\mathrm{c}}|{\text{XRF}}^{\mathrm{f}},C^{\mathrm{m}},{\text{XRF}}^{\mathrm{m}}\right)\propto p(\mathit{\theta },{\mathit{\sigma }}_{\mathrm{c}}|{\text{XRF}}^{\mathrm{m}}\left|C^{\mathrm{m}}\right)\\ \cdot p\left({\text{XRF}}^{\mathrm{f}}|C^{\mathrm{f}},\mathit{\theta },{\mathit{\sigma }}_{\mathrm{c}}\right)p\left(C^{\mathrm{f}},C^{\mathrm{m}}|{\mathit{\sigma }}_{\mathrm{c}}\right)p\left({\mathit{\sigma }}_{\mathrm{c}}\right).\end{array}\end{array}$$

The first term on the right-hand side is estimated separately and represents the posterior distribution of the modern calibration relationship parameters, which is then not further learnt from the fossil data in the second part of the model fit. Given the different parts of the modelling approach, we split the following section into two, firstly fitting the modern calibration period (Sect. 2.3.2) and secondly using what is learnt from this stage to reconstruct fossil climate (Sect. 2.3.3).

2.2.2 Calibration model fitting

Like all quantitative transformations of palaeoclimate, the first step is to understand the relationship between the proxy and the climate variable. In our modelling approach, this relationship is learnt from the first term on the right-hand side of Eq. (2) $p(\mathit{\theta },{\mathit{\sigma }}_{\mathrm{c}}|{\text{XRF}}^{\mathrm{m}},C^{\mathrm{m}})$ and includes not only the causal relationship between the individual µXRF-CS elements and climate but also the covariance between the elements. The data used for this section of the model are from the most recent period and must be aligned with an overlapping period of instrumental climate (C^m), and we call this our calibration dataset.

This step assumes that some of the variability observed in the proxy data is controlled by the climate variable; this is sometimes referred to as a “forward” model. Here, we want to estimate the posterior distribution of the θ parameters $({\mathit{\beta }}_{\mathrm{0}},{\mathit{\beta }}_{\mathrm{1}},{\mathit{\beta }}_{\mathrm{2}},{\mathit{\mu }}_{\mathrm{0}})$ and the climate variability parameter σ_c from a joint probability distribution using the following:

$$\begin{array}{}\text{(3)}& \begin{array}{l}p\left(\mathit{\theta },{\mathit{\sigma }}_{\mathrm{c}}|{\text{XRF}}^{\mathrm{m}},C^{\mathrm{m}}\right)\propto p\left({\text{XRF}}^{\mathrm{m}}\right|C^{\mathrm{m}},\mathit{\theta })\cdot p\left(C^{\mathrm{m}}|{\mathit{\sigma }}_{\mathrm{c}}\right)\\ \cdot p\left(\mathit{\theta }\right)p\left({\mathit{\sigma }}_{\mathrm{c}}\right).\end{array}\end{array}$$

We use p(θ) to represent the prior distribution of the parameters ${\mathit{\beta }}_{\mathrm{0}},{\mathit{\beta }}_{\mathrm{1}},{\mathit{\beta }}_{\mathrm{2}},{\mathit{\mu }}_{\mathrm{0}}$, with σ_c and p(C^m|σ_c) representing the prior distribution on modern climate (we use a random walk with standard deviation σ_c at each time point). $p\left({\text{XRF}}^{\mathrm{m}}\right|C^{\mathrm{m}},\mathit{\theta })$ is our likelihood distribution, and, finally, the parameter's posterior distribution is represented by $p(\mathit{\theta },{\mathit{\sigma }}_{\mathrm{c}}|{\text{XRF}}^{\mathrm{m}},C^{\mathrm{m}}$).

To approximate the relationship between the clr-transformed µXRF-CS data and the climate, we use a multivariate normal polynomial regression model for each of the µXRF elements:

$$\begin{array}{}\text{(4)}& \begin{array}{l}{\text{XRF}}_i^{\mathrm{m}}\sim \text{MVN}(M_i,\mathrm{\Sigma })\\ M_i=[{\mathit{\mu }}_{i\mathrm{1}},{\mathit{\mu }}_{i\mathrm{2}},\mathrm{\dots },{\mathit{\mu }}_{i\mathrm{11}}]\\ {\mathit{\mu }}_{ij}={\mathit{\beta }}_{\mathrm{0}j}+{\mathit{\beta }}_{\mathrm{1}j}\cdot C\left(t_i\right)+{\mathit{\beta }}_{\mathrm{2}j}C(t_i{)}^{\mathrm{2}}.\end{array}\end{array}$$

The mean term μ_ij captures the relationship between climate and assumes a quadratic relationship with a single mode when β_2j<0. We use Σ to represent the covariance matrix of the relationship between each of the different elements which are not explained by μ_ij. We acknowledge that other more complex models could be used to fit the relationship between the climate and the µXRF-CS elements rather than a polynomial model explained here. However, when experimenting with a more complicated P-spline model, we experienced overfitting and a significant reduction in the computational speed, whereas the polynomial regression model is sufficient to capture the relationships between the elements and climate without having a large computational burden.

Vague normal distributions are used for the priors on ${\mathit{\beta }}_{\mathrm{0}},{\mathit{\beta }}_{\mathrm{1}},$ and β₂; an inverse Wishart prior on Σ; and finally a vague uniform prior distribution for σ_c:

$$\begin{array}{}\text{(5)}& \begin{array}{l}{B}_{\mathrm{0}j}\sim N(\mathrm{0},\mathrm{100}),B_{\mathrm{1}j}\sim N(\mathrm{0},\mathrm{100}),B_{\mathrm{2}j}\sim N(\mathrm{0},\mathrm{100})\\ {\mathrm{\Sigma }}^{-\mathrm{1}}\sim \text{Wishart}(R,k+\mathrm{1}).\end{array}\end{array}$$

For the prior distribution on climate, we use a continuous-time random walk:

$$\begin{array}{}\text{(6)}& \begin{array}{l}P\left(C_i^{\mathrm{m}}\right)\sim N(C_{i-\mathrm{1}}^{\mathrm{m}},{\mathit{\omega }}_i)\\ {\mathit{\omega }}_i=\left(t_i^{\mathrm{m}}-t_{i-\mathrm{1}}^{\mathrm{m}}\right)\cdot {\mathit{\sigma }}_{\mathrm{c}}^{\mathrm{2}}.\end{array}\end{array}$$

We give σ_c a vague uniform distribution: ${\mathit{\sigma }}_{\mathrm{c}}\sim U(\mathrm{0},\mathrm{100})$. We choose the use of vague priors in this part of the model because we do not want to make any assumption about the relationship between the µXRF-CS elements and climate; instead, we allow the model to learn only about the data.

2.2.3 Fossil model fitting

Once the model has learnt about the relationship between the µXRF-CS data and climate, the second part of the computational shortcut can commence (Parnell et al., 2015). This firstly involves using the learnt relationship from the calibration period to create marginal data posteriors (MDPs), which represent all the information about fossil climate contained in one layer of µXRF data. Thus, we initially estimate the C^f using only the information within a particular time slice (XRF^f). Using only the information from one time slice at a time allows the model to marginalise over the parameters (θ) and reduce the dimensionality of the data. This step decreases the computational burden of estimating both the climate–proxy relationship and the fossil climate values in the same step. Information on the MDP fitting can be found in Sect. S2 in the Supplement and in more detail in Parnell et al. (2015, 2016).

To accurately capture the climate dynamics of the fossil period, we include a more informed prior for the random walk of fossil climate by re-using the continuous-time random walk from the modern calibration module and combine each of the individual MDP layers once they are corrected. This enables us to create a complete joint posterior distribution of the combined C^f and C^m and fit the model detailed in Eq. (2). As above, the varying time steps are captured via a dynamic precision term:

$$\begin{array}{}\text{(7)}& \begin{array}{l}P\left(C_i^{\mathrm{f}}\right)\sim N\left(C_{i-\mathrm{1}}^{\mathrm{f}},{\mathit{\omega }}_i\right)\\ {\mathit{\omega }}_i=\left(t_i^{\mathrm{f}}-t_{i-\mathrm{1}}^{\mathrm{f}}\right)\cdot {\mathit{\sigma }}_{\mathrm{c}}^{\mathrm{2}}.\end{array}\end{array}$$

To fully learn the climate dynamics standard deviation parameter from both the fossil and the modern data, we set a log-normal prior distribution for σ_c:

$$\begin{array}{}\text{(8)}& {\mathit{\sigma }}_{\mathrm{c}}\sim \text{LN}(a,b).\end{array}$$

The values a and b are chosen to match the posterior distribution from the modern calibration model fit.

The model produces an ensemble of posterior climate paths that cover the fossil and modern periods. This considers the uncertainties in the µXRF-CS proxy–climate relationship with a mild smoothing constraint arising from the random walk prior. The ensemble can then be summarised by taking the median value of the posterior distribution C^f and calculating the 50 % and 95 % credible interval of the reconstruction using the 2.5 %, 25 %, 75 %, and 97.5 % percentiles for plotting.

3 Walk-through example

This next section of the paper provides a walk-through example of each stage of the Bayesian model fitting on real-life µXRF-CS data. In an attempt to make this modelling approach as user-friendly as possible, we have produced the R package SCUBIDO (Simulating Climate Using Bayesian Inference with proxy Data Observations), which synthesises the modelling process into several distinct steps. The package can be downloaded from the GitHub repository, https://github.com/LauraBoyall/SCUBIDO (last access: 15 August 2025), alongside a walk-through example and a link to a video tutorial on how to use the R package.

We first demonstrate this example on the lake sediments of Diss Mere, a small lake in the UK containing Holocene varved sediments. This site has been chosen due to the sediments being annually laminated for much of the Holocene (from approximately 10 000–2000 years before 1950 CE, cal. BP hereafter); it therefore has a refined chronology based on annual layer counts with age uncertainties of less than a few decades (Martin-Puertas et al., 2021), which is important for this modelling approach, as we do not model or consider chronological uncertainty. The averaged sedimentation rate for the varved sequence is 0.4 mm yr⁻¹, with variability between 0.1 and 1.8 mm yr⁻¹ (Martin-Puertas et al., 2021). The most recent 2 millennia are recorded in the top 9 m of the sediment sequence, where the annual laminations are poorly preserved, and counting was not possible. However, the chronology has been constrained through a series of radiometric dating techniques (¹⁴C, ¹³⁷Cs) and tephrochronology, providing a high average sedimentation rate of ca. 0.5 cm yr⁻¹ and described in detail in Boyall et al. (2024) and summarised in Sect. S3. Both the modern sediment depositional processes and palaeosediments have been studied in detail through modern lake monitoring, microfacies analysis, and analysis of the µXRF-CS record, which all highlighted that the main environmental processes explaining the sediment deposition in the lake have not changed through time and respond to climate variations on seasonal to multi-centennial timescales (Boyall et al., 2023; Martin-Puertas et al., 2023; Boyall et al., 2024). Whilst human activity has had an impact on the lake sedimentation in the last 2000 years, i.e. increased detrital input into the lake (Boyall et al., 2024), the lake sedimentation and sediment composition keep responding to the annual lake cycle (monomictic), which is driven by climate parameters such as temperature and wind speed (Boyall et al., 2023). The sensitivity of these sediments to weather and climate variability thus provides scope for testing this modelling approach.

The Diss Mere sediments were scanned using an ITRAX µXRF-Core scanner (Cox Analytical Systems) at the GFZ-Potsdam, and geochemical elements include Si, S, K, Ca, Ti, V, Mn, Fe, Rb, Sr, and Zr at 200 µm resolution with a dwell time of 6 s and were later resampled to 400 µm for processing (Boyall et al., 2024). These elements were chosen based on having a standard error <15 % (Boyall et al., 2024) and not too many null values to perform the clr transformation (Bertrand et al., 2024).

Boyall et al. (2024) found a good visual relationship between the µXRF-CS data, specifically the element calcium (Ca) (linked to temperature-induced authigenic calcite precipitation deposited during spring to early autumn), and annual mean temperature evolution through the Holocene (Davis et al., 2003; Kaufman et al., 2020a; Rasmussen et al., 2007). Whilst this study found the strongest relationship to climate with Ca, all the elements are used in this modelling approach, given that SCUBIDO models the covariance between the elements and learns from these relationships. For the first 2000 years of the geochemical record between ca. 10 300 and 8100 cal a BP, the environmental interpretation of the element data reflected a non-climate local signal associated with the stabilisation of the lake depositional environment during the early Holocene (Boyall et al., 2024). Therefore, we attempt this modelling approach on only the geochemical data from 8100 cal a BP to present. We emphasise to future users of SCUBIDO that they should also conduct a qualitative analysis of the µXRF-CS data and environmental interpretation prior to using SCUBIDO to ensure that their record is climate-sensitive and has not been subjected to significant alterations from human activity.

3.1 Data setup

One of the most fundamental considerations for any type of palaeoclimate reconstruction is the choice of climate variable to reconstruct (e.g. annual mean temperatures, precipitation, growing season), given that different proxies are sensitive to a number of climate drivers (Sweeney et al., 2018). The SCUBIDO modelling approach can easily be adapted to reconstruct different climate parameters with overlapping instrumental data. However, it is important to note that not all lakes are responsive to every climate parameter of interest; thus the outputs may not be useful. For example, we attempted to run SCUBIDO on the Diss Mere µXRF-CS data to reconstruct both annual mean temperature and precipitation. However, the SCUBIDO output for precipitation from Diss Mere was not successful, as the reconstruction was completely flat, not resembling precipitation variability, and there was no predictive power between the elements and instrumental precipitation. Annual mean temperature, on the other hand, worked well, supporting the temperature signal recorded in the µXRF-CS data during the Holocene (Boyall et al., 2024). Another point to highlight at this stage is that we run the Bayesian model using a multivariate dataset made of the elements measured by the µXRF scanner. We do so to avoid any bias through time, as the climate–proxy relationship might not be stable over time. SCUBIDO also includes the relationship between elements (covariance) to deal with this issue. As the top of the µXRF-CS data (most recent period of sediment accumulation) begins at 1932 CE, a long-term instrumental temperature dataset was required to obtain a sufficient length for the model to learn about the climate–proxy relationship. We therefore rely on the Hadley Central England Temperature (HadCET; Met Office Hadley Centre, 2024) dataset, which is the longest monthly temperature dataset available. However, it is worth noting that, whilst this is the best instrumental record that we could use for Diss Mere given the long record, the meteorological stations used in this period of the record are not proximal to the site; therefore some of the local temperature changes which are recorded in the proxy record may not have been recorded by the meteorological station or vice versa.

The first step was to divide the data into two: the modern calibration dataset (containing an age index (t), modern µXRF-CS data (XRF^m), and the overlapping instrumental climate data (C^m)) and the fossil data (containing the age (t) and µXRF-CS data for the remaining data (XRF^f)). As there are many µXRF-CS data points per year, we linearly interpolated the data to resample to annual means and align the XRF^m dataset with the corresponding year in the HadCET dataset. We begin the calibration dataset at 1700 CE, and the top of the µXRF-CS data finishes at 1932 CE, and, because of a short gap where there was no µXRF-CS data present, this meant that the calibration dataset was 193 years long. Temperatures were converted into anomalies from the mean of the calibration period, as this not only removes the arbitrary mean of the temperature reconstruction, making the data more comparable, but it can also better constrain the climate values that the model can predict (see Sect. S2). The fossil data were provided in their original temporal resolution ranging between 5 data points per year to >25 data points per year depending on the sediment accumulation rate. This resulted in 59 461 time slices covering the period between 8100 cal a BP and 1699 CE.

We check the model convergence using $\widehat{R}$ values (Gelman and Rubin, 1992; Brooks and Gelman, 1998) and evaluate the performance of the model using both in-sample and out-of-sample posterior predictive calibration checks (Gelman et al., 1995). We detail this analysis in more detail below.

3.2 Model fitting

The full model was run within the SCUBIDO R package. This package depends on Just Another Gibbs Sampler (JAGS; Plummer, 2003) through the R package “R2jags” (Su et al., 2024) to fit the modern calibration model and part of the fossil modelling stage. We ran the calibration model for 100 000 iterations and ignored the first 40 000 runs to allow the model to settle. We repeated this process four times using different starting values to run the Markov chain Monte Carlo (MCMC) process in parallel. The $\widehat{R}$ values were consistently <1.05, indicating that the algorithm had successfully converged during the MCMC process (Gelman and Rubin, 1992; Brooks and Gelman, 1998; Vehtari et al., 2021; Su et al., 2024). Figure 1 shows the quadratic relationships between the individual µXRF-CS elements and temperature in the calibration period.

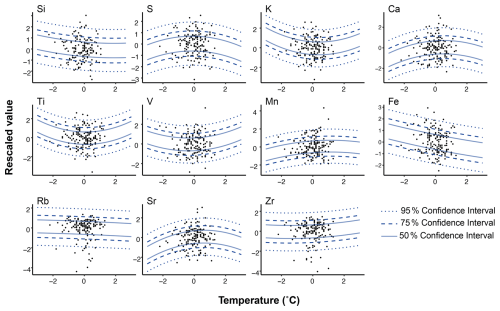
Figure 1 Relationship between the µXRF-CS elements and instrumental annual mean temperature from the calibration period. Individual µXRF-CS elements are plotted against the instrumental climate anomaly data for each year. The quadratic relationships are represented by lines, with the solid, dotted, and dashed lines representing the uncertainty ranges of 50 %, 95 %, and 75 %, respectively. Note that this modelling approach uses multivariate response regression; however, these plots display the individual response between each element and climate, hence the weak relationships plotted.

In more conventional approaches, where µXRF-CS data are used to qualitatively reconstruct climate, only one element, or pair of elements (in the form of a ratio), is used at a time to reconstruct climate (for example, Zander et al., 2024). This would be equivalent to our approach if had we used a diagonal structure for Σ (Eq. 4). Such a diagonal structure treats every element as independent and therefore may falsely reduce the uncertainty in the resulting reconstructions. However, the novel contribution of our model is that it includes a multivariate response regression approach that also models the covariances between the elements, so we argue that it produces more realistic, but also more uncertain, reconstructions. This explains why Fig. 1 shows only weak relationships between the individual 11 elements and temperature. When each of these relationships are combined in the multivariate response regression, our model provides a more precise posterior estimate of climate.

The fossil reconstruction stage for Diss Mere used 2000 iterations and ignored the first 200 runs and repeated this process four times. Fewer iterations are required for this stage for convergence, as the model complexity is substantially reduced compared to the modern calibration stage as MDPs are used. $\widehat{R}$ values were <1.05, indicating satisfactory convergence of the algorithm. The full reconstruction using all the SCUBIDO functions took approximately 16 h on a standard computer using a single core.

3.3 Model validation

As a more rigorous test of the model performance, and to maximise the use of the palaeoclimate reconstructions for climate services and model calibration, we further test its uncertainty calibration properties using an out-of-sample 5-fold cross-validation routine (Mauri et al., 2015; Chevalier et al., 2020). We removed 20 % of the modern data and re-fitted the full model to obtain posterior estimates of the climate variable for years which the model did not see during the training phase. We repeated this step five times, such that each observation year was removed once. We can then compare these out-of-sample predicted climate values with the true values in the modern data and see how often their uncertainty ranges cross with the true values. For example, in an ideal model, 95 % of these values would lie within the 95 % interval, 50 % would lie in the 50 % interval, etc. Although, in real-world data, the estimated proportion inside the credible intervals may be slightly higher or lower, out-of-sample evaluation of climate reconstructions seems not to be a common feature in the literature, but we would strongly advocate this in the future, especially if a goal is for the reconstructions to be used beyond the palaeoclimate community to, for example, help constrain climate model simulations.

The results of the 5-fold cross validation showed that, in 97.4 % of the 193 calibration temperatures, the reconstructions fell within the 95 % credible interval (Fig. 2). The coverage percentage for each individual fold ranged by 5.4 %, from 94.6 %–100 %. This demonstrates the validity of the modelling approach and shows that most of the temperature variability observed in the instrumental record is captured within the confidence intervals of the reconstructed climate.

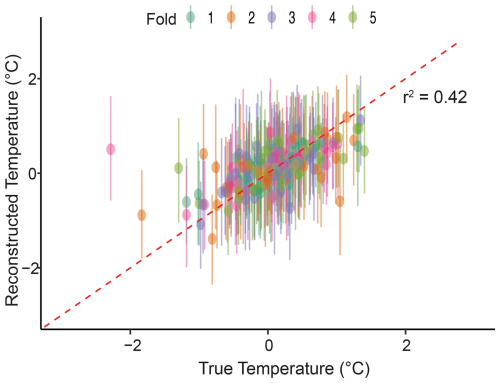
Figure 2 Results from the out-of-sample validation with true instrumental temperatures and reconstructed temperatures. Coloured dots represent the temperature values, and error bars represent the predicted temperature's 95 % uncertainty interval for each of the 5 folds. Note that the dashed red line is not the regression line and instead reflects the 1:1 relationship between true and reconstructed temperatures.

The coefficient of determination (r²) for the true and reconstructed temperature is 0.42 (P≦0.001), which suggests that there is some skill in the model prediction of the median values; however, it does suggest that not all the median values perfectly align with the true instrumental temperature. This is not uncommon for palaeoclimate reconstructions, especially as we are comparing proxy data that can also be affected by non-climate factors, such as human activity and internal lake processes. In addition, we are using instrumental temperature data which are not located proximal to the lake and contain large uncertainties, especially in the earliest years of the HadCET dataset (Parker et al., 1992). Nevertheless, the coverage percentage and overall good fit of the model can provide a reasonable assumption of the validity of this approach.

4 Annually resolved annual mean temperature reconstructions in Europe

4.1 Case site 1: Diss Mere, central England

The reconstruction of annually resolved temperatures for the past 8100 cal a BP given the µXRF-CS from Diss Mere using Bayesian inference is presented in Fig. 3. The median Holocene temperature reconstructed from Diss Mere is 9.65 °C and has a maximum range of 1.68 °C, with temperature anomalies between −1.26 and 0.42 °C (7.90 and 9.58 °C absolute temperatures). Most of the temperatures before ca. 2000 cal a BP are cooler than present (9.16 °C), with only isolated centennial-scale periods where temperatures are warmer (Fig. 3). The centennial to interannual variability is, however, reduced in the last 2 millennia, which may reflect the switch to non-varved sediments at this time. The first millennium of the Common Era is slightly warmer than today, remaining similar to present (Fig. 3).

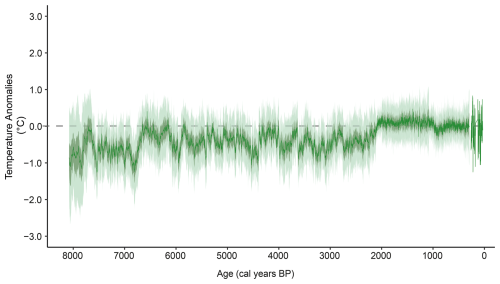
Figure 3 Annually resolved temperature reconstruction from Diss Mere. The dark-green line represents the median reconstruction, with the 50th percentile and 95th percentile in darker green and lighter green, respectively. The data are presented in anomalies for the UK long-term average across 1991–2020, and the dashed grey line marks the centred mean of 0 °C using this period.

4.2 Case site 2: Lake Nautajärvi, southern Finland

We have applied the SCUBIDO approach to reconstruct Holocene annual mean temperature from Nautajärvi, a lake in southern Finland with different lithology and sedimentation processes to those of Diss Mere. Lake Nautajärvi is also a varved lake but shows uninterrupted laminated sediments from the early Holocene to present (Ojala and Alenius, 2005). Except for the first 200 years of the record (9852–9625 cal a BP), when varves were thick (ca. 5 mm) due to a high detrital input during the formation of the lake (Ojala and Alenius, 2005; Ojala et al., 2008b), the sedimentation rate at Nautajärvi (0.2–1.6 mm yr⁻¹) is similar to the varve thickness of Diss Mere (0.1–1.4 mm yr⁻¹). Analysis of both the sediments and the µXRF-CS data from Nautajärvi revealed that the lake, and subsequent sediment record, is responsive to climate variability (Ojala et al., 2008a; Lincoln et al., 2025); thus it is also a good record on which to apply the Bayesian methodology. Table 1 summarises the characteristics of the modelling approach applied on the Lake Nautajärvi varved sediment sequence; for full details about the µXRF-CS data from Nautajärvi, please refer to Lincoln et al. (2025).

Table 1 Summary table of the Lake Nautajärvi data used for the Bayesian reconstruction. More information about the µXRF-CS instrument setup is presented in Lincoln et al. (2025).

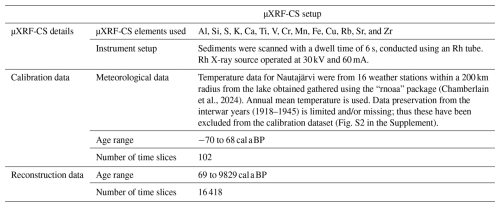
Figure 4 shows the annual temperature reconstruction from Nautajärvi for the past ca. 9800 years overlaid on top of the Diss Mere reconstruction. The average Holocene temperature reconstructed from Nautajärvi is 5.1 °C (Fig. S4) and has a range of 1.60 °C between 4.22 and 6.03 °C (−0.39 and 1.22 °C anomalies), which is within the range of variability observed during the instrumental period. Overall, the reconstructed Holocene temperatures at Nautajärvi are cooler than present, except for the period between ca. 7000 and 4000 cal a BP, where temperatures are warmer and experience greater variability.

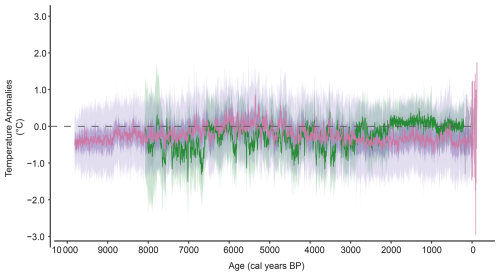
Figure 4 Annually resolved temperature reconstruction from Nautajärvi for the past ca. 9800 years (pink) overlaid on Diss Mere's reconstruction (green). The dark-pink line represents the median reconstruction, with the 50th percentile and 95th percentile in darker pink and lighter pink, respectively. The anomalies are calculated with reference to the 1991–2020 mean from the instrumental data. The dashed grey line marks the 0 °C mean.

The comparison of Nautajärvi and Diss Mere through the Holocene shows slightly different multi-millennial temperature evolutions, where temperatures in England steadily increase, whereas Finland reaches maximum temperatures in the mid-Holocene and then decreases thereafter (Fig. 4). We discuss millennial-scale trends in the next section when we compare our reconstructions with published low-resolution Holocene temperature reconstructions. On multi-decadal to centennial timescales, there is a good agreement between the anomaly values at both sites showing similar trends and amplitude of change, especially with the variability during the mid-Holocene from ca. 4000–6500 cal yr BP (Fig. S5). Larger variability in Diss Mere (England) prior to 6500 cal yr BP compared to Nautajärvi (Finland) might reflect different regional climate sensitivity during a period when the instability of the Laurentide ice sheet and hydrological changes in the Baltic Sea region still had an important role in the reconfiguration of the climate system and spatial distribution of climate patterns in the Northern Hemisphere (Yu and Harrison, 1995; Wastegård, 2022).

4.3 Palaeoclimate comparisons

No previously published reconstructions of annual mean temperature exist for Diss Mere or Nautajärvi, so there can be no comparison to test whether the temperatures produced from the SCUBIDO modelling approach are sensible on longer timescales. Whilst there have been some publications from these lake records which discuss climate variability, the proxies discussed are either not interpreted as temperature (e.g. summer varve thickness from Diss Mere; Martin-Puertas et al., 2023), reflect temperature in the summer season only (e.g. the Ca_clr record from Diss Mere; Boyall et al., 2024), or reconstruct the growing degree-day (e.g. from Nautajärvi in Ojala et al., 2008a) and thus may not capture the same variability and trends as our annual mean temperature reconstructions. Therefore, we compare our reconstruction results with large spatial multi-proxy reconstructions (Temp12k, Kaufman et al., 2020a) and data assimilation results (Last Glacial Maximum Reanalysis (LGMR), Osman et al., 2021; Holocene-DA, Erb et al., 2022) for the same period (Fig. 5). We choose these reconstructions to compare with because they are all based on large-scale data compilations utilising a range of models and proxy types. The Temp12k and Holocene-DA reconstructions both use the Temperature 12k proxy database (Kaufman et al., 2020b), with the Temp-12k reconstruction using a multi-method ensemble to reconstruct temperatures at a centennial resolution (Kaufman et al., 2020a) and the Holocene-DA reconstruction using an updated version of this dataset in a data assimilation framework to combine with transient climate simulations in order to obtain a reconstruction of temperature at a decadal resolution (Erb et al., 2022). On the other hand, the LGMR reconstruction uses only marine proxy records in a data assimilation approach to produce a reconstruction of temperature at a multi-centennial resolution.

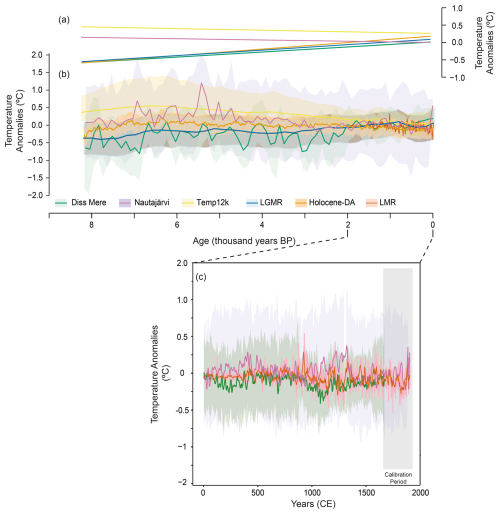
Figure 5 Comparison between different Holocene temperature reconstructions in anomalies. Note that the reference period for all these reconstructions is the mean between 2000–0 cal a BP. (a) Linear relationships between the reconstructed temperature and time for Diss Mere (green), Nautajärvi (purple), LGMR (Osman et al., 2021) (blue), Temp12k (Kaufman et al., 2020) (yellow), and the Holocene-DA (Erb et al., 2022) (orange). (b) The reconstructions from the above studies with Diss Mere and Nautajärvi resampled to 100 years to explore the centennial-scale variability and match the resolution of the other reconstructions. The LGMR and Temp12k are presented at a 200-year resolution. The envelopes for each line in the respective colours represent the uncertainty for each reconstruction. (c) A focus window on the Common Era with the Diss Mere temperature reconstruction with the LMR (Tardif et al., 2019) (orange) for a grid 50 : 60° N, 5° W : 15° E. The solid bold lines are at the 10-year decadal moving average, whereas the transparent envelopes are the original annual resolution.

The multi-millennial trends in the reconstructions are best demonstrated with both Fig. 5a and b, showing the clear evolution of temperatures through the Holocene. Figure 5a shows the slope from linear models conducted on the different reconstructions to explore the evolution of temperature through time. The Diss Mere, Holocene-DA (Erb et al., 2022), and LGMR (Osman et al., 2021) linear models all demonstrate an amelioration of temperature through the Holocene with similar rates of warming, especially during the early to mid-Holocene, where there are almost no differences between the records (Fig. 5a). The Temp-12k reconstruction from Kaufman et al. (2020a) and the Nautajärvi reconstruction from this study deviate from the general increasing trend observed in the other reconstructions and instead show an overall decrease in temperature from the early to late Holocene (Fig. 5a). These records have a more definitive early Holocene Thermal Maximum (HTM) with cooling thereafter in comparison with the other reconstructions, hence the linear model describing a general decrease in temperature through time. As part of the current discussion on the Holocene temperature conundrum (Liu et al., 2020), the differences in temperature evolution between the reconstructions may be a factor of a seasonal bias, which has been already noted for the Temp-12k reconstruction reflecting mostly summer conditions and/or spatial imbalances in proxy distributions, especially in the higher latitudes (Bova et al., 2021; Erb et al., 2022).

The amplitude of variability from the SCUBIDO-produced reconstructions from this study is much larger than the global reconstructions. Ultimately, this is because the LGMR and Temp12k have low temporal resolutions, causing the reconstruction to be smoothed, and contain a range of proxy types. Whilst the Holocene-DA reconstruction technically has data every 10 years, as mentioned in their study (Erb et al., 2022), the reconstruction does not contain robust decadal information from the proxy records and is achieved instead by utilising both proxy and transient models together; thus the low amplitude is still inherent from the low-resolution proxy data used.

The last 2 millennia

Reconstructing palaeoclimate for the Common Era (past 2000 years) has been the focus of many climate studies (e.g. Smerdon and Pollack, 2016; PAGES2k Consortium, 2017; Tardif et al., 2019; Anchukaitis and Smerdon, 2022). To test the Bayesian reconstructions from this study through a period of increased anthropogenic disturbance, we compare the reconstructions to the Last Millennium Reanalysis (LMR; Tardif et al., 2019) (Fig. 5c). Whilst the LMR and the Bayesian reconstructions are annual, we decide to compare at a 10-year resolution to reduce noise and explore the main decadal-scale trends between each record. Despite increased anthropogenic disturbance to the lake system over the past 2000 years at Diss Mere (Boyall et al., 2024) and a disruption to the proxy signal and lake functioning, the comparison between the overall trend of the LMR and Bayesian temperature reconstructions is good and showed similar temporal evolutions (Fig. 5c).

In the first millennium (0–1000 CE), the LMR is much less variable than the Bayesian reconstructions, and this can probably be attributed to the very low number of proxy records used for the first few hundred years of the reconstruction (Tardif et al., 2019). Between ca. 500 and 1000 CE, each of the reconstructions are very similar (Fig. 5c) and follow the 1000 CE temperature decrease. There are some periodic increases in temperature at around 1100–1300 CE, mostly seen at Nautajärvi, but these might reflect the Medieval Climate Anomaly, as they begin to decrease across all reconstructions at ca. 1300 CE.

The good consistency between the records highlights that, despite the different sediment varve characteristics, varve formation processes, and interactions between sedimentation and human activity, the Bayesian approach is able to reconstruct a quantified local to regional climate record from the µXRF-CS.

5 Conclusions and recommendations for future use of SCUBIDO

This study presents the first attempt at reconstructing quantitative annual mean temperatures from multivariate µXRF-data from sediment records using Bayesian inference. Several methodological decisions were made when building SCUBIDO which we believe can help contribute to the advancement of climate reconstructions within the community. The most important choice was to use Bayesian inference not only to obtain a single temperature estimate at each time point, but also to obtain a full posterior distribution to properly quantify uncertainties. In addition, we designed the model to include all geochemical elements and have SCUBIDO model their covariances instead of relying on prior assumptions about relationships, and the final choice was to synthesise SCUBIDO into an R package for the community. We believe that this was the best way to be as user-friendly as possible, as we think others could find this approach interesting and help make new annually resolved palaeoclimate reconstructions.

The ability of the Bayesian theorem to handle various types of data, changing time steps/resolutions, and gaps within datasets has been utilised in this study; for example, there are periods within the µXRF-CS records from both Diss Mere and Nautajärvi which have short gaps and periods where the sedimentation rates are variable, resulting in changing time steps. However, this was easily mitigated against by using a Bayesian framework.

In this paper, we apply SCUBIDO to two proxy records to reconstruct Holocene annual mean temperature in Europe, and the results showed consistency with previously published palaeoclimate reconstructions on a multi-millennial timescale. However, given the model and the high-resolution proxy data from this study, it provides a much more detailed overview of temperature evolution through the Holocene by increasing the resolution to annual at a single site. Of course, the records to which we compared our model (Holocene-DA, Temp12k, and LGMR) have the advantage of also being spatial reconstructions and not just temporal like in our study. The goal would be for more people in the palaeoclimate community to use SCUBIDO and thus produce more reconstructions of an annual resolution to then be incorporated into these large data compilations.

Whilst we encourage other groups to use this approach with their µXRF-CS records, there are some precautions which should be taken, since SCUBIDO does not provide a physical model between the climate and geochemical sediment composition. Like all palaeoclimate reconstructions using different statistical techniques, there is still some assumption that the proxy–climate relationship does not deviate too much through time to what is observed in the calibration period. This is important to consider when sites have experienced substantial alterations in human activity or other depositional changes, and we recommend carefully checking that the major shifts in the climate reconstruction are explained from climate or are rather explained by changes in the sedimentology (e.g. transitions from varved to non-varved deposits and changes in the varve microfacies). Because of this, we encourage users to qualitatively interpret their µXRF-CS records to see whether the lake remains sensitive to climate through time, to find the climate parameter to which the lake is sensitive, and be cautious of the results if there are substantial human-induced changes to the µXRF-CS record.

Finally, because µXRF-CS data are highly site-specific and sensitive to local systems, it is not possible to calibrate one site and apply that calibration period to another µXRF-CS lake record which may be common in other proxies, e.g. pollen (Parnell et al., 2016).

Future developments of the SCUBIDO approach should include integrating age uncertainty into the model, as age ensembles are currently not used. This means that, at present, lake data with stronger chronological age models would likely produce better reconstructions, as aligning the calibration instrumental climate data with the correct layers of µXRF-CS data is important. This is an important consideration for future users who do not have a varve sequence or a tight chronology in their lake records. Another potential avenue for future development using SCUBIDO is to incorporate additional meteorological datasets and model them alongside temperature. Since other meteorological processes likely contribute to the noise in the reconstruction, capturing their joint dependencies may lead to improved reconstruction accuracy.