the Creative Commons Attribution 3.0 License.
the Creative Commons Attribution 3.0 License.
Sensitivity of the Eocene climate to CO2 and orbital variability
John S. Keery
Philip B. Holden
Neil R. Edwards
The early Eocene, from about 56 Ma, with high atmospheric CO2 levels, offers an analogue for the response of the Earth's climate system to anthropogenic fossil fuel burning. In this study, we present an ensemble of 50 Earth system model runs with an early Eocene palaeogeography and variation in the forcing values of atmospheric CO2 and the Earth's orbital parameters. Relationships between simple summary metrics of model outputs and the forcing parameters are identified by linear modelling, providing estimates of the relative magnitudes of the effects of atmospheric CO2 and each of the orbital parameters on important climatic features, including tropical–polar temperature difference, ocean–land temperature contrast, Asian, African and South (S.) American monsoon rains, and climate sensitivity. Our results indicate that although CO2 exerts a dominant control on most of the climatic features examined in this study, the orbital parameters also strongly influence important components of the ocean–atmosphere system in a greenhouse Earth. In our ensemble, atmospheric CO2 spans the range 280–3000 ppm, and this variation accounts for over 90 % of the effects on mean air temperature, southern winter high-latitude ocean–land temperature contrast and northern winter tropical–polar temperature difference. However, the variation of precession accounts for over 80 % of the influence of the forcing parameters on the Asian and African monsoon rainfall, and obliquity variation accounts for over 65 % of the effects on winter ocean–land temperature contrast in high northern latitudes and northern summer tropical–polar temperature difference. Our results indicate a bimodal climate sensitivity, with values of 4.36 and 2.54 ∘C, dependent on low or high states of atmospheric CO2 concentration, respectively, with a threshold at approximately 1000 ppm in this model, and due to a saturated vegetation–albedo feedback. Our method gives a quantitative ranking of the influence of each of the forcing parameters on key climatic model outputs, with additional spatial information from singular value decomposition providing insights into likely physical mechanisms. The results demonstrate the importance of orbital variation as an agent of change in climates of the past, and we demonstrate that emulators derived from our modelling output can be used as rapid and efficient surrogates of the full complexity model to provide estimates of climate conditions from any set of forcing parameters.
- Article
(1487 KB) - Full-text XML
- BibTeX
- EndNote
In the early Eocene, several episodes of global warming coincided with carbon isotope excursions (CIEs), pulses of isotopically light carbon injected into the atmosphere and oceans, and recorded in high-resolution marine and terrestrial sediments (Kennett and Stott, 1991). In one large CIE, at the Palaeocene–Eocene transition at ∼ 56 Ma, the Palaeocene–Eocene Thermal Maximum (PETM), evidence from both tropical (e.g. Zachos et al., 2003) and polar (e.g. Sluijs et al., 2006) regions indicates that temperatures increased by ∼ 5 ∘C in less than 10 kyr. Although the greenhouse gas (GHG) sources and the duration of the onset phase of the PETM are uncertain, the relatively short timescale and global extent of the PETM strongly suggest that a large and sudden increase in GHGs in the atmosphere was the primary climatic forcing factor (Zachos et al., 2007). Since the PETM is the most recent period in Earth's history for which estimated atmospheric GHG concentrations are similar in magnitude to those of the present day, and expected to arise from fossil fuel burning, the PETM may provide a valuable analogue for anthropogenic climate change (e.g. McInerney and Wing, 2011; Zeebe et al., 2016; Zeebe and Zachos, 2013).
The CIEs of the early Eocene show similar regularity in their timing to periodic changes in the Earth's orbit around the Sun (Lourens et al., 2005), and the search for causal relationships between orbital cycles and Paleogene climate is an active area of research (e.g. Lauretano et al., 2015; Laurin et al., 2016; Lunt et al., 2011).
Although the climatic state in the early Eocene cannot be directly measured, much information on temperature and biogeochemical conditions can be inferred from measurements of proxy data: preserved natural records of climate variability, which can be linked to the property of interest through physical processes (Jones and Mann, 2004). However, there are major uncertainties in proxy data from the Eocene due to incomplete preservation and alteration over time, with additional uncertainties as to the seasonality of contributory processes, and for ocean proxies, the depth at which the property of interest, e.g. temperature, influences the proxy (Dunkley Jones et al., 2013). Climate models therefore have an important role to play in exploring the mechanistic functioning of palaeoclimates (Huber, 2012).
Climate simulations with high temporal and spatial resolution can be obtained from general circulation models (GCMs), but the requirement of GCMs for powerful computers and long runtimes makes them difficult to deploy for large ensembles of model simulations and restricts their ability to investigate the large uncertainties in forcings and model parameterisations. Such ensembles are more practical with more heavily parameterised and hence more computationally efficient Earth system models of intermediate complexity (EMICs) (Weber, 2010), although we note that Araya-Melo et al. (2015) and Lord et al. (2017) have deployed the GCM HadCM3 in ensemble-based studies of orbital forcing effects on climates of the Pleistocene and late Pliocene, respectively.
In this study, we deploy an EMIC, PLASIM-GENIE (Holden et al., 2016), in an ensemble of model runs to investigate the effects of varying GHG concentration and orbital parameters on the palaeoclimate of the Earth, with an Eocene configuration of the oceans and continents. We reduce the dimensionality of the model output by computing simple scalar metrics to denote key climatic features of each ensemble member, and we apply singular value decomposition (SVD) to identify the principal components (PCs) of temperature and precipitation fields in the full ensemble, for comparison with the variation in the forcing parameters.
By applying the linear modelling and emulation methods of Holden et al. (2015), we regress both the simple scalar metrics and the SVD-reduced dimension model outputs onto the forcing parameters, and from the derived relationships, we infer main effects denoting the effect of each explanatory term in the linear model and total effects denoting the effect of each forcing parameter, on the variation in the scalar metrics and on the temperature and precipitation output fields. We demonstrate that emulators derived in respect of tropical precipitation metrics can be used to estimate Eocene monsoonal responses to any combination of GHG and orbital forcing parameter values.
2.1 Climate of the early Eocene
During the Eocene, the Earth remained in the “greenhouse” state, which had persisted since the early Cretaceous, with polar air temperatures remaining above 0 ∘C for most of the year (Wing and Greenwood, 1993), no permanent polar ice caps, reduced Equator–pole temperature gradients and lower ocean–land temperature contrasts, inferred from fossil and isotope indicators of temperature and environmental conditions. Climate modellers have experienced difficulty in simulating Cretaceous and Palaeogene “equable climates” (Sloan and Barron, 1990; Wing and Greenwood, 1993) with sufficient warming at high latitudes, without overheating the tropics, although Huber and Caballero (2011), hereafter HC11, have demonstrated that with sufficiently high levels of CO2 (as a proxy for all forms of radiative forcing), climate models can generate global air temperature distributions in broad agreement with the proxy temperature measurements.
The onset of the PETM, at approximately 55.9 Ma (Westerhold et al., 2009), is recognised as the boundary between the Palaeocene and Eocene epochs (Aubry et al., 2007), and is characterised by a large CIE, indicating large GHG emissions, accompanied by a sudden rise in global temperature (Kennett and Stott, 1991), extensive extinction and origination of nanoplankton (Gibbs et al., 2006) and widespread ocean anoxia (Dickson et al., 2012). There is some evidence from analysis and modelling of the timing and duration of variations in δ13C and δ18O observed in nanoplankton fossils that some of the GHG emissions were initially in the form of CH4 (Dickens, 2011; Lunt et al., 2011; Thomas et al., 2002), which is rapidly oxidised in the atmosphere to CO2. The PETM is also marked by enhanced precipitation and continental weathering (Carmichael et al., 2016; Chen et al., 2016; Penman, 2016), rapid and sustained surface ocean acidification (Penman et al., 2014; Zachos et al., 2005), and shares many features of the global-scale oceanic anoxic events of the Cretaceous and Jurassic periods (Jenkyns, 2010); see McInerney and Wing (2011) for a review of PETM research.
The duration of the onset phase of the PETM is uncertain. Cui et al. (2011) have suggested that the peak rate of addition of CO2 to the atmosphere was much lower than the present-day rate of anthropogenic GHG emissions, but this is disputed by Sluijs et al. (2012). Zeebe et al. (2016) have estimated that the initial release of carbon at the onset of the PETM lasted at least 4 kyr, at a rate which was little more than 1∕10 of the present rate of anthropogenic emissions, so the Earth may already be in a “no-analogue” state, with anthropogenic climate change likely to exceed that of the PETM. However rapid the onset, the greenhouse conditions of the early Eocene, and particularly the PETM, provide an opportunity to apply lessons from the past, with a view to improving predictions of the future (Lunt et al., 2013).
2.2 Palaeogeography of the early Eocene
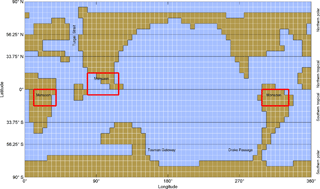
The arrangement of the continents and oceans in the early Eocene was broadly similar to that of the present, with the Earth's land mass divided into the same major continents and with most of the land mass in the Northern Hemisphere. India had not yet collided with the Eurasian continent, and the closure of the Tethys Ocean was not yet complete. Such tectonic movements may have effected some changes to the climate system. In particular, the configuration of ocean gateways strongly influences modes of ocean circulation and hence affects energy transport throughout the climate system (Lunt et al., 2016; Sijp et al., 2014).
2.2.1 Continental and ocean configurations during the early Eocene
Although the Bering Strait was closed throughout the Palaeogene (Marincovich et al., 1990), and the Western Interior Seaway linking the Arctic to the Pacific was closed by the end of the Cretaceous (Slattery et al., 2015), the Arctic Ocean was connected to the major oceans during the early Eocene through the Turgai Strait, also known as the Western Siberian seaway (Akhmetiev et al., 2012; Radionova and Khokhlova, 2000). The Lomonosov Ridge, from which core samples have been obtained by the Arctic Coring Expedition (ACEX) of the Integrated Ocean Drilling Program (IODP) Expedition 302 (Backman et al., 2008), was on the edge of the Arctic basin rather than across the pole as in the present configuration (O'Regan et al., 2008).
Both the Drake Passage between South America and Antarctica (Barker and Burrell, 1977) and the Tasman Gateway between Australia and Antarctica (Exon et al., 2004) were closed during the early Eocene, preventing the development of an Antarctic Circumpolar Current and allowing greater Southern Hemisphere meridional heat transport than in the modern world.
2.2.2 Orbital configurations
Throughout Earth's geological history, oscillations in the relative positions of the Earth and Sun have influenced both the Earth's climate and rates of sedimentation in some climate-sensitive environmental settings (Hinnov and Hilgen, 2012). The main oscillations are the eccentricity of the Earth's orbit around the Sun, with periods of ∼ 100 and 405 kyr, the obliquity or tilt of the Earth's axis of rotation, with a period of ∼ 40 kyr, and precession, the relative timing between perihelion and the seasons, with a period of ∼ 20 kyr (Berger et al., 1993). By correlating oscillations preserved in the geological record with computed time series of changes in insolation received by the Earth, an absolute astronomical timescale may be constructed for recent time spans with a complete sedimentary record, but where the geological evidence is incomplete, or where uncertainties in the orbital model are too great further back in time, only a relative timescale may be derived (Hilgen et al., 2010). An absolute astronomical solution has been computed back to 50 Ma (Laskar et al., 2011), and an absolute age of 55.53 ± 0.05 Ma has been proposed for the onset of the PETM at the start of the Eocene epoch by Westerhold et al. (2012).
Lourens et al. (2005) noted the apparent astronomical pacing of global warming events in the late Palaeocene and early Eocene, with correlations to both the long and short periods of eccentricity. Sexton et al. (2011) suggested that although the smaller hyperthermal events of the early Eocene were driven by cycles of carbon sequestration and release in the ocean, paced by the eccentricity cycles, the PETM was likely to have been driven by carbon injection from a sedimentary source. Laurin et al. (2016) applied a method which allows the phase of the 405 kyr eccentricity cycle to be identified from interference patterns and frequency modulation of the ∼ 100 kyr eccentricity cycle, and concluded that four hyperthermals in the early Eocene were initiated at 405 kyr eccentricity maxima, but in a study of terrestrial sediments with apparent correlation to the ∼ 100 kyr eccentricity cycle, Smith et al. (2014) suggested that hyperthermals occurred during eccentricity minima rather than maxima.
3.1 The PLASIM-GENIE model
PLASIM-GENIE (Holden et al., 2016) is an intermediate complexity atmosphere–ocean global circulation model (AOGCM). We apply the model at a spectral T21 atmospheric resolution, which corresponds to a triangular truncation applied at wave number 21 and a horizontal resolution of 5.625∘, with 10 layers, and a matching ocean grid with 32 depth levels. We apply the calibrated parameter set of Holden et al. (2016). The component modules are as follows.
“Plasim” (Fraedrich, 2012) is built around the 3-D primitive equation atmosphere model PUMA (Fraedrich et al., 2005). The radiation scheme considers two wavelength bands in the short wave and uses the broad band emissivity method for long wave. Fractional cloud cover is diagnosed. Other parameterised processes include large-scale precipitation, cumulus and shallow convection, dry convection and boundary layer heat fluxes.
“Goldstein” is a 3-D frictional-geostrophic ocean model (Edwards and Marsh, 2005; Marsh et al., 2011), dynamically similar to classical GCMs, except that it neglects momentum advection and acceleration. Barotropic flow around the four continental islands (Fig. 1) is derived from linear constraints that arise from integrating the depth-averaged momentum equations.
“Goldsteinseaice” (Edwards and Marsh, 2005) solves for the fraction of the ocean surface covered by ice within a grid cell and for the average sea-ice height. A diagnostic equation is solved for the ice surface temperature. Growth or decay of sea ice depends on the net heat flux into the ice (Hibler III, 1979; Semtner Jr., 1976). Sea-ice dynamics are represented by diffusion and advection by surface currents.
“Ents” (Williamson et al., 2006) models vegetative and soil carbon densities, assuming a single plant functional type. Photosynthesis depends upon temperature (with a double-peaked response representing boreal and tropical forest), atmospheric CO2 concentration and soil moisture availability. Self-shading is parameterised. Land surface albedo, moisture bucket capacity and surface roughness are parameterised in terms of the simulated carbon pool densities.
The computational efficiency of PLASIM-GENIE is achieved mainly through low spatial resolution (∼ 5∘) and, relative- to high-complexity Earth system models, simplifying assumptions in physical processes. These include, for instance, simplified parameterisations of radiative transport and convection in the atmosphere, the neglect of momentum transport in the ocean and the representation of all vegetation as a single plant functional type. Climate sensitivity, the response of the climate to a doubling of atmospheric CO2 concentration, including feedbacks, is an emergent property of the model.
3.2 Model configuration
3.2.1 Model grid
This study was designed before Lunt et al. (2017) presented their Deep-Time Model Intercomparison Project (DeepMIP) guidelines for model simulations of the latest Paleocene and early Eocene. However, our palaeogeography is based on the high-resolution digital reconstruction of the early Eocene published by Herold et al. (2014) and which Lunt et al. (2017) recommended should be used as the standard for all palaeoclimate simulations within the DeepMIP framework. We have used the data set of Herold et al. (2014) as an initial configuration for the tectonic layout, topography and bathymetric boundary conditions in our study. We have reduced the resolution of the Eocene palaeogeography provided by Herold et al. (2014) to a configuration of 64 longitude × 32 latitude cells, with each cell representing 5.625∘ in each orientation. Cells at high latitudes therefore represent smaller land areas than cells at low latitudes. Our vertical resolution is 32 ocean depths and 10 atmospheric layers. We have incorporated the ocean gateway configurations discussed in Sect. 2.2.1. The Turgai Strait is open in our configuration and is the only connection between the Arctic Ocean and other oceans. The Drake Passage and Tasman Gateway are both closed.
The palaeogeography (Fig. 1) comprises four land masses: North (N.) America and Eurasia; Antarctica combined with South (S.) America and Australia; Africa; and India. Red rectangles in Fig. 1 indicate the boundaries of areas used to calculate simple metrics of centennially averaged seasonal precipitation, as empirical indicators of African, Asian and S. American monsoons.
3.2.2 Forcing and other input parameters
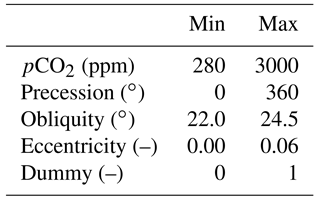
In order to investigate the sensitivity of the Eocene climate to variation in atmospheric CO2 and orbital parameters, we have constructed an ensemble of 50 model configurations, each with a unique set of forcing parameters comprising atmospheric CO2, eccentricity (e), obliquity (ε) and precession (ω), the angle on the Earth's orbit around the Sun between the moving vernal equinox and the longitude of perihelion (Berger et al., 1993). When e is zero, the Earth's distance from the Sun is constant at all points on the orbit, so there is no precessional effect. The magnitude of precessional effects is controlled by e, while phase is controlled by ω, so precessional effects are commonly described by the precession index given by esin ω. The precession index is at its maximum value when perihelion occurs at the December solstice, its minimum value when perihelion is at the June solstice and has a value of 0.0 when perihelion is at either the March or September equinox. The only orbital parameter which alters the total annual solar radiation received by the Earth is e, although the range of variation is very small. We include e and ω as separate and independent forcing parameters, rather than combined as the precession index, or in the form ecos ω. An additional dummy parameter is included to test for possible overfitting of relationships between forcing parameters and model output fields.
Although the maximum mass of CO2 injected into the atmosphere during CIEs, and in particular the PETM, remains uncertain, there is broad agreement that the atmospheric concentration of CO2 did not exceed 3000 ppm (e.g. Gehler et al., 2016) and that it did not fall below the pre-industrial level of 280 ppm at any time during the early Eocene. We allocate these values as the limits of a uniform range from which our ensemble of CO2 values is selected.
Since the absolute astronomical timescale for the early Eocene has an uncertainty which is greater than the periods of the obliquity and precession cycles, and there remains disagreement as to which phases of the eccentricity cycles are related to CIEs, there are no combinations of the orbital forcing parameters which can be known a priori to be of greater importance in their effects on the Eocene climate, in general, and on their contributions to the initiation, duration and termination of the CIEs in particular. We therefore select values of orbital parameters independently and from the full range of each parameter's variation during the early Eocene.
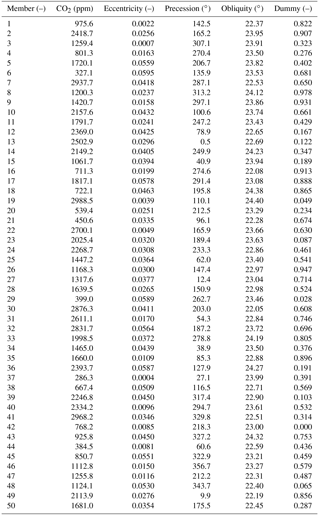
To ensure the best coverage of the five-dimensional state space comprised of the four forcing parameters and the additional dummy parameter in a limited number of model runs, we apply the Latin hypercube method (McKay et al., 1979), a constrained Monte Carlo sampling scheme in which the range to be sampled for each variable is divided into non-overlapping intervals, and one value from each interval is randomly selected (Wyss and Jorgensen, 1998). This provides adequate coverage of the state space more efficiently than can be achieved by a simple Monte Carlo sampling approach (Rougier, 2007). The present study has been designed to facilitate direct comparison between the results for specific ensemble members and their direct counterparts in a future study using the EMIC model GENIE-1 (Edwards and Marsh, 2005), which will include additional forcing parameters not used by this PLASIM-GENIE study. We have applied an iterative method to generate a pair of corresponding hypercubes with 5 and 11 dimensions for the PLASIM-GENIE and GENIE-1 studies, respectively, in which the minimum Euclidean distance between any two points is maximised, and linear correlation between any two parameters is minimised. We note that our selection of values for ω, an angular parameter, is from 0 to 360∘, treated as a linear range, with the consequence that the maximin criterion within the Latin hypercube algorithm is incorrectly calculated. However, given the dimensionality of our experimental design, this is unlikely to result in a significant reduction in the efficiency with which design points are distributed throughout the very sparsely populated state space. We draw readers' attention to an approach presented by Bounceur et al. (2015), in which independent values of esin ω, ecos ω and ε are sampled, with rejection of absolute values of esin ω and ecos ω which equal or exceed the maximum value of e. This experimental design allows values of e and ω for any design point to be identified by trigonometric analysis, while efficiently sampling the state space. Details of the steps taken to generate the hypercubes are provided in Appendix A. The absolute value of the r correlation coefficient does not exceed 0.1 for any pair of input (forcing and dummy) parameters. Uniform ranges for each of the forcing parameters and the dummy parameter are shown in Table 1, and the values applied in all 50 PLASIM-GENIE ensemble members are shown in Table 2.
Table 2Forcing factors and dummy values for each member in the ensemble. Precession is indicated by ω, the angle between the moving vernal equinox and the longitude of perihelion.
The intensity of radiation emitted by the Sun has increased steadily over time, and we apply the linear model of Gough (1981) and select a solar constant of 1358.68 W m−2. We note that Lunt et al. (2017) have recommended that a modern value of 1361.0 W m−2 should be applied to studies within the DeepMIP framework, in order to facilitate comparison between simulations with modern and pre-industrial levels of CO2, and to offset the absence of elevated levels of CH4.
3.2.3 Running the models
Each simulation was run for a spin-up period of 1000 years to reach a quasi-steady state, with key output fields recorded as seasonal averages for each of the 3-month periods December, January and February (DJF) and June, July and August (JJA), representing both winter and summer seasons in both the Northern Hemisphere and Southern Hemisphere. Although model output includes time series of some fields and output values every 100 years, in this study, only the field values recorded at the end of the 1000 years of modelling are used for analysis of the results.
3.3 Analysis of model output
Comparison of the forcing parameters applied in the ensemble with the model output fields can be more efficiently achieved by reducing the dimensionality of the model output while retaining information on key components of the climate system.
3.3.1 Simple metrics
In studies of the Earth's modern climate, it is recognised that the tropical–polar temperature difference (TPTD) influences poleward energy flux, and the ocean–land temperature contrast (OLC) affects monsoon intensity (Jain et al., 1999; Karoly and Braganza, 2001; Peixoto and Oort, 1992). Although atmospheric circulation patterns in the early Eocene will have differed from those in the modern world, in selecting latitude regions to represent the TPTD, we adopt the approach of Abbot and Tziperman (2008), who configured their model of the Cretaceous climate with latitude ranges of 0–30, 30–60 and 60–90∘, the approximate boundaries of the Hadley, Ferrel and polar cells observed in the modern world (Peixoto and Oort, 1992). On our model grid in which each cell spans 5.625∘ of latitude, for the purposes of deriving scalar metrics, we define the tropical regions to be between 0.0 and 33.75∘ north and south, and the polar regions to be between 56.25 and 90∘ north and south.
From the output values of air temperature in the lowest level of the atmosphere, weighted by grid cell area, we derive scalar values for each model run, of global annual mean air temperature (MAT), Northern Hemisphere and Southern Hemisphere seasonality (mean area-weighted DJF–JJA temperature differences in the above-defined polar regions), TPTD for summer and winter in each hemisphere, and OLC for summer and winter in tropical and polar regions in each hemisphere.
Monsoons are related to seasonal variations in tropical and subtropical winds and precipitation (Trenberth et al., 2006). Wang and Fan (1999) noted that the choice of an index to denote monsoon behaviour in the modern world is difficult and arbitrary, with commonly applied indices based on average summer precipitation, maximum summer precipitation, winter–summer difference in precipitation or wind circulation patterns within defined geographical areas. In this study, we derive simple scalar metrics to denote indices for monsoons for Asia, Africa and South America by subtracting winter rainfall from summer rainfall, for defined geographical regions, denoted in Fig. 1, and selected for their similarity to monsoonal regions in the modern continental configuration.
3.3.2 Singular value decomposition, linear modelling and model emulation
We perform a singular value decomposition to identify the PCs and empirical orthogonal functions (EOFs) of temperature and precipitation fields in the full ensemble, although we note that climate variability may not be due to physical processes which vary orthogonally, and identification of PCs can be influenced by aspects of the experimental design. A detailed presentation of the use of this method in the analysis of climate data is given by Hannachi (2004).
We use the linear modelling method of Holden et al. (2015) to regress both the simple scalar metrics and the SVD reduced dimension model outputs onto the forcing parameters. Values of the forcing parameters CO2, e and ε (with its very small angular range considered to be approximately linear) were normalised to the range [−1, 1] and combined with sinω and cosω to form 50-element column vectors representing the forcing factors. Each 2-D (32 × 64) result field for each ensemble member was unrolled to form a column vector of 2048 elements, comprising a single column within a 2048 × 50 matrix of full ensemble values.
SVD was applied to decompose the full ensemble matrix for each 2-D result field, providing a 2048 × 50 matrix of PCs, a 50 × 50 matrix of PC scores and a 50 × 50 matrix of diagonal values.
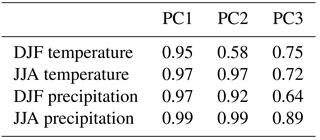
Linear modelling was applied to determine relationships between the normalised forcing factors and the first six columns of the PC scores, including products of pairs of forcing factors and squares of each forcing factor, with the best fitting relationships selected according to the Akaike information criterion (Akaike, 1974), then refined using Bayes information criterion (Schwarz, 1978). Burnham and Anderson (2003) provide a detailed discussion of the application of information criteria in model selection. The resulting relationship provides a simple emulator which can be used to estimate a PC score for the 2-D model field, given a single set of forcing parameter values. Applying derived emulators in respect of temperature and precipitation for both seasons, demonstrated high correlation between emulated PC scores and PC scores derived directly through SVD (Table 3).
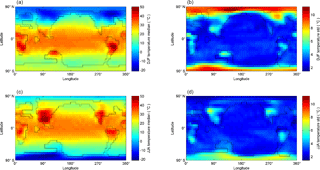
Figure 2Ensemble temperature medians (a, c) and standard deviations (b, d) in DJF (a, b) and JJA (c, d).
Our emulator approach uses linear regression, rather than a Gaussian process (GP), and is therefore simpler than the methods applied by Bounceur et al. (2015) in a study of the response of the climate–vegetation system in interglacial conditions to astronomical forcing, and by Araya-Melo et al. (2015) in their study of the Indian monsoon in the Pleistocene. Unlike linear models, GP models are intrinsically stochastic and give a more accurate quantification of their own error in emulating the input data. However, GP models can become computationally demanding in high-dimensional space, and their results can be more difficult to interpret.
In order to analyse the results of each of our linear models, we apply the method described in detail by Holden et al. (2015) to derive the main effects (Oakley and O'Hagan, 2004), which provide a measure of the variation in the linear model output due to each of the terms (first order, second order and cross products), derived from their coefficients, and total effects (Homma and Saltelli, 1996), which separate the effect of each forcing parameter on the variation in the model output. Although the forcing factors are all scaled within the range [−1, 1], the trigonometrical precession terms are not uniformly distributed across this range. We have therefore computed the variances of the first-order, second-order and cross-product terms directly for all parameters; rather than applying the respective approximations of 1∕3, 1∕9 and 4∕45, we have applied these values as scaling factors in calculating the main effects and total effects.
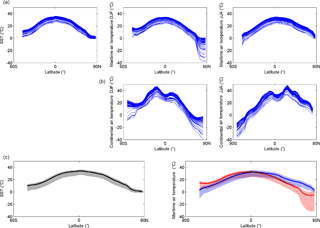
Figure 3(a) Full ensemble distributions of mean latitude values of global annual mean sea surface temperature (SST), with mean latitude maritime surface air temperature in DJF and JJA. (b) Mean latitude continental surface air temperature in DJF and JJA. (c) Ensemble medians and 5 and 95 % percentiles of global annual mean SST and maritime surface air temperature in DJF (red) and JJA (blue).
4.1 Model output – temperature and precipitation
Analysis of the model results has focused on variation in surface air temperature and precipitation in both winter and summer in each hemisphere, although it should be noted that our experiment has not been designed such that mean values in our ensemble output represent direct estimates of the Eocene climate mean. In the left column of Fig. 2, median temperatures at each grid cell for the full ensemble are plotted for DJF (Fig. 2a) and for JJA (Fig. 2c), with the standard deviations plotted in the right column column (Fig. 2b and d).
Ranges of median temperatures over land are greater than over the oceans, but TPTD is smaller in both seasons and both hemispheres than simulated in the modern world (see Fig. 2, Holden et al., 2016). It is apparent from the standard deviation field that the tropical–polar temperature difference varies substantially across the ensemble, particularly in northern winter. The temperature distributions are similar to those of the 2240 ppm CO2 simulation of HC11, regarded as their “mid-to-late Eocene” analogue (they consider elevated CO2 as a proxy for all radiative forcing, including uncertain climate sensitivity). The principal difference is in high northern latitude winter temperatures; the Arctic ocean remains above freezing in HC11. We note that the Arctic winter median air temperature is below freezing over both land and sea in the PLASIM-GENIE ensemble (see Fig. 3), and the Arctic does not remain ice free throughout the year in any of the 50 simulations in our study. Tropical temperatures in excess of 35 ∘C were simulated in some cases, as in HC11, which they regarded as their “most troubling result”, although they note observational data are currently insufficient to rule this out. Finally, we note that multi-model ensembles have found significant inter-model differences including, for instance, a 9 ∘C spread in global average temperature under the same CO2 forcing (Lunt et al., 2012). Quantification of model-related uncertainty is beyond the scope of the present study.
Full ensemble distributions of mean latitudinal distributions of annual mean sea surface temperature (SST), with mean latitudinal distributions of maritime and continental surface air temperature in both DJF and JJA, are plotted in Fig. 3, together with ensemble medians and 5 and 95 % percentiles of global annual mean SST and maritime surface air temperature in both DJF and JJA. The greater range of temperatures below rather than above median values reflects our use of a uniform range of CO2 forcing values and the logarithmic response of temperature to increasing CO2 concentration. There is substantial variation of mean temperature across the ensemble, around 20∘ over land, but the temperature offset varies little with latitude outside of polar regions where snow and ice greatly reduce winter temperatures in the colder simulations. The variation in TPTD across the ensemble thus appears to be essentially driven by the strength of snow and ice albedo feedbacks.
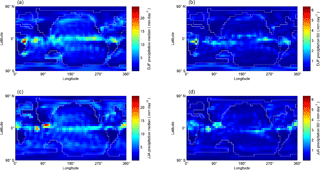
Figure 4Ensemble precipitation medians (a, c) and standard deviations (b, d) in DJF (a, b) and JJA (c, d).
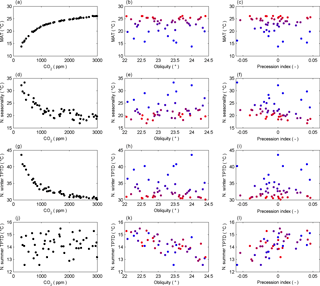
Figure 5Correlation between three forcing factors (CO2, obliquity and precession index; in columns from left to right) and the simple metrics (MAT, northern seasonality, northern winter tropical–polar temperature difference and northern summer tropical–polar temperature difference; in rows from top to bottom). CO2 is plotted in colour in the obliquity and precession plots (blue is low; red is high).
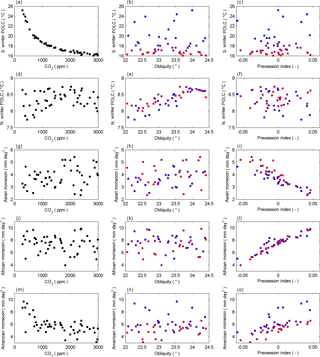
Figure 6Correlation between three forcing factors (CO2, obliquity and precession index; in columns from left to right) and the simple metrics (southern winter polar OLC, northern winter polar OLC, Asian monsoon index, African monsoon index and the S. American – hereafter referred to as “American” – monsoon index; in rows from top to bottom). CO2 is plotted in colour in the obliquity and precession plots (blue is low; red is high).
Our ensemble distributions of sea and air temperatures are in broad agreement with the values from the Eocene model studies compared by Lunt et al. (2012), hereafter L12, and with the tables of marine and terrestrial proxy data compiled by L12 and HC11, covering the early Eocene, and including some records from the very latest Paleocene but not including the PETM. Our palaeogeography specifically represents the early Eocene, but our range of CO2 and orbital inputs is more representative of the variation in forcing across the whole era. L12 have summarised variations of SST with latitude from their proxy data set, in their Fig. 1, including large error bars representing uncertainty which they attribute to assumptions about seawater chemistry, possible non-analogous behaviour between modern and ancient systems, and uncertainty in calibrations of relationships between proxy data and properties of the palaeoclimate. Our median values of SST are close to the median estimates of SST in L12 at midlatitudes, and well within the uncertainty indicated by error bars at high latitudes.
Median values and standard deviations of precipitation at each grid cell are plotted in Fig. 4. Higher precipitation values and variation are largely confined to the tropics, especially to regions associated with monsoons in the present day: Africa and S. America in DJF, and southeast (S.E.) Asia in JJA.
4.2 Simple metrics
In Figs. 5 and 6, CO2, obliquity (ε) and precession index (esin ω) are plotted against MAT, northern seasonality, northern winter TPTD and northern summer TPTD (Fig. 5), and southern winter polar OLC, northern winter polar OLC, Asian monsoon index, African monsoon index and the S. American (hereafter referred to as “American”) monsoon index (Fig. 6). Subplots for obliquity and precession index in Figs. 5 and 6 denote the CO2 level on a continuous colour scale. The dominant effect of CO2 on MAT and northern seasonality is apparent in Fig. 5, and it can also be seen that CO2 strongly affects the northern TPTD in the winter, but not in the summer, when the combined influence of obliquity and precession index is discernible, suggesting that temperature proxies with seasonal bias may have a significant orbital imprint. The plot of atmospheric CO2 against northern winter TPTD shows a change in gradient at approximately 1000 ppm CO2 and 32 ∘C. This may be related to the logarithmic dependence of radiative forcing on CO2 concentration, the disappearance of ice above some threshold level and a minimum level of land surface albedo related to maximum vegetation cover. A possible sea-ice-related threshold mechanism influencing both SST and maritime air temperature in high northern latitudes may be observed in Fig. 3, and this is strongly associated with the increase in northern winter TPTD at low CO2 levels. Zeebe et al. (2017) have analysed a high-resolution benthic isotope record covering the late Palaeocene – early Eocene and have concluded that orbitally paced cycles are unlikely to have been driven by high-latitude mechanisms, but our PLASIM-GENIE modelling suggests that while northern TPTD is not orbitally paced in the winter, being controlled by CO2, it is orbitally paced in the summer, by a combination of obliquity and precession.
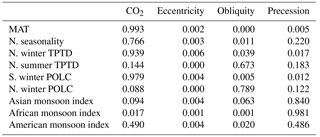
It can be observed in Fig. 6 that there is strong correlation between CO2 and southern winter polar OLC. The African and Asian monsoon indices are both correlated with the precession index, a well-established feature of Quaternary records (e.g. Cruz et al., 2005). The American monsoon index is fairly strongly correlated with the precession index at high levels of CO2 and negatively correlated with CO2 at low levels of CO2. In each of the other examples, there is no apparent correlation between the simple metric and two of the three forcing factors. We have selected these simple metrics with visible correlations to the forcing parameters for further analysis with the linear modelling and emulation methods. Total effects on the simple metrics have been calculated for each of the forcing parameters, with eccentricity and precession considered separately, rather than combined within the precession index, and are shown in Table 4.
The total effects of CO2 on MAT, northern winter TPTD and southern winter polar OLC, and of precession on both the Asian and African monsoon indices are all very high (> 0.90), and the total effects of obliquity on northern winter polar OLC and northern summer TPTD are both fairly high (> 0.65), providing quantitative confirmation of the correlations visible in Figs. 5 and 6.
4.3 Climate sensitivity and mean air temperature
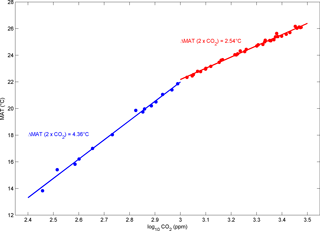
Figure 7 shows the relationship between CO2 (plotted on a logarithmic scale) and MAT, with an abrupt change of gradient clearly visible at a CO2 concentration of 1000 ppm. From the two gradients, we derive climate sensitivity values for a doubling of CO2 concentration at CO2 levels below 1000 ppm and at CO2 levels above 1000 ppm, of 4.36 and 2.54 ∘C, respectively. We note that our modelled values of carbon in vegetation in the ENTS module remain low outside of the tropics at low CO2 concentration, but as CO2 concentration increases, land areas at higher latitudes reach maximum values of carbon in vegetation, with all land areas showing no further capacity for increased carbon in vegetation at an atmospheric concentration of ∼ 1000 ppm. The increase in land vegetation cover, with corresponding reduction in albedo, acts as a positive feedback to rising temperature caused by increasing CO2, but this feedback mechanism ceases to operate when all available land is at its maximum vegetation capacity, with a consequent reduction in the climate sensitivity.
For a pre-industrial atmospheric CO2 concentration of 280 ppm, the value of MAT indicated by our results for our early Eocene palaeogeography is 14.0 ∘C. Holden et al. (2016) applied an identically configured PLASIM-GENIE to a modern geography, and their results show that with a pre-industrial CO2 concentration, the model climate sensitivity is 3.8 ∘C, and MAT is 12.9 ∘C.
Our results also indicate values of global MAT for double and 4 times the pre-industrial levels of CO2 of 18.5 and 22.5 ∘C, respectively; both these values are within the ranges of results for land near-surface air temperature in the modelling studies compared by L12 and shown in their Fig. 2b.
4.4 Singular value decomposition
Figure 8 shows the first three PCs of surface air temperature in DJF and JJA, with the percentages of temperature variation explained by each PC. Each of these plots illustrates the PC scaled by the standard deviation of the PC scores, thereby reflecting the variability across the ensemble. Note the variable scales for each of the subplots. In both DJF and JJA, PC1 explains over 95 % of the variance, with TPTD clearly visible in both hemispheres in DJF but apparent only in the Southern Hemisphere in JJA. OLC is apparent in the plots of PC1 in both DJF and JJA. OLC is discernible in PC2 for DJF temperature, which explains 2.4 % of variance, but less apparent, at least in the Southern Hemisphere, for JJA temperatures, in which PC2 explains 2.6 % of the variance. For temperature in both DJF and JJA, PC3 explains less than 1 % of the variance, with some indication of TPTD and OLC in DJF, but only of weak OLC at high latitudes in JJA. It is worth noting that even though lower-order PCs explain small percentages of global variances, these PCs are generally associated with specific regions where they are comparably important to the first PC.
In their presentation of the SVD method applied in this study, Holden et al. (2015) investigated the effects of orbital parameters on the Earth's climate in the present day but without including CO2 as a forcing parameter in their ensemble, and found that obliquity had a dominant effect on the PC score of annual average surface air temperature. In our study of the Eocene climate, CO2 is strongly correlated with northern seasonality (Fig. 5), and obliquity is weakly correlated with TPTD in JJA (Fig. 5) and with OLC in DJF (Fig. 6). The first three PCs of precipitation in DJF and JJA are shown in Fig. 9. PC1 explains approximately 55 % of the variance in both seasons, with PC2 and PC3 explaining over 20 and over 5 %, respectively, in both seasons. In both PC2 and PC3, areas of high seasonal contrast appear to correspond to areas which experience monsoons in the modern world.
Table 5R correlation values for PC scores for temperature and precipitation in DJF and JJA. Values where R2 ≥ 0.5 are shown in bold.
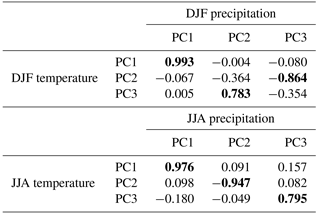
Table 6R correlation values for forcing factors and PC scores. Values where R2 ≥ 0.5 are shown in bold.
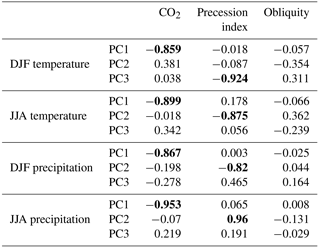
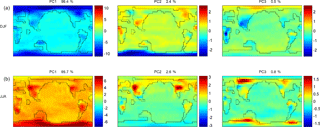
Figure 8The first three principal components of DJF temperature (a) and JJA temperature (b). Percentages of variance explained by each principal component are shown above each plot.
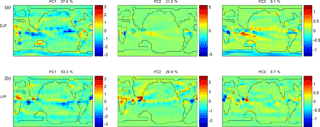
Figure 9The first three principal components of DJF precipitation (a) and JJA precipitation (b). Percentages of variance explained by each principal component are shown above each plot.
Correlations between the PC scores of temperature and precipitation are provided in Table 5. The first PC scores of temperature, reflecting a global warming signal, are highly correlated with the first PC scores for precipitation, suggesting that these PCs reflect a strengthening of the hydrological cycle in response to warming. Similar considerations reveal connections between lower-order PC scores, though we note that the second (third) component of DJF temperature is associated with the third (second) component of DJF precipitation. In order to address the drivers of these modes, we first consider the correlation coefficients, r, between forcing factors and the PC scores, shown in Table 6. These demonstrate that for each output there is a mode of variability driven by CO2 and another mode driven by precession, suggesting they reflect global warming (and associated hydrological strength) and precessional forcing of the monsoon system.
There is strong correlation (r2 > 0.5) between CO2 and the first PC scores of temperature in DJF and JJA. There are also strong correlations between precession index and the third PC scores for DJF temperature, and between precession index and the second PC scores for JJA temperature.
CO2 is strongly correlated with the first PC scores of precipitation in both DJF and JJA, and there is a strong relationship between precession index and the second PC scores of precipitation in both DJF and JJA. An increase in the second PC scores for JJA precipitation in the Asian monsoon region (Fig. 9) corresponds to a decrease in the second PC scores for JJA temperature (Fig. 8), and as already noted, the second PC scores for both temperature and precipitation in JJA are strongly correlated to the precession index. This temperature reduction during the Asian monsoon was also observed by Holden et al. (2014) and attributed to a reduction in incoming solar radiation associated with increased cloud cover and surface evaporation.
4.5 Linear modelling and emulation
The relationships between the forcing parameters (with precession expressed as both sinω and cosω) and the simple metrics, and between the forcing parameters and the PC scores of 2-D fields, derived through linear modelling, include first- and second-order terms of forcing factors, together with products of forcing factors. In all cases, most of the main effects are confined to the first-order terms, and in no case does eccentricity have a significant effect independently of either of the precession terms. All significant effects of the precession terms are accompanied by a small effect of eccentricity.
In Fig. 10, we plot the main effects of the forcing parameters on the first three PCs of temperature and precipitation for DJF. Figure 11 shows the main effects of the forcing parameters on the first three PCs of temperature and precipitation plotted for JJA.
In both seasons, PC1 for temperature and precipitation can be almost entirely explained by CO2, reinforcing the earlier conclusion that these describe a connected mode, global warming with associated effects on the hydrological cycle. The main effects also suggest connections between the modes of variability of temperature and precipitation in lower-order components. In both seasons, and apparent in both variables, there is a mode that is driven by precession; we interpret this as a monsoon signal, given precessional forcing and spatial patterns of rainfall that are characteristic of modern monsoons (Figs. 8 and 9). In JJA, this is the second component of both variables. The mode is associated with precipitation variability of ∼ 2.5 mm day−1 and temperature variability of ∼ 3 ∘C, with increased precipitation associated with a surface air cooling (note the negative correlation in Table 3, so that positive change in one field is associated with negative change in the other). In both cases, the local magnitude of variability is comparable to that driven by CO2. In DJF, the precessional signal is again apparent in the second mode of precipitation but the third mode of temperature. This mode is notable in that it drives changes in simulated precipitation over east Africa (5 mm day−1) that exceed CO2-driven variability. The remaining modes are more complex and may not represent a clear mode of variability that can be straightforwardly attributed. For instance, the third-order mode of JJA temperature is driven by an interaction between CO2 and obliquity, but in precipitation can be explained by a combination of precession and CO2.
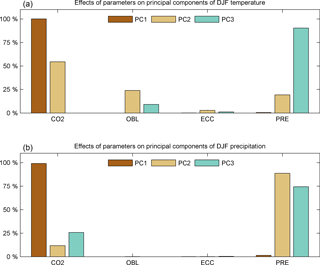
Figure 10Main effects of forcing parameters on the first three principal components of DJF temperature (a) and DJF precipitation (b).
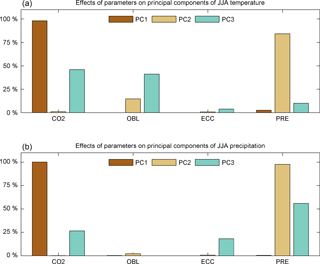
Figure 11Main effects of forcing parameters on the first three principal components of JJA temperature (a) and JJA precipitation (b).
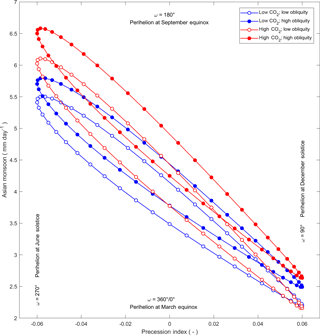
Figure 12Emulated values of the Asian monsoon index, for the full range of the precession index (esin ω), at low and high values of CO2 and obliquity (ε).
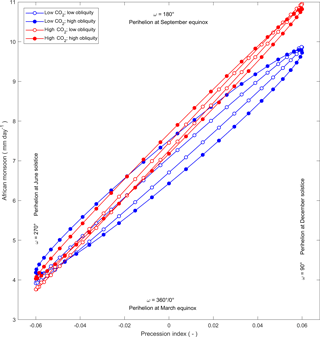
Figure 13Emulated values of the African monsoon index, for the full range of the precession index (esin ω), at low and high values of CO2 and obliquity (ε).
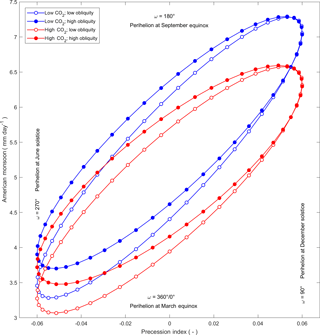
Figure 14Emulated values of the American monsoon index, for the full range of the precession index (esin ω), at low and high values of CO2 and obliquity (ε).
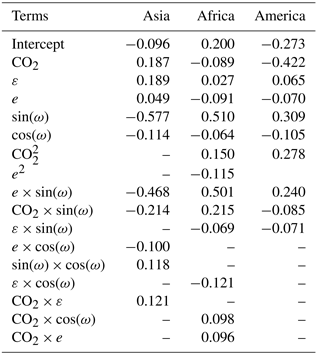
All of the terms in the linear models derived from the forcing factors and the three monsoon indices are shown in Table 7. The Asian and African models are dominated by precession terms, roughly equally distributed between first-order sin(ω) and the cross product of e and sin(ω), with being approximately 5 and 8 times larger than for the Asian and African models, respectively. The American model identifies significant influence of CO2, in both the negative first-order and positive second-order terms, with a similar magnitude of influence from combined precession terms, and with being approximately 3 times larger than . All of the models have small contributions from first or second order, or cross products of ε, and from those terms of e, in addition to significant contributions from esin (ω). The terms in the models clearly reflect the relationships between the three monsoon indices and the two forcing factors, CO2 and esin (ω), shown in Fig. 6.
We apply these linear models as emulators to estimate values of monsoon indices corresponding to the full range of precession (ω), with eccentricity fixed at its high limit of 0.06, low and high values of CO2 (300 and 3000 ppm), and low and high values of obliquity (22.0 and 24.5∘). Precession index (esin ω) and emulated values of the Asian, African and American monsoon indices for all four combinations of high and low CO2 and obliquity are plotted in Figs. 12, 13 and 14, respectively. The elliptical form of each of the plots is controlled by model terms which include cos(ω) and identify seasonal processes in the development of the monsoons. Running each of the emulators with all of the terms in cos(ω) excluded, generates points on a straight line between each apex of the ellipses generated by the full emulator. In each of the 12 plots in Figs. 12–14, ω increases anticlockwise from a value of 0∘ in the centre of the lower arc of the ellipse (with perihelion at the March equinox), through a value of 180∘ in the centre of the upper arc (with perihelion at the September equinox). Relationships between the precession index and the monsoon indices which are visually suggested in Fig. 6 are shown with clear structure in Figs. 12, 13 and 14. In each of the monsoon areas, the highest levels of precipitation occur when perihelion coincides with the summer solstice, in June for the Asian monsoon in the Northern Hemisphere and in December for the African and American monsoons in the Southern Hemisphere. For the Asian and African monsoons, precipitation is increased by high CO2, particularly when perihelion is at the summer solstice, but for the American monsoon, high CO2 decreases precipitation. The plots of the emulated African and American monsoons (Figs. 13 and 14) show the lowest and highest degrees of non-stationarity, respectively, due to the relative magnitude of the cos(ω) terms in the linear models.
Our ensemble of 50 model runs of the EMIC PLASIM-GENIE has used an early Eocene palaeogeography incorporating recent understanding of the configuration of the continents and ocean gateways, with climate forcing by a randomly selected combination of atmospheric GHG emissions and orbital parameters for each model run. Relationships between forcing parameters and scalar summaries of model results have been derived through linear modelling.
Given the input range of CO2, our results show that, at the global scale, variability in patterns of surface air temperature is strongly dominated by a single mode of variation with a strong imprint of TPTD, focused in northern winter, that is entirely controlled by CO2 (> 95 % variance in both seasons). We note, however, that regions under the influence of monsoon systems exhibit precession-driven temperature variability that is comparable in magnitude to the variability driven by CO2 (in large part, the high proportion of variance explained by the CO2 mode arises because the signal is global). In contrast to the unimodal dominance of CO2 on the modelled global temperature fields, precipitation shows a somewhat more nuanced response. The first mode of precipitation, while still controlled entirely by CO2, is much less dominant (maximum 57 % variance in DJF cf 21 % for PC2). In the second and third spatial modes of precipitation variability, CO2 is still important, but no more so than orbital parameters, with PC2 controlled more strongly by precession index.
The importance of orbital forcing to precipitation signals is seen more clearly in the OLC and monsoon indices. In spite of large variation in atmospheric CO2, variation in obliquity accounts for well over half of the variation in high northern latitude ocean–land temperature contrast, and the variation in precession is the dominant influence on seasonal variation in precipitation in tropical Africa and Asia, and combines with CO2 to influence seasonal precipitation in tropical N. and S. America. Our results strongly suggest the presence of monsoons in the early Eocene, but these climatic features would have developed without the effects of orography and high-altitude plateau heating which are important factors in the modern south Asian monsoon (Boos and Kuang, 2010).
We note that the relative amplitude of the CO2-driven modes depends critically on the actual amplitude of CO2 variability in the period of interest. While the ranges for orbital parameters are well defined, this is less true of CO2 variability over the Eocene. If atmospheric CO2 remained within a narrower range throughout the period, for example, in the range 700 to 1800 ppm, indicated for the early Eocene by Anagnostou et al. (2016) in a recent study using boron isotopes, then outside of short-lived hyperthermals, the relative influence of CO2 and orbital inputs might have been more evenly balanced. Our modelling results suggest that climate sensitivity is state dependent, with a value of 4.36 ∘C in a low CO2 state and 2.54 ∘C in a high CO2 state, due to a positive feedback mechanism in which albedo reduces as vegetation increases to its maximum value when CO2 concentration reaches 1000 ppm.
We have demonstrated that emulators derived from linear modelling of the PLASIM-GENIE ensemble results can be used as a rapid and efficient method of estimating climate conditions from any set of forcing parameters, without the need for further deployment of the EMIC.
PLASIM-GENIE is to our knowledge the most sophisticated climate model that has been applied to an ensemble of Eocene simulations, but we note that increasing computing power is now enabling ensembles of simulations with moderately higher resolution models, such as HadCM3 (3.75∘ × 2.5∘) (e.g. Araya-Melo et al., 2015; Lord et al., 2017), to be run, although with some limitation in the model years in each simulation. It will never be possible to apply state-of-the-art climate models to large ensembles because, given the continual striving for the highest possible resolution, single simulations with such models will always be at the limits of what is practicable with available computing power. EMICs therefore have an important role in furthering our understanding of past, present and future climate systems, and in the rapid identification of influencing factors and modes of response which may be targeted for study by slower but more powerful models.
Our study of the early Eocene climate and the PETM using PLASIM-GENIE has shown that variability in orbital parameters can exert significant climatic influence, particularly in regard to tropical temperature and precipitation, and they should not be ignored in modelling studies of climates of the past.
Details on access to the model code and instructions on compiling the model are given in Holden et al. (2016).
This study has been designed together with a future study using the EMIC model GENIE-1 (Edwards and Marsh, 2005). The GENIE-1 model will use all four of the forcing parameters and the dummy parameter, used in the present study, together with an additional six forcing parameters not used by the PLASIM-GENIE study. For PLASIM-GENIE, we have run 50 simulations with five parameters, while in GENIE-1 we will run 100 simulations with 11 parameters, so that the number of runs in each ensemble is approximately 10 times the input dimension (Loeppky et al., 2012).
The overall design for both studies is based on a maximin Latin hypercube
with 100 rows and 11 columns produced by repeatedly invoking the lhsdesign
function in MATLAB (MathWorks), with the command
hyperCube = lhsdesign(100, 11, “criterion”,
“maximin”, “iterations”, 100)
to select from 100 iteratively generated hypercubes the one which best fits the maximin criterion, i.e. where the minimum Euclidian distance between points in hyperspace is at a maximum. This MATLAB command is repeated until the absolute value of correlation between columns falls below a selected value, or until a selected number of attempts has been made. The ability of this “brute force” approach to produce a hypercube which satisfies the maximin criterion, with the required low correlation between columns, decreases rapidly with an increasing number of columns and a decreasing target correlation, but in several minutes it can generate a hypercube with 100 rows, each representing a design point for an ensemble member, and 11 columns, each representing a forcing or dummy parameter, with correlation between any two parameters not exceeding 0.1.
We then modify the overall design by first picking a subset of 50 of the 100 design points to give good coverage of the PLASIM-GENIE subspace. We randomly select an initial point and iteratively select from the remainder, without replacement, the point which provides the largest increase in the number of populated sectors across all the two-dimensional projections of PLASIM-GENIE parameter space defined by dividing each two-dimensional subspace into 6 × 6 equal sectors.
This defines a template comprising a 50-member subset of 11 parameter values.
Copying the template and discarding the six parameters which are only used in the GENIE-1 ensemble yields the final hypercube design for the PLASIM-GENIE ensemble, comprising 50 sets of five parameters.
A second copy of the template forms the top half of the GENIE-1 hypercube, and the bottom half is partially constructed by duplicating only the five PLASIM-GENIE parameters from the first 50 rows, with the remaining six parameters determined by choosing a previously unselected point, without replacement, from the initial 100 × 11 hypercube that maximises the Euclidean distance between the pair of points in the subspace of the remaining six parameters.
Following this procedure, the two hypercubes for the PLASIM-GENIE and GENIE-1 studies both show very good state-space coverage and low correlation, and each member of the PLASIM-GENIE ensemble has two corresponding members in the GENIE-1 ensemble, with identical values for the parameters in common, but widely differing sets of values for the parameters only used by GENIE-1.
JK and PH designed and prepared the ensemble configurations and analysed the model outputs with advice from NE. JK prepared the paper with contributions from both co-authors.
The authors declare that they have no conflict of interest.
The authors gratefully acknowledge support from NERC, with funding for
project NE/K006223/1. We are very grateful to the reviewers are Michel Crucifix and David De Vleeschouwer, and to the editor Arne Winguth, for their thorough and
constructive comments which have helped to improve the manuscript.
Edited by: Arne Winguth
Reviewed by: Michel Crucifix and David De Vleeschouwer
Abbot, D. S. and Tziperman, E.: A high-latitude convective cloud feedback and equable climates, Q. J. Roy. Meteor. Soc., 134, 165–185, https://doi.org/10.1002/qj.211, 2008.
Akaike, H.: A new look at the statistical model identification, IEEE T. Automat. Contr., 19, 716–723, 1974.
Akhmetiev, M. A., Zaporozhets, N. I., Benyamovskiy, V. N., Aleksandrova, G. N., Iakovleva, A. I., and Oreshkina, T. V.: The Paleogene history of the Western Siberian seaway – A connection of the Peri-Tethys to the Arctic Ocean, Austrian J. Earth Sci., 105, 50–67, 2012.
Anagnostou, E., John, E. H., Edgar, K. M., Foster, G. L., Ridgwell, A., Inglis, G. N., Pancost, R. D., Lunt, D. J., and Pearson, P. N.: Changing atmospheric CO2 concentration was the primary driver of early Cenozoic climate, Nature, 533, 380–384, https://doi.org/10.1038/nature17423, 2016.
Araya-Melo, P. A., Crucifix, M., and Bounceur, N.: Global sensitivity analysis of the Indian monsoon during the Pleistocene, Clim. Past, 11, 45–61, https://doi.org/10.5194/cp-11-45-2015, 2015.
Aubry, M.-P., Ouda, K., Dupuis, C., Berggren, W. A., and Couvering, J. A. V.: The Global Standard Stratotype-section and Point (GSSP) for the base of the Eocene Series in the Dababiya section (Egypt), Episodes, 30, 271–286, 2007.
Backman, J., Jakobsson, M., Frank, M., Sangiorgi, F., Brinkhuis, H., Stickley, C., O'Regan, M., Løvlie, R., Pälike, H., Spofforth, D., Gattacecca, J., Moran, K., King, J., and Heil, C.: Age model and core-seismic integration for the Cenozoic Arctic Coring Expedition sediments from the Lomonosov Ridge, Paleoceanography, 23, 1–15, https://doi.org/10.1029/2007PA001476, 2008.
Barker, P. and Burrell, J.: The opening of Drake passage, Mar. Geol., 25, 15–34, 1977.
Berger, A., Loutre, M. F., and Tricot, C.: Insolation and Earth's orbital periods, J. Geophys. Res.-Atmos., 98, 10341–10362, 1993.
Boos, W. R. and Kuang, Z.: Dominant control of the South Asian monsoon by orographic insulation versus plateau heating, Nature, 463, 218–222, https://doi.org/10.1038/nature08707, 2010.
Bounceur, N., Crucifix, M., and Wilkinson, R.: Global sensitivity analysis of the climate–vegetation system to astronomical forcing: an emulator-based approach, Earth Syst. Dynam., 6, 205–224, https://doi.org/10.5194/esd-6-205-2015, 2015.
Burnham, K. P. and Anderson, D. R.: Model selection and multimodel inference: a practical information-theoretic approach, Springer, New York, 2003.
Carmichael, M. J., Lunt, D. J., Huber, M., Heinemann, M., Kiehl, J., LeGrande, A., Loptson, C. A., Roberts, C. D., Sagoo, N., Shields, C., Valdes, P. J., Winguth, A., Winguth, C., and Pancost, R. D.: A model–model and data–model comparison for the early Eocene hydrological cycle, Clim. Past, 12, 455–481, https://doi.org/10.5194/cp-12-455-2016, 2016.
Chen, Z., Ding, Z., Yang, S., Zhang, C., and Wang, X.: Increased precipitation and weathering across the Paleocene-Eocene thermal maximum in central China, Geochem. Geophy. Geosy., 17, 2286–2297, https://doi.org/10.1002/2016GC006333, 2016.
Cruz, F. W., Burns, S. J., Karmann, I., Sharp, W. D., Vuille, M., Cardoso, A. O., Ferrari, J. A., Silva Dias, P. L., and Viana, O.: Insolation-driven changes in atmospheric circulation over the past 116,000 years in subtropical Brazil, Nature, 434, 63–66, https://doi.org/10.1038/nature03365, 2005.
Cui, Y., Kump, L. R., Ridgwell, A. J., Charles, A. J., Junium, C. K., Diefendorf, A. F., Freeman, K. H., Urban, N. M., and Harding, I. C.: Slow release of fossil carbon during the Palaeocene-Eocene Thermal Maximum, Nat. Geosci., 4, 481–485, https://doi.org/10.1038/NGEO1179, 2011.
Dickens, G. R.: Down the rabbit hole: Toward appropriate discussion of methane release from gas hydrate systems during the Paleocene-Eocene thermal maximum and other past hyperthermal events, Clim. Past, 7, 831–846, https://doi.org/10.5194/cp-7-831-2011, 2011.
Dickson, A. J., Cohen, A. S., and Coe, A. L.: Seawater oxygenation during the Paleocene-Eocene thermal maximum, Geology, 40, 639–642, https://doi.org/10.1130/G32977.1, 2012.
Dunkley Jones, T., Lunt, D. J., Schmidt, D. N., Ridgwell, A., Sluijs, A., Valdes, P. J., and Maslin, M.: Climate model and proxy data constraints on ocean warming across the Paleocene–Eocene Thermal Maximum, Earth-Sci. Rev., 125, 123–145, https://doi.org/10.1016/j.earscirev.2013.07.004, 2013.
Edwards, N. R. and Marsh, R.: Uncertainties due to transport-parameter sensitivity in an efficient 3-D ocean-climate model, Clim. Dynam., 24, 415–433, https://doi.org/10.1007/s00382-004-0508-8, 2005.
Exon, N. F., Kennett, J. P., and Malone, M. J.: Leg 189 synthesis: Cretaceous–Holocene history of the Tasmanian Gateway, in: Proceedings of the Ocean Drilling Program, Scientific Results, 189, edited by: Exon, N. F., Kennett, J. P., and Malone, M. J., Ocean Drilling Program, College Station, TX 2004.
Fraedrich, K.: A suite of user-friendly global climate models: hysteresis experiments, Eur. Phys. J. Plus, 127, 1–9, https://doi.org/10.1140/epjp/i2012-12053-7, 2012.
Fraedrich, K., Kirk, E., Luksch, U., and Lunkeit, F.: The portable university model of the atmosphere (PUMA): Storm track dynamics and low-frequency variability, Meteorol. Z., 14, 735–745, https://doi.org/10.1127/0941-2948/2005/0074, 2005.
Gehler, A., Gingerich, P. D., and Pack, A.: Temperature and atmospheric CO2 concentration estimates through the PETM using triple oxygen isotope analysis of mammalian bioapatite, P. Natl. Acad. Sci. USA, 113, 7739–7744, https://doi.org/10.1073/pnas.1518116113, 2016.
Gibbs, S. J., Bown, P. R., Sessa, J. A., Bralower, T. J., and Wilson, P. A.: Nannoplankton extinction and origination across the Paleocene-Eocene thermal maximum, Science, 314, 1770–1773, 2006.
Hannachi, A.: A primer for EOF analysis of climate data, University of Reading, Reading, 2004.
Herold, N., Buzan, J., Seton, M., Goldner, A., Green, J., Müller, R., Markwick, P., and Huber, M.: A suite of early Eocene (∼ 55 Ma) climate model boundary conditions, Geosci. Model Dev., 7, 2077–2090, https://doi.org/10.5194/gmd-7-2077-2014, 2014.
Hibler III, W.: A dynamic thermodynamic sea ice model, J. Phys. Oceanogr., 9, 815–846, 1979.
Hilgen, F. J., Kuiper, K. F., and Lourens, L. J.: Evaluation of the astronomical time scale for the Paleocene and earliest Eocene, Earth Planet. Sc. Lett., 300, 139–151, https://doi.org/10.1016/j.epsl.2010.09.044, 2010.
Hinnov, L. A. and Hilgen, F. J.: Chapter 4 – Cyclostratigraphy and Astrochronology, in: The Geologic Time Scale 2012, edited by: Gradstein, F. M., Ogg, J. G., Schmitz, M. D., and Ogg, G. M., Elsevier, Boston, 2012.
Holden, P., Edwards, N., Garthwaite, P., Fraedrich, K., Lunkeit, F., Kirk, E., Labriet, M., Kanudia, A., and Babonneau, F.: PLASIM-ENTSem v1. 0: a spatio-temporal emulator of future climate change for impacts assessment, Geosci. Model Dev., 7, 433–451, https://doi.org/10.5194/gmd-7-433-2014, 2014.
Holden, P. B., Edwards, N. R., Garthwaite, P. H., and Wilkinson, R. D.: Emulation and interpretation of high-dimensional climate model outputs, J. Appl. Stat., 42, 2038–2055, https://doi.org/10.1080/02664763.2015.1016412, 2015.
Holden, P. B., Edwards, N. R., Fraedrich, K., Kirk, E., Lunkeit, F., and Zhu, X.: PLASIM–GENIE v1.0: a new intermediate complexity AOGCM, Geosci. Model Dev., 9, 3347–3361, https://doi.org/10.5194/gmd-9-3347-2016, 2016.
Homma, T. and Saltelli, A.: Importance measures in global sensitivity analysis of nonlinear models, Reliab. Eng. Syst. Safety, 52, 1–17, 1996.
Huber, M.: Progress in greenhouse climate modeling, in: Reconstructing Earth's Deep-Time Climate – The State of the Art in 2012, edited by: Ivany, L. C. and Huber, B. T., The Paleontological Society, Boulder, CO, 2012.
Huber, M. and Caballero, R.: The early Eocene equable climate problem revisited, Clim. Past, 7, 603–633, https://doi.org/10.5194/cp-7-603-2011, 2011.
Jain, S., Lall, U., and Mann, M. E.: Seasonality and interannual variations of Northern Hemisphere temperature: Equator-to-pole gradient and ocean-land contrast, J. Clim., 12, 1086–1100, 1999.
Jenkyns, H. C.: Geochemistry of oceanic anoxic events, Geochem. Geophy. Geosy., 11, 1–30, https://doi.org/10.1029/2009GC002788, 2010.
Jones, P. D. and Mann, M. E.: Climate over past millennia, Rev. Geophys., 42, 1–42, 2004.
Karoly, D. J. and Braganza, K.: Identifying global climate change using simple indices, Geophys. Res. Lett., 28, 2205–2208, 2001.
Kennett, J. and Stott, L.: Abrupt deep-sea warming, palaeoceanographic changes and benthic extinctions at the end of the Palaeocene, Nature, 353, 225–229, https://doi.org/10.1038/353225a0, 1991.
Laskar, J., Fienga, A., Gastineau, M., and Manche, H.: La2010: a new orbital solution for the long-term motion of the Earth, Astron. Astrophys., 532, A89, 1–15, https://doi.org/10.1051/0004-6361/201116836, 2011.
Lauretano, V., Littler, K., Polling, M., Zachos, J. C., and Lourens, L. J.: Frequency, magnitude and character of hyperthermal events at the onset of the Early Eocene Climatic Optimum, Clim. Past, 11, 1313–1324, https://doi.org/10.5194/cp-11-1313-2015, 2015.
Laurin, J., Meyers, S. R., Galeotti, S., and Lanci, L.: Frequency modulation reveals the phasing of orbital eccentricity during Cretaceous Oceanic Anoxic Event II and the Eocene hyperthermals, Earth Planet. Sc. Lett., 442, 143–156, https://doi.org/10.1016/j.epsl.2016.02.047, 2016.
Loeppky, J. L., Sacks, J., and Welch, W. J.: Choosing the sample size of a computer experiment: A practical guide, Technometrics, 51, 366–376, 2012.
Lord, N. S., Crucifix, M., Lunt, D. J., Thorne, M. C., Bounceur, N., Dowsett, H., O'Brien, C. L., and Ridgwell, A.: Emulation of long-term changes in global climate: Application to the late Pliocene and future, Clim. Past, 13, 1539–1571, https://doi.org/10.5194/cp-13-1539-2017, 2017.
Lourens, L. J., Sluijs, A., Kroon, D., Zachos, J. C., Thomas, E., Röhl, U., Bowles, J., and Raffi, I.: Astronomical pacing of late Palaeocene to early Eocene global warming events, Nature, 435, 1083–1087, https://doi.org/10.1038/nature03814, 2005.
Lunt, D., Elderfield, H., Pancost, R., Ridgwell, A., Foster, G., Haywood, A., Kiehl, J., Sagoo, N., Shields, C., and Stone, E.: Warm climates of the past – a lesson for the future?, Philos. T. R. Soc.-A, 371, 20130146, https://doi.org/10.1098/rsta.2013.0146, 2013.
Lunt, D. J., Ridgwell, A., Sluijs, A., Zachos, J., Hunter, S., and Haywood, A.: A model for orbital pacing of methane hydrate destabilization during the Palaeogene, Nat. Geosci., 4, 775–778, https://doi.org/10.1038/ngeo1266, 2011.
Lunt, D. J., Dunkley Jones, T., Heinemann, M., Huber, M., LeGrande, A., Winguth, A., Loptson, C., Marotzke, J., Roberts, C., and Tindall, J.: A model–data comparison for a multi-model ensemble of early Eocene atmosphere–ocean simulations: EoMIP, Clim. Past, 8, 1717–1736, https://doi.org/10.5194/cp-8-1717-2012, 2012.
Lunt, D. J., Farnsworth, A., Loptson, C., Foster, G. L., Markwick, P., O'Brien, C. L., Pancost, R. D., Robinson, S. A., and Wrobel, N.: Palaeogeographic controls on climate and proxy interpretation, Clim. Past, 12, 1181–1198, https://doi.org/10.5194/cp-12-1181-2016, 2016.
Lunt, D. J., Huber, M., Anagnostou, E., Baatsen, M. L. J., Caballero, R., DeConto, R., Dijkstra, H. A., Donnadieu, Y., Evans, D., Feng, R., Foster, G. L., Gasson, E., von der Heydt, A. S., Hollis, C. J., Inglis, G. N., Jones, S. M., Kiehl, J., Kirtland Turner, S., Korty, R. L., Kozdon, R., Krishnan, S., Ladant, J. B., Langebroek, P., Lear, C. H., LeGrande, A. N., Littler, K., Markwick, P., Otto-Bliesner, B., Pearson, P., Poulsen, C. J., Salzmann, U., Shields, C., Snell, K., Stärz, M., Super, J., Tabor, C., Tierney, J. E., Tourte, G. J. L., Tripati, A., Upchurch, G. R., Wade, B. S., Wing, S. L., Winguth, A. M. E., Wright, N. M., Zachos, J. C., and Zeebe, R. E.: The DeepMIP contribution to PMIP4: experimental design for model simulations of the EECO, PETM, and pre-PETM (version 1.0), Geosci. Model Dev., 10, 889–901, https://doi.org/10.5194/gmd-10-889-2017, 2017.
Marincovich, L., Brouwers, E. M., Hopkins, D. M., and McKenna, M. C.: Late Mesozoic and Cenozoic paleogeographic and paleoclimatic history of the Arctic Ocean Basin, based on shallow-water faunas and terrestrial vertebrates, in: The Geology of North America, L: The Arctic Ocean Region, edited by: Grantz, A., Sweeney, J. F., and Johnson, G. L., Geological Society of America, 1990.
Marsh, R., Müller, S., Yool, A., and Edwards, N.: Incorporation of the C-GOLDSTEIN efficient climate model into the GENIE framework: “eb_go_gs” configurations of GENIE, Geosci. Model Dev., 4, 957–992, https://doi.org/10.5194/gmd-4-957-2011, 2011.
MathWorks: lhsdesign, https://uk.mathworks.com/help/stats/lhsdesign.html, last access: 17 August 2017.
McInerney, F. A. and Wing, S. L.: The Paleocene-Eocene Thermal Maximum: A perturbation of carbon cycle, climate, and biosphere with implications for the future, Annu. Rev. Earth Pl. Sc., 39, 489–516, https://doi.org/10.1146/annurev-earth-040610-133431, 2011.
McKay, M. D., Beckman, R. J., and Conover, W. J.: A comparison of three methods for selecting values of input variables in the analysis of output from a computer code, Technometrics, 21, 239–245, 1979.
Oakley, J. E. and O'Hagan, A.: Probabilistic sensitivity analysis of complex models: a Bayesian approach, J. Roy. Stat. Soc. Ser. B, 66, 751–769, 2004.
O'Regan, M., Moran, K., Backman, J., Jakobsson, M., Sangiorgi, F., Brinkhuis, H., Pockalny, R., Skelton, A., Stickley, C., and Koç, N.: Mid-Cenozoic tectonic and paleoenvironmental setting of the central Arctic Ocean, Paleoceanography, 23, 1–15, https://doi.org/10.1029/2007PA001559, 2008.
Peixoto, J. P. and Oort, A. H.: Physics of Climate, American Institute of Physics, New York, 1992.
Penman, D. E.: Silicate weathering and North Atlantic silica burial during the Paleocene-Eocene Thermal Maximum, Geology, 44, 731–734, G37704, https://doi.org/10.1130/G37704.1, 2016.
Penman, D. E., Hönisch, B., Zeebe, R. E., Thomas, E., and Zachos, J. C.: Rapid and sustained surface ocean acidification during the Paleocene-Eocene Thermal Maximum, Paleoceanography, 29, 357–369, https://doi.org/10.1002/2014PA002621, 2014.
Radionova, E. and Khokhlova, I.: Was the North Atlantic connected with the Tethys via the Arctic in the early Eocene? Evidence from siliceous plankton, GFF, 122, 133–134, https://doi.org/10.1080/11035890001221133, 2000.
Rougier, J.: Probabilistic inference for future climate using an ensemble of climate model evaluations, Climatic Change, 81, 247–264, https://doi.org/10.1007/s10584-006-9156-9, 2007.
Schwarz, G.: Estimating the dimension of a model, Ann. Stat., 6, 461–464, 1978.
Semtner Jr., A. J.: A model for the thermodynamic growth of sea ice in numerical investigations of climate, J. Phys. Oceanogr., 6, 379–389, 1976.
Sexton, P. F., Norris, R. D., Wilson, P. A., Pälike, H., Westerhold, T., Röhl, U., Bolton, C. T., and Gibbs, S.: Eocene global warming events driven by ventilation of oceanic dissolved organic carbon, Nature, 471, 349–352, https://doi.org/10.1038/nature09826, 2011.
Sijp, W. P., Anna, S., Dijkstra, H. A., Flögel, S., Douglas, P. M., and Bijl, P. K.: The role of ocean gateways on cooling climate on long time scales, Global Planet. Change, 119, 1–22, https://doi.org/10.1016/j.gloplacha.2014.04.004, 2014.
Slattery, J. S., Cobban, W. A., McKinney, K. C., Harries, P. J., and Sandness, A. L.: Early Cretaceous to Paleocene paleogeography of the Western Inteior Seaway: The interaction of eustasy and tectonism, in: Cretaceous Conference: Evolution and Revolution, edited by: Bingle-Davis, M., Wyoming Geological Association, Casper, WY, 2015.
Sloan, L. C. and Barron, E. J.: “Equable” climates during Earth history?, Geology, 18, 489–492, 1990.
Sluijs, A., Schouten, S., Pagani, M., Woltering, M., Brinkhuis, H., Damsté, J. S. S., Dickens, G. R., Huber, M., Reichart, G.-J., and Stein, R.: Subtropical Arctic Ocean temperatures during the Palaeocene/Eocene thermal maximum, Nature, 441, 610–613, https://doi.org/10.1038/nature04668, 2006.
Sluijs, A., Zachos, J. C., and Zeebe, R. E.: Constraints on hyperthermals, Nat. Geosci., 5, 231–231, https://doi.org/10.1038/ngeo1423, 2012.
Smith, M. E., Carroll, A. R., Scott, J. J., and Singer, B. S.: Early Eocene carbon isotope excursions and landscape destabilization at eccentricity minima: Green River Formation of Wyoming, Earth Planet. Sc. Lett., 403, 393–406, https://doi.org/10.1016/j.epsl.2014.06.024, 2014.
Thomas, D. J., Zachos, J. C., Bralower, T. J., Thomas, E., and Bohaty, S.: Warming the fuel for the fire: Evidence for the thermal dissociation of methane hydrate during the Paleocene-Eocene thermal maximum, Geology, 30, 1067–1070, 2002.
Trenberth, K. E., Hurrell, J. W., and Stepaniak, D. P.: The Asian monsoon: Global perspectives, in: The Asian Monsoon, edited by: Wang, B., Springer, New York, 2006.
Wang, B. and Fan, Z.: Choice of South Asian summer monsoon indices, B. Am. Meteorol. Soc., 80, 629–638, 1999.
Weber, S. L.: The utility of Earth system Models of Intermediate Complexity (EMICs), Wiley Interdisciplinary Reviews, Climate Change, 1, 243–252, https://doi.org/10.1002/wcc.24, 2010.
Westerhold, T., Röhl, U., McCarren, H. K., and Zachos, J. C.: Latest on the absolute age of the Paleocene–Eocene Thermal Maximum (PETM): new insights from exact stratigraphic position of key ash layers +19 and −17, Earth Planet. Sc. Lett., 287, 412–419, https://doi.org/10.1016/j.epsl.2009.08.027, 2009.
Westerhold, T., Röhl, U., and Laskar, J.: Time scale controversy: Accurate orbital calibration of the early Paleogene, Geochem. Geophy. Geosy., 13, 1–19, https://doi.org/10.1029/2012GC004096, 2012.
Williamson, M. S., Lenton, T. M., Shepherd, J. G., and Edwards, N. R.: An efficient numerical terrestrial scheme (ENTS) for Earth system modelling, Ecol. Model., 198, 362–374, https://doi.org/10.1016/j.ecolmodel.2006.05.027, 2006.
Wing, S. L. and Greenwood, D. R.: Fossils and fossil climate: the case for equable continental interiors in the Eocene, Philos. T. R. Soc.-B, 341, 243–252, 1993.
Wyss, G. D. and Jorgensen, K. H.: A User's Guide to LHS: Sandia's Latin Hypercube Sampling Software, Sandia National Laboratories, Albuquerque, NM, 1998.
Zachos, J. C., Wara, M. W., Bohaty, S., Delaney, M. L., Petrizzo, M. R., Brill, A., Bralower, T. J., and Premoli-Silva, I.: A transient rise in tropical sea surface temperature during the Paleocene-Eocene thermal maximum, Science, 302, 1551–1554, 2003.
Zachos, J. C., Röhl, U., Schellenberg, S. A., Sluijs, A., Hodell, D. A., Kelly, D. C., Thomas, E., Nicolo, M., Raffi, I., Lourens, L. J., McCarren, H., and Kroon, D.: Rapid Acidification of the Ocean during the Paleocene-Eocene Thermal Maximum, Science, 308, 1611–1615, https://doi.org/10.1126/science.1109004, 2005.
Zachos, J. C., Bohaty, S. M., John, C. M., McCarren, H., Kelly, D. C., and Nielsen, T.: The Palaeocene–Eocene carbon isotope excursion: constraints from individual shell planktonic foraminifer records, Philos. T. R. Soc.-A, 365, 1829–1842, https://doi.org/10.1098/rsta.2007.2045, 2007.
Zeebe, R. E. and Zachos, J. C.: Long-term legacy of massive carbon input to the Earth system: Anthropocene versus Eocene, Philos. T. R. Soc.-A, 371, 20120006, https://doi.org/10.1098/rsta.2012.0006, 2013.
Zeebe, R. E., Ridgwell, A., and Zachos, J. C.: Anthropogenic carbon release rate unprecedented during the past 66 million years, Nat. Geosci., 9, 325–329, https://doi.org/10.1038/ngeo2681, 2016.