Distinguishing the combined vegetation and soil component of δ¹³C variation in speleothem records from subsequent degassing and prior calcite precipitation effects

The carbon isotopic signature inherited from soil and epikarst processes may be modified by degassing and prior calcite precipitation (PCP) before its imprint on speleothem calcite. Despite laboratory demonstration of PCP effects on carbon isotopes and increasingly sophisticated models of the governing processes, to date, there has been limited effort to deconvolve the dual PCP and soil–epikarst components in measured speleothem isotopic time series. In this contribution, we explore the feasibility, advantages, and disadvantages of using trace element ratios and δ⁴⁴Ca to remove the overprinting effect of PCP on measured δ¹³C to infer the temporal variations in the initial δ¹³C of drip water prior to degassing and PCP. In nine examined stalagmites, the most widely utilized PCP indicators $\mathrm{Mg}/\mathrm{Ca}$ and δ⁴⁴Ca covary as expected. However, Sr $/$ Ca does not show consistent relationships with δ⁴⁴Ca so PCP is not the dominant control on Sr $/$ Ca. From δ⁴⁴Ca and $\mathrm{Mg}/\mathrm{Ca}$, our calculation of PCP as f_Ca, the fraction of initial Ca remaining in solution at the time the stalagmite layer is deposited, yields multiple viable solutions depending on the assumed δ⁴⁴Ca fractionation factor and inferred variation in D_Mg. Uncertainty in the effective fractionation of δ¹³C during degassing and precipitation contributes to uncertainty in the absolute value of estimated initial δ¹³C. Nonetheless, the trends in initial δ¹³C are less sensitive to these uncertainties. In coeval stalagmites from the same cave spanning the 94 to 82 ka interval, trends in calculated initial δ¹³C are more similar than those in measured δ¹³C and reveal a common positive-anomaly initial δ¹³C during a stadial cooling event. During deglaciations, calculated initial δ¹³C implies a trend of greater respiration rates and higher soil CO₂, although the higher interglacial drip water saturation favors more extensive PCP. Initial δ¹³C can be estimated for active and fossil speleothems from a range of settings, wherever there is confidence that $\mathrm{Mg}/\mathrm{Ca}$ and/or δ⁴⁴Ca provides a quantitative indication of past changes in PCP. Further study of Mg partitioning in speleothems will improve the robustness of $\mathrm{Mg}/\mathrm{Ca}$ as a PCP proxy.

1 Introduction

Changes in vegetation productivity and soil processes significantly influence the δ¹³C of drip water. The δ¹³C of CO₂ in the soil and karst reflects the relative contributions of isotopically light respired CO₂ and isotopically heavier atmospheric CO₂. Conditions which favor higher vegetation productivity, including deeper-rooted trees (Meyer et al., 2014), and faster rates of heterotrophic and autotrophic respiration in soils will lead to higher soil pCO₂ and a lower δ¹³C of CO₂. In contrast, in less productive and slower respiring systems, the atmospheric CO₂ and its higher δ¹³C will be more significant C sources in the soil. This soil and vegetation signature imparted to the drip water is also imprinted on speleothem δ¹³C. In the temperature range characterizing the middle and high latitudes, respiration rates and vegetation density are highly sensitive to temperature, and speleothem δ¹³C has been exploited to serve as a temperature proxy in midlatitude speleothems (Genty et al., 2003, 2006). Sufficient soil moisture is also required for high soil CO₂ (Romero-Mujalli et al., 2019). In addition to its direct effect on the δ¹³C of soil CO₂, higher soil CO₂ concentrations also lead to more open system dissolution of karst host rock carbonate, which further contributes to lower δ¹³C of the drip water dissolved inorganic carbon (DIC).

Superimposed on soil and karst process are in-cave processes which subsequently modify the δ¹³C of DIC and thereby speleothem δ¹³C, since coupled degassing and precipitation of CaCO₃ progressively enriches the δ¹³C of the remaining dissolved inorganic carbon. This process has been demonstrated in lab experiments (Polag et al., 2010; Hansen et al., 2019) and in “farmed calcite” in cave environments (Mickler et al., 2004, 2006) and can be modeled as a Rayleigh process. Extensive quantitative modeling of this processes has been conducted in purpose built models (Mühlinghaus et al., 2007, 2009; Scholz et al., 2009; Sade et al., 2022) and embedded in broader models (Owen et al., 2018). Our interest here is to extend the previous analysis by relating the evolution of the δ¹³C of bicarbonate to the evolution of the Ca in solution. In this way, we can evaluate the viability of using trace element and Ca isotopic data as independent indices of the progression of coupled CO₂ degassing and prior calcite precipitation (PCP).

In this contribution, we explore the potential and limitations of simple, easy to use approaches to distinguish temporal variations in δ¹³C attributable to soil and epikarst vs. in-cave processes. We acknowledge that effects to recover the absolute initial δ¹³C will be challenging in most applications. Therefore we focus on the simpler goal of separating the temporal trends in PCP from those due to soil and epikarst components within a given stalagmite. We present new analyses of PCP proxies δ⁴⁴Ca and $\mathrm{Mg}/\mathrm{Ca}$ on nine stalagmites from a single cave system which experienced the same climate regime and represent a range of climate states from glacial through interglacial. Using these stalagmites as examples, we evaluate approaches for estimating the quantitative extent of PCP and degassing in fossil stalagmites in which initial drip water chemistry and partition coefficients are not independently constrained. For three time intervals including Termination II (TII), Marine Isotope Stage (MIS) 5b–c, and the last deglaciation, we present δ¹³C time series and compare trends of coeval δ¹³C records with and without deconvolution of in-cave as well as soil and epikarst processes.

2 Background on evolution of δ¹³C with progressive CO₂ degassing and PCP

2.1 Rayleigh fractionation of carbon isotopes during CO₂ degassing and prior calcite precipitation

The δ¹³C value of dissolved inorganic carbon in drip water, dominantly bicarbonate, will evolve with the coupled precipitation of calcite and evolution of CO₂(g) from the drip water. Because the C removed by CO₂ degassing is isotopically much lighter than the bicarbonate pool, the δ¹³C value of the dissolved bicarbonate increases. The net total fractionation, ε_tot is the weighted mean (by the number of C atoms) of the individual fractionations between bicarbonate and CO₂(g) and between calcite and bicarbonate, respectively (Scholz et al., 2009):

$$\begin{array}{}\text{(1)}& {\mathit{\epsilon }}_{\mathrm{tot}}=\mathrm{1}/{\mathrm{2}}^{\mathrm{13}}{\mathit{\epsilon }}_{{\mathrm{CO}}_{\mathrm{2}}\left(\mathrm{g}\right)/{\mathrm{HCO}}_{\mathrm{3}}^{-}}+\mathrm{1}/{\mathrm{2}}^{\mathrm{13}}{\mathit{\epsilon }}_{{\mathrm{CaCO}}_{\mathrm{3}}\left(\mathrm{s}\right)/{\mathrm{HCO}}_{\mathrm{3}}^{-}}.\end{array}$$

The first of these fractionations is strongly temperature-dependent. The second bicarbonate–calcite fractionation factor showed negligible temperature dependence in seeded experiments (Romanek et al., 1992) but modest temperature dependence in earlier studies and which were used in compilations (Emrich et al., 1970; Rubinson and Clayton, 1969; Mook and Rozanski, 2001). Thus, the net fractionation evolves from −3.5 ‰ at 25 ^∘C to −5.2 ‰ at 5 ^∘C using temperature-sensitive calcite fractionation factors, but from −3.5 ‰ at 25 ^∘C to −4.6 ‰ at 5 ^∘C when the calcite fractionation factor is invariant. The evolution of the δ¹³C of the bicarbonate in drip water has been modeled by a Rayleigh process, in which the dependence of the δ¹³C of bicarbonate is a function of the remaining HCO${}_{\mathrm{3}}^{-}$ in solution (Mühlinghaus et al., 2007, 2009). Newer models have added the effect of isotopic exchange between cave air and the drip water (Hansen et al., 2017). Finally, advection–diffusion–reaction models simulate the dynamic speleothem formation from a flowing thin film, including the evolution from degassing, precipitation, and exchange with atmosphere (Sade et al., 2022). This latter model confirms that the evolution of δ¹³C of speleothem calcite is very closely correlated to the extent of PCP once >20 % of initial DIC has precipitated.

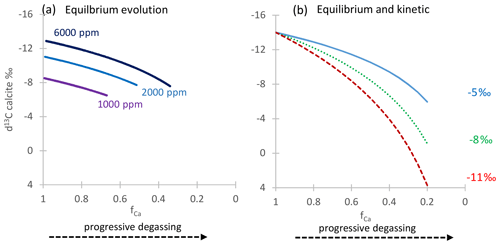
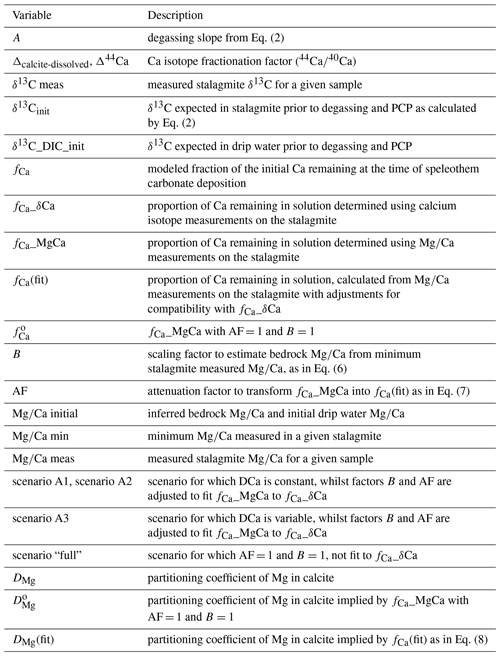
Figure 1 (a) Simulation of the equilibrium evolution of δ¹³C in calcite with increasing PCP for three initial δ¹³C values of DIC corresponding to different pCO₂ of soil, with the soil CO₂ isotopic composition following the typical Keeling line (e.g., Pataki et al., 2003). Calculations were completed in CaveCalc (Owen et al., 2018). The fraction of initial Ca remaining at the time of speleothem deposition (f_Ca) is the index of PCP. (b) Example simulation of the evolution of δ¹³C in calcite from a single initial δ¹³C of DIC following Eq. (3); an equilibrium degassing and precipitation fractionation slope A (−5 ‰) is contrasted with two possible kinetically enhanced fractionation slopes (−8 ‰ and −11 ‰).

Previous modeling has focused on the evolution of δ¹³C bicarbonate as a function of the remaining DIC. In contrast, here we focus on the evolution of δ¹³C bicarbonate as a function of the Ca remaining in the solution. The Ca remaining in solution allows us to estimate the extent of calcite precipitation, and from this we estimate the degree of degassing (and carbonate precipitation) the solution has undergone prior to deposition of the speleothem. We target Ca as the indicator because trace element ratios and Ca isotopic systems may preserve proxy information about the Ca remaining in solution. CaveCalc (Owen et al., 2018) simulates this process and examples are given in Fig. 1a. We therefore relate the Rayleigh-driven progressive enrichment in δ¹³C of bicarbonate with the progressive depletion of Ca in the drip water. f_Ca is the fraction of initial Ca remaining in solution. This relationship is

$$\begin{array}{}\text{(2)}& {{\mathit{\delta }}^{\mathrm{13}}\mathrm{C}}_{\mathrm{init}}={{\mathit{\delta }}^{\mathrm{13}}\mathrm{C}}_{\mathrm{meas}}-A\cdot \ln \left(f_{\mathrm{Ca}}\right),\end{array}$$

in which δ¹³C_init is the composition for a case of negligible degassing and CaCO₃ precipitation (f_Ca=1), and δ¹³C_meas corresponds to the δ¹³C at a given value of f_Ca (Table 1 provides a summary of abbreviations used in this paper). The term A describes the rate of evolution of δ¹³C with progressive degassing and CaCO₃ precipitation. We subsequently refer to term A as the degassing slope. A range of values have been proposed for A, from equilibrium precipitation and degassing in CaveCalc to greater kinetically enhanced fractionation during degassing suggested by some laboratory (Hansen et al., 2019) and field (Mickler et al., 2019) studies (Figs. 1b and S1 in the Supplement). The support for each of these values and implications are discussed at length in Sect. 5.3. To test the influence of different degassing slopes on the magnitude of the PCP effect, we complete a sensitivity analysis with a range of values for the parameter A.

Table 1 List of variables and abbreviations.

2.2 Indicators of PCP

2.2.1 $\mathrm{Mg}/\mathrm{Ca}$ and Sr $/$ Ca

As discussed previously (Stoll et al., 2012), the signal of PCP imprinted on a stalagmite includes calcite precipitation truly prior to landing of the water drop on the stalagmite surface, as well as the “extent of precipitation” occurring from the drop on the stalagmite surface before it is displaced from the active growth axis by flow. As the combined signal is manifest in the stalagmite, hereafter we discuss both true PCP and the extent of precipitation processes under the term “PCP”.

$\mathrm{Mg}/\mathrm{Ca}$ is the most widely applied indicator of degassing and PCP. Due to the low partition coefficient of Mg in calcite (e.g., as low as 0.012; Day and Henderson, 2013), the precipitation of calcite leads to an increase in the solution $\mathrm{Mg}/\mathrm{Ca}$. The Rayleigh equation (Eq. 2) relates the fraction of initial Ca remaining in solution (f_Ca_MgCa) to the initial drip water $\mathrm{Mg}/\mathrm{Ca}$ (e.g., prior to degassing) and measured solution $\mathrm{Mg}/\mathrm{Ca}$ when the partition coefficient D is known.

$$\begin{array}{}\text{(3)}& f_{\mathrm{Ca}\mathrm{\_}\mathrm{MgCa}}={{\displaystyle \frac{\mathrm{Mg}/{\mathrm{Ca}}_{\mathrm{speleothem}}}{\mathrm{Mg}/{\mathrm{Ca}}_{\mathrm{initial}}\cdot D_{\mathrm{Mg}}}}}^{\frac{\mathrm{1}}{\left(D_{\mathrm{Mg}}-\mathrm{1}\right)}}\end{array}$$

Figure 2a illustrates an example evolution. $\mathrm{Mg}/\mathrm{Ca}$ is most robust as a quantitative indicator of PCP in a given stalagmite when the initial drip water $\mathrm{Mg}/\mathrm{Ca}$ (prior to degassing) remains constant and when there is minimal variation in the partition coefficient of Mg. In cave analogue laboratory experiments, D_Mg increases by about 17 % with a 10 ^∘C temperature increase (Day and Henderson, 2013). Additionally, in farmed calcite a 60 %–70 % increase in the D_Mg was observed as calcite $\mathrm{Mg}/\mathrm{Ca}$ increases from 10 to 30 mmol mol⁻¹ (Wassenburg et al., 2020). If D_Mg increases with solution $\mathrm{Mg}/\mathrm{Ca}$, it would amplify the $\mathrm{Mg}/\mathrm{Ca}$ due to increasing PCP. This dependence of D_Mg on $\mathrm{Mg}/\mathrm{Ca}$ has also been shown in some non-cave analogue laboratory experiments (Alkhatib et al., 2022). For inference of PCP, the measured Mg in the stalagmite should be fully in the calcite and not in detrital minerals, a criterion which can be effectively checked using other detrital-sensitive indicators like Al $/$ Ca.

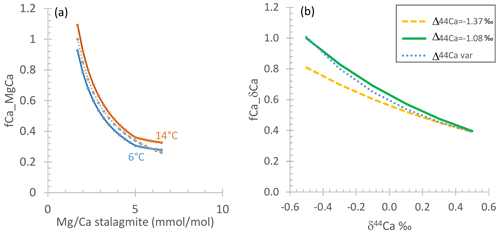
Figure 2 (a) Example variation in $\mathrm{Mg}/\mathrm{Ca}$ with f_Ca from Rayleigh simulations of progressive calcite precipitation at 6 ^∘C (lowermost curve) and 14 ^∘C (uppermost curve) using the D_Mg of Day and Henderson (2013); an example is shown for $\mathrm{Mg}/\mathrm{Ca}$ drip water 400 mmol mol⁻¹. Also shown with a dashed line is the “index” approximation produced by Eq. (5). (b) Example estimation of f_Ca from δ⁴⁴Ca, illustrating the effect of the fractionation factor on the calculated f_Ca for two examples of constant fractionation and one case in which the fractionation factor systematically evolves from Δ_{calcite-dissolved} of −1.37 to −1.08 with increasing PCP and concomitant slowing of the growth rate. The example shown is for a bedrock δ⁴⁴Ca of 0.58.

A formulation similar to Eq. (1) can be made for other divalent cations with partition coefficients significantly less than 1, such as Sr $/$ Ca and Ba $/$ Ca. The coherence of changes in $\mathrm{Mg}/\mathrm{Ca}$, Sr $/$ Ca, and to a lesser extent Ba $/$ Ca is often interpreted to signify that PCP is the controlling process (Sinclair, 2011; Wassenburg et al., 2020). Deviations from expected PCP control may reflect variation in the partition coefficients of Sr (or Ba). Increased DSr with a higher growth rate or saturation state is widely seen in non-cave analogue laboratory experiments (Tang et al., 2008a; Tesoriero and Pankow, 1996; Lorens, 1981). An up to 5-fold increase in DSr is simulated for a 2 order of magnitude increase in growth rate (Nielsen et al., 2013) based on ion-by-ion growth models and non-cave analogue experiments. According to this model, the magnitude of the growth rate dependence depends on the forward and reverse reaction rates, which are sensitive to temperature and solution chemistry. Additionally, in-cave measurements suggest that the DSr increases with increasing calcite $\mathrm{Mg}/\mathrm{Ca}$ ratio. A tripling of calcite $\mathrm{Mg}/\mathrm{Ca}$ from 1.4 to 4.2 mmol mol⁻¹ leads to an 18 % increase in DSr, and a tripling of $\mathrm{Mg}/\mathrm{Ca}$ from 10 to 30 mmol mol⁻¹ leads to an 80 % increase in DSr (Wassenburg et al., 2020). A similar increase in DSr with higher $\mathrm{Mg}/\mathrm{Ca}$, observed in laboratory growth in a seawater-like matrix, is attributed to the increased accommodation of larger Sr ions in the crystal lattice when the lattice is distorted by incorporation of Mg ions which are smaller than Ca (Mucci and Morse, 1983).

The use of $\mathrm{Mg}/\mathrm{Ca}$ (or Sr/Ca) as a quantitative indicator of PCP also requires that the initial drip water $\mathrm{Mg}/\mathrm{Ca}$ attained by karst rock dissolution prior to PCP remain constant for a given drip water site and stalagmite over the time period of interest. Yet, in karst rocks composed of heterogeneous carbonate mineralogy, there is potential for variation in initial drip water trace element to Ca ratios. In karst rocks composed of both dolomite and calcite, the slower dissolution kinetics of dolomite may lead to greater relative dolomite contribution with longer water residence times, leading to higher drip water $\mathrm{Mg}/\mathrm{Ca}$ and higher drip water $\mathrm{Mg}/\mathrm{Sr}$ with longer water residence times (Tremaine and Froelich, 2013; Fairchild and Treble, 2009). In young reef limestone, primary aragonite and high-Mg calcite dissolve more rapidly than diagenetic low-Mg calcite, potentially contributing to temporal evolution of initial, undegassed drip water ratios over time due to progressive meteoric diagenesis of primary phases (Sinclair et al., 2012). Where bedrock is heterogeneous, it can be useful to define the initial (undegassed, without PCP) drip water chemistry as resulting from the mixture of the multiple bedrock components, e.g., the bedrock mixing fraction (Tremaine and Froelich, 2013). In a synthesis of published drip water time series, in 30 out of 32 drip locations (from 11 different cave systems), bedrock mixing fractions remained constant to within 3 %, and the temporal variations in $\mathrm{Mg}/\mathrm{Ca}$ were driven by variable extent of PCP (Tremaine and Froelich, 2013). This compilation suggests that in a large majority of investigated settings, for an individual drip, seasonal and interannual variations in water residence time do not significantly affect the initial $\mathrm{Mg}/\mathrm{Ca}$ attained through karst dissolution. In the cave system from which our example stalagmite records derive, drip water monitoring similarly suggests stable bedrock mixing fractions at each drip location (Kost et al., 2023b).

In monitoring studies, a constant drip water $\mathrm{Mg}/\mathrm{Sr}$ ratio over periods of strongly varying drip rate and water residence time is an indicator of constancy in the proportion of dolomite–calcite dissolution. When partition coefficients of Mg and Sr in speleothems are constant over time, constancy of $\mathrm{Mg}/\mathrm{Sr}$ ratio of speleothems may be a useful indicator that PCP, rather than differential dissolution, is the main process responsible for $\mathrm{Mg}/\mathrm{Ca}$ variations (Tremaine and Froelich, 2013). However, variable $\mathrm{Mg}/\mathrm{Sr}$ in stalagmites may also be caused by strong variations in the partition coefficients of Sr, an interpretation supported by the dependence of stalagmite $\mathrm{Mg}/\mathrm{Sr}$ and inferred DSr on growth rate in many stalagmites (Sliwinski et al., 2023). In such cases, variation in stalagmite $\mathrm{Mg}/\mathrm{Sr}$ ratios does not necessarily indicate variation in the drip water $\mathrm{Mg}/\mathrm{Sr}$ ratios or variation in the dolomite and calcite relative contribution. Thus, we suggest that monitoring of drip water systems may serve as the most meaningful check of the potential stability of the bedrock mixing fraction and initial drip water trace element to Ca ratios.

2.2.2 Calcium isotopes

δ⁴⁴Ca has also been employed as an indicator of PCP, since there is a fractionation of Ca isotopes during the dehydration of the ion for it to be incorporated in the crystal lattice. The lighter isotope desolvates more rapidly and is thereby preferentially incorporated in the calcite lattice (Hofmann et al., 2012). Consequently, with progressive removal of Ca into calcite, the remaining dissolved Ca evolves to an isotopically heavier composition (Owen et al., 2016) (Fig. 2b). The quantitative calculation of f_Ca from calcium isotopes (f_Ca_δCa) is most robust when the Ca isotopic composition of the host rock is known, initial δ⁴⁴Ca from dissolution is constant (i.e., always congruent), and the fractionation factor for Ca isotopes during dehydration and calcite precipitation is constant and known. The fractionation factor may be expressed as α or as Δ_{calcite-dissolved}.

Previous applications of δ⁴⁴Ca in speleothem studies have focused on the Holocene and have monitored cave drip water and farmed calcite to calculate the dissolved calcite fractionation factor in that particular cave setting and drip site (Owen et al., 2016; de Wet et al., 2021). Studies then apply this constant fractionation factor to calculate f_Ca_δCa in stalagmite. For fossil, non-active stalagmites, the fractionation factor cannot be measured in farmed calcite and must be assumed or based on information from farmed calcite in the same or similar cave settings. A summary of field and experimental fractionation factors is given in Table S1 in the Supplement. In one monitoring study, Δ_{calcite-dissolved} of farmed calcite varied among different drips in a modern cave (de Wet et al., 2021). Models of desolvation and attachment during crystal growth suggest that at higher net precipitation rates, the effective fractionation is greater (DePaolo, 2011). This has been observed in non-cave analogue laboratory experiments (Tang et al., 2008b) and simulated in models which suggest that a 2 order of magnitude increase in net precipitation rates leads to a decrease in Δ_{calcite-dissolved} from −0.75 ‰ to −1.45 ‰ (Mills et al., 2021). According to this model, the magnitude of the growth rate dependence – specifically the absolute range of growth rate at which Δ_{calcite-dissolved} varies strongly – depends on the forward and reverse reaction rates, which are sensitive to temperature and solution chemistry (DePaolo, 2011). For a given growth rate, lower temperatures strengthen the water solvation structure, leading to greater fractionation. A laboratory study suggests that a 10^∘ cooling leads to a Δ_{calcite-dissolved} decrease of 0.17 ‰ (Tang et al., 2008b). Yet over a seasonal 7.5 ^∘C cave air temperature cycle in Heshang Cave, no seasonal difference in Δ^44–40Ca was resolved within analytical error (Owen et al., 2016).

2.2.3 Previous comparisons of PCP indicators

Both δ⁴⁴Ca and $\mathrm{Mg}/\mathrm{Ca}$ have been simultaneously employed to study Holocene stalagmites (HS4 in Heshang Cave) (Owen et al., 2016; Li et al., 2018) and last interglacial stalagmites from northern India (Magiera et al., 2019). These studies report good quantitative agreement in estimated f_Ca_δCa and f_Ca_MgCa. Relative to glacial–interglacial transitions, the Holocene and last interglacial experienced more stable temperatures and potentially also more stable drip water initial oversaturation, with both factors potentially contributing to constant calcite water Δ⁴⁴Ca fractionation factors. Heshang Cave contains dolomite host rock, and varying water residence times could potentially alter bedrock mixing fraction, altering the initial $\mathrm{Mg}/\mathrm{Ca}$ of drip water prior to degassing. However, if this process were significant, it would lead to deviation in the f_Ca calculated from $\mathrm{Mg}/\mathrm{Ca}$ compared to that calculated from δ⁴⁴Ca. The consistency of f_Ca estimates from $\mathrm{Mg}/\mathrm{Ca}$ and δ⁴⁴Ca suggests that variations in water–rock contact times did not result in appreciable variation in the bedrock mixing fraction and initial $\mathrm{Mg}/\mathrm{Ca}$ from dissolution.

2.3 Limitations of the Hendy test for degassing correction

The sampling of calcite precipitated from the same initial drip water but with a progressive degree of CO₂ degassing and calcite removal has often been attempted through extraction of samples in a single growth layer at successive distances along the growth axis (Hendy, 1971). In theory, the evolution of $\mathrm{Mg}/\mathrm{Ca}$ and δ¹³C could be examined along a growth layer. However, in practice it is difficult and often impossible to follow a single growth layer laterally along the stalagmite, especially since growth layer thickness decreases with increasing distance from the main growth axis (Dorale and Liu, 2009). Furthermore, simulations suggest that for a drip interval from the 1960s, a flow distance in excess of 3 cm from the main axis is required to generate even a 1 ‰ enrichment of δ¹³C through PCP and CO₂ degassing (Mühlinghaus et al., 2009). Finally, because the drip waters experiencing a lot of degassing are less saturated as they flow off axis than drips with little degassing, the off-axis growth may be biased towards times of low degassing and low PCP. For these reasons, it is often impractical to test relationships between δ¹³C and $\mathrm{Mg}/\mathrm{Ca}$ using the Hendy test.

3 Methods

3.1 Geochemical models of speleothems

We employ CaveCalc for simulations of the equilibrium fractionation of carbon isotopes. The CaveCalc package employs the PHREEQC geochemical model to simulate the initial dissolution of karst limestone in equilibrium with a given volume of soil gas of specified pCO₂ and δ¹³C and the subsequent equilibration of this solution with a cave atmosphere of specified pCO₂, leading to precipitation of CaCO₃. Relevant for this study, the CaveCalc package calculates the initial δ¹³C of bicarbonate and initial Ca concentration of the drip water resulting from karst dissolution and the stepwise evolution of both parameters as well as the δ¹³C of the precipitated calcite as the solution equilibrates with the cave atmosphere. These CaveCalc simulations allow us to relate the Rayleigh-driven progressive enrichment in δ¹³C of bicarbonate with the progressive depletion of Ca in the drip water in equilibrium conditions. CaveCalc employs the temperature-dependent calcite–HCO${}_{\mathrm{3}}^{-}$ fractionation as calculated by Mook and Rozanski (2001).

Independent from CaveCalc, a modified version of the I-STAL model (Stoll et al., 2012) is used to simulate PCP variation resulting from changes in initial drip water saturation state and changes in drip interval. The effect of variations in initial drip water Ca, temperature, and drip interval are explored at conditions of cave pCO₂ fixed at ventilated, near interglacial atmospheric concentrations (300 ppm). In I-STAL calculations, the temperature sensitivity of D_Mg follows Day and Henderson (2013).

3.2 Analysis of fossil stalagmites

We compile existing data and report new data on nine stalagmites from NW Spain with growth periods during the Holocene, during late MIS 5, and during the penultimate deglaciation (Tables S2 and S3). Reported stalagmites are from La Vallina Cave, whose setting and lithology are described in a detailed previous monitoring study (Kost et al., 2023b). The cave is hosted in Carboniferous limestones of the Barcaliente Formation. Because the section dips at 80^∘, different sectors of the cave sample stratigraphically different portions of the limestone, which have significant heterogeneity in $\mathrm{Mg}/\mathrm{Ca}$ and some heterogeneity in Sr $/$ Ca and other trace elements. Thus, different drip locations can feature different initial trace element ratios due to congruent dissolution of limestones of differing composition. Despite site-to-site heterogeneity, individual drips monitored over an 18-month period show very limited temporal variation in $\mathrm{Mg}/\mathrm{Sr}$ ratios despite order of magnitude differences in drip rate, suggesting that in this cave, individual drips sample a relatively stable bedrock dissolution source and maintain a constant bedrock mixing fraction. For most stalagmites, age models are previously published, including those for GAE, GAL, and GLO (Stoll et al., 2013, 2015), as well as GAR and GUL (Stoll et al., 2022). For BEL, GLD, and ROW, age model constraints are given in Table S2. The slowly growing fossil stalagmites consist of dense calcite and show no evidence of columnar porous fabrics. Stalagmite calcite for GAR and GAL consist of predominantly columnar compact to columnar open fabrics (Sliwinski and Stoll, 2021). Similar fabrics are confirmed in GUL and GAE (Sliwinski et al., 2023). Samples ROW, BEL, and NYM exhibit growth rates (12–40 µm yr⁻¹) similar to GAR, GAL, GUL, and GAE and feature similar dense, nonporous macroscopic textures. The much more slowly growing GLO and GLD likewise feature dense, compact calcite comparable to sample GLA with a similar growth rate and are described as columnar and columnar open (Kost et al., 2023a, b).

For geochemical analyses, we sampled approximately 1 mg of powder. Trace element ratios ($\mathrm{Mg}/\mathrm{Ca}$, Sr $/$ Ca) were determined by dissolution of powders in 2 % HNO₃ and analysis on an Agilent 8800 inductively coupled mass spectrometer (ICP-MS) at ETH Zurich in collision mode. On splits of the same powders, we measured δ¹³C and δ¹⁸O using a Thermo Fisher Scientific Gas Bench II with methods previously described and precision of 0.08 ‰ for both isotopes (Breitenbach and Bernasconi, 2011).

In eight stalagmites, we selected several intervals of contrasting $\mathrm{Mg}/\mathrm{Ca}$ to additionally measure δ⁴⁴Ca. From the same aliquot used for $\mathrm{Mg}/\mathrm{Ca}$ analysis, ∼500 µg of powder was dissolved in distilled 2M HNO₃. An automated Ca–Sr separation method (PrepFAST MC, Elemental Scientific, Omaha, NE, USA) was used to separate Ca from Sr, Mg, and other matrix elements to avoid isobaric interferences with the multi-collector inductively coupled mass spectrometer (MC-ICP-MS). SRM 915b solutions were purified in parallel with the samples to provide a combined column chemistry and analytical accuracy assessment. Ca isotope ratios were determined using a Nu Instruments MC-ICP-MS (the University of Oxford) with a desolvating nebulizer as described previously (Reynard et al., 2011). Solutions were run at 10±1 ppm concentration, and the samples were measured with standard sample bracketing. A minimum of five analyses were conducted on each aliquot. δ⁴⁴/⁴⁰Ca is reported normalized to NIST SRM 915a and was calculated from measured ${\mathit{\delta }}^{\mathrm{44}/\mathrm{42}}$Ca as ${\mathit{\delta }}^{\mathrm{44}/\mathrm{40}}$Ca = ${\mathit{\delta }}^{\mathrm{44}/\mathrm{42}}$Ca ⋅ ((43.956–39.963)/(43.956–41.959)) (Hippler et al., 2003). To determine accuracy and external precision, secondary standards NIST SRM 915b and HPSnew (in-house standard) were used. Uncertainty in Ca isotope data is quoted as the t-distribution-derived 95 % confidence interval on the mean of repeat measurements calculated using either the standard deviation or all repeat measurements on each sample.

Additionally, we incorporate published δ¹³C, f_Ca_δCa, and $\mathrm{Mg}/\mathrm{Ca}$ data from Heshang stalagmite HS4 (Owen et al., 2016; Noronha et al., 2014).

3.3 Calculation of f_Ca from δ⁴⁴Ca, $\mathrm{Mg}/\mathrm{Ca}$, and Sr $/$ Ca

$\mathrm{Mg}/\mathrm{Ca}$ measurement is much faster than δ⁴⁴Ca, and therefore it is common to have $\mathrm{Mg}/\mathrm{Ca}$ measured for every δ¹³C_init measured in the stalagmite. We therefore carry out examples employing $\mathrm{Mg}/\mathrm{Ca}$ as the preferred measurement for deriving a continuous record of δ¹³C_init. At the same time, using δ⁴⁴Ca to derive the PCP-corrected δ¹³C_init may be more robust because the δ⁴⁴Ca of the initial solution can be derived from the measured bedrock, and the isotopic composition of the bedrock is expected to be more homogeneous than $\mathrm{Mg}/\mathrm{Ca}$, leading to less uncertainty in the initial solution, and because Ca is a major element.

We calculate f_Ca_δCa from δ⁴⁴Ca measurements using a constant bedrock δ⁴⁴Ca equal to average bedrock (0.58 ‰) reported previously (Lechleitner et al., 2021). Use of the highest or lowest measured bedrock δ⁴⁴Ca leads to a ±0.05 range in absolute f_Ca_δCa values. Because bedrock δ⁴⁴Ca is not expected to change at a given location over time, we do not expect this factor to contribute to temporal variations in δ⁴⁴Ca. The Δ_{calcite-dissolved} for these fossil stalagmites is not independently constrained. Therefore, we complete a sensitivity analysis using the range of Δ_{calcite-dissolved} observed in laboratory calcite growth and ion-by-ion growth models. Table S1 lists the four values of Δ_{calcite-dissolved} which we evaluate.

Inference of the f_Ca_MgCa from $\mathrm{Mg}/\mathrm{Ca}$ using the Rayleigh formula requires knowledge of the partition coefficient and the initial drip water $\mathrm{Mg}/\mathrm{Ca}$, which are both difficult to infer for fossil stalagmites.

Because the D_Mg is very low and the exponent in the Rayleigh formula (Eq. 3) is therefore very close to −1, the following provides a close approximation for f_Ca:

$$\begin{array}{}\text{(4)}& f_{\mathrm{Ca}\mathrm{\_}\mathrm{MgCa}}={\displaystyle \frac{{\mathrm{MgCa}}_{\mathrm{initial}}}{{\mathrm{MgCa}}_{\mathrm{sample}}}}.\end{array}$$

For a D_Mg of 0.025, this approximation deviates from the Rayleigh equation by 0.01 at f_Ca=0.36 and deviates by lesser degrees for higher f_Ca_MgCa (e.g., dashed gray line in Fig. 2a).

Because of heterogeneity in cave bedrock, we calculate f_Ca_MgCa assuming there may be differences in the initial drip water $\mathrm{Mg}/\mathrm{Ca}$ for each stalagmite location. Time series data for each stalagmite indicate a range of $\mathrm{Mg}/\mathrm{Ca}$ values. In a first approach, we assume that the minimum $\mathrm{Mg}/\mathrm{Ca}$ of a stalagmite corresponds to a situation of negligible degassing and PCP, that the D_Mg is constant, and therefore that the numerator can be approximated by the minimum $\mathrm{Mg}/\mathrm{Ca}$ for the stalagmite:

$$\begin{array}{}\text{(5)}& f_{\mathrm{Ca}\mathrm{\_}\mathrm{MgCa}}={\displaystyle \frac{{\mathrm{MgCa}}_{\min }}{{\mathrm{MgCa}}_{\mathrm{sample}}}}.\end{array}$$

By default in this approximation, the maximum f_Ca_MgCa calculated for any stalagmite is 1. Therefore, we consider the consequences for calculated f_Ca_MgCa if the measured minimum $\mathrm{Mg}/\mathrm{Ca}$ in the stalagmite corresponds to precipitation from a solution which has already experienced PCP. We assess this impact with a scaling factor B (between 0.5 and 1) to approximate the initial bedrock dissolution $\mathrm{Mg}/\mathrm{Ca}$ from the minimum $\mathrm{Mg}/\mathrm{Ca}$ measured in the stalagmite and apply a constant B for the stalagmite:

$$\begin{array}{}\text{(6)}& {\mathrm{MgCa}}_{\mathrm{initial}}={\mathrm{MgCa}}_{\min }\cdot B.\end{array}$$

f_Ca_SrCa may also be calculated from Sr $/$ Ca measurements in an approach analogous to $\mathrm{Mg}/\mathrm{Ca}$. Because of the higher DSr, Eq. (5) is a less accurate approximation for Sr; e.g., for a DSr of 0.1, there would be a 0.04 deviation of the f_Ca_SrCa by Eq. (5) (f_Ca=0.30) compared to the Rayleigh formula at f_Ca_SrCa = 0.265.

Finally, we also evaluate the possibility of temporal variation in D_Mg in a given stalagmite, testing the scale of variation in D_Mg which would be consistent with f_Ca_δCa estimations from δ⁴⁴Ca. In this f_Ca(fit), the curvature or slope of the relationship in Fig. 2a is modified by an attenuation factor AF.

$$\begin{array}{}\text{(7)}& f_{\mathrm{Ca}}\left(\mathrm{fit}\right)=B-\left({\displaystyle \frac{\left(B-\frac{{\mathrm{MgCa}}_{\mathrm{initial}}}{{\mathrm{MgCa}}_{\mathrm{sample}}}\right)}{\mathrm{AF}}}\right)\end{array}$$

The relative change in D_Mg needed for the fit is given as

$$\begin{array}{}\text{(8)}& {\displaystyle \frac{D_{\mathrm{Mg}}\left(\mathrm{fit}\right)}{D_{\mathrm{Mg}}^{\mathrm{o}}}}={\displaystyle \frac{f_{\mathrm{Ca}}\left(\mathrm{fit}\right){\mathrm{MgCa}}_{\mathrm{init}}^{\mathrm{o}}}{f_{\mathrm{Ca}}^{\mathrm{o}}{\mathrm{MgCa}}_{\mathrm{init}}\left(\mathrm{fit}\right)}},\end{array}$$

where $f_{\mathrm{Ca}}^{\mathrm{o}}$ indicates the f_Ca_MgCa for the full scenario, with AF = 1 and B=1. This AF gives a linear increase in D_Mg with $\mathrm{Mg}/\mathrm{Ca}$; however, other forms of dependence could also fit the data, since we have δ⁴⁴Ca for only two points for most of the analyzed stalagmites.

3.4 Estimation of δ¹³C_init from δ¹³C_meas and estimated f_Ca

We use $\mathrm{Mg}/\mathrm{Ca}$ to derive continuous PCP-corrected δ¹³C_init, but we employ the few existing δ⁴⁴Ca measurements for each stalagmite to validate and adjust the precise relationship between $\mathrm{Mg}/\mathrm{Ca}$ and PCP yielding f_Ca(fit) in order to achieve a more robust estimate of δ¹³C_init. In detail, we use the $\mathrm{Mg}/\mathrm{Ca}$ to calculate f_Ca in four different ways: f_Ca_MgCa from the minimum stalagmite $\mathrm{Mg}/\mathrm{Ca}$ and constant D_Mg (termed “full” with both B and AF = 1) and additionally from three other f_Ca(fit) values using Eq. (7) (termed A1, A2, and A3) in which the parameters B and AF are adjusted to provide f_Ca_MgCa compatible with f_Ca_δCa. For each stalagmite, the values of B and AF employed for A1, A2, and A3 are given in Table 2.

Table 2 Parameters for elaboration of f_Ca based on δ⁴⁴Ca and $\mathrm{Mg}/\mathrm{Ca}$.

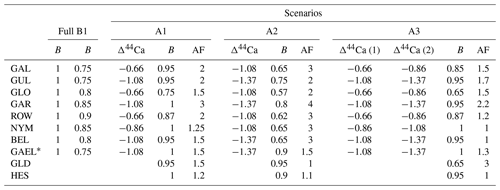
^* Fit with $\mathrm{Mg}/\mathrm{Ca}$ min substituted by the $\mathrm{Mg}/\mathrm{Ca}$ 5th percentile value of 6 mmol.

For each of these four possible f_Ca scenarios, we additionally calculate δ¹³C_init using three possible values of the degassing slope (A) in Eq. (3): −5 ‰, −8 ‰, and −11 ‰ (e.g., in Fig. 2b). This exercise illustrates the consequences of a range of possible equilibrium and disequilibrium fractionation behaviors.

4 Results

4.1 PCP indicators in stalagmites

Within the subsamples measured for both $\mathrm{Mg}/\mathrm{Ca}$ and δ⁴⁴Ca, the δ⁴⁴Ca of measured samples ranges from −0.49 to +0.42. In all of these subsets, the $\mathrm{Mg}/\mathrm{Ca}$ and δ⁴⁴Ca positively correlate (Fig. 3). In all but two stalagmites, Sr $/$ Ca and δ⁴⁴Ca positively correlate. In GUL and GAL, Sr $/$ Ca and δ⁴⁴Ca negatively correlate.

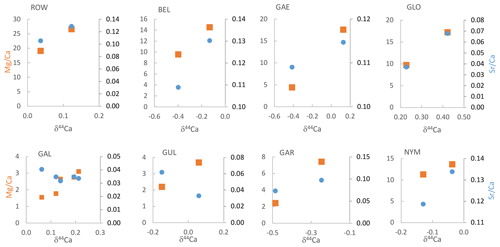
Figure 3 $\mathrm{Mg}/\mathrm{Ca}$ (orange squares on left axes, in mmol mol⁻¹) and Sr $/$ Ca (blue circles on right axes, mmol mol⁻¹) vs. δ⁴⁴Ca (‰) for paired samples from each stalagmite.

In the full geochemical sampling of the nine examined speleothems from La Vallina Cave, $\mathrm{Mg}/\mathrm{Ca}$ variation in a given stalagmite ranges between 1.7-fold and 3.5-fold, with the exception of GAE (12.2-fold range). Six of the nine stalagmites have $\mathrm{Mg}/\mathrm{Ca}$ variations of 2-fold to 3-fold (Table S3). The 1.7- to 3.5-fold range could be fully explained by PCP even with no change in D_Mg, since a 3.5-fold range requires the initial drip water Ca concentration to be greater than 3.5 times the saturation Ca concentration for the cave conditions. Changes in the $\mathrm{Mg}/\mathrm{Ca}$ of the initial drip water prior to degassing from varying bedrock mixing fraction or an enhanced $\mathrm{Mg}/\mathrm{Ca}$ ratio due to increased fluid inclusion density are not required to attain the range of $\mathrm{Mg}/\mathrm{Ca}$ in seven of the eight of the stalagmites. With the exception of Holocene GAL, minimum $\mathrm{Mg}/\mathrm{Ca}$ generally occurs during the glacials and stadials (Table S3). In GAE, the basal 0.5 cm of the stalagmite features an unusually low $\mathrm{Mg}/\mathrm{Ca}$ ratio, which is 12-fold lower than the maximum ratio. If driven solely by PCP, this range would require drip water Ca in excess of 300 ppm during warm periods to drive such a large range in PCP. In this stalagmite, the $\mathrm{Mg}/\mathrm{Ca}$ of this basal portion may reflect a different initial state of the fracture network and mineral surface age over time. GAE was sampled growing on a large block fallen from the ceiling, and first growth after block emplacement may reflect flow through newly opened fracture networks.

The total range in Sr $/$ Ca across each speleothem is between 1.7-fold and 4-fold in all speleothems except GAE (6) (Table S3). The strongest positive correlation between Sr $/$ Ca and $\mathrm{Mg}/\mathrm{Ca}$ is found in GLO, GLD, and BEL. Strong negative correlation occurs in GUL, and modest negative correlation occurs in GAL and GAR.

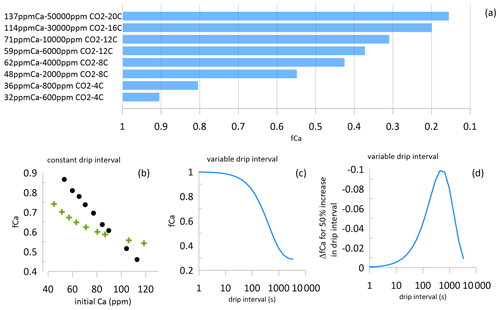
Figure 4 (a) The degree of PCP which is possible based on the initial drip water saturation state simulated by CaveCalc for the initial Ca (ppm), soil pCO₂ for 150 L gas volume, and reaction temperature. The lowest f_Ca is defined as that which would correspond to an instantaneous calcite deposition rate equivalent to 4 µm yr⁻¹, as simulated in I-STAL with Dreybrodt (Romanov et al., 2008) kinetics. (b) The f_Ca simulated for a fixed drip interval of 300 s but variable initial saturation (indexed by Ca concentration). In one case shown with circles, the variable initial Ca corresponds to a progressive decline in temperature from 18 to 5 ^∘C, simulating soil pCO₂ limited by temperature. In a second case shown with green crosses, variable initial Ca corresponds to constant temperature, simulating soil pCO₂ limited by moisture at constant temperature. Simulations assume Dreybrodt kinetics (Romanov et al., 2008) executed in I-STAL with a PCP enhancement factor of 3. (c, d) Illustration of the nonlinearity of PCP relative to drip interval, simulated with Dreybrodt kinetics at a temperature of 12 ^∘C, initial Ca 90 ppm, d=0.01, and a PCP enhancement factor of 3. The drip interval range of maximum PCP sensitivity will vary with modeled temperature and PCP enhancement parameters.

4.2 Calculated f_Ca from PCP indicators

4.2.1 Expected ranges in f_Ca

Because highly oversaturated drip waters have a greater potential for PCP than minimally oversaturated drip waters, f_Ca can vary over a wider range in settings with high oversaturation (e.g., warm climates with higher soil CO₂ and initial drip water Ca; Fig. 4a). In contrast, minimum degassing and high f_Ca will be favored by a very low oversaturation state of the drip, even for slow drip rates (Fig. 4a and b). Minimal degassing is also favored by colder temperatures. In the middle and high latitudes, low oversaturation of drip waters and low PCP are more likely during cold glacial or stadial time periods when CO₂ in soils is depressed due to low temperatures (e.g., Fig. 4b). We consider this expected association of colder climates and higher f_Ca in the quantitative interpretation of f_Ca indices. Alternatively, when soil pCO₂ and drip water initial saturation are regulated by the moisture limitation of soils, then f_Ca varies over a narrower range at a constant drip interval (Fig. 3b). We simulate f_Ca as low as 0.15 in the case of an initial Ca concentration of 137 ppm.

In addition to the oversaturation state, PCP is also dependent on the degassing time. PCP can occur in air-filled voids above the cave as well as on walls and ceilings of the cave prior to the landing of drip water on the studied stalagmite. Here, we discuss the integrated PCP, regardless of where along the flow path PCP has occurred. The susceptibility of a given speleothem to PCP may depend on the geometry of the flow path. Temporal variations in PCP in a given stalagmite are expected to depend on the flow (e.g., drip rate) as well as on the oversaturation. Because the relationship between drip interval and PCP is known to be highly nonlinear (Fig. 4c and d), different coeval stalagmites often have asynchronous variations in PCP indicators or contrasting magnitudes of PCP variation.

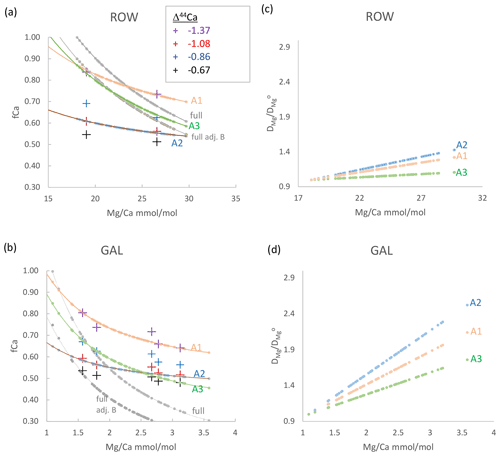
Figure 5 (a, b) f_Ca_δCa (crosses) as well as f_Ca_MgCa and f_Ca(fit) (both with lines) vs. measured $\mathrm{Mg}/\mathrm{Ca}$. Crosses show f_Ca_δCa calculated from δ⁴⁴Ca according to different Δ⁴⁴Ca fractionation factors, vertically ordered according to fractionation factor as given in the legend. Gray curves show calculation of f_Ca_MgCa from $\mathrm{Mg}/\mathrm{Ca}$ assuming $\mathrm{Mg}/\mathrm{Ca}$_min reflects undegassed drip water (“full”, upper gray line) or that undegassed drip water is lower than the minimum $\mathrm{Mg}/\mathrm{Ca}$ by a factor of 0.65 to 0.95 (“full adj. b”, lower gray line; value in Table 2). Pink, blue, and green lines illustrate scenarios A1, A2, and A3, which are potential relationships between f_Ca(fit) and $\mathrm{Mg}/\mathrm{Ca}$ consistent with f_Ca_δCa estimates according to Eq. (7) and fit parameters in Table 2. (c, d) The variation in D_Mg implied by scenarios in (a) and (b), calculated as in Eq. (8) and assuming constant congruent bedrock dissolution to yield a constant initial undegassed $\mathrm{Mg}/\mathrm{Ca}$ ratio of drip water. A 10 ^∘C temperature increase would cause $D/D_{\mathrm{o}}$ to reach 1.22 according to laboratory experiments (Day and Henderson, 2013).

4.2.2 δ⁴⁴Ca

The absolute f_Ca_δCa calculated from a given δ⁴⁴Ca depends on the choice of the calcite dissolved fractionation factor (Table S1). Given bedrock estimated at 0.58 ‰, the measured δ⁴⁴Ca in some samples would imply f_Ca_δCa higher than 1 for the Δ⁴⁴Ca fractionation factor corresponding to the slowest laboratory growth rates (−0.66). For a given stalagmite, choosing a Δ⁴⁴Ca corresponding to slower laboratory growth rates (−0.66, −0.86) yields a wider range of calculated f_Ca_δCa than choosing Δ⁴⁴Ca corresponding to faster laboratory growth rates (−1.08, −1.37). The largest range in f_Ca_δCa is found in GAE, and for a given Δ⁴⁴Ca, the lowest average f_Ca_δCa values are in GAL and GLO (Fig. 5, Appendix A). Because the fractionation factor depends on growth rate and the solution characteristics, it may not be constant throughout the growth period of a stalagmite if there are significant changes in the growth conditions. For a given stalagmite, a slower growth rate during periods of low initial drip water oversaturation might be characterized by less fractionation, e.g., a Δ⁴⁴Ca which is closer to 0, compared to periods of stalagmite growth from solutions with greater oversaturation.

4.2.3 $\mathrm{Mg}/\mathrm{Ca}$ and Sr $/$ Ca

Using Eq. (4) and the minimum $\mathrm{Mg}/\mathrm{Ca}$ for each stalagmite as an estimation of a nondegassed f_Ca_MgCa = 1, the high-$\mathrm{Mg}/\mathrm{Ca}$ stalagmites BEL and ROW exhibit a range in f_Ca_MgCa from 0.95 to 0.6 (Fig. 5; Appendix A) and GLO exhibits a similar range (Appendix A). As mentioned previously, in GAE, the total $\mathrm{Mg}/\mathrm{Ca}$ range exceeds that expected from PCP if the minimum $\mathrm{Mg}/\mathrm{Ca}$ in the basal growth phase is used. We complete a sensitivity analysis calculating f_Ca_MgCa of GAE with the 5th percentile value rather than minimum, which is equivalent to the minimum $\mathrm{Mg}/\mathrm{Ca}$ observed in the upper 82 cm of the stalagmite, including the period of interest presented here. GAR exhibits the highest range in f_Ca_MgCa estimated from measured $\mathrm{Mg}/\mathrm{Ca}$. A smaller range of f_Ca_MgCa and the lowest f_Ca_MgCa are calculated from Eq. (6) when the B factor is <1.

4.2.4 Comparison of f_Ca estimations

We explored which combinations of Δ⁴⁴Ca and assumptions of B and AF lead to coherent estimations of f_Ca_δCa and f_Ca_MgCa of yield f_Ca(fit). We find that in many stalagmites, with AF = 1 the $\mathrm{Mg}/\mathrm{Ca}$ leads to a wider range in f_Ca_MgCa than f_Ca_δCa (e.g., Figs. 5 and S1). Covariation in D_Mg with $\mathrm{Mg}/\mathrm{Ca}$ is one process which could cause AF to be greater than 1.

Estimates of f_Ca_δCa and f_Ca_MgCa for stalagmites BEL, ROW, and NYM are consistent with no systematic variation in D_Mg (i.e., an AF ≈ 1) if the calcite dissolved fractionation factor Δ⁴⁴Ca varies by 0.2 ‰ between the sample of lowest and highest PCP (scenario A3; Fig. 5, Table 2). Alternatively, if Δ⁴⁴Ca is constant (scenarios A1, A2), then f_Ca_δCa and f_Ca_MgCa estimates are consistent only when AF is 1.25 to 3, which implies a systematic variation in D_Mg with $\mathrm{Mg}/\mathrm{Ca}$ (Fig. 5). For other stalagmites (Fig. S1), if the calcite dissolved fractionation factor Δ⁴⁴Ca varies by 0.2 ‰ between the sample of lowest and highest PCP (Fit A3), some variation in D_Mg is still required (AF 1.5–2.2); for the assumption of constant Δ⁴⁴Ca in each stalagmite, a larger range of AF is required (1.5 to 3, with a single higher value of 4 required for GAR). For GAE, only a $\mathrm{Mg}/\mathrm{Ca}$ min of 6 mmol mol⁻¹, which is the 5th percentile value, enabled calculation of a PCP factor consistent with δ⁴⁴Ca.

The concomitant changes in D_Mg for these scenarios range from 1 (e.g., constant D_Mg) to over a 2.5-fold increase in D_Mg over the range of $\mathrm{Mg}/\mathrm{Ca}$ in the stalagmite (Fig. 5). GAL and GAR have the most significant increases in D_Mg, whereas BEL, NYM, and ROW feature the lowest. Most scenarios require an increase in D_Mg larger than that expected from reasonable (5 to 10^∘) temperature dependence of D_Mg alone; for example, according to an experimental cave analogue calculation, a 10^∘ warming would lead to a D_Mg/D_Mg of 1.22 (Day and Henderson, 2013). Holocene stalagmite GAL features a large simulated range in D_Mg despite only limited regional temperature change.

We acknowledge that we have limited f_Ca_δCa for each stalagmite, and therefore our particular scenarios are intended to illustrate potential compatible solutions but do not cover all the possible ranges. The variation in D_Mg may be exaggerated because datasets with higher numbers of paired δ⁴⁴Ca and $\mathrm{Mg}/\mathrm{Ca}$ such as GAL show coherency but also some scatter around this relationship, which may be interpreted as a steeper or shallower relationship in our limited dataset.

4.3 Estimation of δ¹³C_init in measured speleothems

Following the use of scenarios A1, A2, and A3 to generate the f_Ca used in Eq. (3), we generated time series records of δ¹³C_init for eight stalagmites spanning three time periods of interest – the late glacial to the Holocene, the penultimate glacial to the interglacial transition, and a stadial event occurring between 87 and 85 ka BP. For clarity in time series figures, we illustrate the three scenarios only for the −8 ‰ degassing slope. For one scenario (A1) we illustrate the range in δ¹³C_init for degassing slopes from −5 ‰ to −11 ‰. This range is variable over time in a given stalagmite because the choice of degassing slope (−5 ‰, −8 ‰, −11 ‰) impacts the δ¹³C_init significantly for low f_Ca and to a lesser degree for higher f_Ca.

We begin by comparing the range of δ¹³C_init calculated for growth during interglacials and present the time series trends for selected individual stalagmites.

4.3.1 Interglacials

The median δ¹³C_init among interglacial samples (here averaging 9–4 ka and 129 to 125 ka) is strongly dependent on the degassing fractionation slope A (Fig. 6). For the three f_Ca scenarios (A1, A2, A3) in which $\mathrm{Mg}/\mathrm{Ca}$-based f_Ca is attenuated for consistency with δ⁴⁴Ca, with a −5 ‰ slope, median δ¹³C_init ranges from −9 ‰ to −13 ‰, and for the −11 ‰ slope, δ¹³C_init is in the −11.5 ‰ to −16 ‰ range. For scenario full, the −5 ‰ and −8 ‰ δ¹³C_init overlap with modern nondegassed calcite predicted from δ¹³C_DIC measurements, whereas for −11 ‰, scenarios A1 and full lead to δ¹³C_init which is 5 ‰ to 7 ‰ more negative than modern δ¹³C calcite of undegassed drip. Use of the “full” f_Ca scenario with no attenuation of the f_Ca from $\mathrm{Mg}/\mathrm{Ca}$ and the slope of −11 ‰ leads to extreme negative δ¹³C_init for GAR, GAL, GUL, and GAE but not BEL or GLD. With this f_Ca scenario, a slope of −5 ‰ or −8 ‰ yields δ¹³C_init within the ranges described above.

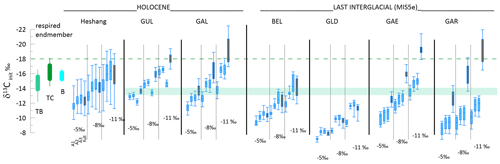
Figure 6 Comparison of calculated δ¹³C_init for interglacial samples spanning 9 to 5 ka and 129 to 125 ka with the calculated composition for calcite for modern δ¹³C_DIC composition under forested portions of the cave (green horizontal band), as well as the calcite calculated for limited degassing of drip waters equilibrated with soil pCO₂ (10 000 ppm) of composition consistent with the δ¹³C of respired end-members in temperate broadleaf (TB), temperate conifer (TC), and boreal (B) ecosystems (Pataki et al., 2003) illustrated as vertical ranges. For each stalagmite, the whisker plots show distribution of δ¹³C_init for three f_Ca scenarios consistent between $\mathrm{Mg}/\mathrm{Ca}$ and δ⁴⁴Ca (A1, A2, A3; blue shading) as well as the f_Ca derived from the full unadjusted $\mathrm{Mg}/\mathrm{Ca}$ record (gray shading) for three different degassing slopes. Shown are the median as well as the upper and lower quartile, and whiskers show 99 % and 1 % for the four different f_Ca scenarios and three different slopes of degassing fractionation. The dashed green line gives the upper limit of calcite expected to form from drip waters in the temperate conifer ecosystem; interglacial δ¹³C_init is not expected to be more negative than this value.

4.3.2 Three coeval time series during MIS 5b–c

Three stalagmites spanning the 94 to 82 ka interval feature contrasting trends in measured δ¹³C (Fig. 7). An excursion to more positive measured δ¹³C is noted around 89 to 86 ka BP in GLO, the stalagmite with the most constant $\mathrm{Mg}/\mathrm{Ca}$. However, the brief positive anomaly is not well expressed in measured δ¹³C GAE because of a high-amplitude long-term trend over this time interval. Yet, in δ¹³C_init, all three stalagmites show a similar positive anomaly. The δ¹³C_init with a slope of −8 or −11, for all f_Ca scenarios, leads to a double-structure positive δ¹³C anomaly at 89 to 86 ka and a constant background δ¹³C_init from 94 to 82 ka. The δ¹³C_init for these simulations in GAE exhibits a more similar trend to that of GLO and ROW.

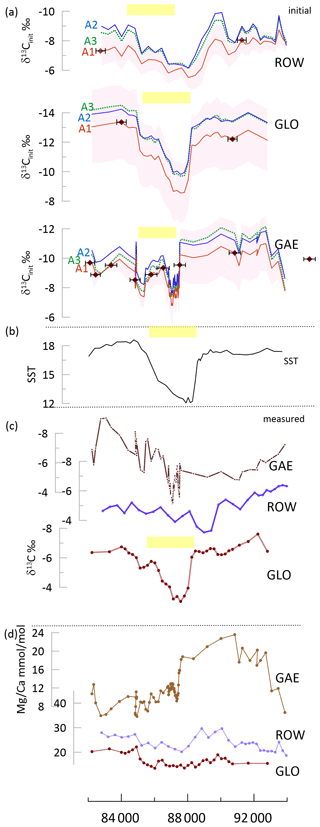
Figure 7 Stadial event in the time interval 94 to 82 ka in ROW, GLO, and GAE. (a) The δ¹³C_init for three f_Ca scenarios (A1 and A2 solid lines, A3 dashed line) for each stalagmite; the line shows the result for a degassing fractionation slope of −8 ‰, and shading for the A1 scenario shows the range using other degassing slopes of −5 ‰ (more positive) and −11 ‰ (more negative). Diamond symbols on the red curve indicate the position of U $/$ Th dates and the uncertainty in the age. (b) The SST record from the Iberian Margin (Martrat et al., 2007). (c) The measured δ¹³C for the three stalagmites; small symbols indicate measured samples. (d) $\mathrm{Mg}/\mathrm{Ca}$ for the three stalagmites; small symbols indicate measured samples. A box-and-whisker plot is given in Fig. S2. In (a) through (c), yellow bars highlight the inferred position of the stadial cooling event in each record, given uncertainty in the age model.

A comparison of the range of f_Ca in each scenario, the resulting range in δ¹³C_init, and the correlation of measured δ¹³C with the δ¹³C_init is given in Fig. S2. The most pronounced change between measured δ¹³C and the δ¹³C_init is simulated for GAE, in which correlation of δ¹³C_init and measured δ¹³C is below 0.2 for all degassing slopes except −5 ‰. The case of GAE contrasts with that of GLO, in which the correlation remains above 0.5 for all scenarios consistent with δ⁴⁴Ca (e.g., scenarios A1, A2, and A3). This reflects the greater range in f_Ca for GAE than for GLO.

4.3.3 Deglaciation

For the Holocene stalagmite GUL, there is a significant temporal trend of $\mathrm{Mg}/\mathrm{Ca}$ increase from the Bølling–Allerød (B/A) into the Holocene (Figs. 8 and S3). Measured δ¹³C was comparable in the B/A and the Holocene, but for all scenarios and degassing slopes, the δ¹³C_init exhibits greater contrast between the early glacial and the Holocene, as the calculated δ¹³C_init of the Bølling–Allerød (B/A) is more positive than that of the Holocene.

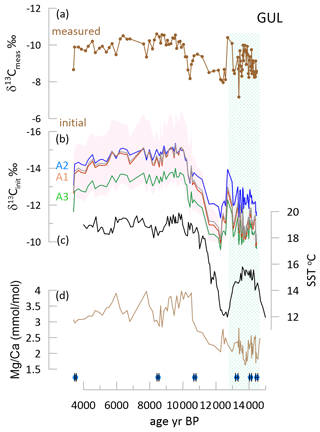
Figure 8 Glacial to Holocene transition in GUL. (a) The measured δ¹³C for GUL. (b) The δ¹³C_init for three f_Ca scenarios; the line shows the result for a degassing fractionation slope of −8 ‰, and shading for the A3 scenario shows the range using other degassing slopes of −5 ‰ (more positive) and −11 ‰ (more negative). (c) The alkenone-based SST for the southern Iberian Margin (Cacho et al., 1999). (d) the $\mathrm{Mg}/\mathrm{Ca}$ for GUL. At the base the position of U $/$ Th age points and their uncertainty are indicated with diamond symbols. A box-and-whisker plot is given in Fig. S3. Green shading highlights the B/A period.

A similar steepening of the temporal trend in δ¹³C_init occurs for stalagmite GLD spanning the penultimate deglaciation. GLD measured δ¹³C features a very stable average value punctuated by two positive anomalies, while $\mathrm{Mg}/\mathrm{Ca}$ exhibits a decrease over the deglaciation. The δ¹³C_init features a significant negative shift between 136 and 130 ka. With this significant change in trends among δ¹³C_init and measured δ¹³C, correlation coefficients drop well below 0.5 for two scenarios at the −8 slope of degassing and correlations approach 0 at the −11 ‰ slope (Figs. 9 and S4).

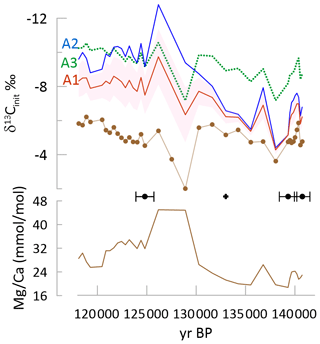
Figure 9 Penultimate glacial to interglacial transition in GLD showing the measured δ¹³C (brown curve with symbols indicating measured samples), with colored lines for δ¹³C_init for the three f_Ca scenarios A1, A2, and A3 (dashed line) for a degassing fractionation slope of −8 ‰. Shading for the A3 scenario shows the range using other degassing slopes of −5 ‰ (more positive) and −11 ‰ (more negative). Black diamonds indicate the position of U $/$ Th dates and their uncertainty; the black cross indicates a tie point based on δ¹⁸O as indicated in Table S2. $\mathrm{Mg}/\mathrm{Ca}$ is also shown with a solid brown line. A box-and-whisker plot is given in Fig. S4.

5 Discussion

5.1 Interpretation of δ¹³C_init and coherence of coeval speleothem signals and regional climate

The calculated δ¹³C_init is formulated to reflect the isotopic signal of DIC prior to significant evolution via degassing and PCP. Warmer interglacial climates characterized by higher soil pCO₂ promote more negative δ¹³C_DIC and increase the degree of drip water saturation, which promotes greater PCP for a given drip interval (Fig. 4). For some locations with drip intervals very sensitive to PCP, these processes may exert comparable magnitude but opposing influence on measured stalagmite δ¹³C and lead to nearly constant measured δ¹³C despite significant changes in temperature (Martrat et al., 2007) and vegetation (Goni et al., 2008; Tzedakis et al., 2018). We suggest that such a process may have contributed to the similar average measured δ¹³C in GUL in late glacial and Holocene time intervals (Fig. 6) and also to the similar glacial and interglacial measured δ¹³C in GLD (Fig. 7). Both of these stalagmites are characterized by large increases in $\mathrm{Mg}/\mathrm{Ca}$ in the interglacial, indicating significant enhancements of PCP.

For stalagmite GUL growing during the last deglaciation, all of the examined calculations of δ¹³C_init yield a temporal pattern more consistent with independent evidence of cooler regional temperatures during the late glacial B/A compared to the early Holocene (Fig. 7) (Martrat et al., 2007; Ausín et al., 2019; Cacho et al., 1999). The aggregate δ¹³C_init of both stalagmites spanning TI (GAL and GUL) exhibits a stronger correlation with regional sea surface temperature (SST) than the measured δ¹³C (Fig. 10).

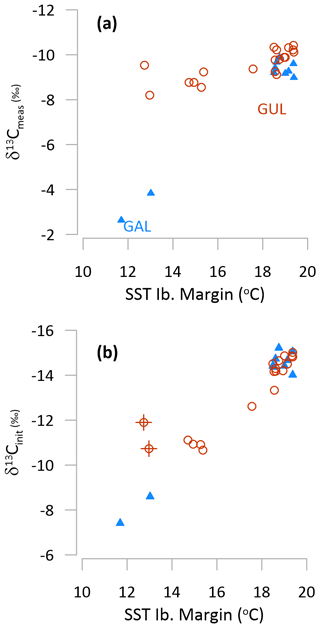
Figure 10 Comparison in 500 kyr fixed time bins of (a) measured δ¹³C and (b) δ¹³C_init vs. regional Iberian Margin SST (Cacho et al., 1999) over the last glacial to interglacial transition in GAL (blue triangle) and GUL (red circle). In (b) we show a −8 ‰ degassing slope and scenario A1. Other scenarios for GAL are illustrated in Fig. S5. In (b), crosses denote two samples of age 12.25 and 12.75 ka, for which the offset may reflect uncertainty in the age interpolation as shown in Fig. 8.

Because the extent of degassing and PCP can be strongly conditioned by the drip rate and drip chemistry supplying an individual stalagmite, the extent and temporal variations of PCP may differ significantly among coeval stalagmites, leading to contrasting measured δ¹³C among coeval stalagmites, even in the case of similar temperature and vegetation forcing of the initial drip water δ¹³C_DIC. Between 94 and 82 ka, the Greenland Stadial (GS) 22 event is a salient cooling feature in regional SST records (Martrat et al., 2007). Yet, only one of the three stalagmites spanning this age range exhibits a clear positive anomaly in measured δ¹³C: stalagmite GLO, which features stable $\mathrm{Mg}/\mathrm{Ca}$ over this time interval. Stalagmite GAE features a long-term trend towards negative measured δ¹³C not observed in GLO or ROW, and GAE also features a significant decrease in $\mathrm{Mg}/\mathrm{Ca}$ (Fig. 7). The calculated δ¹³C_init of GLO does not alter the trend seen in measured δ¹³C. However, the δ¹³C_init of ROW features the positive anomaly typical of stadial cooling. Significantly, despite the strong long-term trend in measured δ¹³C, the calculated δ¹³C_init of GAE also resolves a positive anomaly consistent with the timing of the GS22 cooling. These more coherent temporal trends are resolved in the three records regardless of the f_Ca scenario employed.

These results for multiple coeval stalagmites suggest that calculation of δ¹³C_init has the potential to improve reproducibility among coeval records and resolve signals of important regional changes in temperature and vegetation effects in the soil and epikarst environment.

5.2 Coherency of quantitative PCP estimations and impact on deconvolving PCP effects in δ¹³C

5.2.1 Quantitative PCP indicators in this sample set

The calculation of δ¹³C_init relies on quantitative estimation of PCP. PCP should exert a similar effect on ratios of divalent cations with low partition coefficients like $\mathrm{Mg}/\mathrm{Ca}$ and Sr $/$ Ca. However, many published $\mathrm{Mg}/\mathrm{Ca}$ and Sr $/$ Ca records do not exhibit strong positive correlation (Sinclair, 2011). In our dataset, the greater correlation of $\mathrm{Mg}/\mathrm{Ca}$ and Sr $/$ Ca in some of the high-$\mathrm{Mg}/\mathrm{Ca}$ stalagmites may reflect the proportionally greater effect of calcite $\mathrm{Mg}/\mathrm{Ca}$ on the D_Sr in higher-$\mathrm{Mg}/\mathrm{Ca}$ stalagmites (e.g., Wassenburg et al., 2020). A 3-fold reduction in Ca due to PCP is attainable for reasonable degrees of soil pCO₂ and drip water saturation in our interglacial climates, and therefore a 3-fold range in $\mathrm{Mg}/\mathrm{Ca}$ or Sr $/$ Ca due to PCP is possible. Over a 3-fold range in $\mathrm{Mg}/\mathrm{Ca}$ in low-$\mathrm{Mg}/\mathrm{Ca}$ stalagmites (e.g., 2 to 6 mmol mol⁻¹ $\mathrm{Mg}/\mathrm{Ca}$), existing compilations suggest that the D_Sr increases by 20 %. Yet, for a 3-fold increase in $\mathrm{Mg}/\mathrm{Ca}$ in the high-$\mathrm{Mg}/\mathrm{Ca}$ stalagmites (e.g., 10 to 30 mmol mol⁻¹ $\mathrm{Mg}/\mathrm{Ca}$) the D_Sr would increase by 80 %. Because $\mathrm{Mg}/\mathrm{Ca}$ and δ⁴⁴Ca are always positively correlated, but Sr $/$ Ca and δ⁴⁴Ca are not positively correlated in all samples, we conclude that growth-rate-driven variations in D_Sr can strongly overprint the PCP-driven trends in Sr $/$ Ca in some stalagmites. For a given f_Ca, faster growth rates would promote a lower δ⁴⁴Ca and a higher D_Sr, fueling inverse correlation. Because Ca and Sr are dominantly bedrock-sourced in this setting, this reversal from the expected PCP relationship cannot be attributed to variable contribution of other element sources but must reflect the operation of processes at the solution–calcite interface. Similarly, deviation of Sr $/$ Ca and $\mathrm{Mg}/\mathrm{Ca}$ from the PCP slope, or variation in the Sr $/$ Mg ratio, does not conclusively require variation in non-bedrock sources in either element but could reflect partitioning effects which for Sr are decoupled from PCP, as suggested by strong growth rate dependence of Sr partitioning in stalagmites from this cave (Sliwinski et al., 2023).

In our dataset, temperature variation in D_Mg could explain some, but not all, of the apparent amplification in the $\mathrm{Mg}/\mathrm{Ca}$-based f_Ca compared to δ⁴⁴Ca-based f_Ca. Significant amplification is observed within the Holocene when temperature variation is limited. Additionally, in many cases the required range in D_Mg is larger than the 22 % increase predicted from reasonable-amplitude (e.g., <10^∘) temperature increases according to laboratory calibrations (Day and Henderson, 2013). One candidate explanation for higher-magnitude changes in D_Mg may be the up to 2-fold increase in the D_Mg with increasing calcite $\mathrm{Mg}/\mathrm{Ca}$ (Wassenburg et al., 2020). This effective partitioning increase may reflect true lattice partitioning and/or increased Mg in fluid inclusions. The existing field data do not precisely constrain the slope of this increase in D_Mg or define if the slope is indeed linear. For future absolute estimation of f_Ca from $\mathrm{Mg}/\mathrm{Ca}$, improved constraints on the variation of D_Mg are required from laboratory and field studies. In field monitoring studies, true variation in D_Mg can be most accurately determined when observations adequately control for both the initial solution $\mathrm{Mg}/\mathrm{Ca}$ and the integrated water $\mathrm{Mg}/\mathrm{Ca}$ during calcite precipitation, which may be higher than the initial $\mathrm{Mg}/\mathrm{Ca}$ if a significant amount of the Ca is precipitated on the stalagmite from each solution aliquot. Future field monitoring and farmed calcite studies should also evaluate whether calcite fabrics could provide independent evidence of variation in D_Mg, since some stalagmites show a relationship between fabrics and Sr partitioning (Frisia et al., 2022).

In addition to variation in D_Mg, temporal changes in the $\mathrm{Mg}/\mathrm{Ca}$ of undegassed drip water could also contribute to discrepancies between f_Ca from δ⁴⁴Ca and $\mathrm{Mg}/\mathrm{Ca}$ (e.g., the requirement for AF > 1). We observe only a greater, never lower, magnitude of $\mathrm{Mg}/\mathrm{Ca}$ change than that expected from changes in f_Ca alone. In the La Vallina Cave system, drip water monitoring shows very constant drip water $\mathrm{Mg}/\mathrm{Sr}$ ratios seasonally despite order of magnitude changes in drip water flow rates (Fig. 12 in Kost et al., 2023b). This suggests that despite variation in water residence times, there is not widespread or significant variation in bedrock mixing fraction.

5.2.2 Suggested approach for fossil stalagmites

$\mathrm{Mg}/\mathrm{Ca}$ is a widely measured PCP-sensitive indicator. However, it can be unreliable in host rocks which feature significant components of widely varying solubility and $\mathrm{Mg}/\mathrm{Ca}$ if the bedrock mixing fraction varies over time. This can produce variation in the initial drip water $\mathrm{Mg}/\mathrm{Ca}$ attained by bedrock dissolution before evolution of drip water by PCP. Large temporal variations in drip water $\mathrm{Mg}/\mathrm{Sr}$ ratios at a single drip during monitoring may be one sign of varying bedrock mixing fraction. $\mathrm{Mg}/\mathrm{Ca}$ can also be unreliable as a PCP indicator if a large fraction of the Mg in the stalagmite is present in detrital minerals rather than in the calcite. Stalagmite $\mathrm{Mg}/\mathrm{Ca}$ which covaries with Al $/$ Ca or Si $/$ Ca may indicate an important detrital component of Mg. In these two situations, it is not recommended to use $\mathrm{Mg}/\mathrm{Ca}$ for quantitative PCP estimation.

In settings where bedrock mixing fraction is stable and detrital minerals are not a significant source of Mg in the stalagmite, the quantitative estimation of f_Ca nonetheless entails uncertainty. For stalagmites in which only $\mathrm{Mg}/\mathrm{Ca}$ is measured and δ⁴⁴Ca is not determined, the constancy or range of variation in D_Mg will represent one source of uncertainty in the calculation of δ¹³C_init. The calculation of f_Ca from $\mathrm{Mg}/\mathrm{Ca}$ can be adjusted by an attenuation factor as in Eq. (7). An attenuation factor > 1 is likely required if measured $\mathrm{Mg}/\mathrm{Ca}$ leads to calculation of a larger f_Ca range than expected. For example, f_Ca<0.20 would require initial drip water Ca concentrations > 100 ppm. If a bedrock adjustment factor in Eq. (7) is used, it may need to be coupled with an attenuation factor (other than 1) so that absolute f_Ca does not reach values lower than expected for the cave and climatic context. This uncertainty will be reduced as future research better constrains the variation of D_Mg with $\mathrm{Mg}/\mathrm{Ca}$.

5.3 What is the magnitude of the PCP+degassing effect on δ¹³C?

5.3.1 Do interglacial stalagmites constrain the degassing δ¹³C slope?

For interglacial stalagmites, we can estimate the lowest expected δ¹³C_init and use this limit to evaluate the range of reasonable degassing slopes. The δ¹³C_DIC of drip water has been measured under forested sections of the cave, with sample collection techniques to limit degassing (Kost et al., 2023b). From this, we estimate the δ¹³C_init for calcite forming under similar drip water δ¹³C_DIC. Additionally, we hypothesize that pre-anthropogenic land use at this location would have led to soil pCO₂ in the 8000 to 10 000 ppm range during the mid-Holocene and previous interglacials (Lechleitner et al., 2021). We therefore calculate the composition of calcite forming from DIC in equilibrium with open-system dissolution (e.g., 150 L gas volume and resulting 3 % dead carbon percentage) of limestone by 10 000 ppm soil CO₂ of isotopic composition corresponding to modern respired end-members in three ecosystems (Pataki et al., 2003) (Fig. 6).

We find that interglacial stalagmites cannot rule out any of the investigated degassing slopes. The stalagmites from our monitored cave which include long Holocene growth phases are GAL and GUL, which require low to moderate attenuation factors (1.3 to 3) for calculation of f_Ca from $\mathrm{Mg}/\mathrm{Ca}$. When the f_Ca calculated from $\mathrm{Mg}/\mathrm{Ca}$ includes the estimated AF for coherency with δ⁴⁴Ca as in Table 2, then the −8 ‰ slope for all GUL and GAL samples falls within the range of calcite composition expected from modern drip water with limited degassing (Fig. 6). With the −11 ‰ slope, the median δ¹³C_init approaches −17 ‰, which, although higher than modern drip water predictions, is still compatible with DIC derived from equilibration with respired CO₂ from temperate broadleaf and conifer ecosystems (Pataki et al., 2003). With the −5 ‰ slope, the median δ¹³C_init is slightly below that implied for calcite on the basis of modern monitoring. Results for stalagmites spanning the last interglacial also indicate that the −8 ‰ to −11 ‰ slopes yield δ¹³C_init coherent with expected interglacial calcite. BEL, which requires little attenuation, best matches expected range with −11 ‰. But, our comparison does reveal that unreasonable corrections which are more negative than expected for the respired CO₂ component result from the combination of the −11 ‰ degassing slope and f_Ca calculated from measured $\mathrm{Mg}/\mathrm{Ca}$ without the use of AF (scenario “full”) for some low-$\mathrm{Mg}/\mathrm{Ca}$ stalagmites.

A similar analysis for the Holocene Heshang Cave, for which both $\mathrm{Mg}/\mathrm{Ca}$ and f_Ca data are available, yields δ¹³C_init with the −5 ‰ slope of −12 ‰ and with the −11 ‰ slope δ¹³C_init of −15 ‰, both within the range of calcite composition expected from high-CO₂ soils with respired CO₂ composition from temperature broadleaf or tropical ecosystems (Pataki et al., 2003) (Fig. 6), consistent with the C3 evergreen broadleaf vegetation overlying Heshang Cave (Li et al., 2014).

Thus, the available interglacial datasets so far do not preclude the kinetically enhanced slope of −11 ‰ for fractionation during degassing and PCP. In fact, for the last interglacial, for many stalagmites, the higher slopes yield δ¹³C_init more consistent with expected interglacial soil pCO₂. Although the degree of open vs. closed dissolution cannot be inferred for last interglacial samples, if it is in the range of Holocene and late glacial samples from this and nearby caves (Lechleitner et al., 2021), the δ¹³C_init is not expected to differ by more than 1 ‰from that calculated for the relatively open 10 000 ppm soil CO₂ CaveCalc model.

5.3.2 Previous laboratory and field calibrations

The CaveCalc simulation assumes that the loss of carbon from drip water is attained via CO₂ degassing and calcite precipitation in a 1:1 ratio, with close coupling of the processes, and that fractionation is occurring at equilibrium according to laboratory-estimated fractionation factors. Empirical laboratory and field results are sensitive to true degassing and PCP as well as the isotopic consequences of exchange between drip water and cave atmosphere. We are aware of one published field study in which drip water was sampled before and after a ∼3 m transit across a subvertical flowstone surface in a cave with average temperature of 22.5 ^∘C (Mickler et al., 2019). In this transect, Ca and DIC were directly measured and δ¹³C DIC was determined from total evolution as CO₂ in flushed vials. Ca concentrations were on average 20 % lower after the ISST flowstone transit, and the median estimated degassing slope was −9.9 ‰ in the eight monthly paired samples. The slopes estimated on individual sampling dates (ranging from −7.7 to −13.7) did not correlate with drip water oversaturation or the estimated ratio of Ca to DIC decrease on those dates. The slope in this study is more than double that of CaveCalc at comparable temperatures. One interpretation is that the rapid initial phases of degassing occur at kinetically enhanced fractionation factors (Mickler et al., 2019). A similar experiment conducted on one day in La Vallina Cave was also consistent with a slope of −11 ‰based on sampling at a cave temperature of 12 ^∘C and modest saturation (55 ppm Ca in drip water vs. 21 ppm for equilibrium at cave temperature and pCO₂ ppm) (Kost et al., 2023b). During this sampling, cave air was ventilated to nearly atmospheric CO₂ concentrations and isotopic composition. These laboratory and field results suggest that, given current available data, the CaveCalc slopes may need to be considered the minimum slopes required to correct for degassing and PCP effects on carbon isotopes.

The laboratory experiment best simulating the coupled evolution of δ¹³C DIC, calcite δ¹³C, and f_Ca allowed highly supersaturated solutions to degas and precipitate CaCO₃ as they flowed along a marble plate, with electrical conductivity measurements estimating the degree of Ca depletion along the flow path in a parallel experimental setup with flow over a glass plate (Hansen et al., 2019). The δ¹³C of DIC was measured by precipitation in SrCO₃ and analysis as solid phase. The slope A in the 10 experiments, based on the evolution of δ¹³C of DIC, ranged from −4.63 ‰ to −13.2 ‰or from −5.9 ‰ to −16 ‰ based on evolution of δ¹³C of calcite, although precise estimation of the latter slope is complicated by the measurement of precipitated calcite δ¹³C and conductivity in separate experimental setups which may have experienced slightly different locations of calcite precipitation (Sade et al., 2022). Many of these estimated experimental fractionations are considerably higher than those predicted by CaveCalc.

A dynamical model (Sade et al., 2022) was developed to simulate the laboratory experiments (Hansen et al., 2019). This model derived a single relationship between PCP and DIC evolution using f_DIC in contrast to our calculated index based on Ca consumption, f_Ca. In this model formulation, the degassing slope relative to ln (f_DIC) averages −8.7 ‰ from f=1.0 to f=0.3, but the slope is not constant. Rather, at f_DIC between 0.8 and 1, there is an inverse slope as net DIC evolution is modeled to lead to more negative, rather than more positive, δ¹³C of speleothem calcite. Over the subsequent phase of PCP (f_DIC 0.8 to 0.3), the average modeled degassing slope relative to f_DIC would be −10.1 ‰; however, it flattens to −4 ‰ in the range of f_DIC 0.33 to 0.4. If this model is representative of cave flowstone formation, it may suggest that some of the calculated differences in degassing slopes in field experiments may result from measurements of solutions sampled in different stages of drip water Ca and DIC evolution. Alternatively, it is possible that some differences in degassing slopes reflect different degrees of coupling between degassing and CaCO₃ precipitation. The influence of factors inhibiting CaCO₃ precipitation, potentially including elevated Mg concentrations or certain dissolved organic compounds, on the degassing slope remains to be investigated.

If there were significant variations in the degassing slope experienced by a given stalagmite over time, it could complicate efforts to estimate trends in δ¹³C_init using Eq. (2). Yet, our speleothem time series are broadly consistent with the narrow range of variation of degassing slope within a given stalagmite, since correction of −5 ‰ in one part of the time series and −11 ‰ in another would alter the trends and reduce coherence among the records in Fig. 7. This coherence with a single slope may reflect the limited range of variation in f_Ca inferred for our stalagmites. For example, for all stalagmites except GAE, the A2 scenarios and the majority of data from A3 scenarios fall between f_Ca of 0.4 and 0.8. If coincident with f_DIC of 0.4 to 0.8, these samples would all be within the range of similar slope (−10 ‰ to −11.5 ‰) predicted by the dynamical model simulation. Sampled stalagmite growth may often be biased to periods when f_Ca>0.4, which lead to higher precipitation rates and more calcite deposition. The consistency of our interglacial data with steeper degassing slopes than CaveCalc may reflect the reality that much calcite precipitation will happen when cave pCO₂ is much lower than drip water pCO₂, a situation in which drip water exchange with isotopically heavier cave air could be a significant contributor to a steep degassing slope.

A future calculation of the dynamical model prediction (Sade et al., 2022) of δ¹³C evolution relative to f_Ca, rather than f_DIC, as a PCP indicator would provide a helpful reference for future calculation of δ¹³C_init. This could elucidate whether a nonlinear relationship should be used to calculate δ¹³C_init from ln (f_Ca) and δ¹³C_meas. It would clarify if calcite precipitated at high f_Ca, analogous to that precipitated at high f_DIC, should be excluded from the correction because of compensating effects of kinetic fractionation factors and evolution of f_Ca in the range of high f_Ca. Scenarios employing a B≤0.8 by default have a maximum f_Ca largely outside the range of inverse slope.

5.3.3 Suggested approach

Trends in δ¹³C_init are less sensitive to the choice of the degassing slope but the absolute value of δ¹³C_init is strongly dependent on the choice of degassing slope. At the moment, the absolute δ¹³C_init can be reconstructed with low confidence. However, the reconstructed δ¹³C_init can be used to rule out combinations of f_Ca scenarios and degassing slopes which lead to “overcorrection” to δ¹³C_init values which are more negative than DIC equilibrated with a reasonable respired soil pCO₂ composition for the ecosystem type. Until further constraints to assess the slope of δ¹³C and Ca co-evolution during degassing and PCP which characterizes typical cave environments are available, a sensitivity analysis employing a range of degassing slopes will provide the greatest transparency for assessing δ¹³C_init.

6 Conclusions

We provide a first analysis of the potential estimation of speleothem δ¹³C_init, the δ¹³C which characterized drip water DIC prior to significant degassing and PCP. δ¹³C_init is proposed as a useful interpretable variable derived from speleothem isotope measurements because trends in δ¹³C_init are expected to be more reproducible than measured δ¹³C among coeval stalagmites from a given region and because δ¹³C_init is more sensitive to the vegetation, soil, and epikarst processes which in many regions may be sensitive to temperature in addition to moisture. Calculation of δ¹³C_init for a given sample or growth increment requires a quantitative indicator of the extent of PCP experienced in that growth increment and knowledge of the general rate of change in δ¹³C with progressive degassing and PCP.

In fossil stalagmites, the extent of PCP, as the Rayleigh f_Ca, can be approximated for a particular growth increment using the measured $\mathrm{Mg}/\mathrm{Ca}$ and the minimum $\mathrm{Mg}/\mathrm{Ca}$ measured in the entire stalagmite. f_Ca can also be estimated from δ⁴⁴Ca given reasonable choices of the calcite dissolved fractionation factor. In several of the stalagmites examined here, the f_Ca calculated from $\mathrm{Mg}/\mathrm{Ca}$ shows an amplified range compared to that calculated from δ⁴⁴Ca. An increase in D_Mg with increasing $\mathrm{Mg}/\mathrm{Ca}$, as proposed in previous studies (Wassenburg et al., 2020), is one viable explanation for this systematic trend. This observation warrants further investigation to improve confidence in future estimates of f_Ca from $\mathrm{Mg}/\mathrm{Ca}$, which is the most widely available PCP indicator for stalagmites.

At the moment, there is uncertainty in the degassing slope or rate of change in δ¹³C with progressive degassing and PCP. Values may range from −5 ‰ to −11 ‰. The stalagmites investigated here could be consistent with any value in this range. Because these different possible degassing slopes affect the absolute value of the calculate δ¹³C_init, currently there is uncertainty in the exact value. However, the trends in δ¹³C_init are less sensitive to the choice of degassing slope.

Despite these uncertainties, δ¹³C_init provides more consistent time series among coeval stalagmites and with regional climate records. In one example δ¹³C_init reconciles three divergent measured stalagmite δ¹³C records in the 94 to 82 ka time interval, yielding three δ¹³C_init time series which feature a pronounced positive anomaly corresponding to the regional cooling of Greenland Stadial 22. In western Europe, over the warming trend of deglaciations, the trend towards more negative δ¹³C_DIC due to higher soil respiration and soil CO₂ may be fully or partially compensated for in stalagmite δ¹³C due to the increased PCP from the more oversaturated drip waters. The calculation of δ¹³C_init reveals the trend of increasing respiration rates and soil pCO₂. Over the last deglaciation, the δ¹³C_init matches the millennial structure in regional SST more closely than the measured δ¹³C.

As better constraints emerge on the degassing slope and on Mg partitioning, δ¹³C_init estimates will become more precise and should improve the utility of the high volume of stalagmite δ¹³C measurements made simultaneously with δ¹⁸O in all labs.

Appendix A

Table A1 Measured δ⁴⁴Ca, $\mathrm{Mg}/\mathrm{Ca}$, and Sr $/$ Ca, as well as the calculated f_Ca for differing Δ⁴⁴Ca and B (bedrock factors).