Sensitivity to species selection indicates the effect of nuisance variables on marine microfossil transfer functions

The species composition of many groups of marine plankton appears well predicted by sea surface temperature (SST). Consequently, fossil plankton assemblages have been widely used to reconstruct past SST. Most applications of this approach make use of the highest possible taxonomic resolution. However, not all species are sensitive to temperature, and their distribution may be governed by other parameters. There are thus reasons to question the merit of including information about all species, both for transfer function performance and for its effect on reconstructions.

Here we investigate the effect of species selection on planktonic foraminifera transfer functions. We assess species importance for transfer function models using a random forest technique and evaluate the performance of models with an increasing number of species. Irrespective of using models that use the entire training set (weighted averaging) or models that use only a subset of the training set (modern analogue technique), we find that the majority of foraminifera species does not carry useful information for temperature reconstruction. Less than one-third of the species in the training set is required to provide a temperature estimate with a prediction error comparable to a transfer function that uses all species in the training set. However, species selection matters for paleotemperature estimates. We find that transfer function models with a different number of species but with the same error may yield different reconstructions of sea surface temperature when applied to the same fossil assemblages. This ambiguity in the reconstructions implies that fossil assemblage change reflects a combination of temperature and other environmental factors. The contribution of the additional factors is site and time specific, indicating ecological and geological complexity in the formation of the sedimentary assemblages. The possibility of obtaining multiple different reconstructions from a single sediment record presents a previously unrecognized source of uncertainty for sea surface temperature estimates based on planktonic foraminifera assemblages. This uncertainty can be evaluated by determining the sensitivity of the reconstructions to species pruning.

1 Introduction

Any method to infer quantitative paleoenvironmental information from (fossil) species assemblages relies on the use of a modern (or near modern) training set to identify a statistical relationship between the species assemblage and the environmental variable to be reconstructed. There is a range of methods varying broadly in the way the training set is used to define the relation between the species community and the environmental parameter of interest. In this context, one aspect of the training set design that has received little formal attention is species selection. In applications based on marine microfossils, the assumption has been that (nearly) all species potentially carry useful information, and training sets have been designed to include as many species as practically possible (Kučera et al., 2005a). However, there are fundamental, theoretical reasons to question whether the inclusion of all species is necessary for accurate reconstructions. Firstly, species may respond to environmental variables other than the one of interest and therefore confound the reconstruction. Such species would negatively impact the predictive power of the transfer function model. Secondly, species could be opportunistic or have a wide ecological niche and hence provide little information on the environmental variable to be reconstructed. These species would add little to no information to constrain the reconstruction. The premise of full taxonomic resolution has been recently tested by Juggins et al. (2015), who demonstrated that transfer function techniques are variably sensitive to the influence of non-informative taxa. These authors used highly diverse assemblages from coastal and lacustrine environments in which the proportion of uninformative or confounding taxa can be expected to be high and species selection for transfer function models is intuitively appropriate.

However, marine microfossil assemblages (notably planktonic foraminifera) are less diverse and the species display a low degree of endemicity. In these circumstances, it would appear important to retain as many species in the training set as possible. Indeed, up to now, species pruning in marine microplankton applications has been done, if at all, for practical rather than ecological reasons. Species were removed or lumped because of low abundance, preservation, or taxonomic issues (Hayes et al., 2005; Vernal et al., 2001; Zielinski et al., 1998). However, the minimum number of taxa required for a robust transfer function model, or the influence of non-informative or nuisance taxa on such models, has never been formally evaluated. This is remarkable, considering that many species of marine microplankton appear to have similar responses to the modelled variables and that there is also evidence for responses to multiple variables (Telford et al., 2013; Siccha et al., 2009; Steinke et al., 2008). Furthermore, from a practical point of view, reducing the number of species in the model may improve counting statistics and reduce counting time. Finally, reducing taxonomic resolution may also be beneficial for the application of automated identification and counting systems (e.g. Beaufort and Dollfus, 2004; Hsiang et al., 2016) and enable the use of legacy datasets with incomplete taxonomy. The lack of a formal evaluation of species pruning in marine microfossil studies is also relevant because of the prolific use of different transfer function techniques. The evaluation of species pruning by Juggins et al. (2015) was carried out for “global models” for which the entire training set is used to define the species response curve to an environmental variable. Such methods are used on marine microfossil applications as well (e.g. the Imbrie and Kipp method after Imbrie and Kipp, 1971; weighted averaging (WA), or artificial neural networks after Malmgren and Nordlund, 1997). However, in marine studies the most popular approach is the modern analogue technique (MAT). This approach uses similarity measures to identify a small “local” subset of samples from the training set to derive the environmental variable to be reconstructed. Such a local approach is fundamentally different and could be sensitive to species pruning in the training set in a different way.

Here we evaluate species importance for transfer function performance for two widely differing methods (WA and MAT) representing both ends of the spectrum between local and global methods. We start by assessing species importance to determine the ranking of species for transfer function performance. We then investigate why some species are more important than others. Finally, because the behaviour of transfer functions models cannot be assessed within the modern training set only, we assess the influence of species selection on paleotemperature reconstructions.

We use planktonic foraminifera as a model group, but the results from this study are likely of wider relevance to paleoecological reconstructions based on marine microfossils. Planktonic foraminifera are ideal for this purpose because of the existence of a large global training set (Siccha and Kučera, 2017a) and because of strong evidence that their distribution in surface sediments can be predicted by sea surface temperature alone (Bé and Hutson, 1977; Morey et al., 2005).

2 Data and methods

To derive the transfer functions, we use planktonic foraminifera assemblage data from core top sediments recently compiled in the ForCenS dataset (Siccha and Kučera, 2017a). Multi-species categories and morphotypes were removed, and in the case of replicate samples (at the same location) one sample was randomly selected. Annual mean temperature was assigned to each sample in the training set based on data from climatology (Stephens et al., 2002) averaged over the upper 50 m and within a 100 km radius of each core top sample. To test the effect of species selection on the performance of the transfer function outside of the calibration dataset, we analysed three fossil datasets. To evaluate the effect on assemblages with different diversity, we use two downcore records from the Atlantic: M35003-4 from the Caribbean (Hüls and Zahn, 2000), which spans 0–55 ka, and a longer 0–180 ka record from the Iberian Margin: MD95-2040 (De Abreu et al., 2003a). To evaluate the effect on past spatial sea surface temperature (SST) patterns, we reanalyse the MARGO Last Glacial Maximum (LGM) dataset from the North Atlantic Ocean (Kučera et al., 2005a). The taxonomy of all fossil samples was harmonized with the ForCenS dataset following the same criteria as in Siccha and Kučera (2017a). Species not reported to be present in the downcore assemblages were assumed to be absent.

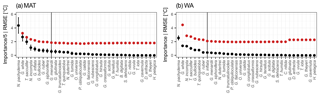
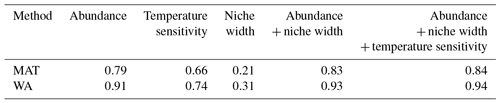
Figure 1 Species importance (black) and transfer function performance (red) for models including all species to the left of the point (e.g. the first red point for the MAT transfer function for the North Atlantic denotes the prediction error (root mean square error; RMSE) of a model with N. pachyderma and G. ruber (white). Error bars on the species importance show the standard deviation of 10 replicates; see “Data and methods” for details. The dark vertical lines indicate the species needed for a transfer function model in which including more species only leads to a marginal reduction in the reconstruction error (arbitrarily set at when the prediction error is within 10 % of the minimum). Note that for display purposes the species importance for MAT has been divided by a factor of 5.

To determine how many and which species are needed for the transfer function models we start with assessing species importance following the approach described by Juggins et al. (2015). Briefly, this involves randomly selecting 1∕3 of the species in the training set and dividing this reduced training set into a part that is used to build the transfer function model including approximately 63 % of the samples and an out-of-bag (OOB) part that is used to evaluate the model. The proportion of each species in the OOB selection is then randomly permuted and the performance of the model is reassessed. Species for which the permutation leads to an increase in the prediction error are considered important. The species importance is derived from the average difference in prediction between the OOB and the permuted OOB samples across 1000 bootstrap samples of the training set. The entire approach is repeated 10 times in order to get an error estimate of the species importance. For WA we use inverse deshrinking to obtain the environmental variables, and for MAT we use the five closest analogues determined using squared chord distance. We note that the way the species importance is assessed and the transfer function models with different numbers are designed implicitly uses a rest group of non-included species. This is because the calculations are based on the relative abundances of the species in the training set with the full taxonomic resolution. This procedure simulates a situation in which the total number of fossils in the studied group has been determined, but only a subset of the species has been counted.

Next, we use the species importance to build transfer function models with a successively increasing number of species. We start with the two most important species and increase the number according to the species importance ranking. The performance of each model (i.e. the prediction error) was assessed using h-block cross-validation to account for the effect of spatial autocorrelation in the training set (Telford and Birks, 2009). We used a cut-off distance of 850 km, which was shown to be appropriate for the North Atlantic (Trachsel and Telford, 2016). Because of the presence of cryptic species with specific ecological preferences, we have carried out the analyses separately for individual ocean basins following Kučera et al. (2005a), assigning the new Red Sea samples of ForCenS to the Indian Ocean. The discussion below focusses on the North Atlantic Ocean because of the abundance of both core top and downcore data, but the species ranking for the other oceans is provided in the Supplement. All calculations were carried out in R (R core team, 2016) using the packages rioja (Juggins, 2017), raster (Hijmans, 2017), vegan (Oksanen et al., 2018), and ggplot2 (Wickham, 2016).

Table 1 Factors explaining species importance: coefficient of determination of linear regression between species importance and maximum abundance, thermal niche width, and temperature sensitivity.

3 Results and discussion

3.1 Species importance ranking

Irrespective of which regional training set is used, for both WA and MAT only a small number of species appears important (Fig. 1 and the Supplement). As shown by the example of the North Atlantic, cross-validation of the transfer function models with an increasing number of species shows that there is a large tail of low-importance species that do not add information and hence do not lead to improved transfer function performance (Fig. 1). In general, it appears that reconstructions with similar errors to the full species reconstruction can be achieved with less than a third of the total number of species. The species importance ranking varies somewhat by method and region but is generally similar (Supplement). In the North Atlantic there is a 90 % overlap of the species in the top 10.

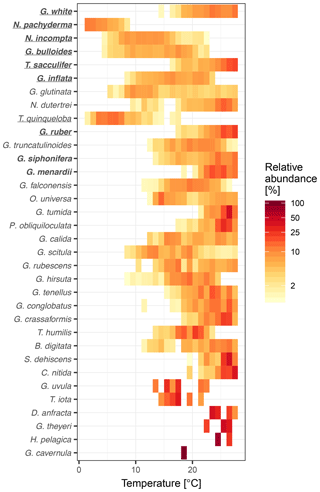
Figure 2 Species thermal niche ranked by average sedimentary abundance (top to bottom). Colours indicate average abundance (on a logarithmic scale) within 1 ^∘C bins. The essential species (see Fig. 1) for MAT are marked in bold and those for WA are underlined. Despite their apparently well-defined thermal niche, rare species are not essential for transfer functions and those that are important are all abundant.

To understand why some species are more important than others, we consider their overall maximum abundance, the width of their thermal niche in the training set, and their temperature sensitivity as potential predictors of importance. We assume that the thermal niche of a species has a Gaussian shape and define temperature sensitivity based on how well the species abundance in temperature space can be described by a simple Gaussian curve. This analysis reveals that abundance (Fig. 2) is the best predictor of species importance (Table 1). Indeed, multiple regression models that include all three variables perform only marginally better than a model using abundance alone. However, we note that all three variables are correlated to some degree. Interestingly, abundance and temperature sensitivity are positively correlated (r=0.84), implying that the thermal niche of abundant species is better defined compared to rare species (Fig. 3a). We also observe that temperature sensitivity and thermal niche width are correlated. Counter-intuitively, this correlation is positive: species with a narrow thermal niche appear less temperature sensitive (r=0.60; Fig. 3b). We attribute this pattern to a combination of low abundance of species with narrow thermal niches (sensitivity being correlated with abundance) and the possibility that their distribution is not primarily governed by temperature, assuming that the narrow thermal niche may be an artefact of adaptation to specific oceanic regions or regimes only secondarily correlated with temperature. However, we also note that the detection of rare species is prone to uncertainty due to the limited number of specimens counted, and the characterization of their ecological niche is thus inherently more difficult.

Figure 3 Relationships between temperature sensitivity and (a) maximum relative abundance and (b) thermal niche width of planktonic foraminifera species in the ForCenS dataset. The positive correlation between temperature sensitivity and abundance suggests that the thermal niche of abundant species is better defined than that of rare species, rendering abundance a good predictor of species importance. Panel (b) suggests that species with a narrow thermal niche are relatively insensitive to temperature, suggesting that the distribution of these, often rare, species may not be not primarily governed by temperature.

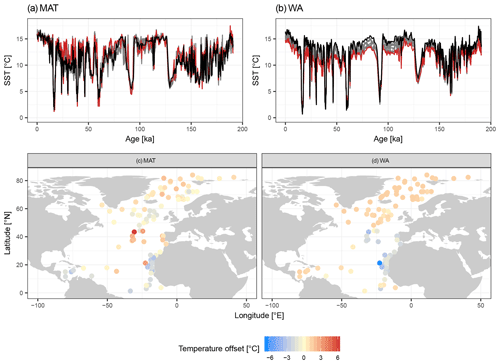
Figure 4 Species selection affects SST reconstructions: examples from two independent datasets showing the effect on temporal and spatial patterns in reconstructed SST. (a, b) SST reconstructions for core MD95-2040 from the Iberian Margin using 33 possible transfer function models with the number of species increasing according to their ranking. Red lines show the reconstructions with essential species only, dark grey lines the reconstructions with more species, and the black line is the “final” reconstruction with all species. (c, d) Spatial pattern of the difference between the SST reconstruction for the LGM with the minimum and with all species included.

The importance ranking also reveals that there are many uninformative species but very few – if any – real nuisance species, i.e. species that lead to an increase in the prediction error when included in the transfer function model. The single possible species in this category is Globoconella glutinata in the case of WA (Fig. 1), but this may in part reflect the complex shape of its thermal niche. Globoconella glutinata is a species with a very wide thermal tolerance and a high degree of cryptic diversity (Darling et al., 2017; André et al., 2014), suggesting that its response to temperature may be complex.

3.2 Effect on reconstructions

Despite the apparent lack of importance of many species in the transfer function model development, their inclusion matters for the reconstruction based on fossil assemblages. Transfer function models with pruned species numbers yield reconstructions that are systematically different from reconstructions with all species included (Fig. 4). The differences can be up to several degrees Celsius and variable in time and space, with important implications for paleoceanographic interpretations. As expected, the average difference between a reconstruction with all species included and pruned species reconstructions decreases with an increasing number of species (Fig. 5). Importantly, species pruning not only results in more variability in the reconstructions, but also leads to a real bias towards either lower or higher temperatures than a reconstruction with all species (Fig. 5).

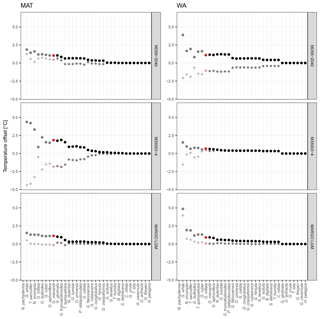
Figure 5 Effect of species selection on SST reconstruction. Graphs show mean difference between reconstructions using species-pruned transfer function models and the model that includes all species. The results are ordered according to species importance, with each dot representing the result from a transfer function model with the species up to the marked point (similar to Fig. 1). Grey symbols are the reconstructions with fewer than the minimum number of species and red symbols the reconstructions with the minimum number of species. Dots are the average of the mean absolute difference, and diamonds are the mean difference.

Inclusion of the most important species leads to a rapid decrease in the difference between species-pruned and all-species reconstructions, but unlike the species importance assessment (Fig. 1), adding more species leads to further stepwise decreases in the difference (Fig. 5). Importantly, steps in reconstruction difference occur with the addition of different species in different cores, indicating that they result from specific downcore changes in the assemblage composition. The exception appears to be G. glutinata in the case of WA, which leads to an increase in both the prediction error and the difference of the reconstruction, supporting its potential rating as a nuisance species.

When adding species to the transfer function model, the reduction in the difference from the reconstruction with all species is initially accompanied by a reduction in the prediction error (Fig. 6). However, once the most important species are included, the prediction error stabilizes, whilst the difference continues to decrease. This means that for the same fossil assemblage, multiple different reconstructions with the same prediction error are possible. This pattern is visible in datasets from different faunistic and climatic regions and different time spans. Moreover, it holds for both methods, suggesting that it is a general pattern of the effect of species selection on SST reconstructions using planktonic foraminifera assemblages. In WA species pruning has a greater effect on the reconstruction error than in MAT, but for both methods species pruning leads to different reconstruction with the same error. Taken at face value and in the absence of independent evidence, such inherent ambiguity renders it impossible to decide which of the reconstructions is more realistic. This adds a previously unrecognized source of uncertainty to quantitative assemblage-based reconstructions.

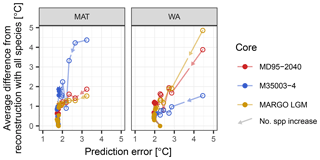
Figure 6 General effect of species pruning on reconstructions and on the prediction error. Each dot represents a reconstruction with n species and its associated prediction error; arrows indicate the direction of increasing species numbers and decreasing species importance. The first point details a transfer function model with two species, and one species is added at each subsequent point. Open symbols highlight reconstructions with the essential species, the inclusion of which leads to a reduction in the prediction error. The reconstruction with minimum error and a minimum number of species is marked by a star. All other reconstructions are plotted as dots. Note that for MAT and WA the inclusion of the essential species leads to a reduction of the prediction error, but once these species are included there are still multiple reconstructions with the same error possible.

3.3 Sensitivity to species pruning

To evaluate the cause of the sensitivity of reconstructions to species selection, we calculate for each fossil sample a sensitivity measure based on the standard deviation of the reconstructions using a different number of species and evaluate its predictability by properties of the assemblages (Fig. 7). The pruning sensitivity for all fossil datasets is higher for MAT than for WA (Fig. 7) despite the fact that the minimum number of essential species is higher for MAT. This suggests that MAT is inherently more sensitive to species pruning, perhaps because the method does not rely on extrapolation to define a species niche.

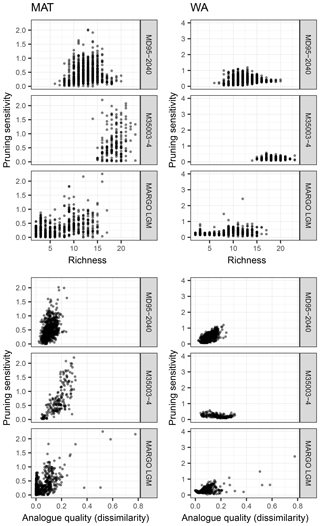
Figure 7 Exploring the effect of species richness and analogue quality on the sensitivity to species pruning. This sensitivity is defined as the standard deviation of the reconstructions with more than the minimum required number of species (i.e. based on transfer function models with uninformative species, which are those to the right of the red dot in Fig. 4). Analogue quality is defined as the average dissimilarity from the five most similar samples in the training set; zero values thus mean perfect analogues. A clear effect of richness cannot be observed, yet for some of the downcore reconstructions (MD95-2040 and M35003-4) poor analogues appear associated with higher pruning sensitivity, particularly for MAT.

Intuitively, it would be expected that the effect of species pruning is larger in low-diversity assemblages. However, for both techniques and all datasets, pruning sensitivity is unrelated to the number of species present in the fossil sample (Fig. 7). The fact that pruning sensitivity is not related to richness confirms that diverse assemblages contain many unimportant (redundant or uninformative) species. Especially for MAT, it could be expected that fossil samples with a composition that differs most from the training set is most sensitive to pruning. This could be so if some species that are judged as uninformative in the training set carry environmentally relevant information downcore. Indeed, we observe such an effect of analogue quality, with poorer analogue assemblages being more sensitive to pruning (Fig. 7). As expected, the effect is stronger for MAT, but it is most clear in the downcore records. However, the fact that the effect is generally weak combined with the absence of a clear common pattern in species pruning sensitivity (Fig. 7) highlights the difficulty of attributing assemblage changes to a single environmental factor and suggests that each site, or time slice, has unique species turnover dynamics. The uniqueness of species dynamics in each dataset is also reflected in the different position of the distinct steps in the difference between the reconstructions with all species and the pruned reconstructions (Fig. 4). Because these steps are not accompanied by a change in the transfer function performance, they indicate changes in the fossil assemblages that either reflect a temperature sensitivity of the species that is not captured in the training set (inadequate training set) or are not related to temperature (non-analogue condition; Hutson, 1977). Non-analogue situations could arise either secondarily from post-depositional changes in the assemblages or primarily and reflect a biological response to an environmental variable other than temperature, which is not apparent in the training set because of temporally variable covariation between this predictor variable and temperature.

Post-depositional changes in species assemblages could arise from processes like dissolution (Berger, 1968) or sediment (and thus fossil) mixing due to bioturbation (Hutson, 1977; Kučera et al., 2005a). The effect of mixing should be most pronounced around intervals of assemblage change and may create fossil species assemblages with poor analogues in the training set. We have assessed to what degree analogue quality (dissimilarity from the training set) varies as a function of change in the assemblages for the downcore records investigated here (Fig. 8). The observed relationship has a sign consistent with our hypothesis but is weak and not apparent in each time series, suggesting that analogue quality varies as a function of multiple parameters and does not simply reflect sediment mixing. Furthermore, we consider the effect of dissolution on the fossil samples negligible and rule out expatriation as the cause of the observed patterns because expatriation is unlikely to have changed considerably in time. We thus infer that the major reason for the observed ambiguity of the reconstructions is the effect of nuisance (non-temperature) variables on fossil assemblage composition.

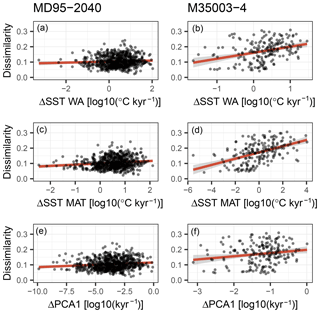
Figure 8 A possible role for sediment mixing in determining analogue quality (dissimilarity; see Fig. 6). Sediment mixing would create poor analogue assemblages when different species communities are mixed. The difference between subsequent species communities in the sediment core is defined here in two ways: (i) as the difference in inferred temperature (a–d) and (ii) as the first derivative of the loadings of the first axis of a principal component analysis (PCA) on the species abundances (e–f). A linear regression including a 95 % confidence interval is shown as a red line with grey shading. Only for core M35004-3 is a weak positive relationship visible, indicating that sediment mixing is a possible contributor to creating poor analogue assemblages but cannot explain them entirely.

3.4 Implications for paleoecological reconstructions

Despite its intuitive simplicity and in spite of apparent statistical support (Morey et al., 2005), relating species assemblage change to a single environmental variable is not trivial (Juggins, 2013; Telford and Birks, 2009, 2005; Telford et al., 2013). This means that quantitative reconstructions based on transfer functions must be interpreted with caution and evaluated in view of additional, independent evidence. Our analysis provides further evidence for the temporal emergence of apparently non-temperature-related changes in fossil planktonic foraminifera assemblages that are not captured by calibration (Telford et al., 2013; Steinke et al., 2008; Siccha et al., 2009). The ambiguity in reconstruction due to species selection thus highlights the potential of environmental variables that appear unimportant in shaping species communities today to explain changes in past assemblages. An important question is therefore how can this ambiguity be considered when interpreting individual reconstructions? We recommend, as a first step, using the approach outlined here (ranking of species importance for each basin is provided in the Supplement) to quantify the sensitivity of reconstructions to pruning and using this as an indication of the influence of secondary or nuisance variables on the reconstruction. This requires that the data are available at full taxonomic resolution, and we therefore explicitly encourage researchers to continue counting all species.

Although a method to translate the effect of pruning into a mechanistic and quantifiable uncertainty estimate is not currently available, one may conclude that reconstructions that are highly sensitive to species pruning indicate that the observed assemblage changes cannot be attributed solely to the environmental variable that is to be reconstructed.

Ultimately, we need a more mechanistic understanding of the factors that determine species assemblage composition in the sediment. Importantly, planktonic foraminifera species inhabit vertically and seasonally distinct habitats (Jonkers and Kučera, 2015; Rebotim et al., 2017). Thus, in many cases the species in a sediment assemblage have never actually lived together and their abundance is thus unlikely to reflect the same forcing. Moreover, the controls on vertical and seasonal abundance variability are species specific, adding even more complexity to deriving a single environmental variable from an assemblage of different species. Ecological models that explicitly simulate assemblages from multiple environmental variables (Kretschmer et al., 2018; Lombard et al., 2011) may improve our capabilities to quantitatively reconstruct past environmental change from species assemblages. In a climate modelling context, such forward modelling of fossil assemblages is likely more fruitful than directly comparing the inferred temperatures.

4 Conclusions

There are both theoretical and practical reasons to investigate whether full taxonomic resolution is required to infer paleoenvironmental data from microfossil assemblages. We have addressed this issue using planktonic foraminifera, but we believe that our results are also relevant to other groups of (marine) microfossils. We have ranked species according to their importance for transfer function model development and shown that less than a third of the species is needed to derive a model that performs as well as (or better than) a model with full taxonomic resolution. Nevertheless, even though the addition of more species has little effect on the transfer function model performance, sea surface temperature reconstructions with an increasing number of species are different. Thus, multiple different reconstructions are possible and their reliability cannot be assessed by transfer function performance in the training set. Our analysis suggests that fossil assemblages do not uniquely reflect a single environmental variable (sea surface temperature in this case) but rather provide an integrated response to biotic (but not temperature related) and abiotic (sediment mixing) factors. We have identified a new way to detect uncertainty (ambiguity) in transfer function reconstructions due to nuisance variables. The sensitivity of reconstructions to species selection can be quantified using the approach outlined here, facilitating an assessment of the robustness of the reconstruction.