The colors of proxy noise

The complex biological and physical processes that preserve paleoclimate information over centuries or longer introduce variations in proxy time series that are unrelated to the true climate. These non-climatic variations act on different timescales and are often referred to as “noise” of a specific color, based on similarities between a time series' power spectrum and the electromagnetic spectrum of light. For example, “white noise” equally affects all timescales, where “red noise” dominates only on long timescales, similar to longwave red light. Noise spectra in proxy records have far-reaching implications in paleoclimate research, but noise characteristics are often assumed based on first principles rather than estimated directly, risking either inflating or underestimating error at particular frequencies. Here, we provide concrete definitions of the various types of timescale-dependent errors that are present in proxy data, and review the literature on methods for quantifying noise terms. We then synthesize the results of several published studies that use a common empirical approach for estimating the noise spectrum in ice-core, coral, and tree-ring data. We posit that the colors of proxy noise are archive-specific, with white noise dominating in depositional archives such as ice cores and marine sediment cores, while red noise is more common in biological archives such as tree rings and corals. Our synthesis supports assigning specific colored noise terms in proxy system models, data assimilations and other experiments.

1 Introduction

Paleoclimate proxy records archive past climate information via biophysical or depositional pathways and preserve it in rings, layers or strata. The processes that create these records integrate non-climatic variability alongside the climate signal either during the archiving process, or afterwards as the physical record is modified over time (Cook, 1987; Evans et al., 2013). Recovering paleoclimate information from these archives requires sophisticated data processing and modeling techniques intended to extract climate-related variance from noisy time series (von Storch et al., 2004; Cook and Kairiukstis, 1990; Hughes and Ammann, 2009; Dee et al., 2016). Recognizing that these methods may be imperfect, the challenge lies in rigorously quantifying and minimizing the impact of non-climatic variations on the signal of past climate change.

Modification of climate signals in proxy time series can result in the addition of variance from random or unrelated fluctuations, loss of variance through smoothing, shifts in timing due to irregularities in the deposition or uncertainties in dating, or a combination of these effects (Fig. 1). We regard a process that adds variance on top of an existing climate signal as a “noise process”, whereas the loss of variance through smoothing also constitutes error (i.e., any difference between the true and reconstructed climate at a given timescale), but not noise, per se. Smoothing processes are typically deterministic to some extent. For example, two co-located ice-core records with similar physical properties are both affected by same isotopic diffusion and their correlation at a certain time-scale will not be affected in the absence of additional noise (Whillans and Grootes, 1985). It is further possible to correct individual records for deterministic errors if the process is well-understood (Schiffelbein, 1985; Meko, 1981; Dolman et al., 2021a; Shaw et al., 2024). By contrast, noise is typically independent, generating differences between nearby records as well as to the true climate signal. Observation and measurement errors are best represented by stochastic, uncorrelated noise unless they represent systematic bias, for example due to a change in the measurement apparatus. Because these types of noise are typically independent, averaging, or “stacking” individual records reduces noise while retaining the climate signal.

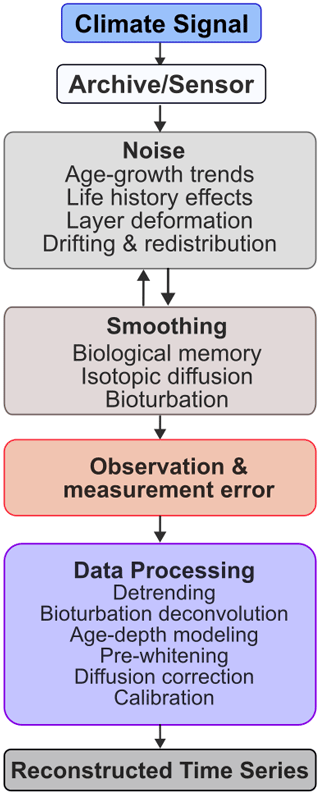
Figure 1 Conceptual diagram showing integration of different types of timescale-dependent proxy errors alongside climate signals via stochastic noise and subtractive smoothing.

Both noise and smoothing processes incorporate unique timescale-dependent uncertainties alongside climate signals. For example, trees integrate multi-decadal age-growth trends alongside climate variations, such that tree-ring time series are typically “detrended” before they are used in reconstructions (Fritts, 1976; Cook and Kairiukstis, 1990; Speer, 2010). Incomplete removal of age-growth trends results in long-term biases in tree-ring data, even if interannual correlations with climate data remain reasonably strong (Melvin and Briffa, 2008, 2014a, b). By contrast, physical smoothing processes such as isotopic diffusion or bioturbation in sediments act on fast timescales by removing climate information from within deposited layers (Johnsen et al., 2000; Whillans and Grootes, 1985; Hutson, 1980; Peng and Broeker, 1984). Smoothing dampens the climate signal at annual to centennial timescales, becoming less influential on longer timescales such that millennial-scale shifts in climate are retained (Schiffelbein and Hills, 1984; Laepple and Huybers, 2013; Münch and Laepple, 2018; Bothe et al., 2019).

These timescale-dependent variations can be analyzed in the spectral domain and referred to using colors by loose analogy to the frequency spectrum of light (Fig. 2). Time series with relatively more low- than high-frequency variability are considered to be “red”, by analogy to long-wave red light, whereas a “white” time series implies that power spectral density is distributed evenly across the frequency space.

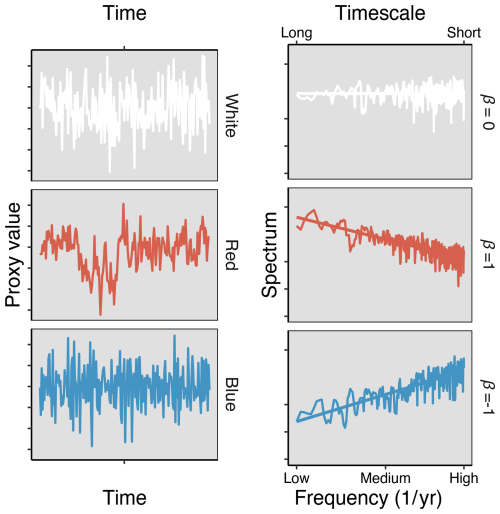
Figure 2 Spectral noise models with correlation structures referred to by analogy to colored light. Left panels show a simulated time series with the noise spectra shown in the right panels. Top: white noise with no correlation with timescale (β = 0). Middle: red noise (sometimes referred to as pink noise) with a positive relationship to timescale (β = 1). Bottom: blue noise with a negative relationship to timescale (β = −1). Note that β values for noise spectra are calculated as the slope of a linear model on a log-log plot, and expressed as β = slope × −1, following the convention where β describes the relationship between power and increasing timescale.

Low-frequency temperature variability is generally understood to exhibit increasing power with timescale, meaning that noise-free temperature proxy spectra would theoretically display a red spectrum (Pelletier, 1998; Huybers and Curry, 2006; Zhu et al., 2019). Noise, because it originates from a variety of sources may display different correlation structures. The integration of noise and climate signals may either further “redden” or “whiten” the spectrum by modifying the correlation structure of the raw time series. The relationship between power spectral density S(f) and frequency f is often summarized using a power-law scaling exponent β such that $S\left(f\right)\sim f^{-\mathit{\beta }}$ (Box 1) (Vautard and Ghil, 1989; Fraedrich and Blender, 2003; Hébert et al., 2021). The exponent β represents the relationship between frequency (or time period) and power spectral density, which appears as a linear relationship plotted on a log–log scale. By convention, the exponent is defined as the negative of the relationship with frequency such that a positive exponent represents increasing variance with timescale. Red noise processes are represented with a positive slope value (β>0); the term “pink noise” is sometimes used specifically for β=1 (Zhu et al., 2023). Red noise is a common noise model that implies autocorrelated errors that affect low-frequencies at a greater magnitude. (Mann et al., 2007; von Storch et al., 2009; Smerdon, 2012). By contrast, a “white” noise process implies errors uncorrelated in time such that the variance is distributed evenly across the frequency space (β=0), similar to the spectrum of white light. White noise is the simplest and most commonly-applied noise model in paleoclimate research (Fisher et al., 1985, Ammann and Whal, 2007; von Storch et al., 2004; Mann et al., 2005; Lee et al., 2008; Smerdon, 2010, 2012). Finally, blue noise refers to processes with relatively higher variability at high frequencies (β<0). Blue noise, which is less commonly used, is characterized by an anti-correlated structure, implying rapidly vanishing effects with increasing timescale (Mann and Rutherford, 2002; Mann et al., 2007).

Box 1 Summarizing the timescale-dependency of proxy noise using spectral power-laws.

Our understanding of proxy noise characteristics has evolved out of the need to reconcile diverging results in records that should, in principle, contain the same climate signal. For certain processes, such as the effects of measurement error, aliasing due to under-sampling, or depositional noise from roughness at the snow surface, the noise power spectrum can be derived from first principles and expressed in closed-form solutions (Fisher et al., 1985; Schiffelbein, 1985; Kunz et al., 2020; Dolman et al., 2021b). In cases where the physical and biological processes affecting proxies are well-understood, a more flexible approach is to use proxy system models (PSMs) (Jones et al., 2009; Vaganov et al., 2011; Evans et al., 2013; Tolwinski-Ward et al., 2011; Dee et al., 2016, 2017; Dolman and Laepple, 2018). In this case, climate data sets of temperature and precipitation from instrumental data, climate models or stochastic simulations are used as input to the PSM, and synthetic proxy time series are simulated. The spectrum of the noise can then be estimated through comparison to the climate time series (Dee et al., 2017). By omitting processes that are not well-understood, PSMs may underestimate the noise level. For example, stratigraphic noise in ice-core-based proxies can account for more than half of the isotope signal (Hirsch et al., 2023) but stratigraphic processes are not represented in current isotope PSMs (Dee et al., 2015). To account for “known unknowns” recent studies have added estimates of noise with specific spectral properties to mimic these extraneous sources of variability in PSM output, using models or reanalysis data as external validation (Dee et al., 2018; Evans et al., 2014; Zhu et al., 2023; Bothe et al., 2019).

Alternatively, empirical proxy noise spectra can be derived by relying solely on proxies by exploiting the spatial correlation of climate signals in nearby records, building on the assumption that non-climatic noise is independent between records. This approach has the advantage of being able to exploit the full length of paleoclimate time series without relying on climate models or short instrumental time series, and without the assumption that physical processes themselves are well-understood. One limitation is that this method relies on the availability of replicated or nearby records that have low time-uncertainty, such as corals, tree rings, banded ice cores or laminated sediments. If empirical noise estimates are consistent with those derived from mechanistic models this both validates the processes represented in PSMs creates a strong basis for using the resulting noise spectra in a variety of research applications.

In this study, we synthesize noise estimates derived directly from multiple proxy types and interpret their spectral characteristics in the context of known biological and physical processes. This provides a basis for evaluating signal fidelity and for refining assumptions commonly made in proxy system models and other experiments. We present noise estimates published in three studies where noise terms were derived using a simple empirical approach that partitions shared signal from independent variance on all timescales (Münch and Laepple, 2018), which we describe in the extended data section (Appendix A). We show results for published ice cores from Münch and Laepple (2018), tree rings (McPartland et al., 2024), and corals (Dolman et al., 2025). By presenting these findings alongside evidence from first principles and existing literature we aim to deepen a collective understanding of the behavior of proxy noise.

The tree-ring and coral data were sourced from global databases compiled by the Past Global Changes (PAGES) initiative (PAGES2k Consortium, 2017; Walter et al., 2023), and the ice-core data represent two large clusters of cores from Antarctica and Greenland (Graf et al., 2002; Weißbach et al., 2016; Hörhold et al., 2023) (Appendix B). Full details on each result are provided in the aforementioned studies. We focus our discussion on the noise spectra and resulting signal-to-noise ratio. Evaluating the climate signal spectra would ideally involve comparison with data and models, which are beyond the scope of this paper. In the extended data section, we reproduce the signal spectra and sample density at each frequency to provide all information involved in the noise spectra calculations and their uncertainty estimates (Appendix C).

2 The colors of proxy noise across paleo archives

Our review of published noise estimates demonstrates that tree rings and corals exhibit clear red noise spectra with positive scaling exponent β values of 0.8 and 0.5 respectively (Fig. 3a, b) such that the power of the noise increases with timescale (McPartland et al. (2024), Dolman et al. (2025). As the noise increases more than the climate signal, this leads to a decline of the signal-to-noise ratio (SNR) (Fig. 3d, e). Tree-ring and coral records result from the growth or accretion of layers by an individual organism over time such that life history or changes in the biological archiving system may affect proxy formation. Evidence suggests that proxy records composed of repeated measurements made on single long-lived organisms through time are susceptible to ontogenetic effects, the legacies of past disturbances, or slow changes in the behavior of the sensor.

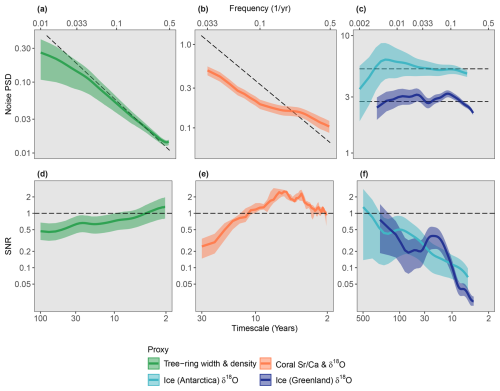
Figure 3 Estimates of proxy noise spectra (a–c) and timescale-dependent signal-to-noise ratios (d–f). Top: (a) mean noise spectra for tree-ring width and density records from the northern hemisphere, (b) mean noise spectra for tropical coral δ¹⁸O and strontium/calcium (Sr $/$ Ca) ratios, (c) noise spectra for ice core δ¹⁸O from Dronning Maud Land (light blue) in Antarctica and the North Greenland Traverse (dark blue). Dashed lines on the top row of panels represent an idealized spectral power-law with a slope β = 1 for proxies containing predominantly red noise (i.e. tree rings and corals), and with β = 0 for proxies (i.e. ice cores) containing predominantly white noise. Bottom: Timescale-dependent signal-to-noise ratios (SNR) for (d) tree rings, (e) corals, and (f) ice cores. Dashed lines represent an SNR of 1. Confidence intervals on all spectra represent the 10th and 90th percentiles from a parametric bootstrapping estimation method. Detailed methods for estimating proxy noise and SNR values can be found in McPartland et al. (2024) (tree rings) and Dolman et al. (2025) (corals).

In dendroclimatology, the pitfalls associated with tree ontogeny have been well-documented (Fritts, 1976; Cook et al., 1995; Esper and Frank, 2009). Cambial age impacts both tree-ring width and density such that detrending to remove juvenile age trends is a near universal practice (Cook and Kairiukstis 1990). Even after detrending, residual age effects could partially explain the persistent low-frequency bias observed in tree-ring records (Franke et al., 2013; Ault et al., 2013). Detrending itself can also introduce biases at medium-frequencies, particularly when fitting raw time series with negative exponential curves or rigid spline functions (Cook and Peters, 1997; Melvin and Briffa, 2008, 2014a, b; Esper, 2003; Briffa and Melvin, 2011). Techniques such as “signal-free” detrending have aimed at boosting low-frequency variability while minimizing bias (Melvin and Briffa, 2008), but despite retaining more low-frequency variance, tests of this method indicated only minor improvements in signal strength and signal-free chronologies retained their red-noise spectra (McPartland et al., 2020, 2024). By extension, red noise is likely a feature of bivalve and sclerosponge chronologies, which contain similar age-growth trends to those found in trees and are detrended using the methods originally developed in dendrochronology (Jones, 1983; Rypel et al., 2008; Hollyman et al., 2018; McCulloch et al., 2024).

Tree rings are also smoothed on fast timescales as a result of the carryover, or “memory”, of prior years' growth. Biological memory adds temporal autocorrelation to tree ring time series which has the effect of steepening the slope of the noise spectra by dampening high frequency power spectral density (Zhang et al., 2015; Lücke et al., 2019; McPartland et al., 2024). “Pre-whitening” chronologies by adjusting their temporal autocorrelation structure to match the climate target improves the interannual correlation between data and proxy (Meko, 1981), but by virtue of removing additional variability at high-frequencies, decreases the ratio of high to low power spectral density that defines the noise slope term β.

Coral aragonite records might similarly be affected by changes in the biology of individual or descendent polyps over time resulting in a slow drift in the temperature response of the proxy which would appear as low-frequency variability. Such changes could be growth-rate related due to reaction-kinetic effects (Goodkin et al., 2005; Hayashi et al., 2013; Maier et al., 2004; Saenger et al., 2008; Suzuki et al., 2005), result from changes in the calcification process (Lough, 2004), or persistent baseline shifts in trace element ratios following thermal stress events (D'Olivo and McCulloch, 2017; D'Olivo et al., 2019) perhaps mediated by changes in the composition of photosynthetic symbionts (Berkelmans and van Oppen, 2006; Cohen, 2002; Little et al., 2004).

The stacks of ice cores from both Greenland and Antarctica that we analyzed show a high white noise level where β is approximately equal to zero (Fig. 3e, f) (Münch and Laepple, 2018). As the climate variations become more pronounced on longer timescales, this leads to an increasing signal-to-noise ratio with time. We argue that proxies that are primarily the result of deposition, rather than growth or accretion primarily contain white noise stemming from stratigraphic processes. Precipitation intermittency and post-depositional redistribution in ice cores result in adjacent measurements that represent water from different precipitation events (Laepple et al., 2018; Casado et al., 2020; Zuhr et al., 2023). By extension, in marine sediments where foraminifera or diatoms are deposited from the water column, each sample represents a new set of individuals such that biological effects are uncorrelated between measurements. From process-based experiments, it has been demonstrated that noise in sediment records is also predominantly white with the signal level increasing as more individuals are measured (Kunz et al., 2020; Dolman et al., 2021b). In both ice and sediment core records of near-surface temperature, seasonal depositional cycles are much stronger than any interannual or even millennial climate change and the sparse subsampling of the seasonal signal leads to aliasing of independent noise within the signal of annual variation (Kunz et al., 2020). Precipitation intermittency and depositional redistribution break up the signal of the large seasonal cycle that would appear as a spike in the spectrum at annual timescales if the signal were recorded without disruption. Instead, the spike is redistributed as white noise across all frequencies (Casado et al., 2020; Münch et al., 2021).

We identified fewer examples of blue noise processes in the paleoclimate literature. Because its effects diminish quickly with time, blue noise does not introduce error past fast timescales. An example of a true blue noise process is the infilling of troughs on ice sheets as wind redistributes snow causing blue noise in noise in annual layer thickness records from ice cores (Fisher et al., 1985). Blue noise models have occasionally been tested alongside red and white noise to account for a variety of potential types of error affecting high-frequencies, and to improve the fit between synthetic proxy records and climate model data (Mann et al., 2007; Mann and Rutherford, 2002).

Like blue noise, smoothing processes predominantly affect high frequencies and becomes less significant with timescale. Biological memory in trees, diffusion in ice cores, and bioturbation in sediments are all examples of smoothing processes that lead to correlated errors between the climate and the proxy signal which can theoretically be accounted for using deterministic modeling (Matalas, 1962; Berger et al., 1977; Meko, 1981; Ruddiman et al., 1980; Whillans and Grootes, 1985). Given such a model, the smoothing effect can be reversed, as we applied in this example to ice core data to reverse the effects of diffusion (Shaw et al., 2024) (see Appendix A). If, as in the case of diffusion, the smoothing process affects the signal and the noise equally, the SNR is unbiased at all timescales regardless of whether or not a correction for the smoothing effect is applied. However, when noise is introduced after smoothing (e.g. measurement noise), the attenuated climate signal on the high-frequency side will be masked by a relatively stronger noise level, biasing the SNR spectrum downwards toward high frequencies. In any case, knowledge about and accounting for smoothing processes in paleoclimate time series is critical for evaluating the short-term effects of climate forcing events such as volcanic eruptions (Esper et al., 2015; Zhang et al., 2015; Lücke et al., 2019), but is potentially less critical for reconstructing low-frequency variations in climate.

3 Time uncertainty and noise color

Dating for all three proxy types discussed here is primarily achieved by some kind of band dating, or by counting annual cycles in geochemical tracers. If bands or cycles are missed, or double counted, this introduces time-uncertainty and an additional source of error in the reconstructed climate time series (Comboul et al., 2014). Time uncertainty has little effect on the shape of individual power spectra when the spectra are broadband, as is typical for climate time series (Rhines and Huybers, 2011). However, it reduces coherence between records, diminishing high-frequency power in stacked spectra and biasing SNR estimates downward at shorter timescales (Münch and Laepple, 2018; Fig. D1). The effect of time-uncertainty acts as a linear transfer function on the stacked spectra and can be estimated and corrected for if the time uncertainty is known, although this was not applied here (Appendix D). For the ice-core records analyzed here, the time-uncertainty is due to potential variations in the accumulation rate between volcanic tie-points and is negligible for frequencies below $\mathrm{1}/\mathrm{10}$ years (Münch and Laepple, 2018, their Fig. B1).

For the sub-annual resolution coral records used here, age models mostly come from counting annual cycles in the geochemical tracers. However, for most coral records there are no independently dated tie-points and so it is not possible to directly estimate counting error rates and correct for time-uncertainty. Simulations with potential error rates derived from corals show that the slope of the SNR is biased in the opposite direction to the one we estimate (Fig. D1) and that even for very large error rates of 1 in 10 years' time-uncertainty cannot account for the low SNR at decadal timescales. Time uncertainty is arguably less of an issue for tree-ring records as they are considered to be precisely dated and dendrochronologists routinely employ statistical cross-dating techniques to identify and eliminate dating errors (Holmes et al., 1986). Through this process locally absent rings are identified during cross-dating and assigned a no-data value to avoid affecting the final chronology. The strength of the tree-ring SNR on sub-decadal timescales is indicative of this dating precision.

For proxy archives that are not annually resolved such as reconstructions from non-varved terrestrial and marine sediment cores, the irregular spacing of samples in time and larger dating uncertainties makes stacking unsuitable for this type of noise estimation, representing a limitation of this approach. Alternative methods, such as estimating the SNR as a function of time uncertainty (Reschke et al., 2019), or applying tuning methods that align proxy records by maximizing covariance and assess significance against surrogate data (Haam and Huybers, 2010), may still allow for empirical SNR estimation in these cases.

4 Implications of colored noise for climate reconstruction

The spectrum of temperature on local to global scales is generally accepted to be red (Huybers and Curry, 2006; Cheung et al., 2017; Hasselmann, 1976). For proxies with predominantly white-noise spectra such as ice cores and sediments, this implies that the SNR increases with timescale. This explains why ice cores are faithful recorders of millennial climate variability (e.g. EPICA community members, 2006), while they fail in many regions to reconstruct interannual to decadal changes (Stenni et al., 2017). By contrast, in proxies that contain red noise, the SNR will rise more slowly or even decline with timescale if the power of the noise rises more steeply than the signal, as we demonstrate in tree rings and corals. These proxies are better recorders of fast time-scale variability where the ratio of signal to noise is highest. For example, corals can deliver unique information on tropical climate dynamics such as the El Niño Southern Oscillation (ENSO) (Fig. 3), but have challenges reproducing multidecadal trends (Scott et al., 2010). The color of the noise thus influences the timescales at which a robust climate signal can be reconstructed because it introduces a frequency-dependence to the SNR.

Information about proxy noise can be used to guide future study design (e.g. what proxies can be used to answer a climatic hypothesis) and to optimize the sampling and measuring design (e.g. how many cores are needed; what is the optimal sampling resolution to minimize noise). It can also be used to estimate time scale-dependent uncertainty in climate reconstructions. For individual proxy time series where the signal increases more strongly with timescale than the noise, when the signal spectrum is “redder” than the noise, binning to a coarser timestep or by applying stronger smoothing reduces the noise. This improves the SNR, albeit at the cost of losing information at shorter timescales. The extent to which uncertainty is reduced by binning or smoothing depends on the relative spectral slopes of both the signal and noise.

Knowing the color and level of proxy noise is valuable in a variety of research contexts in paleoclimatology. For example, accurate noise models are important for pseudo-proxy experiments (PPEs) in which climate model output is transformed into pseudo-proxy time series to test the skill of reconstruction methods and evaluate models (Jones et al., 2009; Smerdon, 2012). Often PPEs rely on sensitivity tests using different noise levels or spectral colors (Riedwyl et al., 2009; Smerdon et al., 2010; Mann and Rutherford, 2002; Gómez-Navaro et al., 2017). Red noise is often tested alongside white or sometimes blue noise, but typically using a first-order autoregressive (AR(1)) process with a fixed spectral slope (β = 2) (Mann et al., 2007; Riedwyl et al., 2009). However, this can lead to underestimation of the actual noise, especially at low frequencies where the spectrum of an AR(1) process levels out. More recent PPEs have integrated full PSM complexity with realistic noise estimates (Bothe et al., 2019; Zhu et al., 2023). Finally, accurate noise estimation is important in data assimilations and field reconstructions to bring reconstructed time series into better alignment with calibration datasets, and to propagate uncertainty in estimates of past climate variability (Goosse et al., 2010; King et al., 2021).

5 Conclusion

Building on prior insights from proxy system modeling, and with reference to a first-principles based understanding of proxy formation, we present here an overview of how colored noise is represented in different types of paleoclimate archives. Incorporating empirical, proxy-specific noise models as presented here into a range of paleoclimate research activities will help to move away from the assumption that noise is white or follows a first-order autoregressive process, which can lead to misinterpreting noise as signal and propagating biases into results. These noise models, or models derived using similar stacking and variance-partitioning methods, can be used account for the range of unique biological and physical processes affecting proxies in pseudo proxy experiments, data assimilation frameworks, and reconstructions efforts to improve the representation of patterns of past climate variability.

Appendix A: Estimating the spectrum of noise

We apply the method of Münch et al. (2018) of combining clustered proxy records into regional stacks and analyzing their variance in the frequency domain. This builds on the assumption that the proxy signal is a function of four main components: the climate signal, additive noise that arises during the proxy creation and archiving stages, measurement noise, and any smoothing processes that act during archiving but not on the measurement noise; i.e.

$$\begin{array}{}\text{(A1)}& P=f\left(C,N,\mathrm{\Sigma };G\right)=G\left(C+N\right)+\mathrm{\Sigma }\end{array}$$

where P, C, N, and Σ stand for the power spectral densities of the proxy signal, the climate signal, the proxy noise, and the measurement noise, respectively, and where G is a transfer function that describes a specific smoothing process such as biological memory, diffusion, or bioturbation.

Given a regional cluster of n proxy records with a similar climate between sites, the mean power spectrum, M, averaged across all individual records' spectra, will yield a precise estimate of the proxy spectrum P. By contrast, the power spectrum, S, of the stacked record from averaging all records in the time domain, will also contain the full climate signal, but with the noise proportions reduced by a factor of n. By combining both quantities one can derive expressions for the climate and noise spectra (Münch and Laepple, 2018),

$$\begin{array}{}\text{(A2)}& \begin{array}{rl}& C={\displaystyle \frac{n}{n-\mathrm{1}}}{G}^{-\mathrm{1}}\left(S-{\displaystyle \frac{M}{n}}\right);\\ & N={\displaystyle \frac{n}{n-\mathrm{1}}}{G}^{-\mathrm{1}}\left(M-S-{\displaystyle \frac{n-\mathrm{1}}{n}}\mathrm{\Sigma }\right)\end{array}\end{array}$$

with the ratio of C:N yielding the frequency-resolved signal-to-noise ratio (SNR). A common smoothing process equally biases the signal and the noise spectrum, if not corrected for by means of the inverse transfer function G⁻¹, and hence its effect cancels out in the SNR spectrum. We note that time uncertainty between individual proxy records can be another source of smoothing in the stacked record, but it is less straightforward to include into our methodology (Münch and Laepple, 2018) and is neglected here.

Appendix B: Data

B1 Tree Rings

For the tree-ring data we analyzed the tree-ring records contained within the Past Global Changes 2k (PAGES2k) database, a large database compiled to reconstruct global temperature variations during the last two millennia. This network of 647 unique paleoclimate records from around the globe includes 450 tree-ring time series, of which we used 421 records of tree-ring width and density located across the Northern hemisphere (PAGES 2k Consortium et al., 2013, 2017; Neukom et al., 2019). Spatial clusters were defined using 250 km radii, such that no two sites were more than 500 km apart. Tree-ring width and density records were clustered separately so that the proxies weren't mixed within clusters. This resulted in 253 clusters containing a minimum of 3, and a maximum of 30 sites per cluster. The average number of sites per cluster was 8. There were 18 density and 235 ring width clusters. The average length of the overlapping period was around 450 years. The results of all clusters of both proxy types were averaged at the end to derive the signal, noise and SNR. Uncertainty was calculated using a parametric bootstrapping approach. (McPartland et al., 2024).

B2 Corals

We used the coral records contained within the PAGES Coral Hydro 2k database to obtain coral SNR estimates (Walter et al., 2023). The Coral Hydro2k database contains 54 oxygen (δ¹⁸O) and strontium calcium (Sr $/$ Ca) records from the global tropics. The database was compiled to reconstruct sea surface temperature and ocean hydroclimate variability for the past two centuries. Due to fewer records, 1000 km spatial clusters were used, resulting in 64 clusters. δ¹⁸O and Sr $/$ Ca records were clustered separately and the results were averaged. More information on the coral data curation is contained in Dolman et al. (2025).

B3 Ice Cores

As an example in ice-core derived temperature proxies, we use stable isotope records from the Dronning Maud Land region in Antarctica (“DML data” in the following; Graf et al., 2002) and from central-north Greenland (“NGT data” in the following; Weißbach et al., 2016; Hörhold et al., 2023).

The DML data consist of 15 records, 12 of which cover the time period from 1800 to 1998 CE and 3 records cover 1000–1998 CE. We combine both datasets by using the individual spectral results (Münch and Laepple, 2018) of the shorter records on timescales below decadal and of the longer records on the supra-decadal timescales. We apply the diffusion correction as in Münch and Laepple (2018) but do not use their time-uncertainty correction.

The NGT data comprise 14 cores covering the time span from 1505 to 1979 CE, including original records from the North Greenland Traverse published in Weißbach et al. (2016) as well as the extended NGT records from exploiting new drillings as presented in Hörhold et al. (2023). The corresponding NGT spectra shown in Hörhold et al. (2023) were not diffusion-corrected; here, to be able to compare the NGT spectra to those from the DML data, we apply a diffusion correction to the NGT spectra following the method given in Münch and Laepple (2018) with diffusion length estimates calculated as described in Hörhold et al. (2023). Note that the SNR spectrum shown in Hörhold et al. (2023) used the ratio of the integrated signal and noise spectra, which is related to the correlation with the climate signal (Münch and Laepple, 2018), whereas here we show the direct ratio of the spectra.

Appendix C: Signal, noise and signal-to-noise ratio estimation

Full results for the uncorrected signal, noise and SNR estimates for tree rings, corals and ice-core data (Fig. C1a–d). Spectra in Fig. 3 represent truncated versions which have been cut off where sample density in corals and tree rings drop off (shaded regions), as seen in the spectral density plots (Fig. C1 bottom panels). In both corals and tree rings, the SNR rises again due to the reduction in replication and dominance by single or a small number of records with higher SNR than average (Fig. C1a, b) (see McPartland et al., 2024; Fig. 2e, f). Confidence intervals on all spectra represent the 10th and 90th percentiles from a parametric bootstrapping estimation method. In addition to the truncation due to low sample size, the lowest two spectral estimates on all spectra are removed during SNR calculation and confidence interval estimation a the multitaper approach introduces a small bias at the lowest frequencies (Percival and Walden, 1993).

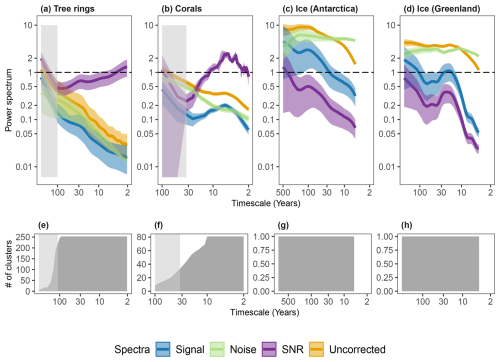
Figure C1 Timescale-dependent signal, noise and SNR estimates with sample density plots for tree rings (a, e), corals (b, f), and ice-core δ¹⁸O data from Dronning Maud Land in Antarctica (c, g) and the North Greenland Traverse (d, h). Panels (a)–(d) show signal (blue), noise (green) and SNR (purple) curves, with the uncorrected “proxy” spectra (yellow). Confidence intervals on all spectra represent the 10th and 90th percentiles from a parametric bootstrapping estimation method. The light grey shading indicates the cut-off point for spectral estimates presented in Fig. 3 when sample density decreases and the results become more uncertain. Detailed methods for estimating proxy noise and SNR values can be found in McPartland et al. (2024) (tree rings), Münch et al. (2018) (ice cores) and Dolman et al. (2025) (corals).

Appendix D: Simulated effects of time uncertainty on timescale-dependent signal-to-noise ratios

To illustrate the potential effects of time uncertainty on estimates of signal-to-noise ratio we used the approach of Comboul et al. (2014) as implemented by Münch and Laepple (2018). Münch and Laepple (2018) show that relative time-uncertainty between records in a stack acts as a linear transfer function, reducing power in the stack at high frequencies. The precise shape of the transfer function depends on the counting error rate, and on the lengths of the time series, as longer time series allow larger relative errors to accumulate. It does not depend on the power spectrum of the initial “true” signal. Here we show the effect on SNR for 100-year time series with band counting error rates of 1 in 10, 50 and 100 years, with equal probability of missing or double counting a band. The effect on estimated SNR is shown relative to a hypothetical true SNR of 1.

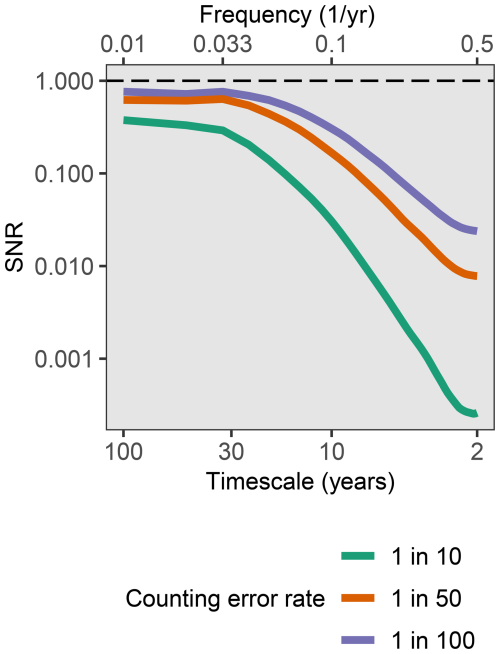
Figure D1 The influence of time-uncertainty on SNR estimated by the stacking method. Here time uncertainty is simulated for a set of 100-year depositional records with band counting error rates of 1 in 10, 50 and 100, and a true SNR of 10 at all frequencies. The simulation was carried out following Münch and Laepple (2018) which implements the counting error model of Comboul et al. (2014).