A novel conceptual model for Dansgaard–Oeschger event dynamics based on ice-core data

This study introduces a novel dynamical systems model designed to capture the highly non-periodic nature of Dansgaard–Oeschger (DO) events. Such events are difficult to model adequately due to their variable durations (some lasting around 1 century, while others span multiple millennia) and the occurrence of short precursor events that precede longer DO events despite similar boundary climate conditions. Utilising a simplified two-equation framework derived from the Stommel model, our approach integrates an internal control parameter which acts as a feedback parameter on the Antarctic Bottom Water (AABW) formation. Through both analytical and numerical methods, we establish a suitable parameter domain within which the newly adjusted models can accurately replicate the palaeoclimatic records of DO events as described by summary statistics derived from ice-core data. The analysis also shows that, without the novel control parameter, the model does not have a suitable parameter domain in which it can reproduce the wide range of event characteristics seen in the ice-core record. The study provides new insights into the underlying mechanisms driving these highly significant climate phenomena and the necessary timescale in which they are forced by allowing the new model's parameters to vary through time. This allows our model to achieve unprecedented precision in capturing a realistic sequence of DO events with timing characteristics matching those of the observational record. This refined model not only enhances our understanding of the DO cycles but also demonstrates the potential of simple dynamical systems to simulate complex climate interactions.

1 Introduction

The Atlantic Meridional Overturning Circulation (AMOC) is a critical component of the global climate system, responsible for transporting vast amounts of heat and influencing the oceanic and atmospheric circulation worldwide (Pedro et al., 2018; Broecker, 1998; Li and Born, 2019, and references therein). Variations in the AMOC have far-reaching effects on regional and global climate patterns, including surface temperature and precipitation (Pratap et al., 2023; Bellomo et al., 2023; Frankignoul et al., 2013). Therefore, understanding the behaviour of the AMOC and its response to various climate forcings in the past is essential for the prediction of future climate change and its impacts on society and ecosystems.

It has been proposed that the strength of the AMOC is linked to the observed abrupt changes in climate over the northern Atlantic during the last glacial (Henry et al., 2016). These Dansgaard–Oeschger (DO) events are characterised by a dramatic rise in temperature that transitions from a cooler stadial phase to a warmer interstadial phase, with temperature changes of around 5–16.5 K occurring over the North Greenland Ice Core Project (NGRIP) drilling site, sometimes within a couple of decades (Kindler et al., 2014). The abrupt warming is followed first by a gradual cooling, then often by an abrupt jump back to the cool stadial, after a period that can last from a century to millennia (Rasmussen et al., 2014). Notably, the DO events show comparable shape and magnitude while exhibiting substantial irregularity in duration and in the time between events. Coinciding with the DO events, Antarctica exhibits a contrasting climatic pattern, where interstadial warm phases in the Northern Hemisphere correspond to phases of cooling conditions in the south, and vice versa. This observed interhemispheric connection through an ocean thermal reservoir is well captured in the empirical bipolar seesaw (BPS) model (Stocker and Johnsen, 2003; Pedro et al., 2018, 2022).

Several conceptual models based on a few coupled ordinary differential equations have been proposed to model DO cycles (Mitsui and Crucifix, 2017; Kwasniok, 2013; Berglund and Gentz, 2010; Roberts and Saha, 2017). In a broad sense, some emphasise the bimodality as in Stommel's model of the thermohaline circulation (Stommel, 1961), and others emphasise the oscillatory nature of the DO events (Roberts and Saha, 2017). Other studies focus on the stochastic nature of the events and whether these climate events arise from purely random processes (Ditlevsen, 1999) or are significantly influenced by external factors (Schulz, 2002). While some aspects of these events can be modelled as stochastic, the sequence and modulation over time appear to be strongly shaped by external climatic effects (Mitsui and Crucifix, 2017; Lohmann and Ditlevsen, 2018). Another method employed in the dynamical systems regime accentuates the stochastic nature of climate transitions, providing a bridge between deterministic dynamical systems and real-world data that exhibits random variability (Kwasniok, 2013).

These models neglect the BPS interhemispheric elements, which are critical for a complete understanding of global climate interactions during these abrupt events (Pedro et al., 2018). Including the Antarctic climate record as well, fast–slow dynamical models, such as the FitzHugh–Nagumo model, have been proposed (Mitsui and Crucifix, 2017), which also fits well with the self-sustained DO oscillations found in a comprehensive ocean model (Vettoretti et al., 2022).

Advances in global climate modelling, particularly with the Community Climate System Model 4 (CCSM4) (Gent et al., 2011; Vettoretti and Peltier, 2018; Vettoretti et al., 2022), have successfully simulated spontaneous, unforced DO events within the climate system (Vettoretti and Peltier, 2016); for an overview of other models, see Malmierca-Vallet et al. (2023). Analysis of the CCSM4's phase-space trajectories, in particular, comparing the AMOC strength against the Antarctic Bottom Water (AABW) strength, has led to the development of a simplified model whose phase-space behaviour aligns closely with that predicted by more comprehensive models like CCSM4 (Vettoretti et al., 2022). This indicates that simpler dynamical systems models can effectively encapsulate the core dynamics of DO events despite the complexity inherent in comprehensive models. For simple models, a difficult aspect of the DO cycles to capture is the existence of the so-called precursor events, a term coined by Capron et al. (2010). These events are short interstadials lasting 100 to a couple of hundred years, followed by a brief stadial phase, directly followed by an interstadial of longer duration (typically more than 1000 years). The extreme examples – which are the ones highlighted in Capron et al. (2010) – are the precursors to interstadials 23 and 21, denoted GI-23.2 and GI-21.2 following Rasmussen et al. (2014), but the short events, GI-16.2, GI-15.1, and, to some degree, GI-17.2, within Marine Isotope Stage (MIS) 3 share the key characteristics, being short interstadials just prior to interstadials of much longer duration. The precursor events are shown in red in Fig. 1. This behaviour is not easily captured in simple models without requiring the addition of large amounts of noise or unrealistically quick changes to the model's control parameters, neither of which are aligned with our understanding of the underlying physical system.

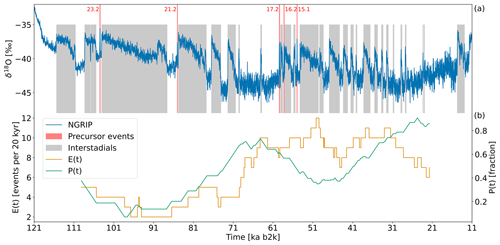
Figure 1 The ice-core record. (a) The δ¹⁸O record from NGRIP with the classification of interstadials by Rasmussen et al. (2014). All ages are given in thousands of years relative to the year 2000 CE (denoted ka b2k). The precursor interstadial events from left to right, GI-23.2, GI-21.2, GI-17.2, GI-16.2, and GI-15.1, are shown in red. (b) The number of DO events, E(t), and the fraction of time spent in stadial conditions, P(t), within running 20 kyr long windows, following Lohmann and Ditlevsen (2018).

In this paper, we present a simple two-equation model of the Atlantic Ocean circulation. Our model is derived from a formulation similar to a simple ocean box model (Stommel, 1961) but incorporates a time-dependent dynamic forcing that introduces variations between monostable fixed points and limit cycles. Our model introduces a novel control parameter that represents a feedback between changes in the AMOC and AABW. Our objective is to capture more of the observed variability in DO events in terms of duration and temporal spacing and ultimately to reproduce precursor events. We provide a physical process-based motivation for our model from modifications to the system described in Vettoretti et al. (2022). We also perform a stability analysis of our model to evaluate its theoretical behaviour under varying boundary conditions following the methodology established in Berglund and Gentz (2010). Specifically, we utilise a novel visualisation technique that involves solving the eigenvalues of the system's Jacobian and illustrates the parametric stability of the phase space of the dynamical system.

2 Methods

We first describe the statistical methodology used to characterise and examine the dynamics of DO events. Our method applies a statistical framework for comparing our conceptual model outcomes with the palaeoclimate records from the NGRIP ice-core record. Then, the conceptual model of Vettoretti et al. (2022) is introduced as a simplified, buoyancy-driven box model, adapted to simulate the rapid transitions and slow climatic shifts associated with DO events. The conceptual model and its connection to the physical world are first discussed in Sect. 2.2 in order to explain the overall model design and behaviour with only the necessary mathematical details. We then argue for why an extra factor has to be added to the model: a critical component of our analysis is the introduction of the α parameter, which modulates the model's sensitivity to changes in Southern Ocean (SO) buoyancy fluxes, directly impacting the dynamics of AABW formation and the AMOC strength. A more rigorous theoretical approach is developed in Sect. 2.3. Readers not interested in the theoretical background can skip Sect. 2.3 and jump directly to Sect. 3.

2.1 The statistical framework

As a basis for our analysis of the characteristics of the modelled and observed DO variability, we make use of the statistical framework proposed by Lohmann and Ditlevsen (2018). This allows a quantitative comparison of the behaviour of our conceptual model with the palaeoclimate records from NGRIP. Here, the observations are regarded as a specific realisation of a stochastic process, acknowledging that another realisation of the climatic evolution of the last glacial period would likely come out differently. Thus, a model should not necessarily reproduce the NGRIP record but rather have similar characteristics, and, rather than over-fitting to observations, our focus is on a few so-called summary statistics, characterising the observed record and the underlying dynamics. Therefore, we have constructed the model such that it is computationally light enough that robust statistics can be obtained for a large number of realisations.

In our statistical framework, the time series are characterised by two summary statistical parameters: the number of DO events E(t) in a 20 kyr window centred at a given time t and the fraction of time spent in stadial-like conditions P(t) within the same 20 kyr window. We use this statistical framework to compare our model with the NGRIP ice-core records, thereby enabling us to assess the likelihood that the observed summary statistics could be drawn from the distribution of summary statistics produced by the model as seen in Fig. 1. We then utilise a grid-search method to explore the parameter space and identify the optimal set of parameters that best fit the data. We constrain the grid search using the parameter intervals derived from the stability analysis (Sect. 2.3.5).

2.2 The physical conceptual model

Here we present a thorough introduction to the simple model briefly introduced in Vettoretti et al. (2022) and describe the relationship between the model physics and the time series it generates. Then, we briefly explain our extension of the model of Vettoretti et al. (2022). We do this with a minimum of formalism and concepts from dynamical system theory. Readers with an interest in the detailed derivation and stability analysis of the set of governing equations for the dynamical system are referred to Sect. 2.3.

The model consists of two non-dimensional governing equations. The non-dimensionality is discussed in more detail in Sect. 2.3.2:

$$\begin{array}{}\text{(1)}& {\displaystyle }\dot{\mathrm{\Delta }b}=-B-\left|q\right|(\mathrm{\Delta }b-b_{\mathrm{0}})+\mathit{\sigma }\mathrm{d}W,\text{(2)}& {\displaystyle }\dot{B}={\displaystyle \frac{\mathrm{1}}{\mathit{\tau }}}(\mathrm{\Delta }b-\mathit{\gamma })+\mathit{\sigma }\mathrm{d}W.\end{array}$$

The first variable is the meridional buoyancy gradient, Δb, which describes the buoyancy difference between the northern and southern Atlantic, akin to changes in the AMOC. Δb is driven by the transport factor q (explained further in Sect. 2.3.2), which, depending on the value of Δb, can reverse the direction of transport (illustrated in Fig. 2) and thereby induce the abrupt changes in the AMOC we wish to simulate. The second variable is the buoyancy flux, B, which describes the combined heat and freshwater flux into or out of the ocean surface. B is applied to the SO with a corresponding balance to the north and is physically related to changes in the AABW formation. Through this mechanism, our model incorporates the fundamental principles of the BPS (Vettoretti et al., 2022). b₀ is a tuning parameter, introduced to shift the system along the Δb axis. The factor dW is Gaussian noise added at each time step scaled by σ. This represents the internal climatic variability and can lead to noise-induced tipping; see the end of Sects. 2.3.5 and 3.1 for more details on the properties of the noise.

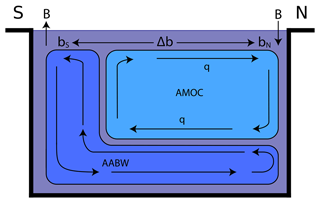
Figure 2 The box model. The Stommel-like box model illustrates the simplified physical transport system described by the governing equations. The focus is on the meridional buoyancy difference (Δb) between the northern and southern Atlantic regions driven by the transport factor q. The buoyancy flux, B, describes the combined heat and freshwater flux into or out of the ocean surface, applied to the SO with a corresponding balance to the north.

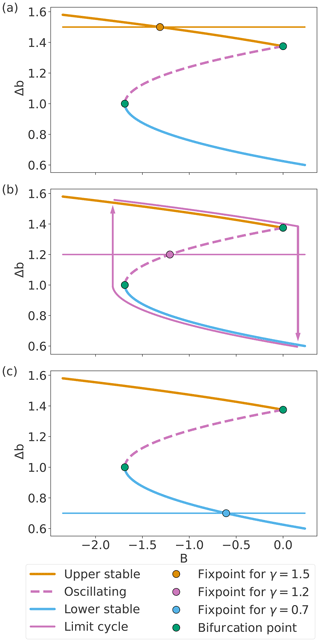
Figure 3 Different regimes of the simple model. The Δb nullcline (the multi-coloured inverted S-shape) and its stability regimes are constant through the three panels. (a) When the horizontal B nullcline intersects the upper part of the Δb nullcline, the system is in a stable interstadial state. (b) If the intersection takes place in the middle, the system oscillates and follows the limit cycle. (c) If the intersection of the nullclines is located on the lower part of the Δb nullcline, the system is in a stable stadial state. As γ changes (the cases $\mathit{\gamma }=\mathrm{1.5},\mathrm{1.2},\mathrm{0.7}$ are shown), the B nullcline moves up and down, and bifurcations take place at the green points which separate the three regimes.

The presence of $\mathrm{1}/\mathit{\tau }$ in the so-called slow equation, Eq. (2), with τ≫1, means that the two equations describe a slow–fast system; thus any change in the Δb parameter will be much faster than a corresponding change in the B parameter, mimicking the fast response of an interstadial onset, compared to the much slower corresponding BPS response in and around Antarctica. The behaviour of the system is controlled by the relative position of the two nullclines ($\dot{\mathrm{\Delta }b}=\mathrm{0}$ and $\dot{B}=\mathrm{0}$) as seen in Fig. 3. The Δb nullcline corresponds to the inverted S-shaped curve, while the B nullcline corresponds to the flat horizontal line. In this paper, we refer to the Δb nullcline as the slow manifold, the curve where the system evolution is dominated by the slow parameter, following the formalism outlined in Berglund and Gentz (2010). We note that nullclines and manifolds are generally not identical for finite values of τ, but the difference is not important in this case, especially due to the presence of noise. As $\dot{B}=\mathrm{0}\iff \mathrm{\Delta }b=\mathit{\gamma }$, γ can be seen as a control parameter (in Vettoretti et al., 2022, taken to be the CO₂ concentration expressed in units of buoyancy) that moves the B nullcline up and down. The location of the intersection of the two nullclines determines the dynamics of the model. When the nullcline intersects the slow manifold in either the upper or lower part (either above or below the corresponding bifurcation points marked by green points in Fig. 3), the model has a stable fixed point and will tend towards this fixed point. These represent a stable interstadial or stadial state, as seen in Fig. 3a and c, respectively.

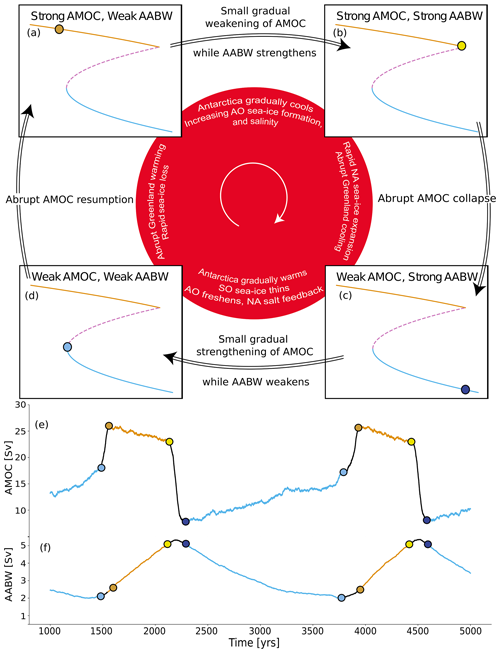
Figure 4 Schematic representation of the behaviour of the model. The sequence from panel (a) to panel (d) showcases the system's progression between stadials and interstadials when it is in the oscillatory regime (as shown in Fig. 3b). The coloured points demonstrate how various segments of the time series (e–f) align with the different states (a–d) as the system oscillates along the slow manifold. The inner part details key physical processes driving the transitions within the comprehensive climate model, which has been shown to have the same qualitative behaviour as our conceptual model (Vettoretti et al., 2022).

When the B nullcline intersects the middle part of the slow manifold, shown as the dashed line in Fig. 3b, the fixed point is unstable and the system will perform oscillations by following the limit cycle, shown as the two arrows in Fig. 3. The diagram in Fig. 4 demonstrates the relationship between the model's phase space and the resultant time series it generates when it is oscillating. In panels (a), (b), (c), and (d), we observe how the state of the system traverses around the limit cycle, with each transition between points linked to the specific events happening here. The inner red section of this panel shows the physical processes associated with these transitions, as inspired by the comprehensive model simulations in Vettoretti et al. (2022). Meanwhile, the generated time series are seen in panels (e) and (f), marked by coloured points and intervals aligned with the system's position on the limit cycle.

This simple model has its limitations in terms of mimicking observed DO variability by exhibiting a high degree of periodicity when the system is oscillating and by having limited variability in the duration of the interstadial–stadial configurations: when γ attains higher values, the system exhibits longer interstadials and short stadials, and vice versa. To better mimic the behaviour seen in ice-core records, one can force the system with a high-amplitude, fast-varying γ value, which is not consistent with the idea that γ represents the CO₂ concentration. To address this limitation, we propose adding another term, $\mathit{\alpha }B/\mathit{\tau }$, to Eq. (2), representing a feedback mechanism that changes the rate at which the ocean takes up heat or gives off heat during a DO cycle. The α parameter affects the rate of change of AABW production, reducing the rate of change of buoyancy flux in interstadials and increasing it in stadials. Physically, it is associated with an SO warming or freshwater-flux parameter, described in more detail in Sect. 2.3.4. We call α the “slope parameter” because it leads to a non-zero slope of the B nullcline, as seen in Fig. 5. By introducing the combination of changing the magnitude of the slope and moving the nullcline up and down, it is possible to more dynamically control the durations of both the stadials and interstadials and the periodicity of DO events through time.

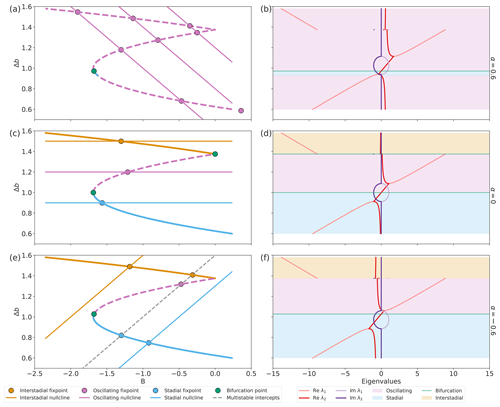
Figure 5 The phase space of the system and the eigenvalues of the Jacobian for three different configurations of the model: (a, b) α=0.6, (c, d) α=0 (equivalent to the cases in Fig. 3), and (e, f) $\mathit{\alpha }=-\mathrm{0.6}$. (a, c, e) Phase space of Δb and B showing the Δb and B nullclines, bifurcation points, and fixed points in different colours based on their stability. (b, d, f) The stability is determined from the system's Jacobian 𝒥 which has two eigenvalues whose real and imaginary components are shown.

2.3 Detailed model description and stability analysis

In the following sections, we provide an in-depth description of our extended model, which is formulated in terms of buoyancy, and the link between the non-dimensional model formulation and the physical world. We then introduce the slope parameter α as an extra term in the governing equations and analyse the extended model's stability. Readers mainly interested in how the model performs compared to the observed DO cycle can move directly to the results in Sect. 3.

2.3.1 The buoyancy framework

We employ a simplified box model with the flow driven by buoyancy differences based on the principles of the multi-vessel Stommel model (Stommel, 1961), as described in Vettoretti et al. (2022). The conceptual model (illustrated in Fig. 2) is formulated in terms of buoyancy and buoyancy fluxes, with Δb defined as the meridional gradient between the buoyancy of the southern box (b_S) and the northern box (b_N). The southern box's buoyancy is greater than the northern box's buoyancy; ergo, Δb is always positive in our standard conceptual model. Therefore, one might think of this difference in physical terms as sinking in the north with denser northern waters returning at intermediate depths, e.g. Stommel (1961). The buoyancy flux (B) captures the haline and thermal forcing of the ocean surface. Classically, boxes are forced by an equal amount of freshwater leaving a southern or equatorial box and entering a northern box, with the density gradient mainly being driven by salinity changes (Cessi, 1994). In a similar methodology, here the buoyancy flux always removes buoyancy at the southern box, while the northern box gains buoyancy, and the transport q (which may be positive or negative) keeps this Δb gradient in balance, either in a strong positive (interstadial) or weak positive (stadial) state. As outlined in Fig. 4, there are four essentially different states of the DO cycle. Starting our description in the mode of strong AMOC and weak AABW (a), corresponding to the beginning of an interstadial period, the southern buoyancy flux is weak and the circulation is largest (q>0). As the system is autonomous, the AMOC decreases, and the southern buoyancy flux begins to increase and removes more buoyancy from the southern box (in Fig. 2, the buoyancy flux moves buoyancy out of the SO, decreasing b_S). While the transport acts to move some of the less buoyant water from the southern box to the northern box, it does not fully compensate for the decreasing buoyancy in the southern box, and the circulation weakens. This is typically understood as a freshwater feedback, where the freshwater transport is out of the northern box southwards, which creates a feedback where more salt is brought into the North Atlantic by a stronger AMOC. This results in a feedback of more freshwater transport out of the northern box with the stronger AMOC. Here we describe how the buoyancy decreases (or density increases) in the southern box, so this mimics a transport of freshwater to the northern box, which weakens the circulation. This is the negative salt-advection feedback.

Conversely, the equal and opposite buoyancy flux in the north is adding buoyancy to the northern box, the combination of which weakens the buoyancy gradient to bring us to a strong (but not maximum) AMOC and strong AABW mode (b); here q=0, and there is no salt-advection feedback. The system then tips abruptly into the mode with weak AMOC and strong AABW (c), and q reverses (the positive salt-advection feedback). The buoyancy flux removal in the southern box remains strong while the system transitions to the lower stable branch. The flow then gradually moves buoyancy, via the positive salt-advection feedback, from the northern box to the southern box to slowly increase the positive buoyancy gradient. At the same time, the buoyancy flux (AABW) begins to weaken in the southern box; conversely, the buoyancy flux into the northern box strengthens. The strong reversed flow begins to weaken, and we enter a mode with weak but slightly strengthened AMOC and weak AABW (d). As the system approaches the lower bifurcation point and then jumps to the upper part of the slow manifold, the transport switches sign (q>0) and the removal of buoyancy remains weak while the circulation is strongest (when Δb is large), and the cycle repeats.

The behaviour of the conceptual DO box model can be related to physical processes. The removal of buoyancy in the southern box represents AABW formation through the removal of buoyancy at the surface, which one might physically think of as brine rejection from forming sea ice, or the removal of heat from the ocean surface by katabatic winds blowing downslope over the Antarctic Peninsula, forming latent-heat polynyas. The increase in buoyancy associated with a positive buoyancy flux into the northern box can be related to the transport of thick Arctic sea ice into regions of North Atlantic Deep Water formation. Removal of heat would act to decrease buoyancy, but haline influences on buoyancy dominate at high latitudes. The transport q can be related to the F_ov parameter used in many studies that investigate the bistability of the AMOC, e.g. Cimatoribus et al. (2014). It can reflect the convergence or divergence of salt into the North Atlantic which helps to act as positive or negative feedback.

2.3.2 Model formalism

Based on the physical arguments, in Sect. 2.2 we derived the set of stochastic ordinary differential Eqs. (1) and (2) for the conceptual model of Vettoretti et al. (2022). Ignoring for a moment the stochastic noise terms, the deterministic part of the model is of the general form $\frac{\mathrm{d}y}{\mathrm{d}t}=\left(f\right(y)-x)$, $\frac{\mathrm{d}x}{\mathrm{d}t}=(y-\mathit{\gamma })/\mathit{\tau }$. With the choice $f\left(y\right)=a(y-y^{\mathrm{3}})+b$, the model becomes the FitzHugh–Nagumo model, previously used in simple models of DO events (Mitsui and Crucifix, 2017). Instead, our model is formulated as a simplified box model with the flow driven by buoyancy differences based on the principles of the multi-vessel Stommel model (Stommel, 1961), as described in Vettoretti et al. (2022), but with model overturning described in terms of the meridional buoyancy gradient rather than density (as in Stommel, 1961) using the following equivalency:

$$\begin{array}{}\text{(3)}& \mathrm{\Delta }b={\displaystyle \frac{-g}{{\mathit{\rho }}_{\mathrm{0}}}}\mathrm{\Delta }\mathit{\rho },\end{array}$$

where g is the gravitational acceleration and ρ₀ is a reference density.

The parameters used in our model are inferred from the comprehensive modelling study of DO variability (see the Supplement of Vettoretti et al., 2022). In the CCSM4 simulations of glacial climate, a linear relationship between the meridional buoyancy gradient (Δb) in the Atlantic and the strength of the AMOC was observed. A relation for the box-model transport was presented ($q=q_{\mathrm{0}}+q_{\mathrm{1}}(\mathrm{\Delta }b-b_{\mathrm{0}}$)) as a process-based relationship with salt-advection feedback, where the non-dimensional constants are $q_{\mathrm{0}}=-\mathrm{9}$ and q₁=12. Inserting $q=q_{\mathrm{0}}+q_{\mathrm{1}}(\mathrm{\Delta }b-b_{\mathrm{0}})$ into Eq. (1), we arrive at the first equation of the non-dimensional conceptual model of Vettoretti et al. (2022):

$$\begin{array}{}\text{(4)}& \dot{\mathrm{\Delta }b}=-B-|q_{\mathrm{0}}+q_{\mathrm{1}}(\mathrm{\Delta }b-b_{\mathrm{0}}\left)\right|(\mathrm{\Delta }b-b_{\mathrm{0}})+\mathit{\sigma }\mathrm{d}W,\end{array}$$

where we have introduced a Wiener process, dW, with a scalable σ parameter to describe the internal variability of the system.

In the following section, we explain the relationship between the flow parameter, q, and the strength of the AMOC. Additionally, we will outline the process of converting the non-dimensional equations into the appropriate physical units.

2.3.3 Coupling of flow with AMOC strength and redimensionalisation

In the simple model, we can replicate the range of values of the AMOC in the comprehensive model simulations of the DO oscillation by introducing constants that describe the characteristic scales of transport (ψ₀,ψ₁) in the ocean to obtain physically meaningful values. The AMOC is then a function of the buoyancy gradient through the following relationship: ${\mathit{\psi }}_{\mathrm{0}}=-\mathrm{4.5}\times {\mathrm{10}}^{\mathrm{6}}{\mathrm{m}}^{\mathrm{3}}{\mathrm{s}}^{-\mathrm{1}}$, ${\mathit{\psi }}_{\mathrm{1}}=\mathrm{20.0}\times {\mathrm{10}}^{\mathrm{6}}{\mathrm{m}}^{\mathrm{3}}{\mathrm{s}}^{-\mathrm{1}}$, AMOC${}_{\dim }={\mathit{\psi }}_{\mathrm{0}}+{\mathit{\psi }}_{\mathrm{1}}\mathrm{\Delta }b$. This redimensionalisation of the AMOC ensures that it is positive definite at all times as in the real ocean, where the non-dimensional q is a transport which can switch directions as in the classic Stommel model and represents a transport of buoyancy in either direction (the thermal and haline modes). The buoyancy and buoyancy flux can be redimensionalised to physical units with the characteristic values used to non-dimensionalise the physical equations, b_c=0.004 m s⁻² and $B_c=\mathrm{3.8}\times {\mathrm{10}}^{-\mathrm{10}}$ m⁻² s⁻³.

Additionally, connection is made in our formulation between the buoyancy flux and AABW production or transport suggesting that the density change in the southern box is related to AABW production and therefore there is an interplay between the AABW and AMOC strength (Klockmann et al., 2018; Nadeau and Jansen, 2020). Following Vettoretti et al. (2022), AABW production is proportional to B. The non-dimensional buoyancy flux can be transformed to AABW units (Sv) as follows:

$$\begin{array}{}\text{(5)}& {\mathrm{AABW}}_{\dim }={\mathit{\psi }}_A+\mathit{\chi }A{\displaystyle \frac{B_c}{b_c}}B,\end{array}$$

where χA is a scaled area of the Atlantic where buoyancy is fluxed downwards, with the following values, $A=\mathrm{7.0}\times {\mathrm{10}}^{\mathrm{12}}$ m², χ=2.5, and ${\mathit{\psi }}_A=\mathrm{5.0}\times {\mathrm{10}}^{\mathrm{6}}$ m³ s⁻¹, as derived in the Supplement of Vettoretti et al. (2022).

In this parametrisation, the flow q reaches zero at the end of the interstadial period at the upper bifurcation point (see Fig. 3), which results in bifurcation-induced tipping into the stadial period. At this point, the flow reverses (q<0, but the AMOC remains positive). While the transport q in the non-dimensional form used here transports buoyancy, it captures freshwater transport between boxes and is therefore related to the salt-advection feedback used in other simple models and in comprehensive models used to assess bistability of the AMOC (Dijkstra, 2007).

2.3.4 The role of the α parameter

To alter the periodicity of oscillations within the simple model and to capture other physical time-dependent processes associated with buoyancy fluxes in the SO, we introduce an additional term, $\mathit{\alpha }B/\mathit{\tau }$, to Eq. (2), as discussed at the end of Sect. 2.2. This modification leads to our updated version of the slow-timescale equation:

$$\begin{array}{}\text{(6)}& \dot{B}={\displaystyle \frac{\mathrm{1}}{\mathit{\tau }}}(\mathrm{\Delta }b+\mathit{\alpha }B-\mathit{\gamma })+\mathit{\sigma }\mathrm{d}W,\end{array}$$

which, together with Eq. (4), forms our set of model equations.

Incorporating the new parameter into the B equation transforms the nullcline from a constant to a linear relation ($\mathrm{\Delta }b=\mathit{\gamma }-\mathit{\alpha }B$). The nullcline represents areas where the rate of change in B ($\dot{B}$) switches between positive and negative. Essentially, the vertical distance to the nullcline indicates the magnitude of this rate of change in B; a smaller distance implies a slower rate of change. By introducing a slope to the nullcline, this distance – and consequently the rate of change in B – becomes variable rather than fixed. This adjustment allows more control of the dynamics throughout interstadial and stadial periods, making the model's simulation of these periods more adaptable to varying climatic conditions. Secondly, the non-zero slope of the B nullcline leads to the formation and elimination of intersections with the slow manifold within very small changes in α and γ compared to the case with the horizontal nullcline. For example, for appropriate values of the slope, it becomes possible for the model to go from having a single stable fixed point on the upper part of the slow manifold to a single stable fixed point on the lower part of the slow manifold with small changes in α and γ. Lastly, the new B nullcline allows the system to have two stable fixed points simultaneously, one in the upper part and one in the lower part of the slow manifold, transforming the system to a purely noise-driven bistable system, creating non-periodic oscillations.

The α parameter plays a crucial role in representing a key influence on the buoyancy of the SO. An increase in α affects the buoyancy flux (or AABW), dampening buoyancy changes during interstadials and amplifying them during stadials. This results in prolonged interstadials and shortened stadials, indicating that SO warming or an additional buoyancy flux associated with sea-ice formation could play a significant role, should similar mechanisms operate in the real world. An increase in α could be indicative of increased meltwater flow from melting Antarctic sea ice, pointing to a significant accumulation of either freshwater or heat. This condition is further demonstrated when there is an intersection of the B nullcline with the upper part of the slow manifold. In such instances, the robustness of the increased meltwater flow is sufficient to prevent a collapse of the AMOC, possibly by hindering sea-ice formation or through other mechanisms. In such scenarios, the AMOC remains in a slightly reduced mode compared to the onset of a DO event, maintaining a quasi-interglacial or “modern” state.

2.3.5 Stability analysis

The governing Eqs. (4) and (6) of our model represent a slow–fast system where the analysis can be split into fast changes in Δb, analogous to the stadial–interstadial transitions, and slow changes along the stable parts of a slow manifold, which dictate the behaviour of the system on longer timescales. To constrain the domain of relevant values of the control parameters, we analyse the stability of the dynamical system. This is done by finding the eigenvalues λ_1,2 of the Jacobian, 𝒥, for the model including the slope term given by

$$\begin{array}{}\text{(7)}& \mathcal{J}\equiv \left(\begin{array}{cc}\frac{\partial \dot{\mathrm{\Delta }b}}{\partial \mathrm{\Delta }b}& \frac{\partial \dot{\mathrm{\Delta }b}}{\partial B}\\ \frac{\partial \dot{B}}{\partial \mathrm{\Delta }b}& \frac{\partial \dot{B}}{\partial B}\end{array}\right)=\left(\begin{array}{cc}x& \mathrm{1}/\mathit{\tau }\\ -\mathrm{1}& \mathit{\alpha }/\mathit{\tau }\end{array}\right),\end{array}$$

where

$$\begin{array}{}\text{(8)}& x=-|q_{\mathrm{0}}+q_{\mathrm{1}}(\mathrm{\Delta }b-b_{\mathrm{0}}\left)\right|-q_{\mathrm{1}}\mathrm{\Lambda }\left(\mathrm{\Delta }b\right)(\mathrm{\Delta }b-b_{\mathrm{0}}),\end{array}$$

with

$$\mathrm{\Lambda }\left(\mathrm{\Delta }b\right)=\left\{\begin{array}{ll}\mathrm{0}& \mathrm{if}\mathrm{\Delta }b=\frac{-q_{\mathrm{0}}}{q_{\mathrm{1}}}+b_{\mathrm{0}}\\ \mathrm{sign}(q_{\mathrm{0}}+q_{\mathrm{1}}(\mathrm{\Delta }b-b_{\mathrm{0}}\left)\right)& \mathrm{otherwise}\end{array}\right..$$

The panels in the right part of Fig. 5 show the eigenvalues of 𝒥 as Δb changes. In all panels, the real parts of λ_1,2 are different for low Δb values, become identical for values of Δb close to 1, and then differ again for large Δb values. When the two are not identical, $\left|\mathit{Re}\right({\mathit{\lambda }}_{\mathrm{1}}\left)\right|$ diverges with larger $\left|\mathrm{\Delta }b\right|$ values, while $\left|\mathit{Re}\right({\mathit{\lambda }}_{\mathrm{2}}\left)\right|$ remains small. The imaginary parts of the eigenvalues (purple lines) are zero for most values of Δb, but when the real parts coalesce around Δb=1, and at the point of non-differentiability, the imaginary parts are also non-zero (purple points).

To determine the stability of the state, we look at three cases: if Re(λ)<0 the system is stable, and for Re(λ)>0 the state is unstable. Lastly, if λ is purely imaginary, then the system is undergoing a bifurcation. Firstly, we analyse the situation with α=0, Fig. 5c and d, to compare it with the literature (Mitsui and Crucifix, 2017; Vettoretti et al., 2022). For Δb<1, the system is in a stable state (blue region). This corresponds to the lower part of the slow manifold. Then, when Δb=1, λ_1,2 becomes purely imaginary and the system undergoes a bifurcation (green horizontal line). Increasing Δb, the system becomes unstable (purple region). Here, the system will always converge to the limit cycle and exhibit oscillatory DO-like behaviour. At $\mathrm{\Delta }b=\frac{-q_{\mathrm{0}}}{q_{\mathrm{1}}}+b_{\mathrm{0}}=\mathrm{1.38}$, the manifold is non-differentiable; therefore $\frac{\partial \dot{\mathrm{\Delta }b}}{\partial \mathrm{\Delta }b}$ is undefined. Kowalczyk and Glendinning (2011) show that a non-smooth bifurcation occurs and that the derivative, $\frac{\partial \dot{\mathrm{\Delta }b}}{\partial \mathrm{\Delta }b}$, should be defined to 0. After the bifurcation, we again have a stable system (yellow region), now in the interstadial state.

When α≠0, the stability changes, as shown in Fig. 5b and f. The eigenvalues as a function of Δb have the same shape as for α=0 but shift with the size of α. The combined movements of the real and imaginary parts result in a drastic change in the stability of the manifold. For $\mathit{\alpha }=-\mathrm{0.6}$, Fig. 5e and f, the lower part of the manifold becomes stable for a larger interval of Δb values. In the same way, the lower bifurcation happens at this higher value for Δb. The bifurcation at the non-differentiability (Δb=1.38) disappears as α changes the real part of the eigenvalues for the Jacobian (Kowalczyk and Glendinning, 2011) to be non-zero.

For α=0.6, Fig. 5a and b, the stability of the whole manifold changes. The entire manifold becomes unstable (purple shading), and the system diverges instead of converging to a fixed point or the limit cycle. A very small part of the lower manifold is still stable when the real part of λ₂ (dark red) is negative. This allows a half-stable limit cycle, where, if the system is inside the limit cycle, it converges out to the limit cycle, but if it is outside, it diverges. This condition results in a highly unstable system, as the noise-driven variability can quickly push the system outside of the limit cycle. Relating this scenario to the physical explanation of α, the α parameter leads to a feedback mechanism that not only maintains but actively accelerates the AMOC. Such continuous acceleration is considered unphysical, as it implies an unsustainable increase in the system's intensity.

From these observations, we derive the region where the behaviour of the system will exhibit cyclic behaviour and respond to changes in the control parameters. From the previous analysis, α is constrained to $[-\mathrm{1},\mathrm{0}]$. We argue in Sect. 3.1 that the upper bound is a good choice. To keep the nullcline inside the relevant area of the system, γ is constrained to [0.6,3].

The noise in the system comes from a Wiener process, dW. At each time step it adds a random number drawn from a unit Gaussian that is scaled with a parameter, σ. To ensure that our model exhibits behaviour that is governed by its deterministic structure rather than by random fluctuations, we set a limit on the parameter σ, which controls the intensity of the noise in the model. If σ is too high, the model behaves like a random walk, leading to abrupt and unrealistic transitions in the system. Through a search of the domain of the summary statistics presented in Sect. 3.1, we selected a value for σ that best replicates the behaviour observed in the ice-core record.

3 Results

In this section, we present the findings of our simulations and analyses aimed at exploring the behaviour of the AMOC in response to varying control parameters. We begin by detailing the results of our simulation studies in Sect. 3.1, where we examine the effects of introducing the slope parameter α into our model and its implications on the summary statistics. This section also discusses the structural changes in the achievable results from varying parameters and how we use this analysis to set a fixed noise level. Following this, in Sect. 3.2, we explore how an idealised forcing can produce results resembling the dynamics of the last glacial period.

3.1 Output space

To see the effect of introducing the α parameter, we run simulations across the extensive parameter space delineated by the stability analysis. Each simulation generates a non-dimensional AMOC time series. Each run is initiated such that it ends at 11 703 b2k, at the beginning of the Holocene (Rasmussen et al., 2014). The model runs with a constant time step of 20 years, which comes from a balance between run time and the stiffness of the system. Therefore we start the simulation at 119 123 b2k, with initial conditions $(\mathrm{\Delta }b,B)=(\mathrm{1},\mathrm{0})$. This is the closest to the transition out of the Eemian that a whole number of 20-year steps from 11 703 b2k can come. The simulations are therefore run for 5371 steps. The simulations were carried out using a stochastic Runge–Kutta method without adaptive stepping to mitigate the stiffness of the system (Ansel et al., 2024; Kidger et al., 2021; Li et al., 2020). As we initialise in GS-26, the initial conditions are chosen to be in a stadial state. Using two threshold values for the stadial and interstadial states, as outlined in Mitsui and Crucifix (2017), we automatically classify when the AMOC time series is in stadial and interstadial periods, respectively. From this classification, we calculate the E^′(t) and P^′(t) series for each run. For the remainder of this paper, primed values will denote E and P values for the modelled time series.

The modelled temporal averages ${\mathit{\mu }}_E^{\prime }$ and ${\mathit{\mu }}_P^{\prime }$ for each set of control parameters are shown in Fig. 6, with the left column coloured by the γ value and the right coloured by the σ value of the simulation. Each ${\mathit{\mu }}_E^{\prime }$ and ${\mathit{\mu }}_P^{\prime }$ value pair is an ensemble average of 100 individual runs for a specific set of parameters. The model is run for 10⁴ different sets of γ, α, and σ in the domain found in Sect. 2.3.5.

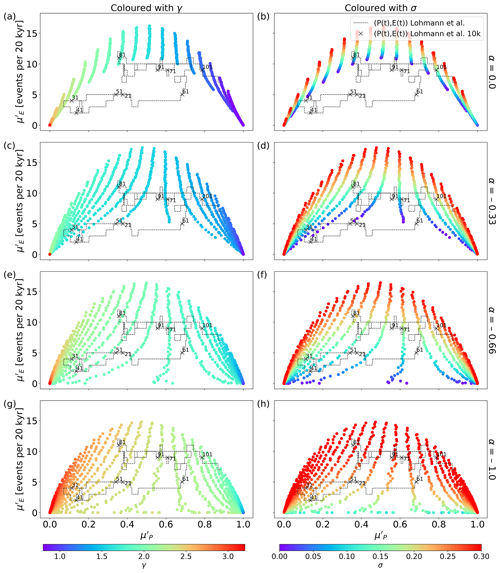
Figure 6 Achievable ${\mathit{\mu }}_P^{\prime }$ and ${\mathit{\mu }}_E^{\prime }$ pairs. A scatter plot of ${\mathit{\mu }}_P^{\prime }$ and ${\mathit{\mu }}_E^{\prime }$, with the (P(t),E(t)) time series from Fig. 1 superimposed. The numbers mark the ages at 10 kyr spacing. Each pair is coloured by the value of γ (left column) or σ (right column) used in the corresponding model run. The value of α decreases from top (α=0) to bottom $(\mathit{\alpha }=-\mathrm{1})$.

The simulations are unstable for α=0 and γ>1.85 and have been omitted. We also show the temporal evolution of (P(t),E(t)) values calculated from the ice-core record as described in Lohmann and Ditlevsen (2018) and as also shown in Fig. 1. For α=0 (Fig. 6a and b), the model's outcomes appear to arch around the values derived from the ice-core record. For some periods, e.g. around 81 ka b2k, the model can capture the (P(t),E(t)) pair found in the ice-core record. However, for most time periods, this is not possible. Clear arches for each noise level are seen in the right panel, while almost vertical bands of similar ${\mathit{\mu }}_P^{\prime }$ corresponding to each γ value are seen in the left panel. This is a clear consequence of the model properties. γ controls the magnitude of the gradient along the slow manifold, and, if γ is near the upper bifurcation point in the unstable region, the system will have a small gradient along the upper part of the manifold but a large gradient along the lower part. This in turn leads to longer interstadials and shorter stadials. With larger σ, the system becomes more volatile, and it will jump from the stable parts of the manifold more readily, leading to more events in a given time interval. Interpolating and extrapolating to uncharted parts of the parameter domain is fairly straightforward: with decreasing γ, ${\mathit{\mu }}_P^{\prime }$ moves to higher values, and increasing the σ will increase ${\mathit{\mu }}_E^{\prime }$. Either way, it would not be possible with α=0 to reach most of the observed (P(t),E(t)) values.

Including the slope parameter allows the model to better capture the observed behaviour and thereby match the (P(t),E(t)) values. Decreasing the α parameter extends the arches downward, so each line of constant γ now reaches lower values of ${\mathit{\mu }}_E^{\prime }$. In the middle and lower panels, the observed values are now more fully represented by the possible values found in the model. The correlations observed between ${\mathit{\mu }}_P^{\prime }$ and γ and between ${\mathit{\mu }}_E^{\prime }$ and σ are still maintained. As α decreases, γ has to increase to keep the B nullcline in the relevant region of the phase space where DO events occur, as γ controls the intercept of the B nullcline with the Δb axis of the phase space. This is also illustrated in the left column of Fig. 5, where the overall γ values increase with decreasing α value. In the right column, we can see that increasing α moves the entire arch downwards and replaces the upper parts of the arch with higher noise levels. Thus for $\mathit{\alpha }<-\mathrm{1}$ it would require an even higher value of σ for enough events to happen to capture the period around 101 ka b2k. This higher value will make the system even more noise-driven. From the superimposed (P(t),E(t)) time series in Fig. 6, it is apparent that there is no single panel which encompasses the entirety of the observed dynamics in a single colour, representing a fixed set of control parameters.

The results shown in Fig. 6 and discussed above come from stationary models, where the given set of parameters $\mathit{\{}\mathit{\sigma },\mathit{\gamma },\mathit{\alpha }\mathit{\}}$ is constant over the entire simulation. This allowed us to analyse the behaviour of the new model with non-zero α compared to the old one without the sloping nullcline. However, due to the variable nature of the glacial climate, there is no reason to believe that the parameters are stationary, and it is thus less relevant to try to fit the stationary model to the observed P((t),E(t)) values. What we conclude from this analysis is that a dynamically forced model with the addition of the α parameter should be able to simulate the behaviour seen in the ice-core record, as the time series of summary statistics is now within the achievable domain illustrated in Fig. 6.

When trying to fit an idealised forcing to optimally resemble the dynamics of the ice-core record, we experienced that the α and γ parameters relied so heavily on the noise level that any optimisation algorithm would choose a random noise level, optimising only the α and γ parameters, and thus risk getting stuck in a local minimum. It was not possible to optimise on the α and γ parameters first and then optimise on the noise level, as this led to non-optimal solutions. Therefore, we decided to use the arches from Fig. 6 as an argument for choosing a constant σ=0.2 for our further analysis: because the yellow points in the right panels together span the entire area, it should be possible with σ=0.2 to find a pair of γ and α that can reproduce the dynamics of the ice-core record at any time. A more accurate picture from the simple model could be achieved if we had a better estimate of the appropriate noise levels for stadial and interstadial periods. Previous studies suggest a higher variability in stadial states compared to interstadial states (Ditlevsen et al., 2002). Ideally, this would lead us to allow different noise levels in each state. Preliminary analysis of the noise level observed in global climate models or ice-core data presents a more complicated picture. Specifically, the noise in the AMOC does not necessarily seem to be directly linked to the variability in the Greenlandic ice-core records. Therefore, due to the lack of a method to numerically estimate or computationally derive distinct values for each state, we have opted to use a constant noise level for both states.

3.2 Fitting the forcing

Many attempts have been made to link the control parameters of simple models to physical quantities, including e.g. global ice volume, insolation, and CO₂ concentration (Lohmann and Ditlevsen, 2018; Vettoretti et al., 2022; Mitsui and Crucifix, 2017). Adding to the complexity is the possibility that a combination of these forcings could be at play simultaneously, making the task of testing each one through trial and error impractical. Therefore, we take another approach by fitting an idealised time-dependent forcing via α(t) and γ(t). We choose to describe α and γ with one point every ∼3.6 kyr and make a cubic spline interpolation between these points. This allows us to resolve periodic variations in the forcing with a period on the order of 14 kyr. We have chosen this resolution to allow the forcing to have variations on orbitally relevant timescales but not on the typical scale of the DO events.

We use a Bayesian algorithm to determine α(t) and γ(t) forcing that minimises the root-mean-square error (RMSE) between the ensemble mean of E^′(t) and P^′(t) of the model simulations and the observed E(t) and P(t). Given that P^′(t) and P(t) naturally range between 0 and 1, we normalise E^′(t) and E(t) by dividing each by the maximum observed value of E(t). This ensures that the two variables contribute equally to the optimisation process when calculating the root-mean-square error. The α(t) and γ(t) series contains 30 values that are constrained by the analysis from Sect. 2.3.5. After the Bayesian optimisation, a random Gaussian noise perturbation with a standard deviation of 0.075 is added to the first parameter of γ(t) 15 times, the best of these are found, and the parameter is updated. This is then done sequentially in time to all parameters, first for γ(t) and then for α(t), to find even better optima than those found by the Bayesian optimiser. The results of this can be seen Fig. 7. The ensemble resembles the observations as E(t) consistently falls within E^′(t). There are periods around 91 and 21 ka b2k where the modelled P^′(t) fails to capture the observations. This is further discussed below. The interpolated γ(t) and α(t) can be found in panel (c) and show that variations with large amplitudes and frequencies are required to fit the P(t) and E(t) of the observations. Panel (d) shows the member of the ensemble of the simulations with the lowest RMSE between the simulated and observed E(t) and P(t) values. Two precursor interstadials can be seen at 107 and 97 ka b2k, with approximate durations of 496 and 817 years followed by 323- and 371-year-long stadials that lead into interstadials with durations of approximately 7.7 and 5.1 kyr. This demonstrates the model's ability to produce a DO event sequence that somewhat resembles short precursor-style events followed by long interstadials as observed in the ice-core record.

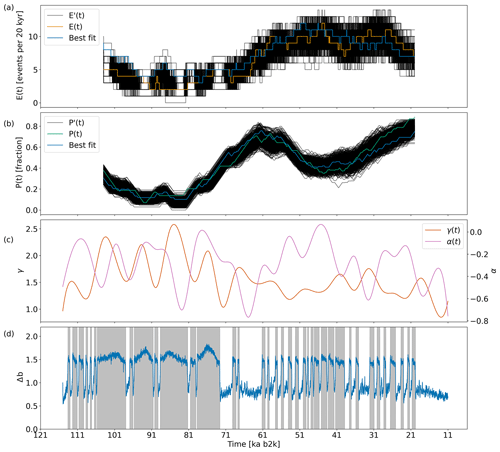
Figure 7 Optimal time-dependent forcing α(t) and γ(t). The top two panels (a) and (b) show the events E(t) and stadial fraction P(t) found in data and in an ensemble of simulations, with fixed α(t) and γ(t) but different realisations of the random noise. Highlighted in blue are the E^′(t) and P^′(t) of the realisation with the lowest RMSE compared with the observations. (c) Cubic spline interpolation between the 30 points in each time series for α(t) and γ(t). (d) Time series generated using the forcing in panel (c) giving the best fit of E^′(t) and P^′(t) to the observed values. The model time runs from the beginning to the end of the last glacial.

4 Discussion

One of the most profound features of the DO cycles is their highly non-periodic nature with interstadial durations and event spacing spanning several orders of magnitude. We show that, by optimising the forcing and adding a novel parameter, our conceptual model of the AMOC-driven DO dynamics can mimic the ice-core record in terms of its non-periodicity. The idealised forcing makes the model produce summary statistics matching those of the observations. We do not claim that this idealised forcing can be directly linked to the likely natural forcings that were acting on the climate system during the glacial, e.g. ice volume, CO₂ concentration, and insolation. It does, however, show that the model output can span a realistic range of situations, with a forcing varying by periods longer than 14 kyr. The glacial climate system was likely forced by a complex combination of forcing factors possibly combined in a non-linear and non-stationary way. In addition, the level of internal variability, which plays a key role in the model behaviour, may have varied between stadials and interstadials and possibly also on longer time scales. However, as outlined in Sect. 3.1, here we determine an idealised forcing while keeping the noise parameter σ constant with a value of 0.2. We suspect that other σ values, or a time-varying σ(t) combined with different γ(t) and α(t), can produce summary statistics that match the observed characteristics even better. Also, our fitting method does not take into account the multi-dimensional first- and second-order correlations between the control parameters that arise from both the simple geometry of the nullclines and the strong correlations between ${\mathit{\mu }}_E^{\prime }$ and ${\mathit{\mu }}_P^{\prime }$ shown in Sect. 3.1. We therefore simply show that it is possible to get a simple model to fit the behaviour of the ice-core records to a greater extent than previously shown in the literature. To further improve the idealised forcing, we suggest starting with a reformulation of the equations to decouple α and γ, maintaining the nullcline's proximity to the slow manifold's critical range as α varies. This would effectively transform the system so that the origin would lie in the middle of the manifold close to the unstable part. As α varies, the B nullcline would therefore remain in the relevant region without necessitating large variations in γ.

Unforced DO events produced by current Earth system models are highly periodic, and the periodicity of the DO behaviour in the simple model configuration – and our suggestion of how to break this periodicity in the model – is therefore also relevant for the question of how more comprehensive models can be improved. The Earth system model of Vettoretti et al. (2022) has been linked to the simple model used here with α=0 via its similar phase-space behaviour. Our analysis shows that, to mimic the non-periodicity of the ice-core record, the simple model needs α<0. By looking for a similar feedback mechanism to the feedback represented by the α term in the simple model, the comprehensive models might be able to better replicate the non-periodic dynamics observed in the ice-core record. A first step could be a thorough study of the parameters influencing the ocean circulation in the southern Atlantic and SO.

A weakness of our optimisation scheme (which is based on simply minimising the overall RMSE of the summary statistics of the generated time series; see Fig. 7) is that it does not regard each modelled time series as an actual time series but as a series of individual data points without any temporal structure. This approach might result in a low RMSE, suggesting a close fit between the model's ensemble predictions and the summary statistics of the observed record. However, it falls short of accurately recreating the actual observed data series. The method does not favour high accuracy in a single time series but a rather low variability across the collective range of the ensemble; see best-fit lines in Fig. 7a and b. Our examination of the current literature and theoretical models has failed to provide a method for determining whether a specific time series originates from a population of time series. Therefore, we have opted for the analytical approach used here.

.

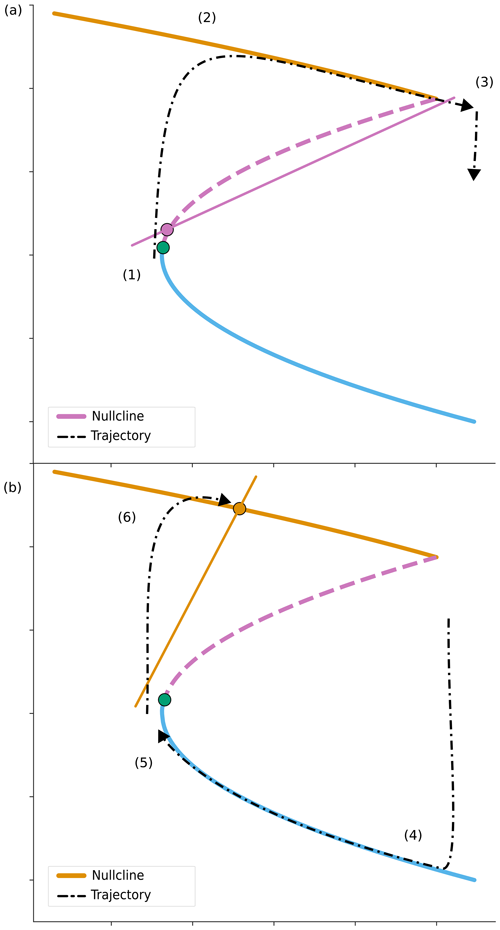
Figure 8 Illustration of type I precursor events. Initially, the system oscillates around the limit cycle, possibly relatively fast, beginning under stadial conditions (1). The system jumps to interstadial conditions (1→2) and experiences a full interstadial period before tipping (3→4) and reaching stadial conditions again. During the tipping (3→4), the nullcline moves and an upper fixed point emerges, making the interstadial stable. The system experiences a full stadial before tipping (5) and transitioning to interstadial conditions for the second time, where it remains for an extended time (6).

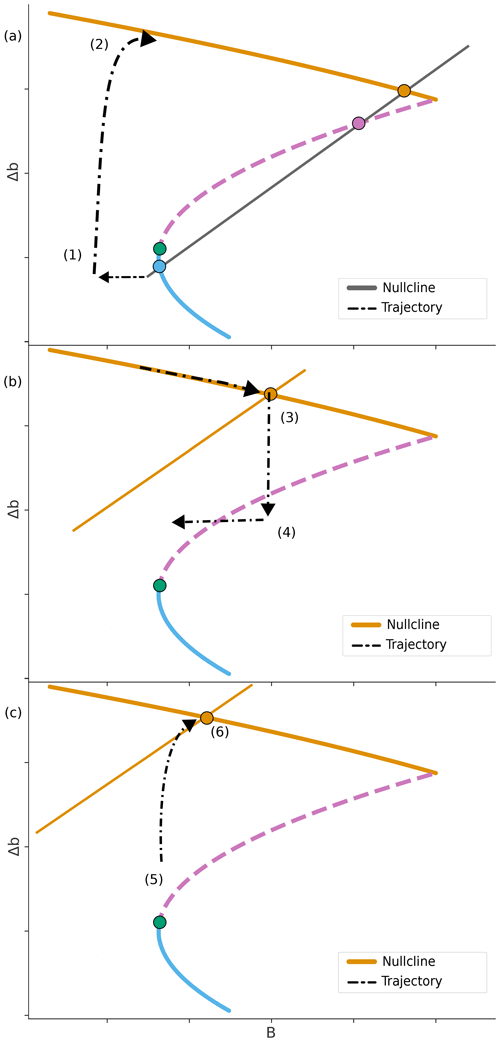
Figure 9 Illustration of type II precursor events. Initially, the system experiences a noise-induced transition from stadial to interstadial conditions (1→2). Subsequently, the system moves to a stable fixed point (2→3) while the nullcline ascends, resulting in the disappearance of the lower stable fixed point. Another noise-induced leap propels the system across the slow manifold (3→4). This crossing induces a brief period resembling stadial conditions (4→5). Ultimately, the system moves back to interstadial conditions (5→6) and stabilises in an interstadial state for a prolonged period (6).

Previous simple models have not been able to produce precursor events without large and rapid variations in control parameters. The α parameter's effect on the B derivative and the possibility of having multiple fixed points allow our model to produce DO events with duration and spacing similar to those in the observational record, including the precursor events. These modelled precursor events present themselves in two different ways, which are described here. In type I precursor events (seen in Fig. 8), the system goes around the limit cycle akin to a regular DO event after which the system's stability changes and the system transitions into a stable interstadial state. Type I events will have the same amplitude as the other DO onsets, with a duration based on the time it takes to run a full course around the limit cycle. The difference between models with α=0 and α<0 is that, for α=0 and a B-nullcline location close to the upper slow manifold, the model can only produce events with a very long interstadial duration, while a sloping nullcline close to the point of non-differentiability (marked by situation (a) in Fig. 8) can produce short interstadials. The type II events, on the other hand, have even shorter interstadial duration, more similar to the ones seen in the ice-core records, and are purely noise-induced. They come in different varieties: type IIa (seen in Fig. 9) occurs when the system has two stable fixed points close to the turns in the manifold and the system is in a stadial state. Here, a small amount of noise can induce a DO onset, and, if the system quickly jumps again, it barely crosses the slow manifold. If a bifurcation makes the lower stable fixed point vanish during this process (or turns it into an unstable fixed point), the system will return to interstadial conditions, having exhibited very short stadial and interstadial periods. A similar situation (type IIb) can occur if the system has a single stable fixed point in the upper part of the manifold. This must be far enough away from the non-differentiability to prohibit noise-induced horizontal jumps off the slow manifold but still close enough to the unstable part of the manifold to allow vertical noise-induced transitions. Afterwards, the system will tend toward the stable interstadial-state fixed point again. These jumps would tend to have a lower amplitude than the corresponding situation with two stable fixed points, as smaller jumps can lead the system to cross the unstable part of the manifold before tending towards the upper stable fixed point again. Type IIb is analogous to type IIa but starting in interstadial conditions (3), as seen in Fig. 9.

When type I precursor events occur, the AABW model proxy exhibits changes akin to the normal BPS response as the system evolves around the limit cycle. This is not observed in the Antarctic ice-core record. As the type II precursor events are predominantly noise-induced vertical jumps, with a small change in the AABW based on the location of the upper stable fixed point, the only sizeable response is seen in the AMOC, with little to no response in the AABW. This appears more like the situation seen in the ice-core records, but, due to the relatively slow and muted response of the Antarctic climate to AMOC changes, this could also be a consequence of the short duration of the precursor events.

Both kinds of type II precursor events can explain the response seen in the ice-core record, as both are linked closely to the transition into highly stable interstadial conditions. Type IIa can only occur in the specific case of a noise-induced jump happening while the system has two stable fixed points but is transitioning to a stable interstadial state. IIb can only happen while having a single stable fixed point in the upper manifold that moves further up the manifold, implying the system is moving towards longer interstadial periods. Conditions producing type IIa and IIb precursor events require that an upper stable fixed point exists, with a small vertical distance to the unstable part of the manifold, as they require the system to cross it. Therefore, the scenarios will only lead to precursors to long interstadials when the upper fixed point moves upwards on the slow manifold. On the contrary, if the system is already in a long stable interstadial, the nullcline will be too far from the unstable part of the manifold for this to occur.

Neither type of event adequately reproduces the precursor patterns observed in the ice-core record. Type I captures the correct amplitude but fails to replicate both the short interstadial and stadial periods that precede the longer interstadial phase. Type II events, on the other hand, successfully mimic the brief climatic intervals but do not fully reach the cold level of stadial conditions reflected in the data. When considering the type II precursor events, the primary distinctions between ordinary DO events and these precursors lie in the mechanisms that trigger them. A typical DO event can occur due to “natural” oscillations (when the moving location of the B-nullcline results in an unstable fixed point), or it can arise from noise-induced transitions. These transitions occur when there is a stable fixed point near the turns of the manifold. The noise-induced transitions can be triggered by fluctuations either in the Δb or in the B direction as long as these fluctuations lead to crossing the bifurcation threshold. However, from the previous analysis, precursor events of type II solely result from noise-induced fluctuations in the Δb direction, meaning these are purely triggered by variability in the AMOC.

5 Conclusions

Our results demonstrate why modelling the ice-core record using conventional FitzHugh–Nagumo-style models has been difficult. There is a strong second-order correlation between the ${\mathit{\mu }}_E^{\prime }$ and ${\mathit{\mu }}_P^{\prime }$ value pairs that can be produced by the usual control parameters, γ and σ. The $({\mathit{\mu }}_E^{\prime },{\mathit{\mu }}_P^{\prime })$ set attainable by the simple model does not contain the observed (E(t),P(t)) pairs, thereby making it impossible to match the data without allowing unphysically extreme and rapid changes in the control parameters over decadal to centennial scales – faster than any known climate driver impacting the AMOC. The most difficult aspect to represent for these models is the highly non-periodic nature of the DO events, especially the precursor events. Adding a slope does not break the second-order correlation, but it changes the set of possible $\left(E^{\prime }\right(t),P^{\prime }(t\left)\right)$ pairs. This allows the model to capture all observed E(t) and P(t) values. To explore the physical processes associated with the novel α parameter, our focus would be on improving the understanding of how variations in temperature, salinity, and freshwater fluxes in the surface layer of the Southern Ocean impact the formation of deep water. Fitting an idealised time-variable forcing with a resolution of 3.5 kyr allows the model to almost reproduce the statistical measures observed in the data. Additionally, it produces hitherto unmodelled precursor events, an example of which can be seen in panel (d) of Fig. 7 at 95 ka.

Additionally, our analysis has demonstrated that the α parameter's influence on the B derivative is crucial in producing precursor events that mimic the durations and spacings observed in the ice-core records. In describing the modelled precursor events, we differentiate between two types of precursor events. Type I events exhibit the full amplitude and duration of typical DO onsets as determined by variations in the location of the B nullcline and α. Type II precursor events, on the other hand, are purely noise-induced and reveal the sensitivity of the system to stochastic disturbances, leading to short interstadial states similar to those recorded in the ice-core record.

We observe that, unlike the normal DO events, which may arise from either systemic oscillations or noise-induced shifts near bifurcation points, the precursor events in our model are exclusively triggered by noise-induced fluctuations in the Δb direction. This points to the unique role of AMOC variability as the driving force behind these events.

Appendix A: List of abbreviations and their full forms.

Abbreviation	Full Form
AABW	Antarctic Bottom Water
AMOC	Atlantic Meridional Overturning Circulation
BPS	Bipolar seesaw
CCSM4	Community Climate System Model 4
DO	Dansgaard–Oeschger
NGRIP	North Greenland Ice Core Project
MIS	Marine Isotope Stage
SO	Southern Ocean
NA	North Atlantic