the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
A novel explainable deep learning framework for reconstructing South Asian palaeomonsoons
Kieran M. R. Hunt
Sandy P. Harrison
We present novel explainable deep learning techniques for reconstructing South Asian palaeomonsoon rainfall over the last 500 years, leveraging long instrumental precipitation records and palaeoenvironmental datasets from South and East Asia to build two types of models: dense neural networks (“regional models”) and convolutional neural networks (CNNs). The regional models are trained individually on seven regional rainfall datasets, and while they capture decadal-scale variability and significant droughts, they underestimate inter-annual variability. The CNNs, designed to account for spatial relationships in both the predictor and target, demonstrate higher skill in reconstructing rainfall patterns and produce robust spatiotemporal reconstructions. The 19th and 20th centuries were characterised by marked inter-annual variability in the monsoon, but earlier periods were characterised by more decadal- to centennial-scale oscillations. Multidecadal droughts occurred in the mid-17th and 19th centuries, while much of the 18th century (particularly the early part of the century) was characterised by above-average monsoon precipitation. Extreme droughts tend to be concentrated in southern and western India and often coincide with recorded famines. The years following large volcanic eruptions are typically marked by significantly weaker monsoons, but the sign and strength of the relationship with the El Niño–Southern Oscillation (ENSO) vary on centennial timescales. By applying explainability techniques, we show that the models make use of both local hydroclimate and synoptic-scale dynamical relationships. Our findings offer insights into the historical variability of the Indian summer monsoon and highlight the potential of deep learning techniques in palaeoclimate reconstruction.
- Article
(8672 KB) - Full-text XML
- BibTeX
- EndNote
1.1 The Indian summer monsoon
The Indian, or South Asian, summer monsoon occurs each year between June and September. It brings about 80 % of annual rainfall to the subcontinent, supporting the lives and livelihoods of over a billion people (Turner and Annamalai, 2012). While the Indian monsoon can be thought of as a large-scale convectively coupled land–sea breeze, there is strong heterogeneity in both space and time which is forced through both internal and external variability (Rind and Overpeck, 1993; Webster et al., 1998).
The inter-annual variability of the monsoon, averaged over the whole of India, is slight – 1 standard deviation amounts to only about 10 % (Webster et al., 1998). Yet intraseasonal variability, mostly forced by the boreal summer intraseasonal oscillation (BSISO), can be many times larger (Kikuchi et al., 2012; Kikuchi, 2021; Hunt and Turner, 2022). This can lead to extended periods of substantially below- or above-average rainfall (Krishnamurthy and Goswami, 2000; Goswami and Ajayamohan, 2001; Pai et al., 2016), such as the month-long break of August 2023, when the whole country received only 64 % of its typical August rainfall, or the twin low-pressure systems (LPSs) in August 2018 that resulted in Kerala receiving more than twice the typical rainfall for the first 3 weeks of the month (Hunt and Menon, 2019).
Monsoon heterogeneity is also forced externally through multiple teleconnections or large-scale modes of variability across the tropics and extratropics, identified in both palaeoclimates and present-day climates. These modes are not strictly orthogonal, nor are they mutually exclusive, and the strength of the teleconnections can vary on multidecadal timescales. Large-scale forcing and teleconnections, however, explain the majority of inter-annual variance in the summer monsoon. These include, but are not limited to, the El Niño–Southern Oscillation (ENSO; Webster and Yang, 1992; Torrence and Webster, 1999; Turner et al., 2005; Xavier et al., 2007), the Indian Ocean Dipole (IOD; Ashok et al., 2001; Cherchi et al., 2021), solar forcing (Rind and Overpeck, 1993; Agnihotri et al., 2002), and related latitudinal variations in the Intertropical Convergence Zone (ITCZ; Fleitmann et al., 2007), as well as multidecadal variability in the Atlantic (Gupta et al., 2003; Archer and Fowler, 2004; Wang et al., 2005), Pacific (Krishnan and Sugi, 2003; Krishnamurthy and Krishnamurthy, 2014), and West African monsoon (Crétat et al., 2020, 2024).
1.2 Palaeoclimate reconstructions of the Indian monsoon
Robust palaeoclimate reconstructions of the Indian summer monsoon are challenging because of the small number of datasets from the Indian peninsula (Wang et al., 2010; Rehfeld et al., 2013; Dixit and Tandon, 2016), regional variability within the monsoon (Ramesh and Yadava, 2005; Banerji et al., 2020), and strong inter-annual variability (Ramesh and Yadava, 2005; Dimri et al., 2022). These problems are further compounded because the impact of the monsoon on humans is predominantly felt on seasonal timescales, but there are few palaeoclimate records with sufficient resolution to detect such a signal. Tree rings and speleothems can have sub-annual or annual resolution, but there are few such records available for India.
Tree rings, speleothems, and palaeoclimate records with lower resolution, such as lake and marine deposits, have proved useful in constraining changes in decadal variability. Studies using such records (e.g. Burns et al., 2002; Anderson et al., 2010; Dixit and Tandon, 2016; Kaushal et al., 2018; Banerji et al., 2020; Rawat et al., 2021) have shown a consistent and coherent strengthening of the summer monsoon during the Medieval Warm Period (MWP; ca. 950–1250 CE) and a weakening during the Little Ice Age (LIA; ca. 1500–1850 CE). These responses are generally understood to be caused by shifts in the ITCZ in response to changing solar forcing (Haug et al., 2001), but it is unclear if this is a local response (Sinha et al., 2011) or driven by ENSO (Burns et al., 2002). The summer monsoon has also experienced periods of extended drought (Sinha et al., 2011) and deluge (Sridhar and Chamyal, 2018) outside the MWP and LIA. These were mostly regional in nature, however, and thus do not always correlate well with indices such as all-India rainfall records. Furthermore, the interpretation of palaeoenvironmental records in terms of monsoon changes is complicated because the records can be influenced by changes specific to the depositional setting, local hydrological conditions, and regional signals, as well as changes in the relative importance of monsoonal and non-monsoonal sources (Dixit and Tandon, 2016; Wolf et al., 2023). Nevertheless, longer-term changes in monsoon strength during the Holocene have been reconstructed from speleothem records (Kaushal et al., 2018), specifically increased monsoon intensity during the early Holocene (12–6 ka) with a gradual decrease in rainfall from the mid-Holocene to the present day. Variability was higher in the late Holocene (after ca. 5.6 ka) due to changes in solar irradiance, ENSO, and the Pacific Decadal Oscillation (PDO).
The history of the monsoon over the last 2 centuries has been reconstructed at annual or near-annual resolution using tree rings from fir and spruce across the Himalaya (Sano et al., 2012, 2017; Brunello et al., 2019; Sano et al., 2020; Fan et al., 2022; Thomte et al., 2022; Dhyani et al., 2023). These records show a general increase in aridity in the past 2 centuries and increased variability in the last few decades. However, the reconstructed precipitation records do not correlate well with each other, in part because of the impact of local conditions and inter-specific differences on tree growth but also reflecting regional variations in rainfall across the Himalaya. A 500-year tree ring record from southern India (Borgaonkar et al., 2010), which correlates well with all-India rainfall over the instrumental record and has therefore been interpreted as a monsoon signal, showed no evidence of the increase in aridity over the last 2 centuries indicated by the Himalayan records. Instead, it has been interpreted as indicating weak monsoons with high variability from 1750–1850, followed by a period of strong monsoons at the end of the 19th century.
Cook et al. (2010) combined these various lines of information using a point-by-point regression on a network of tree rings, including three from peninsular India, to construct a gridded Monsoon Asia Drought Atlas spanning 1300–2005 CE at a resolution of 2.5°. They identified major Indian droughts in 1756–1758 (the “Strange Parallels” drought), 1790–1796 (the “East India” drought), and 1876–1878 (the “Great Drought”). They also found that the monsoon was sensitive to different flavours of ENSO (i.e. whether the strongest anomalies are in the central Pacific or eastern Pacific). Very long instrumental records, some of which stretch back to 1813 (Sontakke and Singh, 1996; Sontakke et al., 2008), indicate a period of weak monsoons in the middle of the 19th century.
Most monsoon palaeoclimate studies have focused on single or small numbers of records. Even where they have used wider networks (e.g. Cook et al., 2010), they have not quantified or used the spatial relationships between the palaeoclimate records or within the rainfall field, so regional variations in monsoon rainfall are not well documented or understood. Machine learning methods that can leverage this kind of information, even implicitly, could therefore be useful to reconstruct maps of monsoon evolution.
1.3 Data-driven approaches to reconstruct the palaeoclimate
Machine learning approaches have been used in palaeoclimate research for automated palaeoenvironmental record generation, model post-processing, and reconstruction. Automated palaeoenvironmental record generation has typically relied on image detection and classification methods to improve the efficiency and accuracy of extracting chronologies, including layer counting in speleothems (Sliwinski et al., 2023) and tree ring width detection (e.g. Fabijańska and Danek, 2018; Kim et al., 2023; Poláček et al., 2023; Wu et al., 2023), as well as pollen identification (e.g. Tcheng et al., 2016; de Geus et al., 2019; Bourel et al., 2020; Olsson et al., 2021), measuring soil organic carbon content (Lukens et al., 2019; Liu et al., 2022), measuring carbonate content in marine sediment (Lee et al., 2022), and identifying leaf physiognomy (Wei et al., 2021). Machine learning has also been used to create backward models, for example, to estimate tree ring width chronologies from local environmental factors. These have used a range of techniques including multivariate linear regression (Jevšenak et al., 2018), decision trees (Bodesheim et al., 2022), and even deep learning (Li et al., 2023). Nelson et al. (2021) also used a decision-tree-based approach to improve and extend instrumental records.
Machine learning has not been as widely used for model post-processing, although it has been used to improve the temporal resolution of model output using frame interpolation methods (Zheng et al., 2024), to reconstruct output variables through non-linear mappings (Huang et al., 2020), for anomaly detection using a multilayer perceptron (MLP; Bianchette et al., 2023), and for identifying droughts using Markov random fields (Coats et al., 2020). The use of machine learning for palaeoclimate reconstruction is a relatively unexplored field, although Bayesian machine learning methods are potentially more useful for this than linear regression techniques (e.g. Mannila et al., 1998; Chandra et al., 2021; Andermann et al., 2022). Neural-network-based methods, however, were used by Malmgren and Nordlund (1997) to reconstruct summer and winter sea surface temperature over the southern Indian Ocean using a basic MLP. Cortese et al. (2005) used an MLP to estimate North Atlantic summer sea surface temperature from protozoan assemblages over the Holocene. Guiot et al. (2005) used an MLP with 47 palaeoclimate records to reconstruct temperature and temperature-related events (e.g. grape harvests) in western Europe. Carro-Calvo et al. (2013) used a basic MLP to reconstruct winter precipitation in Mediterranean Europe from 1700 CE onwards.
1.4 This study
In this study, we capitalise on the fact that India has some of the longest instrumental rainfall records in the world to test whether deep learning techniques can take advantage of the non-linear relationships between the palaeoenvironmental records and seasonal rainfall, as well as between the palaeoenvironmental records themselves, to overcome the challenges raised by the sparsity of the palaeoclimate records and regional variation in the monsoon and thus generate robust spatiotemporal reconstructions of the Indian summer monsoon over the past 5 centuries.
We first address three methodological questions.
-
How well does a basic multilayer perceptron model time series of regional monsoon rainfall anomalies?
-
Can a convolutional neural network take advantage of the spatial structures within these rainfall anomalies to improve spatial reconstructions beyond commonly used statistical methods?
-
How do the models combine information from the palaeoenvironmental records to build their reconstructions?
To answer these questions, we must first overcome the issue of having a comparatively small training dataset (Sect. 2): ∼150 years for the regional models and only 100 years for the spatial model. We use a variety of techniques to optimise model performance (Sect. 3). We then show that both the regional models (Sect. 4.1) and spatial model (Sect. 4.2) produce robust and stable estimates of monsoon rainfall over the last 500 years. We compare these results to standard statistical models that have often been applied for reconstructions and explore the implications of our approach. We then apply explainable AI methods to our models (Sect. 4.3) and analyse the different kinds of contributions made by individual palaeoclimate records to the final predictions. We then describe the history of the Indian monsoon over the past 500 years (Sect. 4.4) before discussing the implications (Sect. 5) and conclusions of our work (Sect. 6).
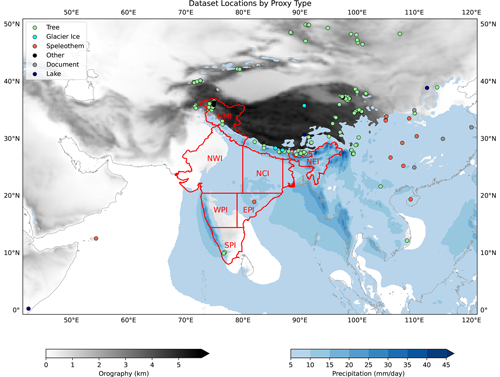
Figure 1Locations of the 155 palaeoclimate proxy records used in this study, coloured by type. Filled blue contours denote isohyets of the summer monsoon (June–September 1940–2022, computed using ERA5), and grey shading denotes orographic height. Also shown, in red, are the seven homogeneous rainfall regions of India (Sontakke et al., 2008).
2.1 Palaeoclimate records
2.1.1 PAGES2k global 2000-year multiproxy temperature database v2.0.0
The PAGES2k dataset (PAGES2k Consortium, 2017) is a collection of temperature reconstructions for the Common Era (1 CE to present) designed to contextualise industrial-era warming within natural climatic variability. Version 2.0.0 of the PAGES2k temperature database augments the earlier PAGES2k 2013 collection of terrestrial records with marine records. It also includes more terrestrial records, new metadata, and improved validation, making the dataset more cohesive and uniformly structured across regions. The dataset comprises 692 records from 648 locations covering all continental regions and major ocean basins. These records, sourced from trees, ice, sediment, corals, speleothems, documentary evidence, and other archives, range in length from 50 to 2000 years with a median length of 547 years. The temporal resolution varies from biweekly to centennial. Almost half of the palaeoclimate time series in this dataset correlate significantly with the HadCRUT4.2 surface temperature (Morice et al., 2012) over the period 1850–2014. The global temperature composites derived from these data show good coherence between high- and low-resolution records across different archive types and geographical locations.
2.1.2 Iso2k global palaeo-water isotope database v1.0.0
The Iso2k database (Konecky et al., 2020) is a collection of stable oxygen (δ18O) and hydrogen (δ2H) isotope records from precipitation, seawater, lake water, soil, and groundwater, reflecting hydroclimate changes over the Common Era. The isotope records are compiled from a variety of natural archives including glaciers, ground ice, cave formations, corals, sclerosponges, mollusc shells, and wood. The database comprises 759 isotope records, with individual datasets having a temporal resolution ranging from sub-annual to centennial.
2.1.3 Northern Hemisphere hydroclimatic variability database v1.0.0
The Northern Hemisphere hydroclimatic variability database (Ljungqvist et al., 2016) comprises 196 hydroclimate reconstructions and 128 temperature reconstructions, with a minimum length of 1000 years, from sources including tree rings, speleothems, and sediments. The temporal resolution varies from annual to multicentennial. All data from this database, as well as from PAGES2k and Iso2k, are available as Linked Paleo Data (LiPD) files. These provide a wealth of metadata and a standard format that makes them machine-readable.
2.1.4 Homogenisation
The three databases were combined, homogenised, and filtered as follows.
-
All .lpd (LiPD) and .txt files in the relevant directories are identified. Each one corresponds to a single palaeoenvironmental record. These are read in using the lipd and pandas Python libraries.
-
Datasets missing a “year” attribute are discarded, as are those that do not extend into the period after 1900 CE, those that have year values after 2020 CE, and those whose year attribute is non-monotonic.
-
The remaining datasets are checked for duplicates, which are removed. Entries are considered duplicates if both the year and record value match one another.
-
Datasets with fewer than three entries are also removed.
-
Datasets are then rebased onto a common timeline (0 CE to 2010 CE, at yearly resolution) using cubic interpolation. Values are not extrapolated, so where the rebased years fall outside the original dataset, the record value is set as missing.
-
Two new tabular files are created, one each for the metadata and the interpolated dataset.
These two files were loaded into the deep learning models, where additional filtering by location, time span, and temporal resolution could be done quickly. We only used datasets that were located between 40–120° E and 10° S–50° N, had a decadal (or better) temporal resolution, and spanned at least 1500 CE to 1995 CE. After this filtering, there were 155 datasets that could be used as predictors to train the models (Fig. 1).
2.2 Rainfall data
2.2.1 IMD
The Indian Meteorological Department (IMD) produces a daily 0.25°×0.25° gridded rainfall dataset for the whole of India (Pai et al., 2014). The dataset covers 1901 to the present and uses around 7000 rain gauges in total. The minimum number of gauges used on any given day (early 1901) is about 1500. The gauge data are gridded using a simple inverse distance method (Shepard, 1968) adjusted to include directional effects and barriers (Rajeevan et al., 2006). The IMD dataset compares well against other overlapping datasets (Pai et al., 2014), except in the far north (mountainous Ladakh, Jammu, and Kashmir) and far northeast (mountainous Arunachal Pradesh), where the terrain makes gauges sparse and unreliable. We aggregated these data to create a training dataset containing the average rainfall during each monsoon season (June to September) for each grid point over India.
2.2.2 ERA5
We used precipitation data over South Asia derived from the ERA5 reanalysis dataset (Hersbach et al., 2020). ERA5 provides hourly data at a horizontal resolution of 0.25°×0.25° from 1940 to the present. We aggregated these data to create a secondary training dataset containing the average rainfall during each monsoon season (June to September) for each grid point over India. ERA5 data are available from https://cds.climate.copernicus.eu/ (last access: 20 December 2024).
2.2.3 Extended homogeneous region timelines
We used the datasets described in Sontakke et al. (2008) for our regional rainfall targets. These provide estimates of summer monsoon rainfall for seven “homogeneous” zones in India (Fig. 1), as well as averaged over the whole country: northern mountainous India (NMI), northwestern India (NWI), north central India (NCI), northeastern India (NEI), western peninsular India (WPI), eastern peninsular India (EPI), and southern peninsular India (SPI). The datasets draw on slightly more than 300 rain gauges spread across India. The datasets for each region have different start dates depending on the availability of records, ranging from 1813 (SPI) to 1848 (EPI). The authors did not assess the reliability of their data, but note that two regions, NEI and NMI, were very sparsely populated with gauges.
2.3 Additional data
Famine data were drawn from two aggregated lists: https://en.wikipedia.org/wiki/Timeline_of_major_famines_in_India_prior_to_1765 (last access: 20 December 2024) and https://en.wikipedia.org/wiki/Timeline_of_major_famines_in_India_during_British_rule (last access: 20 December 2024). In each case, the year(s), affected region(s), and mortality (if known) are given for each famine, along with a list of supporting references. We convert these to a table recording whether a famine occurred in each of the seven regions, or parts thereof, for each year from 1500 to 1945. These data are available at https://doi.org/10.5281/zenodo.12688184 (last access: 20 December 2024). Given the complex relationship between famine and drought, as well as the inconsistencies in recording historical famines, we only used famine data for illustrative purposes.
Volcanic eruptions were drawn from the “Volcanoes of the World” database maintained by Venzke (2024), which compiles information on eruptions globally throughout the Holocene. For our period of study (i.e. 1500 CE onwards), these are mostly from eyewitness reports, with a handful being reconstructed from paeleodata. These data provide a test of reconstruction performance as large eruptions are known to weaken the South Asian monsoon in subsequent years (Liu et al., 2016) and perhaps on interdecadal timescales (Ning et al., 2017).
For the same reason, we also use reconstructed ENSO anomalies from Li et al. (2013). This dataset uses thousands of tree ring datasets to reconstruct ENSO anomalies at annual resolution over the last 700 years. In the present day, positive phases of ENSO (i.e. El Niño) are known to weaken the summer monsoon (e.g. Webster and Yang, 1992), but this is thought to be a dynamic relationship whose strength varies on interdecadal timescales (Krishnamurthy and Goswami, 2000).
In this study, we aim to reconstruct historical monsoon rainfall over India over the last 500 years using deep learning models. Our predictor dataset – i.e. the model input – comprises a wide range of palaeoenvironmental records (Sect. 2.1) interpolated to annual resolution. Our target datasets – i.e. what we want the model to predict – are derived from observed monsoon rainfall (Sect. 2.2) The models were trained and tested by replicating the target datasets over their lengths, and once testing confirmed their predictions were robust, their predictions were extended backwards in time to 1500.
To achieve this reconstruction, we tested two different architectures for the model. The first was a regional model, built using a dense multilayer perceptron, and was trained to replicate longer instrumental time series of precipitation over the homogeneous regions (Sect. 2.2.3). The second was a spatial model, built using a decoding convolutional neural network, trained to replicate gridded precipitation data (Sect. 2.2.1). To avoid overfitting on small training datasets, we employed a range of common techniques including bagging, dropout, and regularisation. Finally, to understand how the models make their predictions given certain inputs, we employed an explainability method known as Shapley analysis. These models and techniques are described in greater detail in the sections below.
3.1 Bagging
Bagging, or bootstrap aggregation, is a way to reduce the risk of model overfitting. Neural networks trained on small datasets have a high risk of overfitting. Bagging promotes diversity among models by training each one on a different dataset. This diversity causes the errors of each model to be at least partially orthogonal, and as a result, averaging the errors across the ensemble reduces the overall variance.
Bagging begins with bootstrap sampling, where the convention is to draw multiple bootstrap samples from the original training dataset with replacement, meaning the same instance can be selected multiple times in each bootstrap sample. This procedure is not suitable for very small training datasets. Therefore, to keep the bias as low as possible, the bootstrap samples for the regional models are constructed by removing a random 10-year period for testing and another random 5-year period for validation. The number of training samples then varies depending on the region, with a maximum of 167 years and a minimum of 132. For the spatial models, each bootstrap sample has just a single test year and 4 validation years. This leaves 90 years of training data. The purpose of having distinct validation and training datasets also arises from the desire to avoid overfitting. As the models are trained, the loss function is computed on both the training dataset (which the training process is designed to minimise) and the validation dataset. If the validation loss starts to increase while the training loss continues to decrease, that is a sign that the model is starting to overfit. However, because the model has thus been tuned on the validation data, a true fair test requires that it is distinct from the test dataset, which must remain hidden from the model.
Separate models were then trained on each bootstrap sample. Because the bootstrap samples have random years taken out for testing and validation, each model sees a slightly different version of the data. This process results in a diverse ensemble of models, in a process similar to cross-validation. Once all the models are trained, bagging makes predictions by aggregating the individual predictions of all the models in the ensemble. For regression problems, this typically involves taking some average of the predictions of all models. In the timeline ensemble, we used the multi-model median, with the ensemble spread giving a measure of the uncertainty.
3.2 Dropout
We also used dropout to prevent overfitting, a technique where a fraction of neurons in a layer are randomly deactivated during training, with a specified probability, p, which is a tuneable hyperparameter, at each training step. This random deactivation forces the network to learn more robust and generalisable features, since the network learns to distribute the representation across all neurons instead of relying on any specific set of neurons (Liu et al., 2023). The randomness introduced by dropout helps break the complex co-adaptations among neurons, which can be particularly problematic when the training data are limited (Brigato and Iocchi, 2021). Dropout mitigates the tendency for neurons to become overly specialised to work well together on the training data, which causes them to perform poorly on new, unseen data, by promoting a form of ensemble learning within the network, where each sub-network (obtained by dropping a different set of neurons) learns to operate independently.
3.3 Regularisation and loss
The conventional choice of loss function for most regression tasks is mean squared error (MSE). However, even with dropout, our small training dataset still led to substantial overfitting. To overcome this, we added several new terms to the loss function.
Firstly, we used L1 regularisation, a technique that adds a penalty for large parameter values in the model. This encourages the model to focus on the most important features and ignore the less relevant ones. This sparsity is beneficial in reducing overfitting because it encourages the model to become less complex and more generalisable, ignoring palaeoenvironmental records which do not reliably improve the predictions.
The L1 regularisation term is given by
where wi represents the model parameters (i.e. weights) and λ is a tuneable hyperparameter. This is added to the MSE in the loss function, and thus
However, due to the combination of the small training dataset and requirement for a strong regularisation, using this loss function tends to result in the models regressing towards the mean of the target distribution (i.e. zero, as we use standardised rainfall anomalies). To prevent the model from simply predicting the average, we modify the loss function by adding terms that promote matching the observed variance and correlation as follows:
where α, β, and γ are also tuneable hyperparameters. The variance difference, VarDiff, is given by
This component encourages the model to match the variance of the target distribution and thus penalises direct regression to the mean. The correlation loss, CorLoss, is simply taken as
where ρ(ytrue,ypred) is the correlation coefficient between the observed and predicted target distributions. In the regional model, this is a Pearson correlation coefficient computed between the two time series over a given time period. In the CNN auto-encoder model, this is a spatial pattern correlation coefficient computed over the grid points with valid rainfall observations. This component further discourages regression to the mean by encouraging the model to maintain a strong correlation between output and target.
Values for α, β, and γ were found using a simple hyperparameter grid search. For the regional model, we use α=1, β=1, and γ=2. For the CNN auto-encoder model, we use α=1, β=0.75, and γ=0.25. For values of λ, see Sect. 3.4 and 3.5 for the regional and spatial models, respectively. The choice of α is of course arbitrary, since it is the ratios , , and that set the relative importance of the different components in the loss function. Note that to obtain the same results by doubling each of these parameters, we would need to halve the learning rate.
3.4 Regional model ensemble
We used two models to reconstruct monsoon rainfall over the last 500 years. The regional model was used to produce time series of seasonal rainfall (averaged over each June–September) for each of the homogeneous rainfall regions and for the whole of India.
Table 1General form of the architecture of the regional models. Boldface layer types indicate the encoder part of the model, and regular font layer types indicate regularisation or dropout layers. See the text for a definition of terms and Table 2 for a list of the configurations used.

Table 2Hyperparameter configurations used for the regional models. L1 and L2 represent the input and hidden layers, respectively. L1_neurons and L2_neurons are the sizes (i.e. number of neurons) of these layers. L1_activation is the activation function used in the first layer. The italicised column headers indicate regularisation parameters: dropout is the fraction of neurons randomly dropped from the first layer during training, and L1_regularisation is the magnitude of the L1 regularisation term added to the loss function.

The architecture is basic (Table 1) – a dense feedforward neural network with two hidden layers separated by a dropout layer – and extremely cheap to run given the small training dataset. This allowed us to expand the bagged ensemble to include seven different hyperparameter configurations (Table 2), which were identified by a cross-validated grid search.
The full recipe for training and running these regional models is given below. The process was repeated for each regionally averaged rainfall dataset used.
- 1.
Model configuration.
- (a)
Define a set of test and validation periods.
- i.
For each hyperparameter configuration, create a set of 42 test periods – each a list of 10 consecutive years starting with each of the even-numbered years from 1902 to 1984.
- ii.
Choose 2 validation years randomly from the remaining years using a fixed seed to ensure repeatability.
- i.
- (b)
Specify the model hyperparameters (number of neurons, activation functions, dropout rates, and regularisation; see Table 2).
- (a)
- 2.
Model training and evaluation.
- (a)
For each combination of test period and hyperparameter configuration, do the following.
- i.
Split the data into training, validation, and test sets.
- ii.
Preprocess the training data. Normalise each predictor in the training data to have a minimum of 0 and a maximum of 1 using min–max scaling. Then apply the same scaling parameters to the validation and test sets. For precipitation, standardise the training data to have a mean of 0 and a standard deviation of 1, and apply the same standardisation to the validation and test sets.
- iii.
Build and compile the model using the specified hyperparameters and architecture.
- iv.
Train the model with the training data. At the end of each epoch, compute the loss (Sect. 3.3) on the validation data and stop training if this has not improved over the last 250 epochs (Fig. 2).
- v.
Evaluate the model performance on the test set using Kling–Gupta efficiency (KGE) and linear correlation coefficient. Log these scores in a file, along with a unique model identifier and metadata.
- vi.
Save the model weights using the same model identifier.
- i.
- (a)
- 3.
Model selection and prediction.
- (a)
Select models from the log file that meet the desired performance criteria (i.e. KGE > 0 and correlation coefficient > 0.3).
- (b)
Generate predictions for the extended period (1500 to the beginning of the training dataset). Save these predictions to a file.
- (a)
- 4.
Ensemble and result compilation.
- (a)
Load the results for all selected models and average them to create a bagged ensemble average.
- (a)
Figure 2Example verification of one of the regional model ensemble members, trained on IMD gridded gauge precipitation averaged and standardised over northern central India (NCI). (a) Training (blue) and validation (orange) loss curves as a function of epoch number. The dashed grey line indicates the best epoch, as determined by validation loss, from which the model weights are taken. (b) Verification of the trained model against observations (grey) over the training period (blue; 1901–1979), verification period (green; 1980–1984), and testing period (red; 1985–1994). The correlation coefficients between model predictions and observations for each period are given in the legend.
For each ensemble member in each region, certain years within the training dataset were withheld for both validation and testing (see Sect. 3.4). The ensemble for each regional model then comprises members whose validation r>0.5 or the 10 best-performing members, whichever yielded the greater number.
3.5 CNN auto-encoder ensemble
The creation of maps of rainfall anomalies, rather than a single area-averaged value, is a more complex task and therefore requires more complex network architecture – convolutional layers within a convolutional neural network (CNN). Convolutional layers apply a set of learnable filters to the input data, where each filter slides (convolves) across the input to produce feature maps that capture various patterns or features. The resulting feature maps are then passed through activation functions to introduce non-linearity and enable the network to learn complex representations of the input data and then perform e.g. classification tasks. They thus reduce the dimensionality of the input, usually in a way that results in a useful latent space, e.g. detecting phases of ENSO from satellite images. Here, however, we want the network to decode rather than encode by taking low-dimensional palaeodata and extracting a high-dimensional representation from them (i.e. rainfall maps). We thus invoke the deconvolution (or transposed convolution; Conv2DTranspose in Table 3). This expands input features to a larger spatial resolution. Like the convolutional layer, it achieves this by using a set of learnable filters (whose size, or “kernel”, must be pre-defined) that slide over the input data but simultaneously upscale by padding or striding. Specifically, transposed convolutional layers reverse the downsampling effect of standard convolutions by inserting zeros between input elements or adjusting strides, allowing the filters to produce outputs with larger spatial dimensions and reconstruct higher-resolution feature maps from lower-dimensional data.
The full CNN architecture (Table 3) comprises two parts: firstly, dense encoding layers transform the input palaeodata into a simplified representation (latent space), and then a stack of deconvolutional layers decodes the latent space into a rainfall anomaly map. A final cropping layer is required to adjust the size of the output to match the dimensions of the IMD training dataset (135 longitude × 129 latitude). As this model contains both encoding and decoding elements, it is referred to as an auto-encoder.
Although the CNN is substantially more complex than the regional model, the training and running are almost identical. The only differences are as follows.
-
The increased training time arising from greater model complexity means only one set of hyperparameters is used. These values are given in Table 3.
-
The choice of testing and validation years reflects both the increased model complexity and the shorter training dataset. Now, each model has 1 validation year and 5 test years. Every year (1901–1994) is used as a validation year four times. The associated testing years start 1, 3, 5, or 7 years after and are then separated by 20 years, wrapping around if necessary. Thus, the first model has 1901 as its validation year and 1902, 1922, 1942, and 1962 as its testing years.
-
As described in Sect. 3.3, the functional form of the loss function is the same, but the parameters vary slightly.
-
The criteria for a model being used in the ensemble are (1) having a spatial pattern correlation coefficient greater than 0.3 and (2) having a variance difference (for the standardised anomaly) of less than 0.1. Both are computed using the validation year.
Like the regional models, the spatial model comprises a number of ensemble members, each withholding small but different sets of years for validation and testing. As the model never sees data from testing years, performance for these years should be indicative of performance outside of the training dataset, i.e. from 1500–1900.
Two basic linear regression models, commonly used in palaeoclimate studies, were used to compare with the timeline and spatial models. Specifically, we used a generic multivariate linear regression model, where regression is computed directly for each pixel in the training data, and a PCA-based approach, where the training dataset dimensionality is reduced by decomposing it into eight EOFs, with regression computed over their corresponding principal components (from which the predicted field is reconstructed through the original EOFs). The choice of eight EOFs was made through inspection. Although model performance was not particularly sensitive to this choice, using many more or many fewer leads to reduced skill.
We thus use four models: linear regression and PCA as standard techniques, regional models as they are fast, and CNNs as they are robust.
3.6 Shapley value analysis
3.6.1 Overview
Shapley values are widely used to assess the significance or contribution of specific variables in a model by estimating the marginal contribution from a given predictor in forcing a prediction away from the mean of all predictions (Shapley, 1953; Roth, 1988; Lundberg and Lee, 2017). The sum of all the Shapley values for all predictors for a given prediction, , is therefore equal to the difference between the predicted value and the predictand mean, i.e. . We used the shap Python package (https://github.com/shap/shap, last access: 20 December 2024), whose KernelExplainer function estimates Shapley values using a kernel method. This is particularly useful for models where other forms of Shapley value estimation are computationally infeasible due to their complexity. It works by building a local linear model that approximates changes in the output of the main model when a feature value is altered. This local model uses a background dataset to integrate out selected features, allowing it to estimate the impact of including or not including a given feature and thus its marginal contribution.
3.6.2 Implementation
We used two separate implementations. The “backward” method takes a model prediction and uses Shapley analysis to compute the contribution of each palaeoenvironmental record to that prediction. Averaged over all predictions, this provides an estimate of the relative importance of each palaeoenvironmental record within the model for making rainfall predictions at each point. We did this using the regional models as, although they are less robust than the CNN, the aggregation of the results by region means they are less prone to noise and small-scale spatial errors. This method shows which palaeoclimate records are not being used by the models and thus which may be defective or otherwise not useful (e.g. tree growth occurring entirely outside of the monsoon season). This information could be useful for future modelling efforts since it can determine a posteriori which palaeoclimate records to exclude. The “forward” method identifies the mean impact of a given palaeoenvironmental record on the predictions of each pixel in the CNN ensemble mean. This provides insights into how the model is using the palaeoclimate records and thus how the model differs from and improves upon conventional multivariate linear regression or PCA techniques.
4.1 Regional model
Five of the eight ensemble means had r>0.5 over their respective test periods, with only one having r<0.4. These values, while not exceptional, are better than some inter-observational agreement measures (Baudouin et al., 2020). Many of the reconstructed intervals of low rainfall coincide with famines (Fig. 3). The worst individual drought–famine year was 1630, in the middle of a multidecadal drought that persisted over the subcontinent throughout much of the mid-17th century (see e.g. Singhvi and Kale, 2010). However, the seven regional models (Fig. 3) tend to underestimate rainfall compared to the instrumental record, as does the all-India model. This seems to be an issue of timescale: the palaeoenvironmental records themselves capture decadal and multidecadal variability well but strongly underestimate inter-annual variability. However, although the records are not necessarily good matches for monsoonal rainfall and there is poor coverage over much of the peninsula, the models generally do reasonably well. The size of the available training data has little impact on the model skill.
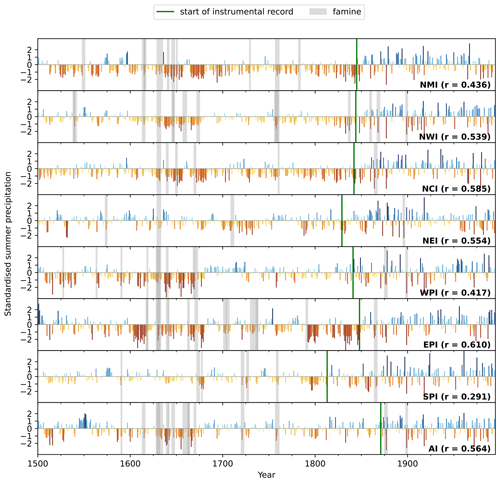
Figure 3Estimated seasonal precipitation anomalies from the regional model ensembles. For each of the seven homogeneous regions as well as all of India (AI), the ensemble median is given by the coloured bars. Observed values, taken from the reconstructed time series in Sontakke et al. (2008), are given to the right of the green line. Where standardised anomalies lower than −0.5 in either the modelled or observed time series co-occur with known regional or national famines, these are marked with grey bands. Stated r values measure the correlation between coincident actual and model test values.
The worst-performing region, SPI, has the longest training dataset, and the best-performing region, EPI, has one of the shortest. There is also no clear relationship between the number of records in a region and model skill. This suggests that the problem lies in the quality or usefulness of the records from each region (see Sect. 4.3). The fact that the regional model method works reasonably well suggests that the palaeoclimate records contain sufficient information to reconstruct regional monsoon anomalies using the more complex spatial model to take advantage of the spatial relationships within the rainfall field itself (Sect. 4.2).
4.2 Spatial model
4.2.1 Evaluation
The 5 years (1906, 1926, 1946, 1966, 1986) used to test the single CNN ensemble member (Fig. 4) represent a range of conditions, with two deficient monsoons in 1966 and 1986 and three surplus monsoons in 1906, 1926, and 1946, each with their largest anomalies in different regions. In 1906, the spatial model captures the dry anomaly over Jammu and Kashmir. However, while it captures the heterogeneous anomaly pattern over the rest of the subcontinent and hence accurately estimates the all-India average, it tends to locate these smaller-scale anomalies incorrectly, leading to a poor spatial pattern correlation coefficient (r=0.07). The other 4 years are better represented, with spatial pattern correlation coefficients of 0.45 to 0.52. The spatial model accurately captures the anomalously wet monsoon troughs in 1926 and 1946 with dry conditions elsewhere, as well as the anomalously dry conditions across most of the peninsula in 1966 and 1986. The locations of the large-scale anomalies in 1946 and 1986 are very well predicted (central India and western India, respectively). In 1966, the dry anomaly is predicted to the south of central India as opposed to the east of central India in the observations. In 1926, the wet anomaly is located over eastern central India as opposed to the whole monsoon core zone (western, central, and northern India, excluding mountains) in the observations.
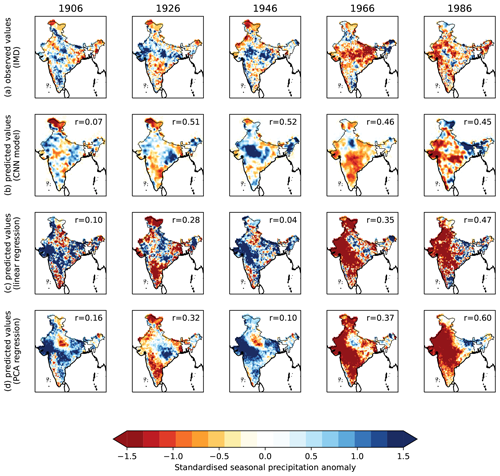
Figure 4Example verification for one of the members of the CNN–IMD ensemble. (a) Observed seasonal rainfall anomalies for the 5 years that were excluded from the model training dataset (computed using the IMD gridded gauge dataset). (b) CNN–IMD model predictions for the same 5 years from one ensemble member. (c) Predictions from a basic linear regression model, with the value of each pixel computed using multivariate linear regression (again excluding these 5 years from fitting). (d) Predictions from a more complex regression model, computed by regressing eight PCAs onto the palaeoclimate data and then reconstructing the anomaly field from the related EOFs. The spatial pattern correlation coefficient with observations is given in the top left for each model year. In all cases, the correlation is computed using data coarsened to 2° resolution using a 9×9 median filter.
The linear regression model (Fig. 4c) performs much less well than the spatial model. Only 1 year has a spatial pattern correlation coefficient close to the best years of the spatial model (r=0.45); the range for the other 4 years is 0.04–0.35. The linear regression model generally captures the observed wet and dry signals, with notable successes in 1926 (wet in central India, dry in the north and south) and 1986 (very dry in western India). However, the locations of the largest anomalies are typically wrong; e.g. it captures the surplus all-India rainfall in 1946 but overestimates it and places the strongest wet anomaly in far western India rather than over the monsoon trough. Similarly, it captures the deficient all-India rainfall in 1966 but makes western (rather than eastern) India very dry. Thus, the linear regression model generally performs less well than the spatial model.
Although PCA regression models are commonly used for spatial palaeoclimate reconstructions, the one used here represents only a marginal (though consistent) improvement compared to the linear regression model (Fig. 4d). The sign of the all-India rainfall anomaly is correct, but, like the linear regression model, the anomalies occur in the wrong place. However, this is just one ensemble member compared across just five seasons. While the mean value of r is higher in the CNN (0.40) than the PCA (0.31) and linear (0.25) models, the latter two do beat the CNN model in 2 of the 5 years.
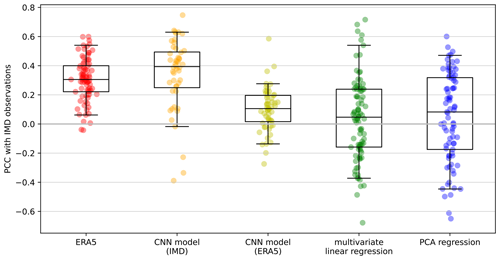
Figure 5Distribution of spatial pattern correlation coefficients between IMD observations and each model (plus ERA5 reanalysis), with each marker indicating the pattern correlation coefficient (PCC) for one monsoon season. The number of markers for each model is the number of years of overlap between the model and observations (1940–2022 for ERA5, 1901–1994 for IMD–CNN and the regression models, and 1940–1994 for ERA5–CNN). For the spatial models, the PCC is computed over the ensemble mean of members that were not trained on the year in question. Similarly for the regression, one model was trained per 5 years of desired output, with the model not seeing those 5 years. As in Fig. 4, the PCC is computed using data coarsened to 2° resolution using a 9×9 median filter. The boxes represent the median and interquartile range, and the whiskers represent the 5th and 95th percentiles.
Therefore, as a further test of the spatial model, we use the whole training dataset via cross-validation (Fig. 5) and add a second CNN trained on precipitation data from ERA5 (hereafter ERA5–CNN) to compare with the original spatial model (hereafter IMD–CNN). We used precipitation data from the ERA5 reanalysis to encompass the uncertainties due to differences between independent observational datasets. For each model, each point in Fig. 5 represents the spatial pattern correlation coefficient for one monsoon season from the subset of members (or for regression, single model) not including that season in their training dataset. The IMD–CNN model is a closer match to the IMD observations than the ERA5 reanalysis; i.e. the error associated with this model is less than the difference between the training dataset and another observational dataset. The median spatial pattern correlation coefficient for the IMD–CNN is about 0.4 compared with about 0.3 for the ERA5 reanalysis. The ERA5–CNN is much weaker, with a median of about 0.1, partly because of the much shorter training dataset and partly because of the differences between the ERA5 training dataset and the IMD evaluation dataset. The two regression models perform similarly to the ERA5–CNN, with median spatial pattern correlation coefficients of about 0.1, though they have a much greater spread than either of the CNN-based spatial models, with some years exceeding 0.5.
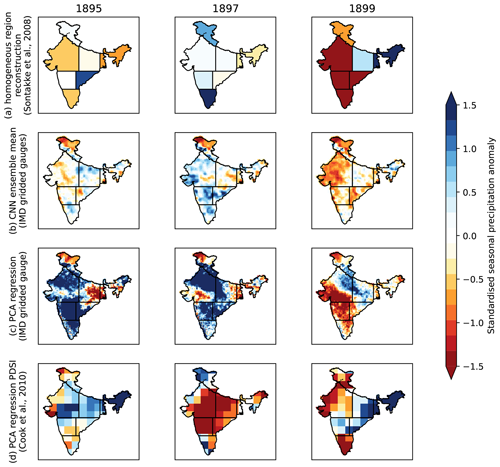
Figure 6Verification of selected models against values for homogeneous regions given in Sontakke et al. (2008). The 3 years shown here (1895, 1897, 1899) are 3 of the last years before the start of the training dataset. (a) Reconstructed regional rainfall anomalies from instrumental records; (b) predicted values from the IMD–CNN ensemble mean; (c) predicted values from the PCA regression model; (d) values of PDSI from Cook et al. (2010).
Comparison against June–September rainfall aggregated from the reconstructed monthly regional time series from Sontakke et al. (2008) provides a test for the IMD–CNN model for cases completely outside the IMD gridded gauge dataset. We use 3 years (1895, 1897, 1899; Fig. 6) that reflect diverse conditions: 1895 was an average monsoon with regional anomalies of both signs in peninsular India, 1897 was a surplus monsoon with all but NEI recording positive rainfall anomalies, and 1899 was a very deficient monsoon with four of the seven regions recording standardised rainfall anomalies of less than −1.5. The IMD–CNN model (Fig. 6b) captures these variations well, especially the wet anomalies in the south in 1897 and the dry anomalies covering all of western and southern India in 1899. It also captures the normal monsoon of 1895, although there are some errors with regional anomalies, especially in EPI. The IMD–CNN model generally has weak performance in NEI and NMI, likely due to relatively sparse observations in these regions in the training dataset but potentially also due to large uncertainties in these regions in the Sontakke et al. (2008) dataset. In general, as is the case for the single ensemble model (Fig. 4), the IMD–CNN model tends to underestimate the magnitude of the anomalies.
The PCA regression model (Fig. 6c) captures the strong and weak monsoons of 1897 and 1899, respectively, including the general locations of the dry anomalies in western India in 1899. However, the model gets the locations of the wet anomalies wrong in 1897, and it predicts widespread wet anomalies in 1895 that were not observed.
The reconstructed Palmer drought severity index (PDSI) from Cook et al. (2010) is not expected to be a strict match (Fig. 6d), since the PDSI includes information on potential evapotranspiration. The PDSI is widely used in palaeoclimate studies because the inclusion of potential evapotranspiration means that it is often better correlated with tree ring records than rainfall alone. The PDSI correlates reasonably well with the instrumental record in 1895 and 1899, though, like the other PCA regression model, the anomalies are often in the wrong locations. In 1897, the strongly negative PDSI does not match the observed slightly surplus monsoon. This may be due to lasting subsurface effects of a very weak 1896 monsoon.
The evaluation of the CNN-based spatial model shows that it performs better than other models, captures signals present in longer instrumental records, and is closer to the training dataset than a state-of-the-art reanalysis. This provides confidence in the use of the spatial model to make full reconstructions.
4.2.2 Reconstruction
We first examine the spatial patterns of extreme years, as shown by the spatial model and observations (Fig. 7). The four driest monsoons in the model – 1758, 1666, 1865, and 1778 – all tend to have their strongest anomalies over western and southern peninsular India. This is broadly consistent with observations, indicating that the model has no consistent bias and is replicating patterns seen in the observations. In contrast, the strongest anomalies in the wettest years in the model occur in several different locations – from the far northwest in 1716 to the southern and central peninsula in 1731. Again, this pattern is consistent with the wettest observed monsoons (compare e.g. 1917 and 1988). Both results are consistent with theory: weak monsoons are characterised by long periods of low rainfall caused by large-scale intraseasonal circulation patterns (e.g. breaks). In contrast, extreme wet anomalies are typically caused by the passage of one or several monsoon low-pressure systems which, depending on their track, can cause heavy rainfall over most of India (Hunt and Fletcher, 2019; Thomas et al., 2021).
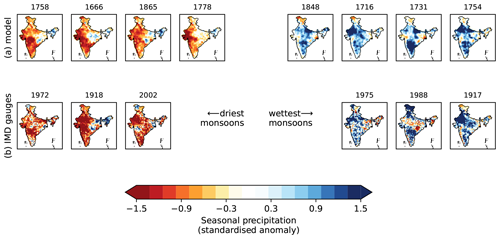
Figure 7Maps of seasonal rainfall anomalies for the wettest and driest monsoon seasons: (a) the CNN ensemble mean (prior to 1901) and (b) the IMD gridded gauge observations. In panels (a) and (b), the population of monsoons is sorted by total seasonal rainfall, i.e. by first converting the anomaly to an absolute amount using the spatial mean and variance computed from observations, thus reversing a preprocessing step before model training.
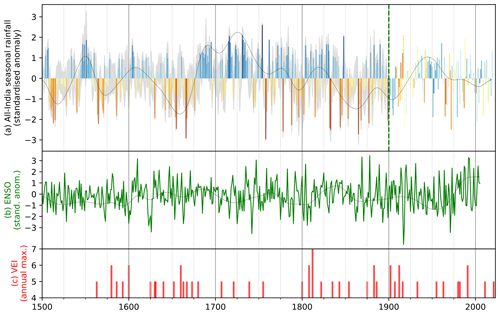
Figure 8All-India monsoon rainfall anomalies from 1500 CE to the present. (a) Anomalies are computed using the CNN ensemble mean, with the IMD instrumental record to the right of the dashed green line. The grey shading indicates the bounds of the 11-member ensemble. (b) Reconstructed and standardised ENSO anomalies for the same period, taken from Li et al. (2013). (c) Major volcanic eruptions with a volcanic explosivity index greater than 4, taken from Venzke (2024). The thin black lines in panels (a) and (b) are 10-year Gaussian low-pass filters (multiplied by a factor of 3).
The model consistently underpredicts the magnitude of the anomalies, likely because it tends to overestimate the spatial scales of precipitation. While observed extreme anomalies are marked by a strong heterogeneity and have high variance at small spatial scales (as well as large ones), this is not the case in the model. This is most likely due to the number of degrees of freedom in the predictor dataset being much lower than in a high-resolution gridded rainfall product.
Nevertheless, since the large-scale signal is reasonable, we can extract the all-India rainfall time series (Fig. 8a) by converting the spatial anomalies to absolute values, taking a spatial mean and re-standardising the values for consistency. There is a marked improvement in capturing the inter-annual variability compared to the original regional model (Fig. 3), suggesting the model has successfully learned important spatial relationships in the training data, but it still somewhat underestimates the observed inter-annual variability (Fig. 8a). The decadal variability and timing of droughts during this period are corroborated by earlier work (e.g. Kathayat et al., 2022).
The reconstructed ENSO anomalies (Fig. 8b) have a correlation with monsoon anomalies that varies centennially: the rolling 30-year correlation (not shown) is negative throughout almost all of the 18th and 20th centuries, but it is positive in the 17th and early 19th centuries. This pattern is consistent with previous studies (Shi and Wang, 2019), in which it is speculated to be modulated by the Pacific Decadal Oscillation.
Similarly, large volcanic eruptions (Fig. 8c) have a significant impact on the reconstructed monsoon anomalies. Lagged composites of monsoon rainfall for each volcanic explosivity index (VEI; not shown) suggest that the impact on the monsoon grows with increasing VEI. In year 0 of VEI5 events, the mean reconstructed monsoon rainfall anomaly falls to −0.11, then to a minimum of −0.18 in year 2, before recovering by year 4. The pattern is different in VEI6 events, which initially cause an increase in monsoon strength, reaching a maximum mean anomaly of +0.25 in year 2. This then starts to fall and becomes negative by year 5, reaching a minimum of −0.56 in year 8, after which it recovers. These coherent responses of the reconstructed monsoon to volcanic eruptions give us further confidence in our reconstruction.
Consistent with the regional model and other studies, conditions were generally dry in the 17th century (particularly 1650–1680), the 18th century was generally wet (particularly 1715–1740), and the 19th century had much stronger inter-annual variability. The dry period in the middle of the 19th century is consistent with long-term gauge records (Sontakke and Singh, 1996). Quite surprisingly, given the general underestimation of inter-annual variability, the driest (1758) and wettest (1754) years predicted by the model are only 4 years apart. The 10 wettest years are 1551, 1715, 1716, 1731, 1732, 1754, 1762, 1848, 1917, and 1988. The 10 driest years are 1655, 1666, 1758, 1778, 1832, 1833, 1844, 1865, 1918, and 1972.
4.3 Explainability
Shapley analysis (Sect. 3.6), which shows the contribution of each palaeo-record to the prediction of the regional models, indicates that the most important records tend to lie in the region of interest (Fig. 9). This is especially true when there are a large number of suitable high-quality palaeoclimate records. For example, in the regions bordering the Himalaya (NMI, NCI, and NEI), where there are several long tree ring datasets, there are many records with high Shapley values. In contrast, records from regions with very few palaeoclimate records do not necessarily show good predictability for that region although they may be important for other regions. An example of this is the single speleothem record from EPI (Jhumar Cave), which shows poor predictability for EPI though it is a useful predictor for the neighbouring WPI region. The lack of predictive power may be because the record does not have a strong causal relationship with regional monsoon rainfall or because the record is not of high enough quality, e.g. because of low resolution. Shapley analysis implies the former case for the EPI speleothem. Sinha et al. (2011) argued that the variability in this record reflects changes in both local and upstream rainfall, and thus it is plausible that the heavier monsoon rainfall of the WPI may end up influencing speleothems in EPI.
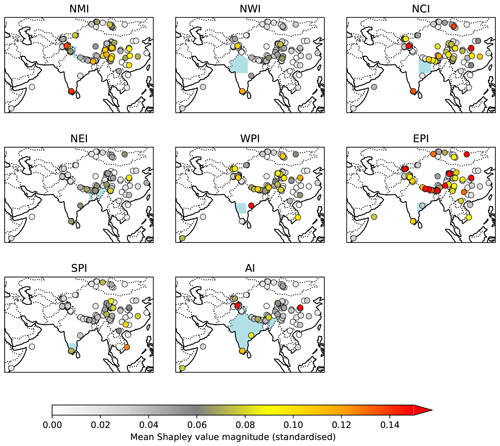
Figure 9Feature importance of each palaeoenvironmental record in each of the regional model ensembles. Shapley analysis is applied to each of the first five models in each ensemble to determine the impact of each predictor on the final predictions. The points are coloured by the mean of the absolute values of these numbers. The Shapley values are standardised in the sense that a value of 0.1 means that, on average, the selected dataset changes the predicted value of standardised seasonally averaged monsoon precipitation in the given regional model by 0.1. The absolute Shapley values are taken before averaging.
Some palaeoclimate records are dynamically linked to rainfall in other regions. The two tree ring records in the Western Ghats, for example, are also useful for estimating rainfall over northern (NMI, NWI, NCI) and eastern (EPI) India. This follows from the basic monsoon circulation: a stronger average monsoon is associated with a stronger Somali jet and hence enhanced moist flow and precipitation over the Western Ghats, as well as a stronger monsoon trough around which this moist flow subsequently recurves, bringing enhanced precipitation to the monsoon core zone, which covers much of NWI, NCI, and EPI. The records in the Arabian Sea and on the Somali coast are likely useful for the same reason. Records in the north can also be useful for modelling rainfall in the south, although this relationship is weaker due to the ratio of records in the two regions.
The model also ingests palaeoclimate records from outside India, most of which are from China. China experiences a summer monsoon (the East Asian monsoon) during roughly the same months as India. The two monsoons are linked both dynamically, via low-pressure systems and wave responses to local diabatic heating, and through shared teleconnections, e.g. with ENSO (Kripalani and Kulkarni, 2001; Shukla et al., 2011; Ha et al., 2018). The model is often able to use these records to constrain the estimates of regional precipitation over India; for example, the EPI model assigns high importance to a number of records over southern and central China.
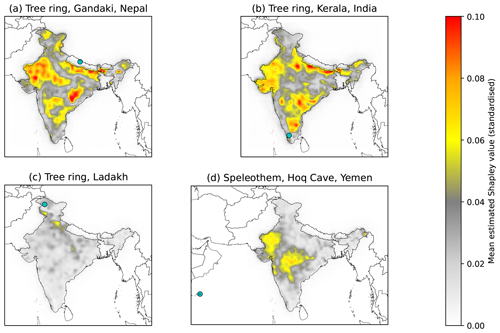
Figure 10Mean estimated Shapley value magnitudes for four of the input palaeoclimate records in the CNN ensemble model. The four records shown are (a) a tree ring dataset in the central Himalayas in central Nepal, (b) a tree ring dataset at the southern edge of the Western Ghats in Kerala, (c) a tree ring dataset in the Hindu Kush in Ladakh, and (d) a speleothem from Hoq Cave on Socotra Island in the western Indian Ocean. The Shapley values are standardised in the sense that a grid point value of 0.1 means that, on average, the selected dataset changes the predicted value of standardised seasonally averaged monsoon precipitation at that grid point by 0.1.
The forward method indicates the approximate importance of specific records for predicting rainfall at each grid point in the spatial model ensemble mean predictions (Fig. 10). As an example, we use a typical central Himalayan tree ring record (Fig. 10a). This dataset has a strong influence on local conditions along the Nepali border. However, it is also important for much of central India, especially along the monsoon core zone. This is likely due to the spatial coherence of seasonal anomalies in this region: a strong monsoon trough, usually manifested through an increased frequency of low-pressure systems crossing the region, results in increased precipitation along both the central Himalayan foothills and the Indo-Gangetic Plain.
This coherence, supported by synoptic-scale dynamics, is highlighted by one of the Keralan tree rings (Fig. 10b). It has a strong local impact, but through its link to the monsoon circulation it is also a useful predictor for much of northern India. In particular, it seems to be useful at predicting extensions of the monsoon trough, with high impact to its west (Gujarat), north (foothills), and south (Deccan Plateau).
However, many palaeoclimate records have only a very localised impact in the model. This is, as expected from the results with the backward model, most common in areas with a high density of records. In such cases, the model finds that they provide only a small local adjustment. In the example of the Ladakhi tree ring records (Fig. 10c), the model uses almost no information from this dataset outside of its immediate neighbourhood, and even there it has a smaller impact than other nearby records.
The Hoq Cave speleothem on Socotra Island (Fig. 10d) is an example of an extra-regional record that has a big impact on model predictions of seasonal rainfall over much of central and western India because of the dynamical linkage between the two regions via the coupling of the Somali jet, which passes directly over Socotra, and the overall circulation strength of the summer monsoon. Precipitation over the two regions is correlated on inter-annual timescales (Fukushima et al., 2019), possibly driven by the IOD and ENSO (Jain et al., 2021), but there is also intraseasonal variability that affects both regions simultaneously, independent of the low-level jet, such as the BSISO (Hunt and Turner, 2022).
4.4 The history of the monsoon
The reconstructions, based on both the time series (Fig. 3) and the CNN (Figs. 6 and 8) models, show considerable inter-annual variability in monsoon precipitation, particularly during the 19th and 20th centuries, but with marked decadal- and centennial-scale variability during the earlier part of the record. The spatial model (Fig. 8) provides a somewhat smoother view of the changes than the regional model (Fig. 3), but there is good agreement between the two series. Across India as a whole, for example, there are intervals of below-average precipitation between 1507 and 1516 CE, with an extended period of drought from the end of the 16th century persisting through most of the 17th century and with a further interval of below-average precipitation in the last decade of the 19th century. Comparison with the regional time series shows that each of these intervals affected different regions of the subcontinent. The earliest drought interval, for example, is registered quite strongly in WPI and NMI and less strongly in NCI, although individual years have below-average rainfall in many of the other regions of the country. The drought characteristic of the end of the 16th century and in the 17th century is registered more widely, including in EPI, WPI, NCI, NWI, and NMI. Drought conditions at the end of the 17th century are strongly registered in EPI and also in NCI, NWI, and NMI, although in these regions the anomalies are smaller though persistent over a longer period. There is a drought period between 1820 and 1840 CE which is strongly registered in EPI but only shows up as individual anomalous years in the all-India composite. Much of the 18th century is characterised by wetter-than-average conditions, and decadal-scale intervals of enhanced monsoons occur between 1542 and 1557 CE, from 1681–1691 CE, from 1700–1718 CE, and in the middle part of the 19th century.
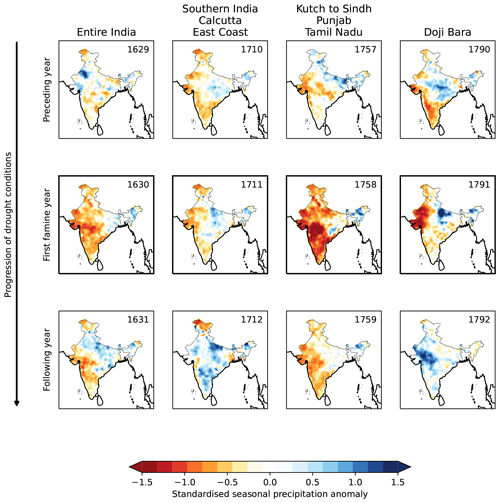
Figure 11Modelled monsoon rainfall anomalies for years associated with four major famines in the 17th and 18th centuries. In each case, the first recorded year of the famine is given in the middle row. Doji Bara is the name given to a famine that affected much of southern and western India.
The reconstructed dry extremes (Fig. 7) align well with known major famines (Fig. 11), with dry anomalies over the regions where famine was recorded. The “Entire India” famine of 1630 appears to have been triggered by widespread dry anomalies reaching from the far south to the far north, with only Bengal and northeastern India having a normal monsoon. Famines were recorded in Gujarat, Punjab, and Tamil Nadu in 1758, and the model predicts strong dry anomalies in these regions in that year, as well as across much of northern India. The Doji Bara or “skull famine”, which started in 1791, was triggered in part by a string of strong El Niños towards the end of the 18th century (Grove, 2007). This led to weak monsoons in 1788 and 1789, affecting western India and southern India, respectively, followed by a weak monsoon in southern India in 1790 and an extremely weak monsoon in western India (with low rainfall across most of the peninsula) in 1791. This extended event led to catastrophic famine in Gujarat, Punjab, and Tamil Nadu, consistent with very large dry anomalies in the model. Our results for the spatial pattern of this drought are in agreement with Kathayat et al. (2022). In contrast to the strong negative anomalies of these three famines, the famine of 1711, which affected southern India, Calcutta, and much of the east coast, was linked to 2 successive years of only mildly reduced rainfall in the these locations. In the cases where famines coincided with periods of deficient monsoon rainfall, the strongest dry anomalies were typically co-located with the regions where the famines were recorded. These were often linked to consecutive years of negative regional anomalies, although this may be an artefact of the underestimation of inter-annual variability in the model.
We have demonstrated the potential of deep learning techniques to produce robust spatiotemporal patterns of palaeomonsoon rainfall over the Indian subcontinent. The reconstructions indicate that the high inter-annual variability characteristic of much of the 19th and 20th centuries is not typical of earlier periods, which displayed more decadal- to centennial-scale variability. Kathayat et al. (2022) also drew attention to this difference in the timescale of variability between the instrumental and pre-instrumental periods, based on a high-resolution speleothem record from Mawmluh. According to our reconstructions, the 17th century was drier, and much of the 18th century was wetter than average. Major droughts identified by the model, for example during the early and late 17th century, correspond to documented famines in the affected regions. Intervals of below-average rainfall are rarely registered across the whole of the subcontinent, however, reflecting the fact that they are caused by different changes in circulation patterns and/or teleconnections. This suggests that the all-India monsoon index is, at best, an oversimplified way of contextualising changes in the monsoon. The spatial patterns produced by the spatial model provide a more nuanced way of examining patterns of change through time.
The spatial variability in the expression of above- or below-average monsoon precipitation also makes it difficult to rely on individual palaeo-records for reconstructions. Snow accumulation rates, as well as dust and chloride records from ice cores from the Tibetan Plateau and the Himalayas, have been interpreted as indicators of changes in the monsoon over recent centuries (Thompson et al., 2000; Davis and Thompson, 2004; Yao and Yang, 2004; Duan et al., 2004; Thompson et al., 2006), but there are large differences in the timing of inferred intervals of above- and below-average precipitation between different sites, which are thought to reflect the impact of complex topography and potentially different precipitation sources (Kaspari et al., 2008). This makes these records difficult to correlate with the overall behaviour of the monsoon across the peninsula. The high-resolution speleothem record from Mawmluh (not included in our training data) shows relatively good concordance with our reconstructions of the timing of weak and strong monsoons over the past 500 years, but again this single record cannot be expected to capture all of the features shown by our reconstructions. Our reconstruction also demonstrates robust and coherent relationships with an earlier ENSO reconstruction (Li et al., 2013) – with which its correlation varies on centennial timescales – and historical data on large volcanic eruptions – which lead to a substantial weakening of the reconstructed monsoon over the following decade.
In our model reconstructions, as in many other palaeoclimate reconstructions, we make the assumption of stationarity. The spatial model learns from the period 1901–1994, and the regional models extend this back a further 50 years or so. Both models assume that the seasonal relationships between palaeoclimate records and precipitation are fixed over this period and that these relationships have held true since 1500 CE. This is an oversimplification. The monsoon has been subject to forcing from aerosols and greenhouse gases over this interval, both of which have a significant impact on seasonal precipitation (Lau and Kim, 2017; Westervelt et al., 2020). Recent changes in rainfall seasonality, specifically a shift from winter rainfall to summer rainfall, are thought to have affected the tree ring records in the western Himalaya, for example (Kotlia et al., 2012; Munz et al., 2017). However, there is evidence that this variability was present in the last century (Brunello et al., 2019; Fan et al., 2022) and is thus represented in the training dataset and should not present a problem for the models. The strength of teleconnections with the East Asian monsoon or ENSO is also not constant. The correlation between summer monsoon rainfall and ENSO varies on decadal timescales (Torrence and Webster, 1999), and Rehfeld et al. (2013) showed that the coupling strength of the South Asian monsoon and East Asian summer monsoon varies centennially as a function of large-scale climatic conditions. However, the Shapley analysis indicates that the models do not depend heavily on these teleconnections.
The reliability of the training datasets will also affect the reliability of the final models. The gridded gauge dataset used as the rainfall target has very few gauges even today in the western and eastern Himalaya, and the situation was even worse in the first half of the 20th century. This may explain why the CNN struggles to capture finer spatial detail in these regions. There may also be considerable dating uncertainties associated with the palaeoclimate records. Ljungqvist et al. (2016) assume an acceptable dating uncertainty of 200 years for the records in their dataset. Although most of the palaeoclimate records included in this study have an annual or near-annual sampling resolution this is not necessarily equivalent to the resolution of the climate signal. The transmission time for water transfer from the surface to the cave means that speleothem records, for example, often have a signal resolution of several years (Baker et al., 2013; Comas-Bru et al., 2019). Similarly, annual tree growth can be affected by sub-optimal conditions in previous years such that the tree ring record provides an attenuated signal of the current year (e.g. Moreau et al., 2020; Schnabel et al., 2022). Furthermore, although the monsoon is the dominant moisture source for tree growth over most of India, this is not necessarily the case in the western and central Himalaya where the covariance of annual and monsoon rainfall is moderate. However, our data-driven models have two advantages. Firstly, because of the strong regularisation, they filter out predictors that have no tractable relationship with the target variable. Secondly, the models combine multiple palaeoclimate records non-linearly to extract local monsoon signals. Other studies have leveraged the dynamical links between the monsoon and more distant records to make reconstructions of changes in the monsoon (e.g. Burns et al., 2002; Fleitmann et al., 2007), but the advantage of data-driven models is being able to combine them with other records to maximise model skill at a given point. Thus, even if many of the palaeoclimate records used are not particularly good indicators of monsoon rainfall and have relatively poor coverage over much of peninsular India, the models still have high skill.
We used two types of deep learning models to produce palaeoclimate reconstructions of the Indian summer monsoon over the last 500 years. These were trained on long instrumental records of monsoon rainfall over India and used records from three palaeoenvironmental datasets covering South and East Asia. Due to the small size of the training dataset, we needed to use techniques that prevent overfitting and improve model performance. These included regularisation (which simplifies the model), custom loss functions (which guide the model learning more effectively), and bagging (which combines multiple models to reduce errors). Both sets of models, therefore, were run as ensembles, from which we report the mean predictions.
The regional models were trained separately on seven regional rainfall datasets, ranging from 120 to 180 years in length, and their all-India sum. This produced reconstructions which captured decadal-scale variability well, identifying the multidecadal droughts of the mid-17th century which affected most of the subcontinent, as well as the dry conditions in the east and north of the country in the first half of the 19th century. However, despite reasonably high correlation with observations across their testing data (r∼0.5), these models largely underestimated inter-annual variability.
The CNN-based spatial model improves on these results by taking account of spatial relationships in the predictors and the rainfall. In testing, the model had a higher spatial correlation coefficient with the IMD observations, with an error smaller than that between different observational datasets. The extreme deficit and extreme surplus years in the spatial model mirrored the spatial characteristics – in both scale and region – of the observations. The all-India monsoon time series produced by the spatial model showed the following features.
-
Multidecadal droughts occurred from approximately 1640–1680 and approximately 1840–1900. The latter period was characterised by much larger inter-annual variability.
-
Multidecadal intervals of above-average rainfall occurred from approximately 1690–1750.
-
The most extreme drought years (1666, 1758, 1778, 1865) were characterised by very strong dry anomalies in southern and western India.
-
There were several events of large inter-annual variability (1754–1758, 1776–1778, 1784–1788, 1828–1833, 1844–1848) where standardised seasonal rainfall of both signs exceeded a magnitude of 1.5.
-
There were also several pairs of consecutive years where the seasonal anomaly fell below −1.5: 1654–1655, 1666–1667, 1758–1759, and 1832–1833.
Some of the identified drought years correspond to recorded famines; the dry anomalies typically occurred in regions where famine was reported, especially in the south and west.
In the regional models, the most important predictors in regions with ample high-quality palaeoclimate records tended to be located in or near those regions due to their strong tie to the regional hydroclimate. However, in both the regional and spatial models, some records had a predictive influence across broader regions, stemming from large-scale dynamical monsoon linkages. Some records in data-sparse regions had high importance if they related to the broader synoptic monsoon environment. This analysis indicates that the models learned physically meaningful teleconnections between local palaeoclimate indicators and regional rainfall patterns.
Code to reproduce the models and figures in this study is publicly available at https://github.com/kieranmrhunt/paleomonsoon (Hunt and Harrison, 2024b).
All data produced by this study are publicly available at https://doi.org/10.5281/zenodo.12688184 (Hunt and Harrison, 2024a).
KMRH conceived the study, designed and trained the model, and created the figures. SPH and KMRH wrote and iterated the manuscript together.
The contact author has declared that none of the authors has any competing interests.
Publisher’s note: Copernicus Publications remains neutral with regard to jurisdictional claims made in the text, published maps, institutional affiliations, or any other geographical representation in this paper. While Copernicus Publications makes every effort to include appropriate place names, the final responsibility lies with the authors.
KMRH is supported by a NERC Independent Research Fellowship (MITRE; NE/W007924/1).
This research has been supported by the Natural Environment Research Council (grant no. NE/W007924/1).
This paper was edited by Nerilie Abram and reviewed by Nick Scroxton and one anonymous referee.
Agnihotri, R., Dutta, K., Bhushan, R., and Somayajulu, B. L. K.: Evidence for solar forcing on the Indian monsoon during the last millennium, Earth Planet. Sc. Lett., 198, 521–527, https://doi.org/10.1016/S0012-821X(02)00530-7, 2002. a
Andermann, T., Strömberg, C. A., Antonelli, A., and Silvestro, D.: The origin and evolution of open habitats in North America inferred by Bayesian deep learning models, Nat. Commun., 13, 4833, https://doi.org/10.1038/s41467-022-32300-5, 2022. a
Anderson, D. M., Baulcomb, C. K., Duvivier, A. K., and Gupta, A. K.: Indian summer monsoon during the last two millennia, J. Quaternary Sci., 25, 911–917, 2010. a
Archer, D. R. and Fowler, H. J.: Spatial and temporal variations in precipitation in the Upper Indus Basin, global teleconnections and hydrological implications, Hydrol. Earth Syst. Sci., 8, 47–61, https://doi.org/10.5194/hess-8-47-2004, 2004. a
Ashok, K., Guan, Z., and Yamagata, T.: Impact of the Indian Ocean dipole on the relationship between the Indian monsoon rainfall and ENSO, Geophys. Res. Lett., 28, 4499–4502, 2001. a
Baker, A., Bradley, C., and Phipps, S. J.: Hydrological modeling of stalagmite δ18O response to glacial-interglacial transitions, Geophys. Res. Lett., 40, 3207–3212, 2013. a
Banerji, U. S., Arulbalaji, P., and Padmalal, D.: Holocene climate variability and Indian Summer Monsoon: an overview, The Holocene, 30, 744–773, 2020. a, b
Baudouin, J.-P., Herzog, M., and Petrie, C. A.: Cross-validating precipitation datasets in the Indus River basin, Hydrol. Earth Syst. Sci., 24, 427–450, https://doi.org/10.5194/hess-24-427-2020, 2020. a
Bianchette, T. A., Pandey, V., Mollan, C., Hall, S., McCloskey, T. A., and Liu, K.-b.: Machine learning based anomaly detection for sedimentological data: Application to a Holocene multi-proxy paleoenvironmental reconstruction from Laguna Boquita, Jalisco, Mexico, Mar. Geol., 464, 107125, https://doi.org/10.1016/j.margeo.2023.107125, 2023. a
Bodesheim, P., Babst, F., Frank, D. C., Hartl, C., Zang, C. S., Jung, M., Reichstein, M., and Mahecha, M. D.: Predicting spatiotemporal variability in radial tree growth at the continental scale with machine learning, Environmental Data Science, 1, e9, https://doi.org/10.1017/eds.2022.8, 2022. a
Borgaonkar, H. P., Sikder, A. B., Ram, S., and Pant, G. B.: El Niño and related monsoon drought signals in 523-year-long ring width records of teak (Tectona grandis LF) trees from south India, Palaeogeogr. Palaeocl., 285, 74–84, 2010. a
Bourel, B., Marchant, R., de Garidel-Thoron, T., Tetard, M., Barboni, D., Gally, Y., and Beaufort, L.: Automated recognition by multiple convolutional neural networks of modern, fossil, intact and damaged pollen grains, Comput. Geosci., 140, 104498, https://doi.org/10.1016/j.cageo.2020.104498, 2020. a
Brigato, L. and Iocchi, L.: A Close Look at Deep Learning with Small Data, 2020 25th International Conference on Pattern Recognition (ICPR), Milan, Italy, 2021, 2490–2497, https://doi.org/10.1109/ICPR48806.2021.9412492, 2021. a
Brunello, C. F., Andermann, C., Helle, G., Comiti, F., Tonon, G., Tiwari, A., and Hovius, N.: Hydroclimatic seasonality recorded by tree ring δ18O signature across a Himalayan altitudinal transect, Earth Planet. Sc. Lett., 518, 148–159, 2019. a, b
Burns, S. J., Fleitmann, D., Mudelsee, M., Neff, U., Matter, A., and Mangini, A.: A 780-year annually resolved record of Indian Ocean monsoon precipitation from a speleothem from south Oman, J. Geophys. Res.-Atmos., 107, ACL–9, https://doi.org/10.1029/2001JD001281, 2002. a, b, c
Carro-Calvo, L., Salcedo-Sanz, S., and Luterbacher, J.: Neural computation in paleoclimatology: General methodology and a case study, Neurocomputing, 113, 262–268, 2013. a
Chandra, R., Cripps, S., Butterworth, N., and Muller, R. D.: Precipitation reconstruction from climate-sensitive lithologies using Bayesian machine learning, Environ. Modell. Softw., 139, 105002, https://doi.org/10.1016/j.envsoft.2021.105002, 2021. a
Cherchi, A., Terray, P., Ratna, S. B., Sankar, S., Sooraj, K. P., and Behera, S.: Indian Ocean Dipole influence on Indian summer monsoon and ENSO: A review, Indian summer monsoon variability, 157–182, https://doi.org/10.1016/B978-0-12-822402-1.00011-9, 2021. a
Coats, S., Smerdon, J., Stevenson, S., Fasullo, J. T., Otto-Bliesner, B., and Ault, T. R.: Paleoclimate constraints on the spatiotemporal character of past and future droughts, J. Climate, 33, 9883–9903, 2020. a
Comas-Bru, L., Harrison, S. P., Werner, M., Rehfeld, K., Scroxton, N., Veiga-Pires, C., and SISAL working group members: Evaluating model outputs using integrated global speleothem records of climate change since the last glacial, Clim. Past, 15, 1557–1579, https://doi.org/10.5194/cp-15-1557-2019, 2019. a
Cook, E. R., Anchukaitis, K. J., Buckley, B. M., D’Arrigo, R. D., Jacoby, G. C., and Wright, W. E.: Asian monsoon failure and megadrought during the last millennium, Science, 328, 486–489, 2010. a, b, c, d
Cortese, G., Dolven, J. K., Bjørklund, K. R., and Malmgren, B. A.: Late Pleistocene–Holocene radiolarian paleotemperatures in the Norwegian Sea based on artificial neural networks, Palaeogeogr. Palaeocl., 224, 311–332, 2005. a
Crétat, J., Braconnot, P., Terray, P., Marti, O., and Falasca, F.: Mid-Holocene to present-day evolution of the Indian monsoon in transient global simulations, Clim. Dynam., 55, 2761–2784, 2020. a
Crétat, J., Harrison, S. P., Braconnot, P., d’Agostino, R., Jungclaus, J., Lohmann, G., Shi, X., and Marti, O.: Orbitally forced and internal changes in West African rainfall interannual-to-decadal variability for the last 6000 years, Clim. Dynam., 62, 2301–2316, 2024. a
Davis, M. E. and Thompson, L. G.: Four centuries of climatic variation across the Tibetan Plateau from ice-core accumulation and d18O records, in: Earth Paleoenvironments: Records Preserved in Mid- and Low-Latitude Glaciers, edited by: Cecil, L. D., Green, J. R., and Thompson, L. G., 145–162, Kluwer, Dordrecht, https://doi.org/10.1007/1-4020-2146-1, 2004. a
de Geus, A. R., Barcelos, C. A. Z., Batista, M. A., and da Silva, S. F.: Large-scale pollen recognition with deep learning, in: 2019 27th European Signal Processing Conference (EUSIPCO), A Coruna, Spain, 1–5, https://doi.org/10.23919/EUSIPCO.2019.8902735, 2019. a
Dhyani, R., Bhattacharyya, A., Joshi, R., Shekhar, M., Chandra Kuniyal, J., and Singh Ranhotra, P.: Tree rings of Rhododendron arboreum portray signal of monsoon precipitation in the Himalayan region, Frontiers in Forests and Global Change, 5, 1044182, https://doi.org/10.3389/ffgc.2022.1044182, 2023. a
Dimri, A. P., Roxy, M., Sharma, A., Pokharia, A., Gayathri, C. R., Sanwal, J., Sharma, A., Tandon, S. K., Pattanaik, D. B., and Mohanty, U. C.: Monsoon in history and present, Journal of Palaeosciences, 71, 45–74, 2022. a
Dixit, Y. and Tandon, S. K.: Hydroclimatic variability on the Indian subcontinent in the past millennium: review and assessment, Earth-Sci. Rev., 161, 1–15, 2016. a, b, c
Duan, K., Yao, T., and Thompson, L. G.: Low-frequency of southern Asian monsoon variability using a 295-year record from the Dasuopu ice core in the central Himalayas, Geophys. Res. Lett., 31, https://doi.org/10.1029/2004GL020015, 2004. a
Fabijańska, A. and Danek, M.: DeepDendro – A tree rings detector based on a deep convolutional neural network, Comput. Electron. Agr., 150, 353–363, 2018. a
Fan, H., Gou, X., Nakatsuka, T., Li, Z., Fang, K., Su, J., Gao, L., and Liu, W.: Different moisture regimes during the last 150 years inferred from a tree-ring δ18O network over the transitional zone of the Asian summer monsoon, J. Hydrol., 613, 128484, https://doi.org/10.1016/j.jhydrol.2022.128484, 2022. a, b
Fleitmann, D., Burns, S. J., Mangini, A., Mudelsee, M., Kramers, J., Villa, I., Neff, U., Al-Subbary, A. A., Buettner, A., Hippler, D., and Matter, A.: Holocene ITCZ and Indian monsoon dynamics recorded in stalagmites from Oman and Yemen (Socotra), Quaternary Sci. Rev., 26, 170–188, 2007. a, b
Fukushima, A., Kanamori, H., and Matsumoto, J.: Regionality of long-term trends and interannual variation of seasonal precipitation over India, Progress in Earth and Planetary Science, 6, 1–20, 2019. a
Goswami, B. N. and Ajayamohan, R. S.: Intraseasonal oscillations and interannual variability of the Indian summer monsoon, J. Climate, 14, 1180–1198, 2001. a
Grove, R. H.: The Great El Niño of 1789–93 and its Global Consequences: Reconstructing an Extreme Climate Event in World Environmental History, The Medieval History Journal, 10, 75–98, https://doi.org/10.1177/097194580701000203, 2007. a
Guiot, J., Nicault, A., Rathgeber, C., Edouard, J. L., Guibal, F., Pichard, G., and Till, C.: Last-millennium summer-temperature variations in western Europe based on proxy data, The Holocene, 15, 489–500, 2005. a
Gupta, A. K., Anderson, D. M., and Overpeck, J. T.: Abrupt changes in the Asian southwest monsoon during the Holocene and their links to the North Atlantic Ocean, Nature, 421, 354–357, 2003. a
Ha, K.-J., Seo, Y.-W., Lee, J.-Y., Kripalani, R., and Yun, K.-S.: Linkages between the South and East Asian summer monsoons: a review and revisit, Clim. Dynam., 51, 4207–4227, 2018. a
Haug, G. H., Hughen, K. A., Sigman, D. M., Peterson, L. C., and Röhl, U.: Southward migration of the intertropical convergence zone through the Holocene, Science, 293, 1304–1308, 2001. a
Hersbach, H., Bell, B., Berrisford, P., Hirahara, S., Horányi, A., Muñoz-Sabater, J., Nicolas, J., Peubey, C., Radu, R., Schepers, D., Simmons, A., Soci, C., Abdalla, S., Abellan, X., Balsamo, G., Bechtold, P., Biavati, G., Bidlot, J., Bonavita, M., De Chiara, G., Dahlgren, P., Dee, D., Diamantakis, M., Dragani, R., Flemming, J., Forbes, R., Fuentes, M., Geer, A., Haimberger, L., Healy, S., Hogan, R. J. , Hólm, E., Janisková, M., Keeley, S., Laloyaux, P., Lopez, P., Lupu, C., Radnoti, G., de Rosnay, P., Rozum, I., Vamborg, F., Villaume, S., and Thépaut, J.-N.: The ERA5 global reanalysis, Q. J. Roy. Meteor. Soc., 146, 1999–2049, 2020. a
Huang, Y., Yang, L., and Fu, Z.: Reconstructing coupled time series in climate systems using three kinds of machine-learning methods, Earth Syst. Dynam., 11, 835–853, https://doi.org/10.5194/esd-11-835-2020, 2020. a
Hunt, K. M. R. and Fletcher, J. K.: The relationship between Indian monsoon rainfall and low-pressure systems, Clim. Dynam., 53, 1–13, 2019. a
Hunt, K. M. R. and Menon, A.: The 2018 Kerala floods: a climate change perspective, Clim. Dynam., 54, 2433–2446, 2019. a
Hunt, K. M. R. and Turner, A. G.: Non-linear intensification of monsoon low-pressure systems by the BSISO, Weather Clim. Dynam., 3, 1341–1358, https://doi.org/10.5194/wcd-3-1341-2022, 2022. a, b
Hunt, K. M. R. and Harrison, S. P.: Data-driven reconstructions of the Indian palaeomonsoon (1500–1995 CE), Zenodo [data set], https://doi.org/10.5281/zenodo.12688184, 2024a. a
Hunt, K. M. R. and Harrison, S. P.: Code to reproduce models and figures, GitHub, https://github.com/kieranmrhunt/paleomonsoon (last access: 20 December 2024), 2024b. a
Jain, S., Mishra, S. K., Anand, A., Salunke, P., and Fasullo, J. T.: Historical and projected low-frequency variability in the Somali Jet and Indian Summer Monsoon, Clim. Dynam., 56, 749–765, 2021. a
Jevšenak, J., Džeroski, S., and Levanič, T.: Predicting the vessel lumen area tree-ring parameter of Quercus robur with linear and nonlinear machine learning algorithms, Geochronometria, 45, 211–222, 2018. a
Kaspari, S., Hooke, R. L., Mayewski, P. A., Kang, S., Hou, S., and Qin, D.: Snow accumulation rate on Qomolangma (Mount Everest), Himalaya: synchroneity with sites across the Tibetan Plateau on 50–100 year timescales, J. Glaciol., 54, 343–352, 2008. a
Kathayat, G., Sinha, A., Breitenbach, S. F., Tan, L., Spötl, C., Li, H., Dong, X., Zhang, H., Ning, Y., Allan, R. J., Damodaran, V., Edwards, R. L., and Cheng, H.: Protracted Indian monsoon droughts of the past millennium and their societal impacts, P. Natl. Acad. Sci. USA, 119, e2207487119, https://doi.org/10.1073/pnas.2207487119, 2022. a, b, c
Kaushal, N., Breitenbach, S. F., Lechleitner, F. A., Sinha, A., Tewari, V. C., Ahmad, S. M., Berkelhammer, M., Band, S., Yadava, M., Ramesh, R., and Henderson, G. M.: The Indian summer monsoon from a speleothem δ18O perspective – a review, Quaternary, 1, 29, 2018. a, b
Kikuchi, K.: The boreal summer intraseasonal oscillation (BSISO): A review, Journal of the Meteorological Society of Japan. Ser. II, 9, 933–972, 2021. a
Kikuchi, K., Wang, B., and Kajikawa, Y.: Bimodal representation of the tropical intraseasonal oscillation, Clim. Dynam., 38, 1989–2000, 2012. a
Kim, D., Ko, C., and Kim, D.: Method for detecting tree ring boundary in conifers and broadleaf trees using Mask R-CNN and linear interpolation, Dendrochronologia, 79, 126088, https://doi.org/10.1016/j.dendro.2023.126088, 2023. a
Konecky, B. L., McKay, N. P., Churakova (Sidorova), O. V., Comas-Bru, L., Dassié, E. P., DeLong, K. L., Falster, G. M., Fischer, M. J., Jones, M. D., Jonkers, L., Kaufman, D. S., Leduc, G., Managave, S. R., Martrat, B., Opel, T., Orsi, A. J., Partin, J. W., Sayani, H. R., Thomas, E. K., Thompson, D. M., Tyler, J. J., Abram, N. J., Atwood, A. R., Cartapanis, O., Conroy, J. L., Curran, M. A., Dee, S. G., Deininger, M., Divine, D. V., Kern, Z., Porter, T. J., Stevenson, S. L., von Gunten, L., and Members, I. P.: The Iso2k database: a global compilation of paleo-δ18O and δ2H records to aid understanding of Common Era climate, Earth System Science Data, 12, 2261–2288, https://doi.org/10.5194/essd-12-2261-2020, 2020. a
Kotlia, B. S., Ahmad, S. M., Zhao, J.-X., Raza, W., Collerson, K. D., Joshi, L. M., and Sanwal, J.: Climatic fluctuations during the LIA and post-LIA in the Kumaun Lesser Himalaya, India: evidence from a 400 y old stalagmite record, Quaternary International, 263, 129–138, 2012. a
Kripalani, R. H. and Kulkarni, A.: Monsoon rainfall variations and teleconnections over South and East Asia, International Journal of Climatology: A Journal of the Royal Meteorological Society, 21, 603–616, 2001. a
Krishnamurthy, L. and Krishnamurthy, V. J. C. D.: Influence of PDO on South Asian summer monsoon and monsoon–ENSO relation, Clim. Dynam., 42, 2397–2410, 2014. a
Krishnamurthy, V. and Goswami, B. N.: Indian monsoon–ENSO relationship on interdecadal timescale, J. Climate, 13, 579–595, 2000. a, b
Krishnan, R. and Sugi, M.: Pacific decadal oscillation and variability of the Indian summer monsoon rainfall, Clim. Dynam., 21, 233–242, 2003. a
Lau, W. K.-M. and Kim, K.-M.: Competing influences of greenhouse warming and aerosols on Asian summer monsoon circulation and rainfall, Asia-Pacific J. Atmos. Sci., 53, 181–194, 2017. a
Lee, A.-S., Chao, W.-S., Liou, S. Y. H., Tiedemann, R., Zolitschka, B., and Lembke-Jene, L.: Quantifying calcium carbonate and organic carbon content in marine sediments from XRF-scanning spectra with a machine learning approach, Sci. Rep., 12, 20860, https://doi.org/10.1038/s41598-022-25377-x, 2022. a
Li, J., Xie, S.-P., Cook, E. R., Morales, M. S., Christie, D. A., Johnson, N. C., Chen, F., D’Arrigo, R., Fowler, A. M., Gou, X., and Fang, K.: El Niño modulations over the past seven centuries, Nat. Clim. Change, 3, 822–826, 2013. a, b, c
Li, S., Brandt, M., Fensholt, R., Kariryaa, A., Igel, C., Gieseke, F., Nord-Larsen, T., Oehmcke, S., Carlsen, A. H., Junttila, S., Tong, X., d'Aspremont, A., and Ciais, P.: Deep learning enables image-based tree counting, crown segmentation, and height prediction at national scale, PNAS nexus, 2, pgad076, https://doi.org/10.1093/pnasnexus/pgad076, 2023. a
Liu, F., Chai, J., Wang, B., Liu, J., Zhang, X., and Wang, Z.: Global monsoon precipitation responses to large volcanic eruptions, Sci. Rep., 6, 24331, https://doi.org/10.1038/srep24331, 2016. a
Liu, X., Zhou, T., Shi, P., Zhang, Y., Luo, H., Yu, P., Xu, Y., Zhou, P., and Zhang, J.: Uncertainties of soil organic carbon stock estimation caused by paleoclimate and human footprint on the Qinghai Plateau, Carbon Balance and Management, 17, 8, https://doi.org/10.1186/s13021-022-00203-z, 2022. a
Liu, Z., Xu, Z., Jin, J., Shen, Z., and Darrell, T.: Dropout Reduces Underfitting, arXiv [preprint], https://doi.org/10.48550/arXiv.2303.01500, 2023. a
Ljungqvist, F. C., Krusic, P. J., Sundqvist, H. S., Zorita, E., Brattström, G., and Frank, D.: Northern Hemisphere hydroclimate variability over the past twelve centuries, Nature, 532, 94–98, 2016. a, b
Lukens, W. E., Stinchcomb, G. E., Nordt, L. C., Kahle, D. J., Driese, S. G., and Tubbs, J. D.: Recursive partitioning improves paleosol proxies for rainfall, Am. J. Sci., 319, 819–845, 2019. a
Lundberg, S. M. and Lee, S.-I.: A Unified Approach to Interpreting Model Predictions, in: Advances in Neural Information Processing Systems, edited by: Guyon, I., Luxburg, U. V., Bengio, S., Wallach, H., Fergus, R., Vishwanathan, S., and Garnett, R., vol. 30, Curran Associates, Inc., https://proceedings.neurips.cc/paper/2017/file/8a20a8621978632d76c43dfd28b67767-Paper.pdf (last access: 20 December 2024), 2017. a
Malmgren, B. A. and Nordlund, U.: Application of artificial neural networks to paleoceanographic data, Palaeogeogr. Palaeocl., 136, 359–373, 1997. a
Mannila, H., Toivonen, H., Korhola, A., and Olander, H.: Learning, mining, or modeling? A case study from paleoecology, in: Discovey Science: First International Conference, DS’98 Fukuoka, Japan, 14–16 December 1998, Proceedings 1, 12–24, Springer, https://doi.org/10.1007/3-540-49292-5_2, 1998. a
Moreau, G., Achim, A., and Pothier, D.: An accumulation of climatic stress events has led to years of reduced growth for sugar maple in southern Quebec, Canada, Ecosphere, 11, e03183, https://doi.org/10.1002/ecs2.3183, 2020. a
Morice, C. P., Kennedy, J. J., Rayner, N. A., and Jones, P. D.: Quantifying uncertainties in global and regional temperature change using an ensemble of observational estimates: The HadCRUT4 data set, J. Geophys. Res.-Atmos., 117, https://doi.org/10.1029/2011JD017187, 2012. a
Munz, P. M., Lückge, A., Siccha, M., Böll, A., Forke, S., Kucera, M., and Schulz, H.: The Indian winter monsoon and its response to external forcing over the last two and a half centuries, Clim. Dynam., 49, 1801–1812, 2017. a
Nelson, D. B., Basler, D., and Kahmen, A.: Precipitation isotope time series predictions from machine learning applied in Europe, P. Natl. Acad. Sci. USA, 118, e2024107118, https://doi.org/10.1073/pnas.2024107118, 2021. a
Ning, L., Liu, J., and Sun, W.: Influences of volcano eruptions on Asian Summer Monsoon over the last 110 years, Sci. Rep., 7, 42626, https://doi.org/10.1038/srep42626, 2017. a
Olsson, O., Karlsson, M., Persson, A. S., Smith, H. G., Varadarajan, V., Yourstone, J., and Stjernman, M.: Efficient, automated and robust pollen analysis using deep learning, Methods Ecol. Evol., 12, 850–862, 2021. a
PAGES2k Consortium: A global multiproxy database for temperature reconstructions of the Common Era, Scientific data, 4, 170088, https://doi.org/10.1038/sdata.2017.88, 2017. a
Pai, D. S., Rajeevan, M., Sreejith, O. P., Mukhopadhyay, B., and Satbha, N. S.: Development of a new high spatial resolution (0.25 × 0.25) long period (1901–2010) daily gridded rainfall data set over India and its comparison with existing data sets over the region, Mausam, 65, 1–18, 2014. a, b
Pai, D. S., Sridhar, L., and Ramesh Kumar, M. R.: Active and break events of Indian summer monsoon during 1901–2014, Clim. Dynam., 46, 3921–3939, 2016. a
Poláček, M., Arizpe, A., Hüther, P., Weidlich, L., Steindl, S., and Swarts, K.: Automation of tree-ring detection and measurements using deep learning, Methods Ecol. Evol., 14, 2233–2242, 2023. a
Rajeevan, M., Bhate, J., Kale, J. D., and Lal, B.: High resolution daily gridded rainfall data for the Indian region: Analysis of break and active monsoon spells, Curr. Sci., 91, 296–306, 2006. a
Ramesh, R. and Yadava, M. G.: Climate and Water Resources of India, Curr. Sci., 89, 818–824, 2005. a, b
Rawat, V., Rawat, S., Srivastava, P., Negi, P. S., Prakasam, M., and Kotlia, B. S.: Middle Holocene Indian summer monsoon variability and its impact on cultural changes in the Indian subcontinent, Quaternary Sci. Rev., 255, 106825, https://doi.org/10.1016/j.quascirev.2021.106825, 2021. a
Rehfeld, K., Marwan, N., Breitenbach, S. F., and Kurths, J.: Late Holocene Asian summer monsoon dynamics from small but complex networks of paleoclimate data, Clim. Dynam., 41, 3–19, 2013. a, b
Rind, D. and Overpeck, J.: Hypothesized causes of decade-to-century-scale climate variability: climate model results, Quaternary Sci. Rev., 12, 357–374, 1993. a, b
Roth, A. E.: The Shapley value: essays in honor of Lloyd S. Shapley, Cambridge University Press, ISBN 9781107717213, 1988. a
Sano, M., Ramesh, R., Sheshshayee, M., and Sukumar, R.: Increasing aridity over the past 223 years in the Nepal Himalaya inferred from a tree-ring δ18O chronology, The Holocene, 22, 809–817, 2012. a
Sano, M., Dimri, A. P., Ramesh, R., Xu, C., Li, Z., and Nakatsuka, T.: Moisture source signals preserved in a 242-year tree-ring δ18O chronology in the western Himalaya, Glob. Planet. Change, 157, 73–82, 2017. a
Sano, M., Xu, C., Dimri, A. P., and Ramesh, R.: Summer monsoon variability in the Himalaya over recent centuries, Himalayan Weather and Climate and their Impact on the Environment, 261–280, https://doi.org/10.1007/978-3-030-29684-1_14, 2020. a
Schnabel, F., Purrucker, S., Schmitt, L., Engelmann, R. A., Kahl, A., Richter, R., Seele-Dilbat, C., Skiadaresis, G., and Wirth, C.: Cumulative growth and stress responses to the 2018–2019 drought in a European floodplain forest, Glob. Change Biol., 28, 1870–1883, 2022. a
Shapley, L.: A Value for n-person games, Contributions to the Theory of Games II, edited by: Kuhn, H. and Tucker, A., in: Contributions to the Theory of Games II, Princeton University Press, Princeton, 307–317, https://doi.org/10.1515/9781400881970-018, 1953. a
Shepard, D.: A two-dimensional interpolation function for irregularly-spaced data, in: Proceedings of the 1968 23rd ACM national conference, 517–524, https://doi.org/10.1145/800186.810616, 1968. a
Shi, H. and Wang, B.: How does the Asian summer precipitation-ENSO relationship change over the past 544 years?, Clim. Dynam., 52, 4583–4598, 2019. a
Shukla, R. P., Tripathi, K. C., Pandey, A. C., and Das, I. M. L.: Prediction of Indian summer monsoon rainfall using Niño indices: a neural network approach, Atmos. Res., 102, 99–109, 2011. a
Singhvi, A. K. and Kale, V. S.: Paleoclimate studies in India: last ice age to the present, Indian National Science Acad., https://www.insaindia.res.in/pdf/Paleoclimate-Final_18-12-09-web.pdf (last access: 20 December 2024), 2010. a
Sinha, A., Berkelhammer, M., Stott, L., Mudelsee, M., Cheng, H., and Biswas, J.: The leading mode of Indian Summer Monsoon precipitation variability during the last millennium, Geophys. Res. Lett., 38, https://doi.org/10.1029/2011GL047713, 2011. a, b, c
Sliwinski, J. T., Mandl, M., and Stoll, H. M.: Machine learning application to layer counting in speleothems, Comput. Geosci., 171, 105287, https://doi.org/10.1016/j.cageo.2022.105287, 2023. a
Sontakke, N. A. and Singh, N.: Longest instrumental regional and all-India summer monsoon rainfall series using optimum observations: reconstruction and update, The Holocene, 6, 315–331, 1996. a, b
Sontakke, N. A., Singh, N., and Singh, H. N.: Instrumental period rainfall series of the Indian region (AD 1813–2005): revised reconstruction, update and analysis, The Holocene, 18, 1055–1066, 2008. a, b, c, d, e, f, g
Sridhar, A. and Chamyal, L.: Implications of palaeohydrological proxies on the late Holocene Indian Summer Monsoon variability, western India, Quatern. Int., 479, 25–33, 2018. a
Tcheng, D. K., Nayak, A. K., Fowlkes, C. C., and Punyasena, S. W.: Visual recognition software for binary classification and its application to spruce pollen identification, PloS one, 11, e0148879, https://doi.org/10.1371/journal.pone.0148879, 2016. a
Thomas, T. M., Bala, G., and Srinivas, V. V.: Characteristics of the monsoon low pressure systems in the Indian subcontinent and the associated extreme precipitation events, Clim. Dynam., 56, 1859–1878, 2021. a
Thompson, L. G., Yao, T., Mosley-Thompson, E., Davis, M., Henderson, K., and Lin, P.-N.: A high-resolution millennial record of the South Asian monsoon from Himalayan ice cores, Science, 289, 1916–1919, 2000. a
Thompson, L. G., Mosley-Thompson, E., Brecher, H., Davis, M., Leon, B., Les, D., Lin, P.-N., Mashiotta, T., and Mountain, K.: Abrupt tropical climate change: Past and present, P. Natl. Acad. Sci. USA, 103, 10536–10543, 2006. a
Thomte, L., Shah, S. K., Mehrotra, N., Bhagabati, A. K., and Saikia, A.: Influence of climate on multiple tree-ring parameters of Pinus kesiya from Manipur, Northeast India, Dendrochronologia, 71, 125906, https://doi.org/10.1016/j.dendro.2021.125906, 2022. a
Torrence, C. and Webster, P. J.: Interdecadal changes in the ENSO–monsoon system, J. Climate, 12, 2679–2690, 1999. a, b
Turner, A. G. and Annamalai, H.: Climate change and the South Asian summer monsoon, Nat. Clim. Change, 2, 587–595, 2012. a
Turner, A. G., Inness, P. M., and Slingo, J. M.: The role of the basic state in the ENSO-monsoon relationship and implications for predictability, Q. J. Roy. Meteor. Soc., 131, 781–804, https://doi.org/10.1256/qj.04.70, 2005. a
Venzke, E.: Volcanoes of the World (v. 5.2.2; 22 August 2024), https://doi.org/10.5479/si.GVP.VOTW5-2024.5.2, distributed by Smithsonian Institution, Global Volcanism Program, 2024. a, b
Wang, Y., Liu, X., and Herzschuh, U.: Asynchronous evolution of the Indian and East Asian Summer Monsoon indicated by Holocene moisture patterns in monsoonal central Asia, Earth-Sci. Rev., 103, 135–153, 2010. a
Wang, Y.-J., Cheng, H., Edwards, R. L., He, Y.-Q., Kong, X.-G., An, Z.-S., Wu, J.-Y., Kelly, M. J., Dykoski, C. A., and Li, X.-D.: The Holocene Asian monsoon: links to solar changes and North Atlantic climate, Science, 308, 854–857, 2005. a
Webster, P. J. and Yang, S.: Monsoon and ENSO: Selectively Interactive Systems, Q. J. Roy. Meteor. Soc., 118, 877–926, https://doi.org/10.1002/qj.49711850705, 1992. a, b
Webster, P. J., Magaña, V. O., Palmer, T. N., Shukla, J., Tomas, R. A., Yanai, M., and Yasunari, T.: Monsoons: Processes, predictability, and the prospects for prediction, J. Geophys. Res.-Oceans, 103, 14451–14510, https://doi.org/10.1029/97JC02719, 1998. a, b
Wei, G., Peng, C., Zhu, Q., Zhou, X., and Yang, B.: Application of machine learning methods for paleoclimatic reconstructions from leaf traits, Int. J. Climatol., 41, E3249–E3262, 2021. a
Westervelt, D. M., You, Y., Li, X., Ting, M., Lee, D. E., and Ming, Y.: Relative importance of greenhouse gases, sulfate, organic carbon, and black carbon aerosol for South Asian monsoon rainfall changes, Geophys. Res. Lett., 47, e2020GL088363, https://doi.org/10.1029/2020GL088363, 2020. a
Wolf, A., Ersek, V., Braun, T., French, A. D., McGee, D., Bernasconi, S. M., Skiba, V., Griffiths, M. L., Johnson, K. R., Fohlmeister, J., Breitenbach, S. F. M., Pausata, F. S. R., Tabor, C. R., Longman, J., Roberts, W. H. G., Chandan, D., Peltier, W. R., Salzmann, U., Limbert, D., Trinh, H. Q, and Trinh, A. D.: Deciphering local and regional hydroclimate resolves contradicting evidence on the Asian monsoon evolution, Nat. Commun., 14, 5697, https://doi.org/10.1038/s41467-023-41373-9, 2023. a
Wu, F., Huang, Y., Benes, B., Warner, C. C., and Gazo, R.: Automated tree ring detection of common Indiana hardwood species through deep learning: Introducing a new dataset of annotated images, Information Processing in Agriculture, https://doi.org/10.1016/j.inpa.2023.10.002, 2023. a
Xavier, P. K., Marzin, C., and Goswami, B. N.: An objective definition of the Indian summer monsoon season and a new perspective on the ENSO–monsoon relationship, Q. J. Roy. Meteor. Soc., 133, 749–764, 2007. a
Yao, T. and Yang, M.: Climatic changes over the last 400 years recorded in ice collected from the Guliya Ice Cap, Tibetan Plateau, in: Earth Paleoenvironments: Records Preserved in Mid- and Low-Latitude Glaciers, edited by: Cecil, L. D., Green, J. R., and Thompson, L. G., 163–180, Kluwer, Dordrecht, https://doi.org/10.1007/1-4020-2146-1_9, 2004. a
Zheng, D., Merdith, A. S., Goddéris, Y., Donnadieu, Y., Gurung, K., and Mills, B. J. W.: Using deep learning to integrate paleoclimate and global biogeochemistry over the Phanerozoic Eon, Geosci. Model Dev., 17, 5413–5429, https://doi.org/10.5194/gmd-17-5413-2024, 2024. a






