Advection and non-climate impacts on the South Pole Ice Core

The South Pole Ice Core (SPICEcore), which spans the past 54 300 years, was drilled far from an ice divide such that ice recovered at depth originated upstream of the core site. If the climate is different upstream, the climate history recovered from the core will be a combination of the upstream conditions advected to the core site and temporal changes. Here, we evaluate the impact of ice advection on two fundamental records from SPICEcore: accumulation rate and water isotopes. We determined past locations of ice deposition based on GPS measurements of the modern velocity field spanning 100 km upstream, where ice of ∼20 ka age would likely have originated. Beyond 100 km, there are no velocity measurements, but ice likely originates from Titan Dome, an additional 90 km distant. Shallow radar measurements extending 100 km upstream from the core site reveal large (∼20 %) variations in accumulation but no significant trend. Water isotope ratios, measured at 12.5 km intervals for the first 100 km of the flowline, show a decrease with elevation of −0.008 ‰ m⁻¹ for δ¹⁸O. Advection adds approximately 1 ‰ for δ¹⁸O to the Last Glacial Maximum (LGM)-to-modern change. We also use an existing ensemble of continental ice-sheet model runs to assess the ice-sheet elevation change through time. The magnitude of elevation change is likely small and the sign uncertain. Assuming a lapse rate of 10 ^∘C km⁻¹ of elevation, the inference of LGM-to-modern temperature change is ∼1.4 ^∘C smaller than if the flow from upstream is not considered.

1 Introduction

Ice cores provide unique and detailed records of past climate (e.g., Alley et al., 1993; Petit et al., 1999; NorthGRIP, 2004; Marcott et al., 2014). Such records are most useful if they represent the change in climate at a fixed geographic location and elevation. Two important non-climatic influences on ice-core records are changes in ice-sheet elevation (Vinther et al., 2009; Steig et al., 2001; Stenni et al., 2011; Parennin et al., 2007; Cuffey and Clow, 1997) and changes in the location of ice origin due to flow (Whillans et al., 1984; Huybrechts et al., 2007; NEEM, 2013; Steig et al., 2013; Koutnik et al., 2016). Many ice cores are drilled near an ice divide to minimize both of these effects: ice thickness varies less in the interior than on the margins (Cuffey and Paterson, 2010), and there is little lateral ice flow near a divide. The change in ice thickness can be evaluated with ice-flow models (Parrenin et al., 2007; Golledge et al., 2014; Briggs et al., 2014; Pollard et al., 2016) or measurements from the ice core itself (Martinerie et al., 1994; Steig et al., 2001; Vinther et al., 2009; Waddington et al., 2005; Price et al., 2007). The magnitude and sign of the elevation change in ice-sheet models varies depending on the specified boundary conditions and model parameters, which have a large uncertainty (DeConto and Pollard, 2016; Kingslake et al., 2018). We assess the ice-sheet elevation change near the South Pole in this paper using the 625-member ensemble of the Penn State ice-sheet model (Pollard et al., 2016). We also focus on the impact of ice flow on the South Pole Ice Core (SPICEcore). We will use the term “advection impact” to refer to variations in the ice-core histories that are due to variations in the deposition location and paleo-elevation for different parcels of ice in the South Pole core, as opposed to temporal change in the climate at the ice-core site.

Ice cores are often drilled far enough from divides that lateral advection is important because of site characteristics (NorthGRIP, 2004; EPICA, 2006; WAIS Divide, 2013; Morse et al., 2002; NEEM, 2013), logistical considerations (Camp Century, Gow et al., 1968; Dye-3, Dansgaard et al., 1969; Byrd, Hammer et al., 1980; Vostok, Lorius et al., 1985), or concern about divide migration over the drill site (Waddington et al., 2001). The importance of advection on ice-core records depends on both the velocity of the ice and the gradient in the constituent or property of interest. For well-mixed atmospheric gases, such as carbon dioxide and methane, there is no direct impact on the histories. The affected histories are primarily those recovered from the ice phase: accumulation rate, water isotopes, surface temperature, and aerosols. Of the cores that have been drilled off of ice divides, the horizontal velocities range from less than 1 (EDML) to 12 m a⁻¹ (Dye-3), and all require correction to obtain the climate history for a fixed geographic location (Whillans et al., 1984; Steig et al., 2001, 2013; Huybrechts et al., 2007; Vinther et al., 2009; NEEM, 2013; Koutnik et al., 2016).

The 1751 m long SPICEcore was obtained at the South Pole between 2014 and 2016. SPICEcore was sited, in part, to take logistical advantage of the South Pole station where the surface velocity is 10 m a⁻¹ in the direction of 40^∘ W (Hamilton, 2004; Casey et al., 2014). Lilien et al. (2018b) inferred the flowline out to 100 km upstream and concluded that Titan Dome is the likely source region for ice reaching the SPICEcore site. Previous measurements of water isotope values upstream of the South Pole are primarily from surface snow samples, which do not provide reliable time-averaged values (Masson-Delmotte et al., 2008; Dixon et al., 2013). A shallow ice core near Titan Dome (US-ITASE 07-4) provides a single estimate of accumulation (0.074 m ice equivalent a⁻¹; Dan Dixon, personal communication, 2013). Here, we assess the advection impact (i.e., non-climate impact) on the accumulation rate, water isotope, and surface temperature histories of SPICEcore using new measurements in the upstream catchment.

2 Methods

To assess the impact of advection on the SPICEcore climate histories, we measured ice velocity, accumulation rates, water isotopes, and firn temperatures in the upstream catchment. The surface ice-flow velocities, inferred flowline, and spatial pattern of accumulation were described by Lilien et al. (2018b; http://www.usap-dc.org/view/dataset/601100, last access: 24 April 2020), and we provide only a brief review below.

2.1 Surface ice-flow velocity and flowline determination

Determining the ice-flow velocity near the South Pole is more difficult than many other locations in Antarctica; there is little satellite coverage due to the geometry of satellite orbits resulting in a data “pole hole”. Rignot et al. (2011) used synthetic aperture radar to compute the surface velocity but utilized a substantially tilted satellite view, resulting in velocity measurements that are not sufficiently precise to define the flowline. To obtain improved velocity measurements in the region, we performed repeat surveys of stakes with GPS during four consecutive field seasons. We installed 56 stakes at 12.5 km intervals along lines of longitude from 110 to 180^∘ E at 10^∘ intervals (Lilien et al., 2018b). The 110 and 180^∘ lines were measured only to 50 km from the South Pole; the others were measured to 100 km (Fig. 1). The measured velocities range from 3 to 10 m a⁻¹, with errors of ±0.02 to 0.25 m a⁻¹ in each horizontal direction.

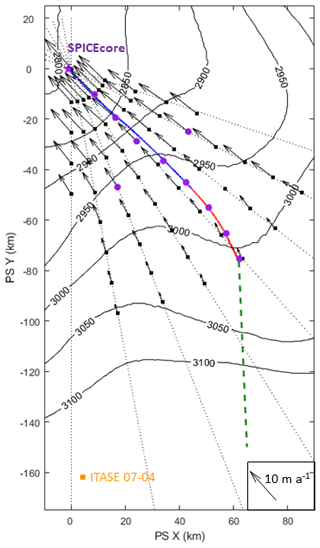
Figure 1 Map of the area upstream of the South Pole. SPICEcore location is indicated by the purple star. The 10 m core locations are purple circles. Stake locations (black squares) were surveyed with GPS in multiple years to measure velocity vectors. Flowline was inferred from the velocity measurements for the past 10.1 kyr (blue, from Lilien et al., 2018b) and 10.1 to ∼25 ka (red). Unconstrained flowline for ∼25 to 55 ka is dashed green. Surface topography contours are from BedMap2 (Fretwell et al., 2013). ITASE 07-04 core at Titan Dome is the orange square. Note that Titan Dome is a broad ridge and the geometry is not well defined in BedMap2; the elevation does not match the 3090 m measured by Dixon et al. (2013).

2.2 Accumulation rate

The accumulation rate along the flowline is derived from radar layers imaged from approximately 20 to 100 m depth with a 200 MHz radar (details can be found in Lilien et al., 2018b). The depth of a radar layer is converted to an accumulation rate using the density profile and depth–age relationship of a core extracted by us on the flowline 50 km upstream from SPICEcore. The firn depth–density profile is assumed to be unchanging along the flowline. The firn density affects the derived accumulation-rate history both through the inferred depth of the layer due to the radar-wave propagation speed and through the conversion to ice-equivalent thickness. These two uncertainties oppose each other but do not necessarily cancel out. Using four additional density profiles near the South Pole, Lilien et al. (2018b; Fig. S4) found the spread in accumulation has a standard deviation of 2.3 % for a layer at ∼20 m depth. Deeper layers have a smaller spread because the density is most variable near the surface. All accumulation rates are given in m a⁻¹ of ice equivalent.

2.3 Water isotopes

Water isotope ratios of δ¹⁸O and δD were measured in cores of approximately 10 m depth at 12.5 km spacing along the flowline, as well as at two sites 15 km perpendicular to the flowline 50 km upstream of SPICEcore, for a total of 10 firn cores. We also report the deuterium excess, using the log definition (d_ln; Markle et al., 2017). The cores were sampled at 0.5 m intervals in the field and allowed to melt in plastic bottles. The measurements were performed at the University of Washington's Isolab with a Picarro L-2120i. The average δ¹⁸O and δD values (vs. Vienna Standard Mean Ocean Water) for each core are presented here. The cores were not dated and thus the water isotopes cannot be averaged over the same ages; averaging using only the upper 5 m for each core instead of the full core produced negligible differences. One outlier from 0.5 to 1 m depth at site 25 km was excluded.

2.4 10 m temperatures

The temperature at approximately 10 m depth was measured in each borehole left by the shallow-core extraction. We averaged the values measured by four thermistors surrounded by a copper shield. The thermistors were left in the borehole for different lengths of time ranging from 28 min to 48 h.

2.5 Analysis of continent-scale ice-sheet models

We use a 625-member ensemble of the Penn State ice-flow model (Pollard et al., 2016) to assess possible ice-sheet changes during the deglacial transition. The model uses a 20 km grid size for West Antarctica, which includes the South Pole region. The accumulation rate applied at 20 ka is approximately half of the modern value (Pollard and DeConto, 2012). The ensemble is used to assess the histories of surface velocity and elevation of the South Pole. The ensemble varies four different ice-dynamic parameters with five values each. The four parameters affect the basal sliding coefficient where ice is no longer grounded (CSHELF); ice shelf melt rate (OCFAC); calving rate factor (CALV); and isostatic rebound (TAUAST). We perform evaluations using both the full ensemble (n=625) and a subset, including only the parameter values identified with the advanced statistical techniques (n=32) to best fit geologic constraints (Table 1; Pollard et al., 2016, their Fig. 3, right column).

Table 1 Pollard et al. (2016) most likely parameter values.

3 Results

3.1 Gradients in upstream climate

3.1.1 Accumulation rate

The accumulation rate along the 100 km flowline for four different internal layers is shown in Fig. 2. The youngest layer is 151 years before 2017 (∼20 m depth) and was used by Lilien et al. (2018b); the 743-year layer is the deepest (∼90 m) layer resolved. Although the layers are relatively young, there can still be a horizontal offset of hundreds of meters to kilometers from where the layer was deposited on the surface. In Fig. 2a, the accumulation rates in the upper panel are plotted at the position of the radar trace. The impact of horizontal advection can be observed as the older layers appear shifted to the left (closer to SPICEcore) compared to the younger layers.

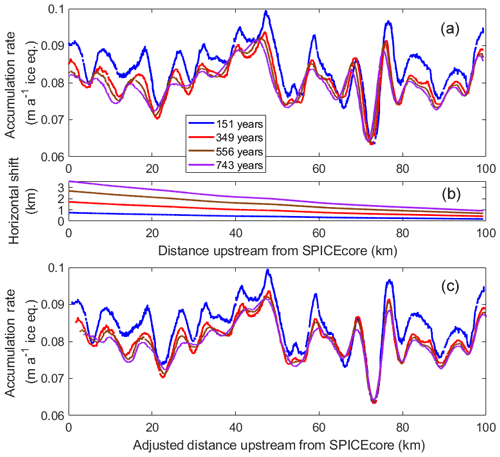
Figure 2 Accumulation rate along flowline. Panel (a) shows the accumulation rate for four radar layers, with ages in years before 2017. Panel (b) shows average horizontal distance traveled. Panel (c) shows the same inferred accumulation as in panel (a), with the position adjusted to account for the horizontal distance traveled.

To account for horizontal advection, the position where the accumulation rate is inferred (i.e., the location of the radar trace) is adjusted. This adjustment is made by multiplying the half age of the layer by the surface velocity at the midpoint of its path from deposition to the current trace location (Fig. 2b). The adjustment ranges from 3.7 km at SPICEcore for the 743-year layer to 0.2 km for the 151-year layer at the upstream end. Shifting the distance of the accumulation records (Fig. 2c) better aligns the peaks and troughs among the four layers. It also highlights that older layers vary less along flow. The depth of a layer reflects the average surface accumulation rate over the distance traveled. Thus, an older layer is flatter because it averages the influence of accumulation on vertical velocity over a longer distance (Waddington et al., 2007). This shows that simply shifting the position of the layers to account for horizontal advection does not fully recover the spatial variations in accumulation.

A more-complete treatment could solve an inverse problem to infer the surface accumulation rate along the flow line that best matches the observed layer thicknesses (e.g., Waddington et al., 2007). We do not address this because here we focus on the advection impact on the SPICEcore record and not a formal evaluation of the surface accumulation patterns consistent with available layers. Lilien et al. (2018b, the Supplement) showed that the 151-year layer was sufficiently deep to record real climate variations, and not noise, but shallow enough to not be significantly affected by lateral flow.

The average accumulation rate of the oldest (743-year-old) layer is 0.080 m a⁻¹ and the spatial linear trend of $-\mathrm{4}\times {\mathrm{10}}^{-\mathrm{6}}$ m a⁻¹ km⁻¹ is negligible. Shorter-wavelength spatial variations are approximately ±20 % of the average value, much larger than the linear trend. Beyond the 100 km of mapped flowline, the only accumulation-rate information is from the US-ITASE 07-04 core near Titan Dome, where an accumulation rate of 0.074 m a⁻¹ was inferred (Daniel Dixon, personal communication, 2013). This is within the range of accumulation rates identified along the flowline, but slightly smaller than the 0.080 m a⁻¹ average along the first 100 km of the flowline. With only a single point measurement, we cannot resolve whether this accumulation rate near Titan Dome is representative of a mean value for a wider area.

We also calculate the accumulation rate for the intervals between successive layers (Fig. 3), which allows temporal trends to be more clearly evaluated. The uncertainty in the accumulation rate is greatest for the 151-year layer because the density measurements are least certain in the lower-density surface snow, and surface firn conditions are more spatially variable. We calculate the uncertainty for an interval based on the density profiles of five different firn cores (the core we drilled at 50 km and four cores from near the South Pole; Severinghaus et al., 2001; Christo Buizert, personal communication, 2017). The uncertainty shading shown in Fig. 3 is the range between the maximum and minimum accumulation rates using the five density profiles. The spatial average of the three older intervals are within uncertainty of each other. The spatial average of the 0 to 151-year interval is always greater than the older three intervals. Because the spatial average of the minimum accumulation rate (based on firn density) for 0 to 151 years is greater than the spatial average of the maximum for the older intervals, we have confidence that the accumulation rate has increased in the past 151 years. The accumulation increase is 8±4 % compared to the previous 592 years (151 to 743 years before 2017). Previous ice-core estimates of accumulation at the South Pole suggested an increase in the past 150 years (e.g., Ferris et al., 2011), but an increase could not be identified with confidence because variations among cores were dominated by spatial, not temporal, effects (van der Veen et al., 1999). Our measurements average over a 100 km distance, allowing the temporal change to be identified.

Table 2 Accumulation increase in the past 151 years relative to previous periods.

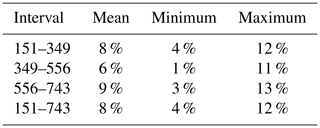
Mean increase uses density profile from the core at 50 km for all layers. Minimum (maximum) increase uses density profile which yields the minimum (maximum) accumulation rate for the 0–151 interval and the density profile which yields the maximum (minimum) for the older layers.

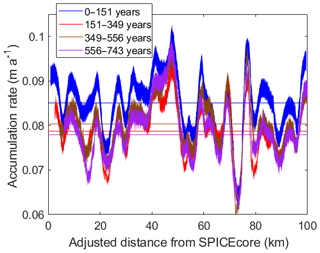
Figure 3 Temporal average accumulation rate for ages between radar layers. Shading indicates uncertainty based on five firn-density profiles. Distance from SPICEcore has been adjusted as in Fig. 2 and described in main text. Horizontal lines indicate spatial average of the accumulation rate using the density profile measured on the firn core at 50 km.

3.1.2 Water isotopes

Measurements of water isotopes require the collection of ice samples and thus have less spatial resolution than the radar-derived accumulation-rate measurements. There is considerable scatter (Fig. 4) in the 0.5 m resolution samples, which have durations of a few years (i.e., 2–4 years) per sample; the differences among 0.5 m samples are likely driven by interannual variations. Using the mean values, a decrease with distance from the South Pole is observed in both δ¹⁸O and δD. The d_ln values show no significant trend upstream.

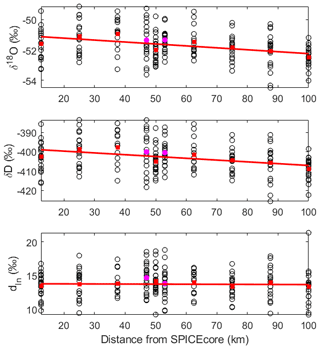
Figure 4 Water isotope values (black circles) and averages (red squares) for shallow cores along the flowline upstream of the South Pole. Cores at 50 km upstream on 120 and 160^∘ E are plotted at 47 and 53 km (magenta circles). Linear slope (thick red line) is from the average values along the flowline only.

The δ¹⁸O and δD values plotted by elevation are shown in Fig. 5. Linear fits to δ¹⁸O and δD yield slopes of $-\mathrm{0.0080}\pm \mathrm{0.0055}\mathrm{‰}$ m⁻¹ and $-\mathrm{0.0579}\pm \mathrm{0.04}\mathrm{‰}$ m⁻¹ respectively (95 % confidence levels). Our value for δ¹⁸O is in between the slope of −0.009 ‰ m⁻¹ from the Masson-Delmotte et al. (2008) database and the slope of −0.007 ‰ m⁻¹ found in their multiple linear regression analysis which includes latitude and distance from the coast. Including the average δ¹⁸O value from the upper 1.2 m of the US-ITASE 07-04 firn core at Titan Dome (−53.15 ‰) in the linear regression changes the slope to −0.0073 ‰ m⁻¹, which is in good agreement with the mean slope. Because the Titan Dome value is an average of the upper 1.2 m and not directly comparable in time to our 10 m average measurements, we use the mean slope of 0.008 ‰ m⁻¹ from the 10 m cores for the advection correction described in the subsequent section.

3.1.3 Surface temperature gradient

The ∼10 m temperatures are shown in Fig. 6. Unfortunately, time constraints in the field forced differences in the measurement procedure between sites, preventing a determination of the gradient in mean annual temperature. Measurements that equilibrated for less than 1.5 h yielded warmer temperatures than those left in boreholes for longer times, and we consider those shorter measurements less reliable. Measurements that were made after leaving the thermistors in the boreholes for longer than 6 h are consistent with a dry adiabatic lapse rate of 10 ^∘C km⁻¹, but we cannot reject a wide range of other values for the lapse rate.

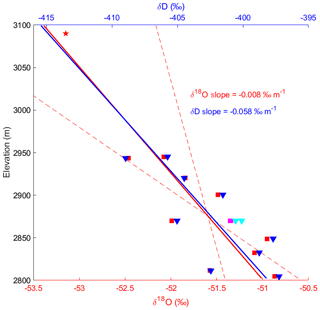
Figure 5 Average δ¹⁸O (red squares) and δD (blue triangles) values from the 10 m cores along the flow line and SPICEcore. Average δ¹⁸O and δD from cores off of the flowline at 50 km upstream (pink squares and cyan triangles). δ¹⁸O of US-ITASE 07-04 core at Titan Dome (red star). Linear fit of 10 m cores along the flow line for δ¹⁸O (red thick line) and δD (blue thick line) do not include Titan Dome or cores from off the flowline. The 95 % confidence intervals of the δ¹⁸O fit (red dashed lines) are shown. Confidence intervals of δD overplot those of δ¹⁸O and are not shown.

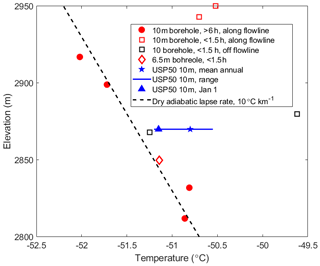
Figure 6 The 10 m temperature measurements. Filled symbols are equilibrated for more than 6 h; open symbols are equilibrated for less than 1.5 h. Red symbols are along the flow line; black symbols are off the flowline. The diamond is a measurement at 6.5 m depth, which is likely ∼0.7 ^∘C colder due to the winter cold wave than if measured at 10 m depth. Blue symbols are from a single thermistor installed at 10 m depth in a back-filled borehole with measurements recorded for more than 1 year; the star is mean annual temperature, the triangle is initial temperature after equilibration, and the horizontal line is the range of temperature recorded. The black dashed line shows a lapse rate of 10 ^∘C km⁻¹.

3.2 Determination of flowline position and age

We divide the reconstruction of the flowline into three segments based on the data available for different distances upstream from SPICEcore:

1. 0 to 65 km (0 to 10.1 ka) which has been constrained by Lilien et al. (2018b);

2. 65 to 100 km (10.1 to ∼25 ka) where we have velocity measurements; and

3. beyond 100 km (older than ∼25 ka) where only limited data from other sources exist.

The uncertainty associated with the reconstruction increases for each segment because of the data available as well as possible changes to the ice-sheet configuration at earlier times. For segment 1, the uncertainty is low because correlation of the SPICEcore layer thicknesses and upstream accumulation pattern provides a unique and tight constraint (Lilien et al., 2018b). For segments 2 and 3, we have no inferences of past ice-sheet velocity. The variation in horizontal velocity with depth does not need to be considered because we are only interested in tracking particles to 1751 m depth in SPICEcore where the modeled horizontal velocity is at least 99 % of the surface velocity. The challenge of determining the flowline position with age is then of estimating the past surface velocity. The modeled surface velocities near the South Pole in the ice-sheet ensemble (Pollard et al., 2016) are slower than observed (mean of 2 m a⁻¹ for the models runs compared to the measured 8 m a⁻¹ at ∼20 km from SPICEcore) and thus cannot be used directly. Instead, we use the relative change in speed between 20 and 10 ka to inform our choice of speed change for this time period. The full ensemble (Fig. 7) shows a large fraction of model runs with faster velocities at 20 ka compared to 10 ka with a mean slowdown of 10 % from 20 to 10 ka. The speed changes in the limited ensemble are bimodal: one group shows speeds at 20 ka between 50 % and 90 % of the speed at 10 ka. The other group shows between no change and 10 % faster speeds at 20 ka compared to 10 ka. The first group is closer to the speed that might be expected if the speed was primarily determined by the accumulation rate through a balance velocity; the second group indicates that dynamic changes are able to counteract the influence of lower accumulation rates at 20 ka. We thus determine the speeds for ages older than 10.1 ka in two ways: no change in speed and speed changes that scale with an approximate accumulation history.

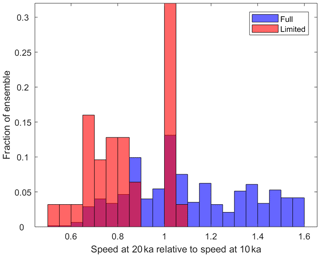
Figure 7 Histograms of modeled speed changes between 10 and 20 ka near the South Pole for the full and limited ensembles (see Sect. 2.5 for full description; Pollard et al., 2016).

3.2.1 Segment 1: 0 to 65 km (0 to 10.1 ka)

The first segment uses the inferred flowline of Lilien et al. (2018b). They used a novel method of correlating the SPICEcore layer thicknesses with the geophysically determined accumulation pattern upstream and found that with a 15 % increase in speed from 10.1 ka to today, the upstream pattern of accumulation explained approximately three-quarters of the variance in the SPICEcore accumulation history. Of particular importance to this study, their work tightly constrains the location where the ice in the core was deposited on the surface of the ice sheet. This has not been possible at previous ice-core sites (e.g., WAIS Divide, EDML, NEEM) where ice-flow models provided the only estimates of past velocity.

The measured velocity field was used to determine the modern flowline. We use the flowline position and age from the preferred scenario of a 15 % Holocene speed up of Lilien et al. (2018b). The position and age were found by starting at the SPICEcore drill site and recursively stepping upstream in 1-year intervals in the direction opposite the velocity vectors to obtain annual positions along the flowline. The velocity direction was fixed in time while the magnitude was linearly decreased to 15 % slower velocities at 10.1 ka. The 10.1 ka ice originated 65 km upstream along the flowline.

3.2.2 Segment 2: 65 to 100 km (10.1 to ∼25 ka)

For ice older than 10.1 ka, the spatial variations in the accumulation rate cannot be clearly correlated with the layer thickness variations in SPICEcore. This is likely because (1) uncertainty in the flowline position increases with distance (age); (2) the relative uncertainty in the surface velocity increases as the velocity decreases with distance upstream; (3) the surface-velocity measurement stakes are farther apart; and (4) the temporal variations in accumulation are likely larger during the isotopic maximum at ∼11 ka and the glacial–interglacial transition (Veres et al., 2013; Fudge et al., 2016). This segment of the flowline spans from 65 km to the limit of the surface velocity measurements at 100 km from the SPICEcore drill site. Without the constraints of the correlation analysis, both the flow direction and past ice-flow velocity are much less certain. Continent-scale ice-sheet models have difficulty reproducing the details of ice flow in the region and are sensitive to boundary forcing assumptions.

We use two different assumptions about the past ice speed to estimate the flowline position with age before 10.1 ka. For both methods, we start with the inferred speed at 10.1 ka from Lilien et al. (2018b; i.e., 15 % slower than measured today) and keep the ice-flow direction fixed in time. The first reconstruction assumes that the speed has been constant in time prior to 10.1 ka. The second reconstruction scales the speed to an estimate of the past accumulation rate, essentially assuming that the speed is controlled by the ice flux necessary to keep the ice sheet in balance.

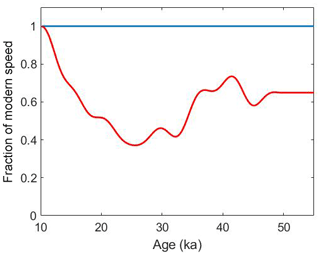
The speed history used is shown in Fig. 8. Winski et al. (2019) only reported the SPICEcore accumulation history for the Holocene (younger than 11.7 ka) because the cumulative thinning layers have experienced becomes increasingly uncertain with depth. Since we are only seeking a plausible estimate of past speed, the increased uncertainty of the thinning function is not a major concern for this work. We obtain an accumulation history for the past 54 kyr by dividing the layer thicknesses of the SP19 timescale (Winski et al., 2019) by a thinning function computed with a Dansgaard-Johnson (1969) model of vertical strain with a kink height of 0.2 and low-pass filtered at 5 ka. Scaling the ice-flow speed to the accumulation rate results in speeds at the Last Glacial Maximum (LGM) of only 40 % of the modern era; thus, ages at the end of the measured flowline, at 100 km from SPICEcore, are 7 kyr older (28 ka) than with the assumption of a constant speed (21 ka).

Figure 8 Fraction of modern speed used to reconstruct flowline position and age for the constant speed scenario (blue) and scaled to accumulation history (red).

3.2.3 Segment 3: beyond 100 km (older than ∼25 ka)

For ice that originated beyond 100 km from SPICEcore, no reliable surface-velocity measurements exist to help define where the ice originated. We examined the utility of the surface topography of BedMap2 (Fretwell et al., 2013) in defining the flow direction by tracking particles along the steepest descent. We computed two flowlines: one going upstream from SPICEcore and the other going downstream from the 10 ka location. They do not agree with each other or with the measured flowline, which is not surprising given the limited data in BedMap2 and the convergent flow. Thus, we do not expect the surface topography to be useful in defining the x and y components of the flowline beyond 100 km, and we assume that the ice has flowed in a straight line from an ice divide (Fig. 1). The position of the ice divide is not well defined, and we assume it is at an additional 90 km distance. We also assume that the speed decreases linearly from its value at 100 km to zero at the divide, equivalent to assuming a balance velocity in an ice sheet with uniform ice thickness and accumulation rate and no convergence or divergence, because we have little information on the bedrock topography upstream. We then apply the same two assumptions for the flow speed used for the second segment: either constant speed or varying based on the accumulation history. These assumptions suggest the oldest SPICEcore ice (54.3 ka) originated a total of 135 to 155 km upstream from SPICEcore.

3.3 Advection impact

The advection impact on the SPICEcore accumulation rate and water isotope histories are quite different from each other. The accumulation rate is sampled with high frequency but shows no long-term trend with distance and elevation. The water isotopes, on the other hand, are sampled infrequently but show a linear trend with distance and elevation. We discuss the advection impact for the two separately.

3.3.1 Accumulation rate

The lack of a linear trend in the accumulation rate along the flowline indicates that no trend should be removed from the SPICEcore accumulation history. However, the variation in accumulation upstream has a major impact on the SPICEcore history. Lilien et al. (2018b) were able to isolate the influence of kilometer-scale upstream variability for the past 10 kyr, which explains a majority of the variance in the SPICEcore accumulation history. Thus, little of the variability in the accumulation history for the past 10 kyr is due to climate. While the residual variance of the SPICEcore accumulation history (the accumulation history after removing the advection impact) might reflect temporal changes in climate, the residual variance is also affected by multiple sources of uncertainty such as the assumptions of a constant spatial pattern of accumulation, a fixed flowline, a linear speed up, and a spatially homogeneous firn-density profile. These uncertainties are sufficiently large and difficult to quantify and we do not interpret the residual as a temporal history of accumulation.

Beyond 10 ka, it is important to understand the potential influences of spatial variations in accumulation in order to avoid erroneous conclusions about temporal variations in the accumulation rate over the past 54 kyr. Since there is no overall trend, we are primarily interested in how the spatial variability could be imprinted in the ice-core history. Spectral analysis of the spatial pattern of accumulation shows that there is significant power at a wavelength of 5 to 10 km. The temporal imprint of the spatial variations on ice-core-derived accumulation rates is then determined by the ice-flow velocity, which is 4 m a⁻¹ for ice of 10 ka age and decreases to 1 m a⁻¹ for ice of 54 ka age. The timescales affected in the accumulation history are ∼1 to 6 kyr during the deglacial transition (10–20 ka) and get longer, reaching 10 kyr, for the glacial SPICEcore ice. The advection impact on the deglacial transition may affect the specific timing of accumulation-rate change, but not the overall temporal trend. For older ages, the advection impact has a similar timescale to millennial-scale climate variations. We thus expect that the advection impact will decrease the coherence between the accumulation-rate history and the temperature history inferred from water isotopes.

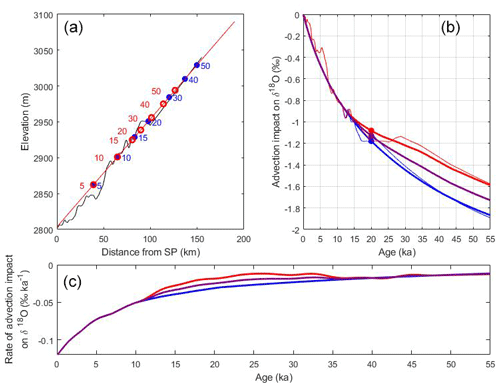
Figure 9 Advection impact for δ¹⁸O. (a) Elevation profile (black) and linear fit (red) used in advection correction. Elevations at 5 kyr intervals for the constant velocity assumption (blue dots) and scaled to accumulation history (red circles). (b) Advection correction using elevations in panel (a). Blue is constant velocity. Red is scaled to accumulation history. Thick lines use linear elevation change; thin lines use measured elevation along flowline. The average of the two assumptions is shown in purple. A negative value indicates the ice recovered in the core fell at a location where the water isotopes are more depleted than the South Pole in the current climate. (c) The rate of the advection impact for the three curves in panel (b).

3.3.2 Water isotopes

The water isotopes are not sampled at a high enough spatial resolution to perform an analysis of millennial-scale variations as was done for the accumulation rate; however, the δ¹⁸O and δD both show linear trends with elevation and distance. Because δ¹⁸O and δD are similar, we will discuss only the advection correction for δ¹⁸O in this section (both are provided in the Supplement). A correction for advection becomes important, particularly for questions such as the magnitude of the glacial–interglacial temperature change. We use a linear fit to elevation data as the base for the advection correction (Fig. 9). The linear fit is continued beyond 100 km at the same slope, reaching an elevation similar to the US-ITASE 07-04 core at 190 km upstream of SPICEcore. We use the linear fit to avoid meter-scale elevation variability being added through the advection correction.

We use the two inferences of the origin positions of ice in SPICEcore described in Sect. 3.2 to find the elevation change through time due to advection. We convert this into an advection impact for δ¹⁸O based on the linear δ¹⁸O–elevation fit (Sect. 3.1.2; Fig. 5), which we assume is constant in time. The two scenarios provide an estimate of the range of plausible advection impacts. While we do not have enough information to define a formal uncertainty on the advection impact, the difference between the two scenarios provides a qualitative uncertainty estimate for the effect of past speed changes. We use the average of these two scenarios as our best estimate of the advection impact and report all three in the archived data file (https://doi.org/10.15784/601266; Fudge et al., 2020).

SPICEcore ice of 20 ka age is approximately 1.1 ‰ more depleted than if it had fallen at the South Pole instead of at ∼95 km upstream and at ∼135 m higher elevation. The uncertainty of this advection impact due to the temporal surface velocity assumption is approximately ±0.1 ‰; however, there is additional uncertainty due to the slope of the elevation–water isotope fit. Because the elevation change is linear with distance, the curvature of the advection impact is determined by the change in ice velocity and the advection impact increases the most rapidly at the youngest ages. The difference over the Holocene (past 11.7 kyr) is 0.85 ‰, while the additional difference to the LGM (20 ka) is only 0.25 ‰. The advection impact for the oldest ice is only about 0.01 ‰ ka⁻¹ and is nearly the same for both velocity assumptions after 35 ka; this is because the ice in the constant-speed scenario has moved closer to the divide where the speed is lower and thus is similar to the lower speed in the accumulation-scaled scenario.

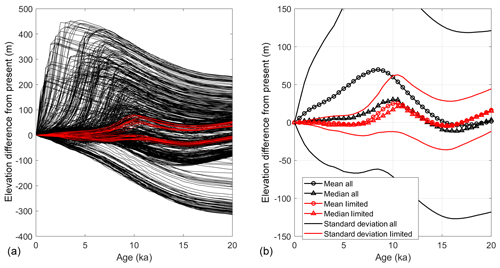
Figure 10 (a) Elevation difference from modern for each model run in the Pollard et al. (2016) ensemble (black, 625 members) and limited ensemble (red, 32 members) of the most likely parameter combinations. (b) Mean (circles), median (triangles), and standard deviation (thin lines) of full ensemble (black) and limited ensemble (red).

3.4 Ice-sheet elevation change

The in situ measurements performed in this study provide little in the way of constraints for past ice thickness change. Lilien et al. (2018b) noted that the inferred 15 % Holocene speedup could be caused by either a modest thickening of ∼100 m or a steeping of a few percent. However, the analysis cannot be used for older ages with larger climate changes and potentially more elevation change. Therefore, we assess the range of plausible elevation change using the output of a 625-member ensemble of a full ice-sheet model (Pollard et al., 2016) as well as a limited ensemble (32 members) of the most likely parameter combinations (see Sect. 2.5). We calculate the mean, median, and standard deviation of the elevation change relative to modern (Fig. 10) for the full and limited ensembles. We note that every member of the limited ensemble has ice thickness changes of less than 100 m in the past 10 kyr.

The full ensemble suggests the ice sheet thickened, and the surface elevation increased, from 15 to 8 ka, before Holocene thinning reduced the ice-sheet elevation back to near 20 ka values. The median change is roughly half the magnitude of the mean with a peak elevation that occurs at about 10 ka. The limited ensemble shows limited variance about the full model median, with less elevation change after 8 ka and a slightly higher elevation at 20 ka. The limited ensemble is bimodal, with the group of runs with a higher elevation at 10 ka corresponding to the basal sliding coefficient of ungrounded areas parameter (CSHELF) equal to −6 and the group of runs with lower elevations at 10 ka from runs with CSHELF equal to −5. The maximum elevation change of the limited ensemble mean is +26 m at 10 ka. The mean elevation is +16 m at 20 ka. In all cases, 1 standard deviation encompasses both higher and lower elevations for all past ages to 20 ka. Therefore, we do not provide an explicit correction for past ice-sheet elevation. An elevation change of 26 m corresponds to a 0.2 ‰ impact for δ¹⁸O using the measured, modern, spatial slope of 0.008 ‰ m⁻¹. This is roughly one-quarter of the advection correction at 10 ka. Thus, uncertainty from possible ice-sheet elevation change should be considered in any interpretation of the water isotope record, but existing ice-sheet models cannot sufficiently constrain the elevation history to warrant an explicit correction.

4 Discussion

Advection has enhanced the glacial–interglacial δ¹⁸O change at SPICEcore by ∼1 ‰ because ice in the core originated at higher elevations with more depleted isotopic values. The total LGM (20 ka) to modern (past 1 kyr) δ¹⁸O change in SPICEcore is approximately 6 ‰ (Kahle et al., 2018). Accounting for advection reduces the fixed-location glacial–interglacial change to 5 ‰. Advection has the opposite impact at the WAIS Divide ice core (WDC), where advection increases the glacial–interglacial change by 1 ‰ to 8 ‰ (Steig et al., 2013; WAIS Divide Project Members, 2013). Understanding the advection impact is important for comparing the magnitude of isotopic change among Antarctic ice cores; WDC has a 1 ‰ greater LGM–modern change than SPICEcore in the measured records, but a 3 ‰ greater change after accounting for advection. Because SPICEcore and WDC have similar source regions and distillation pathways (e.g., Sodemann and Stohl, 2009), the difference between the two cores has the potential to yield insight into the relative elevation change between the West and East Antarctic ice sheets and to further refine the range of plausible model results presented in Fig. 10. A full interpretation of relative isotopic change between SPICEcore and WDC is beyond the scope of this paper, but including the impact of advection is critical for future analysis.

The advection impact on the accumulation history is distinct from that for the water isotopes. There is no linear trend in accumulation in the upstream catchment, and thus no trend to remove from the SPICEcore accumulation history. High-spatial-resolution measurements of the modern upstream accumulation pattern have revealed that the majority of the accumulation variability in the past 10 kyr is caused by advection and not temporal changes (Lilien et al., 2018b). While the upstream pattern and SPICEcore history cannot be correlated for ages older than 10 ka, the spatial pattern is still expected to impact the accumulation history. The dominant timescales affected increase from ∼1 kyr in the Holocene to ∼10 kyr at 50 ka. These timescales are similar to that of millennial climate change and thus we expect the spatial variability of accumulation that is imprinted on the SPICEcore temporal history to decrease the coherence between water isotope (as a proxy for temperature) and accumulation records. Overall, changes in accumulation of less than 20 % on millennial timescales should not be interpreted as a climate signal.

The different character of the advection impacts for water isotopes and accumulation arises because there is no coherent relationship between water isotopes and accumulation rate. This may be because the water isotopes are largely controlled by the condensation temperature (Jouzel et al., 1997), whereas the accumulation rate is affected by wind redistribution and the local surface topography (Hamilton, 2004). In fact, the curvature (second derivative) of the elevation profile along the flowline explains a third of the variance in the modern spatial pattern of accumulation, similar to areas in Greenland (Miege et al., 2013; Hawley et al., 2014).

The impact of elevation change on the isotopic records is not clear. An ensemble of continental-scale ice-sheet model runs showed minimal mean and median elevation changes in the past. The standard deviation of the runs always included changes of both signs. Therefore, we do not suggest a correction for ice-sheet elevation change through time but note that there is uncertainty associated with a possible change that should be considered in subsequent analyses. We also could not determine the temperature lapse rate from our 10 m borehole temperatures; however, we can estimate the temperature impact of advection based on a dry adiabatic lapse rate of 10 ^∘C km⁻¹, which is consistent with our measurements. The LGM ice fell at ∼140 m higher elevation and likely would be ∼1.4 ^∘C colder than if it had fallen at the current elevation of the South Pole.

5 Conclusions

The relatively fast ice speed at the South Pole today causes ice at depth in SPICEcore to have originated at locations up to 155 km away in the direction of Titan Dome and at elevations upstream of up to 230 m higher, assuming the ice-sheet configuration has not changed significantly in the past. Elevation change of the ice sheet through time is likely small and of uncertain sign. Our measurements in the upstream catchment define the flow direction and speed as well as spatial gradients in the accumulation rate and water isotopes. These measurements identify the impact of advection on the SPICEcore records. The accumulation rate has no spatial trend but shows 20 % variations on length scales of 5–10 km; δ¹⁸O shows a −0.008 ‰ m⁻¹ depletion which enhances the measured LGM–Holocene change in the ice core by ∼1 ‰. This work facilitates accurate interpretation of the SPICEcore records as temporal histories of climate at the South Pole.