How large are temporal representativeness errors in paleoclimatology?

Ongoing work in paleoclimate reconstruction prioritizes understanding the origins and magnitudes of errors that arise when comparing models and data. One class of such errors arises from assumptions of proxy temporal representativeness (TR), i.e., how accurately proxy measurements represent climate variables at particular times and time intervals. Here we consider effects arising when (1) the time interval over which the data average and the climate interval of interest have different durations, (2) those intervals are offset from one another in time (including when those offsets are unknown due to chronological uncertainty), and (3) the paleoclimate archive has been smoothed in time prior to sampling. Because all proxy measurements are time averages of one sort or another and it is challenging to tailor proxy measurements to precise time intervals, such errors are expected to be common in model–data and data–data comparisons, but how large and prevalent they are is unclear. This work provides a 1st-order quantification of temporal representativity errors and studies the interacting effects of sampling procedures, archive smoothing, chronological offsets and errors (e.g., arising from radiocarbon dating), and the spectral character of the climate process being sampled.

Experiments with paleoclimate observations and synthetic time series reveal that TR errors can be large relative to paleoclimate signals of interest, particularly when the time duration sampled by observations is very large or small relative to the target time duration. Archive smoothing can reduce sampling errors by acting as an anti-aliasing filter but destroys high-frequency climate information. The contribution from stochastic chronological errors is qualitatively similar to that when an observation has a fixed time offset from the target. An extension of the approach to paleoclimate time series, which are sequences of time-average values, shows that measurement intervals shorter than the spacing between samples lead to errors, absent compensating effects from archive smoothing. Nonstationarity in time series, sampling procedures, and archive smoothing can lead to changes in TR errors in time. Including these sources of uncertainty will improve accuracy in model–data comparisons and data comparisons and syntheses. Moreover, because sampling procedures emerge as important parameters in uncertainty quantification, reporting salient information about how records are processed and assessments of archive smoothing and chronological uncertainties alongside published data is important to be able to use records to their maximum potential in paleoclimate reconstruction and data assimilation.

1 Introduction

Paleoclimate records provide important information about the variability, extremes, and sensitivity of Earth's climate to greenhouse gases on timescales longer than the instrumental period. As the number of published paleoclimate records has grown and the sophistication of numerical model representations of past climates has improved, it has become increasingly important to understand the uncertainty with which paleoclimate observations represent climate variables so that they can be compared to one another and to model output. Additionally, quantifying uncertainty is important for ongoing efforts to assimilate paleoclimate data with numerical climate models (e.g., Hakim et al., 2016; Amrhein et al., 2018).

Paleoclimate records can have errors arising from many different sources: biological effects (e.g.,  Elderfield et al., 2002; Adkins et al., 2003), aliasing onto seasonal cycles (Wunsch, 2000; Fairchild et al., 2006; Dolman and Laepple, 2018), spatial representativeness (Van Sebille et al., 2015), proxy climate calibrations (e.g.,  Tierney and Tingley, 2014), and instrument errors, to name a few. This paper focuses on errors from temporal representativeness (TR), which we define as the degree to which a measurement averaging over one time interval can be used to represent a second target time interval. For instance, in a data assimilation procedure that fits a model to observations at every year, it is important to know the uncertainty associated with relating a decadal-average proxy observation to an annual-average target interval. Furthermore, computing a mean is often the implicit goal of binning procedures that combine observations from within a target time period such as a marine isotope stage, and we expect those observations to have errors that vary with their averaging duration and offsets from the target. Importantly, the term “error” is not meant to connote a procedural error on behalf of a collector or user of observations: given the sparsity of data and the nature of geophysical time series, there is often a good rationale to use one time period to approximate another that is adjacent or has a different duration. Our goal is to understand the uncertainty arising in such a representation in a general framework.

Much of the previous study of errors arising from sampling in time has focused on aliasing, whereby variability at one frequency in a climate process appears at a different frequency in discrete samples of that process. Pisias and Mix (1988) described the consequences of aliasing in a study of deterministic peaks in climate spectra due to Milankovitch forcing. Wunsch and Gunn (2003) described criteria for choosing sample spacing so as not to alias low-frequency variability in sediment cores, and Wunsch (2000) demonstrated how aliasing can lead to spurious spectral peaks in ice core records. Beer et al. (2012) and von Albedyll et al. (2017) describe how running means can reduce aliasing of solar cycle variability in ice core records. In paleoclimate, measurements are often unevenly spaced in time due to changes in archive deposition rates; Jones (1972) showed that aliasing is present and even exacerbated in unevenly sampled records relative to regularly sampled ones. Anderson (2001) and McGee et al. (2013) describe how bioturbation and other diagenetic processes smooth records in time and may reduce aliasing errors.

A second area of previous focus stems from chronological uncertainties, whereby times assigned to measurements may be biased or uncertain. In some cases, such as for radiocarbon dating, estimates of these uncertainties are available from Bayesian approaches that incorporate sampling procedures (Buck, 2004; Buck and Millard, 2004; Bronk Ramsey, 2009); practices for incorporating this information into model–data or data–data comparisons vary, and developing tools for analyzing chronological uncertainty is an active area of research. Huybers and Wunsch (2004) include the effect of uncertainties in tie points in order to align multiple records of Pleistocene oxygen isotopes, and Haam and Huybers (2010) developed tools for estimating the statistics of time-uncertain series. The effect of time uncertainty on estimates of signal spectra is modest in some cases (Rhines and Huybers, 2011), in part because time uncertainty acts to smooth high-frequency variability when computed as an expectation over a record (Moore and Thomson, 1991).

This paper synthesizes effects contributing to TR errors in an analytical model and explores their amplitudes and dependence on signal spectra and sampling timescales. Extending results from time-mean measurements to time series demonstrates how sampling practices can lead to aliasing errors when records are not sampled densely, e.g., when an ocean sediment core is not sampled continuously along its accumulation axis. While we do not claim that TR error is the most important source of uncertainty in paleoclimate records, it does appear to be large enough to affect results in some cases. Moreover, this work is a step towards reducing the number of “unknown unknowns” in paleoclimate reconstruction.

2 Origins of temporal representativeness error

Our focus is first on errors arising when a mean value computed over one time period is used to represent another time period – for instance, when a time average over 20–19 ka (thousand years ago) is used to represent an average over 23–19 ka, the nominal timing of the Last Glacial Maximum (Clark et al., 2012). We define the TR error θ as the difference between x and y:

$$\begin{array}{}\text{(1)}& \mathit{\theta }=x-y,\end{array}$$

where x is the “true” average over the target time interval and the measurement y is affected by one or more types of TR error. As illustrated using a synthetic time series in Fig. 1, our focus is on TR errors arising when the following is true:

• the duration over which an observation averages (τ_y) differs in length from that of the target (τ_x; Fig. 1a);

• the observation is offset from the target by a time Δ (Fig. 1b; these offsets can either be known or, in the presence of chronological uncertainty of observations, stochastic and unknown); and/or

• the paleoclimate archive was smoothed prior to sampling, whether by bioturbation, diagenesis, residence times in karst systems upstream of speleothems (Fairchild et al., 2006), or other effects. In order to perform a 1st-order exploration of smoothing effects, we represent archive smoothing as a moving average over a timescale τ_a. Figure 1c illustrates how smoothing introduces errors for the case in which τ_a=2τ_x.

Visual inspection of Fig. 1 yields some intuitive expectations. As the observational duration τ_y grows small relative to τ_x, one expects TR errors to grow as the observation “feels” more of the variability at high frequencies. TR errors could also be expected to grow as a measurement is increasingly offset from the target in time. But interactions between different types of errors complicate the picture: for instance, in some cases a measurement interval that is short relative to τ_x might have smaller error if it is also offset in time or if it samples an archive that stores a smoothed version of the climate signal. Subsequent sections examine interactions between various TR error sources.

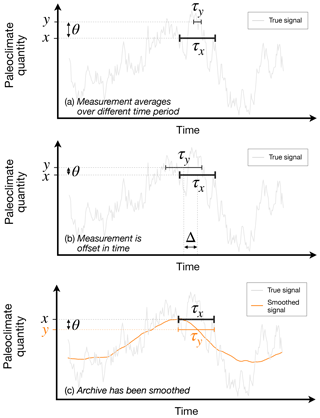
Figure 1 Several factors can contribute to temporal representativeness errors, defined here as the difference θ between a true time-average paleoclimate quantity x and a measurement y that averages over a different time interval. These effects are illustrated using a synthetic autoregressive time series. In each panel, the true quantity x is the same. Panel (a) shows the difference when y averages over a time duration τ_y that is 5 times shorter than the averaging interval τ_x of the target value. Panel (b) shows the error when the observed and target averaging intervals are the same, but the observation is centered on a different value in time. Additional uncertainties, not shown here but discussed in the text, arise if the time offset is a stochastic random variable, as can occur, e.g., with chronological uncertainties from radiocarbon dating. Panel (c) illustrates effects when the observation spans the correct time interval but when the paleoclimate archive being sampled stores a smoothed version of the true signal; here that smoothing has a timescale of τ_a=2τ_x. These errors are merely examples and are not meant to argue, e.g., that offset errors are always greater than errors from different averaging periods.

This list is not exhaustive and neglects, for instance, effects from small numbers of foraminifera in sediment core records and other errors that are inherited from the construction of r(t) from proxy observations. To isolate TR errors we assume that observations directly sample the true climate process, r(t). This approach is intended to be complementary to proxy system models (PSMs; e.g., Evans et al., 2013) that relate proxy quantities to climate variables (“forward operators” in the language of data assimilation). The procedures described may be used to estimate TR uncertainty when PSMs do not; when they do, the model can provide a theoretical grounding for understanding those results. Variances from multiple error sources can be added together under the approximations that they are independent and Gaussian. When these assumptions fail, more holistic forward modeling of errors in PSMs may be necessary.

3 Estimating temporal representativeness error

Because in paleoclimatology we do not have complete knowledge of the underlying climate signal r(t) (it is what we are trying to sample), it is impossible to infer what the TR error is for each measurement as done in the synthetic example (Fig. 1). Instead, our aim is to determine a typical error value, which is important for data assimilation and for comparing models and observations as well as observations to one another. We will characterize TR error θ by estimating its variance, 〈(θ−〈θ〉)²〉, where angle brackets denote statistical expectation. To do this, we approximate r(t) as being weakly statistically stationary, meaning that its mean and variance do not change in time; caveats surrounding this assumption are addressed later in the paper. Under the weak stationarity assumption for the error types considered, the mean error 〈θ〉 is zero, and we can take the expectation by evaluating θ² at all the times in r(t) to compute the variance,

$$\begin{array}{}\text{(2)}& 〈{\mathit{\theta }}^{\mathrm{2}}〉={\displaystyle \frac{\mathrm{1}}{{\mathit{\tau }}_{\mathrm{0}}}}\underset{t_{\mathrm{0}}}{\overset{t_f}{\int }}{\left(x\left(t\right)-y\left(t\right)\right)}^{\mathrm{2}}\mathrm{d}t,\end{array}$$

where t₀ and t_f are the initial and final times in r(t), ${\mathit{\tau }}_{\mathrm{0}}=t_f-t_{\mathrm{0}}$, and x(t) and y(t) are the “target” and “measured” values that would result from sampling r(t) at various times. Intuitively, we are estimating the error in representing x by y (at a single time) as the time-mean squared difference of running means of r(t) (over all times).

In practice, though we do not know r(t), knowledge of its statistics is adequate to estimate 〈θ²〉. Representing TR error in the frequency domain (Appendix A) emerges as an intuitive way to describe errors that also provides closed-form expressions that can be readily integrated to explore the effects of different sampling and time series parameters. A basic result (see Eq. A13) is that in the frequency domain, TR errors are represented as

$$\begin{array}{}\text{(3)}& 〈{\mathit{\theta }}^{\mathrm{2}}〉={\displaystyle \frac{\mathrm{1}}{{\mathit{\tau }}_{\mathrm{0}}}}\underset{\mathrm{0}}{\overset{\mathrm{\infty }}{\int }}H\left(\mathit{\nu },{\mathit{\tau }}_x,{\mathit{\tau }}_y,{\mathit{\tau }}_{\mathrm{a}},\mathrm{\Delta }\right){\left|\widehat{r}\left(\mathit{\nu }\right)\right|}^{\mathrm{2}}\mathrm{d}\mathit{\nu },\end{array}$$

where ν denotes frequency, H is a so-called transfer function, and ${\left|\widehat{r}\left(\mathit{\nu }\right)\right|}^{\mathrm{2}}$ is the power spectral density of the true signal r(t). In effect, the error variance is a weighted sum of the power at different frequencies in r(t), whereby the weights in frequency space (given by H) depend on how the paleoclimate record has been sampled and smoothed. This behavior is typical of aliasing, where variance in the signal at one frequency appears erroneously in a measurement at a different frequency (in this case, at the zero frequency, which is the time mean).

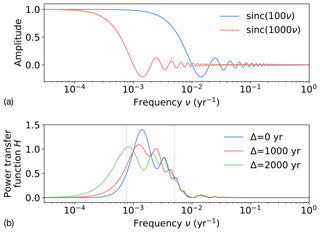
Figure 2 The power transfer function H (Eq. 3) illustrates the dependence of temporal representativeness errors on frequencies in the climate signal and on sampling timescales. In the case in which the offset Δ between the measurement and target is 0, H is a squared difference of sinc functions sinc(τν) as in Eq. (A13), illustrated in (a) for τ=100 years and τ=1000 years. (b) Transfer functions for three different values of the time offset Δ. Grey bars indicate the 1∕200 and 1∕1300 yr⁻¹ frequencies, which approximately bound the frequencies contributing to TR errors in the Δ=0 case.

While the details are left to the Appendix, it is noteworthy that in many practical cases, TR errors can be straightforwardly attributed to signal variability within a particular frequency band. This frequency band behavior emerges because H is a squared difference of sinc functions (Fig. 2a), which has a bump-like shape (Fig. 2b). For instance, if a centennial mean is used to represent a millennial mean, in the absence of archive smoothing, the expected error variance is roughly equal to the variance in r(t) at periods between 200 and 1300 years; the error is the same if a millennial mean is used to represent a centennial mean. Thus, the difference between the sample and target averaging intervals (τ_y and τ_x) sets the frequency band that is aliased onto the mean. These effects are modulated in the presence of archive smoothing, and when there is a time offset in the measurement relative to the target, additional variability is aliased onto errors (Appendix A).

4 Illustrating TR error quantification at the Last Glacial Maximum by sampling a high-resolution paleoclimate archive

Here we explore the procedure for estimating TR errors described in the previous section in the context of estimating mean properties at the Last Glacial Maximum (LGM), the period roughly 20 000 years ago that is associated with the greatest land ice extent during the last glacial period. Following MARGO Project Members (2009) and others, LGM target quantities are defined to be estimates of time means over the 4000-year-long period from 23 000 to 19 000 years ago (23–19 ka):

$$x_{\mathrm{LGM}}={\displaystyle \frac{\mathrm{1}}{\mathrm{4000}}}\underset{-\mathrm{23}\mathrm{000}}{\overset{-\mathrm{19}\mathrm{000}}{\int }}r\left(t\right)\mathrm{d}t.$$

We will consider TR errors arising from representing x_LGM by an observed 1000-year time-mean value that is centered on 21 ka:

$$\begin{array}{}\text{(4)}& y_{\mathrm{LGM}}={\displaystyle \frac{\mathrm{1}}{\mathrm{1000}}}\underset{-\mathrm{20}\mathrm{500}}{\overset{-\mathrm{21}\mathrm{500}}{\int }}r\left(t\right)\mathrm{d}t.\end{array}$$

Qualitatively, errors from this representation have the form illustrated in Fig. 1a. Such an estimate – dated to within the LGM but averaging over only a subset – could reasonably be included in a binned-average compilation of LGM data. However, because statistically robust averaging procedures must downweight uncertain observations according to observational error, including TR errors, is important to avoid biasing any binned averages. Similarly, were we to compare y_LGM to an LGM-mean estimate of r(t) from a model without taking TR errors into account, we might erroneously conclude that the model did not fit the data.

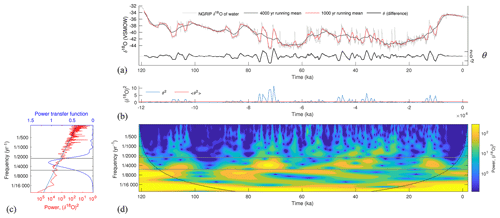
Figure 3 Temporal representativeness error in the time and frequency domains. Errors in representing a 4000-year mean by a 1000-year mean are estimated by computing the difference θ (a, thick black line) between a 4000-year (red line) and 1000-year (thin black line) running mean of the NGRIP δ¹⁸O_ice record (grey). The time average (red line, b) of θ² (blue line) is an estimate (0.7 (‰δ¹⁸O)²) of the temporal representativeness error variance. Large values in θ² correspond to time periods with increased variability, as diagnosed by a wavelet analysis (d), particularly in the band between 2257- and 5298-year periods (grey lines). Panel (c) shows the power transfer function H (dark blue line), the NGRIP spectrum (red line), and the power spectrum ν^−β with β=1.53 derived by a least-squares fit to the NGRIP spectrum.

How large is the TR error in representing x_LGM by y_LGM? We will illustrate the procedure proposed in Sect. 3 by taking a high-resolution climate record to be a true climate signal r(t) and sampling it at longer time averages than the record spacing. Here we will use the North Greenland Ice Core Project (NGRIP; Andersen et al., 2004) 50-year average time series of oxygen isotope ratios (δ¹⁸O). Smoothing the NGRIP record with running means of length τ_x=4000 and τ_y=1000 yields time series of potential target and observation values x(t) and y(t), as defined in Eq. (2) (black and red lines, Fig. 3a). Their difference is the error θ(t) (thick black line, Fig. 3a), and their squared difference is the blue line in Fig. 3b. The time mean 〈θ²〉 (red line, Fig. 3b) is 0.7 ${\left(\mathrm{‰}{\mathit{\delta }}^{\mathrm{18}}\mathrm{O}\right)}^{\mathrm{2}}$ and is the estimate of the error variance.

A prominent feature in Fig. 3b is the time variability of TR error: in some time periods (including the LGM) errors are relatively small, whereas they are markedly larger at, e.g., 80–70 ka. This time variability in errors arises from nonstationarities in the NGRIP oxygen isotope record. The transfer function (blue line, Fig. 3c), shows that for our choices of τ_x and τ_y, variability in the frequency band lying between roughly 2200- and 5300-year periods is responsible for TR errors. A wavelet analysis (Fig. 3d) shows that increased variability in this band is coincident with increases in TR error variance: note, e.g., the correspondence of high wavelet values in that band near −75 000 years with contemporaneous large values in the blue line in Fig. 3b. Evidently, in the presence of nonstationary climate variability, TR errors can vary in time. They may also vary due to changes in sampling procedures over the course of constructing a time series, as discussed in Sect. 6. Observations of intervals with less variability in the TR error frequency band (e.g., the LGM) will be less susceptible to TR errors, an additional quantitative justification for the long-held process of focusing study on time means of periods with relatively less variability.

Next, we will extend our analysis of NGRIP to cover a range of different values of τ_x and τ_y. To compare the NGRIP results to synthetic time series in the following sections with arbitrary units, we will analyze the unitless noise-to-signal standard deviation ratio,

$$\begin{array}{}\text{(5)}& f={\displaystyle \frac{\sqrt{〈{\mathit{\theta }}^{\mathrm{2}}〉}}{\mathit{\sigma }}}.\end{array}$$

Because one motivation of studying the LGM is inferring differences from modern climate, we adopt as our “signal” amplitude the typical anomaly σ between two mean intervals of length τ_x separated by 21 000 years. This quantity is estimated from the NGRIP time series for each value of τ_x.

Figure 4 contours the noise-to-signal ratio f for every combination of τ_x and τ_y between 10 and 4000 years. TR errors depend jointly on values of τ_x and τ_y. Errors are zero for τ_x=τ_y (corresponding to an ideal sampling scheme) and increase monotonically away from those values. Errors are greatest (up to 30 % of signal amplitudes) for small values of τ_y relative to τ_x, where TR error dwarfs the relatively small signal amplitudes that are typical of 21 000-year differences in long-term time averages¹. Subsequent sections extend this analysis to a broader set of sampling parameters (including archive smoothing and time offsets) as well as records with different spectral characteristics.

5 Exploring interactions between sampling parameters and signal spectra

The succinct expression of TR errors in terms of power spectra in Eq. (3) is a clue that the spectral character of paleoclimate processes is an important factor for the amplitude of TR errors. To investigate how errors depend on the spectrum of r(t), we will shift our focus away from observations and consider climate processes with power-law spectra, i.e., those whose power spectral densities ${\left|\widehat{r}\left(\mathit{\nu }\right)\right|}^{\mathrm{2}}$ have the form

$$\begin{array}{}\text{(6)}& {\left|\widehat{r}\left(\mathit{\nu }\right)\right|}^{\mathrm{2}}\propto {\mathit{\nu }}^{-\mathit{\beta }},\end{array}$$

where β is termed the spectral slope (when plotted in log–log space, ν^−β is a straight line with slope −β). We choose this idealized form because spectra consistent with a power-law description are common in climate (Wunsch, 2003). White noise, which partitions variance equally across frequencies, has a spectral slope of 0; signals with a steeper slope (larger β) have a larger fraction of their variance originating from low-frequency variability. Here we consider spectral slopes β=0.5 and β=1.5, motivated by Huybers and Curry (2006), who fit paleoclimate records to spectral slopes between β=0.3 and β=1.6. Climatological spectral features that are not described by power laws, such as peaks due to deterministic astronomical forcing from annual or Milankovitch variability, also contribute to errors (Pisias and Mix, 1988; Wunsch, 2000) but are not specifically considered in these examples. All calculations are performed by numerical integration of Eq. (A13) by global adaptive quadrature.

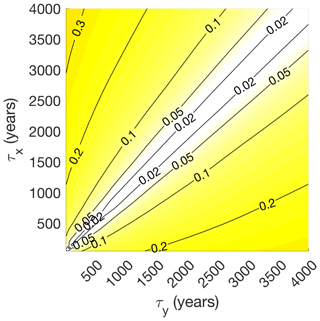
Figure 4 Error-to-signal variance fractions f (Eq. 5) for estimates of time-mean values computed from the NGRIP record of Pleistocene oxygen isotopes contoured as a function of target averaging interval τ_x and observation averaging interval τ_y. A value of 0.1 means that TR error amplitudes are 10 % of the “signal,” which is defined as the typical difference between two time averages over durations τ_x separated by 21 000 years.

5.1 Effects from archive smoothing and signal spectra

Similar to Fig. 4, Fig. 5 contours the noise-to-signal ratio f as a function of τ_x and τ_y, but now for four cases spanning two values of the archive smoothing timescale τ_a (0 and 1000 years) and two values of spectral slope β. Signals with steeper spectral slopes (β=1.5 rather than β=0.5), show smaller f values because TR errors, which originate at relatively high frequencies (Fig. 2), are smaller relative to the greater amount of low-frequency variability in the signal, as also discussed by Wunsch (1978) and Wunsch (2003). The close resemblance between Fig. 5b and the equivalent figure computed from NGRIP (Fig. 4), which has a spectral slope of 1.53 (Fig. 3c), is partly coincidental; analysis of synthetic records with spectral slopes of 1.5 (not shown) reveals variability in f because of variations about the power-law distribution in finite-length, stochastically generated time series, of which NGRIP is arguably one realization. Nevertheless, the agreement shows correspondence between results from paleoclimate data and our idealized approach.

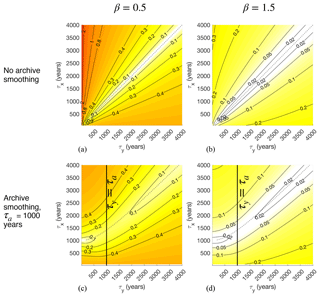
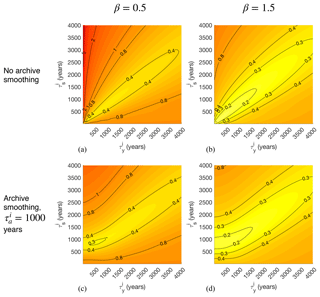
Figure 5 Error-to-signal fractions f for time-mean estimates plotted as a function of target averaging interval τ_x and observation averaging interval τ_y. Climate signal spectra are power-law functions of frequency (${\left|\widehat{r}\left(\mathit{\nu }\right)\right|}^{\mathrm{2}}\propto {\mathit{\nu }}^{-\mathit{\beta }}$) with spectral slopes β equal to 0.5 (a, c) and 1.5 (b, d). Panels (a–b) correspond to a case with no archive smoothing (τ_a=0), while panels (c–d) correspond to a case in which the signal r(t) is smoothed by a running mean over τ_a=1000 years. Values to the left of the bold line at τ_y=τ_a lie in the “smoothed regime” wherein archive smoothing qualitatively affects results. Timescales were chosen to be relevant to the problem of time-mean estimation at the Last Glacial Maximum, ca. 20 ka. Dotted lines show values of ${\stackrel{\mathrm{̃}}{\mathit{\tau }}}_y$ derived to minimize error estimated according to Eq. (A20).

Dependencies on τ_x and τ_y change when we include archive smoothing (Fig. 5a and c; schematized in Fig. 1c). These effects are evident primarily for τ_y<τ_a. In that “smoothed” regime, the largest values of f for small τ_y are reduced because archive smoothing removes some of the high-frequency variability that would otherwise be felt by observations and erroneously aliased onto the mean. Another effect is that τ_y=τ_x no longer minimizes f everywhere; in the smoothed regime, smaller values of τ_y lead to reduced TR error. This is because archive smoothing already provides a measure of time averaging so that when τ_x=1000, the value of τ_y that minimizes error is close to zero because anything longer would be “oversmoothing” the record and effectively giving a longer time average than τ_x. Archive smoothing also reduces the sensitivity of errors to the choice of τ_y for τ_y<τ_a. Finally, the presence of smoothing means that arbitrarily short choices of τ_x can no longer be resolved without error, as evidenced by the monotonic growth of error as τ_x decreases from τ_a.

To the extent that these simple experiments reflect actual paleoclimate sampling procedures, one could attempt to sample time-mean intervals to avoid TR errors. In the absence of archive sampling, the (trivial) result is that τ_y should be equal to τ_x. But the danger of oversmoothing means that this rule is not always appropriate for τ_a≠0. Appendix A derives Eq. (A20), an approximate expression for the error-minimizing value, ${\stackrel{\mathrm{̃}}{\mathit{\tau }}}_y=\sqrt{{\mathit{\tau }}_x^{\mathrm{2}}-{\mathit{\tau }}_{\mathrm{a}}^{\mathrm{2}}}$, that is a function of both the target interval length and smoothing timescale. These values (dotted lines, Fig. 5) are in good qualitative agreement with minimum TR error values.

5.2 Effects from known time offsets

Having explored how choices of τ_x and τ_y contribute to TR errors, we next illustrate effects from chronological offsets when Δ≠0 (schematized in Fig. 1b). Motivated by the LGM timescale, we focus again on the case in which τ_x is fixed to 4000 years and integrate Eq. (A13) varying τ_y between 10 and 6000 years and Δ between 10 and 4000 years for values of $\mathit{\beta }=(\mathrm{0.5},\mathrm{1.5})$ and ${\mathit{\tau }}_{\mathrm{a}}=(\mathrm{0},\mathrm{1000})$.

For all values of τ_a and β, errors grow monotonically away from the values Δ=0, τ_y=τ_x, which corresponds to the case with no TR error² (Fig. 6). As in the previous section, a “smoothed regime” is evident for τ_y≤τ_a across all values of Δ shown: because archive smoothing damps variability in time, the errors from shifting an observation relative to the target become less severe. Another qualitative difference emerges for values of Δ that are greater or less than $\left|{\mathit{\tau }}_x-{\mathit{\tau }}_y\right|/\mathrm{2}$ (blue line, Fig. 6a and c). This boundary designates when the observed time period is sufficiently offset that it begins to fall outside the target interval; at that point, errors grow rapidly as Δ increases. As before, errors are more pronounced for β=0.5 than for β=1.5, with errors larger than the signal (f>1) for small values of τ_y at all values of Δ for β=0.5.

Figure 6 Same as Fig. 5, but illustrating the effects of offsets Δ between target and observational intervals on noise-to-signal ratios. In all cases, the target averaging interval is τ_x=4000, reflecting the nominal length of the Last Glacial Maximum. Values along the line τ_y=τ_x strictly reflect the influence of chronological offsets. The blue line in panel (a) denotes values for which $\mathrm{\Delta }=\left|{\mathit{\tau }}_x-{\mathit{\tau }}_y\right|/\mathrm{2}$, indicating the maximum values of Δ for which the observation interval lies completely within the target interval.

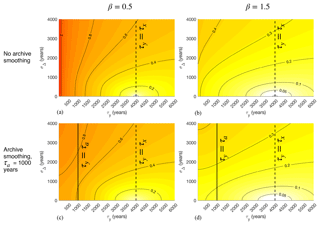
Figure 7 Same as Fig. 5, but illustrating the effects of chronological uncertainties in observations on noise-to-signal ratios. Error fractions f are plotted as a function of the observational averaging interval τ_y and the standard deviation σ_Δ of a Gaussian distribution of time offsets centered on zero. In all cases, the target averaging interval is τ_x=4000, reflecting the nominal length of the Last Glacial Maximum. Values along the line τ_y=τ_x strictly reflect the influence of chronological uncertainty, which is zero when the observational offset is exactly known to be zero (i.e., σ_Δ=0).

5.3 Effects from probabilistic time offsets

When the dating of a measurement is uncertain, a range of Δ values may be possible, as specified by a probability distribution function p(Δ). To explore effects from chronological uncertainty, we assume that p(Δ) is Gaussian about zero with a standard deviation equal to the timescale σ_Δ. We include this uncertainty in TR error variance by taking a second expectation (denoted by _Δ, in addition to the time expectation in Eq. 2) to give

$$\begin{array}{}\text{(7)}& {〈〈{\mathit{\theta }}^{\mathrm{2}}〉〉}_{\mathrm{\Delta }}=\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}p\left(\mathrm{\Delta }\right)〈{\mathit{\theta }}^{\mathrm{2}}〉\mathrm{d}\mathrm{\Delta }.\end{array}$$

In practice, p(Δ) can be multimodal or otherwise non-Gaussian (e.g., from radiocarbon ages; Telford et al., 2004), which could qualitatively change results. While not explored here, such errors can be investigated by integrating Eq. (7) with different choices of p(Δ).

Integrating Eq. (7) and varying σ_Δ and τ_y shows that TR errors in the presence of Gaussian chronological uncertainty p(Δ) with standard deviation σ_Δ are qualitatively similar to those from a fixed offset Δ=σ_Δ (cf. Figs. 6 and 7). The transition in sensitivity to σ_Δ across ${\mathit{\sigma }}_{\mathrm{\Delta }}=\left|{\mathit{\tau }}_x-{\mathit{\tau }}_y\right|/\mathrm{2}$ is less pronounced than for the equivalent in Fig. 6, consistent with the range of lags that is possible for any nonzero σ_Δ. Nevertheless, the intuitively sensible conclusion is that chronological errors will be gravest when uncertainties tend to place measurements outside target intervals. Reduced errors in the smoothed regime τ_y≤τ_a indicate that archive smoothing can reduce effects from chronological errors in some cases.

6 Extension to time series

Paleoclimate time series are sequences of time-mean values; here, we discuss how the TR errors discussed for time-mean estimation affect transient records of climate variability. We show that in the absence of archive smoothing, dense sampling (i.e., setting the averaging interval equal to the spacing between measurements) is a nearly optimal approach to minimize TR errors.

The sampling theorem of Shannon (1949) states that sampling r(t) instantaneously at times separated by a fixed time interval τ_s unambiguously preserves signal information only when r(t) does not contain any spectral power at frequencies greater than 1∕2τ_s (called the Nyquist frequency, ν_Nyq). When this criterion is not met, the discrete signal is corrupted by aliasing, whereby variability in r(t) at frequencies greater than ν_Nyq appears artificially at lower frequencies in the discrete signal. To mitigate aliasing, one can either increase the sampling rate or apply a low-pass “anti-aliasing” filter to r(t) to attenuate power at frequencies higher than ν_Nyq.

In the process of constructing a paleoclimate time series, sampling time-mean values serves a moving average and thereby an anti-aliasing filter. Thus, we expect sample averaging procedures to affect aliasing errors in time series, as also discussed by von Albedyll et al. (2017). Appendix B uses Shannon's theorem to obtain a frequency domain expression for the TR errors for individual time series measurements. The procedure is to (1) define local (in time) values of ${\mathit{\tau }}_s^i$ and ${\mathit{\nu }}_{\mathrm{Nyq}}^i$ for the ith observation and (2) compute the expected errors if an entire time series were sampled using those local properties. To do this, we make the assumption that the sampling interval ${\mathit{\tau }}_s^i$ is locally constant: that is, for the ith measurement yⁱ taken at time tⁱ, yⁱ⁻¹ was taken at time $t^i-{\mathit{\tau }}_s^i$, and yⁱ⁺¹ was taken at time $t^i+{\mathit{\tau }}_s^i$. If the sampling interval changes rapidly, the conclusions from this approach might not apply. Again leaving the details to the Appendix, we note that similar to the time-mean case, the error variance 〈θⁱ²〉 for the ith observation is a weighted integral over the power density spectrum of r(t), as in Eq. (B6). Unlike in the mean estimation case, in which TR errors can be zero, nonzero error is unavoidable with uniform sampling because of differences between the shape of the sinc function and the ideal, abrupt frequency cutoff that minimizes error according to Shannon's theorem.³

To demonstrate sensitivities to sampling parameters we again compute noise-to-signal ratios. In keeping with our local measure of TR error, we take the signal strength to be the standard deviation of the time series that would result if r(t) were sampled with the same averaging and sampling interval as the ith observation over 21 000 years, the approximate duration of the last deglaciation. The results are qualitatively similar to those for the time-mean case, with two main distinctions (cf. Figs. 8 and 5). First, as discussed above, errors are always 10 % or more of signal amplitudes because of errors arising from constructing a time series as a sequence of time-mean values. Second, values of τ_y that minimize errors do not obey τ_y=τ_s but are larger by a factor of roughly 1.2, suggesting that, in the absence of considerations from archive smoothing, the ideal sample would span an interval slightly longer than the sampling interval to minimize errors. In practice, sampling densely (that is, without space between observations) appears to be a good approximation of this error-minimizing strategy.

As in the time-mean case, the effects of archive smoothing are large in a regime of sampling parameter space (τ_y≤τ_a), implying that knowledge of τ_a is important for informing choices of τ_s and τ_y. Clearly, sampling at intervals τ_s<τ_a will result in errors because some of the variability of interest will have been destroyed. Choosing a τ_s that is larger than both τ_y and τ_a will result in aliasing errors. Finally, within the smoothed regime τ_y≤τ_a, TR errors are less sensitive to choices of τ_y than they are for τ_y>τ_a, meaning that sampling discontinuously (i.e., not densely) may not be problematic.

Figure 8 Same as Fig. 5, but illustrating the dependence of the error-to-signal standard deviation ratio for individual measurements in a time series as a function of local time series spacing (${\mathit{\tau }}_s^i$) and the observational averaging time interval ${\mathit{\tau }}_y^i$.

7 Discussion

This paper presents a framework for quantifying temporal representativeness (TR) errors in paleoclimatology, broadly defined as resulting when one time average is represented by another. A simple model illustrates interacting effects from record sampling procedures, chronological errors, and the spectral properties of the climate process being sampled.

We find that TR errors for time-mean estimates can be large relative to climate signals, with noise-to-signal standard deviation ratios greater than 1 in some cases, particularly those in which the observational interval τ_y is smaller than the target interval τ_x. These errors result from aliasing climate variability onto time-mean estimates and can be mitigated to some degree by choices of sampling procedures and by archive smoothing, both of which act as anti-aliasing filters. However, archive smoothing can also destroy information about climate variability, and the combined effects of sampling and smoothing can oversmooth a record and lead to increased errors. TR errors due to sampling are not independent of chronological errors but interact, for instance, in the way that errors grow more quickly as a function of chronological uncertainty amplitude when that uncertainty is likely to place a measurement outside a target interval (Fig. 7). Given that these error variances were estimated using parameters representative of the LGM, it seems possible that TR errors may explain some of the disagreement among proxy measurements within that time period (e.g.,  MARGO Project Members, 2009; Caley et al., 2014), though nonstationarities may cause TR errors to be overestimated for climate intervals like the LGM that appear to be quiescent relative to other time periods. While we do not claim that TR errors are the largest source of error for any particular proxy type or reconstruction problem, they may be in some cases. The tools presented can be used to assess likely error amplitudes.

Though not the principal goal, these analyses provide a basis for sampling practices that minimize errors, for instance for avoiding oversmoothing that can arise through the combined effects of sampling and archive smoothing. When constructing paleoclimate time series, it is important to bear in mind not just the Nyquist frequency but also the role of sampling and smoothing timescales as anti-aliasing filters; these considerations point to dense sampling (i.e., without space between contiguous samples) in order to minimize error in the absence of effects from archive smoothing (Sect. 6). However, many practical considerations motivate paleoclimate sampling strategies and may outweigh the concerns described here. For instance, records sampled densely cannot be used as a starting point for subsequently constructing higher-resolution records. Moreover, the preservation of natural archives for subsequent analyses is important for reproducibility and sharing resources between laboratories but may be complicated by continuous sampling.

To some extent, the simple model for TR error can be generalized to more complex scenarios. If samples are nonuniform in time – for instance, due to large changes in chronology or because material was sampled using a syringe or drill bit with a circular projection onto an archive – then the sinc function in (Eq. 3) can be replaced by Fourier transforms of the relevant function. Similarly, a more complex pattern of archive smoothing can be accommodated by substituting a different smoothing kernel. Non-Gaussian age uncertainties can be incorporated by substituting a different distribution in Eq. (7). Changes in sampling properties through time (as might arise from nonconstant chronologies or sampling procedures) can readily be accommodated because all computations are performed on a point-by-point basis. If sampling or smoothing timescales are unknown, a similar procedure can be adopted as was used for Δ in Eq. (7), whereby a second integration is performed to compute the expectation over an estimated probability distribution of one or more timescales.

Several caveats apply to the uncertainty estimates given. First, the model neglects some effects that may be important, such as inhomogeneities in preserved climate signals owing to, e.g., diagenesis or scarcity of biological fossils. Second, nonstationarity in record spectra leads to time variations in errors, as illustrated in Fig. 3. Third, in the analysis of time series errors, we ignore the possibility that errors covary in time, which can result from chronologies constructed by interpolating ages between tie points; more complete characterizations could be achieved by Monte Carlo sampling of age model uncertainty (Anchukaitis and Tierney, 2013). More broadly, there is a clear need for comprehensive approaches in uncertainty quantification that can reveal interactions among the various sources of uncertainty in paleoclimate records. Forward proxy system models (e.g.,  Evans et al., 2013; Dee et al., 2015; Dolman and Laepple, 2018) are a promising way forward to assess uncertainties holistically.

Results for time series (Sect. 6) hold when record spacing and chronologies do not change too rapidly and when the goal is to obtain a discrete representation of a continuous process. For other objectives, other sampling procedures may be preferred. For instance, “burst sampling,” whereby rapid sequences of observations are taken at relatively long intervals, is used in modern oceanographic procedures to estimate spectral nonstationarities in time (Emery and Thomson, 2014), and unevenly spaced paleoclimate observations can be leveraged to give a range of frequency information using variogram approaches (Amrhein et al., 2015) or the Lomb–Scargle periodogram (e.g.,  Schulz and Stattegger, 1997).

Representativity errors due to aliasing are not limited to the time domain, and similar procedures may be useful for quantifying errors due to spatial representativeness by considering how well proxy records can constrain the regional and larger scales typically of interest in paleoclimatology. An analogous problem is addressed in the modern ocean by Forget and Wunsch (2007), and Zhao et al. (2018) considered spatial representativeness in choosing how to weight deglacial radiocarbon time series in spatial bin averages. A challenge of any such approach is that the spatial averaging functions (analogous to our τ_y but occupying three spatial dimensions) represented by proxy records are often not well known; Van Sebille et al. (2015), for instance, explore how ocean advection determines three-dimensional patterns represented by sediment core observations. Because spatial patterns and timescales of ocean and climate variability are linked, it may ultimately be necessary to consider the full four-dimensional spatiotemporal aliasing problem.

The hope is that these procedures may prove useful for 1st-order practical uncertainty quantification. A challenge is estimating the signal spectrum ${\left|\widehat{r}\right|}^{\mathrm{2}}$, which itself can be affected by aliasing (Kirchner, 2005). One approach is to use spectra from other records that are more highly resolved or were sampled densely, e.g., from a sediment core at an adjacent site, or a record believed to record similar climate variability. Alternately, measurements of archive properties that can be made cheaply and at high resolution – such as magnetic susceptibility, wet bulk density, and other proxy properties that are routinely made on sediment cores – could prove useful for estimating ${\left|\widehat{r}\right|}^{\mathrm{2}}$ if those properties are related linearly to r(t) (Herbert and Mayer, 1991; Wunsch and Gunn, 2003). Another challenge is that the sampling parameters that we have shown affect errors are often not published alongside paleoclimate datasets, thus turning systematic errors (where parameters like τ_y are known) into stochastic errors because a range of possible values must be explored. Publishing all available information about sampling practices, age model construction, and assessments of archive smoothing will greatly aid uncertainty quantification efforts.

Appendix A: Expressing time-mean temporal representativeness errors in the frequency domain

This Appendix describes an analytical approach for estimating temporal representativity errors in the context of estimating time means. These errors have a compact representation in the frequency domain that rationalizes interactions between sampling procedures, time uncertainty, and signal spectra in contributing to errors. Fore more on the theorems and properties of Fourier analysis that are referenced, see, e.g., Bracewell (1986).

A1 Derivation

Define a mean value m(t,τ) of a climate variable r(t) as a function of the duration τ and the time t on which that duration is centered:

$$\begin{array}{}\text{(A1)}& m\left(t,\mathit{\tau }\right)=\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}\mathrm{\Pi }\left(t^{\prime },\mathit{\tau }\right)r\left(t+t^{\prime }\right)\mathrm{d}{t}^{\prime },\end{array}$$

where Π(t,τ) is a normalized “boxcar” function centered on t=0 with width τ,

$$\begin{array}{}\text{(A2)}& \mathrm{\Pi }\left(t,\mathit{\tau }\right)=\left\{\begin{array}{ll}\mathrm{1}/\mathit{\tau }& \left|t\right|\le \mathit{\tau }/\mathrm{2}\\ \mathrm{0}& \left|t\right|>\mathit{\tau }/\mathrm{2}.\end{array}\right.\end{array}$$

The operation in Eq. (A1) defines a moving average m(t,τ) and is known as a convolution, hereafter denoted as a star:

$$\begin{array}{}\text{(A3)}& m\left(t,\mathit{\tau }\right)=\mathrm{\Pi }\left(t,\mathit{\tau }\right)\star r\left(t\right).\end{array}$$

Then let the target quantity x(t) be a mean of r(t) over an interval of length τ_x centered on t, and let an observation y(t) be an average over a different duration τ_y centered on a different time t+Δ:

$$\begin{array}{}\text{(A4)}& {\displaystyle }x\left(t\right)=m\left(t,{\mathit{\tau }}_x\right),\text{(A5)}& {\displaystyle }y\left(t\right)=m\left(t+\mathrm{\Delta },{\mathit{\tau }}_y\right).\end{array}$$

Figure A1 Illustration of the frequency dependence of errors in representing an instantaneous measurement of a process r(t) at a time t by another measurement r(t+Δ). Each line represents a different frequency component of r(t): grey vertical lines represent sampling times, and colored circles represent the values of components at those times. At frequencies $\mathit{\nu }=\frac{n}{\mathrm{\Delta }}$ for $n=\mathrm{0},\mathrm{1},\mathrm{2},\mathrm{\dots }$, (a), the Fourier components of x(t) will be exactly in phase when sampled at a time lag Δ, so these components do not contribute to the error variance $〈{\left(r\left(t\right)-r\left(t+\mathrm{\Delta }\right)\right)}^{\mathrm{2}}〉$. By contrast, at frequencies $\mathit{\nu }=\frac{n}{\mathrm{\Delta }}+\frac{\mathrm{1}}{\mathrm{2}\mathrm{\Delta }}$ (b), the Fourier components are exactly out of phase, so these components tend to contribute most to the error variance. At intermediate frequencies, contributions lie between the two extremes, leading to a cosine function of error contribution as a function of frequency (Eq. A22).

The Fourier transform will be written using both the operator 𝔉 and a hat. Denoting frequency by ν, it is defined as

$$\mathfrak{F}\left(x\left(t\right)\right)\equiv \widehat{x}\left(\mathit{\nu }\right)=\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}x\left(t\right)e^{-\mathrm{2}\mathit{\pi }i\mathit{\nu }t}\mathrm{d}t.$$

Parseval's theorem states that the integral of a squared quantity in the time domain is equal to the integral of the squared amplitude of the Fourier transform of that quantity, so after substituting Eq. (A5) we can write Eq. (2) as

$$\begin{array}{}\text{(A6)}& {\displaystyle }〈{\mathit{\theta }}^{\mathrm{2}}〉={\displaystyle \frac{\mathrm{1}}{{\mathit{\tau }}_{\mathrm{0}}}}\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}\left(m(t,{\mathit{\tau }}_x)-m\left(t+\mathrm{\Delta }t,{\mathit{\tau }}_y\right)\right){}^{\mathrm{2}}\mathrm{d}t,\text{(A7)}& {\displaystyle }={\displaystyle \frac{\mathrm{1}}{{\mathit{\tau }}_{\mathrm{0}}}}\underset{\mathrm{0}}{\overset{\mathrm{\infty }}{\int }}{\left|\mathfrak{F}\left[m(t,{\mathit{\tau }}_x)-m\left(t+\mathrm{\Delta }t,{\mathit{\tau }}_y\right)\right]\right|}^{\mathrm{2}}\mathrm{d}\mathit{\nu }.\end{array}$$

By the Fourier shift theorem,

$$\begin{array}{}\text{(A8)}& \mathfrak{F}\left[m\left(t+\mathrm{\Delta },{\mathit{\tau }}_y\right)\right]=e^{-\mathrm{2}\mathit{\pi }i\mathit{\nu }\mathrm{\Delta }}\mathfrak{F}\left[m\left(t,{\mathit{\tau }}_y\right)\right].\end{array}$$

Then, by the linearity of the Fourier transform,

$$\begin{array}{}\text{(A9)}& 〈{\mathit{\theta }}^{\mathrm{2}}〉={\displaystyle \frac{\mathrm{1}}{{\mathit{\tau }}_{\mathrm{0}}}}\underset{\mathrm{0}}{\overset{\mathrm{\infty }}{\int }}{\left|\widehat{m}(\mathit{\nu },{\mathit{\tau }}_y)-e^{-\mathrm{2}\mathit{\pi }i\mathit{\nu }\mathrm{\Delta }}\widehat{m}\left(\mathit{\nu },{\mathit{\tau }}_x\right)\right|}^{\mathrm{2}}\mathrm{d}\mathit{\nu }.\end{array}$$

By the convolution theorem, convolution in the time domain is equivalent to multiplication in the frequency domain. Thus, the Fourier transform of a time mean as defined in Eq. (A3) is

$$\begin{array}{}\text{(A10)}& {\displaystyle }\widehat{m}\left(\mathit{\nu },\mathit{\tau }\right)=\mathfrak{F}\left[\mathrm{\Pi }\left(t,\mathit{\tau }\right)\star r\left(t\right)\right]\text{(A11)}& {\displaystyle }=\widehat{\mathrm{\Pi }}\left(\mathit{\nu },\mathit{\tau }\right)\cdot \widehat{r}\left(\mathit{\nu }\right).\end{array}$$

Substituting this relation into Eq. (A9) yields

$$\begin{array}{}\text{(A12)}& \begin{array}{rl}〈{\mathit{\theta }}^{\mathrm{2}}〉& ={\displaystyle \frac{\mathrm{1}}{{\mathit{\tau }}_{\mathrm{0}}}}\underset{\mathrm{0}}{\overset{\mathrm{\infty }}{\int }}{\left|\widehat{\mathrm{\Pi }}\left(\mathit{\nu },{\mathit{\tau }}_x\right)-e^{-\mathrm{2}\mathit{\pi }i\mathit{\nu }\mathrm{\Delta }}\cdot \widehat{\mathrm{\Pi }}\left(\mathit{\nu },{\mathit{\tau }}_y\right)\right|}^{\mathrm{2}}\\ & \cdot {\left|\widehat{r}\left(\mathit{\nu }\right)\right|}^{\mathrm{2}}\mathrm{d}\mathit{\nu }.\end{array}\end{array}$$

Finally, we represent smoothing prior to sampling by defining a new climate signal, r^′(t), that has had a running mean applied,

$$r^{\prime }\left(t\right)=\mathrm{\Pi }\left(t,{\mathit{\tau }}_{\mathrm{a}}\right)\star r\left(t\right).$$

Substituting ${\widehat{r}}^{\prime }\left(\mathit{\nu }\right)$ into Eq. (A12) and applying the convolution theorem gives

$$\begin{array}{}\text{(A13)}& \begin{array}{rl}〈{\mathit{\theta }}^{\mathrm{2}}〉& ={\displaystyle \frac{\mathrm{1}}{{\mathit{\tau }}_{\mathrm{0}}}}\underset{\mathrm{0}}{\overset{\mathrm{\infty }}{\int }}\left|\widehat{\mathrm{\Pi }}\left(\mathit{\nu },{\mathit{\tau }}_x\right)-e^{-\mathrm{2}\mathit{\pi }i\mathit{\nu }\mathrm{\Delta }}\cdot \widehat{\mathrm{\Pi }}\left(\mathit{\nu },{\mathit{\tau }}_{\mathrm{a}}\right)\right.\\ & {\left.\cdot \widehat{\mathrm{\Pi }}\left(\mathit{\nu },{\mathit{\tau }}_y\right)\right|}^{\mathrm{2}}{\left|\widehat{r}\left(\mathit{\nu }\right)\right|}^{\mathrm{2}}\mathrm{d}\mathit{\nu }.\end{array}\end{array}$$

Numerical integration of Eq. (A13) is used in the text to illustrate dependencies of TR error on sampling parameters.

A2 Interpretation

The integrand of Eq. (A13) is the product of two components. The second, ${\left|\widehat{r}\left(\mathit{\nu }\right)\right|}^{\mathrm{2}}$, is the power spectral density of r(t), which describes the variance contained at frequencies in r(t). The first component is a power transfer function,

$$\begin{array}{}\text{(A14)}& \begin{array}{rl}H\left(\mathit{\nu },{\mathit{\tau }}_x,{\mathit{\tau }}_y,{\mathit{\tau }}_{\mathrm{a}},\mathrm{\Delta }\right)& =\left|\widehat{\mathrm{\Pi }}\left(\mathit{\nu },{\mathit{\tau }}_x\right)-e^{-\mathrm{2}\mathit{\pi }i\mathit{\nu }\mathrm{\Delta }}\cdot \widehat{\mathrm{\Pi }}\left(\mathit{\nu },{\mathit{\tau }}_{\mathrm{a}}\right)\right.\\ & {\left.\cdot \widehat{\mathrm{\Pi }}\left(\mathit{\nu },{\mathit{\tau }}_y\right)\right|}^{\mathrm{2}},\end{array}\end{array}$$

which describes how power at different frequencies in r(t) contributes to 〈θ²〉. The Fourier transform of the boxcar function is a sinc function,

$$\begin{array}{}\text{(A15)}& \widehat{\mathrm{\Pi }}\left(\mathit{\nu },\mathit{\tau }\right)=\text{sinc}\left(\mathit{\tau }\mathit{\nu }\right)={\displaystyle \frac{\sin \left(\mathit{\pi }\mathit{\tau }\mathit{\nu }\right)}{\mathit{\pi }\mathit{\tau }\mathit{\nu }}},\end{array}$$

which converges towards 1 at frequencies below 1∕τ and oscillates with decreasing amplitude about 0 at higher frequencies (Fig. 2a).

When τ_x and τ_y are adequately separated so that the transfer function has a simple band-pass shape as seen in Fig. 2b, the “cutoff frequencies” ${\mathit{\nu }}_{\mathrm{low}}^{†}$ and ${\mathit{\nu }}_{\mathrm{high}}^{†}$ are useful to diagnose how sampling procedures contribute to TR error. These are the frequencies on either side of the band at which the transfer function is equal to 0.5. In the presence of zero time offsets, the cutoff frequencies can be estimated by solving

$$\begin{array}{}\text{(A16)}& {\displaystyle }H\left({\mathit{\nu }}_{\mathrm{low}}^{†}\right)\approx {\left|\text{sinc}\left({\mathit{\tau }}_x{\mathit{\nu }}_{\mathrm{low}}^{†}\right)-\mathrm{1}\right|}^{\mathrm{2}}={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}},\text{(A17)}& {\displaystyle }H\left({\mathit{\nu }}_{\mathrm{high}}^{†}\right)\approx {\left|\text{sinc}\left({\mathit{\tau }}_y{\mathit{\nu }}_{\mathrm{high}}^{†}\right)\right|}^{\mathrm{2}}={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}},\end{array}$$

which yields ${\mathit{\nu }}_{\mathrm{low}}^{†}=\mathrm{0.755}{\mathit{\tau }}_x^{-\mathrm{1}}$ and ${\mathit{\nu }}_{\mathrm{high}}^{†}=\mathrm{0.443}{\mathit{\tau }}_y^{-\mathrm{1}}$. (In the case in which τ_x is less than τ_y, then ${\mathit{\nu }}_{\mathrm{low}}^{†}=\mathrm{0.755}{\mathit{\tau }}_y^{-\mathrm{1}}$ and ${\mathit{\nu }}_{\mathrm{high}}^{†}=\mathrm{0.443}{\mathit{\tau }}_x^{-\mathrm{1}}$).

We can expect that the presence of archive smoothing might reduce errors originating from high frequencies in r(t), thereby reducing ${\mathit{\nu }}_{\mathrm{high}}^{†}$ and narrowing the band of aliased frequencies. In the presence of archive smoothing, the expression for ${\mathit{\nu }}_{\mathrm{high}}^{†}$ becomes

$$\begin{array}{}\text{(A18)}& H\left({\mathit{\nu }}_{\mathrm{high}}^{†}\right)={\left|\text{sinc}\left({\mathit{\tau }}_{\mathrm{a}}{\mathit{\nu }}_{\mathrm{high}}^{†}\right)\text{sinc}\left({\mathit{\tau }}_y{\mathit{\nu }}_{\mathrm{high}}^{†}\right)\right|}^{\mathrm{2}}={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}.\end{array}$$

An approximate solution using a Taylor series representation is

$$\begin{array}{}\text{(A19)}& {\mathit{\nu }}_{\mathrm{high}}^{†}\approx {\displaystyle \frac{\mathrm{0.443}}{\sqrt{{\mathit{\tau }}_{\mathrm{a}}^{\mathrm{2}}+{\mathit{\tau }}_y^{\mathrm{2}}}}},\end{array}$$

which illustrates a combined effect from sampling and archive smoothing for determining which frequencies contribute to TR errors. Thus, when τ_y and τ_a are small relative to τ_x, archive smoothing reduces TR errors, consistent with numerical integrations (comparing Fig. 5a and b with Fig. 5c and d).

Using Eq. (A19), we can estimate an ideal sampling interval ${\stackrel{\mathrm{̃}}{\mathit{\tau }}}_y$ in the presence of archive smoothing by minimizing the width of the frequency band that contributes to TR error. Setting $\mathrm{0.443}{\stackrel{\mathrm{̃}}{\mathit{\tau }}}_x^{-\mathrm{1}}$ (i.e., the cutoff frequency in the case in which the combined averaging effect of sampling and smoothing gave the desired averaging interval τ_x) equal to $\mathrm{0.443}({\mathit{\tau }}_y^{\mathrm{2}}+{\mathit{\tau }}_{\mathrm{a}}^{\mathrm{2}}{)}^{-\frac{\mathrm{1}}{\mathrm{2}}}$ and solving yields

$$\begin{array}{}\text{(A20)}& {\stackrel{\mathrm{̃}}{\mathit{\tau }}}_y=\sqrt{{\mathit{\tau }}_x^{\mathrm{2}}-{\mathit{\tau }}_{\mathrm{a}}^{\mathrm{2}}}\text{for}{\mathit{\tau }}_x>{\mathit{\tau }}_{\mathrm{a}}.\end{array}$$

Numerical experiments (see the dotted lines in all panels of Fig. 5) support the robustness of this approximation for two different signal spectra.

To study the error contribution from a time offset Δ, consider the limit at which τ_x, τ_y, and τ_a approach zero, corresponding to instantaneous observations in time, so that 〈θ²〉 approaches

$$\begin{array}{}\text{(A21)}& 〈{\mathit{\theta }}^{\mathrm{2}}〉={\displaystyle \frac{\mathrm{1}}{{\mathit{\tau }}_{\mathrm{0}}}}\underset{\mathrm{0}}{\overset{\mathrm{\infty }}{\int }}{\left|\mathrm{1}-e^{-\mathrm{2}\mathit{\pi }i\mathit{\nu }\mathrm{\Delta }}\right|}^{\mathrm{2}}{\left|\widehat{r}\left(\mathit{\nu }\right)\right|}^{\mathrm{2}}\mathrm{d}\mathit{\nu }.\end{array}$$

Expanding ${\left|\mathrm{1}-e^{-\mathrm{2}\mathit{\pi }i\mathit{\nu }\mathrm{\Delta }}\right|}^{\mathrm{2}}$ and simplifying gives

$$\begin{array}{}\text{(A22)}& 〈{\mathit{\theta }}^{\mathrm{2}}〉={\displaystyle \frac{\mathrm{1}}{{\mathit{\tau }}_{\mathrm{0}}}}\underset{\mathrm{0}}{\overset{\mathrm{\infty }}{\int }}\left(\mathrm{2}-\mathrm{2}\cos \left(\mathrm{2}\mathit{\pi }\mathit{\nu }\mathrm{\Delta }\right)\right){\left|\widehat{r}\left(\mathit{\nu }\right)\right|}^{\mathrm{2}}\mathrm{d}\mathit{\nu }\end{array}$$

so that the power transfer function is $H=\mathrm{2}-\mathrm{2}\cos \left(\mathrm{2}\mathit{\pi }\mathit{\nu }\mathrm{\Delta }\right)$ and the expected error due to Δ is a cosinusoidally weighted function of the signal power spectrum. H takes a minimum value of 0 at frequencies

$${\mathit{\nu }}_{\min }=\mathrm{0},{\displaystyle \frac{\mathrm{1}}{\mathrm{\Delta }}},{\displaystyle \frac{\mathrm{2}}{\mathrm{\Delta }}},\mathrm{\dots }{\displaystyle \frac{n}{\mathrm{\Delta }}}$$

for integer values of n; at these frequencies, measurements spaced by Δ in time are in phase and are therefore exactly correlated (Fig. A1a). The weights take a maximum value of 4 at frequencies

$${\mathit{\nu }}_{\max }={\displaystyle \frac{\mathrm{1}}{\mathrm{2}\mathrm{\Delta }}},{\displaystyle \frac{\mathrm{3}}{\mathrm{2}\mathrm{\Delta }}},{\displaystyle \frac{\mathrm{5}}{\mathrm{2}\mathrm{\Delta }}},\mathrm{\dots }{\displaystyle \frac{n}{\mathrm{\Delta }}}+{\displaystyle \frac{\mathrm{1}}{\mathrm{2}\mathrm{\Delta }}},$$

where measurements separated by Δ are always exactly out of phase (Fig. A1b). At those frequencies, the underlying signal r(t) is projected twofold onto the error so that its variance contribution is multiplied fourfold. These variations in frequency contributions modulate effects from smoothing and sampling timescales (Fig. 2b).

Appendix B: Expressing time series temporal representativeness errors in the frequency domain

This Appendix extends the analytical approach for estimating temporal representativity errors from estimating time means to time series. Define the associated moving average time series that would result if all of r(t) were sampled as the i^th observation yⁱ to be

$$\begin{array}{}\text{(B1)}& y^i\left(t\right)=\mathrm{\Pi }\left(t,{\mathit{\tau }}_y^i\right)\star \mathrm{\Pi }\left(t,{\mathit{\tau }}_{\mathrm{a}}^i\right)\star r\left(t\right),\end{array}$$

where we have included a contribution from archive smoothing so that its Fourier transform is

$$\begin{array}{}\text{(B2)}& {\widehat{y}}^i\left(\mathit{\nu }\right)=\widehat{\mathrm{\Pi }}\left(\mathit{\nu },{\mathit{\tau }}_y^i\right)\cdot \widehat{\mathrm{\Pi }}\left(\mathit{\nu },{\mathit{\tau }}_{\mathrm{a}}^i\right)\cdot \widehat{r}\left(\mathit{\nu }\right).\end{array}$$

By Shannon's sampling theorem, an accurate discrete representation of r(t) results from sampling all frequencies in r(t) less than or equal to the local Nyquist frequency ${\mathit{\nu }}_{\mathrm{Nyq}}^i=\mathrm{1}/\left(\mathrm{2}{\mathit{\tau }}_s^i\right)$. As such, the target value xⁱ for the ith measurement yⁱ is the value of r(t) sampled at tⁱ after filtering r(t) to remove high-frequency variability. The Fourier transform of a time series of values of xⁱ is

$$\begin{array}{}\text{(B3)}& {\widehat{x}}^i\left(\mathit{\nu }\right)=G\left(\mathit{\nu },{\mathit{\tau }}_s^i\right)\widehat{r}\left(\mathit{\nu }\right),\end{array}$$

where the “ideal” transfer function G(ν,τ_s) is the Heaviside function:

$$\begin{array}{}\text{(B4)}& G(\mathit{\nu },{\mathit{\tau }}_s)=\left\{\begin{array}{ll}\mathrm{1}& \mathit{\nu }<\mathrm{1}/\left(\mathrm{2}{\mathit{\tau }}_s^i\right)\\ \mathrm{0}& \mathit{\nu }\ge \mathrm{1}/\left(\mathrm{2}{\mathit{\tau }}_s^i\right),\end{array}\right.\end{array}$$

which is ideal in the sense that it eliminates variability at frequencies greater than ${\mathit{\nu }}_{\mathrm{Nyq}}^i=\mathrm{1}/\left(\mathrm{2}{\mathit{\tau }}_s^i\right)$. Then we define TR error at the ith measurement to be

$$\begin{array}{}\text{(B5)}& {\mathit{\theta }}^i=x^i-y^i.\end{array}$$

As in the previous section, we estimate the variance of θⁱ by taking the expected value as if the entire record had been sampled using the local values ${\mathit{\tau }}_s^i$ and ${\mathit{\tau }}_y^i$. Then, equivalent to Eq. (A13),

$$\begin{array}{}\text{(B6)}& \begin{array}{rl}〈{\mathit{\theta }}^{i\mathrm{2}}〉& ={\displaystyle \frac{\mathrm{1}}{{\mathit{\tau }}_{\mathrm{0}}}}\underset{\mathrm{0}}{\overset{\mathrm{\infty }}{\int }}{\left|G\left(\mathit{\nu },{\mathit{\tau }}_s^i\right)-\widehat{\mathrm{\Pi }}\left(\mathit{\nu },{\mathit{\tau }}_{\mathrm{a}}^i\right)\cdot \widehat{\mathrm{\Pi }}\left(\mathit{\nu },{\mathit{\tau }}_y^i\right)\right|}^{\mathrm{2}}\\ & {\left|\widehat{r}\left(\mathit{\nu }\right)\right|}^{\mathrm{2}}\mathrm{d}\mathit{\nu }.\end{array}\end{array}$$