A 2600-year summer climate reconstruction in central Japan by integrating tree-ring stable oxygen and hydrogen isotopes

Oxygen isotope ratios (δ¹⁸O) of tree-ring cellulose are a novel proxy for summer hydroclimate in monsoonal Asia. In central Japan, we collected 67 conifer wood samples, mainly Chamaecyparis obtusa, with ages encompassing the past 2600 years. The samples were taken from living trees, archeological wood, architectural wood, and buried logs. We analyzed stable isotope ratios of oxygen (δ¹⁸O) and hydrogen (δ²H) in tree-ring cellulose in these samples (more than 15 000 rings in total) without using a pooling method and constructed a statistically reliable tree-ring cellulose δ¹⁸O time series for the past 2500 years. However, there were distinct age trends and level offsets in the δ¹⁸O record, and cellulose δ¹⁸O values showed a gradual decrease as an individual tree matures. This suggested it is difficult to establish a cellulose δ¹⁸O chronology for low-frequency signals by simple averaging of all the δ¹⁸O time series data. In addition, there were opposite age trends in the cellulose δ²H, and δ²H gradually increased with tree age. There were clear positive correlations in the short-periodicity variations between δ¹⁸O and δ²H, probably indicating a common climate signal. A comparison of the δ¹⁸O and δ²H time series in individual trees with tree-ring width suggested that the opposite age trends of δ¹⁸O and δ²H are caused by temporal changes in the degree of post-photosynthetic isotope exchange with xylem water (physiological effect), accompanied by changes in stem growth rate that are influenced by human activity in the forests of central Japan. Based on the assumptions that cellulose δ¹⁸O and δ²H vary positively and negatively with constant proportional coefficients due to climatological and physiological effects, respectively, we solved simultaneous equations for the climatological and physiological components of variations in tree-ring cellulose δ¹⁸O and δ²H in order to remove the age trend. This enabled us to evaluate the climatic record from cellulose δ¹⁸O variations. The extracted climatological component in the cellulose δ¹⁸O for the past 2600 years in central Japan was well correlated with numerous instrumental, historical, and paleoclimatological records of past summer climate at various spatial and temporal scales. This indicates that integration of tree-ring cellulose δ¹⁸O and δ²H data is a promising method to reconstruct past summer climate variations on annual to millennial timescales, irrespective of the growth environment. However, analytical and statistical methods need to be improved for further development of this climate proxy.

1 Introduction

In general, it is not straightforward to extract low-frequency climate signals from tree-ring time series because there are typically age trends in tree-ring width. To overcome this, the regional curve standardization (RCS) method is used to determine the typical growth curve in a region for a tree species, which is subtracted from the tree-ring width time series of individual trees to explicitly estimate climatological influences (Esper et al., 2003), but it is difficult to fully preserve low-frequency climate signals of tree-ring width and density.

Tree-ring cellulose oxygen isotope ratios (δ¹⁸O) are a novel proxy for past summer hydroclimate, and it has been reported that such data are not affected by age trends (Young et al., 2011; Kilroy et al., 2016; Xu et al., 2016; Büntgen et al; 2020) or only show short-lived juvenile effects of higher δ¹⁸O values (Szymczak et al., 2012; Duffy et al., 2017). These juvenile effects are interpreted to be related to the less-developed root system of young trees and the evaporative enrichment of ¹⁸O in soil water in the near surface. However, Esper et al. (2010) demonstrated the presence of long-term age trends, whereby δ¹⁸O gradually decreases for hundreds of years after germination, as well as significant level offsets between different individual trees, in a conifer species. This requires three analytical criteria to evaluate the age trends and level offsets in the tree-ring cellulose δ¹⁸O data: (1) well-replicated data, (2) non-pooled data, and (3) composite chronologies from multiple species and regions. However, given that subsequent studies of tree-ring cellulose δ¹⁸O have reported that age trends are negligible, the mechanisms responsible for long-term age trends remain unclear.

In Japan, it has been difficult to establish millennial-scale tree-ring chronologies applicable to reconstructing past changes in summer climate, even though such information is critical for rice paddy cultivation and for historical and archeological studies in Japan. Although there are ancient archeological and architectural woods that have been used for dendrochronological analysis of wooden artifacts with ages of 1000–2000 years (Mitsutani, 2000; NNRICP, 1990), these have not been utilized for past climate reconstructions. This is because tree-ring widths measured in trees from normal Japanese forests do not have a high sensitivity to climate. Moreover, the ecological and artificial disturbance of tree growth in dense Japanese forests prevents reconstructions of past climate based on the relatively small number of old sub-fossil wood samples that are available.

However, tree-ring cellulose δ¹⁸O data are sensitive to summer hydroclimate in Asia (Treydte et al., 2006; Grießinger et al., 2011; Li et al., 2011; Xu et al., 2011; Sano et al., 2012; Liu et al., 2017), including in Japan (Nakatsuka et al., 2004; Tsuji et al., 2008; Yamaguchi et al., 2010; Li et al., 2015). High correlation coefficients for tree-ring cellulose δ¹⁸O data amongst different individual trees and species make it possible to reconstruct past summer climate using only a small number of sub-fossil trees. Therefore, during the past decade we have analyzed tree-ring cellulose δ¹⁸O in various types of conifer wood with large tree-ring numbers (mainly Chamaecyparis obtusa), including from living trees, archeological wood, architectural wood, and buried logs, in order to reconstruct past variations in summer hydroclimate in central Japan (Nakatsuka, 2015, 2018).

We do not use the pooling method (Szymczak et al., 2012; Loader et al., 2013) for the tree-ring isotope measurements. Instead, we analyze all the tree rings in the wood samples using a novel method, involving direct cellulose extraction from 1 mm thick wood sections (Kagawa et al., 2015). This allows us to evaluate age trends in individual trees and offsets between different individuals in the tree-ring cellulose δ¹⁸O data, following the criteria proposed by Esper et al. (2010). This approach has shown that most old trees in Japan (mainly Chamaecyparis obtusa) are significantly affected by long-term age trends and level offsets such that it is not possible to reconstruct long-term summer climate variations without taking these effects into accounts.

However, we have also found that hydrogen isotope ratios (δ²H) of tree-ring cellulose, which have been measured simultaneously with the δ¹⁸O data, have age trends opposite to those of δ¹⁸O and that δ²H is positively and negatively correlated with δ¹⁸O in terms of short- and long-periodicity variations, respectively. This δ¹⁸O and δ²H relationship provides insights into the mechanisms responsible for age trends in tree-ring cellulose δ¹⁸O data and makes it possible to remove the age trends in such data.

Here, we compare δ¹⁸O and δ²H data for tree-ring cellulose and elucidate the mechanisms responsible for age trends in tree-ring cellulose δ¹⁸O data. We then propose and apply a new method to the tree-ring cellulose δ¹⁸O and δ²H time series for reconstructing climate over the past 2600 years in central Japan. This enables us to remove the age trend and extract the climatological component of the tree-ring cellulose δ¹⁸O data using many ecologically and artificially disturbed trees that are available for the last several thousand years, even in Japan.

2 Samples and chemical analyses

2.1 Collection of tree-ring samples

A total of 67 tree samples covering the past 2600 years were collected in central Japan (Fig. 1). These samples consist of living trees, architectural wood, archeological wood, and buried logs (Table S1 in the Supplement). Most of the trees are Japanese cypress (Chamaecyparis obtusa), but there are some samples of other conifer species (Chamaecyparis pisifera, Sciadopitys verticillata, and Cryptomeria japonica). All samples contain hundreds of rings. Although some samples have already been dated by traditional dendrochronological methods using tree-ring width (Mitsutani, 2000; NNRICP, 1990), the new tree-ring δ¹⁸O time series were used in the final dendrochronological determination of their ages (Roden, 2008; Yamada et al., 2018), which provided results consistent with the tree-ring width dating results (Fig. S1).

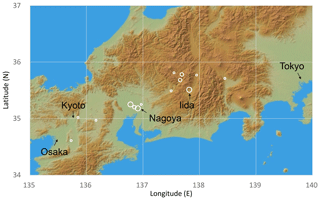
Figure 1 Sample sites of this study. Open circles indicate locations of wood samples, shown by the latitude and longitude of governmental offices in the municipalities where samples were collected because most samples were not living trees for which the actual growth location can be identified. The size of the open circles indicates the sample numbers for each site (large 10–15; medium 4–9; small 1–3). This figure was constructed using the JAXA AW3D30 DSM data map.

2.2 Measurement of tree-ring cellulose δ¹⁸O and δ²H

Here, we analyzed cellulose δ¹⁸O and δ²H for all tree rings in all wood samples using a novel method, involving direct cellulose extraction from 1 mm thick wood laths (Kagawa et al., 2015), without using the pooling method. Firstly, 1 mm thick cross-sectional laths perpendicular to the cellulose fibers were sliced from all wood samples regardless of ring width and age and directly subjected to chemical treatment to remove components other than cellulose. In order to keep the original shape of samples during chemical treatments, 1 mm thick wood laths were put between two Teflon punching sheets and set into test tubes. Given that buried wood sometimes shows extraordinary δ¹⁸O values due to alteration of chemical components and/or deposition of iron oxides (Savard et al., 2012; Yapp, 2001), we carefully selected less-degraded wood segments and completely removed all components other than cellulose. A 100–300 µg fragment of cellulose representing the whole annual layer was then cut from the cellulose lath year by year using a fine blade under a microscope (Fig. S2). Each sample was wrapped in silver foil for δ¹⁸O and δ²H measurements using a mass spectrometer combined with a pyrolysis elemental analyzer (TCEA/Delta V Advantage; ThermoFisher Scientific, Bremen, Germany). In this study, we analyzed both δ¹⁸O and δ²H values for each cellulose sample simultaneously by making the focus of the mass spectrometer automatically jump between outflows of H₂ and CO gases from the pyrolysis elemental analyzer. After measurements of every eight samples, a cellulose standard (cellulose reagent; Merck) with known δ¹⁸O and δ²H was analyzed to calibrate analytical drift and calculate the δ¹⁸O and δ²H of samples against the international standard of VSMOW, following Eqs. (1) and (2). Analytical reproducibility (1σ) based on repeated measurements of homogeneous cellulose samples is ca. ± 0.15 and ± 1.5 ‰ for δ¹⁸O and δ²H, respectively. Absolute accuracies of δ¹⁸O and δ²H may be a little bit worse because we use only one working standard to minimize the memory effect in the δ²H measurement. However, it does not influence the discussion of this study because we do not utilize absolute isotope values but focus only on their temporal variations.

$$\begin{array}{}\text{(1)}& {\displaystyle }{\mathit{\delta }}^{\mathrm{18}}{\mathrm{O}}_{\mathrm{vsmow}}\left(\mathrm{‰}\right)=\left\{{\displaystyle \frac{{\left({}^{\mathrm{18}}\mathrm{O}{/}^{\mathrm{16}}\mathrm{O}\right)}_{\mathrm{sample}}}{{\left({}^{\mathrm{18}}\mathrm{O}{/}^{\mathrm{16}}\mathrm{O}\right)}_{\mathrm{vsmow}}}}-\mathrm{1}\right\}\times \mathrm{1000}\text{(2)}& {\displaystyle }{\mathit{\delta }}^{\mathrm{2}}{\mathrm{H}}_{\mathrm{vsmow}}\left(\mathrm{‰}\right)=\left\{{\displaystyle \frac{{\left({}^{\mathrm{2}}\mathrm{H}{/}^{\mathrm{1}}\mathrm{H}\right)}_{\mathrm{sample}}}{{\left({}^{\mathrm{2}}\mathrm{H}{/}^{\mathrm{1}}\mathrm{H}\right)}_{\mathrm{vsmow}}}}-\mathrm{1}\right\}\times \mathrm{1000}\end{array}$$

Given that cellulose contains 30 % OH-group hydrogen that is exchangeable with experimental water during chemical treatment, it is necessary to remove the OH group by nitration of the cellulose (synthesis of nitrocellulose) before the isotope measurements (Epstein et al., 1976; DeNiro, 1981). However, it was nearly impossible to nitrate all the cellulose samples analyzed in this study due to the very small sample amount (Fig. S2) and the extremely large sample number (15 924 rings for isotopic measurements). Moreover, it was desirable to measure both δ¹⁸O and δ²H simultaneously for each sample, not only to reduce the sample number to half, but also to treat the δ¹⁸O and δ²H data as completely originating from the same sample, as discussed later, but the nitration of cellulose makes it impossible to measure its δ¹⁸O together with δ²H due to the contamination of oxygen in the NO₂ group. However, we can expect that all OH-group hydrogen in a cellulose lath will have a unique δ²H value, as it would have been replaced by the hydrogen of homogeneous water in the test tube during the process of cellulose extraction such that the measured tree-ring cellulose δ²H time series will retain the original isotopic variations, although the amplitude of these variations will decrease by up to 70 % and the absolute values will have been modified (Filot et al., 2006). We confirmed that there are consistent correlations in δ²H variations between cellulose and nitrocellulose produced using the traditional nitration method (Epstein et al., 1976; DeNiro, 1981) for two tree samples (Fig. 2), although the correlation coefficients are lower than that from a more sophisticated method to fix the δ²H value of the OH group in cellulose (Filot et al., 2006). This demonstrates that it is possible to reconstruct original variations in tree-ring cellulose δ²H data without nitrating the cellulose to a certain degree. However, considering the possible analytical uncertainties in cellulose δ²H data of this study, we restrict the usage of δ²H data to the calibration of long-term age trends in cellulose δ¹⁸O, as discussed later.

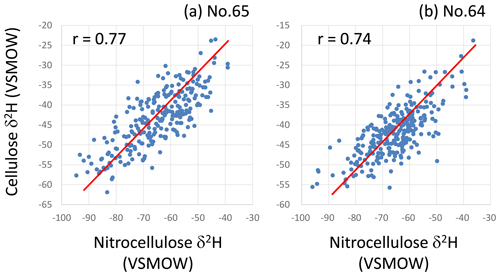
Figure 2 Correlations between hydrogen isotope ratios (δ²H) of tree-ring cellulose and nitrocellulose in two Japanese cypress trees. (a) No. 65 and (b) no. 64 in Table S1. Red lines indicate the slope observed when all OH-group hydrogen in cellulose is exchanged with hydrogen with a unique δ²H value.

3 Results and discussion

3.1 Variations in the tree-ring cellulose δ¹⁸O and δ²H data

After constraining the exact dates for all the tree rings by the cross-dating method using δ¹⁸O data (Fig. S1; Bunn, 2008), we compared all tree-ring cellulose δ¹⁸O and δ²H time series (Fig. 3a and c).

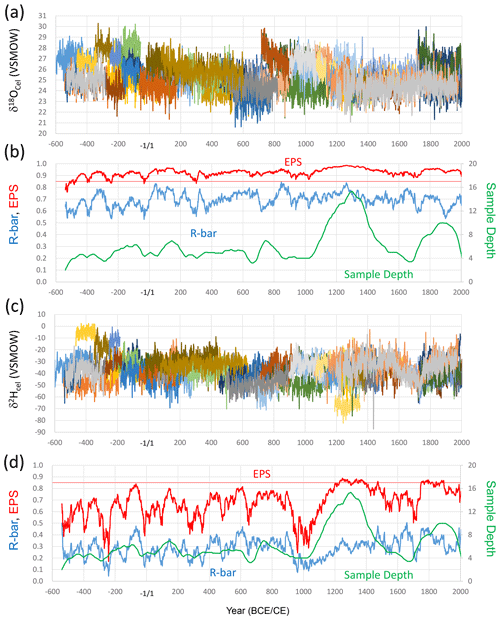
Figure 3 The tree-ring cellulose δ¹⁸O and δ²H time series and their statistical properties. (a) Tree-ring cellulose δ¹⁸O time series of the 67 analyzed trees. (b) R bar (average correlation coefficients between different individual trees), EPS (see text), and sample depth (tree sample numbers) in the corresponding periods for the tree-ring cellulose δ¹⁸O dataset. (c) Tree-ring cellulose δ²H time series of the 67 analyzed trees. (d) R bar, EPS, and sample depth for the tree-ring cellulose δ²H dataset. All data in panels (b) and (d) were calculated for a total period of 51 years, including 25 years before and after the year shown.

Given that the average correlation coefficient (R bar) amongst the different δ¹⁸O time series is ca. 0.6–0.8, the expressed population signal (EPS) (Wigley et al., 1984), defined as $N\times R/[\mathrm{1}+(N-\mathrm{1})\times R]$, where the N and R values are the number of time series and R bar, respectively, is > 0.85 for almost all periods during the past 2500 years (Fig. 3b), indicating that the δ¹⁸O data in Fig. 3a are sufficient to establish accurate δ¹⁸O chronologies. However, there are distinct long-term age trends in that the δ¹⁸O values gradually decrease as the trees mature, as also noted by Esper et al. (2010). These effects must be detrended in order to reconstruct long-term climate variations using the δ¹⁸O data. There are also significant offsets in absolute δ¹⁸O values for each year amongst different trees, probably reflecting differences in the sample location and magnitude of the age trend. Given that the original locations of the trees cover a wide region from coastal to inland areas and low to high altitudes (Fig. 1), this would result in different precipitation δ¹⁸O values and relative humidity (Waseda and Nakai, 1983; Araguás-Araguás et al., 2000; Shu et al., 2005). This would account for the offset absolute δ¹⁸O values of tree-ring cellulose in different trees.

The R bar for the different δ²H time series is ca. 0.2–0.4, resulting in lower EPS values (Fig. 3d), which must reflect more complicated post-photosynthetic changes in isotopic ratios in hydrogen than in oxygen (Roden et al., 2000), as discussed later, but may be partly owing to the analytical uncertainty from the direct measurement of cellulose hydrogen including the OH group in the δ²H measurements. However, there are also distinct age trends, which are opposite to those exhibited by δ¹⁸O in that δ²H values gradually increase as the trees mature.

3.2 Relationship between short- and long-periodicity δ¹⁸O and δ²H variations

To investigate the environmental causes of the age trends in tree-ring cellulose δ¹⁸O and δ²H data, we decomposed the δ¹⁸O and δ²H time series into short- and long-periodicity variations (Figs. 4, S3, S4, and S5). These trees (no. 65 and nos. 43, 49, 40; Table S1) are Japanese cypress (Chamaecyparis obtusa) from Nagano and Gifu Prefectures. In all cases, short-periodicity variations (i.e., < 11 years) in the tree-ring cellulose δ¹⁸O and δ²H data show a clear positive correlation, indicating that both the δ¹⁸O and δ²H variations reflect a common climatological signal (i.e., precipitation isotope ratios and relative humidity) as reported in previous studies (e.g., An et al., 2014). However, the long-periodicity variations (i.e., > 11 years) in the tree-ring cellulose δ¹⁸O and δ²H data show negative correlations (Figs. 4b and S3b), suggesting the influence of opposite age trends in Fig. 3. However, the negative correlations are not very clear in Figs. S4b and S5b, probably because the climatological signals also overlap the long-periodicity variations and make the correlation between the tree-ring cellulose δ¹⁸O and δ²H positive to a certain degree.

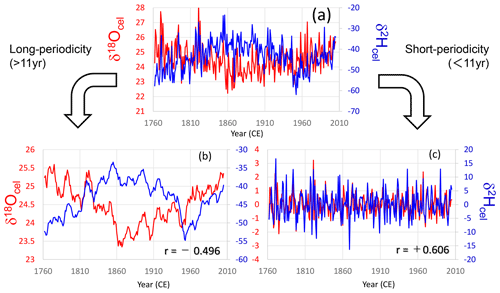
Figure 4 Comparison between tree-ring cellulose δ¹⁸O (red) and δ²H (blue) time series in tree sample no. 65. (a) Raw data, (b) long-periodicity components (> 11 years; 11-year running mean), and (c) short-periodicity components (< 11 years; deviation from the 11-year running mean).

Figures 4b, S3b, S4b, and S5b show that δ¹⁸O and δ²H often changed oppositely in the long-periodicity variations, regardless of the tree age. Therefore, the long-term opposite variations in the tree-ring cellulose δ¹⁸O and δ²H data are not a simple age trend. As such, it is impossible to apply the RCS or negative exponential curve proposed by Esper et al. (2010) to remove the apparent age trend of tree-ring cellulose δ¹⁸O in central Japan.

To date, the age trend in tree-ring cellulose δ¹⁸O data has been explained by the relatively shallow root system of juvenile trees and the evaporative enrichment of ¹⁸O in soil water at the near surface. However, this cannot explain the long-term variations in tree-ring cellulose δ¹⁸O and δ²H data in this study (Figs. 4, S3, S4, and S5) because the soil water evaporation must increase both δ¹⁸O and δ²H. As illustrated in Sect. S1 and Fig. S6, the long-term opposite variations in tree-ring cellulose δ¹⁸O and δ²H are tightly related to changes in tree-ring width (growth rate of trees), suggesting that they are influenced by some physiological effect corresponding to long-term changes in tree growth rate.

3.3 Mechanical model of cellulose δ¹⁸O and δ²H

What physiological mechanism can explain the long-term opposite variations in the δ¹⁸O and δ²H values? Tree-ring cellulose δ¹⁸O and δ²H values can be expressed using the following equations, which are modified and simplified from Roden et al. (2000):

$$\begin{array}{}\text{(3)}& {\displaystyle }\begin{array}{rl}{\mathit{\delta }}^{\mathrm{18}}{\mathrm{O}}_{\mathrm{cel}}& =f\left({\mathit{\delta }}^{\mathrm{18}}{\mathrm{O}}_{\mathrm{rain}}+{\mathit{\epsilon }}_{\mathrm{ho}}\right)\\ & +\left(\mathrm{1}-f\right)\left[{\mathit{\delta }}^{\mathrm{18}}{\mathrm{O}}_{\mathrm{rain}}+\left({\mathit{\epsilon }}_{\mathrm{eo}}+{\mathit{\epsilon }}_{\mathrm{ko}}\right)\left(\mathrm{1}-h\right)+{\mathit{\epsilon }}_{\mathrm{ao}}\right],\end{array}\text{(4)}& {\displaystyle }\begin{array}{rl}{\mathit{\delta }}^{\mathrm{2}}{\mathrm{H}}_{\mathrm{cel}}& =f\left({\mathit{\delta }}^{\mathrm{2}}{\mathrm{H}}_{\mathrm{rain}}+{\mathit{\epsilon }}_{\mathrm{hh}}\right)\\ & +\left(\mathrm{1}-f\right)\left[{\mathit{\delta }}^{\mathrm{2}}{\mathrm{H}}_{\mathrm{rain}}+\left({\mathit{\epsilon }}_{\mathrm{eh}}+{\mathit{\epsilon }}_{\mathrm{kh}}\right)\left(\mathrm{1}-h\right)+{\mathit{\epsilon }}_{\mathrm{ah}}\right],\end{array}\end{array}$$

where cel and rain indicate the tree-ring cellulose and precipitation, respectively; h is the relative humidity during photosynthesis; f is the proportion of oxygen atoms in carbohydrate exchanged with xylem water during post-photosynthetic processes before cellulose synthesis, which is assumed to be equal to that of the hydrogen atoms; ε_eo (ε_eh) and ε_ko (ε_kh) are isotopic fractionation factors for oxygen (hydrogen) during equilibrium water vapor evaporation from water and kinetic water vapor diffusion through leaf stomata, respectively; and ε_ao (ε_ah) and ε_ho (ε_hh) are isotopic fractionation factors for oxygen (hydrogen) between water and carbohydrates during photosynthesis in the leaf and the post-photosynthetic processes before cellulose synthesis, respectively. Values of ε_eo, ε_ko, ε_ao, and ε_ho are +9, +29, +27, and +27, respectively, while ε_eh and ε_kh are +80 and +25, respectively, and ε_ah and ε_hh are approximately −150 and +150, respectively (Roden et al., 2000).

Given that we can assume that all the isotopic fractionation factors are constant, δ¹⁸O_cel and δ²H_cel are determined only by climatological factors (δ¹⁸O_rain, δ²H_rain, and h) when f is constant. Because there are always positive correlations between δ¹⁸O_rain and δ²H_rain (Dansgaard, 1964) and any change in h produces changes in δ¹⁸O_cel and δ²H_cel in Eqs. (3) and (4) in the same direction, we can expect that there are also positive correlations between δ¹⁸O_cel and δ²H_cel when f is constant. In fact, even in trees that have negative correlations between δ¹⁸O_cel and δ²H_cel for the long-periodicity variations, we observe clear positive correlations in the short-periodicity variations (Figs. 4c, S3c, S4c, and S5c), suggesting that f does not change on annual timescales and the short-periodicity variations in δ¹⁸O_cel and δ²H_cel are controlled solely by climatological factors.

However, if f increases over the long term due to some physiological reason, it can be inferred from Eqs. (3) and (4) that δ¹⁸O_cel decreases while δ²H_cel increases. This is because, for oxygen, the magnitude of isotopic fractionation between water and carbohydrates is the same (+27) for photosynthesis (ε_ao) and post-photosynthesis processes (ε_ho), and the increase in f reduces the effect of leaf water ¹⁸O enrichment, $({\mathit{\epsilon }}_{\mathrm{eo}}+{\mathit{\epsilon }}_{\mathrm{ko}})(\mathrm{1}-h)$ in Eq. (3), resulting in lower δ¹⁸O_cel. However, for hydrogen, the magnitude of isotopic fractionation between water and carbohydrates during post-photosynthesis processes (${\mathit{\epsilon }}_{\mathrm{hh}}=+\mathrm{150}$) is significantly larger than that during photosynthesis (${\mathit{\epsilon }}_{\mathrm{ah}}=-\mathrm{150}$) such that the increase in f results in higher δ²H_cel. This causes long-term opposite trends in δ¹⁸O_cel and δ²H_cel data (Figs. 3, 4b, S3b, S4b, and S5b), which can be interpreted as a long-term change in the rate of post-photosynthetic isotopic exchange between carbohydrates and xylem water (f). Possible physiological mechanisms for this include an increase in the rate of utilization of stored carbohydrates for stem cellulose synthesis (Nabeshima et al., 2018), rather than directly using photosynthetic products for rapid tree growth during the juvenile period. The change in the f value could also occur in the period following an abrupt improvement in the growth environment due to logging of neighboring trees (see Sect. S1 and Fig. S6).

Although the long-periodicity variations in δ¹⁸O_cel and δ²H_cel are influenced by predominant physiological effects (Figs. 4b, S3b, S4b, and S5b), this does not mean that the long-periodicity variations in δ¹⁸O_cel and δ²H_cel do not contain climatological components. In fact, climate varies at all timescales such that long-term variations in δ¹⁸O_cel and δ²H_cel inevitably include climatological components. It is therefore challenging to resolve the climatic signals from the physiological effects. In dendrochronological studies based on tree-ring width, RCS is used to separate and estimate climatological components in tree-ring width time series (Esper et al., 2002; Grudd et al., 2002; Büntgen et al., 2005). However, it is difficult to create a regional standardized δ¹⁸O_cel curve like the RCS for the samples analyzed in this study because the physiological effects on δ¹⁸O_cel are not solely an age trend and also reflect past human disturbances to the trees such as logging activity (see Sect. S1; Totman, 1989).

3.4 Classification of δ¹⁸O and δ²H variations into climatological and physiological components

To extract the climatological component of the variations in the tree-ring cellulose δ¹⁸O data, we modified the model of cellulose δ¹⁸O and δ²H in Eqs. (3) and (4) into climatological and physiological components. Given there are four variables (δ¹⁸O_rain, δ²H_rain, h, and f) in Eqs. (3) and (4), we first define their variations as follows:

$$\begin{array}{}\text{(5)}& {\displaystyle }{\mathit{\delta }}^{\mathrm{18}}{\mathrm{O}}_{\mathrm{rain}}={\mathit{\delta }}^{\mathrm{18}}{\mathrm{O}}_{\mathrm{rain}\left(\mathrm{0}\right)}+\mathrm{\Delta }{\mathit{\delta }}^{\mathrm{18}}{\mathrm{O}}_{\mathrm{rain}},\text{(6)}& {\displaystyle }{\mathit{\delta }}^{\mathrm{2}}{\mathrm{H}}_{\mathrm{rain}}={\mathit{\delta }}^{\mathrm{2}}{\mathrm{H}}_{\mathrm{rain}\left(\mathrm{0}\right)}+\mathrm{\Delta }{\mathit{\delta }}^{\mathrm{2}}{\mathrm{H}}_{\mathrm{rain}},\text{(7)}& {\displaystyle }h=h_{\left(\mathrm{0}\right)}+\mathrm{\Delta }h,\text{(8)}& {\displaystyle }f=f_{\left(\mathrm{0}\right)}+\mathrm{\Delta }f,\end{array}$$

where δ¹⁸O_rain(0), δ²H_rain(0), h₍₀₎, and f₍₀₎ are δ¹⁸O_rain, δ²H_rain, h, and f in a fixed year (0), respectively, and Δδ¹⁸O_rain, Δδ²H_rain, Δh, and Δf are deviations in δ¹⁸O_rain, δ²H_rain, h, and f from the fixed year (0) to an arbitrary year, respectively. By substituting Eqs. (5)–(8) into Eqs. (3)–(4) and neglecting the second-order minor terms (ΔfΔh, ΔfΔδ¹⁸O_rain, and ΔfΔδ²H_rain), Eqs. (3) and (4) can be rewritten as follows:

$$\begin{array}{}\text{(9)}& {\displaystyle }\begin{array}{rl}{\mathit{\delta }}^{\mathrm{18}}{\mathrm{O}}_{\mathrm{cel}}& =f_{\left(\mathrm{0}\right)}\left({\mathit{\delta }}^{\mathrm{18}}{\mathrm{O}}_{\mathrm{rain}\left(\mathrm{0}\right)}+{\mathit{\epsilon }}_{\mathrm{ho}}\right)\\ & +\left(\mathrm{1}-f_{\left(\mathrm{0}\right)}\right)[{\mathit{\delta }}^{\mathrm{18}}{\mathrm{O}}_{\mathrm{rain}\left(\mathrm{0}\right)}+\left({\mathit{\epsilon }}_{\mathrm{eo}}+{\mathit{\epsilon }}_{\mathrm{ko}}\right)\left(\mathrm{1}-h_{\left(\mathrm{0}\right)}\right)\\ & +{\mathit{\epsilon }}_{\mathrm{ao}}]\\ & +\left[\mathrm{\Delta }{\mathit{\delta }}^{\mathrm{18}}{\mathrm{O}}_{\mathrm{rain}}-\mathrm{\Delta }h\left({\mathit{\epsilon }}_{\mathrm{eo}}+{\mathit{\epsilon }}_{\mathrm{ko}}\right)\left(\mathrm{1}-f_{\left(\mathrm{0}\right)}\right)\right]\\ & +\mathrm{\Delta }f\left[{\mathit{\epsilon }}_{\mathrm{ho}}-{\mathit{\epsilon }}_{\mathrm{ao}}-\left({\mathit{\epsilon }}_{\mathrm{eo}}+{\mathit{\epsilon }}_{\mathrm{ko}}\right)\left(\mathrm{1}-h_{\left(\mathrm{0}\right)}\right)\right],\end{array}\text{(10)}& {\displaystyle }\begin{array}{rl}{\mathit{\delta }}^{\mathrm{2}}{\mathrm{H}}_{\mathrm{cel}}& =f_{\left(\mathrm{0}\right)}\left({\mathit{\delta }}^{\mathrm{2}}{\mathrm{H}}_{\mathrm{rain}\left(\mathrm{0}\right)}+{\mathit{\epsilon }}_{\mathrm{hh}}\right)\\ & +\left(\mathrm{1}-f_{\left(\mathrm{0}\right)}\right)[{\mathit{\delta }}^{\mathrm{2}}{\mathrm{H}}_{\mathrm{rain}\left(\mathrm{0}\right)}+\left({\mathit{\epsilon }}_{\mathrm{eh}}+{\mathit{\epsilon }}_{\mathrm{kh}}\right)\left(\mathrm{1}-h_{\left(\mathrm{0}\right)}\right)\\ & +{\mathit{\epsilon }}_{\mathrm{ah}}]\\ & +\left[\mathrm{\Delta }{\mathit{\delta }}^{\mathrm{2}}{\mathrm{H}}_{\mathrm{rain}}-\mathrm{\Delta }h\left({\mathit{\epsilon }}_{\mathrm{eh}}+{\mathit{\epsilon }}_{\mathrm{kh}}\right)\left(\mathrm{1}-f_{\left(\mathrm{0}\right)}\right)\right]\\ & +\mathrm{\Delta }f\left[{\mathit{\epsilon }}_{\mathrm{hh}}-{\mathit{\epsilon }}_{\mathrm{ah}}-\left({\mathit{\epsilon }}_{\mathrm{eh}}+{\mathit{\epsilon }}_{\mathrm{kh}}\right)\left(\mathrm{1}-h_{\left(\mathrm{0}\right)}\right)\right].\end{array}\end{array}$$

We can now introduce new equations for the climatological and physiological components in the tree-ring cellulose δ¹⁸O and δ²H time series, as follows:

$$\begin{array}{}\text{(11)}& {\displaystyle }\mathrm{\Delta }{\mathit{\delta }}^{\mathrm{18}}{\mathrm{O}}_{\mathrm{cel}\left(\mathrm{climate}\right)}=\mathrm{\Delta }{\mathit{\delta }}^{\mathrm{18}}{\mathrm{O}}_{\mathrm{rain}}-\mathrm{\Delta }h\left({\mathit{\epsilon }}_{\mathrm{eo}}+{\mathit{\epsilon }}_{\mathrm{ko}}\right)\left(\mathrm{1}-f_{\left(\mathrm{0}\right)}\right),\text{(12)}& {\displaystyle }\mathrm{\Delta }{\mathit{\delta }}^{\mathrm{2}}{\mathrm{H}}_{\mathrm{cel}\left(\mathrm{climate}\right)}=\mathrm{\Delta }{\mathit{\delta }}^{\mathrm{2}}{\mathrm{H}}_{\mathrm{rain}}-\mathrm{\Delta }h\left({\mathit{\epsilon }}_{\mathrm{eh}}+{\mathit{\epsilon }}_{\mathrm{kh}}\right)\left(\mathrm{1}-f_{\left(\mathrm{0}\right)}\right),\text{(13)}& {\displaystyle }\mathrm{\Delta }{\mathit{\delta }}^{\mathrm{18}}{\mathrm{O}}_{\mathrm{cel}\left(\mathrm{physiol}\right)}=\mathrm{\Delta }f\left[{\mathit{\epsilon }}_{\mathrm{ho}}-{\mathit{\epsilon }}_{\mathrm{ao}}-\left({\mathit{\epsilon }}_{\mathrm{eo}}+{\mathit{\epsilon }}_{\mathrm{ko}}\right)\left(\mathrm{1}-h_{\left(\mathrm{0}\right)}\right)\right],\text{(14)}& {\displaystyle }\mathrm{\Delta }{\mathit{\delta }}^{\mathrm{2}}{\mathrm{H}}_{\mathrm{cel}\left(\mathrm{physiol}\right)}=\mathrm{\Delta }f\left[{\mathit{\epsilon }}_{\mathrm{hh}}-{\mathit{\epsilon }}_{\mathrm{ah}}-\left({\mathit{\epsilon }}_{\mathrm{eh}}+{\mathit{\epsilon }}_{\mathrm{kh}}\right)\left(\mathrm{1}-h_{\left(\mathrm{0}\right)}\right)\right],\end{array}$$

where Δδ¹⁸O_cel(climate), Δδ¹⁸O_cel(physiol), Δδ²H_cel(climate), and Δδ²H_cel(physiol) are variations in the tree-ring cellulose δ¹⁸O and δ²H from the fixed year (0) with respect to an arbitrary year due to climatological and physiological factors, respectively. We can then reformulate δ¹⁸O_cel and δ²H_cel as the sum of climatological and physiological components, as follows:

$$\begin{array}{}\text{(15)}& {\displaystyle }{\mathit{\delta }}^{\mathrm{18}}{\mathrm{O}}_{\mathrm{cel}}={\mathit{\delta }}^{\mathrm{18}}{\mathrm{O}}_{\mathrm{cel}\left(\mathrm{0}\right)}+\mathrm{\Delta }{\mathit{\delta }}^{\mathrm{18}}{\mathrm{O}}_{\mathrm{cel}\left(\mathrm{climate}\right)}+\mathrm{\Delta }{\mathit{\delta }}^{\mathrm{18}}{\mathrm{O}}_{\mathrm{cel}\left(\mathrm{physiol}\right)},\text{(16)}& {\displaystyle }{\mathit{\delta }}^{\mathrm{2}}{\mathrm{H}}_{\mathrm{cel}}={\mathit{\delta }}^{\mathrm{2}}{\mathrm{H}}_{\mathrm{cel}\left(\mathrm{0}\right)}+\mathrm{\Delta }{\mathit{\delta }}^{\mathrm{2}}{\mathrm{H}}_{\mathrm{cel}\left(\mathrm{climate}\right)}+\mathrm{\Delta }{\mathit{\delta }}^{\mathrm{2}}{\mathrm{H}}_{\mathrm{cel}\left(\mathrm{physiol}\right)},\end{array}$$

where δ¹⁸O_cel(0) and δ²H_cel(0) are δ¹⁸O_cel and δ²H_cel at the fixed year (0), respectively.

3.5 A method to extract the climatological component from cellulose δ¹⁸O

Here we propose a new method to calculate the climatological component in variations of tree-ring cellulose δ¹⁸O (Δδ¹⁸O_cel(climate)) by solving simultaneous equations consisting of Eqs. (15)–(16), with two additional equations based on the relationship between Δδ¹⁸O_cel(climate) and Δδ²H_cel(climate) and between Δδ¹⁸O_cel(physiol) and Δδ²H_cel(physiol) (i.e., Eqs. 17–18). This is based on the theoretical and observational understanding that tree-ring cellulose δ¹⁸O and δ²H data correlate positively and negatively due to climatological and physiological factors, respectively. (Note that we restrict the physiological effects to the change in the rate of post-photosynthesis isotope exchange with xylem water here. If there are other types of ecophysiological effects generating a positive relationship between δ¹⁸O_cel and δ²H_cel, such as root deepening or growth season shift, they are counted as parts of the climatological effects here.)

$$\begin{array}{}\text{(17)}& {\displaystyle }\mathrm{\Delta }{\mathit{\delta }}^{\mathrm{2}}{\mathrm{H}}_{\mathrm{cel}\left(\mathrm{climate}\right)}=A\times \mathrm{\Delta }{\mathit{\delta }}^{\mathrm{18}}{\mathrm{O}}_{\mathrm{cel}\left(\mathrm{climate}\right)},\text{(18)}& {\displaystyle }\mathrm{\Delta }{\mathit{\delta }}^{\mathrm{2}}{\mathrm{H}}_{\mathrm{cel}\left(\mathrm{physiol}\right)}=-B\times \mathrm{\Delta }{\mathit{\delta }}^{\mathrm{18}}{\mathrm{O}}_{\mathrm{cel}\left(\mathrm{physiol}\right)},\end{array}$$

where A and B are positive proportional coefficients, as shown in Eqs. (19)–(20) and defined by Eqs. (11)–(14).

$$\begin{array}{}\text{(19)}& {\displaystyle }A={\displaystyle \frac{\mathrm{\Delta }{\mathit{\delta }}^{\mathrm{2}}{\mathrm{H}}_{\mathrm{rain}}-\mathrm{\Delta }h\left({\mathit{\epsilon }}_{\mathrm{eh}}+{\mathit{\epsilon }}_{\mathrm{kh}}\right)\left(\mathrm{1}-f_{\left(\mathrm{0}\right)}\right)}{\mathrm{\Delta }{\mathit{\delta }}^{\mathrm{18}}{\mathrm{O}}_{\mathrm{rain}}-\mathrm{\Delta }h\left({\mathit{\epsilon }}_{\mathrm{eo}}+{\mathit{\epsilon }}_{\mathrm{ko}}\right)\left(\mathrm{1}-f_{\left(\mathrm{0}\right)}\right)}},\text{(20)}& {\displaystyle }B=-{\displaystyle \frac{{\mathit{\epsilon }}_{\mathrm{hh}}-{\mathit{\epsilon }}_{\mathrm{ah}}-\left({\mathit{\epsilon }}_{\mathrm{eh}}+{\mathit{\epsilon }}_{\mathrm{kh}}\right)\left(\mathrm{1}-h_{\left(\mathrm{0}\right)}\right)}{{\mathit{\epsilon }}_{\mathrm{ho}}-{\mathit{\epsilon }}_{\mathrm{ao}}-\left({\mathit{\epsilon }}_{\mathrm{eo}}+{\mathit{\epsilon }}_{\mathrm{ko}}\right)\left(\mathrm{1}-h_{\left(\mathrm{0}\right)}\right)}}\end{array}$$

If A and B are constant, we can solve the simultaneous Eqs. (15)–(18) in order to cancel out the physiological component (Δδ¹⁸O_cel(physiol)) and extract the climatological component (Δδ¹⁸O_cel(climate)), as follows:

$$\begin{array}{}\text{(21)}& \begin{array}{rl}\mathrm{\Delta }{\mathit{\delta }}^{\mathrm{18}}{\mathrm{O}}_{\mathrm{cel}\left(\mathrm{climate}\right)}& ={\displaystyle \frac{{\mathit{\delta }}^{\mathrm{2}}{\mathrm{H}}_{\mathrm{cel}}+B\times {\mathit{\delta }}^{\mathrm{18}}{\mathrm{O}}_{\mathrm{cel}}}{A+B}}\\ & -{\displaystyle \frac{{\mathit{\delta }}^{\mathrm{2}}{\mathrm{H}}_{\mathrm{cel}\left(\mathrm{0}\right)}+B\times {\mathit{\delta }}^{\mathrm{18}}{\mathrm{O}}_{\mathrm{cel}\left(\mathrm{0}\right)}}{A+B}}.\end{array}\end{array}$$

In fact, A might not be constant because there are three variables (Δδ¹⁸O_rain, Δδ²H_rain, and Δh) in Eq. (19). Δδ¹⁸O_rain and Δδ²H_rain may change somewhat independently from each other over a wide spatiotemporal range, and the relationship between Δδ¹⁸O_rain (Δδ²H_rain) and Δh may not be simple in Eq. (19). However, the significant positive correlations in the short-periodicity variations between δ¹⁸O_cel and δ²H_cel (Figs. 4c, S3c, S4c, and S5c) suggest there may be an empirical constant value for A in a restricted study area such as central Japan. In contrast to A, B may be nearly constant because there are no variables in Eq. (20).

Although the assumption that A and B are constant might not be valid, this assumption is needed to explicitly calculate Δδ¹⁸O_cel(climate) using Eq. (21). Hence, we tentatively assumed that A and B are constant and calculated Δδ¹⁸O_cel(climate) over the past 2600 years using Eq. (21). We then verify this by comparison with numerous local, regional, and global meteorological, historical, and paleoclimatological records of past summer climate over various timescales in order to judge whether the simplest assumption, that A and B in Eq. (21) are constant, is practically useful or not for paleoclimatological studies.

3.6 Method to determine the proportional coefficients A and B

To utilize Eq. (21), we need to determine the proportional coefficients A and B in Eqs. (17)–(20). In principle, there are two ways to determine A and B: a theoretical approach based on Eqs. (19)–(20) and an empirical approach based on Eqs. (17)–(18).

We first consider the feasibility of the theoretical approach. It is not easy to determine A using Eq. (19) because there are three variables (Δδ¹⁸O_rain, Δδ²H_rain, and Δh). If the rainwater isotope ratios do not change (both Δδ¹⁸O_rain and Δδ²H_rain=0), then A is equal to $({\mathit{\epsilon }}_{\mathrm{eh}}+{\mathit{\epsilon }}_{\mathrm{kh}})/({\mathit{\epsilon }}_{\mathrm{eo}}+{\mathit{\epsilon }}_{\mathrm{ko}})$, which is $(\mathrm{80}+\mathrm{25})/(\mathrm{9}+\mathrm{29})=\mathrm{2.76}$ (Roden and Ehleringer, 2000). However, if relative humidity does not change (Δh=0), A=Δδ²H_rain∕Δδ¹⁸O_rain, which is equal to 8 if the meteoric waterline is followed (Dansgaard, 1964). Given the wide range of potential A values from 2.76 to 8, we cannot easily theoretically define A. On the other hand, B may be easier to determine theoretically because there are no variables in Eq. (20). For example, if the relative humidity h₍₀₎ is 0.5, B=13 because ε_eo, ε_ko, ε_ao, ε_ho, ε_eh, ε_kh, ε_ah, and ε_hh are +9, +29, +27, +27, +80, +25, ca. −150, and +150, respectively (Roden et al., 2000). However, in fact, it is not easy to fix h₍₀₎ because the relative humidity typically shows large diurnal variations, and the timing of δ¹⁸O incorporation into leaf carbohydrates is unknown. Moreover, the ε_ah and ε_hh values of −150 and +150 are just approximations. For example, while Yakir and DeNiro (1990) obtained values of −171 and +158 for ε_ah and ε_hh, respectively, Estep and Hoering (1981) obtained values of −100 to −120 for ε_ah, and Luo and Sternberg (1992) reported values of +144 to +166 for ε_hh.

Therefore, we used the empirical approach to estimate A and B. The A value in Eq. (17) can be estimated from the relationship between δ¹⁸O_cel and δ²H_cel in the short-periodicity variations because they are positively correlated due to the climate variations shown in Figs. 4c, S3c, S4c, and S5c. In the case of the B value in Eq. (18), the situation is more complex. Although there are apparent negative correlations between δ¹⁸O_cel and δ²H_cel in the long-periodicity variations (Figs. 4b and S3b), these are also affected by long-term climate signals such that it is difficult to resolve the physiological component. Here we propose a practical method to determine the B value. After fixing A, we first set various B values in order to calculate the temporal variations in the climatological component of the tree-ring cellulose δ¹⁸O data (Δδ¹⁸O_cel(climate)) for all 67 tree samples by substituting individual δ¹⁸O_cel and δ²H_cel time series in Fig. 3a and c into Eq. (21). We then combine the Δδ¹⁸O_cel(climate) time series of all 67 trees calculated from each B value using the method described below (Sect. 3.7). Finally, we compare the overall trend of the combined time series of Δδ¹⁸O_cel(climate) data with that of a simple average of all 67 raw δ¹⁸O_cel time series in Fig. 3a in order to find the B value that produced the best match between the two time series. This procedure assumes that, although individual trees possess different age trends and level offsets, averaging of all data from all trees covering all periods and all locations in this study may cancel out these effects and allow climate variations to be discerned, at least in terms of “the overall trend”.

3.7 Method to combine individual tree-ring time series with large level offsets

To reconstruct multi-millennial variations in the climatological component of the tree-ring cellulose δ¹⁸O data (Δδ¹⁸O_cel(climate)), we must combine individual time series from different trees with variable level offsets due to different sample locations. As such, we cannot simply average all data for individual trees because this produces steps in the composite record at both ends of the time series of individual trees. Numerous procedures have been proposed to combine tree-ring time series (e.g., Hangartner et al., 2012); here we propose a new iterative calculation method (Fig. 5).

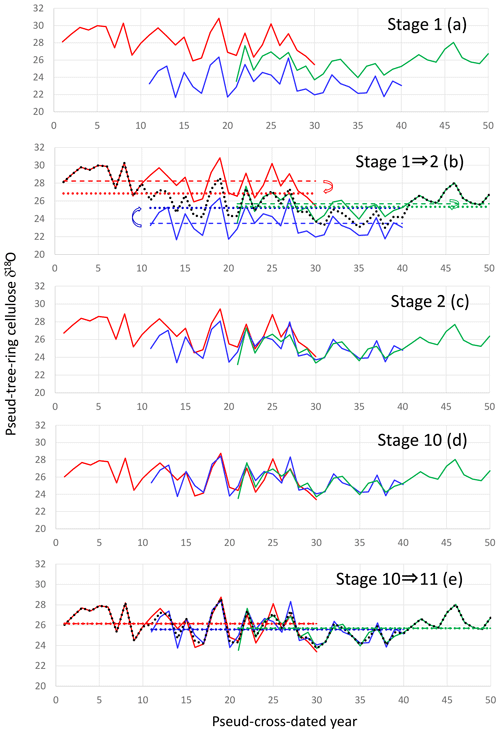
Figure 5 The iterative calculation method used to smoothly combine many individual tree-ring time series with large level offsets. (a) Pseudo-cross-dated tree-ring cellulose δ¹⁸O time series (Stage 1). (b) Averaging of all time series in Stage 1 (black dotted line) and offsetting individual time series in Stage 1 to the position where the average of the individual time series (colored dashed lines) becomes equal to the average of the black dotted line during the corresponding period (colored dotted lines) by retaining the original temporal patterns. (c) Result of offsetting of individual time series from Stage 1 (Stage 2). (d) Result of nine iterative calculations from Stage 1 (Stage 10). (e) Procedure from Stages 10 to 11. We obtain a unique combined time series when the dotted lines become equal to the dashed lines within a finite number of iterations.

Firstly, we simply average all the individual time series to make a preliminary combined time series. Secondly, we offset each individual time series up or down, retaining their original patterns of temporal variations, to the position where the temporal average of the individual time series becomes equal to that of the preliminary combined time series for the corresponding period of the individual tree. Thirdly, we average all the offset individual time series to make a refined combined time series. We iterate this procedure until the temporal average of the individual time series becomes equal to that of the combined time series for the corresponding period, without any further offsetting of the individual time series. If you start from the same original dataset on δ¹⁸O variations of stem segments, the pattern of relative variation in the final combined δ¹⁸O time series is mathematically unique although its absolute value has no meaning. That is, there is no room for artifacts to influence resultant time series. This method assumes that the tree-ring absolute isotope ratios of individual trees are not important because they depend on the sample locations but that the temporal variations are well correlated amongst different trees due to a common regional climate signal.

3.8 Procedure to calculate the climatological component in tree-ring δ¹⁸O (Δδ¹⁸O_cel(climate)) data

Figure 6a shows how the combined time series for Δδ¹⁸O_cel(climate) is constructed. Firstly, we determine A from the short-periodicity variations between δ¹⁸O_cel and δ²H_cel in individual trees. Secondly, we use δ¹⁸O_cel and δ²H_cel to calculate Δδ¹⁸O_cel(climate) for individual trees using various B values in Eq. (21). Thirdly, we combine the Δδ¹⁸O_cel(climate) time series of all trees for each case of different B values. Fourthly, we select the best B value by comparison of the overall trends in the combined Δδ¹⁸O_cel(climate) and average δ¹⁸O_cel data. Finally, we reintegrate the long-periodicity variations in Δδ¹⁸O_cel(climate) calculated using the best B value and short-periodicity variations in δ¹⁸O_cel for all individual trees at an adequate threshold periodicity and combine all individual data again because the physiological factors do not appear to affect the short-periodicity δ¹⁸O_cel variation so that we should keep the original δ¹⁸O_cel variations in the high-frequency domain. In this procedure (Fig. 6a), the iterative calculation used to combine many tree-ring time series in the third step is the most time-consuming because various B values are tested.

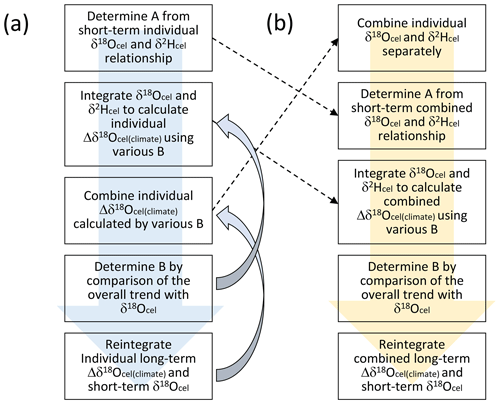
Figure 6 The two procedures used to establish the smoothly combined climatological component of the variations in the tree-ring cellulose δ¹⁸O data (Δδ¹⁸O_cel(climate)). Although the order of procedures is different in panels (a) and (b), the results are the same if we assume unique A and B values for all individual trees.

Although A can be determined independently for each tree, we can only obtain one B value for all the trees. In a practical sense, it is not meaningful to determine A separately for each tree because all the trees were collected within central Japan (Fig. 1). If we assume that A and B are unique for all trees in this study, we can simplify the procedure as shown in Fig. 6b to reduce the time required for the iterative calculation. Considering that all the calculations used to combine and integrate the time series in Fig. 6 are linear, we can change the order of calculation between combination and integration. In fact, if we use common A and B values, the resultant combined time series for Δδ¹⁸O_cel(climate) does not change when using the two procedures (Fig. 6a and b). In Fig. 6b, we first combine the δ¹⁸O_cel and δ²H_cel time series of all trees in Fig. 3 using the method shown in Fig. 5. Secondly, we determine A by investigating the relationship between short-periodicity variations of δ¹⁸O_cel and δ²H_cel in their combined time series. Thirdly, we integrate the combined δ¹⁸O_cel and δ²H_cel records to show temporal variations in Δδ¹⁸O_cel(climate) using various B values. Fourthly, we select the best B value by comparison of the overall trends of the Δδ¹⁸O_cel(climate) time series and average δ¹⁸O_cel. Finally, we reintegrate the long-periodicity variations in Δδ¹⁸O_cel(climate) and short-periodicity variations in combined δ¹⁸O_cel at an adequate threshold periodicity to keep the original δ¹⁸O_cel variation in the high-frequency domain.

3.9 Determination of the climatological and physiological proportional coefficients (A and B)

We combined all the time series for δ¹⁸O_cel and δ²H_cel shown in Fig. 3 using the method illustrated in Fig. 5. The final combined δ¹⁸O_cel and δ²H_cel time series after 1000 iterations are shown in Fig. 7. The long-term variations in the combined δ¹⁸O_cel and δ²H_cel time series obviously reflect the accumulated age trends, in which the δ¹⁸O_cel and δ²H_cel tend to decrease and increase over a long timescale, respectively.

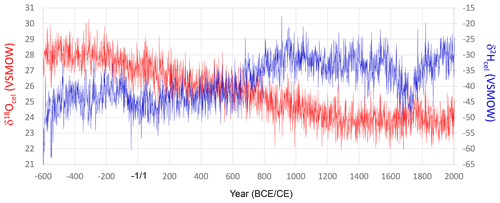
Figure 7 Smoothly combined individual time series of δ¹⁸O_cel and δ²H_cel from Fig. 3a and c using the iterative calculation method shown in Fig. 5. The combined time series is after 1000 iterations (Stage 1000).

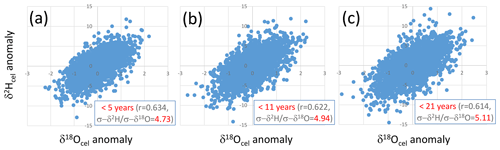
Figure 8 Relationships between short-periodicity components of δ¹⁸O_cel and δ²H_cel that are (a) < 5 years, (b) < 11 years, and (c) < 21 years, defined as the anomalies from the 5-, 11-, and 21-year running means of the combined δ¹⁸O_cel and δ²H_cel time series in Fig. 7, respectively.

We found that the climatological proportional coefficient A in Eq. (17) can be set to 5 because there are positive correlations in the short-periodicity variations of the combined δ²H_cel and δ¹⁸O_cel records with a slope of ca. 5 (Fig. 8), irrespective of the threshold year for extracting the short-periodicity variations (i.e., 5, 11, or 21 years). A value of 5 is within the theoretical range of A of 2.76 to 8 obtained from Eq. (19). We used the δ²H_cel data directly for the calculation of A, although the amplitude of variations in δ²H_cel is reduced to 70 % of that of the original cellulose such that a value of 5 is equivalent to about 7 in the theoretical range.

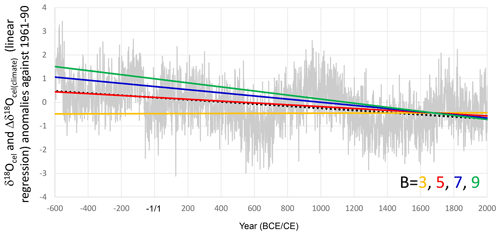
Figure 9 Linear regressions of Δδ¹⁸O_cel(climate) calculated using 3 (orange line), 5 (red line), 7 (blue line), and 9 (green line) as B values, with A = 5 in Eq. (21), and the simple averages of all tree-ring cellulose δ¹⁸O data in Fig. 3a (gray line) with a linear regression (black dotted line).

To determine the most appropriate value for the physiological proportional coefficient B in Eq. (18), we integrated the combined δ¹⁸O_cel and δ²H_cel time series in Fig. 9 using Eq. (21) in order to calculate Δδ¹⁸O_cel(climate) with B values of 3, 5, 7, and 9, as well as an A value 5. We then examined the overall trend in Δδ¹⁸O_cel(climate) and found that it became equal to the overall trend of the average δ¹⁸O_cel (Fig. 3a) when B = 5.4 (Fig. 9). Given the 70 % amplitude reduction of Δδ²H_cel, 5.4 is equivalent to 7.7 from the theoretical estimation. If we assume that ε_eo, ε_ko, ε_ao, ε_ho, ε_eh, ε_kh, ε_ah, and ε_hh are +9, +29, +27, +27, +80, +25, −150, and +150, respectively, then B = 7.7 means that h₍₀₎ is 0.25 in Eq. (20). Given that 0.25 is too low for the relative humidity in central Japan, the values of −150 and +150 for ε_ah and ε_hh, respectively, may be overestimated. However, because the overall trend of the integrated Δδ¹⁸O_cel(climate) using B = 5.4 is equal to that of the average of raw δ¹⁸O_cel values, we use this value of B hereafter.

3.10 Calculation of temporal variations in the climatological component (Δδ¹⁸O_cel(climate))

We calculated the temporal variation in the climatological component (Δδ¹⁸O_cel(climate)) of tree-ring cellulose δ¹⁸O (Fig. 10a) by using A = 5 and B = 5.4, as well as the smoothly combined δ¹⁸O_cel and δ²H_cel time series in Fig. 7 and Eq. (21). We used the temporal average of (δ²H_cel+Bδ¹⁸O${}_{\mathrm{cel}})/(A+B)$ during the 30 years from 1961 to 1990 for (δ²H_cel(0)+Bδ¹⁸O${}_{\mathrm{cel}\left(\mathrm{0}\right)})/(A+B)$ in Eq. (21) so as to make Δδ¹⁸O_cel(climate) the climatological variation in δ¹⁸O_cel from the period between 1961 and 1990.

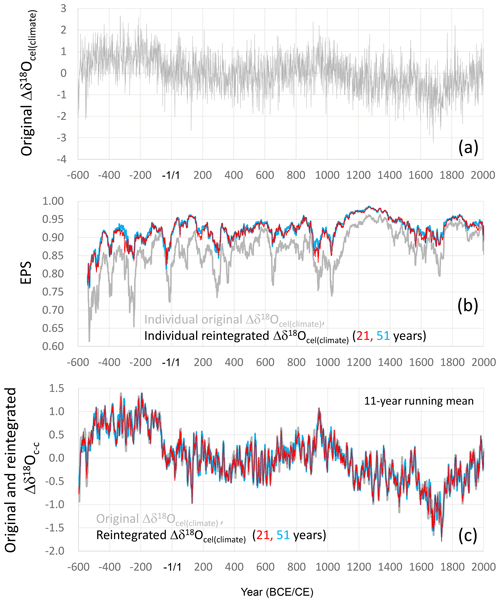
Figure 10 Calculation of the climatological component of the tree-ring cellulose δ¹⁸O data (Δδ¹⁸O_cel(climate)). (a) Time series of Δδ¹⁸O_cel(climate) calculated using Eq. (21), with A = 5.0 and B = 5.4, and the smoothly combined time series of δ¹⁸O_cel and δ²H_cel in Fig. 7. (b) EPS values for the individually calculated time series of Δδ¹⁸O_cel(climate) (gray line) and the individually calculated and reintegrated time series between the long-periodicity component of Δδ¹⁸O_cel(climate) and short-periodicity component of δ¹⁸O_cel, with 21 years (red line) and 51 years (blue line) as the thresholds between long and short periodicity. (c) 11-year running mean of the time series of Δδ¹⁸O_cel(climate) in Fig. 10a (gray line) and those of the reintegrated time series between the long-periodicity component in Δδ¹⁸O_cel(climate) in Fig. 10a and short-periodicity component in the combined δ¹⁸O_cel in Fig. 7, with 21 years (red line) and 51 years (blue line) as the threshold between long and short periodicity. EPS values in panel (b) were calculated for a total period of 51 years, including 25 years before and after the year shown.

The Δδ¹⁸O_cel(climate) variation shown in Fig. 10a was influenced by the δ²H_cel time series, not only for the long-periodicity variation, but also for the short-periodicity variation for which it is not necessary to integrate δ²H_cel. In fact, when we calculated EPS values for all individual Δδ¹⁸O_cel(climate) time series from Eq. (21), we found that the EPS values are significantly lower (Fig. 10b), reflecting the low EPS value of the original δ²H_cel time series (Fig. 3d). The purpose of introducing the δ²H_cel signal into the δ¹⁸O_cel time series is to remove the physiological effects from the long-periodicity variations in δ¹⁸O_cel. Therefore, at two threshold periodicities (21 and 51 years), we tentatively separated the long-periodicity component (21- and 51-year running means) from the integrated Δδ¹⁸O_cel(climate) time series in Fig. 10a and short-periodicity component (deviations from 21- and 51-year running means) from the original combined δ¹⁸O_cel in Fig. 7, and we reintegrated these into a new time series for Δδ¹⁸O_cel(climate) to remove the influence of the δ²H_cel data from the short-periodicity component. We also applied this reintegration procedure between the long-periodicity (Δδ¹⁸O_cel(climate)) and short-periodicity (δ¹⁸O_cel) components to the data for individual trees and calculated the EPS values for the reintegrated Δδ¹⁸O_cel(climate) datasets (Fig. 10b). The resultant EPS values were > 0.85 and much higher than the original Δδ¹⁸O_cel(climate) for almost all periods during last 2500 years when either 21 or 51 years was used as the threshold.

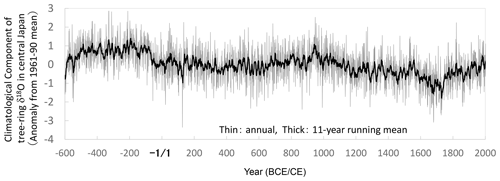
Figure 11 The final combined time series of the climatological component in variations of tree-ring cellulose δ¹⁸O data (Δδ¹⁸O_cel(climate)). This is the reintegrated time series between the long-periodicity component in the original Δδ¹⁸O_cel(climate) data in Fig. 10a and the short-periodicity component in the combined δ¹⁸O_cel data in Fig. 7, with 21 years as the threshold between long and short periodicity.

However, this reintegration procedure may recover potential physiological effects with intermediate periodicities of less than 21 and 51 years. Hence, we compared the long-term variations (periodicity > 11 years) of the two reintegrated Δδ¹⁸O_cel(climate) time series using 21 and 51 years as the thresholds and the original Δδ¹⁸O_cel(climate) time series (Fig. 10a) in Fig. 10c to investigate whether there are significant differences. Each of the three time series shown in Fig. 10c almost coincide over all timescales, indicating there are no significant physiological effects with a periodicity between 11 and 51 years. However, we used 21 years as the threshold for the reintegration of the long- and short-periodicity components in order to robustly remove the influence of physiological effects. It does not result in a lower-quality reintegrated Δδ¹⁸O_cel(climate) record, given the nearly equal EPS values using the 21- and 51-year thresholds in Fig. 10b. We utilized the reintegrated Δδ¹⁸O_cel(climate) time series between the long-periodicity (> 21 years) domain of Δδ¹⁸O_cel(climate) in Fig. 10a and short-periodicity (< 21 years) domain of δ¹⁸O_cel in Fig. 7 as the final time series of the climatological component in the tree-ring cellulose δ¹⁸O data (Fig. 11). (You can see the effects of the integration and reintegration procedures more directly in Fig. S7.)

In contrast to the combined δ²H_cel record (Fig. 7), the multi-centennial variation in the combined δ¹⁸O_cel record (Fig. 7) does not appear to be very similar to that of the climatological component Δδ¹⁸O_cel(climate) (Fig. 11). This is partly because there is an apparent age trend in the combined δ¹⁸O_cel record, which overlaps the multi-millennial climatological decrease in Fig. 9. This means the multi-centennial variations are ambiguous in the combined δ¹⁸O_cel record (Fig. 7). However, there may be an anthropogenic explanation for this, whereby in wetter and cooler periods, the number of trees in Japanese forests might have decreased due to logging for fuel. Rapid tree growth in the resultant more open and lighter forest would have increased δ¹⁸O_cel and decreased δ²H_cel values due to physiological effects (see Sect. S1). The wetter and cooler climate may have also lowered δ¹⁸O and δ²H in leaf water. The combined effects of climate variations and anthropogenic factors on Japanese forests might have reduced and enhanced the multi-centennial variations in δ¹⁸O_cel and δ²H_cel, respectively (Fig. 7). However, we can robustly extract the climatological component Δδ¹⁸O_cel(climate) independently of the local forest history by integrating δ¹⁸O_cel and δ²H_cel data. This is the most important paleoclimatological innovation of our study.

3.11 Comparison of Δδ¹⁸O_cel(climate) with other summer climate records

In dendroclimatological studies focused on interannual variability, statistical methods to calibrate and verify the relationship between tree-ring data and instrumental meteorological observations have been well established. However, there is no commonly accepted statistical method to validate the reliability of long-periodicity (i.e., centennial or millennial) climate reconstructions. In the case of low-frequency data recovered from speleothems, ice cores, and sediments, climate reconstructions are typically not based on correlations with meteorological observations. These reconstructions are verified by different methods, such as mechanical models based on the relationship between oxygen isotope ratios and environmental factors, empirical knowledge of the relationship between pollen assemblages and climate, and experimental studies between biomarker compositions and water temperature. The reconstruction of Δδ¹⁸O_cel(climate) variations is principally based on the mechanical model developed in Eqs. (3)–(21), but it is necessary to validate our results by comparison with other past summer climate records.

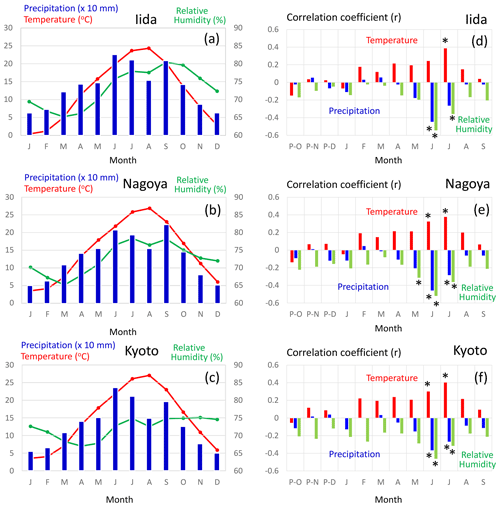
Figure 12 (a–c) Average values of the monthly mean temperature (red), precipitation (blue), and mean relative humidity (green) from 1901 to 2005 CE. (d–f) Correlation coefficients of variations between Δδ¹⁸O_cel(climate) in Fig. 11 and the monthly mean temperature (red), precipitation (blue), and mean relative humidity (green) from 1901 to 2005 CE. The meteorological data were observed at Iida (a, d), Nagoya (b, e), and Kyoto (c, f) (see Figs. 1 and 13b) and recorded in the database of the Japan Meteorological Agency. Asterisks in panels (d), (e), and (f) indicate statistical significance at the > 99 % level (p < 0.01).

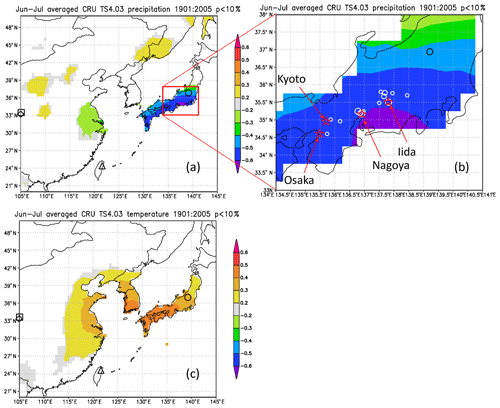
Figure 13 Maps of the spatial correlation (p < 10 %) of Δδ¹⁸O_cel(climate) in Fig. 11 with (a–b) June–July precipitation and (c) June–July mean temperature for 1901–2005 from CRU TS4.03, with sites of reference studies shown as an open square (Huangye Cave), diamond (Wanxiang Cave), triangle (Tsuifong Lake), and circle (Ozegahara peatland). For this analysis, we used Climate Explorer (http://www.knmi.nl/, last access: 21 January 2020) of the Royal Netherlands Meteorological Institute (KNMI) (van Oldenborgh and Burgers, 2005). Sample locations and numbers (Table S1) are shown as white circles (large 10–15; medium 4–9; small 1–3) in panel (b).

Figure 12 shows the sensitivity of Δδ¹⁸O_cel(climate) to local monthly mean temperature, mean relative humidity, and precipitation during the period 1901–2005 at Kyoto, Nagoya, and Iida in central Japan. Δδ¹⁸O_cel(climate) shows significant negative correlations with precipitation and relative humidity and a positive correlation with temperature during summer (Fig. 12d–f) when annual precipitation is at its maximum (Fig. 12a–c), as demonstrated by previous studies of monsoonal Asia (Li et al., 2015; Liu et al., 2017; Pumijumnong et al., 2019; Sano et al., 2012, 2013, 2017; Seo et al., 2019; Xu et al., 2013, 2018, 2019). Spatial correlations of Δδ¹⁸O_cel(climate) with June–July precipitation in East Asia (Fig. 13) indicate that Δδ¹⁸O_cel(climate) in central Japan reflects precipitation in an extended region from the lower reaches of the Yangtze River in China to southern Honshu in Japan, corresponding to the baiu–meiyu front, which is an early summer stagnant rain belt characteristic of the East Asian summer monsoon (Fig. 13a). Δδ¹⁸O_cel(climate) has a significant positive correlation with June–July mean temperature across a wide region of Japan, Korea, and China, suggesting that Δδ¹⁸O_cel(climate) may be a good proxy for the East Asian summer monsoon (Fig. 13c).

The negative correlations of Δδ¹⁸O_cel(climate) with relative humidity and precipitation can be explained by the direct negative relationship between Δδ¹⁸O_cel(climate) and relative humidity in Eq. (11) as well as the amount effect, whereby δ¹⁸O_rain becomes lower when precipitation increases (Dansgaard, 1964; Araguás-Araguás et al., 1998). The highest correlation (< 0.6) area of June–July precipitation is located just to the south of the sample sites (Fig. 13b). This is because, in the summer season, water vapor usually comes from the south (Pacific Ocean) to the sample sites and δ¹⁸O_rain becomes lower when heavy rainfall occurs just before the arrival of the air mass carrying the water vapor. The positive correlation between Δδ¹⁸O_cel(climate) and temperature must be caused by the meteorologically reverse relationship between summer precipitation and temperature in humid monsoonal Asia, including Japan. In fact, the center of the highest correlation area of June–July mean temperature is located slightly to the west of the sample site (Fig. 13c). As such, when the temperature in western Japan is high and characterized by high pressure, the wind blows from the north to the sample site, resulting in dry conditions and low rainfall.

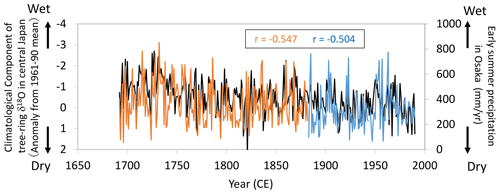
Figure 14 Comparisons of the climatological component of the tree-ring cellulose δ¹⁸O (Δδ¹⁸O_cel(climate)) record in Fig. 11 (black line) with diary-based annual reconstructions (orange line) and meteorological observations (blue line) of early summer precipitation at Osaka (Mizukoshi, 1993). Note that the y axis of Δδ¹⁸O_cel(climate) is inverted to indicate higher precipitation toward the top of the figure.

Given the relationship between Δδ¹⁸O_cel(climate) and modern meteorological observations evident in Figs. 12 and 13, we compared Δδ¹⁸O_cel(climate) in central Japan with long-term historical and paleoclimatological records of summer climate before the 19th century. During the Edo era (1603–1868 CE), people wrote numerous diaries throughout Japan in which daily weather conditions were routinely described. Mizukoshi (1993) compiled many diary weather descriptions for central Japan and reconstructed interannual variations in early summer precipitation for Osaka since 1692 CE (Fig. 14). The diary-based (1692–1882) and instrumentally observed (1883–1990) precipitation reconstructions for Osaka are negatively correlated with Δδ¹⁸O_cel(climate) in central Japan, not only at an interannual timescale, but also at a multi-decadal timescale, indicating that Δδ¹⁸O_cel(climate) records long-term variations in summer climate.

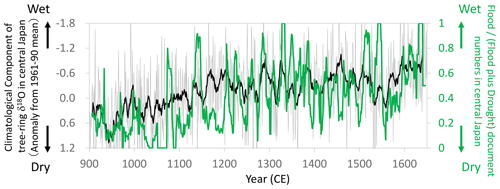
Figure 15 Comparisons of the climatological component of the tree-ring cellulose δ¹⁸O (Δδ¹⁸O_cel(climate)) record in Fig. 11 (gray line: annual; black line: 11-year running mean) with the proportion of flood-related documents (11-year running mean) of total flood- and drought-related documents (11-year running mean) during the summer season (JJA) in central Japan (mostly in and around Kyoto) (Fujiki, 2007). Note that the y axis of Δδ¹⁸O_cel(climate) is inverted to indicate higher precipitation toward the top of the figure.

During the Medieval period from the 11th to 16th centuries in Japan, there were numerous extreme meteorological events (Fujiki, 2007). We used flood- and drought-related disaster records during the summer season (June–August) to construct an index of the “flood disaster ratio”, which is the proportion of flood-related documents to total flood- and drought-related documents. Given that documents are scarcer in the older period, we calculated an 11-year running mean of the flood disaster ratio and compared it with Δδ¹⁸O_cel(climate) (Fig. 15). In the 10th and 11th centuries during the Medieval Climate Anomaly, there were numerous droughts in Japan, corresponding to the highest values of Δδ¹⁸O_cel(climate). After the 11th century, both the documentary records and Δδ¹⁸O_cel(climate) values demonstrate that climate became progressively wetter towards the Edo era in the 17th century.

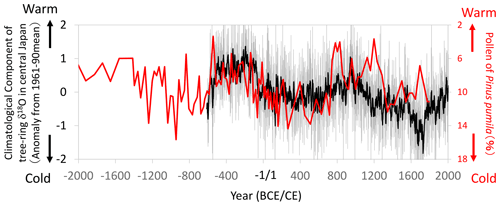
Figure 16 Comparisons of the climatological component of the tree-ring cellulose δ¹⁸O (Δδ¹⁸O_cel(climate)) record in Fig. 11 (gray line: annual; black line: 11-year running mean) with the pollen percentage of a cold-region pine (Pinus pumila) in the Ozegahara peatland (Sakaguchi, 1983, 1989). Location of the pollen record is shown in Fig. 13. Given that P. pumila becomes dominant during cold periods, the y axis for the pollen percentage is inverted to indicate warmer conditions toward the top of the figure.

Although we could not find historical records of extreme climate events prior to the 10th century CE in Japan, Sakaguchi (1983, 1989) reconstructed long-term summer temperature variations using the pollen percentage of a cold-region pine (Pinus pumila) in the Ozegahara peatland of east Japan (Fig. 16). Although the pollen data after the 3rd century CE are not very reliable due to the lower sedimentation rate and human disturbance, the high sedimentation rate before the 2nd century CE enabled us to compare it with Δδ¹⁸O_cel(climate). Both the pollen and Δδ¹⁸O_cel(climate) records show similar variations from the 6th century BCE to 2nd century CE, indicating a warmer and drier climate from the 5th to 2nd century BCE and a cooler and wetter climate after the 1st century BCE (Fig. 16). After the 3rd century CE, both datasets show similar millennial variations, although the temporal resolution of the pollen data is not high.

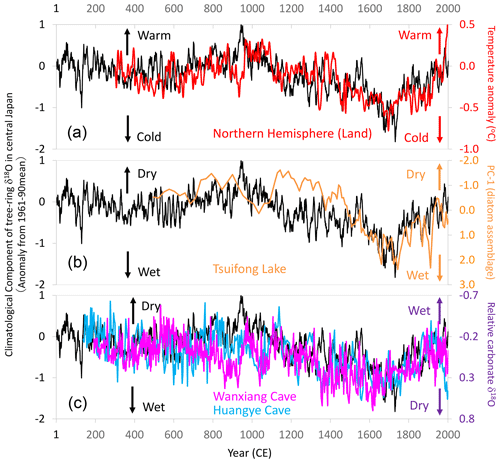
Figure 17 Comparison of centennial- to millennial-scale variations of the climatological component of tree-ring cellulose δ¹⁸O (Δδ¹⁸O_cel(climate)) in central Japan with global and East Asian climate reconstructions. The time series of 11-year running means for Fig. 11 (black line) with (a) air temperature over the Northern Hemisphere defined as NH EIV-land (Mann et al., 2008) (red line), (b) precipitation inferred from a principal component analysis (PC1) of diatom assemblages from Tsuifong Lake in southeastern China (Taiwan) (Wang et al., 2013) (orange line), and (c) precipitation inferred from carbonate δ¹⁸O values of speleothems from Wanxiang (pink line) and Huangye (blue line) caves in northwestern China (Zhang et al., 2008; Tan et al., 2010). Note that the y axes are reversed between the speleothem data and Δδ¹⁸O_cel(climate) in panel (c). Locations of the records in panels (b) and (c) are shown in Fig. 13.

The climatological component of the variations in tree-ring cellulose δ¹⁸O (Δδ¹⁸O_cel(climate)) correlates well with meteorological, historical, and vegetation data over various timescales in central Japan, and it also shows similar long-term patterns as paleoclimatological global temperature and East Asian precipitation data. Figure 17a shows that Δδ¹⁸O_cel(climate) exhibits variations almost identical to air temperature reconstructions for land areas in the Northern Hemisphere (Mann et al., 2008), except for the period of the Medieval Climate Anomaly. Variations in summer precipitation reconstructed from diatom assemblages in lake sediments in Taiwan (Wang et al., 2013) are also similar to the variations in Δδ¹⁸O_cel(climate) in central Japan (Fig. 17b). Two time series of carbonate δ¹⁸O values in speleothems from northwest China (Zhang et al., 2008; Tan et al., 2010) also match the variations in Δδ¹⁸O_cel(climate) (Fig. 17c). Note that the directions of the y axis are reversed between the speleothem and Δδ¹⁸O_cel(climate) data, reflecting the meridional disparity of precipitation patterns in East Asia (Fig. 13a), as demonstrated by Liu et al. (2014) and Chen et al. (2015).

The climatological component of the variations in the tree-ring cellulose δ¹⁸O data (Δδ¹⁸O_cel(climate)) in central Japan (Fig. 11) corresponds well over various timescales with summer precipitation and temperature records in central Japan, which have been derived from various meteorological, historical, and paleo-vegetation archives (Figs. 12–16). This indicates that Δδ¹⁸O_cel(climate) is a reliable proxy for summer climate, such as the activity of the East Asian summer monsoon. Multi-centennial and millennial Δδ¹⁸O_cel(climate) variations are similar to those of paleoclimatological reconstructions of global temperatures and East Asian precipitation (Fig. 17), indicating a drier climate during the Medieval Climate Anomaly and wetter climate during the Little Ice Age in central Japan. As such, Δδ¹⁸O_cel(climate) can be utilized in climatological, historical, and archeological studies.

4 Conclusions

We constructed a statistically reliable multi-millennial tree-ring dataset of cellulose δ¹⁸O in central Japan by analyzing tree rings of 67 trees without using a pooling method. We found that there are distinct age trends in the δ¹⁸O time series. By comparison with the δ²H time series, we showed that the age trend in δ¹⁸O is caused by an increase in the degree of post-photosynthesis isotopic exchange with xylem water before cellulose synthesis as the trees mature. Because the physiological conditions of the post-photosynthesis isotopic exchange are not simply controlled by tree age, but also related to the tree growth environment randomly influenced by human activity, it was not possible to remove the age trend by application of the negative exponential curve or RCS.

Given that tree-ring cellulose δ¹⁸O and δ²H are correlated positively and negatively due to climatological and physiological factors, respectively, we formulated simultaneous equations for the climatological and physiological components of the tree-ring cellulose δ¹⁸O and δ²H data. We solved these equations to cancel out the physiological effects and established a multi-millennial record of the climatological component of tree-ring cellulose δ¹⁸O (Δδ¹⁸O_cel(climate)). The Δδ¹⁸O_cel(climate) time series is well correlated with local, regional, and global variations in summer climate reconstructed by instrumental, historical, and paleoclimatological methods. This suggests that Δδ¹⁸O_cel(climate) has recorded summer climate variations in central Japan during the past 2600 years on annual to millennial timescales.

However, further research is needed to make Δδ¹⁸O_cel(climate) a more reliable index of summer climate. In this study we utilized δ²H_cel as supplementary data just to remove the long-term physiological effects in δ¹⁸O_cel. This is partly because the EPS of δ²H_cel is lower than that of δ¹⁸O_cel, reflecting the larger and more complicated post-photosynthetic isotope fractionations (physiological effects) in hydrogen than in oxygen and the possible analytical uncertainties in δ²H_cel owing to direct measurements of cellulose including the OH group. Therefore, we must further improve our understanding of cellulose hydrogen isotope ratios. Firstly, the analytical procedure of the tree-ring cellulose δ²H measurements needs to be improved. It is desirable to fix the δ²H in the OH group by some sophisticated method (Filot et al., 2006). Secondly, more global tree-ring cellulose δ²H data need to be acquired to expand the δ¹⁸O and δ²H datasets (and Δδ¹⁸O_cel(climate) time series) for different regions and tree species as well as to validate its usefulness. Thirdly, it remains challenging to calibrate long-term Δδ¹⁸O_cel(climate) variations because there are few long-term datasets of meteorological observations.

Although Δδ¹⁸O_cel(climate) is a promising proxy for summer climate that can remove the age trend, previous δ¹⁸O-based dendrochronological reconstructions of past summer climate may still be robust. Most tree-ring δ¹⁸O studies utilized samples collected from natural forests where human disturbance was insignificant in comparison with forests in central Japan. In contrast to the conifer trees studied here and reported by Esper et al. (2010), hardwoods may be intrinsically free from long-term age trends (Duffy et al., 2017; Büntgen et al., 2020). Therefore, in most isotopic dendrochronological studies, the cellulose δ²H data will be a supplementary index to ensure there are no significant age trends (An et al., 2014). However, when such studies are based on a small amount of conifer wood collected from archeological artifacts and/or architectural material, and where the growth environments may have been disturbed by human activities, the simultaneous measurement of δ²H and δ¹⁸O allows Δδ¹⁸O_cel(climate) variations to be used as a proxy for past climate.