Mysteriously high Δ¹⁴C of the glacial atmosphere: influence of ¹⁴C production and carbon cycle changes

Despite intense focus on the ∼190 ‰ drop in atmospheric Δ¹⁴C during Heinrich Stadial 1 at ∼17.4–14.6 ka, the specific mechanisms responsible for the apparent Δ¹⁴C excess in the glacial atmosphere have received considerably less attention. The computationally efficient Bern3D Earth system model of intermediate complexity, designed for long-term climate simulations, allows us to address a very fundamental but still elusive question concerning the atmospheric Δ¹⁴C record: how can we explain the persistence of relatively high Δ¹⁴C values during the millennia after the Laschamp event? Large uncertainties in the pre-Holocene ¹⁴C production rate, as well as in the older portion of the Δ¹⁴C record, complicate our qualitative and quantitative interpretation of the glacial Δ¹⁴C elevation. Here we begin with sensitivity experiments that investigate the controls on atmospheric Δ¹⁴C in idealized settings. We show that the interaction with the ocean sediments may be much more important to the simulation of Δ¹⁴C than had been previously thought. In order to provide a bounded estimate of glacial Δ¹⁴C change, the Bern3D model was integrated with five available estimates of the ¹⁴C production rate as well as reconstructed and hypothetical paleoclimate forcing. Model results demonstrate that none of the available reconstructions of past changes in ¹⁴C production can reproduce the elevated Δ¹⁴C levels during the last glacial. In order to increase atmospheric Δ¹⁴C to glacial levels, a drastic reduction of air–sea exchange efficiency in the polar regions must be assumed, though discrepancies remain for the portion of the record younger than ∼33 ka. We end with an illustration of how the ¹⁴C production rate would have had to evolve to be consistent with the Δ¹⁴C record by combining an atmospheric radiocarbon budget with the Bern3D model. The overall conclusion is that the remaining discrepancies with respect to glacial Δ¹⁴C may be linked to an underestimation of ¹⁴C production and/or a biased-high reconstruction of Δ¹⁴C over the time period of interest. Alternatively, we appear to still be missing an important carbon cycle process for atmospheric Δ¹⁴C.

1 Introduction

The cosmogenic radionuclide radiocarbon (¹⁴C) is a powerful tracer for the study of several ocean processes including deep ocean circulation and ventilation. Past changes in atmospheric ¹⁴C∕C (i.e., Δ¹⁴C_atm, in per mill; corresponding to Δ from Stuiver and Polach, 1977), as recorded in absolutely dated tree rings, plant macrofossils, speleothems, corals, and foraminifera, have been interpreted as possibly reflecting real changes in the ocean's large-scale overturning circulation (Siegenthaler et al., 1980). The extended 54 000-year record of Δ¹⁴C_atm from the latest IntCal compilation (i.e., IntCal13; Reimer et al., 2013) and from two Hulu Cave stalagmites (Cheng et al., 2018), adjusted to the presently accepted value of the radiocarbon half-life of 5700 years (Audi et al., 2003; Bé et al., 2013), suggests that large millennial-scale variations in Δ¹⁴C_atm occurred during the last glacial compared to the relatively small (∼30 ppm) change in atmospheric CO₂ over the same time period (Fig. 1). When interpreting the implications of such changes, it is important to note that Δ¹⁴C_atm is controlled not only by global carbon cycle processes but also by variations in the atmospheric ¹⁴C production rate. Therefore, the use of Δ¹⁴C_atm as an indicator of past oceanic conditions, particularly those associated with air–sea exchange efficiency and deep ocean ventilation rates, requires reliable estimates of the ¹⁴C production rate over time.

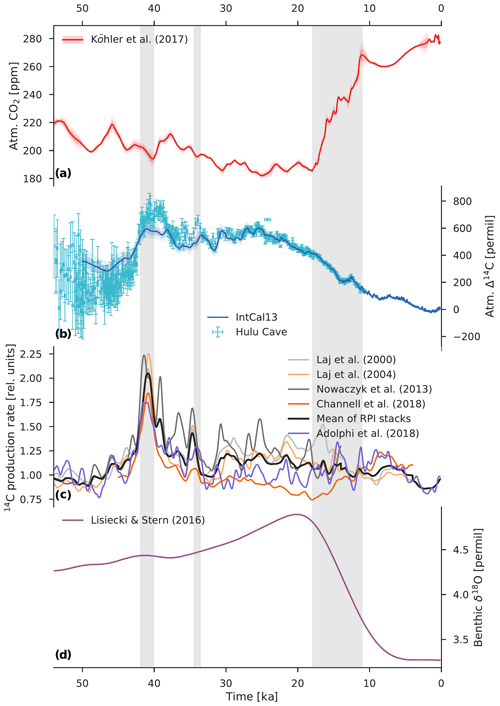
Figure 1 Comparison of various paleoclimate records for the last 54 kyr. (a) Atmospheric CO₂ from the data compilation of Köhler et al. (2017). The light red envelope shows the uncertainty (2σ). (b) Atmospheric Δ¹⁴C reconstructed from ¹⁴C measurements on tree rings, plant macrofossils, speleothems, corals, and foraminifera. The light blue envelope shows the uncertainty (2σ) in the IntCal13 calibration curve (Reimer et al., 2013), whereas the Hulu Cave data (Cheng et al., 2018) are shown with error bars (1σ). Hulu Cave data are consistent with IntCal13 between ∼10.6 and 33.3 ka. For both records Δ¹⁴C values were adjusted to the presently accepted value of the radiocarbon half-life (5700 years). (c) ¹⁴C production rate in relative units reconstructed from paleointensity data (Laj et al., 2000, 2004; Nowaczyk et al., 2013; Channell et al., 2018) and from polar ice-core ¹⁰Be fluxes (Adolphi et al., 2018). The heavy dark gray line is the mean paleointensity-based ¹⁴C production rate. (d) Global benthic δ¹⁸O stack, a proxy for ice volume, from Lisiecki and Stern (2016). Three vertical light gray bars indicate the Laschamp excursion (∼41 ka) when the Earth's geomagnetic dipole field intensity was close to zero, the Mono Lake geomagnetic excursion (∼34 ka), and the last glacial termination (∼18 to 11 ka).

The vast majority of all ¹⁴C production changes are the result of either solar or geomagnetic modulation of the cosmic ray flux reaching the Earth (Masarik and Beer, 1999; Poluianov et al., 2016). Figure 1 shows several different proxy records of the global production rate of ¹⁴C in relative units covering the full range of the ¹⁴C dating method based on geomagnetic field data from marine sediments (Laj et al., 2000, 2004; Nowaczyk et al., 2013; Channell et al., 2018) and on ¹⁰Be and ³⁶Cl measurements in polar ice cores (Adolphi et al., 2018). A fundamental difference between these reconstruction methods is that paleointensity-based estimates of the ¹⁴C production rate, by definition, do not reflect changes in the solar modulation of the cosmic radiation, whereas ice-core ¹⁰Be-based estimates give the combined influence of solar and geomagnetic modulation on radionuclide production. Of note is the striking coherence in all three records (Δ¹⁴C_atm, paleointensity-based production, and ice-core ¹⁰Be-based production) of the Laschamp excursion (∼41 ka), when the Earth's geomagnetic dipole field briefly reversed and its intensity was close to zero (Nowaczyk et al., 2012; Laj et al., 2014). According to reconstructions and production rate models, this large geomagnetic event caused a doubling of the ¹⁴C production rate, leading to the highest Δ¹⁴C_atm values over the last 54 kyr. Relatively high Δ¹⁴C_atm values continued until ∼25 ka, then gradually diminished to preindustrial levels, interrupted by a sharp drop in Δ¹⁴C_atm during Heinrich Stadial 1 (HS1) at ∼17.4 to 14.6 ka (sometimes called the “mystery interval”; Broecker and Barker, 2007). While the Laschamp geomagnetic excursion appears to be responsible for the Δ¹⁴C_atm peak at ∼41 ka, the production rate estimates during much of the pre-Holocene period are subject to considerable uncertainty.

Paleointensity-based reconstructions are sensitive to coring disturbances of poorly consolidated sediments. The last 50 kyr are represented by the relatively slushy uppermost few meters of recovered marine sediment cores (Channell et al., 2018). Channell et al. (2018) preferentially selected cores recovered using conventional piston and square barrel gravity coring methods and from sites with high mean (>15 cm kyr⁻¹) sedimentation rates to minimize the influence of drilling disturbance and reached very different production rates than, e.g., Laj et al. (2000). On the other hand, ice-core ¹⁰Be records are affected by changes in the transport and deposition of atmospheric ¹⁰Be, which may overprint the production rate changes (e.g., Heikkilä et al., 2013). Furthermore, in order to calculate the ice-core ¹⁰Be deposition fluxes, snow accumulation rates must be known for each specific ice core, which themselves have uncertainties on the order of 10 % to 20 % that propagate into the ice-core ¹⁰Be fluxes (Gkinis et al., 2014; Rasmussen et al., 2013). The large uncertainties associated with the reconstruction of past changes in ¹⁴C production hamper our ability to reliably predict the extent to which production changes contributed to high glacial Δ¹⁴C_atm levels. Only if estimates of past changes in ¹⁴C production are robust can one improve assessments of the relative importance of the two fundamental mechanisms responsible for glacial–interglacial Δ¹⁴C changes: (1) production changes and (2) carbon cycle changes.

Earlier model studies have focused heavily on the ∼190 ‰ drop in Δ¹⁴C_atm during HSI and on the deglacial trends in Δ¹⁴C_atm after HS1 (Muscheler et al., 2004; Broecker and Barker, 2007; Skinner et al., 2010; Mariotti et al., 2016; Delaygue et al., 2003; Marchal et al., 2001; Huiskamp and Meissner, 2012; Hain et al., 2014). Historically, the younger portion of the Δ¹⁴C_atm record has received more attention than the glacial section because of the early emphasis on the general climatic trends of the North Atlantic stadials (HS1 and the Younger Dryas, YD) and the Bølling–Allerød (BA) warm period, as well as on the important role of an exceptionally aged (¹⁴C-depleted) deepwater mass in the pulsed rise of atmospheric CO₂ during the last glacial termination (e.g., Skinner et al., 2017). Less research over the last few decades has studied the specific mechanisms responsible for high glacial Δ¹⁴C_atm levels. The model studies that are available point out the difficulties in simulating the correct glacial Δ¹⁴C_atm levels (Hughen et al., 2004; Köhler et al., 2006). These studies demonstrate with box models that glacial levels of Δ¹⁴C_atm cannot be attained without invoking significant changes in ocean circulation, air–sea gas exchange, and carbonate sedimentation. However, the box models were not able to reproduce Δ¹⁴C_atm values higher than 700 ‰, and these results still need to be scrutinized with models of higher complexity. To our knowledge, no three-dimensional ocean biogeochemical model has yet simulated the 50 000-year record of Δ¹⁴C_atm. Many questions remain unanswered, in particular the following: what mechanism can account for the persistence of relatively high Δ¹⁴C_atm values during the millennia after the Laschamp excursion?

The expected timescale for sustaining elevated levels of Δ¹⁴C_atm after a production peak is on the order of thousands of years, a timescale tied to the mean lifetime of ¹⁴C (∼8223 years; Audi et al., 2003; Bé et al., 2013) and the time required for deep ocean ventilation (on the order of 1000 years or more; Primeau, 2005). Specifically, Muscheler et al. (2004) demonstrate that the characteristic time constant for equilibration of Δ¹⁴C_atm after a perturbation in atmospheric production is 5000 years. By this analysis, the Laschamp event, which lasted only about 1500 to 2000 years (Laj et al., 2000), was insufficient to sustain the high Δ¹⁴C_atm values observed over the next ∼15 000 years. The lack of significant changes (only ∼10 %) in atmospheric CO₂ during the time period of interest raises the question of what causes variations in Δ¹⁴C_atm, but not CO₂, on millennial timescales. The obvious answers are cosmic ray modulation and air–sea gas exchange. Ultimately, no explanation for high glacial Δ¹⁴C_atm levels can be complete in the absence of more robust estimates of the pre-Holocene ¹⁴C production rate, as well as a good understanding of the ocean carbon cycle under glacial climate conditions.

One of the major challenges associated with modeling glacial–interglacial climate cycles is that it is currently not possible to reproduce climate and atmospheric CO₂ variations on the basis of orbital forcing alone. Problems include the complexity of the Earth system, making it difficult to represent all the relevant processes in models, and the long timescales involved, making simulations covering tens of thousands of years costly in computation time. Glacial–interglacial simulations with dynamic ocean and land models of intermediate complexity have begun to emerge, but these models are not yet able to reproduce the reconstructed variations in important proxy data or the timing of CO₂ variations during the last glacial termination (Brovkin et al., 2012; Ganopolski and Brovkin, 2017; Menviel et al., 2012). A wide variety of mechanisms, both physical and biological, centered on or connected with the ocean, as well as exchange processes with the land biosphere, marine sediments, coral reefs, and the lithosphere, are thought to play a role in explaining the glacial–interglacial variations in atmospheric CO₂ (Archer et al., 2000; Fischer et al., 2010; Wallmann et al., 2016; Galbraith and Skinner, 2020), but how they interacted over time under the influence of orbital forcing remains elusive. We appear to still be missing a single framework in which these mechanisms are linked to each other in a predictable manner. As long as there are still large gaps in our understanding of the glacial climate and associated ocean carbon cycle, a convenient way to examine the impact of the possible mechanisms on atmospheric CO₂ levels, and here on Δ¹⁴C_atm, is to perform sensitivity experiments and scenario-based simulations with models. This allows us to investigate specific phenomena in idealized settings, permitting us to investigate in detail which parameters and processes are most important in controlling Δ¹⁴C_atm levels.

In this paper we extend previous modeling efforts concerning the record of Δ¹⁴C_atm with respect to three issues: (1) the sensitivity of the Δ¹⁴C_atm response to carbon cycle changes and the potential importance of marine sediments, (2) the simulation of Δ¹⁴C_atm covering the time range of the IntCal13 radiocarbon calibration curve (50 000 years), the primary focus being the explanation for high glacial Δ¹⁴C_atm levels, and (3) a new 50 000-year record of the ¹⁴C production rate, as inferred by deconvolving the reconstructed histories of Δ¹⁴C_atm and CO₂ with a prognostic carbon cycle model and considering the uncertainties associated with the glacial–interglacial ocean carbon cycle. In the following sections we first introduce the Bern3D Earth system model of intermediate complexity and describe the carbon cycle scenarios for forcing it. We then use step changes in the ¹⁴C production rate and in selected parameters of the ocean carbon cycle model to gain insight into the transient and equilibrium response of Δ¹⁴C_atm. After these sensitivity experiments we present the results of paleoclimate simulations forced by available reconstructions of past changes in ¹⁴C production together with reconstructed and hypothetical carbon cycle changes accompanying glacial–interglacial climate cycles. Finally, we present results for a first attempt to reconstruct the glacial history of the ¹⁴C production rate using the Bern3D model forced with reconstructed variations in Δ¹⁴C_atm and CO₂ as well as a wide range of carbon cycle scenarios. We end with a comparison of three fundamentally different (model-based, paleointensity-based, and ice-core ¹⁰Be-based) reconstructions of atmospheric ¹⁴C production.

2 Materials and methods

2.1 Brief description of the Bern3D model

Simulations are performed with the computationally efficient Bern3D Earth system model of intermediate complexity (version 2.0), which is designed for long-term climate simulations over several tens of thousands of years. The Bern3D couples a frictional geostrophic 3-D ocean general circulation model (Edwards et al., 1998; Edwards and Marsh, 2005; Müller et al., 2006), a 2-D energy–moisture balance atmosphere model (Ritz et al., 2011), an ocean carbon cycle model (Müller et al., 2008; Tschumi et al., 2008; Parekh et al., 2008), a chemically active 10-layer ocean sediment model (Heinze et al., 1999; Tschumi et al., 2011; Roth et al., 2014; Jeltsch-Thömmes et al., 2019), and a four-box model representing carbon stocks in the terrestrial biosphere (Siegenthaler and Oeschger, 1987). The coarse-resolution ocean model is implemented on a 41×40 horizontal grid, with 32 logarithmically spaced layers in the vertical. The seasonal cycle is resolved with 96 time steps per year. The tracers carried in the ocean model include temperature, salinity, dissolved inorganic carbon (DIC), dissolved organic carbon (DOC), carbon isotopes (¹⁴C and ¹³C) of DIC and DOC, alkalinity (Alk), phosphate (P), silicate (Si), iron, dissolved oxygen (O₂), preformed dissolved oxygen (O_2,pre), and an “ideal age” tracer. The ideal age is set to zero in the surface layer, increased by Δt in all interior grid cells at each time step of duration Δt, and transported by advection, diffusion, and convection. Atmospheric CO₂, ¹⁴CO₂, and ¹³CO₂ are also carried as tracers in the atmosphere model. For a more complete description of the Bern3D model, the reader is referred to Appendix A.

2.2 Implementation of the ¹⁴C tracer

Natural radiocarbon (¹⁴C) is a cosmogenic radionuclide produced in the atmosphere by cosmic radiation. Once oxidized to ¹⁴CO₂, it participates in the global carbon cycle. Atmospheric ¹⁴CO₂ invades the ocean by air–sea gas exchange, where it is subject to the same physical and biogeochemical processes that affect DIC. The only difference is that ¹⁴C is lost by radioactive decay (half-life of 5700±30 years; Audi et al., 2003; Bé et al., 2013). The governing natural processes, namely atmospheric ¹⁴C production, air–sea gas exchange, physical transport and mixing in the water column, biological production and the export of particulate and dissolved matter from the surface ocean, particle flux through the water column, particle deposition on the seafloor, remineralization and dissolution in the water column and the sediment pore waters, and vertical sediment advection and sediment accumulation, are explicitly represented in the Bern3D model (see Fig. 2). Air–sea gas exchange is parameterized using a modified version of the standard gas transfer formulation of OCMIP-2, with exchange rates that vary across time and space (see Appendix A for more details).

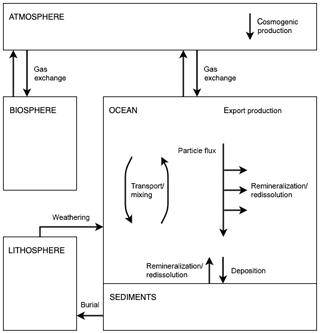
Figure 2 Schematic diagram of the Bern3D carbon cycle model. The fully coupled model includes the major global carbon reservoirs (atmosphere, terrestrial biosphere, ocean, and sediments) and the exchange fluxes between them. Biogeochemical processes, namely air–sea gas exchange, biological export production, and particle flux through the water column, are parameterized by refined OCMIP-2 formulations. Details concerning the model are provided in Sect. 2 and Appendix A.

Radiocarbon measurements are generally reported as Δ¹⁴C, i.e., the ratio of ¹⁴C to total carbon C relative to that of the 1950 CE atmosphere, with a correction applied for fractionation effects, e.g., due to gas exchange and photosynthesis (see Stuiver and Polach, 1977). In this model study, Δ¹⁴C is treated as a diagnostic variable using the two-tracer approach of OCMIP-2. Rather than treating the ¹⁴C∕C ratio as a single tracer, fractionation-corrected ¹⁴C is carried independently from the carbon tracer. The modeled ¹⁴C concentration is normalized by the standard ratio of the preindustrial atmosphere (${}^{\mathrm{14}}{r}_{\text{std}}=\mathrm{1.170}\times {\mathrm{10}}^{-\mathrm{12}}$; Orr et al., 2017) in order to minimize the numerical error of carrying very small numbers. For comparison to observations, Δ¹⁴C is calculated from the normalized and fractionation-corrected modeled ¹⁴C concentration as follows:

$$\begin{array}{}\text{(1)}& {\mathrm{\Delta }}^{\mathrm{14}}\mathrm{C}=\mathrm{1000}\left({}^{\mathrm{14}}{r}^{\prime }-\mathrm{1}\right),\end{array}$$

where ¹⁴r^′ is the ratio of ¹⁴C∕C in either atmospheric CO₂ or oceanic DIC divided by ¹⁴r_std, depending on the reservoir being considered. The approach taken to simulate atmospheric ¹⁴CO₂ is analogous to the approach used for CO₂, except that the equation includes the terms due to atmospheric production and radioactive decay. For simulations in which the sediment model is active, the oceanic DIC tracer sees a constant input from terrestrial weathering, whereas there is no weathering input of DI¹⁴C to the ocean (see Appendix A for more details).

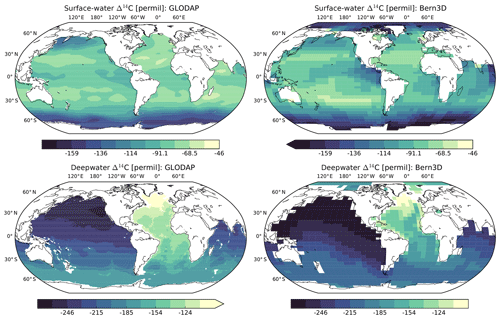
Figure 3 Steady-state distribution of Δ¹⁴C in the surface (<100 m) and deep (>1500 m) ocean for the preindustrial control run (right) compared to the distribution of Δ¹⁴C based on the Global Ocean Data Analysis Project (GLODAP).

In the preindustrial spin-up simulation needed to initialize the Bern3D model, atmospheric CO₂ is held constant at 278.05 ppm and Δ¹⁴C_atm at 0 ‰. During this integration time the ocean inventories of carbon and ¹⁴C adjust to the forcing fields. The resulting changes after >50 000 years of integration are negligibly small. Figure 3 shows the steady-state Δ¹⁴C distribution in the surface (<100 m) and deep (>1500 m) ocean for the preindustrial control run. The large-scale distribution of modeled oceanic Δ¹⁴C broadly resembles the observed pattern in the Global Ocean Data Analysis Project (GLODAP; Key et al., 2004). That final state (i.e., the end of the preindustrial spin-up) is used to diagnose the ¹⁴C production rate for the preindustrial atmosphere such that the rate of ¹⁴C production is balanced by radioactive decay and the net fluxes out of the atmosphere. For transient simulations, an adjustable scale factor is applied to the preindustrial steady-state value of 443.9 mol¹⁴C yr⁻¹ (1.66 $\mathrm{atoms}{\mathrm{cm}}^{-\mathrm{2}}{\mathrm{s}}^{-\mathrm{1}}$) in order to account for production changes induced by solar and/or geomagnetic modulation. These production changes are derived from, e.g., available reconstructions of the ¹⁴C production rate in relative units, as detailed in Sect. 2.5. Note the preindustrial spin-up results in steady-state values for weathering-derived inputs of DIC, Alk, P, and Si of 0.46 Gt C yr⁻¹, 34.37 Tmol Alk yr⁻¹, 0.17 Tmol P yr⁻¹, and 6.67 Tmol Si yr⁻¹, respectively. These terrestrial weathering rates were chosen to balance the sedimentation rates on the seafloor and are held fixed and constant throughout the simulations.

2.3 Model configurations

We focus in this paper on the response of Δ¹⁴C_atm to changes in ¹⁴C production and the ocean carbon cycle. For a deeper mechanistic understanding of the driving processes, step response experiments are first performed (see Sect. 3.1). These simulations include perturbations of the steady-state ¹⁴C∕C distribution under preindustrial conditions. We investigate the impact of step changes in (1) the ¹⁴C production rate (“higher production” scenario), (2) wind stress and vertical diffusivity (“reduced deep ocean ventilation” scenario), and (3) the gas transfer velocity (“enhanced permanent sea ice cover” scenario). After a step change at time 0, the simulations are run to near equilibrium over a 50 000-year integration. The following model configurations and therefore exchanging carbon reservoirs are considered: atmosphere–ocean (OCN), atmosphere–ocean–land (OCN-LND), atmosphere–ocean–sediment (OCN-SED), and atmosphere–ocean–land–sediment (ALL).

Next we examine the influence of changes that are transient in nature. We simulate Δ¹⁴C_atm over the full range of the ¹⁴C dating method (i.e., 50 to 0 ka) (see Sect. 3.2 and 3.3). These transient simulations are initialized at 70 ka using model configuration ALL and forced by reconstructed changes in ¹⁴C production (see Sect. 2.5) over a 70 000-year integration. The first 20 000 years of the integration are considered a spin-up. Although the full record is simulated, we focus our analysis on the millennial-scale variation in Δ¹⁴C_atm before incipient deglaciation at ∼18 ka. Eight model runs are carried out for each production rate reconstruction using different combinations of forcing fields and parameter values as described next.

2.4 Carbon cycle scenarios

In our transient simulations with the Bern3D model, eight scenarios based on different assumptions about the global carbon cycle are considered, the details of which are summarized in Table 1. The goal is to investigate the extent to which changes in the ocean carbon cycle could explain high glacial Δ¹⁴C_atm levels given available reconstructions of past changes in ¹⁴C production. We therefore consider a wide range of carbon cycle scenarios, including some extreme cases. A note of caution: because millennial-scale Δ¹⁴C_atm variations during the last glacial are what we are interested in, we do not attempt to reproduce abrupt climate perturbations such as Dansgaard–Oeschger warming events in the model runs.

Table 1 Summary of model scenarios considered in this study. Initial conditions refer to the boundary conditions used for the precursor spin-up simulation needed to initialize the transient simulation. These correspond either to preindustrial (PI) or last glacial conditions. The paleoclimate forcing fields, i.e., Orb-GHG-Ice, are reconstructed changes in orbital parameters (Berger, 1978), greenhouse gas radiative forcing based on reconstructed atmospheric greenhouse gas histories (Köhler et al., 2017), and varying ice sheet extent scaled using the global benthic δ¹⁸O stack of Lisiecki and Stern (2016). Numbers refer to the scale factor values applied to the tunable model parameters τ (wind stress scale factor), K_V (vertical diffusivity), k_w (gas transfer velocity), rr (CaCO₃-to-POC export ratio), and ℓ_POC (POC remineralization length scale) at the Last Glacial Maximum (LGM). These values were chosen in order to achieve an atmospheric CO₂ concentration close to the LGM level and are varied over time using the global benthic δ¹⁸O stack. See Roth et al. (2014) for the Bern3D model parameter set. In all scenarios, the fully coupled model configuration, including the major global carbon reservoirs (atmosphere, terrestrial biosphere, ocean, and sediments), is used.

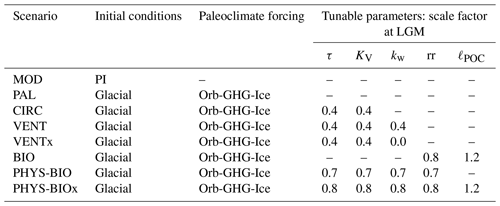
In the first scenario (MOD), the model is run with fixed preindustrial boundary conditions for the Earth's orbital parameters, radiative forcing due to well-mixed greenhouse gases, and ice sheet extent. As a consequence, atmospheric CO₂ remains approximately constant at the preindustrial level of 278.05 ppm over the simulation. The second scenario (PAL) considers reasonably well-known climate forcing over the last glacial–interglacial cycle. Simulations under this scenario are initialized with output from a previous spin-up simulation forced by glacial boundary conditions with respect to orbital parameters (Berger, 1978), ice sheet extent (see below), and greenhouse gas radiative forcing based on the smoothed dataset of atmospheric greenhouse gases by Köhler et al. (2017) as constructed from the original data of Ahn and Brook (2014), Ahn et al. (2012), Bauska et al. (2015), Bereiter et al. (2012), Buizert et al. (2015), Dlugokencky et al. (2016), Lourantou et al. (2010), Lüthi et al. (2010), MacFarling-Meure et al. (2006), Marcott et al. (2014), Monnin et al. (2001, 2004), Rubino et al. (2013), Schneider et al. (2013), and Sigl et al. (2016). In simulations under PAL, the model is integrated until 0 ka following the reconstructed histories of orbital forcing, ice sheets, and radiative forcing due to greenhouse gases. Ice sheets for the preindustrial and Last Glacial Maximum (LGM) states are taken from Peltier (1994) and linearly scaled using the global benthic δ¹⁸O stack of Lisiecki and Stern (2016), which is a global ice volume proxy. Changes in the albedo, salinity, and latent heat flux associated with the ice sheet buildup or melting are also taken into account (Ritz et al., 2011). Note that, although the radiative forcing for CO₂ is prescribed, the atmospheric CO₂ concentration is allowed to evolve freely, except in the simulations described in Sect. 2.5.

Model scenario PAL appears to still be missing an important process or feedback for atmospheric CO₂, as it cannot reproduce the observed low glacial CO₂ level without invoking additional changes (see, e.g., Tschumi et al., 2011; Menviel et al., 2012; Roth and Joos, 2013; Jeltsch-Thömmes et al., 2019). Variations in atmospheric CO₂ govern how fast Δ¹⁴C signatures are passed between the atmosphere and ocean. Gross fluxes of ¹⁴C between the atmosphere and ocean, and vice versa, scale with atmospheric pCO₂ and its ¹⁴C∕C ratio. It is therefore important to reproduce low glacial atmospheric CO₂ concentrations in at least some of the model scenarios, thereby capturing the influence of temporal changes in CO₂ on the air–sea exchange of ¹⁴C. In this study, we consider six scenarios that invoke additional changes to force the model toward the observed low glacial CO₂ concentration. In addition to the PAL forcing, a time-varying scale factor F(t) is applied to some combination of tunable model parameters: wind stress scale factor τ, vertical diffusivity K_V, gas transfer velocity k_w, CaCO₃-to-particulate organic carbon (POC) export ratio (rr), and POC remineralization length scale ℓ_POC. For the preindustrial period, the value of F(t) is fixed at 1, whereas the theoretical LGM value was chosen in order to achieve an atmospheric CO₂ concentration close to the LGM level of ∼190 ppm (see Table 1), as determined by sensitivity experiments. Note that the same values of F(t) apply to any of the model parameters considered in a given scenario. To obtain intermediate values, F(t) is linearly scaled using the global benthic δ¹⁸O stack (see Fig. 1). For the spin-up needed to initialize these simulations, the glacial spin-up simulation of PAL was integrated for 50 000 model years, with tunable parameters adjusted to their appropriate glacial values. Atmospheric CO₂ drawdown of up to ∼100 ppm is achieved over this 50 000-year integration. From that final spun-up state, the model is run forward in time until 0 ka with PAL and F(t) forcing.

The first of these scenarios (CIRC) allows us to test the sensitivity of the model results with respect to changes in ocean circulation. Tunable model parameters τ and K_V were reduced to 40 % of their preindustrial values throughout the global ocean during the LGM (i.e., $F_{\mathit{\tau },K_{\mathrm{V}}}=\mathrm{0.4}$). Such a drastic change in the wind stress field is not realistic. Rather, these changes should be viewed as “tuning knobs” that force the ocean model into a poorly ventilated state with an “older” ideal age and ¹⁴C-depleted deep waters, as suggested for the glacial ocean (e.g., Sarnthein et al., 2013; Skinner et al., 2017). In the model's implementation, a change in wind stress does not affect the gas transfer velocity k_w, unlike in the real ocean where changes in wind stress and wind speed act together. The influence of a change in air–sea exchange efficiency on the model results was investigated in a second scenario (VENT) in which k_w is reduced in the model's north (>60^∘ N) and south (>48^∘ S) polar areas in addition to global reductions of τ and K_V ($F_{\mathit{\tau },K_{\mathrm{V}},k_{\mathrm{w}}}=\mathrm{0.4}$). A 60 % reduction of k_w is unlikely to be correct but is a straightforward way to reduce the model's gas exchange efficiency. In the third scenario (VENTx), reduction of polar k_w to 0 % of its preindustrial value was tested ($F_{\mathit{\tau },K_{\mathrm{V}}}=\mathrm{0.4}$; $F_{k_{\mathrm{w}}}=\mathrm{0.0}$). Here, k_w remains fixed at 0 % during the last glacial and is adjusted to its preindustrial value via a linear ramp across the last glacial termination (∼18 to 11 ka). In this scenario, sea ice would permanently cover 100 % of the Southern Ocean during the last glacial, which is not supported by the sea ice reconstructions of Gersonde et al. (2005) and Allen et al. (2011), and also the high-latitude (>60^∘ N) North Atlantic and Arctic Ocean, for which there is some evidence (Müller and Stein, 2014; Hoff et al., 2016).

We end by investigating the sensitivity of the model results to changes in the parameters controlling the export production of CaCO₃ and the water column remineralization of POC. Model scenario BIO considers changes in the CaCO₃-to-POC export ratio (and thus also the CaCO₃-to-POC rain ratio; Archer and Maier-Reimer, 1994) (F_rr=0.8) and POC remineralization length scale (Roth et al., 2014) ($F_{{\mathrm{\ell }}_{\text{POC}}}=\mathrm{1.2}$). These changes impact the global carbon cycle by influencing the vertical gradients of DIC, Alk, and nutrients in the water column. A change in the fluxes of POC and CaCO₃ to the seafloor drives a change in the magnitude of their removal by sedimentation on the seafloor. A modest reduction in the export ratio during the last glacial is compatible with reconstructed variations in carbonate ion concentrations (Jeltsch-Thömmes et al., 2019). How the depth of POC remineralization changed over time is still unknown. The last two scenarios consider the combined effect of physical and biogeochemical changes: PHYS-BIO ($F_{\mathit{\tau },K_{\mathrm{V}},k_{\mathrm{w}},\mathrm{rr}}=\mathrm{0.7}$) and PHYS-BIOx ($F_{\mathit{\tau },K_{\mathrm{V}},k_{\mathrm{w}},\mathrm{rr}}=\mathrm{0.8}$; $F_{{\mathrm{\ell }}_{\text{POC}}}=\mathrm{1.2}$).

2.5 Measurement- and model-based reconstruction of ¹⁴C production

Our ability to attribute past changes in Δ¹⁴C_atm to climate-related changes in the ocean carbon cycle is limited by our ability to reconstruct a precise and accurate history of the ¹⁴C production rate. Past changes in ¹⁴C production can be estimated from geomagnetic field reconstructions and from ¹⁰Be measurements in polar ice cores. For ice-core ¹⁰Be-based estimates, we use the ice-core radionuclide stack of Adolphi et al. (2018), which is based on ³⁶Cl data from the GRIP ice core (Baumgartner et al., 1998) and on ¹⁰Be data from the GRIP (Yiou et al., 1997; Baumgartner et al., 1997; Wagner et al., 2001; Muscheler et al., 2004; Adolphi et al., 2014) and GISP2 (Finkel and Nishiizumi, 1997) ice cores. It also includes ¹⁰Be data from the NGRIP, EDML, EDC, and Vostok ice cores around the Laschamp geomagnetic excursion (Raisbeck et al., 2017). It has been extended to the present using the ¹⁰Be stack of Muscheler et al. (2016). All ice cores were first placed on the same timescale (GICC05) before ¹⁰Be fluxes were calculated. This 70 000-year ¹⁰Be stack provides relative changes in ¹⁴C production rates under the assumption that ¹⁴C and ¹⁰Be production rates are directly proportional, as indicated by the most recent production rate models (e.g., Herbst et al., 2017).

For paleointensity-based estimates, we employ (1) the North Atlantic Paleointensity Stack, or NAPIS, by Laj et al. (2000) as extended by Laj et al. (2002), (2) the Global Paleointensity Stack, or GLOPIS, by Laj et al. (2004), (3) a high-resolution paleointensity stack from the Black Sea (Nowaczyk et al., 2013), and (4) a paleointensity stack from Iberian Margin sediments (Channell et al., 2018). In principle, stacks of widely distributed cores (NAPIS and GLOPIS) are expected to yield a better representation of the global geomagnetic dipole moment, whereas the paleointensity stacks from the Black Sea and the Iberian Margin avoid some of the problems associated with coring disturbances. The four different paleointensity stacks were converted to ¹⁴C production rates using the production rate model of Herbst et al. (2017), the local interstellar spectrum of Potgieter et al. (2014), and assuming a constant solar modulation potential of 630 MeV.

An alternative approach to estimating the ¹⁴C production rate is to combine an atmospheric radiocarbon budget with a prognostic carbon cycle model. Here simulations are performed with the Bern3D model and forced by reconstructed changes in Δ¹⁴C_atm and CO₂, as well as reconstructed and hypothetical carbon cycle changes, over the last 50 kyr. Both the IntCal13 calibration curve (Reimer et al., 2013) and the recent Hulu Cave Δ¹⁴C_atm dataset (Cheng et al., 2018) are used. Note that although the forthcoming IntCal20 calibration curve (Reimer et al., 2020) will be the new standard atmospheric radiocarbon record for the last 55 000 years, essentially all data underlying IntCal20 before 13.9 ka are tied to the Hulu Cave dataset, either via timescales (Lake Suigetsu plant macrofossil data) or marine reservoir corrections (marine records). Hence, the IntCal20 and Hulu Cave Δ¹⁴C_atm records are very similar, and using IntCal20 would not impact our conclusions.

The ¹⁴C production rate Q is calculated each model year from the air–sea ¹⁴CO₂ flux (F_as), the atmosphere–land ¹⁴CO₂ flux (F_ab), the loss of ¹⁴C due to radioactive decay, and the change (${\dot{I}}_{\mathrm{a}}$) in the atmospheric ¹⁴C inventory (I_a):

$$\begin{array}{}\text{(2)}& {\displaystyle }{\displaystyle }Q=F_{\text{as}}+F_{\text{ab}}+\mathit{\lambda }{I}_{\mathrm{a}}+{\dot{I}}_{\mathrm{a}},\end{array}$$

where λ is the radioactive decay constant for ¹⁴C, i.e., $\mathit{\lambda }=\ln \mathrm{2}/\mathrm{5700}\text{years}=\mathrm{1.2160}\times {\mathrm{10}}^{-\mathrm{4}}$ yr⁻¹. The radioactive decay term λI_a and the change in inventory ${\dot{I}}_{\mathrm{a}}$ follow the reconstructed Δ¹⁴C_atm and CO₂ records, whereas F_as and F_ab are explicitly computed by the model. The F_as term depends strongly on the carbon cycle scenario under consideration (see Sect. 2.4 and Table 1). For comparison with other reconstructions, Q is converted into a relative value by normalizing it by the preindustrial value.

3 Results and discussion

3.1 Atmospheric Δ¹⁴C response to step changes

We use step changes in the ¹⁴C production rate, and in selected carbon cycle parameters, to gain insight into the characteristic magnitude and timescale of the corresponding Δ¹⁴C_atm changes (Fig. 4). Besides variations of the production rate, changes in ocean circulation and air–sea gas exchange are considered the most important factors affecting Δ¹⁴C_atm. Their effect on Δ¹⁴C_atm can be understood in terms of their effect on the reservoir sizes involved in the global carbon cycle and on the exchange rates between the reservoirs. We investigate the relative importance of the major global carbon reservoirs (atmosphere, terrestrial biosphere, ocean, and sediments) by considering four different model configurations (see Sect. 2.3), with particular emphasis on the role of marine sediments.

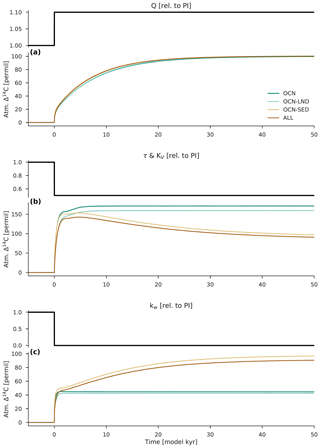
Figure 4 Response of atmospheric Δ¹⁴C to step changes in ¹⁴C production, followed by step changes in the tunable model parameters of the ocean carbon cycle. (a) ¹⁴C production Q is increased at time 0 from 100 % to 110 % of its preindustrial value (“higher production” scenario). (b) Wind stress scale factor τ and vertical diffusivity K_V are decreased at time 0 from 100 % to 50 % of their preindustrial values (“reduced deep ocean ventilation” scenario). (c) Gas transfer velocity k_w is decreased at time 0 from 100 % to 0 % of its preindustrial value at the North Pole (>60^∘ N) and South Pole (>48^∘ S; “enhanced permanent sea ice cover” scenario). Four model configurations are considered. The dark turquoise line shows the model results using the atmosphere–ocean (OCN) configuration, the light turquoise line is the atmosphere–ocean–land (OCN-LND) configuration, the light brown line is the atmosphere–ocean–sediment (OCN-SED) configuration, and the dark brown line is the atmosphere–ocean–land–sediment (ALL) configuration.

In model studies, the process of sedimentation (defined here as the difference between deposition and the remineralization and dissolution of material on the seafloor) is often neglected because it is a relatively minor flux. In the Bern3D model, sedimentation removes only about 0.46 Gt C yr⁻¹ and 45.31 mol ¹⁴C yr⁻¹ in the preindustrial steady state. Indeed, the interaction with the ocean sediments has little influence on the global mean value of oceanic Δ¹⁴C and therefore Δ¹⁴C_atm, as long as the total oceanic amount of carbon remains approximately constant (Siegenthaler et al., 1980); however, this is not always true, particularly in the case of millennial-scale climate perturbations. This is demonstrated by the differences between the model runs with and without sediments (i.e., ALL vs. OCN-LND and OCN-SED vs. OCN) as shown in Fig. 4. The response of Δ¹⁴C_atm to various perturbations depends on the magnitude of the change in the ocean carbon inventory, with a larger change achieved by considering the interaction with the ocean sediments and the imbalance between weathering and sedimentation (see Fig. 5e, f). In order to facilitate our discussion, we will make only direct comparisons between model runs ALL and OCN-LND, which both include the four-box terrestrial biosphere model. We note that the ¹⁴C exchange rate between the atmosphere and the terrestrial biosphere is only of minor importance for long timescales of millennia and more.

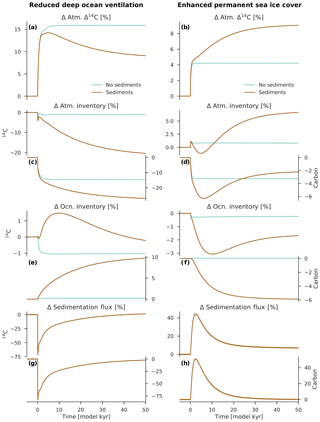
Figure 5 Changes in carbon reservoir sizes and the sedimentation flux for the scenarios “reduced deep ocean ventilation” (a, c, e, g) and “enhanced permanent sea ice cover” (b, d, f, h). The change in atmospheric Δ¹⁴C is also shown (a, b). Anomalies are expressed here as differences relative to the preindustrial steady state (in percent). Turquoise lines show the model results using configuration OCN-LND (without sediments), and brown lines are configuration ALL (with sediments). The y axis on the left-hand side of each panel refers to changes in the ¹⁴C inventory, whereas the y axis on the right-hand side of each panel refers to changes in the carbon inventory or flux.

3.1.1 Change in ¹⁴C production

At steady state, the relative change in Δ¹⁴C_atm is equal to the relative change in the ¹⁴C production rate, irrespective of the individual reservoirs considered. Figure 4 shows that Δ¹⁴C_atm increases by about 100 ‰ (or 10 %) when the production rate is increased by 10 %. In model run ALL, Δ¹⁴C_atm increases approximately exponentially to its new steady-state value with a characteristic time constant T of about 6170 years (i.e., $\mathrm{1}-\mathrm{1}/e\approx \mathrm{63}$ % of the total change in Δ¹⁴C_atm occurs within 6170 years). This e-folding timescale is close to the mean lifetime of ¹⁴C (∼8223 years), which is modulated by the time required for Δ¹⁴C to equilibrate between the atmosphere and the ocean (i.e., the timescale for deep ocean ventilation, of the order of hundreds of years to 1000 years or more). In the next section, we will investigate the effect of ocean carbon cycle processes on Δ¹⁴C_atm.

Note that for simplicity, we investigated only step changes in atmospheric production, although in reality ¹⁴C production varies continuously over time due to changes in the solar and/or geomagnetic modulation of the cosmic radiation. This results in a non-steady-state value of Δ¹⁴C_atm.

3.1.2 Change in ocean circulation

The exchange rate between the surface and deep ocean is mainly determined by physical transport and mixing processes. The overall effect of these processes is to transport ¹⁴C-enriched surface waters to the thermocline and deep ocean, where waters are typically ¹⁴C-depleted. In addition, the nutrient supply by transport and mixing plays an important role in determining the production and export of biogenic material from the surface ocean, constituting a second pathway for transporting ¹⁴C to the deep ocean.

In the Bern3D model, the tunable model parameters affecting the ventilation of the deep ocean include a scale factor τ for the wind stress field and vertical diffusivity K_V. Figure 4 shows the Δ¹⁴C_atm response after a sudden decrease in τ and K_V by 50 %. Although a halving of τ and K_V does not represent a realistic change, the resulting state of the ocean's large-scale overturning circulation can be interpreted in terms of the “ideal age” of water, which represents the average time since a water mass last made surface boundary contact. The new steady-state ideal age after a halving of τ and K_V is almost 3 times greater than the preindustrial steady-state value (i.e., ∼1664 years vs. ∼613 years). This “aging” of the ocean is achieved through a weakening and shoaling of the global meridional overturning circulation, as evident from a moderate reduction in the meridional overturning stream function for the Indo-Pacific Ocean from about 14 to 9.5 Sv (1 Sv = 10⁶ m³ s⁻¹), and a very strong reduction from about 18 to 8 Sv in the Atlantic meridional overturning stream function, consistent with evidence for the glacial ocean. Here, as expected, the overall effect of deepwater aging is a stronger vertical Δ¹⁴C gradient in the water column and a subsequent increase in Δ¹⁴C_atm. The exact nature of the Δ¹⁴C_atm response, however, depends on the carbon reservoirs considered.

If the ocean sediment reservoir is neglected, the time required for Δ¹⁴C_atm to adjust to step changes in τ and K_V is relatively short. Δ¹⁴C_atm increases rapidly to its new steady-state value of ∼159 ‰, with a time constant T of about 600 years. This increase in Δ¹⁴C_atm can be explained by the fact that, owing to a weaker and shallower overturning circulation, a comparatively large amount of carbon is moved from the atmosphere to the ocean. More specifically, the atmospheric carbon inventory decreases by 14.6 %, whereas the atmospheric ¹⁴C inventory decreases by only 1.1 % (Fig. 5c). The ¹⁴C being produced in the atmosphere is therefore diluted by a smaller carbon inventory, increasing the atmospheric ¹⁴C∕C ratio; this asymmetry in the drawdown of CO₂ and ¹⁴CO₂ is what permits the increase in Δ¹⁴C_atm. Since the ocean carbon inventory changes by only +0.2 %, the mean Δ¹⁴C value for the global ocean is nearly unaffected: a decrease of only ∼11 ‰ in the new steady state (Fig. 6g).

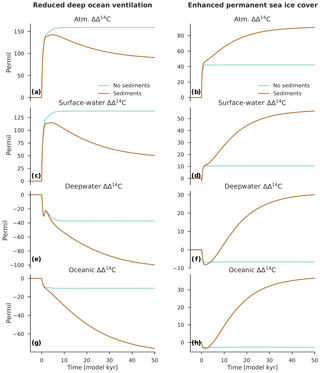
Figure 6 Change in Δ¹⁴C for the atmosphere, surface ocean, deep ocean, and global ocean for the scenarios “reduced deep ocean ventilation” (a, c, e, g) and “enhanced permanent sea ice cover” (b, d, f, h). Anomalies are expressed here as differences relative to the preindustrial steady state (in per mill). Turquoise lines show the model results using configuration OCN-LND (without sediments), and brown lines are configuration ALL (with sediments).

In the model run in which the sediment model is active, there are two distinct time constants. A rapid increase in Δ¹⁴C_atm occurs by ∼143 ‰ in the first few hundred years, then Δ¹⁴C_atm gradually decreases to its final value of ∼91 ‰ after tens of thousands of years. Reduced deep ocean ventilation is again responsible for the rapid Δ¹⁴C_atm change and the respective time constant ($T=\sim \mathrm{480}$ years). The second time constant of ∼23 390 years is due to the relatively long time required for the ocean carbon inventory to adjust to the ocean-circulation-driven imbalance between weathering and sedimentation.

The process of ocean circulation interacts with the efficiency of the ocean's biological carbon pump via its impact on export production, ocean interior oxygen levels, and seawater carbonate chemistry and equilibria. This has important implications for the sedimentation of biogenic material on the seafloor and, on a timescale of tens of thousands of years, the total oceanic amount of carbon. Through this coupling of ocean circulation and seafloor sedimentation via the biological carbon pump, a halving of τ and K_V leads to a 9.8 % increase in the ocean carbon inventory in the new steady state (Fig. 5e). Qualitatively, a reduction in the ocean's overturning circulation leads to a lower surface nutrient supply, which limits the production and export of biogenic material from the surface ocean. This, in turn, decreases the fluxes of POC and CaCO₃ to the seafloor, with major consequences for the magnitude of their removal by sedimentation. At the same time, a constant input of DIC, Alk, and nutrients is added to the ocean from terrestrial weathering, which is no longer balanced by sedimentation on the seafloor (this is what permits a larger ocean carbon inventory). The overall effect is a gradual reduction of oceanic Δ¹⁴C by ∼76 ‰ (Fig. 6g), which dilutes the initial Δ¹⁴C_atm peak by 52 ‰.

3.1.3 Change in gas transfer velocity

It takes about a decade for the isotopic ratios of carbon to equilibrate between the atmosphere and a ∼75 m thick surface mixed layer by air–sea gas exchange (Broecker and Peng, 1974). A consequence of this is that the surface ocean is undersaturated with respect to Δ¹⁴C_atm (see Fig. 3). The choice of gas transfer velocity k_w as a function of wind speed is critical for the efficiency of air–sea gas exchange. A reduction of k_w corresponds to a higher resistance for gas transfer across the air–sea interface, which means that the ¹⁴C produced in the atmosphere escapes into the surface ocean at a slower rate. The effect of a lower k_w is a larger air–sea gradient of Δ¹⁴C and higher Δ¹⁴C_atm values. In contrast, the Δ¹⁴C value for the surface ocean is nearly unaffected so long as the ocean carbon inventory remains approximately constant, since the vertical gradient of Δ¹⁴C in the ocean is dominated by physical transport and mixing processes. Although the exact nature of the gas transfer velocity under glacial climate conditions remains unclear, k_w represents a straightforward way to reduce the model's air–sea exchange efficiency due to theoretical changes in wind stress and sea ice.

Figure 4 shows how Δ¹⁴C_atm responds to a perturbation in the gas transfer velocity. In the model run without sediments, the reduction of k_w to 0 % of its preindustrial value in the model's north (>60^∘ N) and south (>48^∘ S) polar areas leads to a moderate increase in Δ¹⁴C_atm in the new steady state. The amplitude of Δ¹⁴C_atm change is ∼42 ‰, which is achieved with an e-folding timescale T of about 180 years. This relatively short time constant can be explained by the multidecadal timescale required for Δ¹⁴C to equilibrate between the model's atmosphere, upper ocean, and terrestrial biosphere. As shown in Fig. 6, the mean Δ¹⁴C values for the surface, deep, and global ocean in the new steady state are only slightly different from the preindustrial steady-state values, as expected from the fact that the ocean carbon inventory remains relatively stable.

Interestingly, if sediments are included in the model, the final value of Δ¹⁴C_atm is much higher (∼91 ‰). In this case, a perturbation in k_w leads to a very rapid initial increase in Δ¹⁴C_atm (∼42 ‰) and a much slower subsequent increase in Δ¹⁴C_atm (∼49 ‰). The latter has an e-folding timescale T of about 14 200 years. This slow doubling of the initial Δ¹⁴C_atm increase is unexpected but can be explained by the fact that a reduction of k_w also involves a reduction of air–sea O₂ gas exchange in the deepwater formation regions, decreasing the oceanic oxygen that is available for transport to the deep ocean. This, in turn, implies lower oxygen concentrations in the water column and the sediment pore waters, decreasing the rate of POC remineralization in the sediments. Reducing this has the overall effect of enhancing POC sedimentation on the seafloor, causing the ocean carbon inventory to decrease. As shown in Fig. 5f, the total oceanic amount of carbon decreases by 5.9 % in the new steady state, resulting in elevated Δ¹⁴C values for the surface (+56 ‰), deep (+30 ‰), and global (+37 ‰) ocean as well as for the atmosphere (+91 ‰) (see Fig. 6). Note that the increase in Δ¹⁴C_atm is not accompanied by a significant change in the atmospheric carbon inventory, which decreases by only 2.2 % to 3.3 %. The air–sea equilibration timescale for CO₂ by gas exchange is about 1 year for a ∼75 m thick surface mixed layer (Broecker and Peng, 1974), which is much smaller than the ventilation timescale for the deep ocean (on the order of several hundred years or more). One would therefore expect that the oceanic uptake of CO₂ demonstrates only a very small response to changes in k_w.

Overall, findings from these sensitivity experiments demonstrate that (1) the response of Δ¹⁴C_atm to changes in the internal parameters of the ocean carbon cycle, in contrast to ¹⁴C production changes, depends strongly on whether or not the balance between terrestrial weathering and sedimentation on the seafloor is simulated, (2) the e-folding timescale for the initial adjustment of Δ¹⁴C_atm to ocean carbon cycle changes, i.e., changes in ocean circulation and gas exchange, is shorter than that for production changes (i.e., ∼600 and ∼180 years vs. ∼6170 years), (3) air–sea gas exchange, in contrast to ocean circulation, has only a small effect on atmospheric CO₂ given that gas exchange is not the rate-limiting step for oceanic CO₂ uptake, and (4) on timescales of tens of thousands of years changes in the balance between weathering and sedimentation can potentially diminish (or elevate) the Δ¹⁴C_atm value. This is new, important information for future paleoclimate simulations and suggests that changes in Δ¹⁴C_atm may be overestimated (or underestimated) in models that do not simulate the interaction between seafloor sediments and the overlying water column.

3.2 Role of ¹⁴C production in past atmospheric Δ¹⁴C variability

We now consider the component of past Δ¹⁴C_atm variability caused by production changes alone. Figure 7 shows the results of model runs using different reconstructions of the ¹⁴C production rate, as inferred from paleointensity data and from ice-core ¹⁰Be fluxes. The global carbon cycle is assumed to be constant and under preindustrial conditions for these simulations (i.e., scenario MOD is used). Our analysis is restricted to the glacial portion of the record (50 to 18 ka), in part because this is the time period that experiences the largest production changes and in part because we did not attempt to reproduce the ∼80 ppm change in atmospheric CO₂ that occurred during the last glacial termination. As we have already noted, much research over the last decades has attempted to explain the observed glacial–interglacial variations in Δ¹⁴C_atm and CO₂, and this was not the goal of this study.

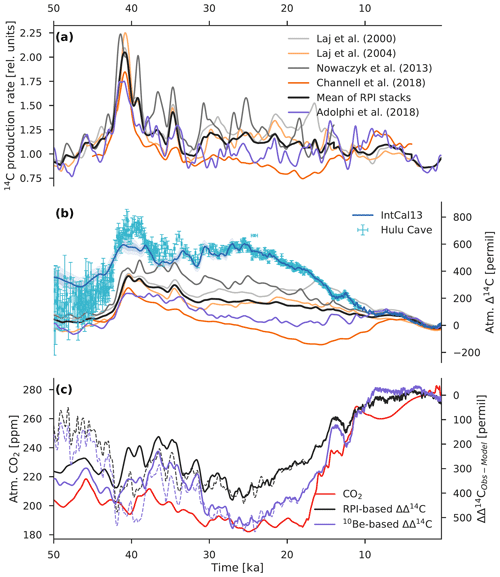
Figure 7 Component of atmospheric Δ¹⁴C variability caused by production changes alone. (a) Relative ¹⁴C production rate as inferred from paleointensity data (gray) and from polar ice-core ¹⁰Be fluxes (purple). The heavy dark gray line is the mean paleointensity-based ¹⁴C production rate. (b) Modeled Δ¹⁴C records based only on ¹⁴C production changes compared with the reconstructed IntCal13 and Hulu Cave Δ¹⁴C records. The modeled records are given by scenario MOD that assumes a constant preindustrial carbon cycle. (c) Difference between reconstructed Δ¹⁴C and model-simulated Δ¹⁴C using averaged paleointensity data (RPI-based ΔΔ¹⁴C; gray) and the ice-core ¹⁰Be data of Adolphi et al. (2018) (¹⁰Be-based ΔΔ¹⁴C; purple) compared with the atmospheric CO₂ record (red). Solid lines show the IntCal13–model difference, whereas dashed lines show the Hulu–model difference. The ΔΔ¹⁴C curve indicates changes in Δ¹⁴C that can be attributed to some combination of carbon cycle changes, uncertainties in the reconstruction of the ¹⁴C production rate, and uncertainties in the IntCal13 and Hulu Cave Δ¹⁴C records.

At first glance, the millennial-scale structure of model-simulated Δ¹⁴C_atm is comparable to that of the reconstructions. These similarities appear to be highest for the oldest portion of the record, roughly before 30 ka. The model reproduces major features of the reconstructed Δ¹⁴C_atm variability such as the large changes associated with the Laschamp (∼41 ka) and Mono Lake (∼34 ka) geomagnetic excursions. These two events are clearly expressed as distinct maxima in all model-simulated records. A more detailed comparison reveals a high correlation between the modeled and reconstructed Δ¹⁴C_atm values between 50 and 33 ka. Of note is the better agreement with the new Hulu Cave Δ¹⁴C_atm dataset compared to the IntCal13 calibration curve (i.e., Pearson correlation coefficient r of 0.96 vs. 0.91). This is likely due to the fact that the Laschamp excursion is smoothed and/or smeared out during the stacking process of the IntCal13 Δ¹⁴C_atm datasets (Adolphi et al., 2018). The correlation between modeled and reconstructed Δ¹⁴C_atm is much weaker during the millennia after the Mono Lake excursion (33 to 18 ka; r=0.52 to 0.64). While it is clear that much of the millennial-scale variation in Δ¹⁴C_atm is driven by past changes in ¹⁴C production, the model fails to reproduce the glacial level of Δ¹⁴C_atm and also does not capture the ∼15 000-year persistent elevation of Δ¹⁴C_atm or the subsequent decrease in Δ¹⁴C_atm after ∼25 ka.

The reconstructions suggest that the highest values of Δ¹⁴C_atm occurred during the Laschamp excursion, with a maximum value of ∼595 ‰ at 41.1 ka found in the IntCal13 record. The Hulu Cave record indicates even higher values for the Laschamp event (${\mathrm{\Delta }}^{\mathrm{14}}{\mathrm{C}}_{\mathrm{atm}}=\sim \mathrm{742}$ ‰ at 39.7 ka). In contrast, the model is able to simulate maximum Δ¹⁴C_atm values of only ∼364 ‰ at 40.4 ka and ∼236 ‰ at 40.5 ka, as predicted by the paleointensity-based and ice-core ¹⁰Be-based production rate estimates, respectively. Although the model is unable to reproduce the reconstructed values of Δ¹⁴C_atm, the modeled amplitude of the variation in Δ¹⁴C_atm in response to the Laschamp event shows reasonable agreement with the reconstructed amplitude of Δ¹⁴C_atm change found in the IntCal13 record (∼240 ‰). The Δ¹⁴C_atm change predicted by paleointensity data has a maximal amplitude of about 320 ‰, whereas the ice-core ¹⁰Be data indicate a smaller amplitude (∼224 ‰). Note that the IntCal13 and model-simulated amplitudes of the Laschamp-related Δ¹⁴C_atm change are about 2 times smaller than that observed in the Hulu Cave record (∼575 ‰), which is more likely to be correct.

Moving on to the full glacial record (50 to 18 ka), there are considerable discrepancies between reconstructed and modeled Δ¹⁴C_atm (ΔΔ¹⁴C; see Fig. 7). The use of ice-core ¹⁰Be data to predict past changes in Δ¹⁴C_atm results in the largest ΔΔ¹⁴C, with offsets between the records as high as ∼544 ‰ to 558 ‰ (root mean square error: RMSE=404 ‰ to 408 ‰). Model-simulated Δ¹⁴C_atm given by paleointensity data varies widely between the four available reconstructions, yielding ΔΔ¹⁴C values of ∼325 ‰ to 639 ‰ (RMSE=206 ‰ to 455 ‰). Note that the upper limit of the paleointensity-based ΔΔ¹⁴C overlaps the ice-core ¹⁰Be-based ΔΔ¹⁴C. Given the uncertainties associated with the reconstruction of past changes in ¹⁴C production, accurate predictions of its contribution to past changes in Δ¹⁴C_atm are challenging. Nonetheless, the substantial systematic offsets between the reconstructed and model-simulated Δ¹⁴C_atm records after ∼33 ka point toward insufficiently high ¹⁴C production rates over this period of time. The question arises as to whether another factor besides geomagnetic modulation of the cosmic ray intensity was responsible for elevated glacial Δ¹⁴C_atm levels. The effect of ocean carbon cycle changes on the evolution of Δ¹⁴C_atm is considered next.

3.3 Carbon cycle contribution to high glacial atmospheric Δ¹⁴C levels

Here we investigate the magnitude and timing of the maximum possible Δ¹⁴C_atm change during the last glacial period, obtained by running the Bern3D model with eight different carbon cycle scenarios (see Table 1). For the sake of clarity, we will discuss only the results of model runs using the mean paleointensity-based ¹⁴C production rate, though all available reconstructions were used. We emphasize that this is not a best-guess estimate of paleointensity-based ¹⁴C production. One should focus on the relative changes in Δ¹⁴C_atm between model scenarios and how specific carbon cycle processes affect the glacial level of Δ¹⁴C_atm.

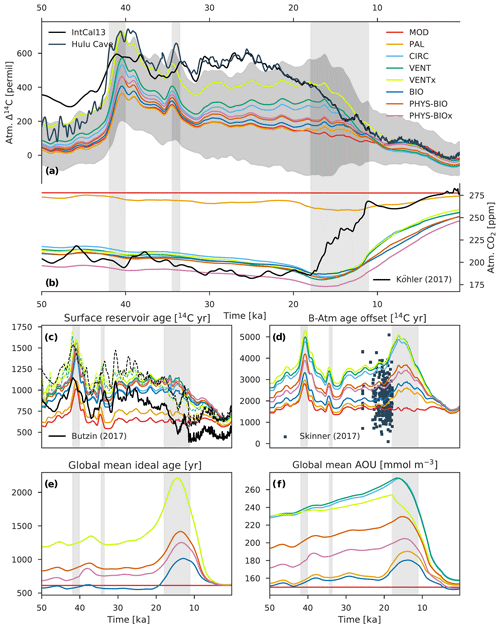
Figure 8 Modeled records of atmospheric (a) Δ¹⁴C and (b) CO₂ compared with their reconstructed histories (black and dark blue lines). Also shown are modeled records of the global average (c) surface reservoir age and (d) B-Atm ¹⁴C age offset compared with a recent compilation of LGM marine radiocarbon data (dark blue squares) by Skinner et al. (2017) and model-based surface reservoir age estimates between 50^∘ N and 50^∘ S (solid black line) and across all latitudes (dashed black line) from Butzin et al. (2017), as well as (e) ideal age and (f) apparent oxygen utilization (AOU). Colored lines show the results of model runs using the mean paleointensity-based ¹⁴C production rate and the eight different carbon cycle scenarios described in Sect. 2.4 and Table 1. The gray envelope in (a) shows the uncertainty (2σ) from all production rate reconstructions and carbon cycle scenarios, providing a bounded estimate of Δ¹⁴C change. The dashed colored lines in (c) show the surface reservoir age results from VENT and VENTx for which atmospheric Δ¹⁴C and CO₂ are prescribed. Radiocarbon ventilation ages are expressed here as radiocarbon reservoir age offsets following Soulet et al. (2016), which are used extensively by the radiocarbon dating community.

Modeled 50 000-year records of Δ¹⁴C_atm and CO₂ as well as their reconstructed histories are shown in Fig. 8. In order to provide a basis for comparison of modeling efforts, the results of model run MOD (which assumes a constant preindustrial carbon cycle) are presented. The influence of ocean carbon cycle changes on Δ¹⁴C_atm was tested in the other model runs. Interestingly, the forcing fields for model run PAL (orbital parameters, greenhouse gas radiative forcing, and ice sheet extent) have only a minimal impact on Δ¹⁴C_atm. The PAL forcing fields also do not achieve sufficiently low glacial CO₂ concentrations. Only a slight reduction of atmospheric CO₂ by ∼20 ppm could be achieved, which unrealistically occurs during the last glacial termination (CO₂=258.07 ppm at 14.6 ka). With hypothetical carbon cycle changes, the agreement between observed and modeled CO₂ during the last glacial period is good (as by design), but the deglacial CO₂ rise is lagged and ∼60 ppm too small at 11 ka. Since this study focuses on glacial Δ¹⁴C_atm levels before incipient deglaciation at ∼18 ka, we will not discuss the lag any further.

Model simulation of high glacial Δ¹⁴C_atm levels can be significantly improved by considering hypothetical carbon cycle changes in conjunction with PAL forcing. The amplitude of Δ¹⁴C_atm change is highest for runs CIRC, VENT, and VENTx. This behavior is due to the fact that, owing to a reduction of τ, K_V, and k_w, strong vertical Δ¹⁴C gradients in the ocean and a large air–sea Δ¹⁴C gradient are established. As shown in Fig. 8, a more sluggish ventilation of deep waters is clearly expressed as an increase in the model ocean's global average ideal age and surface-water and deepwater reservoir ages; the latter two are calculated for the surface ocean and bottom water grid cells, respectively. These are equivalent to radiocarbon reservoir age offsets following Soulet et al. (2016). The deepwater reservoir age (i.e., B-Atm ¹⁴C age offset, or B-Atm) provides a measure of the radiocarbon disequilibrium between the deep ocean and the atmosphere, which arises due to the combined effect of air–sea gas exchange efficiency and the deep ocean ventilation rate, whereas the effect of upper ocean stratification and/or sea ice on air–sea gas exchange is particularly important for surface reservoir ages (i.e., surface R age) (Skinner et al., 2019).

Driven by a reduction in ocean circulation, model run CIRC predicts a substantial increase in B-Atm during the last glacial, which is defined here as 40 to 18 ka to avoid biasing global mean estimates toward Laschamp values. The global average glacial B-Atm predicted by CIRC is ∼3225 ¹⁴C years, representing an increase in B-Atm of ∼1599 ¹⁴C years relative to the preindustrial value of ∼ 1626 ¹⁴C years. Model run VENT predicts a slightly larger increase in glacial B-Atm due to the inhibition of air–sea gas exchange. The “oldest” glacial waters are found in model run VENTx in which air–sea gas exchange is severely restricted, yielding an increase in B-Atm of ∼1912 ¹⁴C years (glacial B-Atm ∼3538 ¹⁴C years). The glacial B-Atm values given by runs CIRC, VENT, and VENTx, as well as the ∼717-year increase in ideal age during the last glacial relative to preindustrial, suggest that the glacial deep ocean was about 2 times older than its preindustrial counterpart. Comparison of our LGM B-Atm estimates (range of 3682 to 3962 ¹⁴C years) with the compiled LGM marine radiocarbon data of Skinner et al. (2017) demonstrates that the carbon cycle scenarios are extreme, although it should be noted that Skinner et al. consider a wider depth range (∼500 to 5000 m) of the ocean than we do. Skinner et al. (2017) predict a global average LGM B-Atm value of ∼2048 ¹⁴C years, an increase of ∼689 ¹⁴C years relative to preindustrial. Turning our comparison to surface reservoir ages, we note that our global average LGM surface R age of ∼1132 ¹⁴C years from runs VENT and VENTx is comparable to the ∼1241 ¹⁴C years obtained by Skinner et al. (2017) for the LGM. The model-based estimates of surface R age from Butzin et al. (2017) indicate a much lower LGM value of ∼780 ¹⁴C years and values ranging from 540 to 1250 ¹⁴C years between 50 and 25 ka. Note that these estimates are based on model-simulated values between 50^∘ N and 50^∘ S. If the polar regions are included in the calculation (see Fig. 8c), their surface R-age estimates become comparable to our glacial values (range of 911 to 1354 ¹⁴C years) and between about 34 and 22 ka can exceed them, even including those from model runs VENT and VENTx, unless Δ¹⁴C_atm and CO₂ are prescribed (dashed colored lines in Fig. 8c) as in the simulation by Butzin et al. (2017).

Indirect evidence for deepwater aging can be provided by the occurrence of depleted ocean interior oxygen levels due to the progressive consumption of dissolved oxygen during organic matter remineralization in the water column. This situation is amplified by the slow escape of accumulating remineralized carbon in the ocean interior (see, e.g., Skinner et al., 2017), leading to higher values of apparent oxygen utilization ($\text{AOU}={\mathrm{O}}_{\mathrm{2},\mathrm{pre}}-{\mathrm{O}}_{\mathrm{2}}$). These two concepts (increased AOU and increased B-Atm) taken together signal a significant reduction in deep ocean ventilation characterized by a decrease in the exchange rate between younger (higher Δ¹⁴C) surface waters and older (¹⁴C-depleted), carbon-rich deep waters. Model runs CIRC, VENT, and VENTx do indeed indicate a large increase in AOU of about 95 mmol m⁻³ from its preindustrial value of ∼150 mmol m⁻³. The reason for this AOU increase is that a reduction of deep ocean ventilation permits enhanced accumulation of remineralized carbon in the ocean interior and therefore a more efficient biological carbon pump. Model runs BIO, PHYS-BIO, and PHYS-BIOx allow us to investigate the impact of other biological carbon pump changes on Δ¹⁴C_atm and CO₂ (i.e., changes in the CaCO₃-to-POC export ratio and POC remineralization length scale). While these changes lead to an effective atmospheric CO₂ drawdown mechanism, model results confirm that their effect on Δ¹⁴C_atm is much less important (see Fig. 8).

Model run VENTx gives the best results with respect to glacial levels of Δ¹⁴C_atm, with a maximum underestimation of ∼202 ‰ to 229 ‰ (RMSE=103 ‰ to 110 ‰) and a relatively good correlation (r=0.79 to 0.91). Only one model parameter was changed for run VENTx compared to runs CIRC and VENT, namely the polar gas transfer velocity k_w was reduced to 0 % of its preindustrial value during the last glacial. In this extreme scenario, we assume that sea ice cover extended in the Northern Hemisphere as far south as 60^∘ N and in the Southern Hemisphere as far north as 48^∘ S, which is not supported by the reconstructions (Gersonde et al., 2005; Allen et al., 2011). Nonetheless, considering extreme assumptions about polar air–sea exchange efficiency under glacial climate conditions is interesting for two reasons: (1) a change in gas exchange hardly affects the atmospheric CO₂ concentration, and (2) an additional change in Δ¹⁴C_atm could possibly be achieved on a timescale of tens of thousands of years by changing the balance between weathering and sedimentation (see Sect. 3.1.3). This behavior has important implications for the glacial atmosphere, which is characterized by high Δ¹⁴C levels in conjunction with low but relatively stable CO₂ concentrations. In contrast to a change in ocean circulation, air–sea gas exchange is a dedicated Δ¹⁴C_atm “control knob” that can be invoked by models for a further increase in Δ¹⁴C_atm without changing atmospheric CO₂. Here, an additional increase in Δ¹⁴C_atm of ∼130 ‰ relative to CIRC and VENT is achieved if gas exchange is permanently reduced to 0 % in the polar regions.

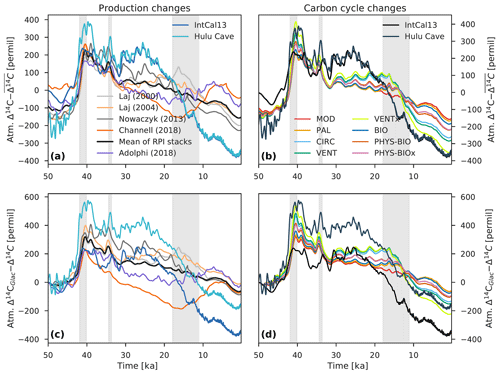
Figure 9 Comparison of atmospheric Δ¹⁴C variability caused by changes in the ocean carbon cycle (b, d) with production-driven changes in atmospheric Δ¹⁴C using scenario MOD (a, c). For the analysis of carbon cycle changes, only the results of model runs using the mean paleointensity-based ¹⁴C production rate are shown. The Δ¹⁴C records in the upper panels (a, b) have been detrended by removing the mean, whereas the lower panels (c, d) show Δ¹⁴C anomalies expressed as differences relative to the Δ¹⁴C value at 50 ka. Three vertical light gray bars indicate the Laschamp (∼41 ka) and Mono Lake (∼34 ka) geomagnetic excursions, as well as the last glacial termination (∼18 to 11 ka).

While the modeled Δ¹⁴C_atm values obtained by VENTx show rather good agreement with the reconstructions between 50 and 33 ka (r=0.92 to 0.96; RMSE=74 ‰ to 102 ‰), considerable discrepancies remain for the younger portion of the record. The analysis shown in Fig. 9 illustrates that even with extreme changes in the ocean carbon cycle it is very difficult to reproduce the reconstructed Δ¹⁴C_atm values after ∼33 ka. During this period of time, VENTx underestimates Δ¹⁴C_atm by up to ∼203 ‰ (RMSE=118 ‰ to 128 ‰) and is very poorly (r=0.1) correlated with the reconstructions, confirming that there are still considerable gaps in our understanding. Although it may be possible that permanent North Atlantic–Arctic and Antarctic sea ice cover extended to lower and higher latitudes than previously reconstructed, we conclude from our model study that even extreme assumptions about sea ice cover are insufficient to explain the elevated Δ¹⁴C_atm levels after ∼33 ka. It appears instead that the glacial ¹⁴C production rate was higher than previously estimated and/or the reconstruction of glacial Δ¹⁴C_atm levels is biased high. The older portion of the Δ¹⁴C_atm record is based on data from archives other than tree rings (i.e., plant macrofossils, speleothems, corals, and foraminifera) (Reimer et al., 2013), providing, except for the Lake Suigetsu plant macrofossil data (Bronk Ramsey et al., 2012), only indirect measurements of Δ¹⁴C_atm. Note that these data show uncertainty in calendar age that propagates into the estimation of past Δ¹⁴C_atm levels.

Large uncertainties in the pre-Holocene ¹⁴C production rate also hamper our qualitative and quantitative interpretation of the Δ¹⁴C_atm record. There is considerable disagreement between the available reconstructions of past changes in ¹⁴C production (Fig. 1). Paleointensity-based estimates typically predict higher ¹⁴C production rates than ice-core ¹⁰Be-based ones. An exception is the paleointensity stack from Channell et al. (2018), which predicts lower production rates. But, irrespective of the scatter, it is clear that all of the ¹⁴C production rate estimates are insufficiently high to explain the elevated Δ¹⁴C_atm levels during the last glacial. Given the uncertainties in these estimates, it is very difficult to quantitatively describe the role of the ocean carbon cycle in determining the Δ¹⁴C and CO₂ levels in the glacial atmosphere.

3.4 Reconstructing the ¹⁴C production rate by deconvolving the atmospheric Δ¹⁴C record

The unresolved discrepancy between reconstructed and model-simulated Δ¹⁴C_atm raises the question of how the ¹⁴C production rate would have had to evolve to be consistent with the IntCal13 calibration curve or the new Hulu Cave Δ¹⁴C_atm dataset. This question is addressed by deconvolving the Δ¹⁴C_atm reconstruction over the last 50 kyr using the Bern3D carbon cycle model forced with reconstructed histories of Δ¹⁴C_atm and CO₂ (see Eq. 2). The carbon cycle scenarios described in Table 1, with the exception of MOD, are used in order to provide an estimate of the uncertainty associated with the model's glacial ocean carbon cycle. We note that the carbon cycle scenarios are not designed to capture the specific features of the last glacial termination, and therefore the results of the deconvolution over this time period must be considered very preliminary (and regarded as tentative). A detailed analysis of the Holocene ¹⁴C production rate is available in the literature (Roth and Joos, 2013). Finally, we consider the uncertainties associated with the older portion of the Δ¹⁴C_atm record by deconvolving both the IntCal13 and Hulu Cave Δ¹⁴C_atm records. Hulu Cave data overlap IntCal13 between ∼10.6 and 33.3 ka (Cheng et al., 2018), as expected from the fact that IntCal13 between 10.6 and 26.8 ka is based in part on Hulu Cave stalagmite H82 (Southon et al., 2012), whereas there are substantial offsets before ∼30 ka.

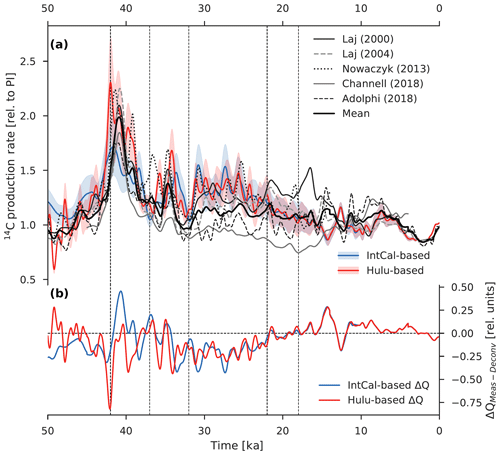
Figure 10 Comparison of ¹⁴C production rate estimates inferred from a deconvolution of the atmospheric Δ¹⁴C record and from paleointensity and ice-core ¹⁰Be data. (a) ¹⁴C production rate calculated as the sum of the modeled air–sea and atmosphere–land ¹⁴CO₂ fluxes as well as the reconstructed change in the atmospheric ¹⁴C inventory and loss of ¹⁴C due to radioactive decay (see Eq. 2). Model-based ¹⁴CO₂ fluxes were obtained by forcing the Bern3D carbon cycle model with reconstructed variations in atmospheric Δ¹⁴C and CO₂ as well as seven different carbon cycle scenarios. Results of model runs using the IntCal13 calibration curve are shown in the light blue envelope (2σ), whereas the light red envelope (2σ) shows the results from simulations using the composite Hulu Cave (10.6 to 50 ka) and IntCal13 (0 to 10.6 ka) Δ¹⁴C record. The heavy black line is the mean of five available production rate reconstructions: Laj et al. (2000, 2004), Nowaczyk et al. (2013), Channell et al. (2018), and Adolphi et al. (2018). (b) Difference between the mean of the measurement-based production rate estimates (heavy black line) and estimates based on the deconvolution of the IntCal13 (IntCal-based ΔQ; blue) and Hulu Cave (Hulu-based ΔQ; red) Δ¹⁴C data.

Figure 10 shows the new, model-based reconstruction of past changes in ¹⁴C production compared with available measurement-based reconstructions. Before the onset of the Laschamp excursion at ∼42 ka, production rates as inferred from the Hulu Cave record are near modern levels, whereas those obtained from the IntCal13 record are somewhat higher than modern. As expected, peak production occurs during the Laschamp event (∼42 to 40 ka), with the Hulu Cave dataset yielding the largest amplitude (factor of ∼2 greater than modern). The IntCal13 record predicts a smaller amplitude of ∼1.6 times the modern value. Both Δ¹⁴C_atm records predict production minima at ∼37 ka (∼7 % higher than modern) and ∼32 ka (∼5 % higher than modern), interrupted by a prominent peak (factors of ∼1.5 and ∼1.4, respectively) during the Mono Lake geomagnetic excursion (∼34 ka), though the details of the timing and structure differ between the two records. Between 32 and 22 ka, model-based estimates of the ¹⁴C production rate are ∼1.3 times the modern value, which then decrease to around modern levels by HS1 (∼18 ka).

Table 2 Production rate estimates in relative units inferred from three fundamentally different reconstruction methods: geomagnetic field data from marine sediments, ¹⁰Be and ³⁶Cl measurements in polar ice cores, and model-based deconvolution of atmospheric Δ¹⁴C. Laj00, Laj04, Now13, and Chn18 refer to the paleointensity-based reconstructions of Laj et al. (2000), Laj et al. (2004), Nowaczyk et al. (2013), and Channell et al. (2018), respectively. Adp18 refers to the ice-core ¹⁰Be-based reconstruction of Adolphi et al. (2018). Int13 and Hul18 refer to the model-based reconstructions from this study using the IntCal13 calibration curve (Reimer et al., 2013) and the new Hulu Cave Δ¹⁴C dataset (Cheng et al., 2018). The bold numbers show the mean production rates during the last glacial (50 to 18 ka).

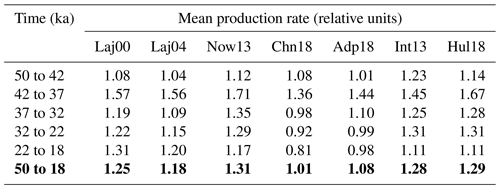
Model-based estimates of ¹⁴C production during the last glacial are typically higher than paleointensity-based and ice-core ¹⁰Be-based ones, as expected from Sect. 3.2. Between 32 and 22 ka, the deconvolutions of the IntCal13 and Hulu Cave Δ¹⁴C_atm records give estimates that are about 17.5 % higher than the reconstructions. It is important to note that the differences between the reconstructions based on proxy data (i.e., paleointensity data and ice-core ¹⁰Be fluxes) are as large as the differences between our deconvolution results and the reconstructions (see Table 2). As shown in Fig. 11, it is extremely difficult to reconcile the discrepancies between measurement- and model-based ¹⁴C production on the basis of carbon cycle changes alone. Nonetheless, the fact remains that two independent estimates of the ¹⁴C production rate (i.e., estimates inferred from paleointensity data and from ice-core ¹⁰Be fluxes) show systematically lower rates than those obtained by our model-based deconvolution of Δ¹⁴C_atm, in particular between 32 and 22 ka. The differences between the production rate results shown in Figs. 10–11 and Table 2 stem from various uncertainties that are discussed next.

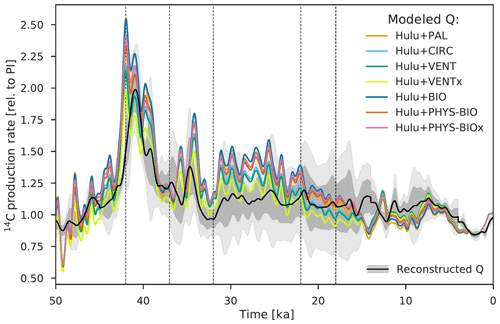
Figure 11 Relative ¹⁴C production rate as inferred from the Bern3D model under seven carbon cycle scenarios (see Sect. 2.4). Estimates shown here are based on the composite Hulu Cave and IntCal13 Δ¹⁴C record. The black line is the mean of the five production rate reconstructions shown in Fig. 10; the gray envelope shows its uncertainty (2σ).

Uncertainties associated with the glacial ocean carbon cycle (Fig. 10, colored shading; Fig. 11, colored lines) are systematic in our approach. The deconvolutions, e.g., of the Hulu Cave Δ¹⁴C_atm record, under different model scenarios are offset against one another, whereas the millennial-scale variability is maintained (see Fig. 11). We do not attempt to resolve uncertainties associated with Dansgaard–Oeschger warming events and related Antarctic and tropical climatic excursions in the model runs. Such climatic events may have influenced the atmospheric radiocarbon budget, but their influence on long-term variations in Δ¹⁴C_atm, and therefore inferred production rates, is presumably limited. As may be expected, the lowest production rates (the lowest F_as values) are found in VENTx and the highest in scenarios PAL and BIO, mirroring the high and low glacial Δ¹⁴C_atm levels achieved by these model scenarios as discussed in Sect. 3.3. Note that there is a large uncertainty in the model-based ¹⁴C production rate stemming from uncertainties associated with the reconstruction of past changes in Δ¹⁴C_atm, in particular the older portion of the Δ¹⁴C_atm record.

A shortcoming of paleointensity-based reconstructions of the ¹⁴C production rate is that they neglect changes in the solar modulation of the cosmic radiation. The solar modulation potential, which describes the impact of the solar magnetic field on isotope production, varied between 100 and 1200 MeV during the Holocene on decadal to centennial timescales, with a median value of approximately 565 MeV (Roth and Joos, 2013). A halving of the solar modulation potential (e.g., from 600 to 300 MeV) increases the ¹⁴C production rate by about 25 % for the modern geomagnetic field strength (Roth and Joos, 2013; see their Fig. 13). This sensitivity remains similar when changes in the strength of the geomagnetic field are limited as during the last ∼35 kyr (Muscheler and Heikkilä, 2011). A shift to lower solar modulation potential could have materialized if the sun spent on average more time in the postulated “grand minimum” mode (Usoskin et al., 2014) during the last glacial than during the Holocene. The sensitivity of isotope production to variations in solar modulation potential became large during the Laschamp event when the intensity of the geomagnetic field was close to zero, and changes in the solar modulation of the cosmic ray flux may have had a discernible impact on the high Δ¹⁴C_atm levels found over this period. A reduction of the solar modulation potential from 600 to 0 MeV would double ¹⁴C production during times of zero geomagnetic field strength (Masarik and Beer, 2009). However, it is likely that changes in the solar modulation potential were insufficient to explain the discrepancy between paleointensity-based production rate estimates and the results of our deconvolution, in particular for the post-Laschamp period and for the reconstruction by Channell et al. (2018). Uncertainties associated with the paleointensity-based reconstructions also stem from uncertainties in estimating the age scales of the marine sediments and the geomagnetic field data.

The ice-core ¹⁰Be-based reconstruction of past changes in ¹⁴C production reflects, by definition, the combined influence of changes in the solar and geomagnetic modulation of the cosmic ray flux reaching the Earth. This method therefore avoids a fundamental shortcoming of reconstructions based on geomagnetic field data. The assumption is that the ¹⁰Be and ³⁶Cl deposited on polar ice and measured in ice cores scales with the amount of cosmogenic isotopes in the atmosphere. A difficulty is to extrapolate measurements from a single location or a few locations to the global atmosphere. Changes in climate influence the atmospheric transport and deposition of ¹⁰Be as well as the snow accumulation rate, which affect the ice-core ¹⁰Be concentration (Elsässer et al., 2015). Furthermore, the sensitivity of ¹⁰Be in polar ice vs. the sensitivity of total production to magnetic field variations, or “polar bias”, is a point of debate, but atmospheric transport models (Heikkilä et al., 2009; Field et al., 2006) and data analyses (Bard et al., 1997; Adolphi and Muscheler, 2016; Adolphi et al., 2018) reach different conclusions about its existence and magnitude. If a polar bias was present, it would lead to an underestimation of the geomagnetic modulation of the ice-core ¹⁰Be flux, and therefore variations in the ¹⁰Be-based ¹⁴C production rate would also be underestimated. However, the mismatch of up to ∼544 ‰ to 558 ‰ between reconstructed and modeled ¹⁰Be-based Δ¹⁴C_atm during the last glacial (see Fig. 7c) appears to be much too large to be reconciled by considering uncertainties in the polar bias alone. Furthermore, this mismatch with reconstructed Δ¹⁴C_atm is qualitatively similar when using paleointensity-based ¹⁴C production rates that do not suffer from a polar bias (Fig. 7c).

Given the uncertainties associated with the proxy records, it may not be surprising that estimates of the ¹⁴C production rate for the last 50 kyr, as obtained by three fundamentally different methods (geomagnetic field data from marine sediments, ¹⁰Be and ³⁶Cl measurements in polar ice cores, and model-based deconvolution of Δ¹⁴C_atm), disagree with one another, typically by order 10 % and sometimes by up to 100 %. At the same time, it is intriguing that two independent estimates of the ¹⁴C production rate (i.e., estimates inferred from paleointensity and ice-core ¹⁰Be data) give values that are systematically lower than what is required to match the Δ¹⁴C_atm reconstruction.

4 Summary and conclusions

It is generally assumed that Δ¹⁴C_atm is controlled by abiotic processes such as atmospheric ¹⁴C production, air–sea gas exchange, and ocean circulation and mixing. Here, results from sensitivity experiments with the Bern3D Earth system model of intermediate complexity suggest that Δ¹⁴C_atm is potentially quite sensitive to the interaction with the ocean sediments on multimillennial timescales. This rather surprising result is due to the coupling of ocean circulation and the sedimentation of biogenic material on the seafloor via the biological carbon pump, which has important implications for the ocean carbon inventory. If the model's ocean carbon cycle is sufficiently perturbed, e.g., by changing the inputs or parameters controlling ocean circulation and/or gas exchange, the imbalance between weathering and sedimentation has a significant impact on the total oceanic amount of carbon. On timescales of tens of thousands of years this slow change in the ocean carbon inventory influences the partitioning of ¹⁴C∕C between the ocean and atmosphere and thus also oceanic Δ¹⁴C and Δ¹⁴C_atm. This is important information for long-term climate studies and paleoclimate modeling efforts concerning Δ¹⁴C_atm. Note that the representation of terrestrial weathering and seafloor sedimentation in the Bern3D model is necessarily simplified compared to reality. Nonetheless, a change in the ocean carbon inventory linked with the weathering–sedimentation balance should be discussed as one of the potentially important factors affecting Δ¹⁴C_atm during the last glacial period.

The reason for the high Δ¹⁴C values exhibited by the glacial atmosphere is still not clear. In order to investigate potential mechanisms governing glacial Δ¹⁴C_atm levels, the Bern3D model is again used as a tool. Results of model simulations forced only by production changes point out that none of the available reconstructions of the ¹⁴C production rate can explain the full amplitude of Δ¹⁴C_atm change during the last glacial. In order to test the sensitivity of the model results with respect to the ocean carbon cycle state, various model parameters, i.e., different sets of physical and biogeochemical parameters, were “tuned” to match the glacial CO₂ level. From this, we find that Δ¹⁴C_atm is most sensitive to changes in physical model parameters, in particular those controlling ocean circulation and gas exchange. In order to achieve a Δ¹⁴C_atm value close to the glacial level, the gas transfer velocity in the polar regions had to be reduced by 100 %. If interpreted as being due to a greater extent of permanent sea ice cover, a reduction in polar air–sea exchange efficiency is a possible explanation for high glacial Δ¹⁴C_atm levels. Although this hypothesis is compelling, such a scenario is not supported by the proxy records of Antarctic sea ice cover (Gersonde et al., 2005; Allen et al., 2011) and the ¹³C∕¹²C ratio of atmospheric CO₂ (Eggleston et al., 2016).

Atmospheric Δ¹⁴C that is modeled at any point in time reflects ¹⁴C production at that point, as well as the legacy of past production and carbon cycle changes. The question arises as to whether our conclusions are affected by unaccounted legacy effects, e.g., linked to the preindustrial spin-up simulation or model-diagnosed production rates. Transient simulations forced by reconstructed changes in ¹⁴C production (Sect. 3.2 and 3.3) are initialized at 70 ka, but their interpretation is restricted to the last 50 000 years of the integration to minimize legacy effects from model spin-up. Available reconstructions of the ¹⁴C production rate in relative units (Sect. 2.5) are applied as a scale factor to the preindustrial steady-state absolute value, which is diagnosed by running the Bern3D model to equilibrium under preindustrial boundary conditions. This approach represents an approximation and equilibrium conditions do not fully apply. Indeed, there is a mismatch between reconstructed and modeled Δ¹⁴C_atm at the preindustrial (see Fig. 8a). This mismatch is on the order of a few percent or less, and adjusting the base level of production accordingly would not remove the large mismatch between reconstructed and modeled Δ¹⁴C_atm during the last glacial. In addition, the uncertainty in the absolute value of the preindustrial production rate is on the order of 15 %, primarily due to the uncertainties in the preindustrial ocean radiocarbon inventory (see Roth and Joos, 2013, Sect. 3.2). This potential systematic bias, however, does not affect our conclusions as we consider normalized production rate changes (see Figs. 7, 10, and 11).

Before model-simulated Δ¹⁴C_atm can be taken seriously, it must be demonstrated that the reconstruction of past changes in ¹⁴C production is reliable. There is, however, a substantial amount of scatter in the paleointensity-based and ice-core ¹⁰Be-based estimates of ¹⁴C production. Here we adopt an alternative approach to estimating the ¹⁴C production rate, which would indeed benefit from further constraints and lines of supporting evidence. Our deconvolution-based approach assumes that the ¹⁴C production rate can be derived from an atmospheric radiocarbon budget constructed using a prognostic carbon cycle model combined with the Δ¹⁴C_atm record. Here, nonequilibrium effects are fully accounted for by transient simulations in which Δ¹⁴C_atm and CO₂ are prescribed following their reconstructed histories (Sect. 3.4). Yet, these simulations indicate that the discrepancy between measurement- and model-based estimates of the ¹⁴C production rate remains for the last glacial (Fig. 10b). This would suggest that unaccounted legacy effects do not significantly affect our conclusions. Our model results imply that the glacial ¹⁴C production rate as inferred from paleointensity data and ice-core ¹⁰Be fluxes may be underestimated by about 15 % between 32 and 22 ka, a time interval that appears to be an important piece of the glacial–interglacial Δ¹⁴C_atm puzzle. Note that our model-based estimates are associated with uncertainties arising from the reconstruction of the older portion of the Δ¹⁴C_atm record and from the model simulation of the glacial ocean carbon cycle (e.g., uncertainties in the glacial ocean circulation and air–sea CO₂ fluxes). An improved understanding of the role of ¹⁴C production in past changes in Δ¹⁴C_atm would open up the possibility of attributing model deficiencies to real changes in the ocean carbon cycle, but there is as yet no emerging single record of the ¹⁴C production rate.

Progress in several different areas may help to resolve the glacial–interglacial radiocarbon problem. Additional records of glacial Δ¹⁴C_atm would help refine the older portion of the IntCal Δ¹⁴C record. Cosmogenic isotope production records may be improved, e.g., by refining estimates of ice accumulation, by developing a better understanding of ¹⁰Be transport and deposition during the glacial, by recovering additional long and continuous records from Antarctic ice cores and including marine ¹⁰Be records, and by obtaining additional geomagnetic field data. An expanded spatiotemporal observational coverage of Δ¹⁴C of DIC in the surface and deep ocean would help narrow the timescales of surface-to-deep transport and the air–sea equilibration of Δ¹⁴C, carbon, and nutrients, thereby guiding model-based analyses. Models should become more sophisticated and detailed in order to successfully reproduce the glacial–interglacial changes in carbon and radiocarbon by including exchange with sediments and the lithosphere, by better representing coastal processes, and by simulating a wide variety of paleo-proxies such as δ¹³C, Nd isotopes, carbonate ion concentration, lysocline evolution, and paleo-productivity proxies in a 3-D dynamic context for model evaluation. What is also missing are methods to quantify how the ocean carbon inventory, which codetermines the ¹⁴C∕C ratio and thus the Δ¹⁴C values in the ocean and atmosphere, has changed over the last 50 000 years. Ultimately, improved knowledge of ¹⁴C production during the last glacial and more robust constraints on the prevailing climate conditions (e.g., ocean circulation, sea ice cover, and wind speed) are necessary to elucidate the processes permitting mysteriously high Δ¹⁴C levels in the glacial atmosphere.

Appendix A: Description of the Bern3D model

The physical core of the Bern3D model is based on the 3-D rigid-lid ocean model of Edwards et al. (1998) as updated by Edwards and Marsh (2005). The forcing fields for the model integration are monthly mean wind stress data taken from NCEP/NCAR (Kalnay et al., 1996). Diapycnal mixing is parameterized with a uniform vertical diffusivity K_V of $\mathrm{2}\times {\mathrm{10}}^{-\mathrm{5}}$ m s⁻¹. The parameterization of eddy-induced transport is separated from that of isopycnal mixing using the Gent–McWilliams skew flux (Griffies, 1998). Running at the same temporal and horizontal resolution, the one-layer energy–moisture balance atmosphere model performs an analysis of the energy budget of the Earth by involving solar radiation, infrared fluxes, evaporation and precipitation, and sensible and latent heat. The zonally averaged surface albedo climatology is taken from Kukla and Robinson (1980). Transport of moisture is performed by diffusion and advection and heat by eddy diffusion.

The Bern3D ocean carbon cycle model is based on the Ocean Carbon-Cycle Model Intercomparison Project (OCMIP-2) protocols. Air–sea gas exchange is parameterized using the standard gas transfer formulation adopted for OCMIP-2, except that the gas transfer velocity k_w parameterization is a linear function of wind speed (Krakauer et al., 2006) to which we have added a scale factor of 0.81 to match the observed global ocean inventory of bomb ¹⁴C (Müller et al., 2008). It is assumed that CO₂ and O₂ are well-mixed in the atmosphere. Surface boundary conditions also include a virtual flux term for biogeochemical tracers (e.g., DIC and Alk) to account for their dilution or concentration due to implicit freshwater fluxes. Following OCMIP-2 biotic protocol, new production is partitioned into particulate and dissolved organic matter. Modifications from the original OCMIP-2 biotic protocol include the prognostic formulation of new/export production as a function of light, temperature, and limiting nutrient concentrations, for which the nutrient uptake follows Michaelis–Menten kinetics. The production of biogenic CaCO₃ and opal is computed on the basis of the modeled particulate organic carbon (POC) production and availability of silicate, with a maximum possible fraction of CaCO₃ material that can be produced. This threshold value is represented by the CaCO₃-to-POC export ratio. In the preindustrial control run, the global mean export ratio (rr) is 0.082.

Biogenic particles that have been produced in the 75 m production zone are redistributed over the water column in order to parameterize the downward particle flux through the water column. A power-law model referred to as the Martin curve is used to describe the vertical POC flux profile, whereas both CaCO₃ and opal export are redistributed over the water column with an exponential curve. POC is remineralized instantaneously back to dissolved form according to Redfield stoichiometry and with a 250 m length scale ℓ_POC (i.e., in 250 m, the POC flux declines by $\mathrm{1}-\mathrm{1}/e\approx \mathrm{63}$ %). Likewise, CaCO₃ and opal are dissolved within one time step, with e-folding depths of 5066 and 10 000 m, respectively. Biogenic particles reaching the model's seafloor form the upper boundary condition of the 10-layer sediment model after Heinze et al. (1999) and Gehlen et al. (2006). The sediment model includes four solid sediment components (POC, CaCO₃, opal, and clay) and is based on the sediment advection and accumulation scheme as in the work of Archer et al. (1993). The rate of POC remineralization in the sediments is primarily determined by the pore water concentration of oxygen, whereas the mineral dissolution rate is governed by the saturation state of sediment pore waters with respect to CaCO₃ or opal. Weathering (dissolution) of carbonate and silicate rocks on land, phosphorous release by chemical weathering of rocks, and volcanic outgassing of CO₂ are simulated as constant inputs of DIC, Alk, phosphate (P), and silicate (Si) to the ocean at rates intended to balance their removal from the ocean by sedimentation on the seafloor. These weathering inputs are added as a constant increment to each surface ocean grid cell along the coastlines. The preindustrial steady state of the model is used to diagnose the weathering rates that are held fixed and constant throughout the simulations. Note that the preindustrial spin-up results in steady-state values for weathering-derived inputs of DIC, Alk, P, and Si of 0.46 Gt C yr⁻¹, 34.37 Tmol Alk yr⁻¹, 0.17 Tmol P yr⁻¹, and 6.67 Tmol Si yr⁻¹, respectively. These values are within the range of observational estimates (see, e.g., Jeltsch-Thömmes et al., 2019). Additional details concerning the sediment model are provided in Tschumi et al. (2011), while the Appendix of Jeltsch-Thömmes et al. (2019) gives a detailed description of the atmosphere–ocean–sediment spin-up.

The exchange of any isotopic perturbation between the atmosphere and the terrestrial biosphere is simulated by use of the four-box model of Siegenthaler and Oeschger (1987). The terrestrial biosphere is represented by four well-mixed compartments (ground vegetation plus leaves, wood, detritus, and soils), with a fixed total carbon inventory of 2220 Gt C. Net primary production is balanced by respiration of detritus and soils and is set to 60 Gt C yr⁻¹.