Sensitivity of a leaf gas-exchange model for estimating paleoatmospheric CO₂ concentration

Leaf gas-exchange models show considerable promise as paleo-CO₂ proxies. They are largely mechanistic in nature, provide well-constrained estimates even when CO₂ is high, and can be applied to most subaerial, stomata-bearing fossil leaves from C₃ taxa, regardless of age or taxonomy. Here we place additional observational and theoretical constraints on one of these models, the “Franks” model. In order to gauge the model's general accuracy in a way that is appropriate for fossil studies, we estimated CO₂ from 40 species of extant angiosperms, conifers, and ferns based only on measurements that can be made directly from fossils (leaf δ¹³C and stomatal density and size) and on a limited sample size (one to three leaves per species). The mean error rate is 28 %, which is similar to or better than the accuracy of other leading paleo-CO₂ proxies. We find that leaf temperature and photorespiration do not strongly affect estimated CO₂, although more work is warranted on the possible influence of O₂ concentration on photorespiration. Leaves from the lowermost 1–2 m of closed-canopy forests should not be used because the local air δ¹³C value is lower than the global well-mixed value. Such leaves are not common in the fossil record but can be identified by morphological and isotopic means.

1 Introduction

Leaves on terrestrial plants are well poised to record information about the concentration of atmospheric CO₂. They are in direct contact with the atmosphere and have large surface-area-to-volume ratios, so the leaf internal CO₂ concentration is tightly coupled to atmospheric CO₂ concentration. Also, leaves are specifically built for the purpose of fixing atmospheric carbon into structural tissue and face constant selection pressure to optimize their carbon uptake relative to water loss. As a result, many components of the leaf system are sensitive to atmospheric CO₂, and these components feed back on one another to reach a new equilibrium when atmospheric CO₂ changes. In terms of carbon assimilation, Farquhar and Sharkey (1982) modeled this system in its simplest form as

$$\begin{array}{}\text{(1)}& A_n=g_{\text{c(tot)}}\times (c_{\text{a}}-c_{\text{i}}),\end{array}$$

where A_n is the leaf CO₂ assimilation rate (µmol m⁻² s⁻¹), g_c(tot) is the total operational conductance to CO₂ diffusion from the atmosphere to the site of photosynthesis (mol m⁻² s⁻¹), c_a is atmospheric CO₂ concentration (µmol mol⁻¹ or ppm), and c_i is leaf intercellular CO₂ concentration (µmol mol⁻¹ or ppm) (see also Von Caemmerer, 2000). Rearranging Eq. (1) for atmospheric CO₂ yields

$$\begin{array}{}\text{(2)}& c_{\text{a}}={\displaystyle \frac{A_n}{g_{\text{c(tot)}}\times \left(\mathrm{1}-\frac{c_{\text{i}}}{c_{\text{a}}}\right)}}.\end{array}$$

Equation (2) forms the basis of two leaf gas-exchange approaches for estimating paleo-CO₂ from fossils (Konrad et al., 2008, 2017; Franks et al., 2014). In the Franks model, conductance is estimated in part from measurements of stomatal size and density, c_i∕c_a from measurements of leaf δ¹³C along with reconstructions of coeval air δ¹³C (see also Eq. 9), and A_n from knowledge of living relatives and its dependency on c_a (Franks et al., 2014). Following Farquhar et al. (1980), the latter is modeled as (Franks et al., 2014; Kowalczyk et al., 2018)

$$\begin{array}{}\text{(3)}& A_n=A_{\mathrm{0}}{\displaystyle \frac{\left[\left(\frac{c_{\text{i}}}{c_{\text{a}}}\right)c_{\text{a}}-{\mathrm{\Gamma }}^{*}\right]\left[\left(\frac{c_{i\mathrm{0}}}{c_{a\mathrm{0}}}\right)c_{a\mathrm{0}}+\mathrm{2}{\mathrm{\Gamma }}^{*}\right]}{\left[\left(\frac{c_{\text{i}}}{c_{\text{a}}}\right)c_{\text{a}}+\mathrm{2}{\mathrm{\Gamma }}^{*}\right]\left[\left(\frac{c_{i\mathrm{0}}}{c_{a\mathrm{0}}}\right)c_{a\mathrm{0}}-{\mathrm{\Gamma }}^{*}\right]}},\end{array}$$

where Γ^* is the CO₂ compensation point in the absence of dark respiration (ppm), and the subscript “0” refers to conditions at a known CO₂ concentration (typically present day). Equations (2) and (3) are then solved iteratively until the solution for c_a converges.

These gas-exchange approaches grew out of a group of paleo-CO₂ proxies based on the CO₂ sensitivity of stomatal density (D) or the similar metric stomatal index (Woodward, 1987; Royer, 2001). Here, the D–c_a sensitivity is calibrated in an extant species, allowing for paleo-CO₂ inference from the same (or very similar) fossil species. These empirical relationships typically follow a power-law function (Wynn, 2003; Franks et al., 2014; Konrad et al., 2017):

$$\begin{array}{}\text{(4)}& c_{\text{a}}={\displaystyle \frac{\mathrm{1}}{k{D}^{\mathit{\alpha }}}},\end{array}$$

where k and α are species-specific constants.

The related stomatal ratio proxy is simplified: D is measured in an extant species (D₀, at present-day c_a0) and then the ratio of D₀ to D in a related fossil species is assumed to be linearly related to the ratio of paleo-c_a to present-day c_a0 (Chaloner and McElwain, 1997; McElwain, 1998):

$$\begin{array}{}\text{(5)}& {\displaystyle \frac{c_{\text{a}}}{c_{a\mathrm{0}}}}=k{\displaystyle \frac{D_{\mathrm{0}}}{D}}.\end{array}$$

Equation (5) can be rearranged to match Eq. (4) but with α fixed at 1. Thus, paleo-CO₂ estimates using the stomatal ratio proxy are based on a one-point calibration and an assumption that α=1; observations do not always support this assumption (e.g., α=0.43 for Ginkgo biloba; Barclay and Wing, 2016). The scalar k was originally set at 2 for Paleozoic and Mesozoic reconstructions so that paleo-CO₂ estimates during the Carboniferous matched that from long-term carbon cycle models (Chaloner and McElwain, 1997). For younger reconstructions, k is probably closer to 1 (by definition, k=1 for present-day plants). We note that the stomatal ratio proxy was originally conceived as providing qualitative information only about paleo-CO₂ (McElwain and Chaloner, 1995, 1996; Chaloner and McElwain, 1997; McElwain, 1998) and has not been tested with dated herbaria materials or with CO₂ manipulation experiments.

At high CO₂, the D–c_a sensitivity saturates in many species, leading to uncertain paleo-CO₂ estimates, often with unbounded upper limits (e.g., Smith et al., 2010; Doria et al., 2011). Stomatal density does not respond to CO₂ in all species (Woodward and Kelly, 1995; Royer, 2001), and because D–c_a relationships can be species specific (that is, different species in the same genus with different responses; Beerling, 2005; Haworth et al., 2010), only fossil taxa that are still alive today should be used. The gas-exchange proxies partly address these limitations: (1) CO₂ estimates remain well-bounded – even at high CO₂ – and their precision is similar to or better than other leading paleo-CO₂ proxies ($\sim +\mathrm{35}/-\mathrm{25}$ % at 95 % confidence; Franks et al., 2014) and (2) the models are mostly mechanistic; that is, they are explicitly driven by plant physiological principles, not just empirical relationships measured on living plants. (3) Because the models retain sensitivity at high CO₂ and do not require that a fossil species still be alive today, much of the paleobotanical record is open for CO₂ inference, regardless of age or taxonomy. (4) Because the models are based on multiple inputs linked by feedbacks, they can still perform adequately even if one or more of the inputs in a particular taxon is not sensitive to CO₂, for example stomatal density (Milligan et al., 2019).

We note that the published uncertainties (precision) associated with the stomatal density proxies are probably too small because they usually only reflect uncertainty in either the calibration regression or in the measured values of fossil stomatal density, but not both; when both sources are propagated, errors often exceed ±30 % at 95 % confidence (Beerling et al., 2009). Also, error rates in estimates from extant taxa for which CO₂ is known (accuracy) are usually smaller with stomatal density proxies than with gas-exchange proxies (e.g., Barclay and Wing, 2016), but this is expected because the same taxa have been calibrated in present-day (or near present-day) conditions. Because the gas-exchange proxies are largely built from physiological principles, they have less “recency” bias; that is, the gas-exchange proxies estimate present-day and paleo-CO₂ with similar certainty when the same methods are used to determine the inputs.

2 Study aims and methods

Leaf gas-exchange proxies for paleo-CO₂ are becoming popular (Konrad et al., 2008, 2017; Grein et al., 2011a, b, 2013; Erdei et al., 2012; Roth-Nebelsick et al., 2012, 2014; Franks et al., 2014; Maxbauer et al., 2014; Montañez et al., 2016; Reichgelt et al., 2016; Tesfamichael et al., 2017; Kowalczyk et al., 2018; Lei et al., 2018; Londoño et al., 2018; Richey et al., 2018; Milligan et al., 2019). However, many elements in these models remain understudied. Here we scrutinize four such elements of the Franks et al. (2014) model and ask the following: how does the model perform across a large number of phylogenetically diverse taxa? And how is the model affected by temperature, photorespiration, and proximity to the forest floor? We next describe the motivation and details of the study design (see also Table 1 for a summary).

Table 1 Attributes of datasets used to test the Franks et al. (2014) model.

n/a: not applicable

2.1 General testing in living plants

Franks et al. (2014) tested the model on four species of field-grown trees (three gymnosperms and one angiosperm) and one conifer grown in chambers at 480 and 1270 ppm CO₂. The average error rate (absolute value of estimated CO₂ minus measured CO₂, divided by measured CO₂) was 5 %. Follow-up work with three field-grown tree species (Maxbauer et al., 2014; Kowalczyk et al., 2018), CO₂ experiments on seven tropical trees species (Londoño et al., 2018), and experiments on two fern and one conifer species (Milligan et al., 2019) indicate somewhat higher error rates (Fig. 1). Combined, the average error rate is 20 % (median 13 %).

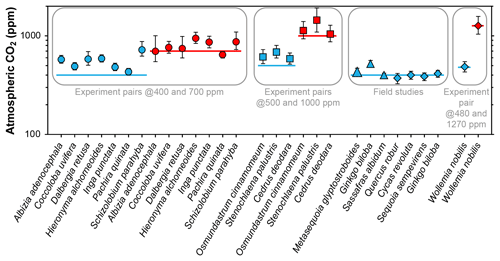
Figure 1 Published CO₂ estimates using the Franks model for extant plants for which the physiological inputs A₀ (assimilation rate at a known CO₂ concentration) and/or g_c(op)∕g_c(max) (ratio of operational to maximum leaf conductance to CO₂) were measured directly. Horizontal lines are the correct CO₂ concentrations. Uncertainties in the estimates correspond to the 16th–84th percentile range. Circles are from Londoño et al. (2018), squares from Milligan et al. (2019), large triangle from Maxbauer et al. (2014), small triangles from Kowalczyk et al. (2018), and diamonds from Franks et al. (2014).

In these studies, two of the key physiological inputs were measured directly with an infrared gas analyzer: the assimilation rate at a known CO₂ concentration (A₀) and/or the ratio of operational to maximum stomatal conductance to CO₂ (g_c(op)∕g_c(max), or ζ), the latter of which is important for calculating the total leaf conductance (g_c(tot)). These two inputs cannot be directly measured on fossils; thus, the error rates associated with Fig. 1 may not be representative for fossil studies. Franks et al. (2014) argue that within plant functional types growing in their natural environment, mean A₀ is fairly conservative, leading to the recommended mean A₀ values in Franks et al. (2014) (12 µmol m⁻² s⁻¹ for angiosperms, 10 for conifers, and 6 for ferns and ginkgos). Along similar lines, the mean ratio g_c(op)/g_c(max) tends to be conserved across plant functional types; Franks et al. (2014) recommend a value of 0.2, which may correspond to the most efficient set point for stomata to control conductance (Franks et al., 2012). This conservation of physiological function is one of the underlying principles in the Franks model.

Here we test this assumption by estimating CO₂ from 40 phylogenetically diverse species of field-grown trees. In making these estimates, we use the recommended mean values of A₀ and g_c(op)∕g_c(max) from Franks et al. (2014) instead of measuring them directly (see also Montañez et al., 2016, for other ways to infer assimilation rate from fossils). Thus, this dataset should be a more faithful gauge for model accuracy as applied to fossils. Of the 40 species, 21 were previously published in Londoño et al. (2018), who collected sun-adapted canopy leaves of angiosperms using a crane in Parque Nacional San Lorenzo, Panama. To test the method in temperate forests, we collected leaves from 11 angiosperm and 7 conifer species from Dinosaur State Park (Rocky Hill, Connecticut), Wesleyan University (Middletown, Connecticut), and Connecticut College (New London, Connecticut) during the summer of 2015. Here, all trees grew in open, park-like settings; one to three sun leaves were sampled from the lower outside crown of each tree. In January of 2015, we also sampled sun-exposed leaves from the tree fern Cyathea arborea in El Yunque National Forest, Puerto Rico (near the Yokahú Tower).

Stomatal size and density were measured either on untreated leaves using epifluorescence microscopy with a 420–490 nm filter or on cleared leaves (using 50 % household bleach or 5 % NaOH) using transmitted-light microscopy. For most species, whole-leaf δ¹³C comes from Royer and Hren (2017); the same leaves were measured for δ¹³C and stomatal morphology. The UC Davis Stable Isotope Facility measured some additional leaf samples. Atmospheric CO₂ concentration (400 ppm) and δ¹³C_air (−8.5 ‰) come from Mauna Loa, Hawaii (NOAA/ESRL, 2019), which we assume are representative of the local conditions under which we sampled (e.g., Munger and Hadley, 2017). Table S1 summarizes for these 40 species all of the inputs needed to run the Franks model, along with the estimated CO₂ concentrations. Uncertainties in the estimates are based on error propagation using Monte Carlo simulations (Franks et al., 2014).

2.2 Temperature

The Franks model can be configured for any temperature. Franks et al. (2014) recommend that the photosynthesis parameters A₀ and Γ^*, and the air physical properties affecting the diffusion of CO₂ into the leaf (the ratio of CO₂ diffusivity in air to the molar volume of air, or d∕v), correspond to the mean daytime growing-season leaf temperature (more precisely, assimilation-weighted leaf temperature). The reasoning behind this is that (i) the assimilation-weighted leaf temperature corresponds to the mean c_i∕c_a derived from fossil leaf δ¹³C, and (ii) both theory (Michaletz et al., 2015, 2016) and observations (Helliker and Richter, 2008; Song et al., 2011) indicate that the control of leaf gas exchange leads to relatively stable assimilation-weighted leaf temperatures (∼19–25 ^∘C from temperate to tropical regions) despite large differences in air temperature. This is mostly due to the effects of transpiration on leaf energy balance. Franks et al. (2014) chose a fixed temperature of 25 ^∘C because much of the Mesozoic and Cenozoic correspond to climates warmer than the present day. When applying the Franks model to known cooler paleoenvironments, improved accuracy may be achieved with leaf-temperature-appropriate values for A₀, Γ^*, and d∕v.

Bernacchi et al. (2003) proposed the following temperature sensitivity for Γ^* based on experiments:

$$\begin{array}{}\text{(6)}& {\mathrm{\Gamma }}^{*}=e^{\left(\mathrm{19.02}-\frac{\mathrm{37.83}}{RT}\right)},\end{array}$$

where R is the molar gas constant ($\mathrm{8.31446}\times {\mathrm{10}}^{-\mathrm{3}}$ kJ K⁻¹ mol⁻¹) and T is leaf temperature (K). Marrero and Mason (1972) describe the sensitivity of water vapor diffusivity to temperature as

$$\begin{array}{}\text{(7)}& d=\mathrm{1.87}\times {\mathrm{10}}^{-\mathrm{10}}\left({\displaystyle \frac{T^{\mathrm{2.072}}}{P}}\right),\end{array}$$

where P is atmospheric pressure, which we fix at 1 atmosphere. Lastly, the temperature sensitivity of the molar volume of air follows ideal gas principles:

$$\begin{array}{}\text{(8)}& v=v_{\text{STP}}\left({\displaystyle \frac{T}{T_{\text{STP}}}}\right)\left({\displaystyle \frac{P}{P_{\text{STP}}}}\right),\end{array}$$

where T_STP is 273.15 K, P_STP is 1 atmosphere, and v_STP is the air volume at T_STP and P_STP (0.022414 m³ mol⁻¹).

Using Eqs. (6)–(8), we can describe how, conceptually, the sensitivities of Γ^* and d∕v to leaf temperature affect estimates of CO₂ from the Franks model. We apply these relationships to a suite of 409 fossil and extant leaves from 62 species of angiosperms, gymnosperms, and ferns. These data come from the current study (see Sect. 2.1 and 2.4) and Londoño et al. (2018), Kowalczyk et al. (2018), and Milligan et al. (2019).

To experimentally test more generally how the Franks model is influenced by temperature, we grew six species of plants inside two growth chambers with contrasting temperatures (Conviron E7/2; Winnipeg, Canada). Air temperature was 28±0.5 ^∘C (1σ) and 20±0.3 ^∘C during the day and 19±0.7 ^∘C and 11±1.1 ^∘C during the night. We note that the difference in leaf temperature was probably smaller than that in air temperature during the day (8 ^∘C; see earlier discussion). We held fixed the day length (17 h with a 30 min simulated dawn and dusk) and CO₂ concentration (500±10 ppm). Light intensity at the heights at which we sampled leaves ranged from 100 to 400 µmol m⁻² s⁻¹. Humidity differed moderately between chambers (76.5±1.8 % and 90.0±3.6 %). To minimize any chamber effects, we alternated plants between chambers every 2 weeks.

Four of the species started as saplings purchased from commercial nurseries: bare-root, 30 cm tall saplings of Acer negundo and Carpinus caroliniana, 30 cm tall saplings of Ostrya virginiana with a soil ball, and bare-root, 10 cm tall saplings of Ilex opaca. We grew the other two species from seed: Betula lenta from a commercial source and Quercus rubra from a single tree on Wesleyan University's campus. All seeds were soaked in water for 24 h and then cold-stratified in a refrigerator for 30 and 60 days, respectively.

All seeds and saplings grew in the same potting soil (Promix Bx with Mycorise; Premier Horticulture; Quakertown, Pennsylvania, USA) and fertilizer (Scotts all-purpose flower and vegetable fertilizer; Maryville, Ohio, USA). They were watered to field capacity every other day, and we discarded any excess water passing through the pots. After 3 months of growth in the chambers, for each species–chamber pair we harvested the three newest fully expanded leaves whose buds developed during the experiment. In most cases, we harvested five plants per species–chamber pair; the one exception was I. opaca, for which we were limited to three plants in the warm treatment and two in the cool treatment.

We measured stomatal size and density on cleared leaves (using 50 % household bleach) with transmitted-light microscopy. Whole-leaf δ¹³C comes from the UC Davis Stable Isotope Facility and the Light Stable Isotope Mass Spec Lab at the University of Florida; the same leaves were measured for δ¹³C and stomatal morphology. We used either a hole punch or razor to remove two adjacent sections of leaf tissue near the leaf centers, avoiding major veins. Because we used the same CO₂ gas cylinder (δ¹³C $=-\mathrm{11.8}$ ‰) and laboratory space (δ¹³C $=-\mathrm{10.4}$ ‰) as Milligan et al. (2019), we used their two-end-member mixing model (1∕CO₂ vs. δ¹³C; Keeling, 1958) to calculate the δ¹³C of the chamber CO₂ at 500 ppm (−10.6 ‰). We used the recommended values from Franks et al. (2014) for the physiological inputs A₀ and g_c(op)∕g_c(max). Table S1 summarizes all of the inputs from this experiment needed to run the Franks model, along with the estimated CO₂ concentrations. The standard errors for the inputs are based on plant means.

To test if leaf δ¹³C and stomatal morphology (stomatal density, stomatal pore length, and single guard cell width) differed between temperature treatments across species, we implemented a mixed model in R (R Core Team, 2016) using the lme4 (Bates et al., 2015) and lmerTest (Kuznetsova et al., 2017) packages, with temperature and species as the two fixed factors. To test if there was a significant difference between CO₂ estimates from the two temperature treatments, we ran a Kolmogorov–Smirnov (KS) test in R. For each species, we first estimated CO₂ for each plant in the warm and cool treatments based on simulated inputs constrained by their means and variances. In the typical case with five plants per chamber, this produced five CO₂ estimates for the warm chamber and the same for the cool chamber. A KS test was then used to test for a significant temperature effect. We repeated this procedure 10 000 times, with 10 000 associated KS tests. The fraction of tests with a p value < 0.05 was taken as the overall p value. An advantage of this approach is that it incorporates both within- and across-plant variation.

2.3 Photorespiration

c_i∕c_a is estimated in the Franks model following Farquhar et al. (1982):

$$\begin{array}{}\text{(9)}& {\mathrm{\Delta }}_{\text{leaf}}=a+(b-a)\times {\displaystyle \frac{c_{\text{i}}}{c_{\text{a}}}},\end{array}$$

where a is the carbon isotope fractionation due to the diffusion of CO₂ in air (4.4 ‰; Farquhar et al., 1982), b is the fractionation associated with RuBP carboxylase (30 ‰; Roeske and O'Leary, 1984), and Δ_leaf is the net fractionation between air and assimilated carbon ($[{\mathit{\delta }}^{\mathrm{13}}{\mathrm{C}}_{\mathrm{air}}-{\mathit{\delta }}^{\mathrm{13}}{\mathrm{C}}_{\mathrm{leaf}}]/[\mathrm{1}+{\mathit{\delta }}^{\mathrm{13}}{\mathrm{C}}_{\mathrm{leaf}}/\mathrm{1000}]$).

Equation (8) can be expanded to include other effects, including photorespiration (Farquhar et al., 1982):

$$\begin{array}{}\text{(10)}& {\mathrm{\Delta }}_{\text{leaf}}=a+(b-a)\times {\displaystyle \frac{c_{\text{i}}}{c_{\text{a}}}}-{\displaystyle \frac{f\mathrm{\Gamma }\ast }{c_{\text{a}}}},\end{array}$$

where f is the carbon isotope fractionation due to photorespiration. Photorespiration occurs when the enzyme rubisco fixes O₂, not CO₂ (i.e., RuBP oxygenase). One product of photorespiration is CO₂ (Jones, 1992), whose δ¹³C is lower than the source substrate glycine. If this respired CO₂ escapes to the atmosphere, the δ¹³C of the leaf carbon becomes more positive. Thus, if c_i∕c_a is calculated using Eq. (8), as is common practice, the calculation may be falsely low, leading to an underprediction of atmospheric CO₂.

Measured values for f vary from ∼9 to 15 ‰ (see compilation in Schubert and Jahren, 2018), which is in line with theoretical predictions (Tcherkez, 2006). At a 400 ppm atmospheric CO₂ and Γ^* of 40 ppm, Eq. (9) implies that ∼1 ‰ of Δ_leaf is due to photorespiration, meaning that c_i∕c_a should be ∼0.04 higher relative to Eq. (8). Here, using the suite of fossil and extant leaves described in Sect. 2.2, we explore how the carbon isotopic fractionation associated with photorespiration affects CO₂ estimates with the Franks model. Because c_i∕c_a is present in both of the fundamental equations (Eqs. 2 and 3), we solve them iteratively until c_i∕c_a converges.

2.4 Leaves that grow close to the forest floor

The composition of air close to the forest floor can differ considerably from the well-mixed atmosphere. Of relevance to the Franks model, soil respiration can lead to a locally higher CO₂ concentration and lower δ¹³C_air (Table 2). This effect is strongest at night, when the forest boundary layer is thickest (e.g., Munger and Hadley, 2017), but we focus here on daylight hours because that is when most plants take up CO₂. In wet tropical forests, which can have very high soil respiration rates, CO₂ during the day near the forest floor can be elevated by tens of parts per million, and the δ¹³C_air can be 2–3 ‰ lower; in temperate forests, the deviations are smaller (Table 2). Above ∼2 m, CO₂ concentrations and air δ¹³C during the daytime largely match the well-mixed atmosphere.

Table 2 Deviations in the δ¹³C and concentration of CO₂ close to a forest floor relative to well-mixed air above the canopy. All measurements were made close to midday.

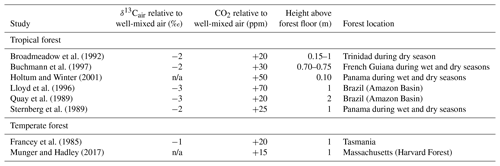
n/a: not applicable

As a result, leaves that grow close to the forest floor may cause the Franks model to produce CO₂ estimates higher than that of the mixed atmosphere for at least two reasons. First, the concentration of CO₂ near the forest floor is elevated; that is, the model may correctly estimate a CO₂ concentration that the user is not interested in. Second, because the δ¹³C_air that a forest-floor plant experiences is lower than the global well-mixed value, if the user chooses the well-mixed value for model input (inferred, for example, from the δ¹³C of marine carbonate; Tipple et al., 2010), then c_i∕c_a and thus atmospheric CO₂ will be overestimated (see Eq. 2).

We sought to test how the Franks model is affected by the forest-floor microenvironment for five tropical angiosperm species and 15 temperate angiosperm and fern species. The tropical leaves were sampled at ∼1–2 m of height from Parque Nacional San Lorenzo, Panama. In contrast to the canopy dataset from San Lorenzo (Sect. 2.1), these CO₂ estimates have not been previously reported. In the summer of 2015, seven fern species were sampled at ∼0.5 m of height from Connecticut College and Wesleyan University. Also, we used leaf vouchers from Royer et al. (2010), who sampled eight herbaceous angiosperm species at ∼0.1–0.2 m of height from Reed Gap, Connecticut. For all 20 species, stomatal and carbon isotopic measurements follow the methods described in Sect. 2.1. Table S1 contains all of the inputs needed to run the Franks model, along with the estimated CO₂ concentrations.

We also investigated if we could include the forest-floor δ¹³C_air effect in our estimates of atmospheric CO₂. We did not measure the CO₂ concentration and δ¹³C_air around our plants, so we could not directly compare our values. But, if the only CO₂ inputs close to the forest floor are from the soil and well-mixed atmosphere, then the system can be modeled as a two-end-member mixing model in which δ¹³C_air has a positive, linear relationship with 1∕CO₂ (Keeling, 1958). If the CO₂ concentration and δ¹³C of both end-members are known, the forest-floor microenvironment should fall somewhere on the modeled line. Importantly, the Franks model provides a second constraint on the system. Here, δ¹³C_air has a negative, nonlinear relationship with 1∕CO₂ because δ¹³C_air is positively related to c_i∕c_a and CO₂. The Franks model thus provides a second calculation for the relationship between δ¹³C_air and estimated CO₂ concentration. The intersection between the two curves should be the correct δ¹³C_air and CO₂ concentration for the forest-floor microenvironment.

To estimate the soil CO₂ end-member, we measured the δ¹³C of soil organic matter collected from the A horizons of 13 soil sites at San Lorenzo and of five each at Reed Gap and Connecticut College. For all soils, we assume a 5000 ppm CO₂ concentration for a depth that is below the zone of CO₂ diffusion from the atmosphere (∼0.3 m; Cerling, 1999; Breecker et al., 2009). The true value for wet temperate and tropical forest soils may be somewhat less or substantially more than 5000 ppm (Medina et al., 1986; Cerling, 1999; Hirano et al., 2003; Hashimoto et al., 2004; Sotta et al., 2004). Because the mixing model uses 1∕CO₂, a much higher CO₂ concentration (e.g., 10 000 ppm) has little impact on our results.

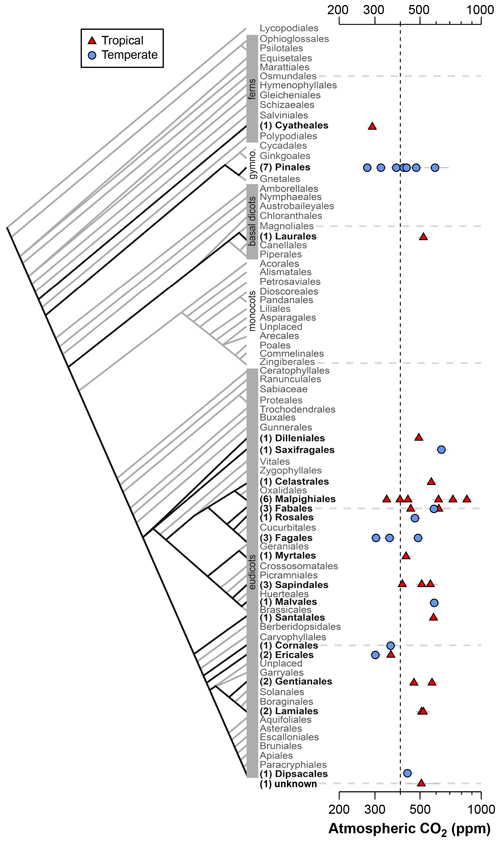
Figure 2 Estimates of CO₂ based on canopy leaves from 40 tree species. Uncertainties in the estimates correspond to the 16th–84th percentile range. Vertical line is the correct concentration (400 ppm). On the left is an order-level vascular plant phylogeny (APW v.13; Stevens, 2001, onwards). The number of measured species is given in parentheses.

3 Results and discussion

3.1 General testing in living plants

Estimates of CO₂ across the 40 tree species sampled in the field range from 275 to 850 ppm, with a mean of 478 ppm and median of 472 ppm (Fig. 2); two-thirds of the estimates (a close equivalent to ±1 standard deviation) range between 353 and 585 ppm. In 28 % of the tested species, the estimated CO₂ concentrations overlap the target concentration (400 ppm) at 95 % confidence; for these species, the CO₂ estimates do not differ significantly from the target. There are no strong differences across taxonomic orders or between leaves from tropical and temperate forests. The mean error rate across the estimates is 28 % (median 24 %), which is higher than estimates that include direct measurements of the physiological inputs A₀ and g_c(op)∕g_c(max) (mean 20 %; median 13 %; Fig. 1). Along similar lines, if the estimates presented in Fig. 1 are reestimated using the values for A₀ and g_c(op)∕g_c(max) recommended by Franks et al. (2014), the mean error rate increases to 37 % (median 33 %). If only the default values of A₀ are used, the median error rate is 27 %, and for only default values of g_c(op)∕g_c(max) it is 22 %.

These results indicate that CO₂ accuracy is generally improved when A₀ and/or g_c(op)∕g_c(max) are measured. These measurements require expensive gas-exchange equipment and are not always easy or practical to make. Moreover, A₀ and g_c(op)∕g_c(max) cannot be measured on fossils. Some gains in accuracy are possible by measuring A₀ and g_c(op)∕g_c(max) on extant relatives of the fossil species (e.g., the same genus). Absent of this, our analysis using the recommended mean values of Franks et al. (2014) indicates an error rate, on average, of approximately 28 %. This is comparable to or better than other leading paleo-CO₂ proxies (Franks et al., 2014).

One reliable way to improve accuracy is to estimate CO₂ with multiple species because the falsely high and falsely low estimates partly cancel each other out. The grand mean of estimates presented in Fig. 2 (478 ppm) is 20 % from the 400 ppm target, which is less than the 28 % mean error rate of individual estimates.

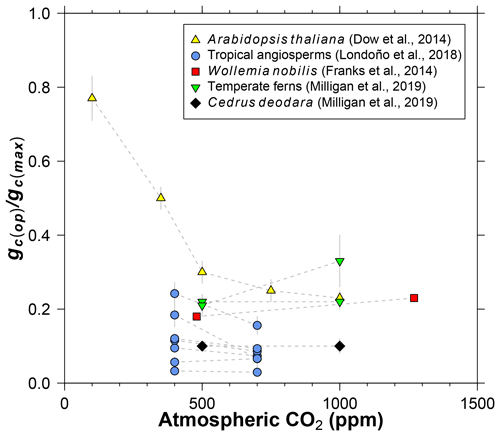
Figure 3 Literature compilation of the sensitivity of g_c(op)∕g_c(max) (ratio of operational to maximum leaf conductance to CO₂) to atmospheric CO₂ concentration.

Dow et al. (2014) observed that g_c(op)∕g_c(max) inversely varies with CO₂ in Arabidopsis thaliana, but primarily at subambient concentrations (yellow triangles in Fig. 3). At elevated CO₂, g_c(op)∕g_c(max) is close to 0.2, which is the value recommended by Franks et al. (2014). Data from 11 species of angiosperms, conifers, and ferns at present-day (or near present-day) and elevated CO₂ concentrations support the view of a limited effect at high CO₂ (Fig. 3; Franks et al., 2014; Londoño et al., 2018; Milligan et al., 2019). More data at subambient CO₂ are needed, but for CO₂ concentrations similar to or higher than the present day, we see no strong reason to include a CO₂ sensitivity in g_c(op)∕g_c(max). The rather low values for Cedrus deodara and many of the tropical angiosperms (<0.1) are likely due to stress imposed by their growth-chamber environment; these g_c(op)∕g_c(max) values are probably not representative of field-grown trees, which tend to be closer to 0.2 (Franks et al., 2014).

3.2 Temperature

The temperature sensitivities of the ratio of diffusivity of CO₂ in air to the molar volume of air (d∕v) and the CO₂ compensation point in the absence of dark respiration (Γ^*) have little effect on estimated CO₂ in the Franks model (Fig. 4). Given that assimilation-weighted leaf temperature only varies about 7 ^∘C across plants today, the differences shown in Fig. 4, which are based on leaf temperatures of 25 and 15 ^∘C, are likely a maximum effect. As such, we consider the use of a fixed leaf temperature (e.g., 25 ^∘C) in the model to be a defensible simplification.

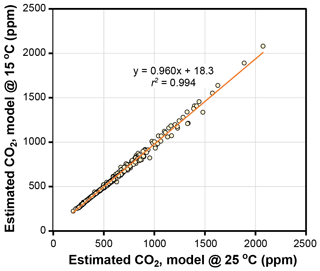
Figure 4 Estimates of CO₂ at leaf temperatures of 25 ^∘C and 15 ^∘C. Each symbol is an extant or fossil leaf. The difference in estimated CO₂ for any leaf is due to the theoretical effects of temperature on gas diffusion (d∕v) and the CO₂ compensation point in the absence of dark respiration (Γ^*) (Eqs. 6–8).

Other inputs in the model may respond to temperature, though. In our growth-chamber experiments for which daytime air temperatures were 28 and 20 ^∘C, the effect on estimated CO₂ was mixed (Fig. 5). In five out of six species, estimated CO₂ was higher in the warm treatment, but for all species these differences were not statistically significant (p>0.05 based on a KS test; see Methods). Incorporating the temperature sensitivities in d∕v and Γ^* had little effect (“adj” estimates in Fig. 5), as expected from Fig. 4.

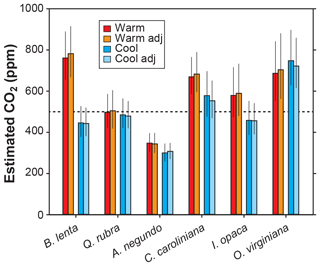
Figure 5 Estimates of CO₂ for plants grown inside growth chambers at daytime air temperatures of 28 and 20 ^∘C. Also shown are estimates after taking into account the temperature sensitivity of gas diffusion (d∕v) and the CO₂ compensation point in the absence of dark respiration (Γ^*) (“adj”; see also Fig. 4). Dashed line is the correct CO₂ concentration (500 ppm). Uncertainties in the estimates correspond to the 16th–84th percentile range.

None of the measured inputs – stomatal density, stomatal pore length, single guard cell width, and leaf δ¹³C – were significantly affected by temperature across all species (p>0.05 for each of the four inputs based on a mixed model; see Sect. 2.2). These small differences probably cannot account for the differences in estimated CO₂ between temperatures. It is more likely that some of the inputs that we did not directly measure, such as assimilation rate (A₀), the g_c(op)∕g_c(max) ratio, or mesophyll conductance (g_m), differ from the true mean value. In the cases for the five species for which estimated CO₂ is higher in the warm treatment, our mean A₀ for the warm plants must be falsely high, or g_c(op)∕g_c(max) or g_m is falsely low.

In summary, we see no strong reason to expand the parameterization of temperature in the model, though more growth-chamber experiments may be warranted. We note that in three out of the six species from the warm treatment, the estimated CO₂ cannot be distinguished from the 500 ppm target at 95 % confidence; for the cool treatment, this is true for four of the species. Also, the across-species means of estimated CO₂ for the warm and cool treatments are reasonably close to the target (590 and 502 ppm, respectively) and overall have a mean error rate of 25 %. This level of uncertainty is similar to our field estimates for which we did not measure A₀ or g_c(op)∕g_c(max) (28 %; see Fig. 2). This too provides support for our recommendation that it is not critical to include a broader treatment of temperature in the model.

Figure 6 Estimates of CO₂ with and without a photorespiration effect (f=9.1 ‰; see Eq. 10). Each symbol is an extant or fossil leaf. Dashed line is y=x.

3.3 Photorespiration

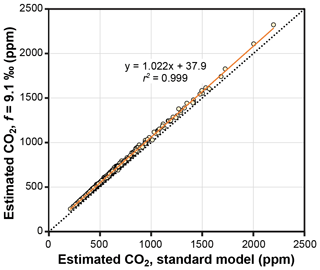
The theoretical effects of photorespiration do not strongly impact estimates of CO₂ in the Franks model. The average effect for our 409 extant and fossil leaves is to increase estimated CO₂ by 2.2 % plus 38 ppm (Fig. 6). At 1000 ppm, for example, estimates would increase by 60 ppm. This calculation assumes a photorespiration fractionation (f) of 9.1 ‰, which is the value estimated for Arabidopsis thaliana (Schubert and Jahren, 2018). If a fractionation towards the upper bound of published estimates is used instead (15 ‰), estimated CO₂ increases on average by 3.8 % plus 61 ppm. Across this range in f, the associated uncertainty in estimated CO₂ is well within the method's overall precision ($\sim +\mathrm{35}/-\mathrm{25}$ % at 95 % confidence; Franks et al., 2014). As such, CO₂ estimates made without these photorespiration effects (i.e., using Eq. 9 instead of Eq. 10) should be reliable, although some improvement is possible using Eq. 10 in cases in which f is accurately known.

We note that both f and Γ^* are also affected by atmospheric O₂ concentration. Because O₂ is directly responsible for photorespiration, f should scale with O₂ (or, more precisely, the O₂ : CO₂ molar ratio). Unfortunately, this effect is poorly constrained (Beerling et al., 2002; Berner et al., 2003; Porter et al., 2017). In contrast, the theoretical effect of O₂ on Γ^* is known: it is linear with an approximate slope of 2 (Farquhar et al., 1982; see their Eq. B13). During the Phanerozoic, O₂ likely ranged from 10 % to 30 %, with lows during the early Paleozoic and early Triassic and highs during the Carboniferous to early Permian and Cretaceous (Berner, 2009; Glasspool and Scott, 2010; Arvidson et al., 2013; Mills et al., 2016; Lenton et al., 2018). Assuming a present-day Γ^* of 40 ppm (at 21 % O₂), Γ^* would be 60 ppm at 30 % O₂ and 20 ppm at 10 % O₂. Running the Franks model on our library of 409 extant and fossil leaves, we find little effect on estimated CO₂: estimates are 7.4 % higher on average at 30 % O₂ than at 10 % O₂ (see also McElwain et al., 2016).

3.4 Leaves that grow close to the forest floor

CO₂ estimates for tropical understory leaves from five species at San Lorenzo, Panama, are very high, ranging from 1903 to 18863 ppm (species mean 6837 ppm). For two of the species, Londoño et al. (2018) also analyzed canopy leaves from trees nearby, and these within-species comparisons highlight the vast discrepancy (Ocotea sp.: 541 vs. 5737 ppm; Tontelea sp.: 622 vs. 18 863 ppm). The primary difference in the inputs between the canopy and understory leaves is the δ¹³C_leaf: Londoño et al. (2018) report a species mean δ¹³C_leaf of −30.0 ‰ for the 21 canopy species versus −35.6 ‰ for the five understory species. This difference leads to very different mean estimates of c_i∕c_a: 0.69 for canopy leaves versus a highly unrealistic (Diefendorf et al., 2010) 0.93 for understory leaves.

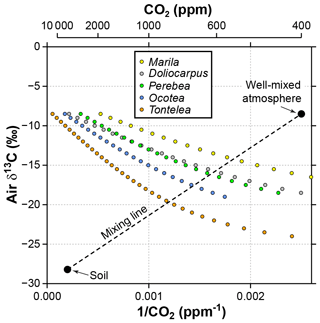
Figure 7 Sensitivity of estimated CO₂ in the Franks model to the δ¹³C of atmospheric CO₂. Estimates come from leaves of five angiosperm species that grew close to the forest floor in Parque Nacional San Lorenzo, Panama. For each species, the step in δ¹³C_air between estimates is 0.5 ‰. The dashed line is a two-end-member mixing model for CO₂ between the soil and well-mixed atmosphere. The intersection between the mixing model and the Franks model should correspond to the CO₂ concentration and δ¹³C_air of the forest-floor microenvironment.

It is likely that the high CO₂ estimates from understory leaves are mostly driven by falsely high δ¹³C_air inputs. Following the mixing model strategy outlined in Sect. 2.4 (and based on a soil organic matter δ¹³C of −28.2 ‰ measured at San Lorenzo), we calculate a species mean δ¹³C_air of −16.7 ‰ (mean of intersection points in Fig. 7). When this δ¹³C_air is used to estimate CO₂ with the Franks model (instead of −8.5 ‰), the species mean drops to 699 ppm. This is somewhat higher than the species mean from canopy leaves in the same forest (563 ppm; red triangles in Fig. 2; Londoño et al., 2018).

Understory leaves from Connecticut temperate forests show similar but less dramatic patterns, which we attribute to a more open canopy with stronger atmospheric mixing. CO₂ estimates for the 15 species range from 447 to 1567 ppm (mean 794 ppm). Our intersection method identifies a mean δ¹³C_air of −11.2 ‰ for the Wesleyan and Connecticut College campuses (based on a soil δ¹³C of −27.6 ‰ measured at Connecticut College) and −10.3 ‰ for Reed Gap (soil δ¹³C $=-\mathrm{26.4}$ ‰). Using these adjusted δ¹³C_air, the species mean of estimated CO₂ drops to 566 ppm, which is somewhat higher than the species mean from canopy leaves in the same areas (449 ppm; blue circles in Fig. 2).

We acknowledge that this analysis is too simple. First, we did not measure the understory CO₂ concentration and δ¹³C_air (this would require repeated measurements during different daytime hours over a growing season to calculate a time-integrated value); instead, we assumed a simple two-end-member mixing model between the soil and well-mixed atmosphere. Second, other factors probably contribute to the differences in estimated CO₂ between canopy and understory leaves. Our predicted δ¹³C_air values are too low (∼8 ‰ and 2 ‰ lower than the well-mixed atmosphere for the tropical and temperate forests) and our estimated CO₂ too high (∼100 ppm higher than that from canopy leaves). In the lowermost 1–2 m of the canopy, previous work suggests up to a −3 ‰ and +70 ppm deviation in tropical forests and −1 ‰ ∕ +20 ppm in temperate forests (Table 1). One input that could help to resolve this discrepancy is the assimilation rate (A₀). We assumed a fixed A₀ of 12 µmol m⁻² s⁻¹ for all leaves, regardless of canopy position. Shade leaves often have lower assimilation rates than sun leaves (Givnish, 1988). Substituting lower A₀ values for understory leaves would lower estimated CO₂ roughly in proportion (Eqs. 2–3). Using lower A₀ values for shade leaves in the model is appropriate, but determining the best value is difficult. Typical A₀ values for leaves growing at the top of the canopy in full sun are far more consistent because photosynthesis in these leaves is usually at its maximum capacity (saturated at full sunlight) for the prevailing atmospheric CO₂ concentration. Because the degree of shadiness near the forest floor is highly variable, photosynthesis (A₀) in these leaves will be acclimated to some fraction of the full-sun maximum in a sun-exposed leaf, but careful thought must go into determining what this fraction is.

We note that our mixing model strategy cannot be applied to fossils because the global atmospheric CO₂ concentration is needed (one end point for dashed line in Fig. 7). Instead, our motivation for the analysis is to demonstrate that (1) leaves growing in the lowermost 2 m of the canopy should be considered with caution in the context of the Franks model, and (2) the failure of the model is due to faulty inputs (mostly δ¹³C_air), not the model itself.

In most fossil leaf deposits, shade morphotypes are comparatively rare (e.g., Kürschner, 1997; Wang et al., 2018) because – relative to sun leaves – they are less durable, do not travel as far by wind, and are produced at a slower rate (Dilcher, 1973; Roth and Dilcher, 1978; Spicer, 1980; Ferguson, 1985; Burnham et al., 1992). Our recommendation is to exclude such leaves. There are several ways to differentiate sun vs. shade morphotypes: overall shape (Talbert and Holch, 1957; Givnish, 1978; Kürschner, 1997; Sack et al., 2006), shape of epidermal cells (larger and with a more undulated outline in shade leaves; Kürschner, 1997; Dunn et al., 2015), vein density (lower in shade leaves; Uhl and Mosbrugger, 1999; Sack and Scoffoni, 2013; Crifò et al., 2014; Londoño et al., 2018), and range in δ¹³C_leaf (high when both sun and shade leaves are present, for example in our study; Graham et al., 2014). Not all shade leaves grow within 2 m of the forest floor, but excluding all such leaves would eliminate the forest-floor bias.

4 Conclusions

The Franks model is reasonably accurate (∼28 % error rate) even when the physiological inputs A₀ (assimilation rate at a known CO₂ concentration) and g_c(op)∕g_c(max) (ratio of operational to maximum leaf conductance to CO₂) are inferred, not measured. Accuracy does improve when these inputs are measured (∼20 % error rate), but such measurements are not possible with fossils and may not always be feasible with the nearest living relatives. A 28 % error rate is broadly in line with (or better than) other leading paleo-CO₂ proxies.

Most of the possible confounding factors that we investigated appear minor. The temperature sensitivities of d∕v (related to gas diffusion) and Γ^* (CO₂ compensation point in the absence of dark respiration) have a negligible impact on estimated CO₂. Our temperature experiments in growth chambers point to larger differences in some species, which must be related to incorrect values for inputs that were not directly measured, such as A₀, g_c(op)∕g_c(max), and g_m (mesophyll conductance). Overall, though, we find that the differences in estimated CO₂ imparted by temperature are generally smaller than the overall 28 % error rate.

Incorporating the covariance between CO₂ concentration and photorespiration leads to only small changes in estimated CO₂. O₂ concentration affects photorespiration and may thus confound CO₂ estimates from the Franks model, but presently the effect is poorly quantified. The effect of O₂ on Γ^* is better known and imparts only small changes in estimated CO₂ across a feasible range in Phanerozoic O₂ of 10 %–30 %.

Leaves from the lowermost 1–2 m of the canopy experience slightly elevated CO₂ concentrations and lower air δ¹³C during the daytime relative to the well-mixed atmosphere. We find that if we use the well-mixed air δ¹³C to estimate CO₂ from leaves that grew near the forest floor, estimates are too high, especially in dense tropical canopies. When we use a two-end-member mixing model to calculate the correct local air δ¹³C, the falsely high CO₂ estimates largely disappear. For fossil applications, shade leaves from the bottom of the canopy should be avoided. Shade leaves are typically rare in the fossil record (relative to sun leaves) and can be identified by their overall shape, the shape of their epidermal cells, their low leaf δ¹³C, and their low vein density.

Conceptually, the Franks model holds considerable promise for quantifying paleo-CO₂: it is mechanistically grounded and can be applied to most fossil leaves. Our tests of the model's accuracy and sensitivity to temperature and photorespiration largely uphold this promise.