Late Miocene–Pliocene climate evolution recorded by the red clay cover on the Xiaoshuizi planation surface, NE Tibetan Plateau

The Pliocene climate and its driving mechanisms have attracted substantial scientific interest because of their potential as an analog for near-future climates. The late Miocene–Pliocene red clay sequence of the main Chinese Loess Plateau (CLP) has been widely used to reconstruct the history of interior Asian aridification and the Asian monsoon. However, red clay sequences deposited on the planation surface of the Tibetan Plateau (TP) are rare. A continuous red clay sequence was recently discovered on the uplifted Xiaoshuizi (XSZ) planation surface in the Maxian Mountains, northeastern (NE) TP. In this study, we analyzed multiple climatic proxies from the XSZ red clay sequence with the aim of reconstructing the late Miocene–early Pliocene climate history of the NE TP and to assess regional climatic differences between the central and western CLP. Our results demonstrate the occurrence of minimal weathering and pedogenesis during the late Miocene, which indicates that the climate was arid. We speculate that precipitation delivered by the paleo East Asian summer monsoon (EASM) was limited during this period and that the intensification of the circulation of the westerlies resulted in arid conditions in the study region. Subsequently, enhanced weathering and pedogenesis occurred intermittently during 4.7–3.9 Ma, which attests to an increase in effective moisture. We ascribe the arid–humid climatic transition near ∼4.7 Ma to the expansion of the paleo-EASM. The warming of the high northern latitudes in response to the closure of the Panama Seaway may have been responsible for the thermodynamical enhancement of the paleo-EASM system, which permitted more moisture to be transported to the NE TP.

1 Introduction

The Pliocene, including the Zanclean (5.33–3.60 Ma) and Piacenzian (3.60–2.58 Ma) stages, is one of the most intensively studied intervals of the pre-Quaternary in climate change research. The Zanclean climate was generally warm and wet and is often used as an analog for near-future climate conditions in terms of carbon dioxide levels, ranging from 280–415 ppm (Tripati et al., 2009; Pagani et al., 2010), and comparable temperatures in the tropical region (Herbert et al., 2010, 2016). On the other hand, the Zanclean was markedly different from today, although several critical changes in thermohaline and atmospheric circulation towards modern conditions were occurring (Haug et al., 2005; Lawrence et al., 2006; Chaisson and Ravelo, 2000). For example, the early Pliocene global mean temperature was approximately 4 ^∘C warmer (Brierley and Fedorov, 2010), and the sea levels are estimated to have been ∼25 m higher, than today (Dowsett et al., 2010). Temperatures at high northern latitudes were considerably higher and therefore continental glaciers were almost absent from the Northern Hemisphere (Ballantyne et al., 2010; Dowsett et al., 2010). The zonal and meridional sea surface temperature gradients in the Northern Hemisphere were weak but gradually became more intensified, changing towards the modern state, which has a much more pronounced spatial temperature contrast (Fedorov et al., 2013; Brierley et al., 2009; Brierley and Fedorov, 2010). The low meridional surface temperature gradient resulted in weaker meridional circulation during this interval (Fedorov et al., 2013; Brierley et al., 2009), and the minor east–west sea surface temperature contrast in the tropical Pacific during this interval is believed to have given rise to a permanent El Niño Southern Oscillation (Lawrence et al., 2006); however, whether permanent El Niño–like conditions were sustained during the Pliocene is controversial (Wara et al., 2005; Watanabe et al., 2011; Zhang et al., 2014). In addition, the episodic uplift of the TP (Li et al., 2015; Zheng et al., 2000; Fang et al., 2005a, b) and gradual closure of the Panama Seaway (Keigwin et al., 1978; O'Dea et al., 2016) were underway. The former had a substantial climatic impact (An et al., 2001; Ding et al., 2001; Liu et al., 2014) and the latter resulted in the reorganization of the global thermohaline circulation system (Haug et al., 1998, 2001). These features imply a spatial change in the organization of the global climate system from the early Pliocene to the present. In this context, it is important to characterize the response of regional climates to these major global climatic and tectonic changes.

East Asia is one of the key regions for studying the aridification of the Asian interior and the Asian monsoon evolution, which are tightly linked to the uplift of the TP, regional climate change, and the evolution of global temperature and ice volume (An et al., 2001; Ding et al., 2001; Li et al., 2008; Clift et al., 2008; Nie et al., 2014; Ao et al., 2016; Sun and Liu, 2006; Sun et al., 2017; Chang et al., 2013; Liu et al., 2014). Previous research has revealed that red clay was widely deposited across the CLP since the late Miocene, indicating that Asian aridification was enhanced (Guo et al., 2001; Song et al., 2007; An et al., 2014; Ao et al., 2016; Li et al., 2017). In the eastern and central CLP, where the climate is dominated by the East Asian monsoon, paleontological evidence, mineral magnetic parameters, and geochemical records from the red clay indicate dry climatic conditions during the late Miocene but generally wet climatic conditions during the early Pliocene (Wang et al., 2006; Guo et al., 2001; Wu et al., 2006; Song et al., 2007; Sun et al., 2010; An et al., 2014; Ao et al., 2016). The most controversial climatic change occurred during the interval from 4.8–4.1 Ma, for which climate reconstructions using different proxies indicate conflicting paleoenvironmental trends. For example, field observations and pollen records indicate an intensified summer monsoon intensity, but low magnetic susceptibility values are more consistent with arid rather than wet climatic conditions (Ding et al., 2001; Ma et al., 2005; Song et al., 2007; Sun et al., 2010). It is thought that dissolution of ferrimagnetic minerals and iron reduction resulting from high precipitation significantly affected the climatic significance of magnetic susceptibility records during this period (Ding et al., 2001). In addition to the East Asian monsoon, the westerlies also had an impact on the climate of East Asia; however, the patterns of climate change in the westerlies-dominated regions were different from the eastern and central CLP during the early Pliocene. Geochemical, stratigraphic, and pollen evidence from the Qaidam and Tarim basins has demonstrated that aridification intensified since the early Pliocene (Fang et al., 2008; Sun and Liu, 2006; Sun et al., 2017; Chang et al., 2013; Liu et al., 2014). Although the general climatic trends of the main CLP and central Asia during this period are well-recorded, paleoclimatic changes in the NE TP, which is at the junction of the zones of westerly and monsoonal influences, remain unclear. Therefore, determining the climatic conditions of the NE TP during the early Pliocene not only improves our understanding of the pattern of regional climate change, but may also provide insights into the responses of the paleo-EASM and the westerlies to TP uplift and changes in the global climate system.

A continuous red clay sequence was recently discovered on the uplifted XSZ planation surface in the NE TP and has been dated via high-resolution magnetostratigraphy (Li et al., 2017). Due to its specific geographical location, the XSZ red clay provides the opportunity to reveal the late Miocene–early Pliocene climate history of the NE TP and to determine the climatic differences between the central and western CLP. In this study, we measured multiple climatic proxies from the late Miocene–Pliocene XSZ red clay core. Our aims were to construct a detailed record of precipitation, chemical weathering, and pedogenesis during 6.7–3.6 Ma and to determine the pattern of regional climate evolution and its possible causal mechanisms.

2 Regional background

The XSZ planation surface is located in Yuzhong County in the western Chinese Loess Plateau (Fig. 1). The main XSZ planation surface is at an altitude of 2800 m in the Maxian Mountains where it has truncated Precambrian gneiss. The Maxianshan are rejuvenated mountains, which protrude into the broad Longzhong Basin; they are located within a climatically sensitive zone because of the combined influences of the Asian monsoon and the northern branch of the midlatitude westerly circulation system. The planation surface is mantled by over 30 m of loess and over 40 m of red clay. Our previous bio-magnetostratigraphic study demonstrates that the red clay sequence covering the XSZ planation surface is dated to ∼6.9–3.6 Ma (Li et al., 2017). Here, we use the XSZ drill core to reconstruct and discuss the patterns of regional climate change during the Miocene–Pliocene. The long, continuous, well-dated record of the drill core is superior to that of the Shangyaotan core analyzed in Li et al. (2017). Yuzhong County lies within the semiarid temperate climate zone at the junction of the eastern monsoon area, the arid area of northwest China, and the cold region of the TP. The mean annual temperature during 1986–2016 was ∼7.0 ^∘C and the annual precipitation was 260–550 mm; 80 % of the precipitation is in summer and autumn (data source: National Meteorological Information Center of the Chinese Meteorological Administration; http://data.cma.cn/, last access: 17 August 2018). The spatial distribution of precipitation is uneven, decreasing from south to north in Yuzhong County. The precipitation amount increases with elevation at a rate of 27 mm per 100 m, attaining a maximum of 800 mm at the top of Maxianshan.

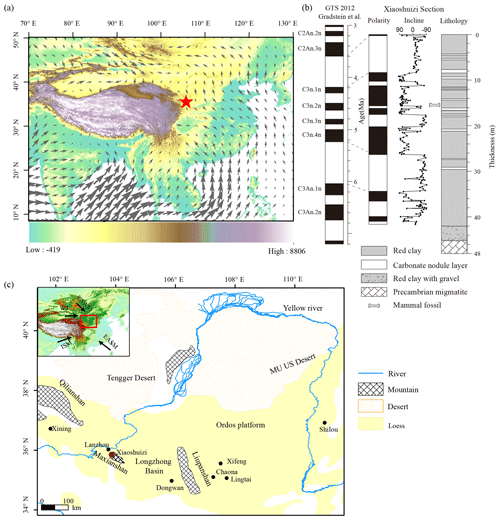
Figure 1 Location of the study area and atmospheric circulation patterns. (a) 850 hPa vector wind averaged from June to August for 1982–2012 based on NOAA Earth System Research Laboratory reanalysis data (https://www.esrl.noaa.gov/psd/, last access date: 20 August 2018). (b) Lithology and magnetostratigraphy of the XSZ drill core. (c) The Chinese Loess Plateau with locations of the studied Xiaoshuizi site and other sections mentioned in the text.

3 Material and methods

The XSZ core (35.8115^∘ N, 103.8623^∘ E and 2758.1 m above sea level) is composed of 42 m of pure red clay, and ∼3 m of red clay and there is an increasing content of angular gravel at the base (Fig. 1b). The red clay interval is composed of brownish red and yellowish clay layers (Fig. 2). The upper 20 m contains numerous horizontal carbonate nodule horizons (B_k), most of which underlie brownish red soil layers (B_w) characterized by loam and a medium angular blocky structure. There are also occasional carbonized plant root channels, elliptical worm burrows, and fossil snail shell fragments. Fe–Mn stains are more frequent in the brownish layers than in the yellowish layers, which is also the case for the carbonized root channels. The red clay across the XSZ planation surface is similar to that of typical eolian red clay in the CLP; both are characterized by numerous carbonate-nodule-rich horizons (Fig. 2b).

Figure 2 Photos of the XSZ planation surface and the red clay. (a) XSZ planation surface. (b) Red clay outcrop, XSZ. (c) Position of the XSZ drill hole. (d) The XSZ drill core.

Samples for grain-size, carbonate content, and magnetic susceptibility measurements were taken at 5 cm intervals, and samples for geochemical analysis were collected at 25 cm intervals. Samples for grain-size measurements were pretreated with 10 % H₂O₂ to remove organic material, with 10 % HCl to remove carbonates, and with 0.05 mol L⁻ of (NaPO₃)₆ for dispersion. They were then measured with a Malvern Mastersizer 2000 grain-size analyzer with a detection range of 0.02–2000 µm. Magnetic susceptibility was measured using a Bartington Instruments MS2 meter and MS2B dual-frequency sensor at two frequencies (470 and 4700 Hz, designated χ_lf and χ_hf, respectively). Three measurements were made at each frequency and the final results were averaged. The frequency-dependent magnetic susceptibility (χ_fd) was calculated as χ_lf–χ_hf. Chemical composition was measured via X-ray fluorescence (XRF) using a Panalytical Magix PW2403 with an error of 0.1 %–0.3 %. The sample preparation procedure for XRF analysis was as follows: bulk samples were heated to 35^∘ for 7 days and then ground with an agate mortar to pass a 75 µm sieve; ∼4 g of powdered sample was then pressed into a pellet with a borate coating using a semiautomatic oil–hydraulic laboratory press (model YYJ-40). All the measurements were conducted at the MOE Key Laboratory of Western China's Environmental Systems, Lanzhou University. Silicate-bound CaO (CaO^*) can be estimated, in principle, by the equation CaO^*(mol) = CaO(mol) − CO₂(calcite mol) − 0.5 CO₂(dolomite mol) − 10∕3 P₂O₅(apatite mol) (Fedo et al., 1995). It is generally calculated based on the assumption that all the P₂O₅ is associated with apatite and all the inorganic carbon is associated with carbonates. Thus, the CaO^* of the XSZ red clay was calculated using the following equivalent equation:

$${\mathrm{CaO}}^{*}\left(\mathrm{mol}\right)=\mathrm{CaO}\left(\mathrm{mol}\right)-{\mathrm{CaCO}}_{\mathrm{3}}\left(\mathrm{mol}\right)-\mathrm{10}/\mathrm{3}{\mathrm{P}}_{\mathrm{2}}{\mathrm{O}}_{\mathrm{5}}\left(\mathrm{mol}\right).$$

The carbonate content was measured with a calcimeter using the volumetric method of Avery and Bascomb (1974) in the Key Laboratory of Mineral Resources in Western China (Gansu Province), Lanzhou University.

We used the coefficient of variation (CV) to measure the variability of the records: the higher the CV, the more variable the record. The CV is defined as

$$\mathrm{CV}=\mathrm{100}{\displaystyle \frac{\text{standard\hspace{0.17em} deviation}}{\text{mean}}}.$$

Each sample age was estimated using linear interpolation to derive absolute ages, constrained by our previous magnetostratigraphic study (Fig. 1). The average temporal resolution of the records is 3.8 kyr. Some 80 % of the sequence has a sampling resolution of 4 kyr or less. After interpolation to a 3 kyr sampling interval, we performed spectral analysis on detrended records of carbonate content and χ_pedo using Redfit based on the Lomb–Scargle Fourier transform combined with a Welch overlapped segment averaging procedure. We applied Gaussian band-pass filters at frequencies of 0.09090–0.01111, 0.02174–0.02778, and 0.04167–0.05556 kyr⁻¹ to extract oscillations associated with the 100, 41, and 21 kyr periodicities, respectively. The significance of the correlations is based on a two-tailed test.

4 Results

Profiles of the various environmental proxies are illustrated in Fig. 3. Notably, there is evidence for a relatively wet interval from ∼16–5 m (4.7–3.9 Ma), which is reflected in the high-frequency occurrence of B_w horizons with a low carbonate content (< 8 %) and intermittent enhancement of magnetic susceptibility. There is a large contrast in carbonate content between B_w and B_k horizons, which corresponds to variations in elemental contents. The B_k horizons, with a higher carbonate content, consist of carbonate nodule layers underlying leached zones in the field and indicate the substantial translocation of carbonate minerals from B_w horizons to B_k horizons due to greater rainfall (He et al., 2013). In addition, the CV of most of the records is greater during this interval than in other intervals (Table 1). These various forms of evidence suggest that the climate became more humid and variable during 4.7–3.9 Ma. The characteristics of the individual proxy records are described in detail below.

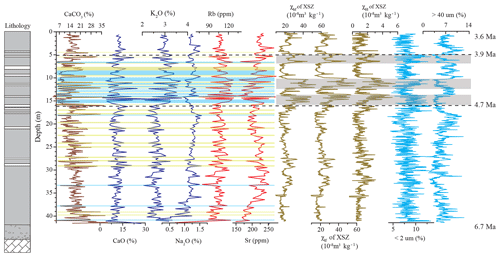
Figure 3 Variations in carbonate content, major element concentration, minor element concentration, magnetic susceptibility, and grain size for the XSZ red clay section (6.7–3.6 Ma). Yellow shading indicates B_k horizons with carbonate content > 21 %; blue shading indicates B_w horizons with carbonate content < 8 %; gray shading indicates intervals with high magnetic susceptibility. Dashed lines are upper and lower boundaries of the relatively wet interval.

Table 1 Average values and coefficients of variation of the geophysical and geochemical data for the XSZ section.

4.1 Carbonate content

The carbonate content of the entire core fluctuates from 1.6 %–39.2 % with an average of 15.9 %. From 42–16 m, the average carbonate content is high (17.1 %) and the carbonate content decreases upwards. The contrast in the carbonate content between the B_w and B_k horizons is generally low; for the B_w horizons, the carbonate content is ∼12 % and values < 8 % are rare. B_k horizons, with a carbonate content of around or above 21 %, are frequent (Fig. 3). From 16–5 m, there are fluctuations in carbonate content of large amplitude (1.6 %–39.1 %) but the average value is low (13.3 %). B_w–B_k horizons are frequent; the B_w horizons have a carbonate content of < 8 %, while that of the B_k horizons is > 21 %. From 5–0 m, the average carbonate content increases to 15.5 %; B_w horizons with a carbonate content < 8 % are absent, and the carbonate content contrast between the B_w and B_k horizons is low.

4.2 Element geochemistry

K₂O ranges from 1.9 %–3.7 % with an average of 2.8 %; Na₂O ranges from 0.14 %–1.54 % with an average of 1.2 %; Rb ranges from 74–134 ppm with an average of 106.2 ppm; and Sr ranges from 141–281 ppm with an average of 212.8 ppm. The variations in CaO exhibit the same trend as carbonate content with high values in B_k horizons and low values in B_w horizons. The variations in Rb and K₂O are synchronous and roughly inverse to those of CaO. The changes in Sr show some similarity with magnetic susceptibility prior to 4.7 Ma but with CaO after 4.7 Ma. Reference to Table 2 shows that CaO is positively correlated with CaCO₃ and Sr and negatively correlated with the other elements. From 16–5 m, CaO and Sr exhibit low values in B_w horizons and high values in B_k horizons, while the opposite is the case for K₂O and Rb. Finally, from 16–5 m, the amplitudes of the fluctuations in CaO, K₂O, Sr, and Rb are greater than in the other intervals.

Table 2 Correlation coefficients for geochemical data for the XSZ section.

Table 3 Results of a significance test for the correlations among CaO^*, CaCO₃, and Sr.

¹ Correlation is significant at the 0.01 level.

4.3 Magnetic susceptibility

The variations in χ_hf, χ_lf, and χ_fd are synchronous. χ_hf ranges from 9.6–53.9 × 10⁻⁸ m³ kg⁻¹ with an average of 21.8 × 10⁻⁸ m³ kg⁻¹; χ_lf ranges from 11.4–59.0 × 10⁻⁸ m³ kg⁻¹ with an average of 23.1 × 10⁻⁸ m³ kg⁻¹; and χ_fd ranges from 0–4.7 × 10⁻⁸ m³ kg⁻¹ with an average of 1.2 × 10⁻⁸ m³ kg⁻¹. From 42–16 m, the three magnetic parameters are relatively low and uniform. χ_hf ranges from 9.6–33.3 × 10⁻⁸ m³ kg⁻¹ with an average of 19.4 × 10⁻⁸ m³ kg⁻¹; χ_lf ranges from 11.4–36.1 × 10⁻⁸ m³ kg⁻¹ with an average of 20.3 × 10⁻⁸ m³ kg⁻¹; and χ_fd ranges from 0–2.8 × 10⁻⁸ m³ kg⁻¹ with an average of 1.0 × 10⁻⁸ m³ kg⁻¹. From 16–5 m, the values of the three parameters, together with their amplitudes of variation, are high. χ_hf ranges from 13.8–53.9 × 10⁻⁸ m³ kg⁻¹ with an average of 27.4 × 10⁻⁸ m³ kg⁻¹; χ_lf ranges from 14.2–59.0 × 10⁻⁸ m³ kg⁻¹ with an average of 29.0 × 10⁻⁸ m³ kg⁻¹; and χ_fd ranges from 0–4.7 × 10⁻⁸ m³ kg⁻¹ with an average of 1.6 × 10⁻⁸ m³ kg⁻¹. Within the intervals of 16–15, 13–11, and 7–5 m, the values of the three parameters increase substantially. From 5–0 m, both the values and amplitudes of variation of the three parameters decrease. χ_hf ranges from 12.8–32.9 × 10⁻⁸ m³ kg⁻¹ with an average of 22.0 × 10⁻⁸ m³ kg⁻¹; χ_lf ranges from 13.6–34.6 × 10⁻⁸ m³ kg⁻¹ with an average of 22.9 × 10⁻⁸ m³ kg⁻¹; and χ_fd ranges from 0–2.5 × 10⁻⁸ m³ kg⁻¹ with an average of 1 × 10⁻⁸ m³ kg⁻¹. Overall, the fluctuations in magnetic susceptibility are substantially different to those of carbonate content, which indicates that the enhancement of magnetic susceptibility was not caused by carbonate leaching.

4.4 Grain size

The clay content (< 2 µm) ranges from 3.8 %–13.5 % with an average of 8.17 %, and the > 40 µm content ranges from 0.7 %–13.9 % with an average of 6 %. The fluctuations in clay content are minor, except for maxima at about 15, 12, and 6 m, which correspond to peaks in magnetic susceptibility (Fig. 3). The coarse silt component (> 40 µm), mainly carried by the East Asian winter monsoon, exhibits a different trend to that of the clay content. In addition, from 21–5 m the fluctuations in the > 40 µm fraction are roughly the inverse of those of magnetic susceptibility. From 42–21 m, the variation of the > 40 µm fraction is characterized by low values and high-frequency fluctuations, whereas above 21 m it exhibits high values and fluctuations of lower frequency.

5 Discussion

5.1 Paleoenvironmental interpretation of the proxies

The carbonate content of aeolian sediments can be readily remobilized and deposited in response to changes in precipitation and evaporation intensity; thus, it is sensitive to changing climatic conditions. Previous studies demonstrated that the carbonate content of loess–red clay sequences of the CLP varies with precipitation (Fang et al., 1999; Sun et al., 2010). The carbonate is mainly derived from a mixture of airborne dust (Fang et al., 1999). Soil micromorphological evidence from Lanzhou loess demonstrates that the carbonate grains in loess are little altered, whereas those in paleosols have undergone a reduction in size as a result of leaching and reprecipitation as secondary carbonate in the lower B_k horizons (Fang et al., 1994, 1999). Furthermore, seasonal alternations between wet and dry conditions are thought to be a key factor driving carbonate dissolution and reprecipitation (Sun et al., 2010). Thus, changes in carbonate content are generally controlled by effective precipitation. When effective precipitation is high, carbonate leaching increases and vice versa. Thus, the carbonate content is an effective proxy for characterizing wet–dry oscillations as well as summer monsoon evolution (Fang et al., 1999; Sun et al., 2010).

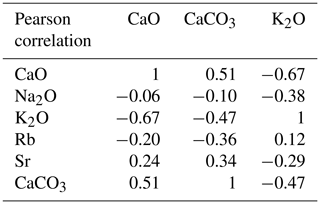
Chemical weathering intensity is generally evaluated by the ratio of mobile (e.g., K, Ca, Sr, and Na) to nonmobile elements (e.g., Al and Rb). In general, Sr shows analogous geochemical behavior to Ca and is readily released into solution and mobilized in the course of weathering; by contrast, Rb is relatively immobile under moderate weathering conditions due to its strong adsorption to clay minerals (Nesbitt et al., 1980; Liu et al., 1993). Thus, the Rb∕Sr ratio potentially reflects chemical weathering intensity. However, Sr may substitute for Ca in carbonates, which may limit the environmental significance of the Rb∕Sr ratio (Chang et al., 2013; Buggle et al., 2011). The correlation between Sr and CaO* (silicate CaO) is significant at the 99 % confidence interval, while the correlation between Sr and CaCO₃ is not significant (Table 3). This means that the variations in Sr are determined by weathering intensity, and therefore we speculate that in our samples the Rb∕Sr ratio mainly reflects weathering intensity (Fig. 4c and d). In addition, the K₂O∕Na₂O ratio is used to evaluate the secondary clay content in loess and is also a measure of plagioclase weathering, thereby avoiding biases due to uncertainties in separating carbonate Ca from silicate Ca (Liu et al., 1993; Buggle et al., 2011). Na₂O is mainly produced by plagioclase weathering and is easily lost during leaching as precipitation increases. By contrast, K₂O (mainly produced by the weathering of potash feldspar) is easily leached from primary minerals and is then absorbed by secondary clay minerals with ongoing weathering (Yang et al., 2006; Liang et al., 2013). In the arid and semiarid regions of Asia, K₂O is enriched in paleosols compared to loess horizons (Yang et al., 2006). Thus, high K₂O∕Na₂O ratios are indicative of intense chemical weathering.

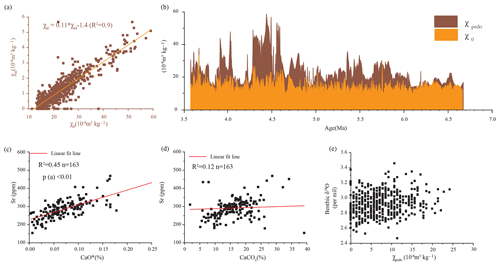
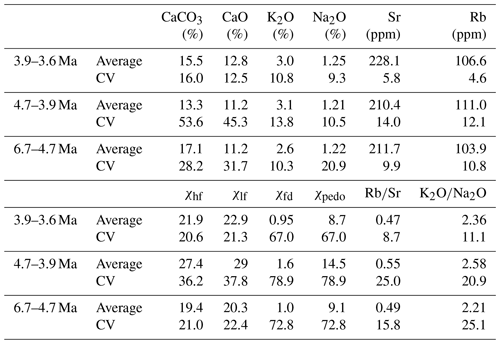
Figure 4 (a) Scatterplot of χ_lf versus χ_fd. (b) Separation of χ_pedo and χ₀. (c) Scatterplot of Sr versus CaO^*. (d) Scatterplot of Sr versus CaCO₃. (e) Scatterplot of benthic δ¹⁸O versus χ_pedo during 6.7–5.2 Ma. χ_pedo is the magnetic susceptibility of pedogenic origin and χ₀ is the magnetic susceptibility of the detrital material.

In the red clay–loess sequence of the CLP, magnetic parameters and the clay content are well-correlated and are thus regarded as proxies for EASM strength (Liu et al., 2004). Aeolian particles usually have two distinct magnetic components consisting of detrital and pedogenic material, respectively (Liu et al., 2004). χ_lf can reflect the combined susceptibility of both components, but changes in χ_lf are mainly affected by changes in the concentration of pedogenic magnetic grains (Liu et al., 2004). The grain-size distribution of pedogenic particles within the superparamagnetic (SP) to single-domain (SD) size range has been shown to be constant (Liu et al., 2004, 2005). Thus, χ_fd can be used detect SP minerals produced by pedogenesis, and therefore the correlation coefficient between χ_lf and χ_fd is a measure of the contribution of such grains (< 0.03 µm for magnetite) to the bulk susceptibility (Liu et al., 2004; Xia et al., 2014). As shown in Fig. 4a, χ_lf is positively correlated with χ_fd, which means that the magnetic susceptibility of the XSZ red clay mainly reflects pedogenic enhancement of the primary aeolian ferromagnetic content via the in situ formation of fine-grained ferrimagnetic material. Thus, the magnetic susceptibility primarily reflects pedogenic intensity. Both the original and pedogenic magnetic signals can be separated using a simple linear regression method (Liu et al., 2004; Xia et al., 2014), which we use to extract the lithogenic (χ₀) and pedogenic magnetite ∕ maghemite (χ_pedo) components. We found that pedogenic magnetite ∕ maghemite accounts for 11 % of the susceptibility (${\mathit{\chi }}_{\mathrm{pedo}}={\mathit{\chi }}_{\mathrm{fd}}/\mathrm{0.11}$).

Pedogenesis results in enhanced secondary clay formation (Sun and Huang, 2006); however, not all of the clay particles are derived from in situ pedogenesis, but rather are inherited from aeolian transport and deposition. Clay particles can adhere to coarser silt and sand particles (Sun and Huang, 2006). In the western CLP, the coarse silt (> 40 µm) content is regarded as a rough proxy for winter monsoon strength (Wang et al., 2002). Therefore, to eliminate this signal from the primary clay particles, the < 2 µm ∕ > 40 µm ratio is proposed to evaluate pedogenic intensity. Furthermore, the similarity of the variations in the < 2 µm ∕ > 40 µm ratio and χ_pedo confirms that in this case the < 2 µm ∕ > 40 µm ratio has the potential to evaluate the pedogenic intensity (Fig. 6).

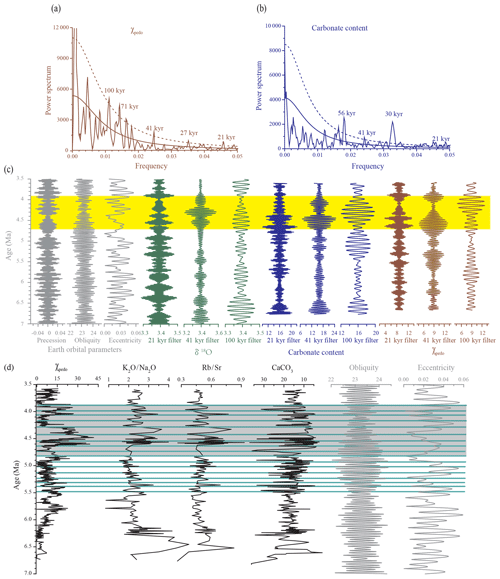
Figure 5 Spectrum analysis results of the XSZ red clay section, (a) χ_pedo and (b) carbonate content. (c) Comparison of orbital parameters (eccentricity, obliquity, and precession; Laskar et al., 2004) with filtered components of the carbonate content, χ_pedo, and δ¹⁸O records (Zachos et al., 2001) in the 18–24, 36–46, and 90–110 kyr bands. Yellow shading denotes increased amplitude of the filtered components of carbonate and χ_pedo within the three orbital bands. (d) Carbonate, weathering, and pedogenic indicators linked to eccentricity and obliquity orbital variations during 4.7–3.9 Ma.

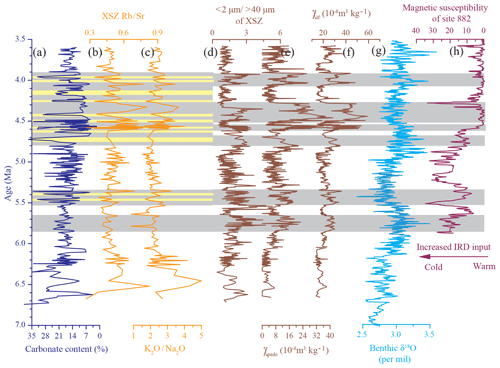
Figure 6 Comparison of the paleoclimatic record of the XSZ red clay section with climate records from elsewhere. (a) Effective precipitation record for the XSZ section. (b–c) Chemical weathering records for the XSZ section. (d–f) Pedogenic intensity records for the XSZ section. (g) Stacked deep-sea benthic foraminiferal oxygen isotope curve compiled from data from DSDP and ODP sites (Zachos et al., 2001). (h) Magnetic susceptibility record from ODP site 882 (Haug et al., 2005). The gray shading indicates relatively wet periods and the light-yellow shading shows intervals of carbonate accumulation.

5.2 Time and frequency domain analysis of carbonate content and χ_pedo

The power spectral analyses of carbonate content and χ_pedo show different dominant cycles (Fig. 5a–b). In detail, χ_pedo is concentrated in the eccentricity (100 kyr), obliquity (41 kyr), and precession (21 kyr) bands, and other periodicities (71 and 27 kyr) are also evident. By contrast, the carbonate signal is concentrated in the precession (21 kyr) and obliquity (41 kyr) bands, but it also exhibits even more prominent periodicities of 56 and 30 kyr. Furthermore, the fluctuations in CaCO₃, weathering, and pedogenesis indices agree well with orbital eccentricity variations during 4.7–3.9 Ma (Fig. 5d). Three orbital periodicities were also detected at other sites in CLP, in the interval from the late Miocene to the early Pliocene, confirming that changes in orbital parameters had a substantial impact on the climate of the CLP (Han et al., 2011).

King (1996) proposed that non-orbital cycles may originate from harmonic effects or interactions of the orbital cycles, while Lu (2004) ascribed them to unstable dust depositional processes followed by varying degrees of pedogenesis in paleosol units. In the XSZ section, the deposition rate is low and uneven, which potentially resulted in the incomplete preservation of the paleoclimatic signal, especially for the relatively short precession cycles. In addition, pedogenesis and postdepositional compaction would also weaken the orbital signals and produce spurious cycles. Moreover, the carbonate content at various depths is affected by leaching, which means that the record integrates soil polygenetic processes, thus obscuring orbital forcing trends related to precipitation amount. Therefore, we speculate that an uneven and low deposition rate, combined with compaction and leaching processes, may have weakened the orbital signals and may be responsible for the presence of non-orbital cycles in the XSZ section.

To investigate the post-6.7 Ma frequency domain evolution of the climate signals in the XSZ section, we filtered the carbonate content and χ_pedo time series at the periods of 100, 41, and 21 kyr using Gaussian band filters centered at frequencies of 0.01, 0.02439, and 0.04762, respectively. We then compared the results with the equivalent filtered components of the stacked deep-sea benthic oxygen isotope record. The results show that the fluctuations of the three filtered components (especially the 41 kyr component) of both proxies change from a low amplitude during 6.7–4.7 Ma to a relatively high amplitude during 4.7–3.9 Ma (Fig. 5c). The enhanced orbital-scale variability of the two proxies from 4.7–3.9 Ma implies increased seasonality and wet–dry contrasts. This shift is not observed in the Earth orbital parameters but is observed in the filtered 41 kyr component of the stacked deep-sea benthic oxygen isotope record (δ¹⁸O). This may mean that the enhancement of wet–dry contrasts at the XSZ site was not driven directly by changes in solar radiation intensity but rather was linked to changes in ice volume or global temperature.

5.3 Late Miocene–Pliocene climate history revealed by the Xiaoshuizi red clay

5.3.1 Multi-proxy evidence for a dry climate during the late Miocene

We used the proxies of pedogenesis and chemical weathering to reconstruct the late Miocene and early Pliocene climatic history of the Xiaoshuizi planation surface. During the late Miocene, relatively high carbonate values with minor fluctuations indicate that the climate was dry, and low Rb∕Sr and K₂O∕Na₂O ratios also support the occurrence of weak chemical weathering. Notably, both the Rb∕Sr and K₂O∕Na₂O ratios show opposite trends to that of carbonate content, meaning that low effective precipitation resulted in weak chemical weathering. Furthermore, the pedogenic proxies (χ_pedo and χ_lf), characterized by low values with minor fluctuations, generally support the occurrence of weak pedogenesis under an arid climate. Thus, the climate at the XSZ site was relatively arid during this interval, resulting in weak chemical weathering and pedogenic intensity. However, there are several subtle differences between the carbonate and pedogenic indices. It is evident that the carbonate content decreases with an increased amplitude of variation after 5.5 Ma, which is consistent with the cycles of carbonate nodules within paleosol horizons observed in the field (Li et al., 2017). It is possible that increased precipitation since 5.5 Ma induced eluviation and the redeposition of carbonate. However, the pedogenic indices indicate that the generally arid climate was interrupted by two episodes of enhanced pedogenesis at 5.85–5.7 and 5.5–5.35 Ma. The subtle differences may result from differences in the sensitivity of magnetic susceptibility and carbonate content to precipitation variability when precipitation is low (Sun et al., 2010). In addition, a coeval mollusk record from the western Liupanshan showed that cold-aridiphilous species dominated, which also indicates that cold and dry climatic conditions occurred in the western CLP during the late Miocene (Fig. 7g).

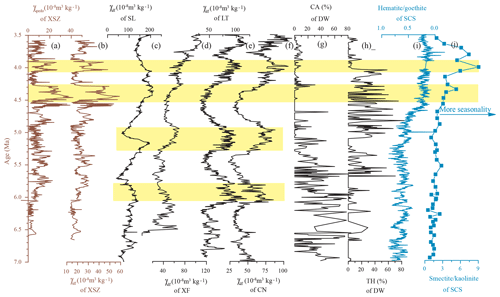
Figure 7 Comparison of late Miocene–Pliocene paleoclimatic records from Asia. (a–b) χ_pedo and χ_lf from the XSZ section. (c–f) χ_lf record from Shilou (Ao et al., 2016), Xifeng (Guo et al., 2001), Lingtai (Sun et al., 2010), and Chaona (Song et al., 2007). (g–h) Percentages of cold-aridiphilous (CA) mollusks and thermo-humidiphilous (TH) mollusks from Dongwan (Li et al., 2008). (i) Hematite ∕ goethite ratio from sediments of the South China Sea (Clift, 2006), and (j) smectite ∕ kaolinite ratio from the South China Sea (Wan et al., 2010; Clift et al., 2014).

Coeval pollen, mollusk, and magnetic records from the central and eastern CLP also indicate generally dry and cold climatic conditions (Wang et al., 2006; Wu et al., 2006; Nie et al., 2014). However, the principal difference is that at the XSZ site, the arid climate was relatively stable, while the climate of the central and eastern CLP was interrupted by several humid stages. For example, two humid stages (6.2–5.8 and 5.4–4.9 Ma) are recorded by the magnetic susceptibility of the red clay in the central and eastern CLP but are absent in the magnetic susceptibility record at the XSZ site (Fig. 7). Notably, the 41 kyr filtered component of thermo-humidiphilous species from Dongwan was damped in the late Miocene (Li et al., 2008). Similarly, the amplitude of the orbital periodicities, filtered from the XSZ carbonate content and χ_pedo records, was obviously damped during 6.7–4.7 Ma. However, the three periodicities in the summer monsoon index from the central CLP show no obvious difference between the late Miocene and Pliocene, but only a slight reduction in variability after 4.2 Ma (Sun et al., 2010). Therefore, we agree that a dry climate prevailed on the CLP during the late Miocene; however, the difference was that the climate in the central and eastern CLP fluctuated more substantially than was the case in the vicinity of the XSZ red clay section.

The especially damped response of the wet–dry climatic oscillations in the western CLP to obliquity forcing may indicate that the influence of the paleo-EASM in the western CLP was negligible. It is widely known that the summer monsoon intensity decreases from southeast to northwest across the CLP. A regional climate model experiment demonstrated that the modern East Asian summer monsoon was not fully established in the late Miocene and had only a small impact on northern China (Tang et al., 2011). A weak paleo-EASM intensity from 7.0–4.8 Ma was revealed by hematite ∕ goethite and smectite ∕ kaolinite ratios at ODP site 1148 in the South China Sea (SCS) (Fig. 7i and j). Therefore, we infer that the paleo-EASM was weak and had only a minor impact on the climate in the study region. In addition, previous studies indicated that the red clay may have been transported by both low-level northerly winds and the upper-level westerlies (Sun et al., 2004; Vandenberghe et al., 2004), and thus the impact of the westerly circulation on the study region cannot be ignored. Notably, the variation of the pedogenic proxies roughly parallels that of the stacked deep-sea benthic foraminiferal oxygen isotope curve (Fig. 6), and χ_pedo has a positive relationship with δ¹⁸O (Fig. 4e). This indicates that when the global temperature was low, pedogenic intensity in the study area increased. It is unreasonable to conclude that precipitation in the study area was dominated by the paleo-EASM and thus we speculate that, during the late Miocene, precipitation transported by the paleo-EASM was limited and that the westerly circulation probably dominated the regional climate.

The simultaneous reduction in amplitude of the 41 kyr filtered components from the western CLP and the deep-sea δ¹⁸O record during the late Miocene likely indicates that the dry climate was related to changes in global temperature and ice volume. A sustained cooling occurred in both hemispheres during the late Miocene, which culminated between 7 and 5.4 Ma (Herbert et al., 2016). δ¹⁸O records from DSDP and ODP sites show an increase of ∼1.0 ‰ during the late Miocene, which resulted from the increased ice volume and the associated decrease in global temperature (Zachos et al., 2001). In the Northern Hemisphere, transient glaciations occurred when the cooling culminated (Herbert et al., 2016). Records from high-latitude regions of the Northern Hemisphere indicate continuously decreasing temperatures and increasing ice volume during the late Miocene (Jansen and Sjøholm, 1991; Mudie and Helgason, 1983; Haug et al., 2005). During the Quaternary, a dry climate prevailed during glacial periods when the global average temperature (especially in summer) was low. Cool summers could result in a small land–sea thermal contrast, which in turn weakened the paleo-EASM. Furthermore, the increased ice volume in the Northern Hemisphere resulted in an increased meridional temperature gradient (Herbert et al., 2016), thus strengthening the westerlies and driving them southwards. This would have prevented the northwestward penetration of the Asian summer monsoon, which is also proposed as the driving mechanism for a weak EASM in northern China during glacial periods (Sun et al., 2015). Thus, the southward shift of the westerlies had a significant impact on the XSZ region. However, moisture sources for the westerly airflow are distant from the CLP (Nie et al., 2014), and only a relatively small amount of moisture was carried to the CLP, resulting in a dry and stable climate in the XSZ region. In conclusion, global cooling and increasing ice volume in the Northern Hemisphere contributed to the dry climatic conditions in the study region.

5.3.2 Intermittently humid climate during the early Pliocene

During the early Pliocene, the proxy evidence indicates that the previously arid climate of the XSZ area became humid from ∼4.7 Ma. The carbonate content was low on average but with large fluctuations, indicating that the climate was generally humid with increased dry–wet oscillations, especially during 4.7–3.9 Ma. Several eluvial–illuvial cycles are evident during 4.7–3.9 Ma; the carbonate content in the eluvial horizons was less than 8 %, whereas in illuvial horizons it was > 21 % (Fig. 6). Research on the migration process of carbonate indicates that a seasonally wet–dry climate is a key factor in driving carbonate dissolution and reprecipitation, and strong seasonally biased precipitation enhances the leaching process and produces thick leached horizons (Rossinsky and Swart, 1993; Zhao, 1995, 1998). The occurrence of high-frequency cycles of carbonate eluviation–redeposition indicates that seasonal precipitation increased during this interval. Furthermore, the variations of Rb∕Sr and K₂O∕Na₂O ratios are very similar to those of carbonate content, which suggests that weathering intensity was related to precipitation amount. Generally, high values of the < 2 µm ∕ > 40 µm ratio, χ_pedo, and χ_lf correspond to large contrasts in carbonate content between eluvial and illuvial horizons; thus, increased precipitation had a significant influence on pedogenic intensity. Seasonal precipitation was intermittently enhanced from 4.7–3.9 Ma, and so was weathering and pedogenic intensity. Pedogenesis and weathering intensity reached a maximum during 4.60–4.25 Ma, as did precipitation intensity, manifested by the enhanced eluviation and carbonate accumulation. Notably, during this interval of peak precipitation (4.6–4.25 Ma), the enhancement of the < 2 µm ∕ > 40 µm ratio is not as strong as that of χ_pedo, which may indicate that the former is of limited value when pedogenic intensity is strong. During 3.9–3.6 Ma, precipitation decreased, and weathering and pedogenic intensity also weakened. Consistent with the records of the XSZ section, mollusk records from Dongwan also indicate the occurrence of warm and humid conditions in the western CLP during the early Pliocene (Fig. 7h).

Palynological and terrestrial mollusk records from the central CLP also indicate relatively humid conditions during the early Pliocene (Wang et al., 2006; Wu et al., 2006). Magnetic susceptibility records from the central and eastern CLP are similar to those from the XSZ section in that both magnitude and variability are high during the early Pliocene. From 4.1–3.9 Ma, the increased magnetic susceptibility indicates that humid climatic conditions prevailed across the entire CLP (Fig. 7). Evidently, when precipitation amount peaked in the vicinity of the XSZ section during 4.60–4.25 Ma, the magnetic susceptibility values at Xifeng, Lingtai, and Chaona were low. However, a record of Fe₂O₃ ratio from Lingtai reveals extremely high values, corresponding to the presence of abundant clay coatings, during 4.8–4.1 Ma; this interval was interpreted as experiencing the strongest EASM intensity in the CLP since 7.0 Ma (Ding et al., 2001). In addition, the relative intensity of pedogenic alteration of the grain-size distribution was the strongest during the interval from 4.8–4.2 Ma in the Lingtai section (Sun et al., 2006). Pollen assemblages at Chaona indicate a substantially warmer and more humid climate from 4.61–4.07 Ma (Ma et al., 2005). These various lines of evidence indicate that during 4.60–4.25 Ma the climate was warm and humid in the central CLP. Gleying has been implicated in reducing the value of magnetic susceptibility as a record of precipitation during this period (Ding et al., 2001). When soil moisture regularly exceeds the critical value, dissolution of ferrimagnetic minerals occurs and the susceptibility signal is negatively correlated with pedogenesis (Liu et al., 2003). This alone indicates that precipitation was likely to have been very high during this interval.

In summary, a wet climate prevailed across the CLP in the early Pliocene. At the same time, the hematite ∕ goethite ratio in the sediments of the South China Sea also indicates enhanced precipitation amount, and the smectite ∕ kaolinite ratio indicates increased seasonality at ∼4.7 Ma (Fig. 7i and j) and thus the enhancement of the paleo-EASM (Clift et al., 2006, 2014). Therefore, we regard the climatic change evident in the XSZ section to reflect the expansion of the paleo-EASM.

Ding (2001) proposed that the uplift of the TP to a critical elevation resulted in an enhanced summer monsoon system during 4.8–4.1 Ma. TP uplift was shown to have had profound effects on the EASM in terms of its initiation and strength, as well as in changing the distribution of the band of high precipitation in East Asia (Li et al., 1991, 2014; An et al., 2001). A detailed modeling study demonstrated that the uplift of the northern TP mainly resulted in an intensified summer monsoon and increased precipitation in northeast Asia (Zhang et al., 2012). From 8.26–4.96 Ma, massive deltaic conglomerates were widely deposited and the sediment deposition rate increased, indicating the uplift of the Qilian Mountains (Song et al., 2001). At the same time, the Laji Mountains underwent pronounced uplift by thrusting at ∼8 Ma, which resulted in the current basin–range pattern (Li et al., 1991; Fang et al., 2005a; Zheng et al., 2000). However, geological and paleontological records indicate that the uplift of the eastern and northern margins of the TP was very minor from the late Miocene to the middle Pliocene (Li et al., 1991, 2015; Zheng et al., 2000; Fang et al., 2005a, b). Therefore, we speculate that uplift of the TP was not the major cause of the expansion of the paleo-EASM at ∼4.7 Ma.

The occurrence of a humid climate across the CLP was synchronous with the gradual closure of the Panama Seaway (Keigwin, 1978; O'Dea et al., 2016). Nie (2014) proposed that the freshening of eastern equatorial and North Pacific surface water, resulting from the closure of the Panama Seaway since 4.8 Ma (Haug et al., 2001), led to sea ice formation in the North Pacific Ocean, which enhanced the high-pressure cell over the Pacific and increased the strength of southerly and southeasterly winds. However, there was a warming trend in the Northern Hemisphere from 4.6 Ma (Haug et al., 2005; Lawrence et al., 2006). The gradual closure of the Panama Seaway resulted in the reorganization of surface currents in the Atlantic Ocean. Notably, the Gulf Stream was enhanced and began to transport warm surface waters to high northern latitudes, thus strengthening the Atlantic meridional overturning circulation and warming the Arctic (Haug and Tiedemann, 1998; Haug et al., 2005). Three independent proxies from an early Pliocene peat deposit in the Canadian High Arctic indicate that Arctic temperatures were 19 ^∘C warmer during the early Pliocene than today (Ballantyne et al., 2010). This warmth is also confirmed by other records from high-northern-latitude regions: diatom abundances and assemblages, pollen data, magnetic susceptibility, and sedimentological evidence from Siberia all indicate that the climate was warm and wet in the early Pliocene (Baikal Drilling Project Members, 1997, 1999). Furthermore, a decrease in the input of ice-rafted debris to the sediments of the subarctic northwest Pacific was synchronous with the expansion of the paleo-EASM during the early Pliocene (Fig. 6). The warming of the Northern Hemisphere and external heating derived from a reduced ice albedo at high northern latitudes enhanced the thermal contrast between the Pacific and Eurasian regions (Dowsett et al., 2010). This large land–ocean thermal contrast was essential for enhancing the paleo-EASM. On the other hand, the unusually warm high northern latitudes and the West Antarctic Ice Sheet expansion by 6–5 Ma (Zachos et al., 2001, 2008) steepened the interhemispheric thermal gradient and further caused the thermal equator to move northward (Chiang and Friedman, 2012; Broecker and Putnam, 2013). This facilitated the northwestward expansion of the paleo-EASM, which is also proposed as the driving mechanism for northwestward migration of the monsoon rain belt for the warm Holocene (Yang et al., 2015). Therefore, we infer that the warming of high northern latitudes in response to the closure of the Panama Seaway may have facilitated the expansion of the paleo-EASM during the early Pliocene. However, there are several uncertainties associated with such an explanation. For example, the timing of the closure of the Panama Seaway is still debated (Bacon et al., 2015; O'Dea et al., 2016), and it is unclear how strongly these changes influenced the paleo-EASM. Addressing these questions requires more geological evidence and precise model simulations of the early Pliocene climate. The value of our study lies in proposing the potential linkage of the evolution of paleo-EASM to changes in temperatures in the high northern latitudes during the early Pliocene.

6 Conclusions

The continuous late Miocene–Pliocene red clay sequence preserved on the planation surface in the NE Tibetan Plateau provides the opportunity to elucidate the history of the Asian monsoon in the western CLP. Multi-proxy records from the XSZ section, together with other paleoclimatic records from the CLP, reveal the major patterns of climatic change from 6.7–3.6 Ma. During the late Miocene, both the amount and variability of precipitation over the XSZ section were small; however, they were much greater in the central and eastern CLP. Thus, the paleo-EASM had little influence on the climate of the western CLP at this time. During the early Pliocene, records from the XSZ section indicate that both the amount and variability of precipitation increased from 4.7–3.9 Ma. The climate was characterized by abrupt increases in the seasonality of precipitation, which attests to a major northwestward extension and enhancement of the summer monsoon. Multiple paleoclimatic proxies clearly show that the strongest summer monsoon occurred during 4.60–4.25 Ma. The expansion of the paleo-EASM may have been caused by warming of the high northern latitudes in response to the closure of the Panama Seaway during the early Pliocene.