the Creative Commons Attribution 3.0 License.
the Creative Commons Attribution 3.0 License.
Interhemispheric effect of global geography on Earth's climate response to orbital forcing
Rajarshi Roychowdhury
Robert DeConto
The climate response of the Earth to orbital forcing shows a distinct hemispheric asymmetry due to the unequal distribution of land in the Northern Hemisphere versus Southern Hemisphere. This asymmetry is examined using a global climate model (GCM) for different climate responses such as mean summer temperatures and positive degree days. A land asymmetry effect (LAE) is quantified for each hemisphere and the results show how changes in obliquity and precession translate into variations in the calculated LAE. We find that the global climate response to specific past orbits is likely unique and modified by complex climate–ocean–cryosphere interactions that remain poorly known. Nonetheless, these results provide a baseline for interpreting contemporaneous proxy climate data spanning a broad range of latitudes, which may be useful in paleoclimate data–model comparisons, and individual time-continuous records exhibiting orbital cyclicity.
- Article
(8298 KB) - Full-text XML
- BibTeX
- EndNote
The arrangement of continents on the Earth's surface plays a fundamental role in the Earth's climate response to forcing. Due to the asymmetric global geography of the Earth, more continental land area is found in the Northern Hemisphere (NH; 68 %) as compared to the Southern Hemisphere (SH; 32 %). These different ratios of land vs. ocean in each hemisphere affect the balance of incoming and outgoing radiation, atmospheric circulation, ocean currents and the availability of terrain suitable for growing glaciers and ice sheets. Subsequently, the climate response of the Earth to radiative forcing is asymmetric (Fig. 1b and c), while the radiative forcing (top-of-atmosphere solar radiation) itself is symmetric across the two hemispheres (Fig. 1a). As a result of the inherent land–ocean asymmetry of the Earth, the climatic responses of the NH and SH differ for an identical change in radiative forcing (Barron et al., 1984; Deconto et al., 2008; Kang et al., 2014; Short et al., 1991).
Charles Lyell was the first to consider the influence of paleogeography on surface temperatures, in the context of the connection between climate and the modern distribution of land and sea (Lyell, 1832). By comparing the climates of the NH and SH, and the distribution of land and sea, Lyell pointed out that the present continental distribution lowers high-latitude temperatures in both hemispheres. He further pointed out that dominance of ocean in the SH leads to mild winters and cool summers. Lyell's work is significant in the context of this paper because it first sparked the debate of continental forcing versus astronomical forcing of climate.
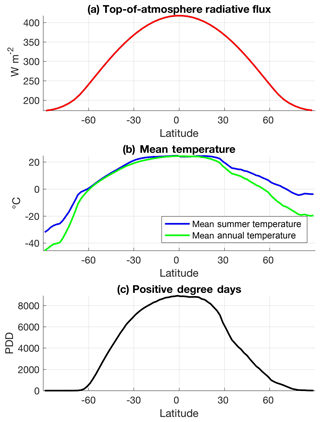
Figure 1(a) Top-of-atmosphere net incoming radiation (annual mean). (b) Mean summer temperatures (blue) and mean annual temperatures (green) computed from GCM simulations with a modern orbit. (c) Positive degree days (PDDs) calculated from GCM simulations with a modern orbit.
Since then, a number of classic studies have shown interhemispheric asymmetry in the climate response of the NH and SH. Climate simulations made with coupled atmosphere–ocean global climate models (GCMs) typically show a strong asymmetric response to greenhouse-gas loading, with NH high latitudes experiencing increased warming compared to SH high latitudes (Flato and Boer, 2001; Stouffer et al., 1989). GCMs also show that the NH and SH respond differently to changes in orbital forcing (e.g., Philander et al., 1996). While the magnitude of insolation changes through each orbital cycle is identical for both hemispheres, the difference in climatic response can be attributed to the fact that the NH is land-dominated while the SH is water-dominated (Croll, 1870). This results in a stronger response to orbital forcing in the NH relative to the SH.
The distribution of continents and oceans has an important effect on the spatial heterogeneity of the Earth's energy balance, primarily via the differences in albedos and thermal properties of land versus ocean (Trenberth et al., 2009). The latitudinal distribution of land has a dominant effect on zonally averaged net radiation balance due to its influence on planetary albedo and its ability to transfer energy to the atmosphere through long-wave radiation, and fluxes of sensible and latent heat. The latitudinal net radiation gradient controls the total poleward heat transport requirement, which is the ultimate driver of winds and ocean circulation (Stone, 1978). Oceans have a relatively slower response to seasonal changes in insolation due to the higher specific heat of water as compared to land, and mixing in the upper ∼10–150 m of the ocean. As a result, in the ocean-dominated SH, the surface waters suppress extreme temperature swings in the winter and provide the atmosphere with a source of moisture and diabatic heating. In the land-dominated NH, the lower heat capacity of the land combined with relatively high albedo results in greater seasonality, particularly in the interiors of large continents (Asia and North America). The land surface available in a particular hemisphere also affects the potential for widespread glaciation, and the extreme cold winters associated with large continents covered by winter snow.
Continental geography has a strong impact on polar climates, as is evident from the very different climatic regimes of the Arctic and the Antarctic. Several early paleoclimate modeling studies using GCMs investigated continental distribution as a forcing factor of global climate (e.g., Barron et al., 1984; Hay et al., 1990). These studies demonstrated that an Earth with its continents concentrated in the low latitudes is warmer and has lower Equator-to-pole temperature gradients than an Earth with only polar continents. Although these early model simulations did not incorporate all of the complexities of the climate system, the results provided valuable insights from comparative studies of polar versus equatorial continents on the Earth and showed that changes in continental configuration has a significant influence on climatic response to forcing.
The asymmetry in the climates of the NH and SH can be attributed to three primary causes: (i) astronomical, i.e., variation in insolation intensity across the NH and SH caused by the precession of the equinoxes (today's perihelion coincides with 3 January, just after the 21 December solstice, leading to slightly stronger summer insolation in the SH); (ii) continental geography, i.e., the effect of continental geography on climate as described above; and (iii) interhemispheric continental geography, i.e., the effect of NH continental geography on SH climate and vice versa. The aim of this study is to gain a better understanding and isolate the effect of interhemispheric continental geography on climate by comparing results from GCM simulations using modern versus idealized (hemispherically symmetric) global geographies. The GCM simulations with modern and idealized (symmetric) geographies are used to quantify the different climate responses to a range of orbits. By comparing the climatic response from simulations with different geographies, we isolate and estimate the effect of interhemispheric continental geography, i.e., the influence of one hemisphere's geography on the climate response of the opposite hemisphere.
One of the main caveats of this study is the lack of a dynamical ocean in our model setup. While this presents certain limitations, the model's computational efficiency has the advantage of allowing for a wide range of orbital parameter space to be explored. We view the inclusion of a full-depth dynamical ocean as a next step, hopefully motivated in part by the results published here. Furthermore, dynamical ocean models introduce an additional level of complexity and model dependencies that we think are best avoided in this initial study.
2.1 Experimental design
GCMs have been used to extensively study the importance of geography on the Earth's climate in the past. In this study, we use the latest (2012) version of the Global ENvironmental and Ecological Simulation of Interactive Systems (GENESIS) 3.0 GCM with a slab ocean component (Thompson and Pollard, 1997) rather than a full-depth dynamical ocean (Alder et al., 2011). The slab ocean predicts sea surface temperatures and ocean heat transport as a function of the local temperature gradient and the zonal fraction of land versus sea at each latitude. While explicit changes in ocean currents and the deep ocean are not represented, the computational efficiency of the slab ocean version of the GCM allows for numerous simulations with idealized global geographies and greatly simplifies interpretations of the sensitivity tests by precluding complications associated with ocean model dependencies. The ocean depth is limited to 50 m (enough to capture the seasonal cycle of the mixed layer). In addition to the atmosphere and slab ocean, the GCM includes model components representing vegetation, soil, snow and thermodynamic sea ice. The 3-D atmospheric component of the GCM uses an adapted version of the NCAR CCM3 solar and thermal infrared radiation code (Kiehl et al., 1998) and is coupled to the surface components by a land-surface-transfer scheme. In the setup used here, the model atmosphere has a spectral resolution of T31 (∼3.75∘) with 18 vertical layers. Land-surface components are discretized on a higher resolution 2∘ × 2∘ grid.
The GCM uses various geographical boundary conditions (described below) in 2∘ × 2∘ and spectral T31 grids for surface and atmospheric general circulation models (AGCMs), respectively. For each set of experiments, the model is run for 50 years. Spin-up is taken into account, and equilibrium is effectively reached after about 20 years of integration. The results used to calculate interhemispheric effects are averaged over the last 20 years of each simulation. Greenhouse-gas mixing ratios are identical in all experiments and set to preindustrial levels with CO2 set to 280 ppmv, N2O to 288 ppbv and CH4 to 800 ppbv (Meinshausen et al., 2011). The default values for CFCl3 and CF2Cl2 values are set to 0 ppm. The solar constant is maintained at 1367 W m−2.
2.2 Asymmetric and symmetric Earth geographies
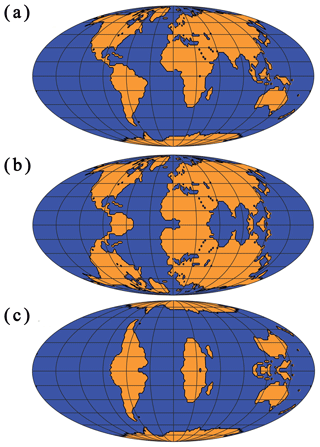
The GCM experiments are divided into three sets: (1) preindustrial CONTROL, (2) NORTH-SYMM and (3) SOUTH-SYMM. The preindustrial CONTROL experiments use a modern global geography spatially interpolated to the model's 2∘ × 2∘ surface grid (Cuming and Hawkins, 1981; Kineman, 1985). The geographical inputs provide the land–ice sheet–ocean mask and land-surface elevations used by the GCM, along with global maps of vegetation distribution, soil texture and other quantities (Koenig et al., 2012).
To simulate the climate of an Earth with meridionally symmetric geographies, we created two sets of land-surface boundary conditions: NORTH-SYMM and SOUTH-SYMM. For the NORTH-SYMM experiments, the CONTROL experiment boundary conditions are used to generate a modified GCM surface mask, by reflecting the NH geography (land–sea-ice mask, topography, vegetation, soil texture) across the Equator into the SH. Similarly, in the experiment SOUTH-SYMM, the land mask and geographic boundary conditions in the SH are mirrored in the NH. The NORTH-SYMM and SOUTH-SYMM boundary conditions are shown in Fig. 2b and c with the CONTROL (Fig. 2a) for comparison. Poleward oceanic heat flux is defined as a function of the temperature gradient and the zonal fraction of land and sea at a given latitude in the model; hence the parameterized ocean heat flux is symmetric in our symmetrical Earth simulations.
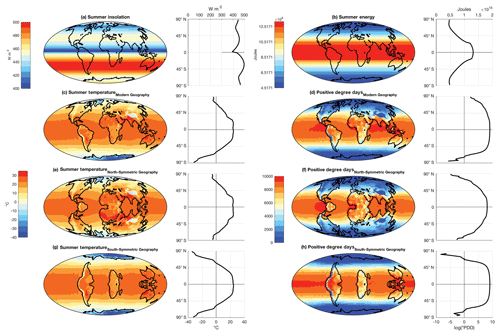
Figure 3(a–d) Demonstration of Earth's asymmetric climate response to symmetric climate forcing. Simulations are forced with modern orbit: (a) summer insolation; (b) summer energy (as defined in Huybers, 2006); (c) summer temperature; and (d) PDD. (e–h) Demonstration of Earth's symmetric climate response to climate forcing when idealized symmetric Earth geographies are used. Simulations are forced by modern-day orbit: (e, f) summer temperature and PDD for NORTH-SYMM simulation, (g, h) summer temperature and PDD for SOUTH-SYMM simulation. The zonal averages are plotted on the right of each panel. Zonal averages of PDD are plotted on a log scale.
In the first experimental setup, we run the GCM with modern-day orbital configuration, i.e., eccentricity is set to 0.0167, obliquity is set to 23.5∘ and precession such that perihelion coincides with the SH summer. The top-of-atmosphere radiation is shown in terms of mean summer insolation and summer energy (Fig. 3a and b). The summer energy is an integrated measure of changes in insolation intensity as well as duration of summer, and is defined as , where Wi is mean insolation measured in W m−2 on day i, and β equals 1 when Wi≥τ and 0 otherwise. τ=275 W m−2 is taken as the threshold for melting to start at the surface of the Earth. Mean summer temperature (ST) is calculated from the GCM as the mean of the average daily temperatures for the summer months in each hemisphere. We define summer by an insolation threshold (325 W m−2) that accounts for the astronomical positions as well as the phasing of the seasonal cycle of insolation. The zonal averages of ST (calculated at each latitude) demonstrate the inherent asymmetry in the Earth's climate between NH and SH, especially evident in the higher latitudes (Fig. 3c). Positive degree days (PDDs) capture the intensity as well as the duration of the melt season, and have been shown to be indicative of the ice-sheet response to changes in external forcing. Figure 3d shows the PDDs for modern orbit, with zonal averages plotted on the log scale. The asymmetry between the NH and SH is captured by the GCM in the calculated PDDs.
Next, we maintain the modern orbit to test the effect of meridionally symmetric continents (Fig. 3e–h). Figure 3e and f shows ST and PDD from a simulation in which the NH geography is reflected in the SH (thus making the Earth geographically symmetric). Figure 3g and h shows ST and PDD from the simulation with symmetric SH continents. Symmetric continents make the climates of the NH and SH symmetric (>95 %). However, due to the current timing of perihelion with respect to the summer solstices, there remains some minor asymmetry. Using an orbit in which perihelion coincides with equinoxes will make the climate truly symmetrical.
4.1 Effect of SH on NH climate
To estimate the effect of SH continental geography on NH climate, we subtract the NH climate of the NORTH-SYMM simulation (symmetric NH continents in both hemispheres) from the CONTROL simulation (asymmetric, modern orbit). In these two simulations, the only difference in setup is the SH continental distribution. Thus the difference in NH climate from the two simulations, if any, can be safely ascribed as the effect of SH continental geography on NH climate. We quantify this interhemispheric effect for ST (for NH) as
Analogous to the effect for ST, the effect for PDD, which we call the “Land Asymmetry Effect” (LAE), is defined as follows:
where and PDDcontrol are the mean daily temperature and PDD from the CONTROL simulation, and and PDDnorth are the mean daily temperature and PDD from the simulation with the North-Symmetric configuration geography (NORTH-SYMM). n is the number of days in the summer months in each hemisphere.
4.2 Effect of NH on SH climate
Similarly, we estimate the effect of NH continental geography on the SH by subtracting the SH climate of the SOUTH-SYMM simulation (symmetric southern continents in both hemispheres) from the CONTROL simulation (asymmetric, modern orbit). In these two simulations, the differences in SH climate in the CONTROL and SOUTH-SYMM simulations, if any, can be ascribed as the “effect of NH continental geography on SH climate”. We quantify this interhemispheric effect for ST (for SH) and the LAE as
where and PDDcontrol are the mean daily temperature and PDD from the CONTROL simulation, and and PDDsouth are the mean daily temperature and PDD from the simulation with the South-Symmetric configuration geography (SOUTH-SYMM).
4.3 Results of modern orbit simulations
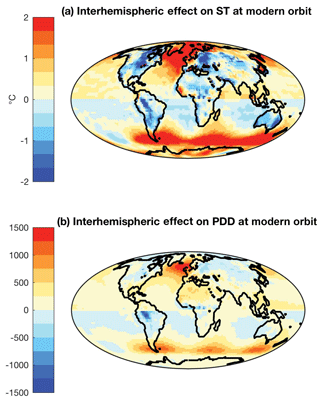
Figure 4a and b shows the interhemispheric effect of continental geography on ST and PDD, respectively. For the NH, the STs are calculated when the insolation intensity over the NH is strongest. The asymmetry in the SH landmasses leads to weakening of the summer warming over North America and Eurasia (blue shaded regions correspond to cooling). Consequently, STs over NH continents are lower by 3–6 ∘C relative to a symmetric Earth. There is a positive warming effect in the North-Atlantic Ocean, and in general the NH oceans are slightly warmer relative to a symmetric Earth. The general trends in the interhemispheric effect on PDD (LAE) (Fig. 4b) mimic those of the STs (Fig. 4a).
Table 1Experimental setup of model boundary conditions and forcings.
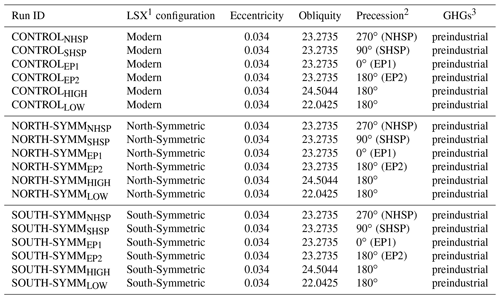
NHSP: NH summer solstice at perihelion; SHSP: SH summer solstice at perihelion; EP1: NH vernal equinox at perihelion and EP2: NH autumnal equinox at perihelion. 1 LSX represents the land-surface transfer scheme. 2 Orbital precession in the GCM is defined here as the prograde angle from perihelion to the NH vernal equinox. 3 GHGs represents greenhouse gases.
For the SH, the STs are calculated when the insolation is most intense over the SH during the year. SH landmasses, except Antarctica, generally show a cooling response during summer, due to NH geography. Over Antarctica, STs are higher in the control simulations than in the symmetric simulations, leading to the inference that there is a warming (increase) in STs due to interhemispheric effect. Also, the Southern Ocean shows a strong positive temperature effect (warming) relative to a symmetric Earth, although this Southern Ocean response might be different or modified if a full-depth dynamical ocean model was used.
Next, we examine the effect of the opposite hemisphere on the Earth's climate response at extreme obliquities (axial tilt) and idealized precessional configurations (positions of the solstices and equinoxes in relation to the eccentric orbit). The orbital parameters used in these experiments are idealized and do not correspond to a specific time in Earth's history. Rather, they are chosen to provide a useful framework for studying the Earth's climate response to precession and obliquity. HIGH and LOW orbits approximate the highest and lowest obliquity in the last 3 million years (Berger and Loutre, 1991). NHSP (NH summer at perihelion) and SHSP (SH Summer at Perihelion) orbits correspond to NH and SH summers coinciding with perihelion, respectively. The other two precessional configurations considered are EP1 and EP2, with the perihelion coinciding with the equinoxes. For the idealized precession simulations, the obliquity is set to its mean value averaged over the last 3 million years. Eccentricity is set to the same moderate value (mean eccentricity over the last 3 million years) for all simulations. Table 1 summarizes the orbits used in the ensemble of model simulations. Here, we focus only on the LAE, as PDD is a better indicator of air temperature's influence on annual ablation over ice sheets than ST, since this metric captures both the intensity and duration of the melt season.
Changes in precession primarily affect seasonal insolation intensity that is well known to be out of phase in both hemispheres (Lyell, 1832). To demonstrate an asymmetry in the climate response to precession, we take the differences between two arbitrarily chosen extremes in the precession cycle (NHSP and SHSP) for both the forcing and the climate response. The forcing (summer energy – J) calculated at the top of the atmosphere is numerically symmetric (but out of phase as expected) in both hemispheres (Fig. 5a). The difference in the PDDs (ΔPDDprecession) is the Earth's climate response to the combined effect of the two precessional motions (wobbling of the axis of rotation and the slow turning of the orbital ellipse). The climate response (ΔPDDprecession) is asymmetric across both hemispheres (Fig. 5b). However, when we run the precessional simulations in an Earth with symmetric continents, the climate response to precession is symmetrical (Fig. 5c and d).
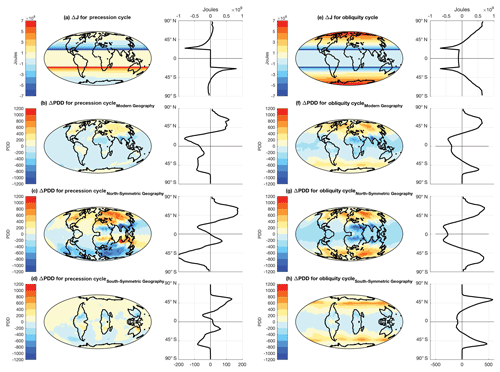
Figure 5Summer energy (J) change for a transition from a SHSP to a NHSP orbit (a); and the corresponding change in positive degree days (PDD) in CONTROL (b); NORTH-SYMM (c) and SOUTH-SYMM (d) simulations. Summer energy (J) change for a transition from LOW to HIGH orbit (e); and the corresponding change in PDD in CONTROL (f); NORTH-SYMM (g) and SOUTH-SYMM (h) simulations.
In contrast to precession, obliquity alters the seasonality of insolation equally in both hemispheres (Fig. 5e). A reduction in the tilt from 24.5∘ (HIGH) to 22∘ (LOW) reduces annual insolation by ∼17 W m−2 and summer insolation by ∼45 W m−2 in the high latitudes. In the tropics, summer insolation increases by up to ∼5 W m−2. Loutre et al. (2004), among others, predicted that global ice volume changes at the obliquity periods could be interpreted as a response to mean annual insolation and meridional insolation gradients. To demonstrate asymmetry in the climate response to obliquity, we take the differences between the highest and lowest obliquities for both the forcing and the climate response. The difference in the PDDs (ΔPDDobliquity) is the Earth's climate response to changes in tilt. Figure 5f shows ΔPDDobliquity and the zonal averages reveal the asymmetry in the obliquity climate response. The same simulations with North-Symmetric Earth (Fig. 5g) and South-Symmetric Earth (Fig. 5h) produce symmetrical climate responses to the obliquity cycle.
The effect of SH continental geography on NH at the idealized orbits is estimated using the same method described above, with the LAE for a given orbit (for NH) calculated as
Similarly, the effect of NH continental geography on SH at the idealized orbits is estimated using the same method described above, with the LAE for a given orbit (for SH) calculated as
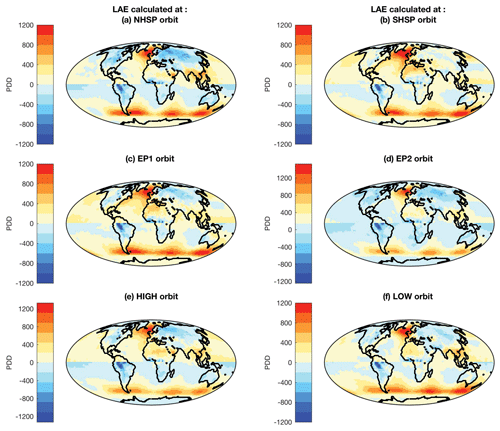
Figure 6a shows the spatial variation in LAE when perihelion coincides with NH summer (NHSP). The NH landmasses show a strong negative response. In this orbit, the NH experiences elevated summer insolation, but the response is attenuated by the interhemispheric effect. This dampening effect is greatest in the interiors of the NH continents. If precession is considered in isolation (i.e., constant obliquity), then according to the astronomical theory of climate the NH should experience “interglacial” conditions when perihelion coincides with NH summer. However, because of the interhemispheric effect, interglacial (warm summer) conditions are muted relative to those on a symmetric Earth. During this orbit, the SH experiences “glacial” (cold summer) conditions due to the weaker summer insolation. The positive effect in the SH leads to weaker cooling relative to a symmetric Earth. Thus, when perihelion coincides with NH summer, the interhemispheric effect dampens the magnitude of “glacial” versus “interglacial” conditions in both hemispheres.
Figure 6b shows the spatial variation in LAE when perihelion coincides with SH summer (SHSP). The NH continents have a weak positive effect, leading to slightly warmer conditions relative to a symmetric Earth. In this orbit, the southern high latitudes experience intense summer insolation. The positive warming effect amplifies the already warm conditions in the SH. Figure 6c and d shows the spatial variation in LAE at the two equinoxes, i.e., when NH vernal equinox is at perihelion (EP1) and when NH autumnal equinox is at perihelion (EP2). The LAE is in general weaker at the equinoxes than at the solstices.
At HIGH obliquity, there exists a negative effect on NH continents (Fig. 6e), which mutes the strong insolation intensity during summer months. In the NH, as a result of continental asymmetry, a decrease in the Equator-to-pole temperature gradient is observed. A lowering of STs and temperature gradient due to the interhemispheric effect has a negative impact on the deglaciation trigger associated with HIGH obliquity orbits. Thus the interhemispheric effect would hinder the melting of ice during high-obliquity orbits. In the SH, the positive interhemispheric effect on PDD over Antarctica and the Southern Ocean leads to overall higher temperatures in the southern high latitudes as compared to a symmetric Earth. Thus, during the HIGH obliquity orbits the positive effect helps deglaciation.
At LOW obliquity, the negative effect over NH continents is generally less intense (Fig. 6f). However, even the modest lowering of summer temperatures caused by the interhemispheric effect would support the growth of ice sheets during low-obliquity orbits. The positive effect (warming) in the southern high latitudes would delay the growth of ice sheets.
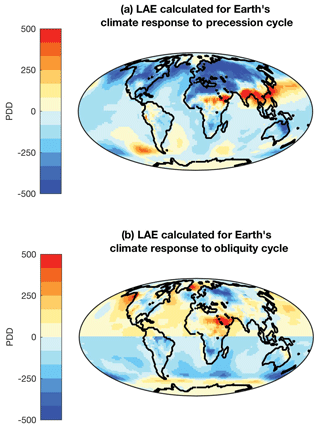
Next, we calculate the LAE for a transition through a precessional cycle. We take two arbitrary end points in the precessional cycle (NHSP and SHSP) and calculate the difference of PDDs between the two simulations (ΔPDDprecession_cycle). The LAE for precessional cycle is therefore calculated as
The LAE shows a strong negative effect in the NH (Fig. 7a). For the NH, this transition from SHSP to NHSP equates to a transition from a cool to a warm climate. The negative interhemispheric effect decreases the |ΔPDD| in the real Earth, thus weakening the effect of precession in the NH. The SH shows a positive effect on PDD at high latitudes. For the SH, the transition from SHSP to NHSP equates to a transition from warmer to cooler climate. The positive interhemispheric effect at high latitudes decreases the |ΔPDD| in the real Earth, thus weakening the effect of precessional cycle in the SH high latitudes.
To calculate the LAE for a transition through the obliquity cycle, we take the highest and lowest obliquities (HIGH and LOW), and calculate the difference of PDDs between the two simulations (ΔPDDobliquity_cycle). The LAE for obliquity cycle is therefore calculated as
The NH shows a small negative effect in the high latitudes, and a positive effect in the low latitudes (Fig. 7b). The transition from LOW to HIGH corresponds to a transition from cold to warm climate. The negative interhemispheric effect decreases the ΔPDD, thus weakening the climate response of the obliquity cycle in the high latitudes. The positive interhemispheric effect increases the ΔPDD, thus strengthening the climate response of obliquity cycle in the low latitudes in the NH. The SH largely shows a negative effect, with a positive effect in the high latitudes. The transition from LOW to HIGH corresponds to a transition from cold to warm climate. The positive interhemispheric effect increases the ΔPDD, thus amplifying the effect of obliquity over Antarctica.
A comprehensive, mechanistic evaluation of the interhemispheric effect is beyond the scope of this initial study. However, as a first step, we test the relationship between the hemispheric LAE and various atmospheric processes by exploring correlations between the interhemispheric responses to orbital forcing, and climatological fields related to changes in radiation (clouds), dynamics (heat and moisture convergence) and feedbacks related to surface processes (sea ice and snow albedos).
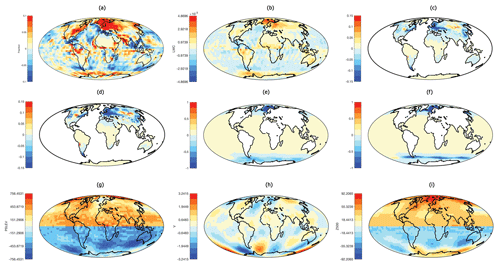
Figure 8The effect of interhemispheric continental distribution on (a) mean annual cloud cover fraction, (b) liquid water content from all cloud types (kg kg−1), (c) fractional snow cover (annual mean), (d) fractional snow cover (averaged over spring months), (e) fractional sea-ice cover (annual mean), (f) fractional sea-ice cover (averaged over spring months), (g) sea level pressure (Pa, annual mean), (h) northward wind (m s−1, annual mean) and (i) 500 hPa geopotential height (m, annual mean).
Numerous studies have shown the impact of variation in the distribution of clouds on climate (e.g., Meleshko and Wetherald, 1981). It is observed that the cloud cover alters in idealized symmetric continent experiments, i.e., the hemispheric asymmetry in the continental geography impacts the distribution of cloud cover (cloud cover is measured as the mean of total cloudiness). Cloud cover affects the climate through two opposing influences; a cooling effect is produced due to reflection of solar radiation, and a warming effect on climate due to reduction of effective temperature for outgoing terrestrial (long-wave) radiation (Wetherald et al., 1980). However, the overall effect of increasing cloud cover is generally considered to cause cooling (Manabe et al., 1967; Schneider, 1972). The hemispheric asymmetry impacts the cloud cover fraction by as much as 10 % at various latitudes (Fig. 8a). The effect of asymmetry increases cloudiness over land poleward of 50∘ N latitude, contributing to negative net radiation and temperature anomalies over the NH continents, and this can be observed both in terms of ST and the PDD. In the SH, total cloudiness decreases over the Southern Ocean due to hemispheric asymmetry, contributing to a positive temperature anomaly over this region. At latitudes below 50∘, the increase in the area-mean flux of outgoing terrestrial radiation is almost compensated by the increase in net insolation flux. Thus, we expect a minor impact of cloud content on the LAE at lower latitudes.
Snow cover reflects ∼80 % to 90 % of the Sun's energy and it has an important influence on energy balance and regional water budgets. Snow cover's effect on surface energy balance has a strong cooling effect; and conversely, decreasing snow cover leads to a decrease in surface albedo and warming. We find that the snow fraction (annual and monthly averages) is also influenced by the hemispheric asymmetry of the continents. There is a decrease in the snow fraction over most of Eurasia and North America due to hemispheric asymmetry (Fig. 8c), leading to warming in the asymmetrical Earth when compared to an Earth with symmetric continents. The effect is more pronounced in the spring months (Fig. 8d), which leads to longer summers, increasing the PDDs in the asymmetric Earth. The relationship between the snow fraction and temperature anomalies is expected to be weaker in the heavily forested regions (such as Northern Asia), where the snow–albedo feedback is less effective (Bonan et al., 1992). Similarly, fractional sea-ice cover has an opposing effect on temperature. Thus, an increase in fractional sea-ice cover due to hemispheric asymmetry causes a negative LAE, as increased albedo reduces net short-wave radiative flux.
Spatial patterns in the LAE are compared with basic dynamical effects of the different geographies. Sea level pressure shows an effect due to hemispheric asymmetry (Fig. 8g), with a general increase in the NH and a decrease in the SH. The resulting change in the time-averaged (mean annual shown here) wind field can be seen in northward winds (Fig. 8h) and imply a dynamical contribution to the LAE anomaly patterns via warm air advection. Spatial patterns in these dynamical linkages can help explain some of the regional anomalies seen in the LAE. For example, we find reduced winds in the North Atlantic leading to reduced heat loss out of that region. This hints at a tropical teleconnection to the westerlies (e.g., Hou, 1998), propagating the impact of low-latitude geography to the midlatitudes of the opposite hemisphere, in this case with an amplifying impact on sea ice and regional warming in the North Atlantic. We observe a positive relationship between the LAE and 500 hPa geopotential height (Fig. 8i), whereby a positive “Z500 effect” indicates that the geopotential heights are regionally higher (implying warm temperatures across the region) when compared to a symmetric Earth, and vice versa. Interhemispheric teleconnections like these have been extensively studied with respect to present-day continental geography (Chiang and Friedman, 2012; Harnack and Harnack, 1985; Hou, 1998; Ji et al., 2014). However, far-field effects such as those arising from interactions between the Hadley circulation and planetary waves (among other dynamical processes) are not adequately resolved at the relatively coarse spatial resolution used in these initial simulations, with monthly meteorological output. A more complete dynamical analysis of the LAE is the subject of ongoing work and a future paper.
The unbalanced fraction of land in the NH versus SH has remained almost unchanged for tens of millions of years. However, the significance of this continental asymmetry on Earth's climate response to forcing has not been previously quantified with a physically based climate model. We find that continental geography of the opposite hemisphere has a control on the climate system's response to insolation forcing, and this may help explain the nonlinear response of the Earth's climate to insolation forcing.
According to classical Milankovitch theory, the growth of polar ice sheets at the onset of glaciation requires cooler summers in the high latitudes in order for snow to persist throughout the year. During warm summers at the high latitudes, the winter snowpack melts, inhibiting glaciation or leading to deglaciation if ice sheets already exist. Thus, the intensity of summer insolation at high latitudes, especially the NH polar latitudes, has been considered the key driver of the glacial–interglacial cycles and other long-term climatic variations. At precessional periods, at which the high-latitude summer insolation intensity primarily varies (Huybers, 2006; Raymo et al., 2006, etc.), the land asymmetry effect plays an important role by amplifying (and weakening at certain times) the effect of summer insolation intensity.
In all the orbital configurations simulated here, we find that the geography of the SH weakens the temperature response of the high NH latitudes to orbital forcing. Consequently, this leads to a larger latitudinal gradient in STs in the NH compared to that of a symmetric Earth. In particular, the amplification (or weakening) of the response to insolation changes at precessional and obliquity periods might explain some of the important features of late Pliocene–early Pleistocene climate variability, when obliquity-paced cyclicity dominated precession in global benthic δ18O records. In Fig. 7, we have demonstrated that the interhemispheric effect causes a suppression of the effects of precessional cycle on the Earth's surface. In other words, the real Earth has a smaller response to a precession cycle as compared to the hypothetical symmetric Earth. We have also showed that the interhemispheric effect causes an amplification of the effects of obliquity cycle on the Earth's surface. In other words, the real Earth has a larger response to the obliquity cycle in the ocean-dominated SH, as compared to the hypothetical symmetric Earth. Consequently, the interhemispheric effect of continental geography contributes to the muting of precessional signal and amplification of obliquity signal recorded in paleoclimate proxies such as benthic δ18O isotope records.
There are various ways in which the Earth's continental asymmetry affects climate. Here, we have shown how these interhemispheric effects influence the Earth's climate response to orbital forcing via the radiative and atmospheric dynamical processes represented in a slab ocean GCM. While computationally challenging, future work should include complimentary simulations with atmosphere–ocean general circulation models to explore the potential modifying role of ocean dynamics on the amplifying and weakening interhemispheric responses to orbital forcing demonstrated here.
The GENESIS GCM model output that was generated for this study is archived under https://doi.org/10.17632/kt8v7ths6p.1 (Roychowdhury and DeConto, 2019).
The authors declare that they have no conflict of interest.
We thank anonymous reviewers for giving constructive comments towards the critical
development of this paper. We thank David Pollard for his help with the GCM simulations.
Edited by: Pascale Braconnot
Reviewed by: three anonymous referees
Alder, J. R., Hostetler, S. W., Pollard, D., and Schmittner, A.: Evaluation of a present-day climate simulation with a new coupled atmosphere-ocean model GENMOM, Geosci. Model Dev., 4, 69–83, https://doi.org/10.5194/gmd-4-69-2011, 2011.
Barron, E. J., Thompson, S. L., and Hay, W. W.: Continental distribution as a forcing factor for global-scale temperature, Nature, 310, 574–575, https://doi.org/10.1038/310574a0, 1984.
Berger, A. and Loutre, M. F.: Insolation values for the climate of the last 10 million years, Quaternary Sci. Rev., 10, 297–317, https://doi.org/10.1016/0277-3791(91)90033-Q, 1991.
Bonan, G. B., Pollard, D., and Thompson, S. L.: Effects of boreal forest vegetation on global climate, Nature, 359, 716–718, https://doi.org/10.1038/359716a0, 1992.
Chiang, J. C. H. and Friedman, A. R.: Extratropical Cooling, Interhemispheric Thermal Gradients, and Tropical Climate Change, Annu. Rev. Earth Planet. Sci., 40, 383–412, https://doi.org/10.1146/annurev-earth-042711-105545, 2012.
Roychowdhury, R. and DeConto, R. M.: Interhemispheric Effect of Global Geography on Earth's Climate Response to Orbital Forcing (GCM Outputs), Mendeley Data, https://doi.org/10.17632/kt8v7ths6p.1, 2019.
Croll, J.: On ocean-currents, part I: ocean-currents in relation to the distribution of heat over the globe, Philos. Mag. J. Sci., 39, 81–106, 1870.
Cuming, M. J. and Hawkins, B. A.: TERDAT: The FNOC system for terrain data extraction and processing, Tech. Rep. M11 Project M254, 2nd Edn., US Navy Fleet Numerical Oceanography Center, Monterey, CA, 1981.
Deconto, R. M., Pollard, D., Wilson, P. A., Pälike, H., Lear, C. H., and Pagani, M.: Thresholds for Cenozoic bipolar glaciation, Nature, 455, 652–656, https://doi.org/10.1038/nature07337, 2008.
Flato, G. M. and Boer, G. J.: Warming asymmetry in climate change simulations, Geophys. Res. Lett., 28, 195–198, https://doi.org/10.1029/2000GL012121, 2001.
Harnack, R. P. and Harnack, J.: Intra- and inter-hemispheric teleconnections using seasonal southern hemisphere sea level pressure, J. Climatol., 5, 283–296, https://doi.org/10.1002/joc.3370050305, 1985.
Hay, W. W., Barron, E. J., and Thompson, S. L.: Results of global atmospheric circulation experiments on an Earth with a meridional pole-to-pole continent, J. Geol. Soc. Lond., 147, 385–392, https://doi.org/10.1144/gsjgs.147.2.0385, 1990.
Hou, A. Y.: Hadley Circulation as a Modulator of the Extratropical Climate, J. Atmos. Sci., 55, 2437–2457, https://doi.org/10.1175/1520-0469(1998)055<2437:HCAAMO>2.0.CO;2, 1998.
Huybers, P.: Early Pleistocene glacial cycles and the integrated summer insolation forcing, Science, 313, 508–511, https://doi.org/10.1126/science.1125249, 2006.
Ji, X., Neelin, J. D., Lee, S.-K., Mechoso, C. R., Ji, X., Neelin, J. D., Lee, S.-K., and Mechoso, C. R.: Interhemispheric Teleconnections from Tropical Heat Sources in Intermediate and Simple Models, J. Climate, 27, 684–697, https://doi.org/10.1175/JCLI-D-13-00017.1, 2014.
Kang, S. M., Seager, R., Frierson, D. M. W., and Liu, X.: Croll revisited: Why is the northern hemisphere warmer than the southern hemisphere?, Clim. Dynam., 44, 1457–1472, https://doi.org/10.1007/s00382-014-2147-z, 2014.
Kiehl, J. T., Hack, J. J., Bonan, G. B., Boville, B. A., Williamson, D. L., and Rasch, P. J.: The National Center for Atmospheric Research Community Climate Model: CCM3, J. Climate, 11, 1131–1149, https://doi.org/10.1175/1520-0442(1998)011<1131:TNCFAR>2.0.CO;2, 1998.
Kineman, J.: FNOC/NCAR global elevation, terrain, and surface characteristics, Digital Dataset, 28 MB, NOAA National Geophysical Data Center, Boulder, 1985.
Koenig, S. J., DeConto, R. M., and Pollard, D.: Pliocene Model Intercomparison Project Experiment 1: implementation strategy and mid-Pliocene global climatology using GENESIS v3.0 GCM, Geosci. Model Dev., 5, 73–85, https://doi.org/10.5194/gmd-5-73-2012, 2012.
Loutre, M.-F., Paillard, D., Vimeux, F., and Cortijo, E.: Does mean annual insolation have the potential to change the climate?, Earth Planet. Sc. Lett., 221, 1–14, https://doi.org/10.1016/S0012-821X(04)00108-6, 2004.
Lyell, C.: Principles of Geology, John Murray, Albemarle Street, London, available at: https://www.bl.uk/collection-items/charles-lyells-principles-of-geology# (last access: 31 January 2018), 1832.
Manabe, S., Wetherald, R. T., Manabe, S., and Wetherald, R. T.: Thermal Equilibrium of the Atmosphere with a Given Distribution of Relative Humidity, J. Atmos. Sci., 24, 241–259, https://doi.org/10.1175/1520-0469(1967)024<0241:TEOTAW>2.0.CO;2, 1967.
Meinshausen, M., Smith, S. J., Calvin, K., Daniel, J. S., Kainuma, M. L. T., Lamarque, J.-F., Matsumoto, K., Montzka, S. A., Raper, S. C. B., Riahi, K., Thomson, A., Velders, G. J. M., and van Vuuren, D. P. P.: The RCP greenhouse gas concentrations and their extensions from 1765 to 2300, Climatic Change, 109, 213–241, https://doi.org/10.1007/s10584-011-0156-z, 2011.
Meleshko, V. P. and Wetherald, R. T.: The effect of a geographical cloud distribution on climate: A numerical experiment with an atmospheric general circulation model, J. Geophys. Res., 86, 11995, https://doi.org/10.1029/JC086iC12p11995, 1981.
Philander, S. G. H., Gu, D., Lambert, G., Li, T., Halpern, D., Lau, N.-C., and Pacanowski, R. C.: Why the ITCZ Is Mostly North of the Equator, J. Climate, 9, 2958–2972, https://doi.org/10.1175/1520-0442(1996)009<2958:WTIIMN>2.0.CO;2, 1996.
Raymo, M. E., Lisiecki, L. E., and Nisancioglu, K. H.: Plio-Pleistocene Ice Volume, Antarctic Climate, and the Global δ18O Record, Science, 313, 492–495, 2006.
Schneider, S. H.: Cloudiness as a Global Climatic Feedback Mechanism: The Effects on the Radiation Balance and Surface Temperature of Variations in Cloudiness, J. Atmos. Sci., 29, 1413–1422, https://doi.org/10.1175/1520-0469(1972)029<1413:CAAGCF>2.0.CO;2, 1972.
Short, D. A., Mengel, J. G., Crowley, T. J., Hyde, W. T., and North, G. R.: Filtering of Milankovitch Cycles by Earth's Geography, Quaternary Res., 35, 157–173, https://doi.org/10.1016/0033-5894(91)90064-C, 1991.
Stone, P. H.: Constraints on dynamical transports of energy on a spherical planet, Dyn. Atmos. Ocean., 2, 123–139, https://doi.org/10.1016/0377-0265(78)90006-4, 1978.
Stouffer, R. J., Manabe, S., and Bryan, K.: Interhemispheric asymmetry in climate response to a gradual increase of atmospheric CO2, Nature, 342, 660–662, https://doi.org/10.1038/342660a0, 1989.
Thompson, S. L. and Pollard, D.: Greenland and Antarctic Mass Balances for Present and Doubled Atmospheric CO2 from the GENESIS Version-2 Global Climate Model, J. Climate, 10, 871–900, https://doi.org/10.1175/1520-0442(1997)010<0871:GAAMBF>2.0.CO;2, 1997.
Trenberth, K. E., Fasullo, J. T., Kiehl, J., Trenberth, K. E., Fasullo, J. T., and Kiehl, J.: Earth's Global Energy Budget, B. Am. Meteorol. Soc., 90, 311–323, https://doi.org/10.1175/2008BAMS2634.1, 2009.
Wetherald, R. T., Manabe, S., Wetherald, R. T., and Manabe, S.: Cloud Cover and Climate Sensitivity, J. Atmos. Sci., 37, 1485–1510, https://doi.org/10.1175/1520-0469(1980)037<1485:CCACS>2.0.CO;2, 1980.
- Abstract
- Introduction
- Model
- Symmetry (and asymmetry) in GCM results
- Modern orbit simulations
- Idealized orbit simulations
- Results of idealized orbit simulations
- LAE for orbital cycles
- Impact of various climatological variables on LAE
- Conclusions
- Data availability
- Competing interests
- Acknowledgements
- References
- Abstract
- Introduction
- Model
- Symmetry (and asymmetry) in GCM results
- Modern orbit simulations
- Idealized orbit simulations
- Results of idealized orbit simulations
- LAE for orbital cycles
- Impact of various climatological variables on LAE
- Conclusions
- Data availability
- Competing interests
- Acknowledgements
- References