the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
The sensitivity of the Greenland Ice Sheet to glacial–interglacial oceanic forcing
Javier Blasco
Alexander Robinson
Jorge Alvarez-Solas
Marisa Montoya
Observations suggest that during the last decades the Greenland Ice Sheet (GrIS) has experienced a gradually accelerating mass loss, in part due to the observed speed-up of several of Greenland's marine-terminating glaciers. Recent studies directly attribute this to warming North Atlantic temperatures, which have triggered melting of the outlet glaciers of the GrIS, grounding-line retreat and enhanced ice discharge into the ocean, contributing to an acceleration of sea-level rise. Reconstructions suggest that the influence of the ocean has been of primary importance in the past as well. This was the case not only in interglacial periods, when warmer climates led to a rapid retreat of the GrIS to land above sea level, but also in glacial periods, when the GrIS expanded as far as the continental shelf break and was thus more directly exposed to oceanic changes. However, the GrIS response to palaeo-oceanic variations has yet to be investigated in detail from a mechanistic modelling perspective. In this work, the evolution of the GrIS over the past two glacial cycles is studied using a three-dimensional hybrid ice-sheet–shelf model. We assess the effect of the variation of oceanic temperatures on the GrIS evolution on glacial–interglacial timescales through changes in submarine melting. The results show a very high sensitivity of the GrIS to changing oceanic conditions. Oceanic forcing is found to be a primary driver of GrIS expansion in glacial times and of retreat in interglacial periods. If switched off, palaeo-atmospheric variations alone are not able to yield a reliable glacial configuration of the GrIS. This work therefore suggests that considering the ocean as an active forcing should become standard practice in palaeo-ice-sheet modelling.
- Article
(5233 KB) - Full-text XML
- BibTeX
- EndNote
Recent observations show that the Greenland Ice Sheet (GrIS) has lost mass at an accelerated rate over the past decades (Rignot et al., 2011; Zwally et al., 2011; Sasgen et al., 2012; Shepherd et al., 2012; van den Broeke et al., 2016). On average, the GrIS contributed to 0.47 ± 0.23 mm a−1 of sea-level rise from 1991 to 2015 (van den Broeke et al., 2016), with an accelerated rate of 0.89 ± 0.09 mm a−1 from 2010 to 2014 (Yi et al., 2015). In the future, the GrIS is expected to continue losing mass, contributing to a sea-level rise relative to the 20th century between 90 and 280 mm by 2100 in the worst-case scenario (RCP8.5) (Bindschadler et al., 2013; IPCC, 2013; Clark et al., 2015; Fürst et al., 2015). This accelerated ice loss is due to a combination of increased surface melting and enhanced ice discharge from marine-terminating glaciers to the ocean (van den Broeke et al., 2016). High surface melting has been attributed to rising atmospheric Greenland temperatures (Box et al., 2009; Hall et al., 2008; Tedesco et al., 2016), which may also increase crevassing and calving at the ice front. Conversely, the recently enhanced discharge of ice into the ocean is thought to be directly connected to warmer Atlantic waters entering Greenland's fjords (Holland et al., 2008a; Rignot et al., 2010; Straneo et al., 2010; Straneo and Heimbach, 2013). Higher oceanic temperatures increase the submarine melting at the calving front of tidewater glaciers, contributing to their acceleration, ice mass discharge into the ocean and potentially grounding-line retreat. This acceleration-and-retreat mechanism has been found in several Greenland glaciers that terminate in the ocean (Rignot and Kanagaratnam, 2006). Jakobshavn Isbræ, West Greenland's fastest glacier, experienced a high rate of basal melting (Motyka et al., 2011) initially induced by the intrusion of warmer waters from the Irminger Sea (Holland et al., 2008a), more than doubling its speed in the last 25 years (Joughin et al., 2012) and suffering a rapid retreat of its terminus. Following enhanced subglacial melting observed in the early 2000s, the Helheim Glacier (southeast Greenland) also doubled its speed (Howat et al., 2005; Sutherland and Straneo, 2012) and suffered peak thinning rates of 90 m a−1 (Stearns and Hamilton, 2007), with its terminus retreating by about 7 km over just 3 years (Howat et al., 2007; Straneo et al., 2016).
The complex mechanisms that lead to ice-shelf thinning, loss of buttressing and potential grounding-line instability have been studied largely for the Antarctic Ice Sheet (AIS) (DeConto and Pollard, 2016; Favier et al., 2014; Hanna et al., 2013; Joughin et al., 2014a; Pritchard et al., 2012; Rignot et al., 2004; Shepherd et al., 2004; Wouters et al., 2015). The thinning of the Larsen C ice shelf (Holland et al., 2015) and its recent calving event (Hogg and Gudmundsson, 2017; Jansen et al., 2015), the collapse of Larsen B and the melting of the Antarctic Peninsula glaciers (Cook et al., 2016), the widespread retreat of Pine Island and other glaciers in West Antarctica (Alley et al., 2015; Joughin et al., 2014b; Rignot et al., 2014) and the thinning of some East Antarctica ice shelves (Rignot et al., 2013) are notable examples of the direct connection between changes in oceanic forcing and glacier-termini adjustment (Alley et al., 2015). Only in the last several years has the scientific community also focused its attention on the ice–ocean interaction in Greenland, motivated by the observed acceleration and retreat of major GrIS outlet glaciers. Although marine-terminating glaciers cover only a small fraction of the entire GrIS, modifications at the ice–ocean boundaries due to oceanic changes may considerably affect the inland ice geometry. The effects induced by outlet-glacier acceleration are transferred onshore by ice-flow dynamics, causing adjustments to the entire inland ice-mass configuration (Nick et al., 2009; Fürst et al., 2013; Golledge et al., 2012). For this reason, a full understanding of the interaction between ice and ocean is crucial to assess the response of the GrIS to past and future climate changes.
Various numerical models have been used to simulate current submarine melt rates (Jenkins, 2011; Rignot et al., 2016; Sciascia et al., 2013; Xu et al., 2012, 2013) and dynamic retreat (Morlighem et al., 2016; Vieli and Nick, 2011) of the GrIS marine-terminating glaciers, as well as ice-dynamic future projections of the whole GrIS (Fürst et al., 2015; Nowicki et al., 2013), due to changes in the oceanic temperatures. However, how this thermal forcing affected the past GrIS configuration has not been explored from a modelling perspective so far. Recently, Bradley et al. (2017) simulated the GrIS evolution for the two last glacial cycles by considering a sub-shelf melt parameterization which is a function of the water depth below the ice shelves. Under this assumption, the submarine melt rate increases when the past sea-level rises. However, their approach does not take into account ocean temperature changes. Other studies have reconstructed the GrIS past evolution as driven essentially by atmospheric forcing (Langebroek and Nisancioglu, 2016; Quiquet et al., 2012, 2013; Robinson et al., 2011; Stone et al., 2013), while the dynamic evolution of the entire GrIS including the influence of the past oceanic forcing too has only been investigated in a simplified manner. To this end, Huybrechts (2002) used a three-dimensional ice-sheet model in which marine extent is controlled by changes in water depth based on past eustatic sea-level variations, while Tarasov and Peltier (2002), Simpson et al. (2009) and Lecavalier et al. (2014) performed a palaeo-reconstruction of the entire GrIS constraining their ice-sheet models with past relative sea-level (RSL) reconstructions. However, submarine melting was not taken into account as an active forcing in these studies.
The main purpose of this work is to assess the impact of ice–ocean interaction on the evolution of the whole GrIS throughout the last two glacial cycles. By implementing a submarine melting rate parameterization suitable for palaeo-climatic studies into a three-dimensional hybrid ice-sheet–shelf model, we evaluate the sensitivity of the GrIS to past climatic variations, including changes in oceanic temperatures (in terms of heat-flux variations), and investigate their capability to trigger grounding-line advance and retreat through time. First, we describe the ice-sheet–shelf model used to simulate the GrIS evolution, focusing on the implementation of the submarine melt rate parameterization, and the sensitivity tests performed for this study (Sect. 2). In Sect. 3, we show the results obtained in each experiment and we compare them with data for the last interglacial (LIG), the Last Glacial Maximum (LGM) and the present day (PD) found in the literature. After discussing the main model uncertainties and caveats (Sect. 4), we summarize the main conclusions of this work (Sect. 5).
2.1 Model
To investigate the oceanic sensitivity of the GrIS throughout the last two glacial cycles, we use the three-dimensional, hybrid, ice-sheet–shelf model GRISLI-UCM. The model is an extension of the GRISLI ice-sheet model (Ritz et al., 2001), which has already been successfully used to simulate the evolution of the past Greenland (Quiquet et al., 2012, 2013) and Antarctic ice sheets (Ritz et al., 2001; Philippon et al., 2006; Alvarez-Solas et al., 2010), as well as the Laurentide Ice Sheet (Alvarez-Solas et al., 2011, 2013). GRISLI-UCM combines the Shallow Ice Approximation (SIA) for slow inland deformational flow and the Shallow Shelf Approximation (SSA) over fast-flowing areas, that is, ice streams and ice shelves, where plug flow is dominant. Since we assume deformational ice-sheet regions to be frozen at the bedrock, no basal sliding is considered for SIA-dominated areas. Basal sliding for ice streams is determined through a basal drag term (τb), defined as a function of the effective pressure (Neff) between ice and water pressure, and the basal horizontal velocity (ub), considered as follows:
where
Dragging at the floating ice-shelf base is considered to be zero. The position of the grounding line is evaluated following a flotation rule dependent on the current sea level and the ice thickness. Calving at the ice front is based on a two-condition thickness criterion (Peyaud et al., 2007; Colleoni et al., 2014). First, an ice-shelf front must have a thickness lower than 200 m to potentially contribute to ice discharge. This threshold is in agreement with the thickness of many observed shelves at their ice–ocean interface. Second, if the ice advected from each upstream point is not sufficient to maintain the ice-front thickness higher than that threshold, the grid point at the front calves. The entire GrIS ice dynamics is solved on a computational grid of 20 km × 20 km horizontal resolution and 21 vertical layers. The glacial isostatic adjustment (GIA) is described by the elastic lithosphere – relaxed asthenosphere method (Le Meur and Huybrechts, 1996), for which the viscous asthenosphere responds to the ice load with a tunable characteristic relaxation time (see Sect. 2.4).
The hybrid scheme uses a weighting function to combine the non-sliding horizontal SIA velocities (uSIA) with the SSA horizontal velocities (uSSA) and is defined as (Bueler and Brown, 2009)
where the weighting function f(uSSA) depends on the module of the SSA component (uSSA) through
ranging between 0 and 1. In this work, the reference velocity uref is set to 100 m a−1. For small values of uSSA, f(uSSA)≈0 and the horizontal velocities are calculated within the SIA, while f(uSSA)≈1 for uSSA≫uref, for which the contribution of SSA dominates.
2.2 Atmospheric forcing
The surface mass balance (SMB) is calculated by the positive degree-day (PDD) scheme (Reeh, 1989) forced by surface atmospheric temperatures and precipitation. This melting scheme is admittedly too simple for palaeo-simulations as it omits the contribution of insolation-induced effects on surface melting, which are important in past warmer periods such as the Eemian (Robinson and Goelzer, 2014). However, since this study focuses on the melting effects induced by past ocean temperature variations, the PDD melt model is sufficient to give a first approximation of surface melt that allows the ice sheet to retreat during interglacial periods in a realistic way. The atmospheric temperature forcing is a spatially and temporally variable field. It is retrieved using an index-anomaly approach in which the present-day climatological field (Tclim, atm) is perturbed by past temperature anomalies derived through a spatially uniform climatic index α(t) (Fig. 1), as follows:
The index α(t) is built through a multiproxy approach. First, we combine the temperature reconstruction for Greenland by Vinther et al. (2009) from 11.7 ka BP to present, the North Greenland Ice Core Project (NGRIP) reconstruction (Kindler et al., 2014) for 115–11.7 ka BP and the North Greenland Eemian Ice Drilling (NEEM) reconstruction (NEEM, 2013) for 135–115 ka BP, and we generate a synthetic temperature anomaly time series for 250–135 ka BP based on Antarctic isotope records following Barker et al. (2011). Second, the composite signal undergoes a windowed low-pass frequency filter ( ka−1) in order to remove the spectral components associated with millennial timescales and below. Finally, the index α is obtained by normalizing the resulting signal to be in agreement with Eq. (5), i.e. α=0 for the LGM and α=1 for the present day. The present-day climatological field is taken from the regional climate model MAR forced by ERA-Interim (Fettweis et al., 2013). TLGM, atm−TPD, atm is the 2-D surface atmospheric temperature (SAT) difference between the LGM and the present, as simulated by the climatic model of intermediate complexity CLIMBER-3α (Montoya and Levermann, 2008). For the precipitation rate, the procedure is similar, but the annual present-day precipitation is scaled by the ratio of the past precipitation to its present value, as in Banderas et al. (2017). At the base of the grounded ice, the melt rate is calculated as a function of the geothermal heat flux, which is prescribed following Shapiro and Ritzwoller (2004), and the local pressure melting point. The submarine melt rate is described in detail in the next subsection.
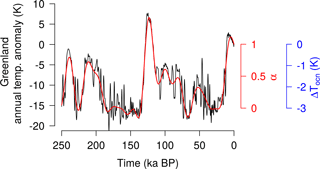
Figure 1The 250 ka Greenland annual temperature anomaly signal built through a multiproxy approach based on the reconstruction by Vinther et al. (2009) from 11.7 ka BP to present, the NGRIP reconstruction (Kindler et al., 2014) for 115–11.7 ka BP, the NEEM reconstruction (NEEM, 2013) for 135–115 ka BP and a synthetic temperature anomaly time series for 250–135 ka BP following Barker et al. (2011) (black line). The red line shows the filtered and normalized climatic index α used to correct the present-day climatological fields when forcing the model. The same signal can be interpreted as the palaeo-oceanic temperature anomaly of Eq. (8) (in blue).
2.3 Oceanic forcing
Several marine basal melting rate parameterizations can be found in the literature. Generally, the submarine melt rate is thought to be directly influenced by the oceanic temperature variations below the ice shelves. Accordingly, most basal melting parameterizations are built as function of the difference between the oceanic temperature at the ice–ocean boundary layer and the temperature at the ice-shelf base, generally assumed to be at the freezing point. The dependence on this temperature difference can be linear (Beckmann and Goosse, 2003) or quadratic (Holland et al., 2008b; Pollard and DeConto, 2012; DeConto and Pollard, 2016; Pattyn, 2017). Because of the increasing temperature anomaly approaching the onshore ice-shelf limit, both schemes ensure a higher basal melting rate close to the grounding line, as suggested by observations (Dutrieux et al., 2013; Rignot and Jacobs, 2002; Wilson et al., 2017).
The marine basal melting rate parameterization used in this work follows a linear approach that accounts separately for sub-ice-shelf areas near the grounding line and for purely floating ice (ice shelves). A linear scheme is the simplest case that allows testing of the GrIS sensitivity to past oceanic temperature changes. The formulation is derived from the net basal melt rate Bgl (m a−1) for ice-shelf cavities close to the grounding line and terminating in shallow ocean zones, expressed by Beckmann and Goosse (2003) as
where Tocn is the oceanic temperature close to the grounding line (K), Tf is the temperature at the ice base, assumed to be at the freezing point (K), and κ is the heat flux exchanged between ocean water and ice at the ice–ocean interface (). Since knowledge of past Tocn and Tf is challenging for the complex heat-flux transfer between ice shelves and the surrounding water, we opted for substituting these quantities and rearranging the equations to make them more suitable for palaeo-studies. A representation of the transient oceanic temperature Tocn can be given by the climatological oceanic temperature Tclim, ocn corrected by the LGM–present temperature anomaly (TLGM, ocn−TPD, ocn) scaled by the same climatic index α=α(t) used to correct the atmospheric climatological fields (Fig. 1). Under this assumption, Eq. (6) can be rewritten as
where
Combining and reorganizing these equations as
we can finally retrieve the expression for the basal melting rate at the grounding line Bgl (m a−1) as used in this work:
Bref (m a−1) is assumed to represent the present-day basal melting rate around the ice sheet, κ represents the sensitivity of the basal melting rate to changes in the oceanic temperature, and ΔTocn (K) expresses the temporal evolution of the melting at the ice base. In this way, Bgl coincides with the present-day melt (Bref) for α=1 and its LGM (21 ka BP) value for α=0. When Bgl is negative, the model allows for refreezing, and the grounding line can advance offshore.
In a more realistic setup, all parameters in Eq. (10) could be described by 2-D spatially variable fields. However, for the sake of simplicity, here we considered all the parameters to be spatially uniform around all the GrIS marine borders, as described in Sect. 2.4. The glacial–interglacial temperature anomaly TLGM, ocn−TPD, ocn (Eq. 8) is set constant to −3 K, which corresponds to the mean value of the reconstructed LGM sea surface temperature (SST) anomalies for the Atlantic Ocean between 60 and 80∘ N latitude (MARGO Project Members, 2009). This value slightly differs from the LGM mean SST anomaly reconstructed by Annan and Hargreaves (2013) (between −1 and −2 K). However, a variation in κ or an identical change in ΔTocn equally affect the oceanic forcing applied to the model. Therefore, considering a different value for ΔTocn would not alter the magnitude of the oceanic sensitivity applied to the GrIS. These simplifications allow here for a spatially uniform, but time-dependent, Bgl.
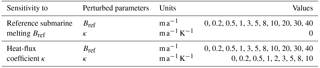
Table 1Summary of all parameter values used to perturb the basal melting rate equation (Eq. 10) in each sensitivity test.
The basal melting rate for purely floating ice shelves (Bsh) is given by the grounding-line basal melt Bgl scaled by a constant factor γ:
In this study, γ is set to 0.1. Hence, we consider that the basal melting rate for ice shelves is 10 times lower than that close to the grounding zone, which is qualitatively in agreement with melt rates observed in some Greenland glaciers (Münchow et al., 2014; Rignot and Steffen, 2008; Wilson et al., 2017). Conversely, the melt rate in the open ocean, that is considered as being beyond the continental shelf break, is prescribed to a high value (50 m a−1) to avoid unrealistic ice growth beyond 1500 m of ocean depth.
2.4 Experimental design
To study how oceanic changes impact the evolution of the GrIS over the last glacial cycles, we performed a set of sensitivity tests by perturbing the two key parameters of the basal melting rate equation (Eq. 10): the estimated present-day submarine melting Bref and the heat-flux coefficient κ. For each experiment, we ran an ensemble of simulations over the GrIS domain throughout the last 250 ka. In this study, the model is initialised with the present-day Greenland topography (Bamber et al., 2013), the characteristic relaxation time for the lithosphere is set to 3000 years, and the model is forced by the past relative sea-level reconstruction of Grant et al. (2014). The first ∼ 100 ka of the simulation are considered as a spin-up and are not analysed. A summary of all the parameter values used in each sensitivity test is shown in Table 1.
First, we analyse the sensitivity of the model to different constant (in space and time) Bref values applied at the base of the ice-sheet marine margins. Due to the scarcity of submarine melt observations along the GrIS coasts, and since the only available estimates have focused on few very rapid tidewater Greenland glaciers that cannot be representative of the basal melt rate for the entirety of GrIS marine areas (Rignot et al., 2010; Motyka et al., 2011; Straneo et al., 2012; Xu et al., 2013; Enderlin and Howat, 2013; Fried et al., 2015; Rignot et al., 2016; Wilson et al., 2017), we assume present-day basal melting rates for Greenland comparable to those from Antarctic ice shelves (Rignot et al., 2013). The range of values of Bref is set between 0 and 40 m a−1, while κ is set to zero to make the ocean contribution constant in time. The resulting basal melting rate is thus equal to the tested Bref value and a condition of no oceanic basal melting around the GrIS is achieved only when both Bref and κ are set to zero.
Second, we study the sensitivity of the GrIS to the basal melt rate sensitivity κ at the ice–ocean interface. The range of tested values for κ is between 0 (expressing a temporally constant basal melting rate) and 10 . The choice of this range reflects the inference made in Antarctica by Rignot and Jacobs (2002) that a variation of 1 K in the effective oceanic temperature changes the melt rate by 10 m a−1 (Eq. 6). Due to the lack of data for Greenland, as a first approximation, we can assume such a value is also realistic there. This is surely a simplification of the problem, as the relation between ocean temperature and melt rate is not universal but depends on many factors, such as the water salinity, the depth, the conformation of the cavity, the water velocity below the ice shelf and subglacial discharge. The sensitivity test for κ is firstly done for Bref=1 m a−1 and then for other Bref values to show that the GrIS response to the melting rate sensitivity κ depends on the chosen reference basal melting rate (see Table 1).
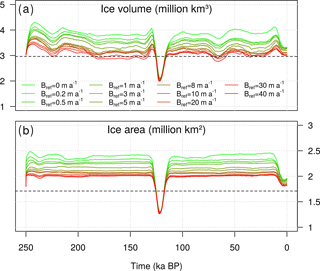
Figure 2Time evolution of (a) grounded ice volume (million km3) and (b) ice-covered area (million km2) simulated for different values of Bref (m a−1) having set κ=0 (see Table 1). Dashed lines show the present-day estimated volume and area of the GrIS (Bamber et al., 2013).
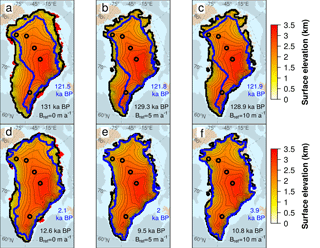
Figure 3Glacial maximum GrIS surface elevation (km) simulated at Termination II (a–c) and Termination I (d–f) for different values of the reference basal melting rate (Bref=0, 5, 10 m a−1) under constant oceanic conditions (κ=0). The timing at which the ice volume reaches its maximum value during a glacial cycle depends on the experiment and is stated in black for each snapshot. Blue lines indicate the GrIS extension at the following peak of deglaciation with its corresponding timing reported in blue. Red zones represent the ice shelves extending beyond the glacial maximum grounding line (black line). Black circles indicate the locations of the Camp Century, NEEM, NGRIP, GRIP and Dye3 ice cores (from north to south).
In this section, we present the results of each sensitivity study aiming to assess the impact of the ocean on the evolution of the GrIS throughout the last two glacial cycles, especially focusing on the LIG, the LGM and the PD GrIS. The present work involved a total of 110 model simulations, although only the most representative cases for each sensitivity study are discussed.
3.1 Sensitivity to the reference submarine melting
In this experiment, the maximum ice volume reached in glacial times ranges between 3.4 and 4.3 million km3 (Fig. 2), 15–45 % higher than the observed current value (Bamber et al., 2013), suggesting that under constant oceanic forcing, the GrIS is limited to a configuration close to that of the present day (Fig. 3). The highest glacial ice volume is reached by imposing a null basal melting to the GrIS margins (Bref=0), which corresponds to a simulation forced solely by palaeo-atmospheric variations. The varying SMB throughout the cycles still results in a changing GrIS ice volume over time. However, during glacials, most grounded ice remains on land above sea level, and only small ice shelves are able to grow (Fig. 3a, d).
For Bref>0, a positive basal melt rate is applied to the marine margins of the whole GrIS throughout the two glacial cycles. The submarine melting not only inhibits the grounding-line advance during the glacials but contributes to thinning the few marine-terminating glaciers still present, constraining the grounding line further inland and resulting in a GrIS extent close to the observed present-day configuration (Fig. 3b, c, e, f). This mechanism can still be quite active during glacial times, such that the ice volume can be even lower than that simulated at the present (Fig. 2). Note that the ice volume is more sensitive to Bref during the glacial periods, as during the interglacial periods the effect of the ocean is limited by the topography of the Greenland itself. Thus, the retreat is almost entirely driven by the surface ablation and the elevation–melt feedback. For low Bref values, the ice lost in a deglaciation is to a large extent determined by the GrIS configuration in the preceding glacial. As high basal melting rates inhibit the ice growth during the cold phase, the higher the Bref is applied to the marine margins, the lower ice loss is simulated in the following interglacial (Fig. 4). However, for Bref=5 m a−1, ice loss becomes insensitive to the melting applied, since the GrIS is also totally land based during glacial periods and any subsequent ice mass loss is therefore uniquely driven by ablation (compare Fig. 3a and b or Fig. 3d and e).
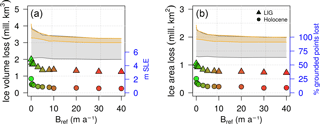
Figure 4Distribution of the ice volume (a) and area (b) lost during the LIG (triangles) and the Holocene (circles) as a function of Bref. Grey and yellow shades show the range between the maximum glacial and the minimum interglacial ice volumes (area) for LIG and Holocene, respectively. The loss is calculated between the time at which the ice volume reaches its maximum value simulated before the deglaciation (between 132 and 128 ka BP for TII and between 13 and 9 ka BP for TI) and its following ice minimum (between 122 and 121 ka BP for the Eemian and between 8 and 0 ka BP for the Holocene). The colours of the points follow the legend of Fig. 2 for clarity. Each ice volume loss has been converted to value of sea-level-equivalent anomaly (m s.l.e. with respect to its simulated present-day volume.
3.2 Sensitivity to the heat-flux coefficient
We next study the sensitivity to the ocean for a fixed Bref value of 1 m a−1 (Fig. 5). This value is within present-day submarine melting rates estimates, between those found in the largest remaining outlet glaciers in Greenland (Wilson et al., 2017) and those of smaller marine-terminating glaciers with presumably much lower ocean-induced melt. Under this assumption, the maximum ice volume simulated in both glacial periods for different κ values ranges between 4 and 5.4 million km3, greatly exceeding the range found for the case with constant oceanic forcing. Prescribing positive or zero uniform submarine melting to the marine boundaries limits the glacial expansion of the GrIS (Figs. 6a and 7a), as discussed in Sect. 3.1. Conversely, by intensifying the oceanic forcing applied to the margins (with increasing values of κ), the glacial ice volume increases. For κ=1 , the model simulates a GrIS glacial expansion to the continental shelf break in which the grounding line has already advanced from the present-day continental boundaries, and large ice shelves are generated in the eastern GrIS, especially in the northeast (Figs. 6b and 7b). The maximum expansion is simulated for the last glaciation, where the grounding line has almost reached the continental shelf break and large ice shelves in the east cover the remaining shallower zones of the bathymetry. For κ=10 , the GrIS extends all the way to the continental shelf break at its glacial maximum, while only a few small floating ice shelves are present (Figs. 6c and 7c).
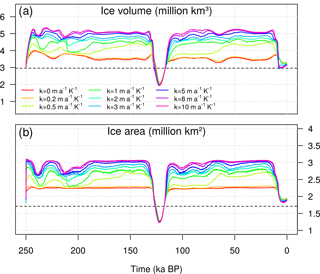
Figure 5(a) Time evolution of GrIS grounded ice volume (million km3) and (b) ice area (million km2) simulated for different values of the heat-flux coefficient κ, having set Bref=1 m a−1. Dashed lines shows the GrIS ice volume and area estimated for the present day (Bamber et al., 2013).
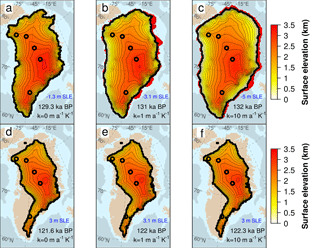
Figure 6GrIS surface elevation (km) simulated at the penultimate glacial maximum (TII) (a–c) and at the LIG minimum (Eemian) (d–f) for three values of the melting rate sensitivity κ having set Bref=1 m a−1. The timing of these snapshots depends on the experiment and is stated in black for each snapshot. Corresponding ice volume (in s.l.e.) is shown in blue. Red zones represent the ice shelves extending beyond the glacial maximum grounding line (black line). Black circles indicate the locations of the Camp Century, NEEM, NGRIP, GRIP and Dye3 ice cores (from north to south).
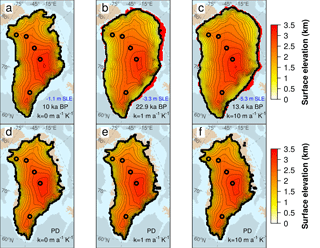
Figure 7GrIS surface elevation (km) simulated at the LGM (TI) (a–c) and present-day GrIS (d–f) for three values of the heat-flux coefficient κ having set Bref=1 m a−1. The timing of the snapshots depends on the experiment and is stated in black for each snapshot. Corresponding ice volume (in s.l.e.) is shown in blue. Red zones represent the ice shelves extending beyond the LGM grounding line (black line). Black circles indicate the locations of the Camp Century, NEEM, NGRIP, GRIP and Dye3 ice cores (from north to south).
A larger ice sheet loses more ice during a deglaciation, leading to an interglacial state that is almost independent of κ (Fig. 5). This response is related to the saturation of the oceanic forcing in warm peaks, when the GrIS is almost totally land-based and the ice loss is hence mostly due to the increase in atmospheric temperature and precipitation. Since glacial accretion affects the ice growth much more than basal melting during the retreat, the ice loss during a deglaciation monotonically increases with increasing κ (Fig. 8). Thus, for larger κ values, more ice grows during glacial periods and more ice is lost, and faster, during the subsequent deglaciation. Mass loss is mostly due to the large number of grounded-ice zones that are converted into ice-free areas during the deglaciation (Fig. 8b). The percentage of grounded points lost until the peak of an interglacial period saturates for κ above 3 in correspondence with preceding glacial GrIS configurations which present a grounding-line expansion to the continental shelf break. The slightly increasing ice loss still observed for higher oceanic sensitivities is mostly related to the ice lost in the GrIS interiors due to the positive elevation–melt feedback.
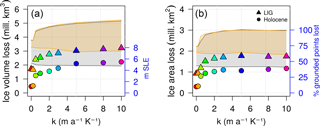
Figure 8Distribution of ice volume (a) and area (b) lost during the LIG and the Holocene as a function of κ, for Bref=1 m a−1. Grey and yellow shades show the deviation between the maximum and the minimum ice volumes (area) for LIG and Holocene, respectively (see Fig. 5). The loss is calculated between the time at which the ice volume reaches its maximum value simulated before deglaciation (between 140 and 128 ka BP for TII and between 19 and 10 ka BP for TI) and the subsequent ice minimum (between 122 and 121 ka BP for the Eemian and between 8 and 0 ka BP for the Holocene). The colours of the points follow the legend of Fig. 5 for clarity.
Due to our melting parameterization (Eq. 10) and to the Bref value chosen, water below the ice shelves is allowed to freeze for κ>0.5 , favouring ice growth and GrIS expansion (Fig. 5). Below this threshold, the model still allows for submarine melting rates across the margins in glacial times and the GrIS expansion is almost totally driven by surface accumulation. However, the sensitivity with respect to κ strictly depends on the value of Bref, as it defines the positive threshold that the glacial GrIS has to overcome to start reacting to the oceanic forcing imposed at the margins (Fig. 9). For Bref=10 m a−1, the GrIS responds to the ocean only for κ>3 , while for Bref=30 m a−1 the GrIS starts to expand only for κ>8 . For high Bref, since a constant high submarine melting is applied overall, the glacial GrIS is almost constrained to the PD configuration and exposure to the ocean is reduced. Only a sufficiently high κ to counteract this strong melting is able to make the GrIS expand and then retreat during the interglacial. Once the reaction has started, the sensitivity of the GrIS to κ increases with increasing Bref; i.e. small variations in the magnitude of κ lead to a fast and large growth of ice during glacials and consequently to a fast and large loss of ice during the deglaciation. Similar results are found for the LIG (not shown).
3.3 Last interglacial
The amount of ice lost during the LIG period increases with the oceanic sensitivity κ. High κ values lead to higher glacial ice volumes and to larger ice losses during the consequent deglaciation (Fig. 8). The range of observed volume changes spans between 4.2 m s.l.e. (for κ=0) and 8 m s.l.e. (for κ=10 ), above the present-day GrIS ice volume. Despite this large ice-loss range, all GrIS configurations simulated at the LIG ice minimum (Eemian) present a similar extension (Fig. 6d–f). In all experiments, a large retreat is observed in the north (especially in the northeast), where melting overcomes the low accumulation rates, and in the southwest, where the ice discharge from the interior is enhanced by the presence of fast ice streams and, in some areas, by the fact that the bedrock is below sea level. Although the position of the land-ice borders at the Eemian is not very sensitive to κ, the corresponding surface elevation fields show some differences depending on κ. For high values of κ, a lower ice elevation is simulated over the GrIS (compare Fig. 6d and f), a tendency that is reflected in a slightly lower ice volume too (Fig. 5).
It is interesting to note that even when imposing a very high κ, the complete disappearance of the GrIS is not simulated. The GrIS is only partly deglaciated and all ice-core sites are still covered by ice (including the discussed ice core locations of Dye3 and NEEM). Since the oceanic-driven retreat is limited by the land-based configuration observed in the interglacials, the retreat during the LIG is mainly controlled by the atmospheric temperatures and precipitations with which the model is forced.
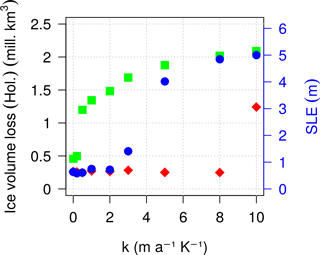
Figure 9Distribution of the ice volume lost in the Holocene as a function of the heat-flux coefficient κ, simulated for three selected reference basal melting rates (Bref=1 m a−1 in green, Bref=10 m a−1 in blue and Bref=30 m a−1 in red). The ice volume loss is calculated between the time at which the ice volume reaches its maximum value before the deglaciation and the present day. The green points are the same as the circles of Fig. 8a (for the Holocene).
The amount of ice lost during the Eemian relative to the present day (Fig. 10), which ranges between 2.9 and 3.2 m s.l.e., is within the uncertainty range of ice volumes suggested by some previous studies (e.g. 1.2–3.5 m s.l.e. for Helsen et al. (2013), 0.4–4.4 m s.l.e. for Robinson et al. (2011) and 0.4–3.8 m s.l.e. for Stone et al., 2013). Also, the timing at which the peak of deglaciation occurs, which spans between 122.3 and 121.6 ka BP in all the simulations, agrees with the timing proposed in many previous studies (Calov et al., 2015; Langebroek and Nisancioglu, 2016; Robinson et al., 2011; Stone et al., 2013; Yau et al., 2016). The time at which the peak of the Eemian occurs in our experiments depends partly on the timing of the atmospheric temperature peak and partly on the duration of the post-glacial rebound, which controls the intrusion of warm waters into the GrIS bays enhancing the ocean-driven retreat. However, the Eemian peak does not depend on the maximum insolation since the PDD scheme used does not account for past insolation changes.
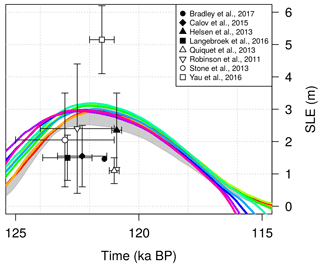
Figure 10GrIS ice volume evolution simulated for different values of the melting rate sensitivity κ during the last interglacial (see Fig. 5 for the line colour legend). The ice volumes have been converted to values of s.l.e. anomaly with respect to the present-day volumes estimated in each specific simulation. Grey shading represents the reference basal melting rates Bref investigated for the case of constant-in-time oceanic forcing (κ=0 ). The upper bound refers to Bref=40 m a−1 and the lower bound to Bref=0 m a−1. Black and white symbols indicate the LIG minimum ice volumes estimated by previous studies. The tight clustering of our estimates compared to previous work is due to the fact that the sole uncertainty is here related to the oceanic forcing through κ.
3.4 Last Glacial Maximum
Although many uncertainties about the GrIS configuration during the last glacial period still exist, several estimates of the sea-level contribution from the GrIS during the last deglaciation can be found in the literature: 2.6 m s.l.e. (Bradley et al., 2017), 2.7 m s.l.e. (Huybrechts, 2002), between 2 and 3 m s.l.e. (Clark and Mix, 2002), 3.1 m s.l.e. (Fleming and Lambeck, 2004), 4.1 m s.l.e. (Simpson et al., 2009), between 3.1 and 4.5 m s.l.e. (Buizert et al., 2018) and 4.7 m s.l.e. (Lecavalier et al., 2014). These estimates come from ice-sheet models of different complexity, with their own dynamics and boundary conditions. Particularly the ice-sheet model used by Simpson et al. (2009) and Lecavalier et al. (2014) is run in combination with a GIA and RSL model and then constrained by past surface elevations derived from ice-core data, observations of past changes in RSL and the present-day GrIS configuration. These models do not solve the dynamics of the ice shelves or the grounding-line migration, which is parameterized. However, their estimates of the GrIS spatial extent can be considered as the most realistic reconstructions of the recent past glacial GrIS so far.
Under constant oceanic conditions, the LGM-PD ice excess simulated by our model at 21 kyr BP spans between 0 and 1.4 m s.l.e. for Bref ranging from 0 to 40 m a−1, increasing with decreasing Bref values (grey shaded region – Fig. 11). This range is well below previous LGM ice volume reconstructions found in the literature (grey points). However, slightly larger ice volumes (0.6–2 m s.l.e.) are found at the peak simulated further in time in the glaciation (∼ 13–10 ka BP). For the case with no submarine melting (Bref=0 m a−1), the maximum ice volume (lower bound of grey shadow, at ∼ 12 kyr BP) is close to those of Huybrechts (2002) and Bradley et al. (2017). In this simulation, the GrIS increases moderately as its extension surpasses its PD borders and the grounding line approaches the continental shelf (Fig. 12a). Nevertheless, the atmospheric forcing alone is not sufficient to make the GrIS expand as expected during the LGM. According to reconstructions, the GrIS extended as far as the continental shelf break in every direction, except in the northeast region where the grounding line remains closer to the coast (Lecavalier et al., 2014). In our simulations, the GrIS reaches a glacial expansion consistent with the literature only for κ≥1 (Fig. 12b). However, the ice volume reached for this oceanic sensitivity is still smaller than the LGM volumes of Simpson et al. (2009) and Lecavalier et al. (2014) (Fig. 11), since only with κ>3 does the model simulate a maximum ice volume comparable to those ranges. The discrepancy in volumes, despite the same extension, could be related to the different dynamics and boundary conditions applied in the two models. Nevertheless, our simulated ice volumes are in agreement with recent estimates corrected for seasonal surface air temperatures in Greenland during the LGM (Buizert et al., 2018).
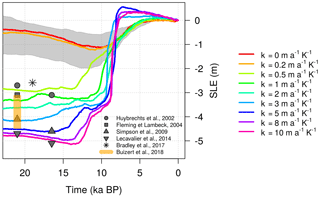
Figure 11GrIS ice volume evolution simulated for different values of the melting rate sensitivity κ during the last deglaciation. The ice volumes have been converted to values of s.l.e. anomaly with respect to the present-day volumes estimated in each specific simulation. As in Fig. 10, grey shading represents the simulations for the different reference basal melting rates (Bref) investigated for the case of constant-in-time oceanic forcing (κ=0). The upper bound refers to Bref=40 m a−1 and the lower bound to Bref=0 m a−1. Grey dots and orange shading indicate estimates of the GrIS ice volume at the LGM (21 ka BP) and at the maximum ice volume reached before the last deglaciation (16.5 ka BP), as suggested by previous work.
The timing of the reconstructed deglaciation can also provide information for comparison. The maximum increases suggested by Simpson et al. (2009) (4.6 m s.l.e.) and Lecavalier et al. (2014) (5.1 m s.l.e.) occur at 16.5 ka BP, while our simulations suggest a timing dependent on κ ranging from 20 to 10 ka BP for very low κ values (Fig. 11). The magnitudes of the oceanic sensitivity that best approximate the evolution of the GrIS before the Holocene are thus between 5 (4.6 m s.l.e. at 17.4 ka BP) and 10 (5.3 m s.l.e. at 14 ka BP). However, some discrepancies between our GrIS glacial extension and that of Lecavalier et al. (2014) are still present (Fig. 12b).
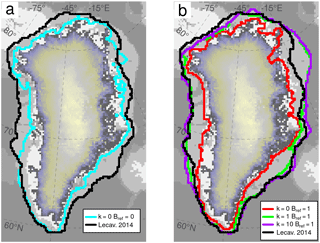
Figure 12GrIS total extent (ice shelves are included) simulated at the peak of the last glaciation for (a) no melting/freezing at the grounding line (cyan) and (b) κ=0, 1 and 10 (red, green and purple lines, respectively) for Bref=1 m a−1. The timing of the glacial maximums is (a) 12 kyr BP and (b) 10, 20 and 14 kyr BP for κ=0, 1 and 10 m a−1, respectively. LGM (21 kyr BP) GrIS grounding-line position estimated by Lecavalier et al. (2014) is shown for comparison (black line).
3.5 Present-day GrIS
Given that the topography of the present-day GrIS is one of the trustworthy measures used to assess the reliability of an ice-sheet model, we compare our present-day GrIS ice thickness and extent simulated for κ=10 to those estimated by Bamber et al. (2013) (Fig. 13). The choice of this particular κ value is based on the discussion above (Sect. 3.4) for the LGM and is supported by the good agreement between the simulated present-day ice volume and observations (Bamber et al., 2013) (Fig. 7f). The simulated extent of the GrIS matches reasonably well the observations. However, notable discrepancies are observed in some sectors. The main differences are found in the northeast, where GRISLI-UCM predicts an ice margin somewhat too far inland, and in the southwest, where our model is not able to make the GrIS retreat as expected. The ice loss in the north is a known problem that appears in many studies when simulating the GrIS during an interglacial (Stone et al., 2010; Born and Nisancioglu, 2012). In the interior, the difference in ice thickness is relatively low. However, the GrIS simulated by our model generally shows thicker ice along the margins, a tendency that propagates inland. Other areas in which our simulated ice thickness is lower than that observed are located in the centre of the continent and in the very southeast corresponding to a mountainous region. However, the focus of our work is not to exactly reproduce the observed present-day GrIS ice volume at the end of the simulations but rather to demonstrate the impact of the ocean on the GrIS past evolution. From this perspective, the simulations arrive at a reasonable representation of the present day and within the range of other models.
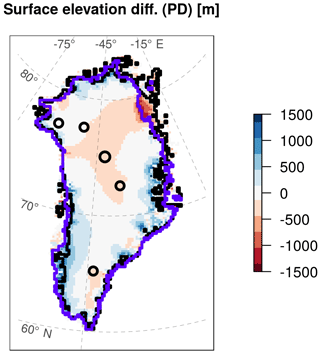
Figure 13Modelled minus observed surface elevation for the present day. Modelled data are taken from the GRISLI-UCM simulation which best estimates the presumed LGM extension (Bref=1 m a−1 and κ=10 ) while the observed surface elevation is taken from Bamber et al. (2013). Purple and black lines represent simulated and observed GrIS extensions, respectively. Black circles indicate the locations of the Camp Century, NEEM, NGRIP, GRIP and Dye3 ice cores (from north to south).
Our model simulates the advance and retreat of the GrIS during the last two glacial cycles. Transient simulations reflect the ice-sheet response to the specific oceanic forcing applied to the model. This reaction is different for glacial and interglacial periods (Fig. 5). Since during the interglacial periods the GrIS is almost totally land based and therefore less exposed to the ocean, the minimum ice volume reflects the oceanic imprint only mildly and is limited to a small range of possible values. On the other hand, the volume reached in glacial periods is much more sensitive to κ. Although the maximum ice volume loss is constrained by the imposed limited extension to the continental shelf break, the large ice loss observed for a high oceanic sensitivity is closely related to the GrIS configuration in the previous glacial, which is essentially marine-based at the margins and therefore more subjected to oceanic changes (Fig. 6c). As water temperatures rise at the beginning of the deglaciation, the basal melting rate increases too (Eq. 10), thinning ice shelves at the boundaries, enhancing outflow of ice and triggering grounding-line retreat. The effects of this ocean-driven retreat are not locally confined but are propagated inland through a dynamic response of the grounded ice sheet. The ice loss at the margins triggers ice advection from the interior which further increases the ice discharge into the ocean, and, as the thickness of the inland ice decreases, the elevation–melt feedback begins. At a given stage of the deglaciation, when the whole ice sheet starts to become land based, this atmosphere-driven retreat becomes the sole driver of ice mass loss. The simulated retreat during this phase is influenced by the choice of the surface melt scheme used in the model. At the peak of the Eemian, the melt determined by the PDD scheme can be 20–50 % lower than the melt calculated if past insolation changes are taken into account (Robinson and Goelzer, 2014). This inaccuracy therefore influences the GrIS contributions to sea-level rise for the last interglacial (Fig. 10), which could be underestimated.
As discussed in Sect. 3.4 and 3.5, the oceanic forcing that seems to best reconstruct the past (LGM) and the present GrIS is achieved for a heat-flux coefficient of 10 . However, the submarine melt scheme used and some simplifications made in its treatment may partly influence our results. Firstly, only a limited range of reference submarine melting rates has been investigated, since only two of the system model parameters have been explored (Table 1). Secondly, our melting parameterization is highly conditioned by the Bref value assumed to represent the present-day submarine melting rate around the GrIS (Fig. 8), as it consequently determines the minimum κ value needed to allow the GrIS to respond to the ocean (Fig. 3). Using a single value for this term is a coarse approximation to reality, but since the detailed distribution of the present-day sub-shelf melt along the coasts does not yet exist for Greenland, the retrieval of a 2-D field would be complex and highly uncertain. However, we have considered the same order of magnitude of melt rates as is proposed in the literature for the AIS, which spans values from negative to above 40 m a−1 in some very active regions (Rignot and Jacobs, 2002). In support of this evidence, similar basal melting rates have been found recently in some GrIS ice tongues (Wilson et al., 2017). Thirdly, the basal melting equation strongly depends on the oceanic temperature anomaly TLGM,ocn−TPD, ocn, which has been prescribed to a spatially constant value of −3 K. Since this term impacts the oceanic sensitivity through κ (Eq. 10), it is clear that the same results obtained in this work would have been reached by fixing one value of κ and instead examining the influence of different levels of the ΔTocn on the GrIS past evolution. Considering a spatially constant SST anomaly represents an idealized simplification of the oceanic forcing for two reasons: the temperature of the water is clearly not uniform along the GrIS coasts and the melt at the grounding line is presumably controlled by water temperature deeper in the ocean column (between 100 and 1000 m in Greenland; Rignot et al., 2016). These issues could be avoided, for example, by using spatially variable (horizontally and vertically) oceanic temperatures from available model outputs for Greenland. To see whether this simplification could influence our results, some tests using 2-D temperatures from CLIMBER-3α snapshots (Montoya and Levermann, 2008) have been run (not shown). Despite some differences in the ice distribution and the time of the retreat, the main results obtained in this work did not change. Finally, another simplification made here is the assignation of the same climatic index α to both atmosphere and ocean. In principle, forcing the ocean with an index derived from past ocean temperatures could be more appropriate. To this end, we ran additional simulations by applying the multiproxy index α for the atmosphere and another index for the ocean calculated from benthic-retrieved ocean temperatures (Waelbroeck et al., 2002). The results of the new simulations show very little differences from the ones reported here, while the same sensitivity to the ocean is preserved (not shown). Thus, such a distinction in forcing does not affect the main outcomes of this work.
Our results may well be model dependent, and some model limitations should be noted. As described in Sect. 2.1, our ice-sheet–shelf model is provided with an internal GIA scheme which accounts for bedrock deformation due to changes in the GrIS ice load. However, since the GrIS rests on the peripheral forebulge of the North American ice sheets (NAIS), such as the Laurentide Ice Sheet, variations in the NAIS ice load induce consequent vertical motions of the lithosphere beneath the GrIS (Lecavalier et al., 2014). The resulting GrIS isostatic adjustment is therefore the combination of these local and non-local responses which make the GIA treatment rather complex. In principle, these non-local effects should be taken into account as they contribute to the sea-level variability, becoming especially relevant at the beginning of deglaciations when the ice mass loss is significantly induced by sea-level rise (Lecavalier et al., 2017). However, for the sake of simplicity, the GrIS isostatic adjustment is assumed here to be only due to local ice mass variations, as other works have done in the past (Greve and Blatter, 2009; Helsen et al., 2013; Huybrechts, 2002; Langebroek and Nisancioglu, 2016; Stone et al., 2013).
The simulated ice volume at the present day is overestimated for all investigated values of κ (Fig. 8). This fact suggests that our model has a tendency to overestimate the ice thickness of the GrIS, especially in the marginal zones of the domain, a well-known phenomenon (Calov et al., 2015). These discrepancies are partly linked to the relatively low model resolution (20 km × 20 km), which limits the accuracy in estimating the margins especially along the fjords, and partly due to the boundary conditions applied to the ice-sheet model, such as the basal sliding. The coarse model resolution prevents the model from resolving fine-scale physical processes at the marine-terminating outlet glaciers that end in narrow fjords, although they are considered as the primary sources of ice discharge today due to oceanic changes. Such an inability of our model may be more relevant when modelling the GrIS retreat during the LIG and the Holocene. The lack of a sub-grid fjord treatment does not allow for a proper analysis of the ice front processes which become relevant when the retreat has reached the continental area above the sea level. Especially when, as in our case, the submarine melt goes abruptly to a high value at the grounding line, the implementation of a sub-grid-scale parameterization would allow the small processes at the fjords to be accurately resolved (Calov et al., 2015; Favier et al., 2016; Gladstone et al., 2017). However, these limitations lead to only second-order effects given the scope of our work.
The parameterization used for the submarine melting rate at the GrIS marine margins is a simplification compared to other temperature-dependent submarine melting schemes. We are aware that the melting rate depends on many regional factors such as the temperature and salinity of the ocean at the ice-shelf margin, the shape of the ice-shelf cavity and the depth of the grounding line, which our equations do not take into account. However, our simple construction allows us to test the sensitivity of the GrIS to the oceanic forcing in a straightforward manner and is found to be particularly suitable for palaeo-studies.
Our basal melting scheme is implemented in such a way that the melting at the grounding line (Eq. 10) is higher than the one set below the ice shelves (Eq. 11). This approach is supported by sub-shelf melting rate estimates (Dutrieux et al., 2013; Reese et al., 2017; Rignot and Jacobs, 2002; Wilson et al., 2017). Moreover, we assume that the ratio between the two is 1:10, which is valid for the present day, but could be inaccurate for glacial times. However, some experiments done with ratios of 1:5 and 1:15 differ very little from the results presented in this work (not shown). Therefore, our parameterization is much less sensitive to the melting rate below the ice shelves with respect to that at the grounding line. On the other hand, a recent study shows the need to make the basal melting decrease smoothly to zero when approaching the grounding line from the ice shelf to avoid resolution-dependent performances (Gladstone et al., 2017). This can be achieved, for example, by considering the submarine melt to be dependent on the water-column thickness beneath the ice shelf, as Bradley et al. (2017) suggested in their work. It is interesting to compare our results with theirs, as we address the same scientific problem, i.e. the impact of submarine melting on the evolution of the past GrIS, from two different points of view. Our submarine melt scheme is implicitly a linear function of the water depth, as, going down through the water column, the melt rate maintains the same value until it reaches a critical zone at which the sub-shelf melt is set to 50 m a−1 to avoid improbable ice expansion (Sect. 2.3). Our work shows that without melting/freezing at the grounding line (for Bref=0 and κ=0), the GrIS is not able to reach the continental shelf break (Fig. 12a). However, it is able to extend past the present-day coastline, similar to the simulations presented by Bradley et al. (2017). Moreover, experiments performed under the same oceanic conditions with increased basal sliding at the margins show that our model allows further expansion during the glacial periods (not shown). On the other hand, the model used by Bradley et al. (2017) has the capability of making the GrIS retreat during interglacial periods only if the submarine meltwater depth relation is exponential and if RSL variations due to both local and non-local effects are considered. On the contrary, a proper retreat during the deglaciations is always achieved in our simulations (Figs. 3 and 6–7), although the GIA does not account for global effects. These discrepancies are probably due not only to the different submarine melt schemes considered in each model but also to the features of the model dynamics, such as the sliding law and the grounding-line migration scheme. Following these assumptions, a sub-grid treatment of the small-scale processes taking place at the grounding line, such as basal sliding, sub-shelf melting, hydrology and migration, will be added in our model in the future. This will provide a more realistic description of grounding-line processes such as the enhanced submarine melting as well as the basal drag at the margin of fast grounded ice.
We should finally remark that the GrIS evolution during the last two glacial cycles has been assessed here only from an oceanic point of view, while the influence of different atmospheric forcings has not been investigated. This simplification may be especially important for the results shown for the LIG and the Holocene, in which the retreat is mostly induced by surface ablation. However, this point will be in the scope of future work.
Here, we assessed the impact of palaeo-oceanic temperature variations on the evolution of the GrIS on a glacial–interglacial timescale. By using a three-dimensional hybrid ice-sheet–shelf model including a parameterization of the basal melting rate at the GrIS marine margins, the model simulates the evolution of the whole ice sheet under temporally variable oceanic conditions. Firstly, the magnitude of the oceanic forcing applied at the ice–ocean interface triggers and drives the grounding-line advance (through water freezing) and retreat (through ice melting). Secondly, it induces a dynamic adjustment of the grounded ice sheet, determining the amount of ice grown (lost) during the cold (warm) stages. Although the GrIS evolution is a result of the atmospheric and oceanic forcings operating together, we have shown that the ocean is a primary driver of the GrIS glacial advance. Not only must the oceanic forcing be activated, but it must be strong enough to reproduce a reliable GrIS evolution throughout the glacial cycles. It is important to remark that other factors which could affect the GrIS evolution have not yet been explored in detail. Sensitivity tests to the atmospheric forcing, glacial isostatic adjustment effects and spatially non-uniform submarine melt rates should be taken into account in the future to analyse the scientific problem from a broad range of points of view. Nevertheless, we have shown that changing oceanic conditions is a fundamental contributor to the evolution of the whole GrIS, suggesting that the oceanic component should be included as an active forcing in palaeo-ice-sheet models.
The GRISLI-UCM code and the analysed data are available from the authors upon request.
IT carried out the simulations, analysed the results and wrote the paper. All other authors contributed to designing the simulations, analysing the results and writing the paper.
The authors declare that they have no conflict of interest.
We would like to thank Catherine Ritz for
providing the original model GRISLI and Rubén Banderas for helping initially with the model. This work was funded
by the Spanish Ministry of Science and Innovation under the project MOCCA
(Modelling Abrupt Climate Change, grant no. CGL2014-59384-R). Ilaria Tabone
is funded by the Spanish National Programme for the Promotion of Talent and
Its Employability (grant no. BES-2015-074097). Alexander Robinson is funded
by the Marie Curie Horizon2020 project CONCLIMA (grant no. 703251). All of
these simulations were performed in EOLO, the HPC of Climate Change of the
International Campus of Excellence of Moncloa, funded by MECD and
MICINN.
Edited by: Alessio
Rovere
Reviewed by: Benoit Lecavalier and Bas de Boer
Alley, R. B., Anandakrishnan, S., Christianson, K., Horgan, H. J., Muto, A., Parizek, B. R., Pollard, D., and Walker, R. T.: Oceanic forcing of Ice-Sheet retreat: West Antarctica and more, Annu. Rev. Earth Planet. Sc., 43, 207–231, https://doi.org/10.1146/annurev-earth-060614-105344, 2015. a, b
Alvarez-Solas, J., Montoya, M., Ritz, C., Ramstein, G., Charbit, S., Dumas, C., Nisancioglu, K., Dokken, T., and Ganopolski, A.: Millennial-scale oscillations in the Southern Ocean in response to atmospheric CO2 increase, Global Planet. Change, 76, 128–136, https://doi.org/10.1016/j.gloplacha.2010.12.004, 2011. a
Álvarez-Solas, J., Montoya, M., Ritz, C., Ramstein, G., Charbit, S., Dumas, C., Nisancioglu, K., Dokken, T., and Ganopolski, A.: Heinrich event 1: an example of dynamical ice-sheet reaction to oceanic changes, Clim. Past, 7, 1297–1306, https://doi.org/10.5194/cp-7-1297-2011, 2011. a
Alvarez-Solas, J., Robinson, A., Montoya, M., and Ritz, C.: Iceberg discharges of the last glacial period driven by oceanic circulation changes, P. Natl. Acad. Sci. USA, 110, 41, 16350–16354, https://doi.org/10.1073/pnas.1306622110, 2013. a
Annan, J. D. and Hargreaves, J. C.: A new global reconstruction of temperature changes at the Last Glacial Maximum, Clim. Past, 9, 367–376, https://doi.org/10.5194/cp-9-367-2013, 2013. a
Bamber, J. L., Griggs, J. A., Hurkmans, R. T. W. L., Dowdeswell, J. A., Gogineni, S. P., Howat, I., Mouginot, J., Paden, J., Palmer, S., Rignot, E., and Steinhage, D.: A new bed elevation dataset for Greenland, The Cryosphere, 7, 499–510, https://doi.org/10.5194/tc-7-499-2013, 2013. a, b, c, d, e, f, g
Banderas, R., Alvarez-Solas, J., Robinson, A., and Montoya, M.: A new approach for simulating the paleo evolution of the Northern Hemisphere ice sheets, Geosci. Model Dev. Discuss., https://doi.org/10.5194/gmd-2017-158, in review, 2017. a
Barker, S., Knorr, G., Edwards, R. L., Parrenin, F., Putnam, A. E., Skinner, L. C., Wolff, E., and Ziegler, M.: 800,000 years of abrupt climate variability, Science, 334, 347–351, https://doi.org/10.1126/science.1203580, 2011. a, b
Beckmann, A. and Goosse, H.: A parameterization of ice shelf-ocean interaction for climate models, Ocean Model., 5, 157–170, https://doi.org/10.1016/S1463-5003(02)00019-7, 2003. a, b
Bindschadler, R. A., Nowicki, S., Abe-Ouchi, A., Aschwanden, A., Choi, H., Fastook, J., Granzow, G., Greve, R., Gutowski, G., Herzfeld, U., Jackson, C., Johnson, J., Khroulev, C., Levermann, A., Lipscomb, W. H., Martin, M. A., Morlighem, M., Parizek, B. R., Pollard, D., Price, S. F., Ren, D., Saito, F., Sato, T., Seddik, H., Seroussi, H., Takahashi, K., Walker, R., and Wang, W. L.: Ice sheet model sensitivity to environmental forcing and their use in projecting future sea level, J. Glaciol., 59, 195–224, https://doi.org/10.3189/2013JoG12J125, 2013. a
Born, A. and Nisancioglu, K. H.: Melting of Northern Greenland during the last interglaciation, The Cryosphere, 6, 1239–1250, https://doi.org/10.5194/tc-6-1239-2012, 2012. a
Box, J. E., Yang, L., Bromwich, D. H., and Bai, L.-S.: Greenland ice sheet surface air temperature variability: 1840–2007, J. Climate, 22, 4029–4049, https://doi.org/10.1175/2009JCLI2816.1, 2009. a
Bradley, S. L., Reerink, T. J., van de Wal, R. S. W., and Helsen, M. M.: Simulation of the Greenland Ice sheet over two glacial cycles: Investigating a sub-ice shelf melt parameterisation and relative sea level forcing in an ice sheet-ice shelf model, Clim. Past Discuss., https://doi.org/10.5194/cp-2017-132, in review, 2017. a, b, c, d, e, f
Bueler, E. and Brown, J.: Shallow shelf approximation as a sliding law in a thermomechanically coupled ice sheet model, J. Geophys. Res., 114, F03008, https://doi.org/10.1029/2008JF001179, 2009. a
Buizert, C., Keisling, B. A., Box, J. E., He, F., Carlson, A. E., Sinclair, G., and DeConto, R. M.: Greenland-wide seasonal temperatures during the last deglaciation, Geophys. Res. Lett., 45, 1905–1914, https://doi.org/10.1002/2017GL075601, 2018. a, b
Calov, R., Robinson, A., Perrette, M., and Ganopolski, A.: Simulating the Greenland ice sheet under present-day and palaeo constraints including a new discharge parameterization, The Cryosphere, 9, 179–196, https://doi.org/10.5194/tc-9-179-2015, 2015. a, b, c
Clark, P. U. and Mix, A. C.: Ice sheets and sea level of the Last Glacial Maximum, Quaternary Sci. Rev., 21, 1–7, 2002. a
Clark, P. U., Church, J. A., Gregory, J. M., and Payne, A. J.: Recent progress in understanding and projecting regional and global mean sea level change, Current Climate Change Reports, 1, 224–246, 2015. a
Colleoni, F., Masina, S., Cherchi, A., Navarra, A., Ritz, C., Peyaud, V., and Otto-Bliesner, B.: Modeling Northern Hemisphere ice-sheet distribution during MIS 5 and MIS 7 glacial inceptions, Clim. Past, 10, 269–291, https://doi.org/10.5194/cp-10-269-2014, 2014. a
Cook, A. J., Holland, P. R., Meredith, M. P., Murray, T., Luckman, A., and Vaughan, D. G.: Ocean forcing of glacier retreat in the western Antarctic Peninsula, Science, 353, 283–286, https://doi.org/10.1126/science.aae0017, 2016. a
DeConto, R. M. and Pollard, D.: Contribution of Antarctica to past and future sea-level rise, Nature, 531, 591–597, https://doi.org/10.1038/nature17145, 2016. a, b
Dutrieux, P., Vaughan, D. G., Corr, H. F. J., Jenkins, A., Holland, P. R., Joughin, I., and Fleming, A. H.: Pine Island glacier ice shelf melt distributed at kilometre scales, The Cryosphere, 7, 1543–1555, https://doi.org/10.5194/tc-7-1543-2013, 2013. a, b
Enderlin, E. M. and Howat, I. M.: Submarine melt rate estimates for floating termini of Greenland outlet glaciers (2000–2010), J. Glaciol., 59, 67–75, https://doi.org/10.3189/2013JoG12J049, 2013. a
Favier, L., Durand, G., Cornford, S. L., Gudmundsson, G. H., Gagliardini, O., Gillet-Chaulet, F., Zwinger, T., Payne, A., and Le Brocq, A. M.: Retreat of Pine Island Glacier controlled by marine ice-sheet instability, Nature Climate Change, 4, 117–121, https://doi.org/10.1038/NCLIMATE2094, 2014. a
Favier, L., Pattyn, F., Berger, S., and Drews, R.: Dynamic influence of pinning points on marine ice-sheet stability: a numerical study in Dronning Maud Land, East Antarctica, The Cryosphere, 10, 2623–2635, https://doi.org/10.5194/tc-10-2623-2016, 2016. a
Fettweis, X., Franco, B., Tedesco, M., van Angelen, J. H., Lenaerts, J. T. M., van den Broeke, M. R., and Gallée, H.: Estimating the Greenland ice sheet surface mass balance contribution to future sea level rise using the regional atmospheric climate model MAR, The Cryosphere, 7, 469–489, https://doi.org/10.5194/tc-7-469-2013, 2013. a
Fleming, K. and Lambeck, K.: Constraints on the Greenland Ice Sheet since the Last Glacial Maximum from sea-level observations and glacial-rebound models, Quaternary Sci. Rev., 23, 1053–1077, https://doi.org/10.1016/j.quascirev.2003.11.001, 2004. a
Fried, M., Catania, G., Bartholomaus, T., Duncan, D., Davis, M., Stearns, L., Nash, J., Shroyer, E., and Sutherland, D.: Distributed subglacial discharge drives significant submarine melt at a Greenland tidewater glacier, Geophys. Res. Lett., 42, 9328–9336, https://doi.org/10.1002/2015GL065806, 2015. a
Fürst, J. J., Goelzer, H., and Huybrechts, P.: Effect of higher-order stress gradients on the centennial mass evolution of the Greenland ice sheet, The Cryosphere, 7, 183–199, https://doi.org/10.5194/tc-7-183-2013, 2013. a
Fürst, J. J., Goelzer, H., and Huybrechts, P.: Ice-dynamic projections of the Greenland ice sheet in response to atmospheric and oceanic warming, The Cryosphere, 9, 1039–1062, https://doi.org/10.5194/tc-9-1039-2015, 2015. a, b
Gladstone, R. M., Warner, R. C., Galton-Fenzi, B. K., Gagliardini, O., Zwinger, T., and Greve, R.: Marine ice sheet model performance depends on basal sliding physics and sub-shelf melting, The Cryosphere, 11, 319–329, https://doi.org/10.5194/tc-11-319-2017, 2017. a, b
Golledge, N. R., Fogwill, C. J., Mackintosh, A. N., and Buckley, K. M.: Dynamics of the last glacial maximum Antarctic ice-sheet and its response to ocean forcing, P. Natl. Acad. Sci. USA, 109, 16052–16056, https://doi.org/10.1073/pnas.1205385109, 2012. a
Grant, K., Rohling, E., Ramsey, C. B., Cheng, H., Edwards, R., Florindo, F., Heslop, D., Marra, F., Roberts, A., Tamisiea, M. E., and Williams, F.: Sea-level variability over five glacial cycles, Nat. Commun., 5, 5076, https://doi.org/10.1038/ncomms6076, 2014. a
Greve, R. and Blatter, H.: Dynamics of ice sheets and glaciers, Springer Science & Business Media, 2009. a
Hall, D. K., Williams, R. S., Luthcke, S. B., and Digirolamo, N. E.: Greenland ice sheet surface temperature, melt and mass loss: 2000–06, J. Glaciol., 54, 81–93, 2008. a
Hanna, E., Navarro, F. J., Pattyn, F., Domingues, C. M., Fettweis, X., Ivins, E. R., Nicholls, R. J., Ritz, C., Smith, B., Tulaczyk, S., Whitehouse, P. L., and Zwally, H. J.: Ice-sheet mass balance and climate change, Nature, 498, 51–59, https://doi.org/10.1038/nature12238, 2013. a
Helsen, M. M., van de Berg, W. J., van de Wal, R. S. W., van den Broeke, M. R., and Oerlemans, J.: Coupled regional climate-ice-sheet simulation shows limited Greenland ice loss during the Eemian, Clim. Past, 9, 1773–1788, https://doi.org/10.5194/cp-9-1773-2013, 2013. a, b
Hogg, A. E. and Gudmundsson, G. H.: Impacts of the Larsen-C Ice Shelf calving event, Nat. Clim. Change, 7, 540–542, https://doi.org/10.1038/nclimate3359, 2017. a
Holland, D. M., Thomas, R. H., De Young, B., Ribergaard, M. H., and Lyberth, B.: Acceleration of Jakobshavn Isbræ triggered by warm subsurface ocean waters, Nat. Geosci., 1, 659–664, https://doi.org/10.1038/ngeo316, 2008a. a, b
Holland, P. R., Jenkins, A., and Holland, D. M.: The response of ice shelf basal melting to variations in ocean temperature, J. Climate, 21, 2558–2572, https://doi.org/10.1175/2007JCLI1909.1, 2008b. a
Holland, P. R., Brisbourne, A., Corr, H. F. J., McGrath, D., Purdon, K., Paden, J., Fricker, H. A., Paolo, F. S., and Fleming, A. H.: Oceanic and atmospheric forcing of Larsen C Ice-Shelf thinning, The Cryosphere, 9, 1005–1024, https://doi.org/10.5194/tc-9-1005-2015, 2015. a
Howat, I. M., Joughin, I., Tulaczyk, S., and Gogineni, S.: Rapid retreat and acceleration of Helheim Glacier, east Greenland, Geophys. Res. Lett., 32, L22502, https://doi.org/10.1029/2005GL024737, 2005. a
Howat, I. M., Joughin, I., and Scambos, T. A.: Rapid changes in ice discharge from Greenland outlet glaciers, Science, 315, 1559–1561, https://doi.org/10.1126/science.1138478, 2007. a
Huybrechts, P.: Sea-level changes at the LGM from ice-dynamic reconstructions of the Greenland and Antarctic ice sheets during the glacial cycles, Quaternary Sci. Rev., 21, 203–231, https://doi.org/10.1016/S0277-3791(01)00082-8, 2002. a, b, c, d
IPCC: Sea Level Change, Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change, Cambridge, UK and New York, NY, USA, 2013. a
Jansen, D., Luckman, A. J., Cook, A., Bevan, S., Kulessa, B., Hubbard, B., and Holland, P. R.: Brief Communication: Newly developing rift in Larsen C Ice Shelf presents significant risk to stability, The Cryosphere, 9, 1223–1227, https://doi.org/10.5194/tc-9-1223-2015, 2015. a
Jenkins, A.: Convection-driven melting near the grounding line of ice shelves and tidewater glaciers, J. Phys. Oceanogr., 41, 2279–2294, https://doi.org/10.1175/JPO-D-11-03.1, 2011. a
Joughin, I., Smith, B. E., Howat, I. M., Floricioiu, D., Alley, R. B., Truffer, M., and Fahnestock, M.: Seasonal to decadal scale variations in the surface velocity of Jakobshavn Isbræ, Greenland: Observation and model-based analysis, J. Geophys. Res., 117, F02030, https://doi.org/10.1029/2011JF002110, 2012. a
Joughin, I., Smith, B. E., and Medley, B.: Marine ice sheet collapse potentially under way for the Thwaites Glacier Basin, West Antarctica, Science, 344, 735–738, https://doi.org/10.1126/science.1249055, 2014a. a
Joughin, I., Smith, B. E., and Medley, B.: Marine ice sheet collapse potentially under way for the Thwaites Glacier Basin, West Antarctica, Science, 344, 735–738, https://doi.org/10.1126/science.1249055, 2014b. a
Kindler, P., Guillevic, M., Baumgartner, M., Schwander, J., Landais, A., and Leuenberger, M.: Temperature reconstruction from 10 to 120 kyr b2k from the NGRIP ice core, Clim. Past, 10, 887–902, https://doi.org/10.5194/cp-10-887-2014, 2014. a, b
Langebroek, P. M. and Nisancioglu, K. H.: Moderate Greenland ice sheet melt during the last interglacial constrained by present-day observations and paleo ice core reconstructions, The Cryosphere Discuss., https://doi.org/10.5194/tc-2016-15, in review, 2016. a, b, c
Lecavalier, B. S., Milne, G. A., Simpson, M. J., Wake, L., Huybrechts, P., Tarasov, L., Kjeldsen, K. K., Funder, S., Long, A. J., Woodroffe, S., Dykei, A. S., and Larsen, N. K.: A model of Greenland ice sheet deglaciation constrained by observations of relative sea level and ice extent, Quaternary Science Rev., 102, 54–84, https://doi.org/10.1016/j.quascirev.2014.07.018, 2014. a, b, c, d, e, f, g, h, i
Lecavalier, B. S., Fisher, D. A., Milne, G. A., Vinther, B. M., Tarasov, L., Huybrechts, P., Lacelle, D., Main, B., Zheng, J., Bourgeois, J., and Dyke, A. S.: High Arctic Holocene temperature record from the Agassiz ice cap and Greenland ice sheet evolution, P. Natl. Acad. Sci. USA, 1, 1–6, https://doi.org/10.1073/pnas.1616287114, 2017. a
Le Meur, E. and Huybrechts, P.: A comparison of different ways of dealing with isostasy: examples from modeling the Antarctic ice sheet during the last glacial cycle, Ann. Glaciol., 23, 309–317, 1996. a
MARGO Project Members: Constraints on the magnitude and patterns of ocean cooling at the Last Glacial Maximum, Nat. Geosci., 2, 127–132, https://doi.org/10.1038/ngeo411, 2009. a
Montoya, M. and Levermann, A.: Surface wind-stress threshold for glacial Atlantic overturning, Geophys. Res. Lett., 35, L03608, https://doi.org/10.1029/2007GL032560, 2008. a, b
Morlighem, M., Bondzio, J., Seroussi, H., Rignot, E., Larour, E., Humbert, A., and Rebuffi, S.: Modeling of Store Gletscher's calving dynamics, West Greenland, in response to ocean thermal forcing, Geophys. Res. Lett., 43, 2659–2666, https://doi.org/10.1002/2016GL067695, 2016. a
Motyka, R. J., Truffer, M., Fahnestock, M., Mortensen, J., Rysgaard, S., and Howat, I.: Submarine melting of the 1985 Jakobshavn Isbræ floating tongue and the triggering of the current retreat, J. Geophys. Res., 116, F01007, https://doi.org/10.1029/2009JF001632, 2011. a, b
Münchow, A., Padman, L., and Fricker, H. A.: Interannual changes of the floating ice shelf of Petermann Gletscher, North Greenland, from 2000 to 2012, J. Glaciol., 60, 489–499, https://doi.org/10.3189/2014JoG13J135, 2014. a
NEEM: Eemian interglacial reconstructed from a Greenland folded ice core, Nature, 493, 489–494, https://doi.org/10.1038/nature11789, 2013. a, b
Nick, F. M., Vieli, A., Howat, I. M., and Joughin, I.: Large-scale changes in Greenland outlet glacier dynamics triggered at the terminus, Nat. Geosci., 2, 110–114, https://doi.org/10.1038/ngeo394, 2009. a
Nowicki, S., Bindschadler, R. A., Abe-Ouchi, A., Aschwanden, A., Bueler, E., Choi, H., Fastook, J., Granzow, G., Greve, R., and Gutowski, G.: Large-scale changes in Greenland outlet glacier dynamics triggered at the terminus, J. Geophys. Res.-Earth, 118, 1025–1044, https://doi.org/10.1002/jgrf.20076, 2013. a
Pattyn, F.: Sea-level response to melting of Antarctic ice shelves on multi-centennial timescales with the fast Elementary Thermomechanical Ice Sheet model (f.ETISh v1.0), The Cryosphere, 11, 1851–1878, https://doi.org/10.5194/tc-11-1851-2017, 2017. a
Peyaud, V., Ritz, C., and Krinner, G.: Modelling the Early Weichselian Eurasian Ice Sheets: role of ice shelves and influence of ice-dammed lakes, Clim. Past, 3, 375–386, https://doi.org/10.5194/cp-3-375-2007, 2007. a
Philippon, G., Ramstein, G., Charbit, S., Kageyama, M., Ritz, C., and Dumas, C.: Evolution of the Antarctic ice sheet throughout the last deglaciation: A study with a new coupled climate – north and south hemisphere ice sheet model, Earth Planet. Sc. Lett, 248, 750–758, https://doi.org/10.1016/j.epsl.2006.06.017, 2006. a
Pollard, D. and DeConto, R. M.: Description of a hybrid ice sheet-shelf model, and application to Antarctica, Geosci. Model Dev., 5, 1273–1295, https://doi.org/10.5194/gmd-5-1273-2012, 2012. a
Pritchard, H. D., Ligtenberg, S. R. M., Fricker, H. A., Vaughan, D. G., Van den Broeke, M. R., and Padman, L.: Antarctic ice-sheet loss driven by basal melting of ice shelves, Nature, 484, 502–505, https://doi.org/10.1038/nature10968, 2012. a
Quiquet, A., Punge, H. J., Ritz, C., Fettweis, X., Gallée, H., Kageyama, M., Krinner, G., Salas y Mélia, D., and Sjolte, J.: Sensitivity of a Greenland ice sheet model to atmospheric forcing fields, The Cryosphere, 6, 999–1018, https://doi.org/10.5194/tc-6-999-2012, 2012. a, b
Quiquet, A., Ritz, C., Punge, H. J., and Salas y Mélia, D.: Greenland ice sheet contribution to sea level rise during the last interglacial period: a modelling study driven and constrained by ice core data, Clim. Past, 9, 353–366, https://doi.org/10.5194/cp-9-353-2013, 2013. a, b
Reeh, N.: Parameterization of melt rate and surface temperature on the Greenland ice sheet, Polarforschung, 59, 113–128, 1989. a
Reese, R., Albrecht, T., Mengel, M., Asay-Davis, X., and Winkelmann, R.: Antarctic sub-shelf melt rates via PICO, The Cryosphere Discuss., https://doi.org/10.5194/tc-2017-70, in review, 2017. a
Rignot, E. and Jacobs, S. S.: Rapid bottom melting widespread near Antarctic Ice Sheet grounding lines, Science, 296, 2020–2023, https://doi.org/10.1126/science.1070942, 2002. a, b, c, d
Rignot, E. and Kanagaratnam, P.: Changes in the velocity structure of the Greenland Ice Sheet, Science, 311, 986–990, https://doi.org/10.1126/science.1121381, 2006. a
Rignot, E. and Steffen, K.: Channelized bottom melting and stability of floating ice shelves, Geophys. Res. Lett., 35, L02503, https://doi.org/10.1029/2007GL031765, 2008. a
Rignot, E., Casassa, G., Gogineni, P., Krabill, W., Rivera, A. U., and Thomas, R.: Accelerated ice discharge from the Antarctic Peninsula following the collapse of Larsen B ice shelf, Geophys. Res. Lett., 31, L18401, https://doi.org/10.1029/2004GL020697, 2004. a
Rignot, E., Koppes, M., and Velicogna, I.: Rapid submarine melting of the calving faces of West Greenland glaciers, Nat. Geosci., 3, 187–191, https://doi.org/10.1038/ngeo765, 2010. a, b
Rignot, E., Velicogna, I., Van den Broeke, M. R., Monaghan, A., and Lenaerts, J. T. M.: Acceleration of the contribution of the Greenland and Antarctic ice sheets to sea level rise, Geophys. Res. Lett., 38, L05503, https://doi.org/10.1029/2011GL046583, 2011. a
Rignot, E., Jacobs, S., Mouginot, J., and Scheuchl, B.: Ice-shelf melting around Antarctica, Science, 341, 266–270, https://doi.org/10.1126/science.1235798, 2013. a, b
Rignot, E., Mouginot, J., Morlighem, M., Seroussi, H., and Scheuchl, B.: Widespread, rapid grounding line retreat of Pine Island, Thwaites, Smith, and Kohler glaciers, West Antarctica, from 1992 to 2011, Geophys. Res. Lett., 41, 10, 3502–3509, https://doi.org/10.1002/2014GL060140, 2014. a
Rignot, E., Xu, Y., Menemenlis, D., Mouginot, J., Scheuchl, B., Li, X., Morlighem, M., Seroussi, H., Broeke, M. v., Fenty, I., Cai, C., An, L., and de Fleurian, B.: Modeling of ocean-induced ice melt rates of five west Greenland glaciers over the past two decades, Geophys. Res. Lett., 43, 6374–6382, https://doi.org/10.1002/2016GL068784, 2016. a, b, c
Ritz, C., Rommelaere, V., and Dumas, C.: Modeling the evolution of Antarctic Ice Sheet over the last 420,000 years. Implications for altitude changes in the Vostok region, J. Geophys. Res., 106, 31943–31964, https://doi.org/10.1029/2001JD900232, 2001. a, b
Robinson, A. and Goelzer, H.: The importance of insolation changes for paleo ice sheet modeling, The Cryosphere, 8, 1419–1428, https://doi.org/10.5194/tc-8-1419-2014, 2014. a, b
Robinson, A., Calov, R., and Ganopolski, A.: Greenland ice sheet model parameters constrained using simulations of the Eemian Interglacial, Clim. Past, 7, 381–396, https://doi.org/10.5194/cp-7-381-2011, 2011. a, b, c
Sasgen, I., van den Broeke, M., Bamber, J. L., Rignot, E., Sørensen, L. S., Wouters, B., Martinec, Z., Velicogna, I., and Simonsen, S. B.: Timing and origin of recent regional ice-mass loss in Greenland, Earth Planet. Sc. Lett., 333–334, 293–303, https://doi.org/10.1016/j.epsl.2012.03.033, 2012. a
Sciascia, R., Straneo, F., Cenedese, C., and Heimbach, P.: Seasonal variability of submarine melt rate and circulation in an East Greenland fjord, J. Geophys. Res.-Oceans, 118, 2492–2506, https://doi.org/10.1002/jgrc.20142, 2013. a
Shapiro, N. M. and Ritzwoller, M. H.: Inferring surface heat flux distributions guided by a global seismic model: particular application to Antarctica, Earth Planet. Sc. Lett., 223, 213–224, https://doi.org/10.1016/j.epsl.2004.04.011, 2004. a
Shepherd, A., Wingham, D., and Rignot, E.: Warm ocean is eroding West Antarctic ice sheet, Geophys. Res. Lett., 31, L23402, https://doi.org/10.1029/2004GL021106, 2004. a
Shepherd, A., Ivins, E. R., Geruo, A., Barletta, V. R., Bentley, M. J., Bettadpur, S., Briggs, K. H., Bromwich, D. H., Forsberg, R., Galin, N., Horwath, M., Jacobs, S., Joughin, I., King, M. A., Lenaerts, J. T. M., Li, J., Ligtenberg, S. R. M., Luckman, A., Luthcke, S. B., McMillan, M., Meister, R., Milne, G., Mouginot, J., Muir, A., Nicolas, J. P., Paden, J., Payne, A. J., Pritchard, H., Rignot, E., Rott, H., Sandberg Sorensen, L., Scambos, T. A., Scheuchl, B., Schrama, E. J. O., Smith, B., Sundal, A. V., van Angelen, J. H., van de Berg, W. J., van den Broeke, M. R., Vaughan, D. G., Velicogna, I., Wahr, J., Whitehouse, P. L., Wingham, D. J., Yi, D., Young, D., and Zwally, H. J.: A reconciled estimate of ice sheet mass balance, Science, 338, 1183–1189, https://doi.org/10.1126/science.1228102, 2012. a
Simpson, M. J. R., Milne, G. A., Huybrechts, P., and Long, A. J.: Calibrating a glaciological model of the Greenland ice sheet from the Last Glacial Maximum to present-day using field observations of relative sea level and ice extent, Quaternary Science Rev., 28, 1631–1657, https://doi.org/10.1016/j.quascirev.2009.03.004, 2009. a, b, c, d, e
Stearns, L. A. and Hamilton, G. S.: Rapid volume loss from two East Greenland outlet glaciers quantified using repeat stereo satellite imagery, Geophys. Res. Lett., 34, L05503, https://doi.org/10.1029/2006GL028982, 2007. a
Stone, E. J., Lunt, D. J., Rutt, I. C., and Hanna, E.: Investigating the sensitivity of numerical model simulations of the modern state of the Greenland ice-sheet and its future response to climate change, The Cryosphere, 4, 397–417, https://doi.org/10.5194/tc-4-397-2010, 2010. a
Stone, E. J., Lunt, D. J., Annan, J. D., and Hargreaves, J. C.: Quantification of the Greenland ice sheet contribution to Last Interglacial sea level rise, Clim. Past, 9, 621–639, https://doi.org/10.5194/cp-9-621-2013, 2013. a, b, c, d
Straneo, F. and Heimbach, P.: North Atlantic warming and the retreat of Greenland's outlet glaciers, Nature, 504, 36–43, https://doi.org/10.1038/nature12854, 2013. a
Straneo, F., Hamilton, G. S., Sutherland, D. A., Stearns, L. A., Davidson, F., Hammill, M. O., Stenson, G. B., and Rosing-Asvid, A.: Rapid circulation of warm subtropical waters in a major glacial fjord in East Greenland, Nat. Geosci., 3, 182–186, https://doi.org/10.1038/ngeo764, 2010. a
Straneo, F., Sutherland, D. A., Holland, D., Gladish, C., Hamilton, G. S., Johnson, H. L., Rignot, E., Xu, Y., and Koppes, M.: Characteristics of ocean waters reaching Greenland's glaciers, Ann. Glaciol., 53, 202–210, https://doi.org/10.3189/2012AoG60A059, 2012. a
Straneo, F., Hamilton, G. S., Stearns, L. A., and Sutherland, D. A.: Connecting the Greenland Ice Sheet and the ocean: a case study of Helheim Glacier and Sermilik Fjord, Oceanography, 29, 22–33, https://doi.org/10.5670/oceanog.2016.97, 2016. a
Sutherland, D. A. and Straneo, F.: Estimating ocean heat transports and submarine melt rates in Sermilik Fjord, Greenland, using lowered acoustic Doppler current profiler (LADCP) velocity profiles, Ann. Glaciol., 53, 50–58, https://doi.org/10.3189/2012AoG60A050, 2012. a
Tarasov, L. and Peltier, R. W.: Greenland glacial history and local geodynamic consequences, Geophys. J. Int., 150, 198–229, 2002. a
Tedesco, M., Doherty, S., Fettweis, X., Alexander, P., Jeyaratnam, J., and Stroeve, J.: The darkening of the Greenland ice sheet: trends, drivers, and projections (1981–2100), The Cryosphere, 10, 477–496, https://doi.org/10.5194/tc-10-477-2016, 2016. a
van den Broeke, M. R., Enderlin, E. M., Howat, I. M., Kuipers Munneke, P., Noël, B. P. Y., van de Berg, W. J., van Meijgaard, E., and Wouters, B.: On the recent contribution of the Greenland ice sheet to sea level change, The Cryosphere, 10, 1933–1946, https://doi.org/10.5194/tc-10-1933-2016, 2016. a, b, c
Vieli, A. and Nick, F. M.: Understanding and modelling rapid dynamic changes of tidewater outlet glaciers: issues and implications, Surv. Geophys., 32, 437–458, https://doi.org/10.1007/s10712-011-9132-4, 2011. a
Vinther, B. M., Buchardt, S. L., Clausen, H. B., Dahl-Jensen, D., Johnsen, S. J., Fisher, D., Koerner, R., Raynaud, D., Lipenkov, V., Andersen, K., Blunier, T., Rasmussen, S. O., Steffensen, J. P., and Svensson, A. M.: Holocene thinning of the Greenland ice sheet, Nature, 461, 385–388, https://doi.org/10.1038/nature08355, 2009. a, b
Waelbroeck, C., Labeyrie, L., Michel, E., Duplessy, J. C., McManus, J., Lambeck, K., Balbon, E., and Labracherie, M.: Sea-level and deep water temperature changes derived from benthic foraminifera isotopic records, Quaternary Sci. Rev., 21, 295–305, 2002. a
Wilson, N., Straneo, F., and Heimbach, P.: Satellite-derived submarine melt rates and mass balance (2011–2015) for Greenland's largest remaining ice tongues, The Cryosphere, 11, 2773–2782, https://doi.org/10.5194/tc-11-2773-2017, 2017. a, b, c, d, e, f
Wouters, B., Martin-Español, A., Helm, V., Flament, T., van Wessem, J., Ligtenberg, S., van den Broeke, M., and Bamber, J.: Dynamic thinning of glaciers on the Southern Antarctic Peninsula, Science, 348, 899–903, https://doi.org/10.1126/science.aaa5727, 2015. a
Xu, Y., Rignot, E., Menemenlis, D., and Koppes, M.: Numerical experiments on subaqueous melting of Greenland tidewater glaciers in response to ocean warming and enhanced subglacial discharge, Ann. Glaciol., 53, 229–234, https://doi.org/10.3189/2012AoG60A139, 2012. a
Xu, Y., Rignot, E., Fenty, I., Menemenlis, D., and Flexas, M.: Subaqueous melting of Store Glacier, west Greenland from three-dimensional, high-resolution numerical modeling and ocean observations, Geophys. Res. Lett., 40, 4648–4653, https://doi.org/10.1002/grl.50825, 2013. a, b
Yau, A. M., Bender, M. L., Robinson, A., and Brook, E. J.: Reconstructing the last interglacial at Summit, Greenland: Insights from GISP2, P. Natl. Acad. Sci. USA, 113, 9710–9715, https://doi.org/10.1073/pnas.1524766113, 2016. a
Yi, S., Sun, W., Heki, K., and Qian, A.: An increase in the rate of global mean sea level rise since 2010, Geophys. Res. Lett., 42, 3998–4006, https://doi.org/10.1002/2015GL063902, 2015. a
Zwally, H. J., Jun, L. I., Brenner, A. C., Beckley, M., Cornejo, H. G., DiMarzio, J., Giovinetto, M. B., Neumann, T. A., Robbins, J., Saba, J. L., Yi, D., and Wang, W.: Greenland ice sheet mass balance: distribution of increased mass loss with climate warming; 2003–07 versus 1992–2002, J. Glaciol., 57, 88–102, https://doi.org/10.3189/002214311795306682, 2011. a





