A question of time and space: a model approach to the synchronous precipitation of gypsum and halite during the Messinian Salinity Crisis

Salt giants, although well studied, still offer some unsolved questions. One example is the Messinian salt giant which formed during the Messinian Salinity Crisis in the Mediterranean Sea. While a common assumption is that gypsum precipitated in the marginal parts of the basin before halite formed in the deeper part of the basin, this could not yet be confirmed. Indeed, it has also been suggested that, while the primary lower gypsum was forming, the deep basin was already accumulating halite. In this study we use box modeling to investigate the distribution of halite and gypsum deposits for different possible configurations of the basin and circulation. Due to a dimensionless description of basin restriction, our results can be transferred to other basins. With this approach we find that under the right conditions all configurations lead to a simultaneous but spatially separated precipitation of gypsum and halite. They would, however, not lead to the spatial pattern that is observed in the Mediterranean, i.e., halite deposition in the deep basins, while gypsum is deposited in the marginal basin. Based on those results we propose a timeline for a salinifying basin. For an average salinity above gypsum but below halite saturation, halite is first formed in a sufficiently restricted marginal part, and only once the average salinity approaches halite saturation can it also form in the open basin due to horizontal salinity gradients. Once the whole basin has reached halite saturation, gypsum only forms in marginal basins with a positive local freshwater budget. Such a mechanism, however, would produce less than 1 m of gypsum within 25 000 years. We thus conclude that a simultaneous, yet spatially separated precipitation of gypsum and halite within one basin is possible but unlikely to have led to the massive primary lower gypsum outcrops in the Mediterranean, while halite formed in the deeper parts of the same sub-basin.

1 Introduction

Although the Mediterranean is known for its equable conditions, this does not apply on geological timescales. In fact, at the end of the Miocene the Mediterranean Sea was in an extreme state compared to today, leading to the youngest known salt giant formation. This event, called the Messinian Salinity Crisis (MSC) (Hsü et al., 1973; Ryan, 2009), has been the subject of study for more than 50 years and took place in a geologically short time span (5.97 to 5.33 Ma – million years before present; Roveri et al., 2008). This has been determined by using astronomical tuning on the onshore MSC record as developed by Krijgsman et al. (2001), which leaves a gap of 600 000 years (600 kyr; we will employ Myr for ranges in millions of years and Ma for dates in millions of years before present as described by Aubry et al., 2009).

The sedimentary record of the MSC includes gypsum deposits in the marginal parts of the basin and in the deep basin mainly halite, which reaches up to 3 km in thickness and adds up to 821 $\pm \mathrm{50}\times {\mathrm{10}}^{\mathrm{3}}$ km³ of late Messinian salt (Haq et al., 2020). In the stratigraphic consensus model, the succession of those evaporites is divided into three stages. In this three-stage model the deposition of the thick halite unit is both preceded and succeeded by a period of dominantly gypsum precipitation (Roveri et al., 2014). In this model the MSC is assumed to start with gypsum precipitation in the marginal basins (stage 1, duration 0.371 Myr) which is then followed by halite precipitation in the deep basin (stage 2, 0.05 Myr). At the end of the crisis (stage 3, 0.22 Myr) the salinity decreased again, and the system experienced another phase of gypsum precipitation (Roveri et al., 2014).

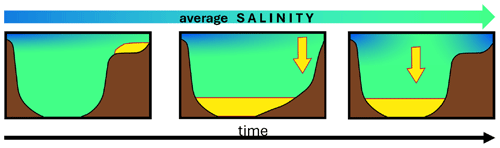
Figure 1 Visualization of the two different conceptual models discussed in this paper. (a) Consensus model. The deposition of gypsum in stage 1 is followed by the deposition of halite in stage 2. (b) Alternative model. The deposition of gypsum overlaps with the deposition of halite.

However, the correlation between the various sedimentary units is never unambiguous, since, for example, we cannot follow the layers of the so-called primary lower gypsum (PLG) from the margins to the deep basin. While the iconic stratigraphic section for the Caltanissetta basin of Sicily shows halite to overlie gypsum (Decima and Wezel, 1971; Decima and Wezel, 1973), these different units are found (in well cores and mines) in places removed by some horizontal distance and their lateral correlation is not observed; i.e., we cannot really exclude the possibility that these two units are each other's lateral equivalent. This idea seemed to get reinforced by a recent study in the Levantine basin (Meilijson et al., 2019), but another study by Manzi et al. (2018) conducted on data in the same area saw the three-stage model confirmed. A more recent study by Oppo et al. (2023), however, reopened this question after investigating the record below the halite deposit in the Levant. This goes to show the complexity of the problem. The coevality of the primary lower gypsum and halite would have implications for the duration of precipitation of the latter and thus would make room for new scenarios for the time corresponding to the first stage while deviating from the consensus model (see Fig. 1).

For these kinds of problems modeling can add valuable insight. They allow us to test interpretations and hypotheses against the principles of physics and explore the behavior of systems theoretically and in a way that is transferrable to similar systems. As such, it is the objective of this paper to apply a model approach to the question of whether it is physically possible that gypsum and halite deposits formed in different depth ranges of the Mediterranean basin at the same time by some form of salinity gradient. A similar approach was adopted by Simon and Meijer (2017), who investigated the spatial distribution of salinity using a box model with prescribed rate of overturning. The latter leaves open the question of whether such overturning would actually develop. It was found that a significantly stratified Mediterranean water column can be established when a slowed-down overturning is assumed. The results also indicate that deposition of halite would take longer than the time span assumed in the three-stage model. In contrast to the study of Simon and Meijer (2017), we use a density-driven dynamic overturning and investigate a broader range of configurations and scenarios. We make our results transferrable to other semi-enclosed basins with an anti-estuarine circulation, i.e., a basin with an outflow more saline than its inflow, e.g., Red Sea (Sofianos and Johns, 2015).

The thermo-haline overturning circulation of this semi-enclosed sea is closely linked to its two-way exchange with the Atlantic Ocean through the Strait of Gibraltar with a dense outflow into the Atlantic, whose imprints can be traced back to the Tortonian (de Weger et al., 2020). This, in combination with the negative freshwater budget of the Mediterranean (Simon et al., 2017), strongly implies a simultaneous inflow from the Atlantic and thus a two-way exchange at the beginning of the MSC. The conversion from Atlantic water to more saline Mediterranean overflow water happens via an overturning cell in the Mediterranean Sea. This thermohaline circulation is driven by a combination of convection and sinking events that transport the newly formed dense water into the deeper basin (Waldman et al., 2018). This process and the interplay between strait exchange and dense-water formation are still very much the subject of studies, e.g., Pinardi et al. (2019).

For this type of overturning circulation there are, roughly speaking, two ways to reach a situation where halite and gypsum are precipitated at the same time. Either the bulk of the Mediterranean Sea has only reached gypsum saturation while there is a part of the basin that is concentrated in a way that it reaches halite saturation (henceforth referred to as scenario A), or the basin has reached halite concentration, while some parts stay below that threshold due to dilution (scenario B).

Scenario A would require an area of deepwater formation where water becomes denser than the water in the deep basin. There are two different configurations in which this can be achieved. The first one is a basin that is driven by convection in a distinct part of the basin itself (A1). Alternatively, the overturning cell is driven by restricted marginal basins from where a density-driven downward flux transports the ions into the deep part of the basin (A2). In possibility (B) a diluted area is required. It is safe to assume that this would be a marginal basin with a positive freshwater budget. In that case, the overturning happens via convection between the open and the deep box. These three configurations as well as their translation to a model setup are illustrated in Fig. 2.

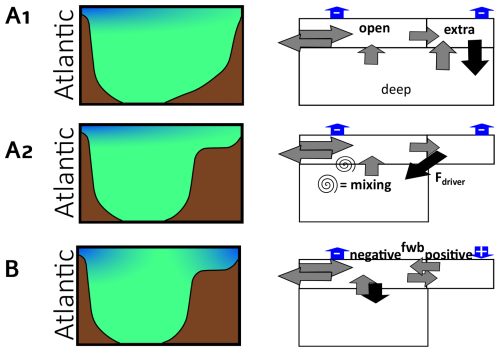
Figure 2 Visualization of the three configurations discussed in this paper. Left: the brown outline represents the Mediterranean Sea with the Atlantic on the left. Shading symbolizes salinity (blue signifies low, green signifies high). Right: the corresponding model setup. The box that reaches halite saturation first is the origin of the density flux that drives the overturning cell (black arrow, driver flux). The grey arrows indicate other fluxes within the Mediterranean Sea, as well as within the Atlantic. The vertical blue arrows represent the freshwater budget (fwb) of the boxes, with the only positive fwb occurring in configuration B in the extra box.

2 Methods

To test whether one of the aforementioned configurations (A1, A2, or B) could lead to coeval precipitation of halite and gypsum, they were translated to numerical models. From previous studies on, for example, sapropels (Dirksen and Meijer, 2020) or the sensitivity of the Atlantic Meridional Overturning Circulation (Chapman et al., 2024), we know that seemingly simple conceptual models can help us to understand even complex systems by reducing them to the main processes and their interaction.

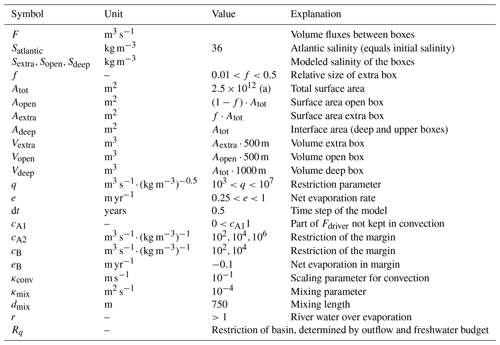
Table 1 Parameters and how they are used in the model. Key to references: (a) – Meijer and Krijgsman (2012).

2.1 Model

For the configurations described in the Introduction, the Mediterranean Sea is represented by three boxes. The main part of the basin is divided into two of them, the open and the deep box. The open box represents the surface and intermediate layer up to a depth of 500 m and is thus in interaction with the Atlantic and influenced by the atmosphere through evaporation and precipitation. The deep box represents the deep water and is not directly influenced by the atmosphere. Those two boxes exchange properties through mixing, and they exchange water through density-driven fluxes, convection, or compensating fluxes, depending on the configuration (see Fig. 1). The so-called extra box describes a smaller volume on the surface that is either a marginal basin (A1 and B) or an area where convection occurs due to a naturally occurring horizontal salinity gradient (A2). The volumes and area, as well as the other parameters used in this model, are listed in Table 1.

All three boxes have a constant volume that is described by their surface or interface area and depth, while their salinities (S_open, S_deep, S_extra) are variable. Each flux, F, that is triggered by a salinity difference (exchange with Atlantic, Q; sinking flux of convection, F_open→deep or F_extra→deep; or dense water sinking) thus triggers fluxes between the other boxes to maintain the volume of each box. All configurations are subjected to a constant net evaporation rate e that acts uniformly across the surface. The only exception is implemented in B, where the extra box has a positive freshwater budget, which results in a negative net evaporation rate.

In configuration A1 the driving flux F_driver is triggered when the salinity of the extra box surpasses that of the deep box. A water flux, scaled by a mixing parameter k_conv, the surface area A_extra of the extra box, and the salinity difference (S_extra−S_lower), sinks into the deep box (it is important to note that this work uses the descriptor κ not in the traditional sense),

$$\begin{array}{}\text{(1)}& F_{\mathrm{driver}}=F_{\mathrm{extra}\to \mathrm{deep}}=k_{\mathrm{conv}}\cdot A_{\mathrm{extra}}\cdot {\displaystyle \frac{S_{\mathrm{extra}}-S_{\mathrm{deep}}}{S_{\mathrm{deep}}}},\end{array}$$

and is partially compensated by an upward flux that is scaled with the factor c_A1:

$$\begin{array}{}\text{(2)}& F_{\mathrm{deep}\to \mathrm{extra}}=\left(\mathrm{1}-c_{\mathrm{A}\mathrm{1}}\right)\cdot F_{\mathrm{driver}}.\end{array}$$

This creates a convection cell with a net downward flux c_A1⋅F_driver as has been described for the Mediterranean Sea (Waldman et al., 2018). The volume of the deep box is then kept constant by an upward flux into the open box, and the volume of the extra box is preserved by a compensating flux from the open box that replaces both the freshwater budget (fwb) and the net downward flux. The downward flux is thus the driver of the circulation. Only the exchange with the Atlantic is not directly dependent on the driver flux. The outflow of this exchange is directly proportional to $\sqrt{S_{\mathrm{open}}-S_{\mathrm{Atl}}}$ as well as a factor, q, describing the strait efficiency.

$$\begin{array}{}\text{(3)}& Q=\sqrt{S_{\mathrm{open}}-S_{\mathrm{Atlantic}}}\cdot q\end{array}$$

The inflow from the Atlantic compensates not only for the outflow, but also for the water volume lost due to evaporation. This creates a stable stratification between the open and the deep box. The resulting salinity gradient leads to mixing at their shared interface. This salt flux j_mix, as also used in Dirksen and Meijer (2020), Matthiesen and Haines (2003), and Tziperman and Speer (1994), depends on the salinity difference, the interface area A_open, a mixing depth d_mix, and the mixing coefficient κ_mix.

$$\begin{array}{}\text{(4)}& j_{\mathrm{mix}}={\mathit{\kappa }}_{\mathrm{mix}}\cdot \left(S_{\mathrm{open}}-S_{\mathrm{deep}}\right)\cdot {\displaystyle \frac{A_{\mathrm{open}}}{d_{\mathrm{mix}}}}\end{array}$$

The salinities S of the three boxes can hence be described by a set of differential equations using the fluxes F as well as mixing the open and the deep box.

$$\begin{array}{}\text{(5a)}& {\displaystyle }\begin{array}{rl}{V}_{\mathrm{open}}& {\displaystyle \frac{\mathrm{d}{S}_{\mathrm{open}}}{\mathrm{d}t}}=\left(Q+e{A}_{\mathrm{tot}}\right)S_{\mathrm{Atlantic}}+c_{\mathrm{A}\mathrm{1}}{F}_{\mathrm{driver}}{S}_{\mathrm{deep}}\\ & -\left(Q+c_{\mathrm{A}\mathrm{1}}{F}_{\mathrm{driver}}+e{A}_{\mathrm{extra}}\right)S_{\mathrm{open}}+j_{\mathrm{mix}}\end{array}\text{(5b)}& {\displaystyle }\begin{array}{rl}{V}_{\mathrm{extra}}& {\displaystyle \frac{\mathrm{d}{S}_{\mathrm{extra}}}{\mathrm{d}t}}=\left(\left(c_{\mathrm{A}\mathrm{1}}\right)F_{\mathrm{driver}}+e{A}_{\mathrm{open}}\right)S_{\mathrm{open}}\\ & -F_{\mathrm{driver}}{S}_{\mathrm{extra}}+(\mathrm{1}-c_{\mathrm{A}\mathrm{1}})\cdot F_{\mathrm{driver}}{S}_{\mathrm{deep}}\end{array}\text{(5c)}& {\displaystyle }{V}_{\mathrm{deep}}{\displaystyle \frac{\mathrm{d}{S}_{\mathrm{deep}}}{\mathrm{d}t}}=-j_{\mathrm{mix}}\end{array}$$

In configuration A2 the driving flux also originates from the extra box which here resembles a marginal basin that has restricted exchange with the rest of the Mediterranean. The exchange is again dependent on the salinity difference between the extra and the deep box and is scaled by a parameter for the restriction c_A2, which changes the flux F_driver,A2 that is driving the circulation in configuration A2 to

$$\begin{array}{}\text{(6)}& F_{\mathrm{driver},\mathrm{A}\mathrm{2}}=c_{\mathrm{A}\mathrm{2}}\cdot \left(S_{\mathrm{extra}}-S_{\mathrm{open}}\right).\end{array}$$

In configuration B the restricted margin has a positive freshwater budget with a negative net evaporation rate e_B, which makes it fresher than the open and the deep box. Since the extra box here is not producing dense water, its outflow is not the driver of the circulation. Instead, the transport of dense water into the deep here happens via mixing and convection between the open and the deep box, which are thus close to each other in salinity.

2.2 Freshened margin

For a more detailed look at configuration B and to answer the question of whether the precipitation of gypsum from such a diluted mixture might be possible, salinity will be viewed as a sum of concentrations.

$$\begin{array}{}\text{(7)}& \begin{array}{rl}S& ={\displaystyle \frac{\sum m_{\mathrm{Salts}}}{V}}=\sum \left[\mathrm{salts}\right]=\left[{\mathrm{CaSO}}_{\mathrm{4}}\right]+\left[\mathrm{NaCl}\right]\\ & +\left[\text{other\hspace{0.17em} salts}\right],\end{array}\end{array}$$

where each ion group (NaCl, CaSO₄) has its own saturation concentration which, when exceeded, triggers precipitation (Raad et al., 2023; Topper and Meijer, 2015, 2013; Leeder, 2009). This allows us to take the riverine ion input into the extra box into account and to identify the freshwater budget that would prevent first halite and then gypsum from precipitating in dependency of the evaporation $\mathrm{EP}=e\cdot A$ [m³ s⁻¹] and river input $R=r\cdot \mathrm{EP},r\ge \mathrm{1}$. Expressing the river inflow R in terms of the evaporitic flux EP allows us to formulate the following expressions in a way that is not dependent on the surface of the basin.

When describing such a state, one can assume that the concentrations of the dissolved salts in question – [NaCl]_extra – and ${\left[{\mathrm{CaSO}}_{\mathrm{4}}\right]}_{\mathrm{extra}}$ as well as the volume do not change over time. Looking at the halite concentration first, said concentration depends on a balance of sinks (precipitation Γ [kg s⁻¹], and ion transport out of the basin, e.g., [NaCl]_extraF_out) and sources (saline inflow from the Mediterranean [NaCl]_openF_in, low-saline river inflow [NaCl]_riverrEP). The same can be said for ${\left[{\mathrm{CaSO}}_{\mathrm{4}}\right]}_{\mathrm{extra}}$, but for reasons of simplicity the derivation of the final expression will be conducted on the example of halite, which can then be readily translated to its gypsum counterpart.

$$\begin{array}{}\text{(8)}& \begin{array}{rl}[\mathrm{NaCl}{]}_{\mathrm{open}}& F_{\mathrm{in}}+[\mathrm{NaCl}{]}_{\mathrm{river}}r\cdot \mathrm{EP}={\mathrm{\Gamma }}_{\mathrm{halite}}\\ & +{\left[\mathrm{NaCl}\right]}_{\mathrm{extra}}{F}_{\mathrm{out}}\end{array}\end{array}$$

With the water volume in the basin being conserved we can express F_out as

$$\begin{array}{}\text{(9)}& \begin{array}{rl}{F}_{\mathrm{out}}& =F_{\mathrm{in}}+\left(R-\mathrm{EP}\right)=F_{\mathrm{in}}+\left(r\cdot \mathrm{EP}-\mathrm{EP}\right)\\ & =F_{\mathrm{in}}+\left(r-\mathrm{1}\right)\cdot \mathrm{EP}.\end{array}\end{array}$$

Using this in addition to the condition that both inflow and outflow are saturated in the salt we are looking at

$$\begin{array}{}\text{(10)}& {\left[\mathrm{NaCl}\right]}_{\mathrm{open}}={\left[\mathrm{NaCl}\right]}_{\mathrm{sat}}\mathrm{and}{\left[\mathrm{NaCl}\right]}_{\mathrm{extra}}={\left[\mathrm{NaCl}\right]}_{\mathrm{sat}}.\end{array}$$

Equation (8) can be simplified to

$$\begin{array}{}\text{(11)}& {\left[\mathrm{NaCl}\right]}_{\mathrm{river}}\cdot r\cdot \mathrm{EP}={\mathrm{\Gamma }}_{\mathrm{halite}}+{\left[\mathrm{NaCl}\right]}_{\mathrm{sat}}\cdot \left(r-\mathrm{1}\right)\cdot \mathrm{EP}.\end{array}$$

With Γ_halite=0 it is possible to identify the point at which precipitation has just not yet started.

$$\begin{array}{}\text{(12)}& {\displaystyle \frac{{\left[\mathrm{NaCl}\right]}_{\mathrm{river}}}{{\left[\mathrm{NaCl}\right]}_{\mathrm{sat}}}}=\mathrm{1}-{\displaystyle \frac{\mathrm{1}}{r}}\end{array}$$

From this we can formulate a condition that applies to a basin that is not yet precipitating halite.

$$\begin{array}{}\text{(13)}& {\displaystyle \frac{{\left[\mathrm{NaCl}\right]}_{\mathrm{river}}}{{\left[\mathrm{NaCl}\right]}_{\mathrm{sat}}}}<\mathrm{1}-{\displaystyle \frac{\mathrm{1}}{r}}\end{array}$$

Analogously, the upper limit when the basin becomes too diluted for gypsum to precipitate,

$$\begin{array}{}\text{(14)}& {\displaystyle \frac{{\left[{\mathrm{CaSO}}_{\mathrm{4}}\right]}_{\mathrm{river}}}{{\left[{\mathrm{CaSO}}_{\mathrm{4}}\right]}_{\mathrm{sat}}}}>\mathrm{1}-{\displaystyle \frac{\mathrm{1}}{r}},\end{array}$$

which defines a range of values for r in which the basin is concentrated enough to precipitate gypsum but diluted enough to not precipitate halite in dependence of the ratio r between river inflow R and net loss to the atmosphere EP.

$$\begin{array}{}\text{(15)}& {\displaystyle \frac{{\left[\mathrm{NaCl}\right]}_{\mathrm{river}}}{{\left[\mathrm{NaCl}\right]}_{\mathrm{sat}}}}<\mathrm{1}-{\displaystyle \frac{\mathrm{1}}{r}}<{\displaystyle \frac{{\left[{\mathrm{CaSO}}_{\mathrm{4}}\right]}_{\mathrm{river}}}{{\left[{\mathrm{CaSO}}_{\mathrm{4}}\right]}_{\mathrm{sat}}}}\end{array}$$

2.3 Dimensionless descriptor for restriction

Just like r can be used to compare marginal basins regardless of their size, we can define another dimensionless metric R_q to describe the degree of restriction of a basin with anti-estuarine circulation.

$$\begin{array}{}\text{(16)}& R_q={\displaystyle \frac{-\mathrm{fwb}}{Q_{\mathrm{out}}}}\end{array}$$

This approach is similar but not identical to metrics that have been used by previous studies (Flecker et al., 2002; Simon and Meijer, 2015; Ebner et al., 2024). If R_q is one, then the influx is twice the size of the outflux to the Atlantic, as it has to compensate for an outflow and fwb that are the same size. For a less restricted basin, this ratio is smaller as the basin is more influenced by the properties of the Atlantic inflow. When the basin is more restricted and the influence of the net evaporation increases, the ratio also increases. This unit-less metric can also be used to compare different basins that are connected via two-way exchange to an oceanic reservoir, regardless of their size.

3 Results

In this section the behavior of the three configurations will first be compared to each other. Subsequently they will be analyzed separately to identify conditions that would lead to a concurrent precipitation of gypsum in the margin and halite in the deep. The section ends with a more in-depth look at the last configuration by making a distinction between the concentration of ions related to gypsum and halite.

3.1 Comparison

To compare the three configurations to each other, two parameters and their influence on the model need to be discussed. Those are the net evaporation e that acts on the surface, which represents the freshwater budget expressed as a rate [m yr⁻¹], and the strait restriction parameter q, which has a somewhat bulky unit [(m³ s⁻¹)/(√ kg m⁻³)] that will be omitted further on.

The more restricted the Mediterranean becomes, meaning the weaker the exchange between Atlantic and Mediterranean Sea is, the higher the average salinity of the system gets. This increase is nonlinear for all configurations, parametrizations, and evaporation rates and only halts when halite saturation is reached. This limit (defined as S_H=350 kg m⁻³) marks the threshold for halite saturation after which salinity would increase much slower than it did before due to the precipitation of halite.

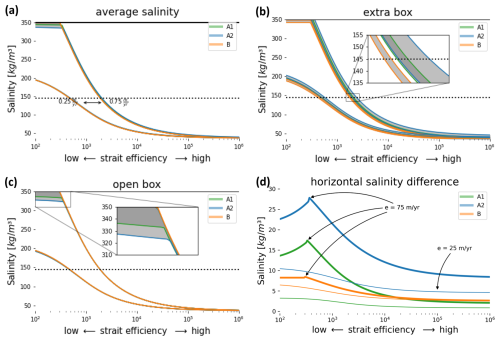
Figure 3 Salinity and salinity differences (y axis) of the three different configurations for different degrees of strait restriction (x axis). Each configuration is run for different sizes of the marginal basin ranging from 1 % to 25 % of the total surface area. The difference in outcome between the two parametrizations is indicated by the grey area between the two corresponding colored lines. Each data point on the lines represents one solution (salinity or salinity difference, y axis) of the configuration that is defined by a strait efficiency (x axis). For each configuration there are two sets of lines that only differ in the net evaporation that was used for the model: (a) the average salinity of the basin, (b) salinity of the extra box, (c) salinity of the upper box, and (d) salinity differences between the two top boxes (results shown for Area_extra=25 %Area_total). Further parameters include A1c =0.1, A2c =10⁴ m³ s${}^{-\mathrm{1}}\cdot$(kg m⁻³)⁻¹, ${\mathrm{Be}}_{\mathrm{extra}}=-\mathrm{0.1}$ m yr⁻¹, and $\mathrm{Bc}={\mathrm{10}}^{\mathrm{4}}\left({\mathrm{m}}^{\mathrm{3}}{\mathrm{s}}^{-\mathrm{1}}\right)/\left(\mathrm{kg}{\mathrm{m}}^{-\mathrm{3}}\right)$.

The direction of the horizontal salinity gradient is what differentiates the two A configurations (Fig. 3, blue and green) from the B configuration (Fig. 3, orange). In both A configurations the extra box is the most saline and thus the first one to reach the halite threshold. In the B case, however, the extra box is diluted compared to the rest of the basin and thus cannot reach halite saturation. The upper and lower box are well mixed in the B configuration. Their salinity develops similarly to the salinity of the extra box in the A configurations.

While the contrast between the average salinity and the constant salinity of the inflow increases, the absolute salinity differences between the boxes also increase, but once halite saturation is reached in the first box, the salinity differences decrease again. The difference would vanish if the whole system reached halite saturation. For the two A configurations the open box would be the last to reach halite saturation, which only happens when the inflow of the Atlantic gets concentrated to halite saturation by the fwb of the open box. The extra box in the B configuration never reaches halite saturation and thus develops a constant salinity difference from the open box once the open box reaches that threshold. This is a systemic difference between the A configurations and the B configuration. However, also within one configuration there are differences between runs, depending on the parametrization. Those differences, however, seem small compared to the influence of the forcing (net evaporation rate e).

3.2 Analysis

To assess which configurations could lead to coeval precipitation of gypsum in a marginal area and halite in the deep basin, we will look at each configuration individually and focus on runs where one or two boxes reach halite saturation while at least one stays below that threshold. In contrast to the previous section, the degree of restriction is now expressed as R_q. With this metric today's Red Sea would plot at 0.37 (e_RedSea=2.06 m yr⁻¹, $A_{\mathrm{RedSea}}=\mathrm{4.5}\times {\mathrm{10}}^{\mathrm{11}}{\mathrm{m}}^{\mathrm{2}}$, Q_RedSea≈0.15 Sv; Sofianos et al., 2002). The Mediterranean Sea is at R_Q=0.11 slightly less restricted (x in Fig. 3a).

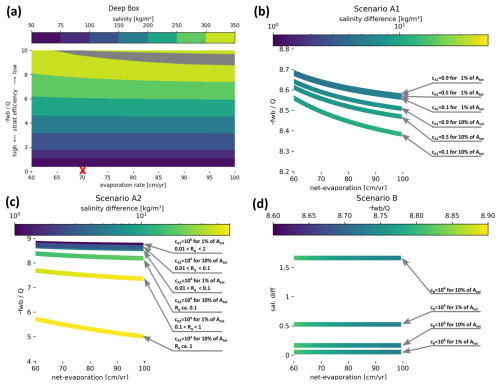
Figure 4 Results of the model for a range of net evaporations and degrees of restriction. The x axis shows the net evaporation rate [cm yr⁻¹] with increasing values towards the right. The y axis indicates how restricted the system is with respect to the Atlantic (ratio between freshwater budget and outflux). (a) Salinity of the lower box for configuration A1 (f=0.9, $A_{\mathrm{extra}}=\mathrm{0.1}\cdot A_{\mathrm{tot}}$). The red x indicates where the present-day Mediterranean Sea would be located. The grey patch marks where one of the upper boxes has already reached the threshold for halite precipitation, while the other one is not yet saline enough. (b, c) Each line shows the lower limit for patches like the one indicated in (a). The color scaling of the lines shows the salinity difference between the two upper boxes. Notice that the color scale differs from the one in panel (a) and that the y axis is adapted to better show the range of results. R_q in (c) describes the restriction of the marginal basin. (d) Compared to the previous two graphs, the meaning of the color scaling and the y axis is switched. Each line now indicates the salinity difference between the open and the extra box at the lower limit of the patches. The color scale shows the conditions needed for the system to reach said lower limit.

3.2.1 A1: convection

In this convection-driven configuration the halite saturation is reached first in the extra box. Hence, halite would form there first and then rain into the deep box, while gypsum could simultaneously form in the open box, which is supplied with “fresh ions” from the Atlantic. This simultaneous precipitation of gypsum and halite in two different boxes can only occur when the exchange between the Mediterranean Sea and the Atlantic is already very restricted (grey patch, Fig. 4). For example, for a net evaporation of 0.6 m yr⁻¹ this exchange would need to be limited to an outflow of less than $\mathrm{5}\times {\mathrm{10}}^{-\mathrm{3}}$ Sv and for 1 m yr⁻¹ ca $\mathrm{8}\times {\mathrm{10}}^{-\mathrm{3}}$ Sv, which is about 3 orders of magnitude less than the outflow today (Schroeder and Chiggiato, 2022) for a net evaporation of 0.7 m yr⁻¹. The lower limit of the grey area indicates the conditions under which the first of the upper boxes reaches halite saturation, the upper limit indicates the conditions under which both boxes have reached halite saturation. This situation is reached when the Atlantic inflow is small enough that its less saline water is concentrated to halite saturation by the loss of fresh water in the open box. The curves in Fig. 4b represent the lower limit of this patch for different parametrizations of the model and thus the least extreme conditions with the largest salinity difference (up 10 kg m⁻³ for A1, Fig. 4b; up to 50 kg m⁻³ for A2, Fig. 4c; up to 1.5 kg m⁻³ for B, Fig. 4d).

When we focus on the range of strait efficiency in Fig. 3b that would lead to the desired outcome, the influence of net evaporation stands out. The decline from left to right is caused by the increasing salinity of the basin that follows stronger evaporation. This means that for lower net evaporation, i.e., going right to left, the basin would have to be more restricted before the extra box could reach halite saturation. The salinity difference for all tested parametrizations is much smaller than 50 kg m⁻³, since the extra box is not restricted towards the open box. The salinity difference increases when more volume is involved in convection (small c_A1), since that slows down the circulation between the three boxes. The size of the area in which convection occurs only has a small influence on the salinity difference. It is thus possible to choose parameter values for configuration A1 in a realistic way that would lead to coeval precipitation of gypsum and halite but only when the whole system is already close to halite saturation due to restricted exchange with the Atlantic.

3.2.2 A2: restricted margin

In this configuration halite saturation is also reached first in the extra box which here acts as a restricted marginal basin. The salinity difference between the two upper boxes mainly depends on the relative strength of the exchange between the open and the extra box (Fig. 3c), which is comparable to the influence of the restriction between the Mediterranean Sea and the Atlantic. The extent of this restricted margin also has an influence on this salinity difference due to the change in surface area that is subjected to evaporation.

Comparing two extra basins with different restrictions but the same surface area (e.g., curves with A_extra=1 %A_tot and c_A2=10⁴ or c_A2=10⁶; Fig. 3c) shows this more clearly. The loss to the atmosphere is the same for both for any given net evaporation, but their outflows differ by 2 orders of magnitude. This creates a larger horizontal salinity difference for the more restricted basin due to the larger difference between in- and outflow. This effect is magnified for a marginal basin with the same restriction but larger area (e.g., curve with c_A2=10⁴ and A_extra=10 % A_tot). For such a basin, the salinity difference between the two upper boxes can exceed 50 kg m⁻³, meaning that the exchange with the Atlantic does not need to be that restricted for the extra box to reach halite saturation. This, however, is an extreme case and would translate to a marginal basin with the extent of the Aegean Sea (Waldman et al., 2018) and an outflow comparable to the discharge of the Evros (Poulos and Kotinas, 2021) that drains into it. Using the same metric for restriction as with the Atlantic–Mediterranean exchange, this would translate to $\left({\mathrm{fwb}}_{\mathrm{marg}}\right)/F_{\mathrm{out}}\approx \mathrm{0.02}$. To rephrase, it can be said that the less restricted the margin is with regard to its size (low ratio between local fwb and exchange), the closer it is to the overall salinity of the basin. For more realistic basins this means that the Mediterranean Sea would need to be close to halite saturation for the marginal basin to reach that threshold.

3.2.3 B: freshened margin

No matter the size or restriction of the extra box (freshened margin), the open box reaches halite saturation always for the same parametrization (Fig. 3d, color scale), while the extra box always stays below that threshold. A plot like in Fig. 3a for this configuration would thus not show an upper end for the grey patch. This is due to the positive local freshwater budget, $e_{\mathrm{B}}=-\mathrm{0.1}$ m yr⁻¹, in the extra box that dilutes the influx from the open box. The resulting salinity difference depends on the relative restriction, just like in the previous configurations.

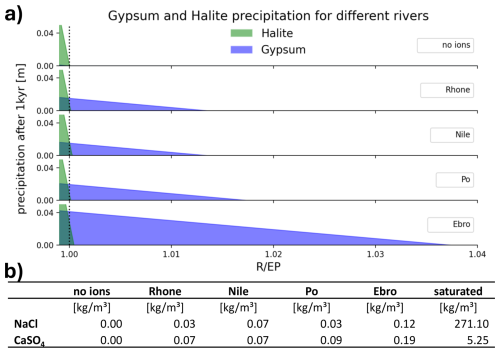
Figure 5 Gypsum and halite precipitation in a margin that is freshened by river water and fed by the Mediterranean Sea which is saturated in gypsum and halite. The x axis shows the ratio between the river inflow and evaporation (corrected for precipitation). When this ratio is 1 (dotted black line), the fwb is 0. For $R/\mathrm{EP}>\mathrm{1}$ the basin experiences less evaporation than river input and has a lower salinity than the inflow from the Mediterranean Sea. The y axis shows the precipitation rate that would result from those conditions [m kyr⁻¹]. The concentrations shown in the table are adapted from Gaillardet et al. (1999) and simplified to fit the model.

In contrast to the previous two configurations, looking at salinities is not enough to determine whether gypsum would precipitate. The salinity in the freshened margin might be above the gypsum threshold, but since it is a diluted brine, it might not be saturated in gypsum anymore. To determine whether that is the case, a closer look at the chemistry of the brine is needed. Since the extra box describes a generic unspecified marginal basin and the chemical composition of the generic river into that basin is not known, the closest approximation is achieved through investigating the behavior of the margin as if it were diluted by typical Mediterranean rivers (Fig. 5).

If the river would carry no ions, then a positive fwb would prevent precipitation of gypsum and halite since the brine would become undersaturated in both minerals. If the river water, however, also brings in ions, one or both concentrations could stay at this threshold and surplus ions would precipitate. This is why for river water compositions closer to the one of the Rhône, Nile, Po, or Ebro rivers (Gaillardet et al., 1999), evaporites could also precipitate when $R/\mathrm{EP}>\mathrm{0}$. In this situation the precipitation rate of halite decreases much faster with increasing relative river inflow than the precipitation rate of gypsum. This becomes especially visible for the example of the Nile, where we assumed comparable concentrations for the two ion groups.

The results in Fig. 5 show two things: firstly, that it is theoretically possible to precipitate gypsum from such a diluted margin without also precipitating halite and, secondly, that the total inflow from rivers can only exceed the loss of fresh water by 0.01 % to 4 % depending on the concentration of Ca²⁺ and ${\mathrm{SO}}_{\mathrm{4}}^{\mathrm{2}-}$ ions in the river water. The smaller the fwb compared to the surface area is, the higher the precipitation rate. The absolute rate depends on the evaporation rate but is of the order of magnitude of 0.1 m kyr⁻¹.

Figure 6 Time component of the system for different degrees of strait efficiency (x axis). Each line is defined by several runs of the model that only differ in restriction between the Mediterranean Sea and Atlantic, while all other parameters are kept the same. Changing the values of these parameters gives the other lines. (a) Time until saturation of gypsum (solid) and halite (dashed) is reached. Each curve tends to an asymptote (one example is added). To the right of an asymptote the strait is too efficient (restriction too limited) to reach gypsum or halite saturation. (b) Duration of simultaneous precipitation of gypsum and halite. Here the illustrative asymptote marks the run that reached simultaneous precipitation in its steady state. For increased readability the axes in the inset window are switched (linear x axis, logarithmic y axis). Key to line style: color indicates configuration, solid and dashed refer to gypsum and halite respectively, and thin and bold refer to the two values of net evaporation.

3.3 Time component

Although this study focuses on steady-state solutions, it is meaningful to consider the timescales involved. We do this by comparing the times the runs take to reach saturation (Fig. 6). Gypsum saturation is reached first for all configurations and parametrizations if the restriction was sufficiently low (Fig. 6a). Runs that were forced with a higher net evaporation rate reached saturation of both gypsum and halite sooner than runs with a lower net evaporation rate but otherwise the same parameter values. For e=0.75 m yr⁻¹ a restriction of several orders of magnitude compared to today's Mediterranean Sea would be necessary to reach gypsum saturation regardless of configuration. It follows from Fig. 6 that, if this restriction happened suddenly, it would take less than a precessional cycle to reach gypsum saturation. In another cycle halite saturation would be reached. Runs that met the conditions in their steady state (Fig. 6a, b, e.g., grey asymptote, corresponding to results shown in Fig. 4b, c, d) precipitate both evaporites in different locations for infinity. The sharp decrease away from the asymptote, however, shows that even small deviations from those favorable conditions would lead to a rapid decrease in this duration as the system soon becomes too saline for gypsum precipitation.

4 Discussion

4.1 Limitations of the model

The models presented here are not a representation of the complexity of the Mediterranean Sea but rather a means to understand some aspects of it. As such it is important to be aware that the dynamic between the eastern and western Mediterranean is not included in the different configurations and that the way salinity is treated does not capture the full thermodynamic reality of brines. Precipitation of halite in the deep basin, for example, is not included in this work, since the salinity cannot increase without the influence of evaporation, and the threshold for precipitation in this work is not dependent on the chemical composition of the brine, pressure, or temperature.

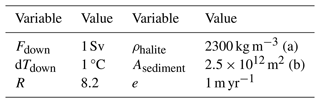
A lower temperature also decreases the ability of the waterbody to dissolve ions by 0.22 kg m⁻³ per 1 °C (based on water chemistry of the Dead Sea; Stiller et al., 1997). This is the cause of one of the governing processes of the Dead Sea (Sirota et al., 2016) and could also play a role in the MSC, since the present Mediterranean shows a vertical salinity gradient (e.g., Margirier et al., 2020; Fach et al., 2021). In the model this would have the effect that halite saturation might be reached first in the deep basin and that precipitation could also occur in the deep basin. The ions for this would be provided by the warmer downflow, which would have an excess of ions when the saturation concentration gets lowered due to cooling when the sinking water mass mixes with the saturated colder one. In the extreme case, we can estimate the precipitation rate caused by that process by assuming a strength for the downward flux, F_down, and temperature difference, dT (see Table 2). With those assumptions it is possible to calculate the ion stream that would be in excess by cooling down the downward flux.

$$\begin{array}{}\text{(17)}& j_{\mathrm{excess}}=F_{\mathrm{down}}\cdot {\displaystyle \frac{\mathrm{d}{c}_{\mathrm{sat}}}{\mathrm{d}T}}\cdot \mathrm{d}{T}_{\mathrm{down}}=\mathrm{2.2}\times {\mathrm{10}}^{\mathrm{5}}{\mathrm{kg}\mathrm{s}}^{-\mathrm{1}}\end{array}$$

Distributing j_excess over the total surface area of the Mediterranean would lead to a sedimentation rate of 10 m kyr⁻¹. This is of the same order of magnitude as ions added via an inflow with marine composition ($c_{\mathrm{NaCl},\mathrm{Atl}}=\mathrm{2.7}$ kg m⁻³; Leeder, 2009) to a basin with e=1 m yr⁻¹ and a restriction that leads to halite saturation (Fig. 3).

$$\begin{array}{}\text{(18)}& \begin{array}{rl}{j}_{\mathrm{added}}& =Q_{\mathrm{in}}\cdot c_{\mathrm{NaCl},\mathrm{Atl}}=\left({\displaystyle \frac{e\cdot A}{\left(\frac{\mathrm{fwb}}{Q}\right)}}+e\cdot A\right)\cdot c_{\mathrm{NaCl},\mathrm{Atl}}\\ & =\mathrm{2},\mathrm{14}\times {\mathrm{10}}^{\mathrm{5}}{\mathrm{kg}\mathrm{s}}^{-\mathrm{1}}\end{array}\end{array}$$

Table 2 Assumptions for the calculation of ion flux from one saturated box to another depending on their temperature difference. Key to references: (a) – Leeder (2009); (b) – Meijer and Krijgsman (2005).

It is however questionable if such a thought experiment is not a simplification of a complex process, since the heat of the cooling stream is dissipating into the surrounding waterbody, raising its temperature and saturation concentration just enough to take the excess ions in. On a smaller scale, however, the dependency of the saturation concentration on temperature can indeed lead to substantial halite deposits (Sirota et al., 2020). Double diffusive processes like salt fingering are too complex (Ouillon et al., 2019) to be represented reliably in this type of model.

Another simplification is the use of constant evaporation rates in contrast to a forcing that reflects the changes in the freshwater budget over time. Studies on the formation of sapropels in the Black Sea, which use a comparable approach, show that the transient response of such a model to changes in the forcing can be complex (Dirksen and Meijer, 2020, 2022). Another study, using a version of configuration A1, however, showed that a sinusoidal freshwater budget influences the amplitude depending on the restriction but not the average over time of signals like salinity (Ebner et al., 2024).

A1 is also similar to the model used in Simon and Meijer (2017). The main difference is in the definition of the driving flux and the exchange with the Atlantic. While their model defines set values, the model presented in this paper scales them more dynamically with salinity differences. Another major difference is the assumption that halite also precipitates from a waterbody that is not in contact with the atmosphere. While this would be allowed in the model presented here, it is not possible since no flux going into the deep box is above the threshold of saturation.

Figure 7 Proposed timeline for a salinifying basin. The different stages correspond to the configurations discussed in this paper in the sequence A2, A1, and B.

4.2 Implications of the model results

As elaborated in the Results section of this paper, all three configurations could lead to a situation in which halite and gypsum would form simultaneously but spatially separate. While the conditions under which this would happen seem similar (high overall salinity), they do differ from each other. This is best presented by their placement on a theoretical timeline of a hypothetical basin that experiences salinification. If we imagine this basin to be at gypsum saturation, it would develop in three steps as salinity keeps increasing (Fig. 7).

• Step 1. A restricted margin with a salinity that is higher than the average reaches halite saturation and starts precipitating halite. When the salinity of the main basin increases further, halite also starts forming in other, less restricted marginal basins.

• Step 2. The salinity in the open basin is now so high that also unrestricted areas reach halite saturation. In those areas the interplay of horizontal and vertical salinity gradients leads to density instabilities and thus convection. The crystals start forming there and rain into the deep basin, where they might partially dissolve again (Topper and Meijer, 2013).

• Step 3. The basin has now reached halite saturation, and halite is the predominant evaporite that forms and rains into the deep. Only some marginal areas that are experiencing a positive local freshwater budget are still precipitating gypsum without halite. This gypsum is now mainly influenced by the chemistry of the river water and how the river inflow compares to the evaporation that occurs on the surface.

The situation in step 1 would lead to halite deposits in sub-basins that only have restricted exchange with the rest of the basin. While it might be possible that the dense, saturated water, leaving such a sub-basin, would form halite as it sinks into the deeper part of the basin and cools, this process would be hindered by the mixing of saturated water with other undersaturated water masses. While this might happen locally, it is unlikely to be a mechanism that forms significant amounts of halite in deeper parts of the basin, where most halite deposits are found in the Mediterranean Sea, with only a few exceptions in elevated basins in, for example, the Balearic Promontory (Raad et al., 2021; Heida et al., 2022; Raad et al., 2023; Raad, 2022). Configuration A2 seems to explain the halite deposits in the Balearic promontory which hosts marginal basins. However, a case study on one of these, the Central Mallorca Depression (Raad, 2022), showed that its halite deposit was most likely caused by a draw down and not by a sill restricting the exchange. In step 3, only minuscule amounts of gypsum would be formed in the marginal areas. The sedimentation rates that would result from such a mechanism are comparable to those that result from the thickness (5 m) of the lower Tripoli Unit in the Lorca basin, which had previously been attributed to a time span of 400 kyr. This rate has been explained, however, by a gap in sedimentation that makes it impossible to define the age of the base of the unit (Rouchy et al., 1998). Even under perfect conditions a sedimentation rate of <4 cm kyr⁻¹ would take more than 25 kyr to deposit 1 m of gypsum. Other estimates for gypsum deposition rates exceed this value by several orders of magnitude (see Table 3).

Table 3 Gypsum precipitation in different studies. Key to references: (a) – Manzi et al. (2012); (b) – de Lange and Krijgsman (2010); (c) – Lugli et al. (2010).

The most interesting step in terms of likelihood and significance of the synchronicity of halite and gypsum thus seems to be the one that corresponds to configuration A1 and is described in step 2. It covers the transition between basinwide gypsum and basinwide halite precipitation that does not depend on local factors, only a horizontal salinity gradient, which unquestionably exists in the Mediterranean Sea (Bonnet et al., 2013). In the context of the MSC this process would add some time to halite formation, as phases 2 and 1 of the consensus model (Roveri et al., 2014) might overlap. How long this overlap can last depends on the strength of the salinity gradient and the pace of the salinity increase. Since the salinity of the Mediterranean would react sensitively to small changes in restriction once it is restricted enough to be close to halite saturation (Meijer, 2012), this overlap likely was insignificantly short. While it is possible for simultaneous precipitation to last for several insolation cycles, our analysis shows this to only apply for a very narrow range of constant restriction. Durations depicted in Fig. 6 are for the case of an instantaneous reduction in strait efficiency, kept constant thereafter. To be able to calculate the duration of simultaneous precipitation of gypsum and halite for a scenario where the connection between the Mediterranean Sea and the Atlantic changed gradually over time, the evolution of the restriction would need to be known in detail.

5 Conclusions

This study allows us to explore the different configurations that could have led to a simultaneous precipitation of gypsum and halite. We find this to potentially occur in all configurations but only for average salinities close to halite saturation. Based on this we propose a timeline for a salinifying basin with restricted margins. The essence of our proposed timeline is that a restricted basin needs to be described by various conceptual models as its salinity increases. From the different configurations we identified, only one (A1) describes the transition between predominantly halite and gypsum precipitation. The other two configurations might have been local effects occurring just before and after this transition but not to a degree that they majorly influenced the MSC strata. Our results do not exclude the possibility of an earlier onset for halite precipitation in the eastern sub-basin, since none of the configurations took the influence of the sill of Sicily into account.

A more comprehensive study should not only include the dynamics between the eastern and western Mediterranean subbasins, but also consider restriction and climatic forcing as a function of time.