the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
The geometry of sea-level change across a mid-Pliocene glacial cycle
Jessica R. Creveling
Jerry X. Mitrovica
Predictions of future sea-level change and ice-sheet stability rely on accurate reconstructions of sea levels for past warm intervals, such as the mid-Pliocene Warm Period (MPWP; 3.264–3.025 Ma). The magnitude of MPWP glacial cycles and the relative contribution of meltwater sources remain uncertain. We explore this issue by modeling processes of glacial isostatic adjustment for a wide range of possible MPWP ice-sheet melt zones, including North America, Greenland, Eurasia, and West Antarctica, as well as the Wilkes Basin, the Aurora Basin, and the embayment of Prydz Bay in East Antarctica. As a case study, we use a series of ice histories together with a suite of viscoelastic Earth models to predict global changes in sea level from the Marine Isotope Stage (MIS) M2 glacial to the MIS KM3 interglacial. At the Whanganui Basin (New Zealand), a location with stratigraphic constraints on Pliocene glacial–interglacial sea-level amplitude, the calculated local-sea-level (LSL) rise is on average ∼ 15 % lower than the associated change in the global mean sea level (GMSL) in the ice-sheet scenarios explored here. In contrast, the calculated LSL rise over the deglaciation from MIS M2 to MIS KM3 at Enewetak Atoll is systematically larger than the GMSL change by 10 %. While no single LSL observation (field site) can provide a unique constraint on the sources of ice melt observed during this period, combinations of observations have the potential to yield a stronger constraint on GMSL change and to narrow the list of possible sources.
- Article
(5814 KB) - Full-text XML
-
Supplement
(1333 KB) - BibTeX
- EndNote
Accurate reconstructions of sea levels for past warm periods offer insight into ice-sheet stability in the face of projected anthropogenic climate change (Dutton et al., 2015). In this regard, the mid-Pliocene Warm Period (MPWP; 3.264–3.025 Ma) serves as a key period of focus. Mid-Pliocene reconstructed atmospheric CO2 levels and global mean annual surface temperatures are comparable to projected 21st-century warming scenarios (350–450 ppm and ∼ 2–3 °C above modern levels, respectively; Pagani et al., 2010; Haywood et al., 2013). As such, estimates of peak global mean sea levels (GMSLs) for the Pliocene have calibrated the sensitivity of global climate models (DeConto and Pollard, 2016). While the differing rates of CO2 forcing and the distinct oceanographic conditions resulting from the closing of equatorial seaways (Haywood et al., 2011; Sarnthein et al., 2009) may reveal the MPWP as an imperfect analogue for the future, the mid-Pliocene period remains a crucial natural laboratory for evaluating the complexity of the Earth's ice age climate system.
A rich literature has sought to quantify GMSL variability during the MPWP using ice-sheet modeling (DeConto and Pollard, 2016; de Boer et al., 2017; Berends et al., 2019a) and a suite of proxy data, including δ18O records, with and without complementary measurements (e.g., Dwyer and Chandler, 2009; Sosdian and Rosenthal, 2009; Rohling et al., 2014; Winnick and Caves, 2015; Miller et al., 2020), phreatic overgrowths on speleothems (Dumitru et al., 2019), sequence-stratigraphic records (e.g., Wardlaw and Quinn, 1991; Naish and Wilson, 2009; Miller et al., 2012; Grant et al., 2019) and coastal-plain terraces and escarpments (e.g., Dowsett and Cronin, 1990; Krantz, 1991; Kaufman and Brigham-Grette, 1993; James et al., 2006; Rowley et al., 2013; Rovere et al., 2014; Hearty et al., 2020; Sandstrom et al., 2021). These studies have evaluated either the total amplitude of sea-level change through Pliocene glacial–interglacial cycles or the absolute peak in sea levels during the Pliocene “super-interglacials”, yet they have achieved little consensus on these values. It is common within these studies to infer the suite of ice-sheet sources of meltwater on the basis of estimates of peak GMSL values (e.g., Naish and Wilson, 2009; Raymo et al., 2011; Miller et al., 2012; Grant et al., 2019); for example, many studies attribute peak GMSL values of up to approximately +10 m relative to the present day to combined melt from the Greenland and West Antarctic ice sheets, with any residual GMSL values (i.e., those exceeding 10 m above present sea levels) attributed to meltwater from the East Antarctic Ice Sheet. More recent studies have included North American and Eurasian ice cover in the sea-level budget (Berends et al., 2019a; LeBlanc et al., 2021).
The persistent disagreement among the various mid-Pliocene sea-level reconstructions may stem from limitations in the proxy records that they are derived from or from corrections applied to these proxies. Although δ18O records accurately reflect glacial timescales (Lisiecki and Raymo, 2005a; Zachos et al., 2001), numerous complexities introduce errors into the mapping of these records to GMSLs (Mix, 1987; Clarke and Marshall, 2002; Waelbroeck et al., 2002; Siddall et al., 2008; Winnick and Caves, 2015). Coupled climate–ice–sea-level models rely on accurate proxy measurements and are sensitive to uncertainties in a wide range of model parameters and climate forcings (e.g., Berends et al., 2019a). Furthermore, inferences of local relative sea levels (RSLs) based on geomorphic or stratigraphic indicators of paleo-sea levels are potentially contaminated by three geophysical processes – tectonics, dynamic topography, and glacial isostatic adjustment (GIA; Raymo et al., 2011; Rowley et al., 2013; Austermann et al., 2017; Richards et al., 2023). Because each process introduces significant geographic variability to sea-level change (i.e., major regional departures from GMSLs), any GMSL inferences from compilations of geological data are subject to uncertainty and/or error in these geophysical corrections.
In this article, we explore in detail possible geometries of MPWP sea-level change arising from the rotational, gravitational, and deformational effects of the GIA process for a wide range of ice-sheet melt zones, including North America, Greenland, Eurasia, and West Antarctica, as well as the Wilkes Basin, the Aurora Basin, and the embayment of Prydz Bay in East Antarctica. Our focus is on the geometry of sea-level change spanning the years from the Marine Isotope Stage (MIS) M2 glacial maximum at 3.295 Ma to the MIS KM3 interglacial at 3.155 Ma; these events represent times of peak sea-level lowstands and highstands, respectively. These modeling experiments complement the common focus on constraining peak sea levels observed during the KM3 interglacial. We first describe the numerical methods adopted in the study, along with the ice history and Earth models that enable sea-level predictions. Next, our procedure for normalizing predictions of sea-level change requires a precise definition of GMSL change; we discuss the definition that we adopted from Pan et al. (2022), which, although framed for interglacials, is relevant to the discussion of Pliocene sea-level change. Finally, we present and compare normalized maps of sea-level change for the individual melt zones listed above and discuss the biases in estimates of Pliocene GMSL change that may be introduced by neglecting the geographic variability inherent in these maps.
2.1 Sea-level model
Our predictions are based on a generalized form of the sea-level equation (Mitrovica and Milne, 2003; Kendall et al., 2005) that accounts for time-varying shoreline migration and perturbations in the Earth's rotation (Mitrovica et al., 2005). We assume a spherically symmetric Maxwell viscoelastic Earth model (Peltier, 1974) and adopt the pseudo-spectral algorithm described by Kendall et al. (2005), with truncation at a spherical harmonic degree and an order of 256. The elastic structure of the Earth model is taken from the seismic model Preliminary reference Earth Model (PREM) (Dziewonski and Anderson, 1981), and in our primary calculations, the viscosity structure is comprised of a 96 km thick elastic lithosphere and uniform upper- and lower-mantle viscosities of 5 × 1020 and 5 × 1021 Pa s, respectively (henceforth referred to as the “reference” model). This primary viscoelastic structure is within the range of models inferred from studies of GIA datasets (Mitrovica and Forte, 2004; Lambeck et al., 2014). However, we also perform an analysis that explores the sensitivity of the normalized sea-level predictions to plausible variations in the viscosity model. These additional 27 models are combinations of specific lithospheric thicknesses (72, 96, and 125 km), upper-mantle viscosities (0.3, 0.5, and 0.8 Pa s), and lower-mantle viscosities (5, 10, and 30 Pa s).
Definitions of how GMSL changes during deglaciation (or glaciation) are complicated by contemporaneous changes in ocean area (i.e., shoreline migration) due to local onlap or offlap of water and the advance or retreat of grounded marine-based ice sheets. Figure 1 is a schematic of the primary definition adopted in this study. This figure shows a cross section through a region with a grounded marine-based ice sheet that retreats, leading to perturbations in the elevations of the solid Earth and the equipotential that defines the sea surface. We followed Pan et al. (2022) in defining GMSL change from MIS M2 to MIS KM3 as the mean change in the volume of the ocean outside the grounding line of the ice sheet prior to the melt event (i.e., the region to the left of the vertical dashed line marked “GL” in Fig. 1a) divided by the average ocean area corresponding to the beginning and end of the time period of interest (Fig. 1a and b, respectively). (We note that, in the simulations discussed below, the ocean areas for MIS M2 and MIS KM3 differ by less than ∼ 1 %, so choosing to divide by the ocean area corresponding to either time, instead of taking the average, would have a negligible impact on the normalization procedure.) This definition of global mean sea-level change, henceforth denoted as GMSLP, reflects our focus on sea-level changes outside marine-based sectors since it accounts for meltwater sequestered in marine regions exposed by the retreat of grounded ice and the flux out of these areas due to post-glacial rebound. We normalize predictions of sea-level change from MIS M2 to MIS KM3 by dividing each prediction by the GMSLP value associated with the GIA simulation. In the “Further discussion and conclusions” section, we consider other possible definitions for GMSL change.
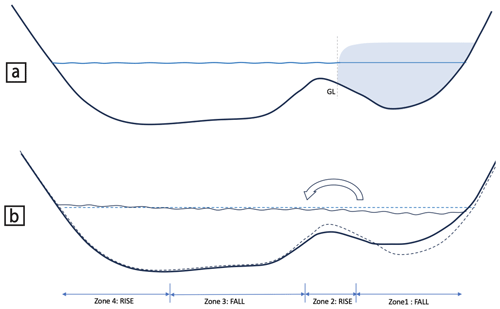
Figure 1Sea-level change in response to the melting of a grounded ice sheet. The sea surface equipotential (blue) and solid surface (black) from before (a) and after (b) the melt event. The labeling at the bottom of panel (a) denotes the ice-sheet grounding line (GL), and panel (b) shows locations of sea-level rise (an increase in the elevation of the sea surface equipotential relative to the solid surface) and fall (a decrease in the elevation of the sea surface equipotential relative to the solid surface). Zones 1–4 are referred to in the text. The arrow at the top of panel (b) indicates the flow of water into the open ocean, driven by the post-glacial uplift of marine sectors previously covered by grounded ice.
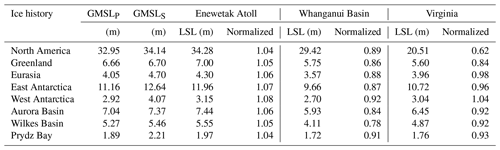
Table 1Computed GMSL changes across a ∼ 100 kyr time period, extending from MIS M2 to MIS KM3, for eight regional ice histories. The two GMSL columns show GMSLP (calculated using the reference Earth model) and GMSLS. The two definitions of GMSL are provided in the text. The last three columns display predicted LSL changes (in meters) and normalized sea-level changes at three sites (Enewetak Atoll, the Whanganui Basin, and Virginia).
2.2 Ice-sheet model
To explore the GMSLP value in response to the collapse of an individual Pliocene ice sheet, we separately modeled ice-sheet variability across eight different regions during the MPWP: Eurasia (the Eurasian ice sheet – EIS), Greenland (the Greenland Ice Sheet – GrIS), North America (the North American ice sheet – NAIS), West Antarctica (the West Antarctic Ice Sheet – WAIS), and East Antarctica (the East Antarctic Ice Sheet – EAIS), as well as three distinct zones within East Antarctica (the Aurora and Wilkes basins and Prydz Bay). Before any computation was performed, we began by establishing the maximum ice cover of individual ice sheets (the GMSL for each ice sheet is listed in Table 1). The maximum ice volume for each ice sheet occurs during MIS M2 (δ18O value of 3.74 ‰, as shown in Fig. 2a), whereas the minimum occurs during MIS MG7 (the peak interglacial sea level during our modeled time period, with a δ18O value of 2.89 ‰, as shown in Fig. 2a).
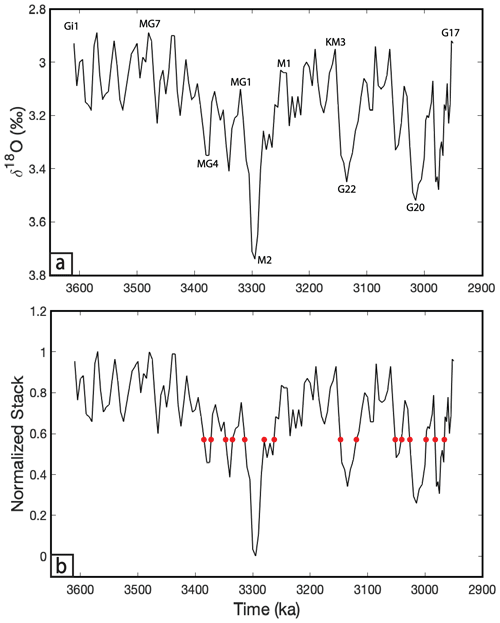
Figure 2The time series used in the model simulations. (a) The LR04 δ18O isotope stack (Lisiecki and Raymo, 2005), extending from 3610 to 2950 ka, with labeled Marine Isotope Stage names. (b) A normalized version of the time series in panel (a), constructed as described in the main text. All points in the time series with the same normalized value have an identical ice geometry (e.g., red points represent times with a normalized value of 0.6 and precisely the same modeled ice geometry).
Next, we adopted a series of Pliocene ice geometries taken from the hybrid ice-sheet–climate model results of Berends et al. (2019b). These included snapshots of the EIS, the GrIS, the NAIS, and Antarctica taken during MIS M2 and MIS KM3 (Fig. 3), as well as ∼ 25 snapshots obtained for several intervening sea-level-equivalent ice volumes. Where the maximum M2 sea-level-equivalent (SLE) ice volume was greater than the Berends et al. (2019b) output (e.g., ∼ 34 m SLE from the NAIS), additional snapshots with larger ice volumes were sourced from Berends et al. (2018), e.g., those for the Last Glacial Maximum. The Antarctica ice geometries were first split along the Transantarctic Mountains to produce separate EAIS and WAIS geometries. The EAIS geometries were further broken down based on underlying topography to delineate the Aurora Basin, Wilkes Basin, and Prydz Bay subregions. Additionally, at the MIS MG7 sea-level highstand, all ice sheets, except for the EAIS, are modeled as entirely deglaciated. For the EAIS, peak interglacial melting only involved the ice sheet's marine-based portion; the land-based EAIS (∼ 47 m SLE) always remained during model interglacials (with the geometry based on the “PRISM” ice-sheet configuration from Dowsett et al., 2010).
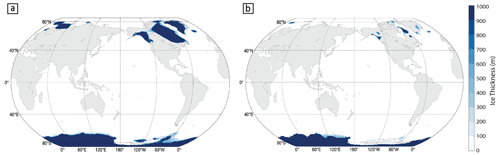
Figure 3Modeled Pliocene ice cover during (a) MIS M2 and (b) MIS KM3. Geometries are based on the hybrid ice-sheet–climate model outputs of Berends et al. (2019b), as described in the text. Note that in this study, each region was modeled separately, but for brevity, the ice-sheet extents are combined in this figure.
We used the benthic oxygen isotope stack from Lisiecki and Raymo (2005) (Fig. 2a) to model time variation in ice volumes from ∼ 300 kyr prior to MIS M2 (i.e., ∼ 3.6 Ma) to ∼ 200 kyr after MIS KM3 (2.95 Ma). (Ice-volume changes prior to this period would have not impacted predictions of sea-level change occurring between MIS M2 and MIS KM3). Specifically, we normalized the magnitude of isotopic variation across this interval to a scale of 0.0–1.0 by subtracting the most depleted δ18O value (2.89 ‰ during MIS MG7) from the interval between ∼ 3.6 and 2.9 Ma; dividing the result by the maximum residual δ18O value corresponding to the MIS M2 glaciation (3.74–2.89 = 0.85 ‰); and, finally, subtracting the resulting value from 1.0. This normalized time series is shown in Fig. 2b. The SLE ice volumes, intermediate between the maximum (MIS M2) and minimum (MIS MG7) glacial conditions shown in Fig. 3, are assumed to scale linearly with the normalized δ18O time series, and ice geometries are smoothly interpolated across time steps of 1 kyr to accomplish this variation. The construction is performed under the additional constraint that the ice geometry is always the same for the same normalized δ18O value (e.g., the model ice geometries are identical at each of the times indicated by the red dots in Fig. 2b).
Finally, the global maps of sea-level change calculated for the ice melt scenarios are normalized by the GMSLP values associated with the respective scenarios (Table 1). Since the sea-level predictions are quasi-linearly related to the net ice mass flux, this normalization procedure yields maps that, outside the immediate vicinity of the melt zone, are relatively insensitive to GMSL changes or, equivalently, the total ice mass flux of the scenario. We demonstrate this insensitivity in the results below. The linearity also allows one to combine, with suitable weighting, the maps for individual melt zones to assess the connection between local-sea-level (LSL) change at any site and total GMSLP for any scenario of interest. This generality is an important point to emphasize because we make no assertion regarding the validity of the total melt volumes in each of the eight scenarios listed in Table 1, and our main conclusions regarding biases in the mapping between local and global sea levels are insensitive to these melt volumes.
With respect to the normalized δ18O time series utilized in this study, there are uncertainties in the LR04-stack-derived frequency and amplitude of glacial–interglacial cycles from 3.3–3 Ma. The stack was put together using 57 different benthic δ18Ocarb and ratios (Lisiecki and Raymo, 2005) and is complicated by uncertainties in fossil species and proxy-specific calibrations, alteration due to diagenesis, and changes in seawater chemistry (Raymo et al., 2018). Additionally, studies of iceberg-rafted debris from areas proximal to the EAIS suggest that, unlike δ18O records from the 3.3–3 Ma time period, glacial–interglacial cycles were not paced by obliquity (40 kyr) but instead by precession (23 kyr; Patterson et al., 2014). Therefore, to accommodate these uncertainties, we performed sensitivity analyses in which we shortened the time duration between MIS M2 and MIS KM3 from 140 to 120 kyr or randomly perturbed the magnitude of the smaller sea-level oscillations between the two Marine Isotope Stages (Fig. 2).
Figure 4 shows maps of sea-level change computed for the eight different regional ice histories, each normalized by the GMSLP value associated with the respective ice history (Table 1). These plots can be interpreted as viscoelastic fingerprints that include both viscous and elastic effects over the period from MIS M2 to MIS KM3. (The term “viscoelastic fingerprints” is used to distinguish the maps from commonly published elastic fingerprints, which are computed for melt events rapid enough for viscous effects to be ignored).
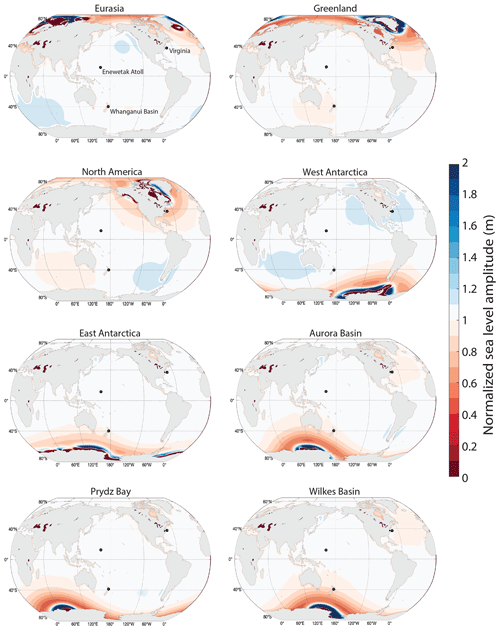
Figure 4Predicted sea-level change from MIS M2 to MIS KM3 for eight different regional ice histories (as labeled above each panel). Predictions are based on the reference viscoelastic Earth model described in the text and, to facilitate comparison, are normalized by the GMSLP value associated with each simulation (Table 1). The three black dots in each panel show the locations of continental-shelf and upper-slope sites discussed in the text.
The normalized maps in Fig. 4 show similar structures in relation to the zones of ice mass flux. In the area once covered by ice, a sea-level fall of high magnitude (off the scale of the plot) is predicted, and as one considers sites progressively further from this region, zones of sea-level rise (blue), which also reach amplitudes off the scale, and zones of sea-level fall (light to dark red) are predicted. Superimposed on these trends is a so-called “quadrantal” sea-level pattern (with a spherical harmonic degree of 2 and an order of 1) due to true polar wander (TPW; Milne and Mitrovica, 1996). TPW contributes to a sea-level fall in the quadrant encompassing ice melt and the anti-polar quadrant, and it contributes to a sea-level rise in the remaining two quadrants. As an example, melting over Laurentia contributes to a TPW-induced sea-level fall over North America and the southern Indian Ocean and to a sea-level rise centered over southern South America and southeastern Asia.
Putting aside the TPW signal, the origin of the complex trends in predicted sea-level change as one moves from the near field to the far field of an ice sheet (Fig. 4), characterized by several changes in sign, is captured in the schematic of Fig. 1. The total change in sea level can be understood as having two contributions. First, a reduction in the ice mass from MIS M2 to MIS KM3 leads to a migration of water from the near field to the far field as the gravitational pull of the ice sheet weakens. This leads to a long-wavelength tilting of the sea surface up toward the far field, as shown in Fig. 1b (wavy blue line). Second, superimposed on this gravitational signal is viscous deformation, comprised of post-glacial rebound in the zone of ice retreat (zone 1), subsidence of a peripheral bulge (zone 2), and relatively minor crustal subsidence due to ocean loading (zone 3). In zone 1, post-glacial rebound and the loss of gravitational pull on the ocean combine constructively to produce a sea-level fall with a peak amplitude more than 10 times greater than the GMSL rise throughout the ice history, shown in red (largely covered by the continental mask used in Fig. 4. In zone 2, peripheral subsidence is of a greater magnitude compared to the water migration away from the near field, and the result is a predicted sea-level rise, as shown in the maps in Fig. 4 (blue contours). In zone 3, the opposite happens: the long-wavelength tilting of the sea surface (and the migration of water) due to the loss of gravitational pull toward the ice sheet once again dominates crustal subsidence, and a sea-level fall is predicted (red zones encircling the blue zones). In zone 3, the predicted sea-level fall also has a contribution from ocean syphoning, i.e., the movement of water away from these regions into the accommodation created primarily by the subsiding peripheral bulges (Mitrovica and Milne, 2002). Finally, water migration into zone 4 dominates other effects, and sea-level rise occurs.
As discussed in the Introduction, the normalization procedure applied in each scenario within Fig. 4 should yield maps that are relatively insensitive to changes in the net volume of melt if the geometry of the ice melt is not fundamentally altered. To highlight this issue, Fig. S1 in the Supplement shows a map analogous to the NAIS scenario in Fig. 4, with the exception that we adopted a melt model with a GMSLP value of 7.71 m. Outside of the region, in the near vicinity of the mass flux, the two normalized maps show nearly identical structures. Of course, the sensitivity is larger at sites close to the mass flux, as we discuss below. Additionally, the sensitivity analyses with a 120 kyr time duration and smaller sea-level oscillations between MIS M2 and MIS KM3 (Fig. 2) revealed that the normalized sea-level maps were negligibly impacted.
The viscoelastic-fingerprint maps in Fig. 4 exhibit significant departures from GMSLs for the period extending from the MIS M2 glacial maximum to the MIS KM3 glacial minimum. The geographic pattern of these departures is governed by the location of the modeled ice melt, and we next turn to the implications of this variability on inferences of the total amplitude of GMSL change that might be derived from local geological indicators of sea-level change. To broaden our assessment of this issue, we incorporated the 27 additional simulations of variable lithospheric thicknesses and mantle viscosities discussed above (see the Methods section for values). Figure 5 shows, for all eight regional ice histories, the full range of normalized sea-level predictions for all 27 Earth models at three sites that host MPWP stratigraphic indicators – one in the near field of Northern Hemisphere ice sheets (Virginia), one in the near field of Antarctica (Whanganui Basin), and one in the far field of all ice sheets (Enewetak Atoll). We note that an inference of sea-level change across the interval from MIS M2 to MIS KM3 has only been made for the Whanganui Basin (Grant et al., 2019); the two additional locales offer an illustration of how the predicted amplitude of local sea-level change across the modeled interval from MIS M2 to MIS KM3 would deviate from GMSLP for the scenarios considered here. The range of the 27 predictions, each normalized by the GMSLP value of the respective scenario, is summarized by the box-and-whisker plots (Fig. 5). The black circle within each box-and-whisker plot refers to the value of sea-level change for the reference Earth model and the individual ice sheet, while the black line represents the median value for all 27 Earth models for an individual ice sheet. The normalization procedure allows us to meaningfully compare the results across these models.
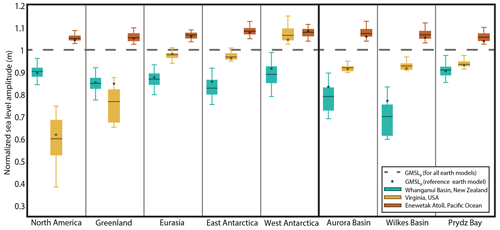
Figure 5Sea-level changes predicted for MIS M2 to MIS KM3 across three geographic sites (see the inset key and Fig. 4 for locations), based upon a range of melt models and viscoelastic Earth models. The box-and-whisker plots show the range of results generated using the 27 different viscoelastic models (discussed in the text). All predictions are normalized by the global mean change, GMSLP, associated with the specific melt and Earth models. The dashed line denotes the result that would occur if the prediction matched the associated GMSLP value; thus, departures from 1.0 represent normalized (fractional) departures from the global mean change in sea level, as defined by Pan et al. (2021).
Predictions obtained at Enewetak Atoll, in the very far field of ice mass changes, are consistently ∼ 0 %–15 % greater than the GMSLP values (Fig. 5). This site is within zone 4 (Fig. 1), but the predictions are influenced in some simulations by rotational effects (Fig. 4). The predictions of sea-level change for the Whanganui Basin have a larger spread than those for Enewetak Atoll and are consistently below the global mean (GMSLP) for all melt models and that for all Earth models. In the case of melting in the Northern Hemisphere (e.g., the EIS, GrIS, and NAIS melt models), the departure from GMSLP is dominated by the sea-level fall associated with rotational effects (Fig. 4). These effects also contribute to the results for Southern Hemisphere melt models, but in those cases, the migration of water away from the zones of melt tends to dominate (zone 3 in Fig. 1), particularly in the case of melt from the Aurora and Wilkes basins (Figs. 4 and 5). In these melt zones, local predictions obtained at the Whanganui Basin vary from ∼ 60 %–98 % of the global mean value. Finally, the predictions obtained in Virginia, on the United States East Coast, show even greater sensitivity to the location of melt. In the simulations involving melt from the NAIS or GrIS, the prediction is dominated by the migration of water away from the area of melt (zone 3 in Fig. 1) and rotational effects, which lead to a sea-level change substantially lower than GMSLP (Fig. 5). Rotational effects dominate the departure from the global mean and contribute to a sea-level fall for all cases of melt within East Antarctica and to a sea-level rise for melt sourced from West Antarctica. We emphasize that these three sites are chosen as illustrative case studies and that the maps in Fig. 4 can be used to assess the relationship between LSL and GMSLP for any site and any of the eight melt scenarios.
As a further illustration of the utility of the maps in Fig. 4, Fig. 6 plots the maximum discrepancy of computed sea-level change from the total GMSLP value based on the reference Earth model and the following unweighted combinations of ice melt models: (1) the GrIS, WAIS, and EAIS (Fig. 6a) and (2) the NAIS, EIS, GrIS, WAIS, and marine-based EAIS (Fig. 6b). (One can repeat the same exercise with any weighted combination of the maps from Fig. 4.) The first combination of ice melt sources reflects the view that only the modern-day ice sheets contributed to melt from MIS M2 to the KM3 interglacial. The second combination incorporates contributions from two additional ice sheets (the NAIS and EIS) across this time period since recent studies have included NAIS and EIS contributions to the sea-level budget (Berends et al., 2019a; LeBlanc et al., 2021). The two maps identify geographic regions in which LSL variation might provide the closest measure of GMSL change from MIS M2 to MIS KM3. For both scenarios, the maximum discrepancy is highest within the near field of the modeled ice mass flux (with both scenarios yielding discrepancies greater than 20 % along, for example, the Antarctic coastline) and lowest in equatorial regions in the far field. In both scenarios, areas in the Indian Ocean extending from Indonesia to Papua New Guinea, the region of the South Pacific Ocean extending from 180–150° W, and some equatorial coastlines are predicted to have experienced a sea-level change from MIS M2 to MIS KM3 within 5 % of the global mean value. In contrast, the discrepancy is large (> 10 %) along the remaining global coastline. Additionally, at Enewetak Atoll and the Whanganui Basin, the scenarios yield consistent deviations from GMSLP of up to 15 % (Fig. 6). (Note that for the Whanganui Basin, the colored area indicating 15 % is partially obscured by the land mask). These discrepancies, and indeed the departure from GMSLP for any other combinations of melt sources at these sites, can be inferred from the individual ice-sheet results provided in Fig. 5.

Figure 6The maximum percentage discrepancy in the reference viscoelastic Earth model's predictions of LSL change for GMSLP from MIS M2 to MIS KM3. The following scenarios of ice melt locations are commonly presented in the published literature: panel (a) corresponds to Greenland, West Antarctica, and marine-based East Antarctica, and panel (b) corresponds to North America, Eurasia, Greenland, West Antarctica, and East Antarctica.
Since the Whanganui Basin is the only site with a published estimate of sea-level change over the deglaciation from MIS M2 to MIS KM3 (Grant et al., 2019), we further explored the discrepancy between GMSLs and LSLs at this site. It is clear from Fig. 5 that any inference of the LSL change at this site will always be smaller than the GMSLP value. To highlight possible departures of site-specific observations from GMSLP, Fig. 7 includes five example scenarios in which combinations of ice-sheet melt, in conjunction with the reference Earth model, predict an LSL rise of ∼ 15 m amplitude over this deglaciation at the Whanganui Basin. The five scenarios presented in Fig. 7 were chosen to represent one set of commonly accepted sources of Pliocene ice-sheet melt (Fig. 7a), a scenario that excludes ice-sheet contributions from North America (Fig. 7b) and East Antarctica (Fig. 7c), and two scenarios that include melt from all ice sheets (Fig. 7d–e). Bar plots (Fig. 7f) provide the GMSLP values for the individual ice sheets in the given scenarios (Fig. 7a–e), as well as the total GMSLP value. This result emphasizes the systematic difference between LSL change at the Whanganui Basin and GMSL values. In these scenarios, the 15 m LSL change at the Whanganui Basin is consistently ∼ 12 % lower than the GMSLP values (16.94, 17.07, 16.92, 17.00, and 17.01 m, respectively, as shown in Fig. 7f).
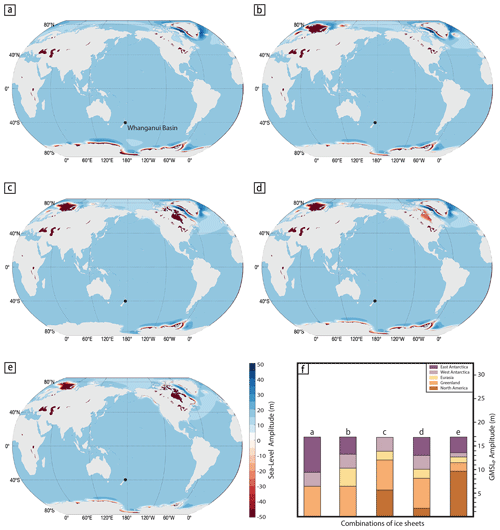
Figure 7Catalog of ice-sheet combinations that produce a LSL change of 15 m amplitude at the Whanganui Basin, New Zealand. (a–e) Global maps of total sea-level change from the MIS M2 glacial to the MIS KM3 interglacial for the five scenarios of ice-sheet melt. Panel (f) shows the global mean change (GMSLP) associated with each of the five melt scenarios and the contributions to the GMSLP values from the regions of melt.
Our analysis has highlighted the geographically variable change in sea level associated with a variety of potential meltwater sources for a major MPWP glacial–interglacial cycle. This variability provides a direct measure of the departure of LSL rise from the global mean change observed anywhere in the global ocean (Fig. 4), including sites that have contributed to estimates of peak and glacial-cycle sea-level change during the MPWP. Discussions about this departure require a robust and transparent definition of GMSL change. The definition we have adopted, GMSLP, involves dividing the total meltwater volume that enters the open ocean outside any exposed marine-based sectors from MIS M2 to MIS KM3 by the area of the ocean (Fig. 1). The appropriateness of this choice is suggested by the normalized sea-level change maps in Fig. 4, which are all characterized by values within a few percent of 1.0 along the Equator. (Mean equatorial ocean values with respect to the normalized maps in Fig. 4 are provided for Eurasia (0.9870), Greenland (0.9695), North America (0.9703), West Antarctica (1.0150), East Antarctica (1.0000), the Aurora Basin (0.9807), Prydz Bay (0.9835), and the Wilkes Basin (0.9717).) That is, at sites furthest from the deformational, gravitational, and rotational effects of GIA, the calculated sea-level change reflects the GMSL change.
Other definitions of GMSL change are, of course, possible. Figure S2 extends Fig. 1 to include two other possibilities. The first, GMSLIAF, involves spreading the ice volume above floatation, as defined at the start of MIS M2, over the global ocean. This ignores the flux of water from exposed marine sectors, which will be a significant limitation given the time duration of the MPWP interval we are considering (∼ 140 kyr) in scenarios with considerable ice-sheet retreat from these sectors. The second definition, GMSLS, takes the full volume of meltwater present between MIS M2 and MIS KM3 and spreads it over the ocean. As in the case of GMSLP, the area of ocean used in the calculation (i.e., whether or not the marine sector is included) will have an effect on GMSLS of ∼ 1 % or less. One can interpret GMSLS as a special case of GMSLP, in which any exposed marine-based sectors rebound sufficiently in the calculation of GMSLP to become subaerial. This will, of course, depend on the volume of the marine accommodation space relative to the total post-glacial uplift of the crust from MIS M2 to MIS KM3. Table 1 also shows the GMSLS values computed for the ice histories described above. The limitation of adopting this definition is most pronounced in the results for West Antarctica, where substantial marine-based regions are exposed throughout the ice history. The difference in the GMSL calculations (4.07–2.92 ≈ 1.15 m) largely reflects, in the calculation of GMSLP, the volume of meltwater that remains during MIS KM3 in the marine-based sectors, which were exposed by the retreat of grounded ice from MIS M2 to MIS KM3. If one were to use GMSLS instead of GMSLP, then the normalized map of the WAIS scenario given in Fig. 4 would show values of ∼ 0.7 (2.92/4.07) rather than 1.0 near the Equator, i.e., the far field, which suggests that GMSLS is not an appropriate metric for GMSL change in this case. The metric GMSLP yields values intermediate between GMSLIAF and GMSLS, and all three definitions of GMSL change will be identical in the case where no grounded marine-based ice is involved in an ice melt scenario. The latter is close to being the case in the GrIS scenario we have adopted.
The Whanganui Basin hosts a well-preserved Pliocene continental-shelf stratigraphy (Naish and Wilson, 2009). Assuming the modern wave climate is similar to the Pliocene climate, Grant et al. (2019) applied a theoretical relationship between modern sediment transport by waves and water depth to temporal variation in grain size in Pliocene core and outcrop samples. This method applied a two-dimensional backstripping method to correct for the effects of tectonic subsidence and sediment compaction in order to estimate the amplitude of LSL change as 13 ± 5 m from MIS M2 to MIS KM3. Grant et al. (2019) noted that, while their analysis strictly provided a measure of local RSL change, their modeling of GIA indicated that the reconstruction also serves as a good approximation of GMSL and, thus, ice-volume fluctuation. The results of Figs. 4–7 indicate that this local measurement will be lower than the associated GMSLP value by an average of ∼ 15 %.
Beyond a robust estimate of GMSL change over the deglaciation from MIS M2 to MIS KM3, a further goal of MPWP paleo-sea-level studies is to constrain the sources of ice mass flux and their relative contributions. For a given site, the greater (smaller) the spread of the box-and-whisker-plot predictions across the various melt scenarios (Fig. 5), the greater (lower) the ability of the observation, when viewed in combination with other observations, to constrain the contributors to sea-level change from the MIS M2 glacial to the MIS KM3 interglacial. As an example, an accurate observation obtained at Enewetak Atoll would provide a powerful constraint on GMSLP because all melt zones provide a consistent scale factor between LSL change and GMSLP. Yet this consistency indicates, conversely, that this datum provides no discriminatory information on the melt source(s). Combining an observation obtained at Enewetak Atoll with one collected in Virginia and/or at the Whanganui Basin might both yield a strong constraint on GMSLP and narrow the possible sources of melt. Further exploration of the results in Fig. 4 will provide other potential sites that could contribute to establishing such constraints in future work.
The code and data for the ice and sea-level models, as well as the code used to produce the figures, is available at https://doi.org/10.5281/zenodo.14233782 (King et al., 2024).
The supplement related to this article is available online at: https://doi.org/10.5194/cp-21-53-2025-supplement.
MEK, JRC, and JXM designed the study, and MEK performed all the simulations. MEK prepared the paper and figures with contributions from JRC and JXM.
The contact author has declared that none of the authors has any competing interests.
Publisher’s note: Copernicus Publications remains neutral with regard to jurisdictional claims made in the text, published maps, institutional affiliations, or any other geographical representation in this paper. While Copernicus Publications makes every effort to include appropriate place names, the final responsibility lies with the authors.
We thank Constantijn J. Berends for the MPWP ice snapshots. We also thank Tim R. Naish and an anonymous reviewer for their constructive comments, which improved this paper. The sea-level code was written by Sam Goldberg, University of Miami (https://doi.org/10.5281/zenodo.14233782, King et al., 2024).
This research was made possible by the US National Science Foundation (award no. 2046244), a Geological Society of America (GSA) Graduate Student Research Grant, and the Oregon State University George and Danielle Sharp Fellowship.
This paper was edited by Alessio Rovere and reviewed by Tim Naish and one anonymous referee.
Austermann, J., Mitrovica, J. X., Huybers, P., and Rovere, A.: Detection of a dynamic topography signal in last interglacial sea-level records, Science Advances, 3, e1700457, https://doi.org/10.1126/sciadv.1700457, 2017.
Berends, C. J., de Boer, B., and van de Wal, R. S. W.: Application of HadCM3@Bristolv1.0 simulations of paleoclimate as forcing for an ice-sheet model, ANICE2.1: set-up and benchmark experiments, Geosci. Model Dev., 11, 4657–4675, https://doi.org/10.5194/gmd-11-4657-2018, 2018.
Berends, C. J., de Boer, B., Dolan, A. M., Hill, D. J., and van de Wal, R. S. W.: Modelling ice sheet evolution and atmospheric CO2 during the Late Pliocene, Clim. Past, 15, 1603–1619, https://doi.org/10.5194/cp-15-1603-2019, 2019a.
Berends, C. J., de Boer, B., Dolan, A. M., Hill, D. J., and van de Wal, R. S. W.: Berends_etal_2019_GMD_supplement, Zenodo [data set], https://doi.org/10.5281/zenodo.2598292, 2019b.
Clarke, G. K. and Marshall, S. J.: Isotopic balance of the Greenland Ice Sheet: modelled concentrations of water isotopes from 30,000 BP to present, Quaternary Sci. Rev., 21, 419–430, https://doi.org/10.1016/S0277-3791(01)00111-1, 2002.
de Boer, B., Haywood, A. M., Dolan, A. M., Hunter, S. J., and Prescott, C. L.: The transient response of ice volume to orbital forcing during the warm late Pliocene, Geophys. Res. Lett., 44, 10486–10494, https://doi.org/10.1002/2017GL073535, 2017.
DeConto, R. M. and Pollard, D.: Contribution of Antarctica to past and future sea-level rise, Nature, 531, 591–597, https://doi.org/10.1038/nature17145, 2016.
Dowsett, H. J. and Cronin, T. M. High eustatic sea level during the middle Pliocene: Evidence from the southeastern US Atlantic Coastal Plain, Geology, 18, 435–438, https://doi.org/10.1130/0091-7613(1990)018<0435:HESLDT>2.3.CO;2, 1990.
Dowsett, H., Robinson, M., Haywood, A. M., Salzmann, U., Hill, D., Sohl, L. E., Chandler, M., Williams, M., Foley, K., and Stoll, D. K.: The PRISM3D paleoenvironmental reconstruction, Stratigraphy, 7, 123–139, https://doi.org/10.29041/strat.07.2.03, 2010.
Dumitru, O. A., Austermann, J., Polyak, V. J., Fornós, J. J., Asmerom, Y., Ginés, J., Ginés, A., and Onac, B. P.: Constraints on global mean sea level during Pliocene warmth, Nature, 574, 233–236, https://doi.org/10.1038/s41586-019-1543-2, 2019.
Dutton, A., Carlson, A. E., Long, A. J., Milne, G. A., Clark, P. U., DeConto, R., Horton, B. P., Rahmstorf, S., and Raymo, M. E.: Sea-level rise due to polar ice-sheet mass loss during past warm periods, Science, 349, aaa4019, https://doi.org/10.1126/science.aaa4019, 2015.
Dwyer, G. S. and Chandler, M. A.: Mid-Pliocene sea level and continental ice volume based on coupled benthic palaeotemperatures and oxygen isotopes, Philos. T. R. Soc. A, 367, 157–168, https://doi.org/10.1098/rsta.2008.0222, 2009
Dziewonski, A. M. and Anderson, D. L.: Preliminary reference Earth model, Phys. Earth Planet. In., 25, 297–356, https://doi.org/10.1016/0031-9201(81)90046-7, 1981.
Grant, G. R., Naish, T. R., Dunbar, G. B., Stocchi, P., Kominz, M. A., Kamp, P. J., Tapia, C. A., McKay, R. M., Levy, R. H., and Patterson, M. O.: The amplitude and origin of sea-level variability during the Pliocene epoch, Nature, 574, 237–241, https://doi.org/10.1038/s41586-019-1619-z, 2019.
Haywood, A. M., Dowsett, H. J., Robinson, M. M., Stoll, D. K., Dolan, A. M., Lunt, D. J., Otto-Bliesner, B., and Chandler, M. A.: Pliocene Model Intercomparison Project (PlioMIP): experimental design and boundary conditions (Experiment 2), Geosci. Model Dev., 4, 571–577, https://doi.org/10.5194/gmd-4-571-2011, 2011.
Haywood, A. M., Hill, D. J., Dolan, A. M., Otto-Bliesner, B. L., Bragg, F., Chan, W.-L., Chandler, M. A., Contoux, C., Dowsett, H. J., Jost, A., Kamae, Y., Lohmann, G., Lunt, D. J., Abe-Ouchi, A., Pickering, S. J., Ramstein, G., Rosenbloom, N. A., Salzmann, U., Sohl, L., Stepanek, C., Ueda, H., Yan, Q., and Zhang, Z.: Large-scale features of Pliocene climate: results from the Pliocene Model Intercomparison Project, Clim. Past, 9, 191–209, https://doi.org/10.5194/cp-9-191-2013, 2013.
Hearty, P. J., Rovere, A., Sandstrom, M. R., O'Leary, M. J., Roberts, D., and Raymo, M. E. Pliocene-Pleistocene Stratigraphy and Sea-Level Estimates, Republic of South Africa With Implications for a 400 ppmv CO2 World, Paleoceanography and Paleoclimatology, 35, e2019PA003835, https://doi.org/10.1029/2019PA003835, 2020.
James, N. P., Bone, Y., Carter, R. M., and Murray-Wallace, C. V.: Origin of the late Neogene Roe Plains and their calcarenite veneer: Implications for sedimentology and tectonics in the Great Australian Bight, Aust. J. Earth Sci., 53, 407–419, https://doi.org/10.1080/08120090500499289, 2006.
Kaufman, D. S. and Brigham-Grette, J.: Aminostratigraphic correlations and paleotemperature implications, Pliocene-Pleistocene high-sea-level deposits, northwestern Alaska, Quaternary Sci. Rev., 12, 21–33, https://doi.org/10.1016/0277-3791(93)90046-O, 1993.
Kendall, R. A., Mitrovica, J. X., and Milne, G. A.: On post-glacial sea level–II, Numerical formulation and comparative results on spherically symmetric models, Geophys. J. Int., 161, 679–706, https://doi.org/10.1111/j.1365-246X.2005.02553.x, 2005.
King, M., Creveling, J., and Mitrovica, J.: meghan-king/plioceneSeaLevel: Data and code release for “The geometry of sea-level change across a mid-Pliocene glacial cycle”, Zenodo [code and data set], https://doi.org/10.5281/zenodo.14233782, 2024.
Krantz, D. E.: A chronology of Pliocene sea-level fluctuations: The US Middle Atlantic Coastal Plain record, Quaternary Sci. Rev., 10, 163–174, https://doi.org/10.1016/0277-3791(91)90016-N, 1991.
Lambeck, K., Rouby, H., Purcell, A., Sun, Y., and Sambridge, M.: Sea level and global ice volumes from the Last Glacial Maximum to the Holocene, P. Natl. Acad. Sci. USA, 111, 15296–15303, https://doi.org/10.1073/pnas.1411762111, 2014.
LeBlanc, D. E.: Cosmogenic nuclides in ocean mud inform ice sheet history, Nature Reviews Earth & Environment, 2, 664–664, https://doi.org/10.1038/s43017-021-00220-5, 2021.
Lisiecki, L. E. and Raymo, M. E.: A Pliocene-Pleistocene stack of 57 globally distributed benthic δ18O records, Paleoceanography, 20, PA1003, https://doi.org/10.1029/2004PA001071, 2005.
Miller, K. G., Wright, J. D., Browning, J. V., Kulpecz, A., Kominz, M., Naish, T. R., Cramer, B. S., Rosenthal, Y., Pelteir, R., and Sosdian, S: High tide of the warm Pliocene: Implications of global sea level for Antarctic deglaciation, Geology, 40, 407–410, https://doi.org/10.1130/G32869.1, 2012.
Miller, K. G., Browning, J. V., Schmelz, W. J., Kopp, R. E., Mountain, G. S., and Wright, J. D.: Cenozoic sea-level and cryospheric evolution from deep-sea geochemical and continental margin records, Science Advances, 6, eaaz1346, https://doi.org /10.1126/sciadv.aaz1346, 2020.
Milne, G. A. and Mitrovica, J. X.: Postglacial sea-level change on a rotating Earth: first results from a gravitationally self-consistent sea-level equation, Geophys. J. Int., 126, F13–F20, https://doi.org/10.1111/j.1365-246X.1996.tb04691.x, 1996.
Mitrovica, J. X. and Forte, A. M.: A new inference of mantle viscosity based upon joint inversion of convection and glacial isostatic adjustment data, Earth Planet. Sc. Lett., 225, 177–189, https://doi.org/10.1016/j.epsl.2004.06.005, 2004.
Mitrovica, J. X. and Milne, G. A.: On the origin of Late Holocene highstands within equatorial ocean basis, Quaternary Sci. Rev., 21, 2179–2190, https://doi.org/10.1016/S0277-3791(02)00080-X, 2002.
Mitrovica, J. X. and Milne, G. A.: On post-glacial sea level: I. General theory, Geophys. J. Int., 154, 253–267, https://doi.org/10.1046/j.1365-246X.2003.01942.x, 2003.
Mitrovica, J. X., Wahr, J., Matsuyama, I., and Paulson, A.: The rotational stability of an ice-age earth, Geophys. J. Int., 161, 491–506, https://doi.org/10.1111/j.1365-246X.2005.02609.x, 2005.
Mix, A. C.: The oxygen-isotope record of glaciation, in: North America and adjacent oceans during the last deglaciation, edited by: W. F. Ruddiman and H. E. Wright, 111–135, https://doi.org/10.1130/DNAG-GNA-K3.111, 1987.
Naish, T. R. and Wilson, G. S.: Constraints on the amplitude of Mid-Pliocene (3.6–2.4 Ma) eustatic sea-level fluctuations from the New Zealand shallow-marine sediment record, Philos. T. R. Soc. A, 367, 169–187, https://doi.org/10.1098/rsta.2008.0223, 2009.
Pagani, M., Liu, Z., LaRiviere, J., and Ravelo, A. C.: High Earth-system climate sensitivity determined from Pliocene carbon dioxide concentrations, Nat. Geosci., 3, 27–30, https://doi.org/10.1038/ngeo724, 2010.
Pan, L., Powell, E. M., Latychev, K., Mitrovica, J. X., Creveling, J. R., Gomez, N., Hoggard, M. J., and Clark, P. U.: Rapid postglacial rebound amplifies global sea level rise following West Antarctic Ice Sheet collapse, Science Advances, 7, eabf7787, https://doi.org/10.1126/sciadv.abf7787, 2021.
Pan, L., Milne, G. A., Latychev, K., Goldberg, S. L., Austermann, J., Hoggard, M. J., and Mitrovica, J. X.: The influence of lateral Earth structure on inferences of global ice volume during the Last Glacial Maximum, Quaternary Sci. Rev., 290, 107644, https://doi.org/10.1016/j.quascirev.2022.107644, 2022.
Patterson, M. O., McKay, R., Naish, T. R., Escutia, C., Jimenez- Espejo, F. J., Raymo, M. E., Meyers, S. R., Tauxe, L., Brinkhuis, H., and IODP Expedition 318 Scientists: Orbital forcing of the East Antarctic ice sheet during the Pliocene and Early Pleistocene, Nat. Geosci., 7, 841–847, 2014.
Peltier, W. R.: The impulse response of a Maxwell Earth, Rev. Geophys., 12, 649–669, https://doi.org/10.1029/RG012i004p00649, 1974.
Raymo, M. E., Mitrovica, J. X., O'Leary, M. J., DeConto, R. M., and Hearty, P. J.: Departures from eustasy in Pliocene sea-level records, Nat. Geosci., 4, 328–332, https://doi.org/10.1038/ngeo1118, 2011.
Raymo, M. E., Kozdon, R., Evans, D., Lisiecki, L., and Ford, H. L.: The accuracy of mid-Pliocene δ18O-based ice volume and sea level reconstructions, Earth-Sci. Rev., 177, 291–302, https://doi.org/10.1016/j.earscirev.2017.11.022, 2018.
Richards, F. D., Coulson, S. L., Hoggard, M. J., Austermann, J., Dyer, B., and Mitrovica, J. X.: Geodynamically corrected Pliocene shoreline elevations in Australia consistent with midrange projections of Antarctic ice loss, Science Advances, 9, eadg3035, https://doi.org/10.1126/sciadv.adg3035, 2023.
Rovere, A., Raymo, M. E., Mitrovica, J. X., Hearty, P. J., O'Leary, M. J., and Inglis, J. D.: The Mid-Pliocene sea-level conundrum: Glacial isostasy, eustasy and dynamic topography, Earth Planet. Sc. Lett., 387, 27–33, https://doi.org/10.1016/j.epsl.2013.10.030, 2014.
Rowley, D. B., Forte, A. M., Moucha, R., Mitrovica, J. X., Simmons, N. A., and Grand, S. P.: Dynamic topography change of the eastern United States since 3 million years ago, Science, 340, 1560–1563, https://doi.org/10.1126/science.1229180, 2013.
Rohling, E. J., Foster, G. L., Grant, K. M., Marino, G., Roberts, A. P., Tamisiea, M. E., and Williams, F.: Sea-level and deep-sea-temperature variability over the past 5.3 million years, Nature, 508, 477–482, https://doi.org/10.1038/nature13230, 2014
Sandstrom, M. R., O'Leary, M. J., Barham, M., Cai, Y., Rasbury, E. T., Wooton, K. M., and Raymo, M. E.: Age constraints on surface deformation recorded by fossil shorelines at Cape Range, Western Australia, Bulletin, 133, 923–938, https://doi.org/10.1130/B35564.1, 2021.
Sarnthein, M., Bartoli, G., Prange, M., Schmittner, A., Schneider, B., Weinelt, M., Andersen, N., and Garbe-Schönberg, D.: Mid-Pliocene shifts in ocean overturning circulation and the onset of Quaternary-style climates, Clim. Past, 5, 269–283, https://doi.org/10.5194/cp-5-269-2009, 2009.
Siddall, M., Rohling, E. J., Thompson, W. G., and Waelbroeck, C.: Marine isotope stage 3 sea level fluctuations: Data synthesis and new outlook, Rev. Geophys., 46, RG4003, https://doi.org/10.1029/2007RG000226, 2008.
Sosdian, S. and Rosenthal, Y.: Deep-sea temperature and ice volume changes across the Pliocene-Pleistocene climate transitions, Science, 325, 306–310, https://doi.org/10.1126/science.1169938, 2009.
Waelbroeck, C., Labeyrie, L., Michel, E., Duplessy, J. C., Mcmanus, J. F., Lambeck, K., Balbon, E., and Labracherie, M.: Sea-level and deep water temperature changes derived from benthic foraminifera isotopic records, Quaternary Sci. Rev., 21, 295–305, https://doi.org/10.1016/S0277-3791(01)00101-9, 2002.
Wardlaw, B. R. and Quinn, T. M.: The record of Pliocene sea-level change at Enewetak Atoll, Quaternary Sci. Rev., 10, 247–258, https://doi.org/10.1016/0277-3791(91)90023-N, 1991.
Winnick, M. J. and Caves, J. K.: Oxygen isotope mass-balance constraints on Pliocene sea level and East Antarctic Ice Sheet stability, Geology, 43, 879–882, https://doi.org/10.1130/G36999.1, 2015
Zachos, J., Pagani, M., Sloan, L., Thomas, E., and Billups, K.: Trends, rhythms, and aberrations in global climate 65 Ma to present, Science, 292, 686–693, https://doi.org/10.1126/science.1059412, 2001.





