A global Data Assimilation of Moisture Patterns from 21 000–0 BP (DAMP-21ka) using lake level proxy records

Global hydroclimate significantly differed from modern climate during the mid-Holocene (6 ka) and Last Glacial Maximum (21 ka). Consequently, both periods have been described as either a partial or reverse analogue for current climate change. To reconstruct past hydroclimate, an offline paleoclimate data assimilation methodology is applied to a dataset of 216 lake status records which provide relative estimates of water level change. The proxy observations are integrated with the climate dynamics of two transient simulations (TraCE-21ka and HadCM3) using a multivariate proxy system model (PSM) which estimates relative lake status from available climate simulation variables. The resulting DAMP-21ka (Data Assimilation of Moisture Patterns 21 000–0 BP) reanalysis reconstructs annual lake status and precipitation values at 500-year resolution and represents the first application of the methodology to global hydroclimate on timescales spanning the Holocene and longer. Validation using Pearson's correlation coefficients indicates that the reconstruction (0.24) is more skillful, on average, than model simulations (0.09), particularly in portions of North America and east Africa, where data density is high and proxy–model disagreement is prominent during the Holocene. Results of the PSM and assimilation are used to evaluate climatic controls on lake status, spatiotemporal patterns of moisture variability, and proxy–model disagreement. During the mid-Holocene, wetter conditions are reconstructed for northern and eastern Africa, Asia, and southern Australia, but in contrast to the model prior, negative anomalies are observed in North America, resulting in drier-than-modern conditions throughout the Northern Hemisphere midlatitudes. Proxy–model disagreement in western North America may reflect a bias in model simulations to stronger sea level pressure gradients in the North Pacific during the mid-Holocene. The data assimilation framework is able to reconcile these differences by integrating the constraints of proxy observations with the dynamics of the model prior to produce a more robust estimation of hydroclimate variability during the past 21 000 years.

1 Introduction

During the past 21 000 years, hydroclimate varied significantly at global, regional, and local scales. These hydrologic changes are well documented by paleoclimate proxy data (e.g., Herzschuh et al., 2023; Shanahan et al., 2015; Street-Perrott et al., 1989) and explored with general circulation model (GCM) simulations (e.g., Bartlein et al., 1998; COHMAP Members, 1988; Harrison et al., 2015) and reflect thermodynamic and dynamic forcings associated with Milankovitch cycles of insolation, retreat of ice sheets, and warming temperature since the Last Glacial Maximum (LGM) (Davis and Brewer, 2009; Harrison et al., 2014; Sun et al., 2021b; Tierney et al., 2020). As a result of these large external forcings, many regions experienced drier or wetter conditions than present during portions of either the deglacial period (21–11.7 ka) or the Holocene (11.7 ka–present). For example, during the LGM, colder temperatures suppressed the hydrologic cycle, causing widespread aridity (Kageyama et al., 2021; Prentice and Jolly, 2000; Yung et al., 1996). However, these changes were not uniform. In regions such as the southwestern United States and southwestern Asia, lower evaporative demand and shifting storm tracks sustained lakes in basins that are dry today (Benson et al., 1990; Li and Zhang, 2020; McGee et al., 2018; Oster et al., 2015; Qin and Yu, 1998). During the early and mid-Holocene, intensified monsoon circulation was widespread throughout the Northern Hemisphere tropics (COHMAP Members, 1988; Zhao and Harrison, 2012), as typified by the African humid period (e.g., deMenocal et al., 2000; Lézine et al., 2011). These anomalies were anti-phased with Southern Hemisphere monsoon regions due to precessional forcing and shifts in the Intertropical Convergence Zone (ITCZ) position (Cheng et al., 2012; Deininger et al., 2020).

Proxy records and GCMs provide complementary information about hydroclimate changes in Earth's recent climate history; paleoclimate proxies integrate the observed environmental response and timing of climate events, whereas models simulate the dynamics associated with prescribed boundary conditions. Although these two data types generally indicate similar large-scale hydroclimate patterns, notable disagreements include Holocene trends in North America (Hermann et al., 2018; de Wet et al., 2023), underestimation of the African humid period by models (Brierley et al., 2020; Coe and Harrison, 2002; Jolly et al., 1998; Tierney et al., 2011), and uncertainty about the direction and magnitude of tropical precipitation anomalies during the LGM (Kageyama et al., 2021). To some extent, these differences reflect known biases in either data type, such as the effect of “no-analogue” environments on proxy calibration (Veloz et al., 2012) or the lack of dynamic vegetation, dust, and lakes in climate models (Lu et al., 2018; Pausata et al., 2016; Specht et al., 2022).

Paleoclimate data assimilation (DA) provides a framework to blend the independent information and strengths provided from each source of information. It does this by quantifying the covariance structure simulated by a model prior and updating the model estimates based on proxy data and their uncertainties, resulting in a gridded reconstruction which is constrained by both the proxy observations and dynamics of the GCM (Hakim et al., 2016). Previous DA applications to geologic timescales produced global datasets of Holocene and LGM–present (Osman et al., 2021) surface temperatures which integrate the temporal variability in proxy observations with the spatial completeness of model data. These results provide a variety of insights into past climate changes, including the relative role of different climate forcings (Osman et al., 2021), potential biases affecting the Holocene temperature conundrum (Erb et al., 2022), and Earth's equilibrium climate sensitivity (Tierney et al., 2020).

Despite extensive comparisons between GCM simulations and hydroclimate proxies during the LGM (e.g., Bartlein et al., 1998; Chevalier et al., 2017; COHMAP Members, 1988) and the Holocene (e.g., Brierley et al., 2020; Hancock et al., 2023; Tarasov et al., 1998), hydroclimate has not been assimilated globally on these timescales. Although model simulations may underestimate the magnitude of Holocene precipitation anomalies for some regions (Harrison et al., 2014; Lu et al., 2019; Morrill et al., 2019), a new data compilation for hydroclimate indicates that models and proxies are more likely to agree about the sign of regional anomalies for precipitation than temperature during the mid-Holocene for most regions (Hancock et al., 2023). These results suggest that some models can accurately simulate the structure of past moisture anomalies when the magnitude of change is significant.

At present, the longest DA-based global hydroclimate reconstruction is the Paleo Hydrodynamics Data Assimilation (PHYDA; Steiger et al., 2018) product of the Common Era (1 to 2000 CE). The PHYDA dataset and other Common Era dynamical DA reconstructions (King et al., 2023) provide valuable information about the inter-annual variability in gridded precipitation and associated hydroclimate indices during a relatively stable period in Earth's climate history. However, the Common Era represents a narrow range of climate states relative to the Holocene (Deininger et al., 2020; Shuman et al., 2018), LGM (Kageyama et al., 2021; Osman et al., 2021), and current warming (Cook et al., 2022; King et al., 2023). The past 2000 years also lacks information about changing hydrodynamics during time periods such as the early and mid-Holocene when Arctic warming was amplified (Miller et al., 2010; Thomas et al., 2018) and intensified monsoon circulation impacted the tropics (Cheng et al., 2012; Zhao and Harrison, 2012), both of which represent observed or projected features of modern climate change (Rantanen et al., 2022; Wang et al., 2021).

To fill this gap, we present a Data Assimilation of Moisture Patterns from 21 000–0 BP (DAMP-21ka) reanalysis, developed by assimilating lake status proxy records using transient simulations from two GCMs as priors. We define lake status as a relative estimate of water depth measured using percentile units and distinct from lake level, which can indicate the absolute surface elevation (Street-Perrott et al., 1989). Extending the reconstruction beyond the Common Era requires the use of different proxy records and proxy system models (PSMs) compared to PHYDA, which relies heavily on tree ring proxies that rarely extend beyond the past 2 millennia (Steiger et al., 2018). Over our timescales of interest (21–0 ka), lake status records in particular have several advantages, including (1) broad spatial distribution; (2) long duration; and, perhaps most importantly, (3) a clear and well-documented connection to hydrologic variability. To assimilate the lake status data, we develop and apply a simple lake status PSM (see Sect. 2.4) based on the framework described by Li and Morrill (2010).

The DAMP-21ka reanalysis reconstructs paleo-lake status, mean annual precipitation, and mean annual temperature. Results focus on the two hydrological variables, and temperature is primarily used to contextualize differences between lake status and precipitation. To reconstruct climate variables other than lake status, the data assimilation methodology relies on the covariance relationship of the simulations for quantifying the lake status relationship to precipitation or temperature between varying locations. These gridded results allow for two key advances in paleoclimate science: (1) a format enabling more direct comparison between the climate anomalies reconstructed in proxy data and simulated by GCMs and (2) the ability to examine plausible climate dynamics associated with observed proxy–model disagreement.

2 Data and methods

2.1 Proxy data

Proxy observations constrain past climate changes by recording environmental variability through a variety of potential pathways, but not all data can be utilized by the DA framework. The most significant requirement for assimilating proxy data is the ability to quantify the relationship between the observed proxy value and the climate state simulated by a GCM, and previous DA methodologies differ in their approach to this problem. Erb et al. (2022) selected data previously calibrated to temperature values which could therefore be directly compared to the output of GCMs. An alternative approach is to apply proxy system models (PSMs) to specific proxy types (Osman et al., 2021). Using PSMs can improve the reconstruction skill if the proxy system is sensitive to multiple climate variables (Dee et al., 2016) but is not always possible given the available proxy data types and PSMs.

Hydroclimate variables have been reconstructed by DA on paleoclimate timescales, but these results relied on datasets of entirely (Tierney et al., 2022) or predominantly (Steiger et al., 2018) temperature proxies; others have been performed regionally in the Arctic where precipitation and temperature are strongly correlated (Badgeley et al., 2020). During the Holocene, nonstationary covariance relationships exist between temperature and precipitation and differ for proxies and models in several regions (Hancock et al., 2023; Herzschuh et al., 2022). In an attempt to extract a predominantly moisture-driven signal spanning the last 21 ka, we assimilate only proxies which are primarily sensitive to hydroclimate; temperature proxies used by Erb et al. (2022) were purposefully excluded in this work.

A review of the Holocene hydroclimate dataset (Hancock et al., 2023) identified three proxy types with widespread distributions and which could theoretically be applied to DA: (1) speleothem and lake δ¹⁸O, (2) pollen assemblages calibrated to mean annual precipitation, and (3) lake status records. The δ¹⁸O records were excluded because of the requirement for an isotope enabled model prior. Although time slice (Osman et al., 2021) and transient (Dee et al., 2015b; He et al., 2021) simulations exist for portions of the LGM–present, there is currently no available isotope-enabled transient simulation for the entire period. The pollen data could be applied to a DA, based on the framework of Erb et al. (2022), which assimilates values previously calibrated to climate variable units. However, straightforward comparisons between these data and available model simulations have already resulted in an extensive literature on pollen-based data–model comparisons, including the evaluation of multiple generations of PMIP simulations (Bartlein et al., 1998; Brierley et al., 2020; Harrison et al., 2015; Mauri et al., 2015; Sun et al., 2021b). For this project, we sought to produce a reconstruction separate from the data used by these previous projects to provide independent results for comparison.

In summary, we assimilate lake status records inferred from shoreline and geomorphic evidence of paleo-water levels. These lake status data provide a widely distributed dataset recording the direct effects of climate change on basin-wide moisture availability, while avoiding a number of secondary inferences needed for interpreting isotope or pollen reconstructions related to calibration, evaporative enrichment, and circulation dynamics (Dayem et al., 2010; Dee et al., 2015a; Liefert and Shuman, 2020; Williams and Shuman, 2008). Pollen records calibrated to reconstruct precipitation were withheld as out-of-sample data to validate the lake-status-based precipitation reconstruction.

2.1.1 Lake status data

A total of 216 lake level records (Table S1 in the Supplement) were selected by searching existing proxy compilations (Hancock et al., 2023; Liefert and Shuman, 2020; Street-Perrott et al., 1989; Qin et al., 1998) to find data with a minimum duration of 10 000 years, at least eight data points in the time series, at least six data points during the Holocene, and a median resolution shorter than 1500 years in the time period spanning 21 000–0 BP. Although the data are spatially biased towards North America (n=62), most terrestrial regions outside of the high latitudes are represented (Fig. 1). Notably, the data density in Africa, a region with typically poor proxy coverage, is substantial. During the past 12 ka, data density remains above 93 %, but the number of available records decreases prior to the Holocene to a minimum of 70 records at 20.25 ka.

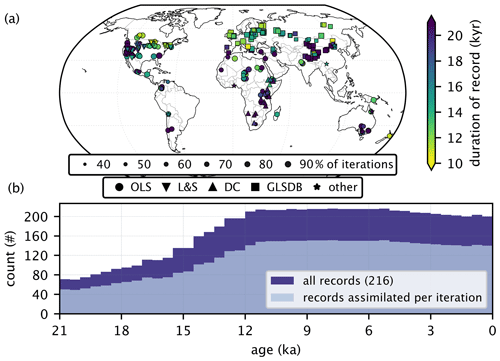
Figure 1 Lake status proxy records. (a) Map showing the spatial distribution of proxy records. Colors indicate the duration of each record, and the size is proportional to the number of iterations each record is used in the assimilation. The shape represents the source of the data, including OLS for the Oxford Lake Status databank, GLS for the Global Lake Status databank, L&S for Liefert and Shuman (2020), and DC for De Cort et al. (2021). Other indicates records from smaller data compilations or individual publications. A reference list for each site is provided in Table S1. (b) Data density plot showing the total number of available proxy records at each time step (dark blue) and the mean number of records used by each iteration of the assimilation (light blue). The difference between these represents the number of proxies records withheld for validation.

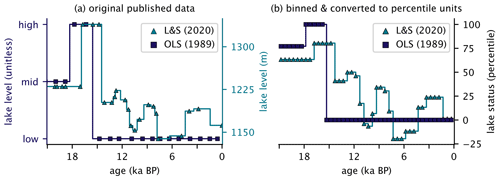
Figure 2 Data pre-processing for two lake records from Pyramid Lake, Nevada, USA. The record from the Oxford Lake Status databank is shown by purple squares (Broecker and Orr, 1958; Street-Perrott et al., 1989). These data were superseded by a newer record (Benson et al., 1990; Briggs et al., 2005) compiled by Liefert and Shuman (2020), which is shown as teal triangles. (a) The original data for the two records. (b) The same records standardized to a common time axis using a nearest-neighbor interpolation and converted percentile unit for assimilation. The mean value during the 11.7–0 ka reference period is then subtracted from each record.

The data are primarily sourced from the Oxford Lake Status databank (OLS) (n=86; Street-Perrott et al., 1989), which provides ordinal data measuring the vertical change in the elevation of the lake surface binned into three categories, namely high (70 %–100 % of total vertical range of lake fluctuation), intermediate (15 %–70 %), and low (0 %–15 %). Although this qualitative metric is limiting, the OLS data provide valuable information in otherwise data-sparse regions such as North Africa (Fig. 1). Prior to assimilation, all proxy values are converted to percentile units, with low and high designations assigned as 0 and 100, respectively. Intermediate values differ for each record according to the percentile scale and the relative number of high and low values (Fig. 2). These data were supplemented with 74 sites from the Global Lake Status Database (GLSDB; Harrison et al., 2003), which provide similar ordinal data but with increased spatial coverage in Eurasia from the inclusion of additional regional data compilations (Tarasov et al., 1996; Yu et al., 2001; Yu, 1995).

If available, OLS and GLSDB data were replaced by newer, higher-resolution records from the same site. An additional 52 records are provided by the more recently created North America (n=28; Liefert and Shuman, 2020), eastern and southern Africa (n=19; De Cort et al., 2021), and Australian (n=5; Clerke, 2023) lake level databases, and another four records from west Africa (Shanahan et al., 2006), South America (Placzek et al., 2006), and Asia (Jiang et al., 2020; H. Xu et al., 2020) were identified according to the defined selection criteria. These data represent a variety of measurement types, ranging between relative lake status estimates similar to the OLS to more precise values of absolute water level elevation. Generally, the newer data provide improved measurement values which are more descriptive and more precise in age compared to the OLS data (Fig. 2a).

Both data types were standardized to a 500-year common time bin with data interpolated using a nearest-neighbor approach. If multiple values were recorded within the same time bin, the mean value was calculated. Finally, the data were converted to percentile units, and the mean value during the 11.7–0 ka reference period was removed (Fig. 2). Although the percentile conversion removes information of more precise measurements, it provides a method of characterizing lake status change, which can be directly compared between different lake status record types and, more importantly, with the PSM developed for the project and the data assimilation framework (see Sect. 2.4).

2.1.2 Validation data

The coarse time resolution of the lake status proxy records prevents comparison to the instrumental period or even reconstructions of the Common Era. Therefore, 30 % of the available lake status records were withheld during the assimilation to evaluate the resulting reconstruction, following Osman et al. (2021). To account for potential biases from the selection of sites used for assimilation and validation, a different sample of 70 % proxy records was used for each iteration (see Sect. 2.2). The mean validation statistic (i.e., correlation coefficient) was then calculated for each record using iterations for which the data were withheld.

For the DAMP-21ka reanalysis, lake status data were assimilated to reconstruct a variety of additional climate fields, including mean annual precipitation. The DA method relies on the covariance between multiple variables to quantify this relationship, but no precipitation (mm a⁻¹) records were included. Therefore, to measure the precipitation reconstruction skill, 350 calibrated pollen records were selected from the Holocene hydroclimate data compilation (Hancock et al., 2023). These records primarily originate from the LegacyClimate 1.0 (Herzschuh et al., 2023) and are supplemented by additional records from sites not included in that dataset (Table S2). Previous studies have used calibrated pollen data to evaluate GCM simulations (e.g., Brierley et al., 2020), and our approach is conceptually similar to validate the reanalysis.

2.2 Data assimilation methodology

Lake status proxies provide valuable observations about hydrologic variations in Earth's past but are spatially limited to the basins which they infill. Data assimilation provides a mathematical technique for using these data to create a spatially complete reconstruction of specific climate variables of interest. The methods used for DAMP-21ka are based on the temperature reconstruction of Erb et al. (2022), which follows previous DA projects for the last millennium (Hakim et al., 2016; Steiger et al., 2014). A detailed explanation of the methodology is described by these references, but a brief explanation of data assimilation, the model prior, and different parameter choices is provided here.

The two major components of data assimilation are the innovation and the Kalman gain. The innovation constrains the results using the observed data and is calculated as the difference between each proxy value and the estimated value from the prior using a PSM. This difference represents the mismatch between the model prior and the proxy at the proxy location. The Kalman gain then quantifies the relationship between the innovation and the target variable for each location using the covariance structure of the model prior. This calculation allows for the translation between proxy variables to a broader climate field. The equations for these calculations are provided in Sect. S1 in the Supplement.

A significant change from the Erb et al. (2022) methodology is the implementation of an ensemble process, so that the DA is performed 10 times. During each iteration, a different sample of proxy records (70 %) and a different sample of climate states (70 %) is selected for the model prior. This technique increases the computational cost of the analysis but provides a more robust framework for uncertainty quantification. If the posterior results for a region are consistent regardless of the specific proxies and model states sampled, the results can be considered more robust than if posterior varies substantially between iterations. We note that previous paleoclimate DA reanalyses have also used a randomized data selection process (Osman et al., 2021; Tardif et al., 2019).

Several modifications to the parameter choices were implemented to optimize the reconstruction for the hydroclimate proxy, target climate variables, and longer time frame. The 500-year time step of reanalysis reflects the coarser resolution of the proxies. The analysis also converts all data to anomalies relative to a longer reference period (11.7–0 ka) than Erb et al. (2022) based on the consistent data density of the lake deposits throughout the entire Holocene (Fig. 1b). A localization radius (w_loc) of 8000 km is implemented for the reanalysis (Gaspari and Cohn, 1999; Tardif et al., 2019). Paleoclimate DA reconstructions differ on the inclusion of w_loc, with some applying a spatial weight (Osman et al., 2021) and others not (Erb et al., 2022; Steiger et al., 2018). Excluding w_loc causes the method to rely more heavily on the model covariance matrix to appropriately determine if a skillful relationship exists between distant locations. This feature may be considered a benefit or detriment, depending on the research goal (Hamill et al., 2001). During the Holocene, transient trends for different regions can impose strong covariances (Herzschuh et al., 2022), which present a challenge for the two regions with the most abundant lake status data, namely North America and North Africa. Proxy records indicate a negative covariance between these regions, based on the Holocene wetting trend for North America and a drying trend for North Africa, but transient models simulate a drying trend for each (Hancock et al., 2023). Using a localization radius allows results in North America and Africa to update independent of each other.

To assess the sensitivity of the method to various combinations of the localization radius and R, a proxy uncertainty parameter, assimilations were performed and evaluated by comparing the results to the withheld proxy data. Based on these results (Table S3), the localization of 8000 km and uncertainty in the 30th percentile were selected to maximize the skill of the precipitation reconstruction. The R value of 30, which is squared for the assimilation, also corresponds to the generalized categorization of the OLS lake status records into thirds.

2.3 Model prior

We develop a time-varying multi-model prior using the methods of Erb et al. (2022). The model prior is constructed using data from two available transient simulations for the LGM to present: (1) TraCE-21k (Transient Climate Evolution over the last 21 000 years; Liu et al., 2009), which used the National Center for Atmospheric Research (NCAR) CCSM3 (Collins et al., 2006) climate model, and (2) a HadCM3 transient deglaciation simulation, which used the UK Met Office's HadCM3 (Hadley Centre Coupled Model, version 3; Snoll et al., 2022). Using a multi-model prior is valuable for limiting the biases of any one model on the result (Bach and Ghil, 2023; Parsons et al., 2021), and this feature is particularly important for a hydroclimate DA because of the wider dispersion of Holocene anomalies between different models for precipitation than temperature (Hancock et al., 2023). By using simulations from multiple models, the resulting covariance structure will provide stronger covariances, where both models agree that there is a strong climate connection, but weaker covariances if the two models disagree. To create the multi-model prior, data from both HadCM (2.5° by 3.75°) and TraCE (∼3.71° by 3.75°) were regridded to a common spatial resolution (2.8125° by 3.75°).

The prior ensemble was developed by sampling 140 multidecadal (50-year) mean climate states within a shifting 5000-year window centered on each time step. This sampling was repeated randomly for each iteration. The choice of a time-varying prior differs from PHYDA (Steiger et al., 2018) but is consistent with DA reconstructions extending beyond the Common Era (Erb et al., 2022; Osman et al., 2021). For longer timescales, changing ice sheet configuration and sea level can alter circulation dynamics and add non-stationarity to the covariance relationship between different locations and climate variables (Herzschuh et al., 2022). The 5000-year prior window length was selected to prevent climate states which include a rapid decline in the Laurentide Ice Sheet prior to 8.5 ka (Gregoire et al., 2018) from influencing the covariance structure during the mid-Holocene (6 ka).

2.4 Lake status PSM

To quantitatively compare proxy records and model data using consistent units, we estimate lake variability from GCM output variables based on a novel proxy system model (PSM). A suitably complex PSM for assimilating the available lake status data has several requirements. The PSM must (1) convert available model output variables into a lake status percentile; (2) be applied globally to any lake; and (3) function independently of any knowledge about lake size, basin topography, runoff efficiency, or seasonal variability. This third requirement eliminates lake balance models that have been used in the past (Morrill et al., 2019). Although these characteristics lead to more mechanistic and realistic models, this information is unavailable for many datasets, and calibrating models at site-specific scales is impractical for global studies (Dee et al., 2015b; Evans et al., 2013).

The resulting PSM (Fig. 3) is derived from Li and Morrill (2010), which provides the following two equations for estimating lake status change from a GCM simulation. The first is a simple steady-state lake water balance equation describing the surface inputs and outputs of any lake as

$$\begin{array}{}\text{(1)}& D=A_{\mathrm{B}}\cdot Q+A_{\mathrm{L}}\cdot \left(P_{\mathrm{L}}-E_{\mathrm{L}}\right),\end{array}$$

where D = discharge, A_B = area of the basin, Q = runoff from the basin into the lake, A_L = area of the lake, P_L = precipitation directly onto the lake, and E_L = evaporation directly from the lake. Because the proxy dataset largely describes closed-basin lakes, D is assumed to be 0, and the water balance equation can be rewritten as

$$\begin{array}{}\text{(2)}& {\displaystyle \frac{A_{\mathrm{L}}}{A_{\mathrm{B}}}}={\displaystyle \frac{Q}{E_{\mathrm{L}}-P_{\mathrm{L}}}}.\end{array}$$

Thus, three variables are needed to calculate the water balance ($A_{\mathrm{L}}/A_{\mathrm{B}}$) of any unknown lake: runoff, E_L and P_L. Runoff and precipitation are both simulated by the two climate models and are available as output variables, but lakes are not simulated by the climate models, so lake evaporation is unavailable. Therefore, we estimate E_L using the Priestley–Taylor equation (Priestley and Taylor, 1972; Vremec and Collenteur, 2022) for potential evapotranspiration (E_potential), which considers net radiation, temperature, relative humidity, and air pressure.

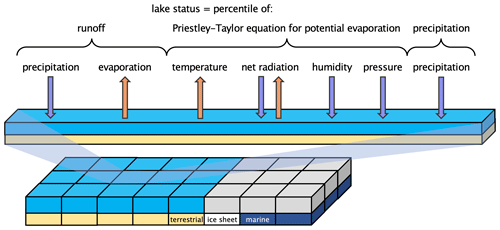
Figure 3 Conceptual diagram of our lake status PSM. Arrows indicate if an increase in the designated variable would result in greater input into the lake (down) or output from the lake (up). Each grid cell is calculated independently, and light gray shading shows that grid cells covered by ocean or substantial snow cover are masked.

Previous water balance studies have used a more computationally expensive lake energy balance model to calculate E_L from paleoclimate simulation output variables (Morrill, 2004). However, by assuming that the lake provides an unlimited supply of water, E_potential can be equated to E_L (McGee et al., 2018). Many of the same GCM outputs are used to calculate E_L in both methods, and the Priestley–Taylor equation can be applied to the global transient data assimilation methodology much more efficiently. We evaluated the ability of the simplified lake status estimation to emulate the more complex energy balance models used by previous studies using Community Climate System Model (CCSM4) CMIP5 simulations of the LGM and preindustrial periods (Brady et al., 2013; Gent et al., 2011). The lake status calculation was applied to these data, and the results were compared to those of Lowry and Morrill (2019).

After calculating $A_{\mathrm{L}}/A_{\mathrm{B}}$, the decadal output for each grid cell is converted into a percentile ranging between 0–100, with 0 representing the decade with the lowest lake status value during the entire 0–21 ka time series and 100 as the highest. Although many of the proxy records provide vertical elevation of the lake level, the classification into lake status rankings allows for the direct comparison with $A_{\mathrm{L}}/A_{\mathrm{B}}$ using the sequential ranking of percentiles:

$$\begin{array}{}\text{(3)}& \mathrm{Lake}\mathrm{status}=\mathrm{percentile}\left({\displaystyle \frac{\mathrm{runoff}}{E_{\mathrm{potential}}-P_{\mathrm{L}}}}\right).\end{array}$$

However, a complication arises when P_L exceeds E_potential, and the $A_{\mathrm{L}}/A_{\mathrm{B}}$ becomes negative (Li and Morrill, 2010). To accommodate this scenario, the calculation of lake status for each grid cell is performed in two steps. First, the data are grouped according to the sign of the E_potential−P_L value and ranked according to their relative values within each group. The data are then re-ranked so that negative values always exceed positive values. This methodology properly sequences each value so that increases in precipitation or runoff or decreases in E_potential will all provide a higher lake status estimate (Fig. S1 in the Supplement).

Both the E_potential and lake status variables are calculated independently of the data assimilation using the decadal means of the model prior, which is the highest resolution publicly available for the runoff variable from TraCE. Higher-resolution lake status values could be calculated using $P/E$ to approximate runoff as these variables are strongly correlated in regions not affected by ice sheets (Fig. S2). However, decadal averages are sufficient for assimilating the low-resolution lake status values for this study. A sea level mask and ice sheet mask are also applied to remove grid cells where no lake is feasible for the prescribed boundary conditions. During the data assimilation, the PSM identifies the correct grid cell and age range for the proxy, and the values are re-ranked within the duration of the proxy record.

2.5 Principal component analysis

To contextualize the results of the data assimilation through time, we evaluate annual precipitation changes using a principal component analysis (PCA). This technique has been used by previous data assimilation studies to synthesize reconstructed spatiotemporal climate variability (Luo et al., 2022; Okazaki and Yoshimura, 2017; Osman et al., 2021) and provides a means of examining how the spatial patterns differ between the prior and the reconstruction without the need to predefine regions. We calculate a global PC1 and PC2 time series (Dawson, 2016) for reconstructed mean annual terrestrial precipitation anomalies. The spatial pattern of the reconstruction is then evaluated using the covariance of precipitation values for each grid cell with each PC time series. We also calculate the covariance of precipitation values in the model prior with each reconstructed PC time series to identify where the two datasets differ.

3 Results and discussion

This study introduces a novel application of PSM and DA methodologies across various timescales, variables, and proxies not previously explored. First, we present results that validate these methodologies and show that the reconstruction is more skillful and than model simulations alone (Sect. 3.1 and 3.2). Then we present time slice results for the LGM (21 ka; Sect. 3.3) and the mid-Holocene (6 ka; Sect. 3.4), two periods of significant scientific interest commonly simulated by model intercomparison projects. Particular focus is placed on comparing how the reconstruction differs from the model prior. Spatial and temporal variability in the effects of precipitation and evaporation on lake level are also examined (Sect. 3.5). The spatial patterns of terrestrial precipitation through time are then evaluated using PCA in Sect. 3.6. Finally, climate dynamics associated with mid-Holocene anomalies in North America are discussed (Sect. 3.7).

3.1 Validation of the PSM

The PSM methodology used by DAMP-21ka represents a simplified version of previous water balance calculations made from the output of paleoclimate GCM simulations (Lowry and Morrill, 2019; Morrill et al., 2019). To accommodate the available data and to efficiently assimilate the proxy data, lake evaporation was estimated by potential evaporation, and the data were converted to percentile units. This second change is necessary to compare the simulated values with the proxy values, but we evaluate the effects of substituting E_potential for E_lake (Fig. 4).

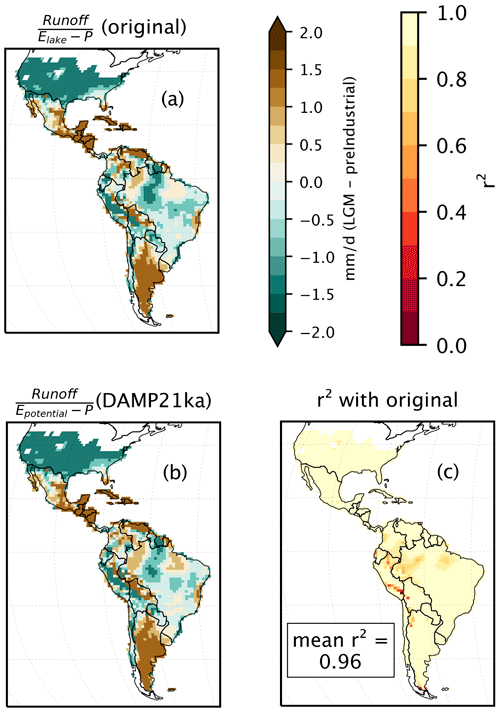
Figure 4 Comparison of lake status PSM equations. Lake status was calculated using runoff and precipitation data of CCSM4 simulations and different evaporation values. (a) Mean LGM minus preindustrial lake status values using lake evaporation data calculated from these simulations by Lowry and Morrill (2019). (b) The same values calculated using E_potential as in this study. (c) For each grid cell, and we calculate an r² value between the two methods using all 200 annual values. A scatterplot of these values is shown by Fig. S4.

Lowry and Morrill (2019) calculated lake evaporation from CMIP5 simulations of the LGM and preindustrial (100 years each) using the lake energy balance model of Morrill (2004). The results of the CCSM4 simulations, which use a similar model to the TraCE simulation (CCSM3), were combined into a 200-year time series, and a series of experiments were performed to compare lake status calculations using the estimated E_lake and E_potential values. The modified lake status values should be able to reproduce the different climates of the LGM and preindustrial, as well as capture the interannual variability.

Potential evaporation skillfully reproduces the temporal variability and spatial patterns of LGM–PI lake evaporation (r²=0.87; Figs. S3 and S4a). By ranking the lake status as percentiles, the effect of using E_potential is further reduced (r²=0.96; Fig. S4a), and the spatial patterns of LGM minus preindustrial anomalies are largely unaffected by the simplified approach (Fig. 4). As a result, we conclude that the impact of substituting potential evaporation for lake evaporation in the lake status calculation is minimal and that our lake status PSM effectively mimics the key characteristics of more sophisticated models.

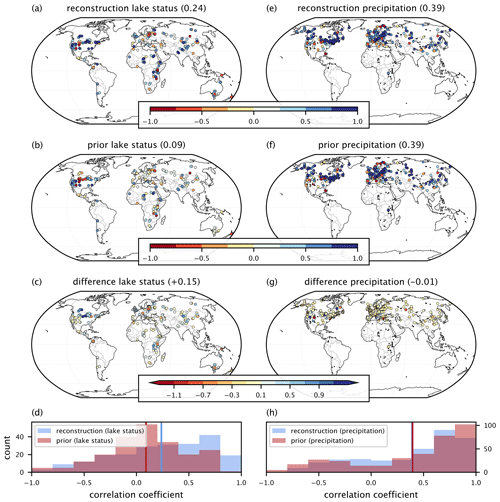
Figure 5 DAMP-21ka validation statistics. Pearson's correlation coefficients calculated for each proxy lake status (a–d) and pollen precipitation (e, h) record. The first row (a, e) shows the correlation between the reconstruction and the withheld proxy values. The second row (b, f) uses the prior values instead of the reconstruction. The third row (c, g) shows the difference so that blue colors indicate improvement, red indicates worsening agreement, and yellow represents no change between the prior and the DAMP-21ka reanalysis. The bottom row shows the histogram of the correlation coefficients for the prior (blue) and reconstruction (red), with the vertical line placed at the mean value, which is also listed in the parenthesis of the panel titles.

3.2 Reconstruction skill

The DAMP-21ka reanalysis provides a more skillful reconstruction of paleo-lake status variability than the model prior alone (Fig. 5). To quantify the agreement between the reconstructed lake status and the proxy lakes, we calculate Pearson's correlation coefficients (r values) for each proxy record using the mean r value from iterations for which the record was withheld. Osman et al. (2021) measured the skill using a variety of metrics, including r², but we note that this value does not consider negative correlation coefficients and therefore could overestimate skill for either the prior or reconstruction by indicating agreement if two values are negatively correlated. The mean value of all sites was then calculated to provide an overall reconstruction r value of 0.24. Although this moderate result provides room for improvement, the correlation is significant (p value < 0.05) for 60 % of records (mean p value = 0.13), and it represents an increase from the same skill metric calculated using a composite HadCM and TraCE time series representative of the model prior (mean r value of 0.09; mean p value of 0.18; 47 % significant). Furthermore, this increase is observed despite the challenges of a limited number of proxy records compared to other global data assimilation products (Erb et al., 2022; Osman et al., 2021) and the tendency for hydroclimate variables to produce lower correlation coefficient results than temperature reconstructions (Steiger et al., 2018). The two regions with the greatest improvement are east Africa and North America (Fig. 5c). The commonality between these areas is that both regions contain numerous lake status records and experienced notable proxy–model disagreement during the Holocene (Hancock et al., 2023). Updating the reanalysis in regions with fewer sites is limited because covariances naturally tend to decrease with distance (North et al., 2011), and the localization radius further reduces the Kalman gain from distant records (Valler et al., 2019). Due to both of these factors, the reconstruction more closely resembles the prior in regions with fewer records, and thus improvements are expected to be minimized.

Precipitation values are evaluated against calibrated pollen records using the same skill metric as for the lake status data (Fig. 5e and f). Overall, the mean correlation between the pollen proxies and the reconstruction (0.39) shows very little difference with that of the model simulations (0.39), but this may reflect the spatial bias of pollen data as regional skill patterns are similar to that of the lake status results. For many of these sites located in Europe and Asia, lake status skill improvement is also lower, possibly due to varied climate signals between nearby proxy records reflective of a low magnitude of change in precipitation. In North America, improvements are greater (Fig. S5), and we advise caution when interpreting precipitation values of the reanalysis outside of regions with skill improvement such as in North America and Africa.

3.3 Last Glacial Maximum (21 ka) anomalies

During the LGM, both thermodynamic and dynamic factors influenced large-scale shifts in hydroclimate, with regionally varying implications for lake levels (Lowry and Morrill, 2019). The globally reduced temperatures decreased evaporation and suppressed the hydrologic cycle (Kageyama et al., 2021), and ice sheets redirected patterns of atmospheric circulation, which increased precipitation amounts for portions of the Northern Hemisphere (Oster et al., 2015).

In the North American midlatitudes, large positive anomalies are simulated by the model prior, reflecting the significant gap between the LGM (21–20 ka) and last millennium (1–0 ka), which are estimated to be among the wettest and driest portions of the time series, respectively, for many grid cells (Fig. 6). By contrast, proxy lakes are more varied, and lake status anomalies in the reanalysis are less positive than in the prior across most of the continent. Several proxy records also indicate that the peak high stands occurred later than what is simulated by models (Fu, 2023). Despite predominantly negative lake status innovations, more positive precipitation anomalies are reconstructed (Fig. 6c and f) for portions of this region, which suggests that both temperature and precipitation are important for controlling lake status during this time.

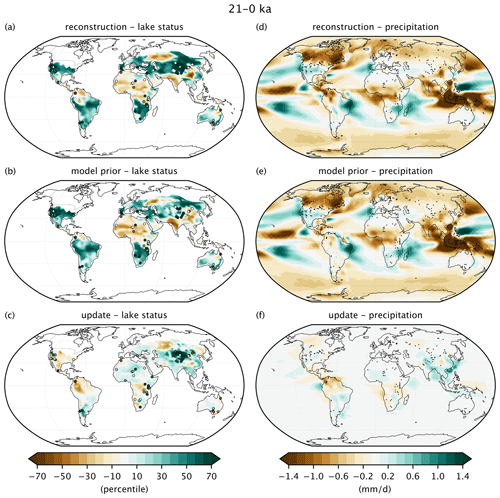
Figure 6 Last Glacial Maximum hydroclimate anomalies. The top row shows the reconstructed mean lake status (a) and annual precipitation (d) anomalies for the Last Glacial Maximum (21–20 ka) subtracted by the last millennium (1–0 ka). (b, d) The same values for the model prior results are shown in the middle row. (c, f) The update describes the difference between these two datasets. The lake status column also shows the proxy values using the same color bar (a, b). For panel (c), these values symbolize the difference between the proxy value and the mean value estimated by the prior from the PSM.

Near the Equator, dry precipitation values are reconstructed by DAMP-21ka during the LGM. Although this pattern is also true of the model prior, the update intensifies the dry anomalies across several regions, including central America and east Africa. These decreases are consistent with the proxy reconstructed lower-lake status, but tropical locations that become wetter from the assimilation, such as eastern South America and southeast Asia, are largely unconstrained by proxy lakes. To investigate the reduced LGM precipitation values in the assimilation, the spatial patterns of the TraCE and HadCM simulations were compared to evaluate the precipitation prior (Fig. S6). This comparison reveals that small anomalies in the multi-model mean actually reflect disagreement between the two simulations. For example, wet anomalies in east Africa simulated by HadCM are offset by dry values from TraCE. The large range of climate states in the model prior increases the uncertainty in the prior, causing the assimilation to rely more heavily on the observations and produce a dry reconstruction consistent with both the lake status proxies and independent evidence from isotope records (Tierney and deMenocal, 2013). The results (and the proxy data) in east Africa support the TraCE simulation, but which model simulation best aligns with the assimilated results varies regionally. For example, in central America and Australasia, the reanalysis produces anomalies which are more consistent with the HadCM simulation. As a result, the reconstruction produces negative precipitation anomalies which are more widespread throughout the tropics than either simulation on its own. This process also underscores the advantage of using a multi-model prior, which better captures structural uncertainties in the models and can better fit the observed values.

3.4 Mid-Holocene (6 ka) anomalies

The mid-Holocene (∼6000 yr BP) is a time period of significant scientific interest (Otto-Bliesner et al., 2017), in part because some features, such as a warmer Arctic, are common between 6 ka and modern warming (Serreze and Barry, 2011). Lake status in North America was lower at many proxy sites during the mid-Holocene (Liefert and Shuman, 2020). Both the TraCE and HadCM transient simulations show spatially variable hydroclimate anomalies, with drier conditions in the southern and central US and wetter conditions along the coastal regions (Hancock et al., 2023). After assimilating the available proxies, the gridded reconstruction indicates that both lower-lake level and precipitation values were widespread throughout the entire continent (Fig. 7). Lakes throughout the Eurasian midlatitudes show a varied response to mid-Holocene climate, and the prior does not differ significantly from the reconstruction. As a result, dry precipitation anomalies are observed throughout most of the terrestrial Northern Hemisphere midlatitudes which contrasts the model prior simulating varied wet (North America) and dry (Eurasia). These results suggest a uniform response throughout the midlatitudes to the orbital forcing of the mid-Holocene (Routson et al., 2019).

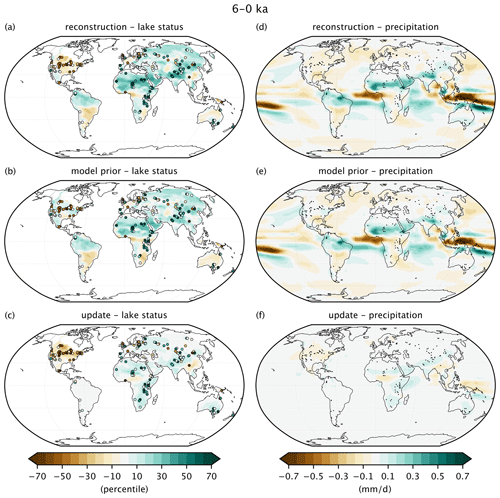
Figure 7 Mid-Holocene hydroclimate anomalies. The top row shows the reconstructed mean lake status (a) and annual precipitation (d) anomalies for the mid-Holocene (6.5–5.5 ka) subtracted by the last millennium (1–0 ka). (b, d) The same values for the model prior results are shown in the middle row. (c, f) The update describes the difference between these two datasets. The lake status column also shows the proxy values using the same color bar (a, b). For panel (c), these values symbolize the difference between the proxy value and the mean value estimated by the prior from the PSM.

In the tropics, the African humid period characterizes a time of increased moisture and vegetation across North Africa which lasted from approximately 15 to 5 ka (deMenocal et al., 2000; Lézine et al., 2011; Shanahan et al., 2015). Both the proxy dataset and the model prior at 6 ka indicate wetter-than-Common-Era anomalies for North America, but model simulations underestimate the magnitude of precipitation needed to sustain the proxy-inferred increase in vegetation during the early and mid-Holocene (e.g., Brierley et al., 2020). Furthermore, in the model prior, wet anomalies in the Sahara region are offset by drier conditions in central and east Africa. Contrasting this spatial pattern, in the reanalysis, increased moisture in both northern and eastern Africa are reconstructed in accordance with the innovation provided by the proxy lake status records. These results are in agreement with other isotopic and elemental abundance proxy results from east Africa which are independent of the reconstruction (Loomis et al., 2015; Russell and Johnson, 2005; Tierney and deMenocal, 2013). Thus, the African humid period may be characterized by both increased precipitation amounts and an increased spatial extent of positive moisture anomalies compared to model simulations.

Available lake records in the Southern Hemisphere are concentrated in Australia. Both lake proxies and models indicate a moisture dipole, with drier conditions in the northeast and wetter conditions in the southeast during the mid-Holocene. The reconstruction strengthens this moisture gradient and suggests that central Australia became wetter rather than drier at 6 ka. Results for the continental interior cannot be validated due to the lack of proxy records from the region (De Deckker, 2022), but the expanded wet anomalies are consistent with the coastal Swallow Lake (Barr et al., 2019).

3.5 Spatial and temporal variability in the effects of precipitation and evaporation on lake level

The lake status PSM represents a balance between hydrologic inputs (precipitation and runoff) and outputs (lake/potential evaporation) within each grid cell. Here we explore the relationship between these variables from the TraCE simulations to better understand controls on lake level variability and to contextualize the results of the assimilation. Sensitivity experiments were performed by comparing the lake status percentiles to similar values calculated if runoff and precipitation (E_varying) or runoff and potential evaporation (P_varying) remained constant. For both experiments, runoff was set to a constant value because this variable incorporates both precipitation and evapotranspiration. Calculations were performed for the entire time series and separately for three segments representing the LGM (21–14 ka), deglacial (14–7 ka), and middle to late Holocene (7–0 ka) to explore non-stationary relationships among these variables.

Throughout the tropics, variability in precipitation dominates the simulated changes in lake level. This is shown by lower mean RMSE values for the P_varying than the E_varying experiments (Fig. 8). For example, in the Sahara, high error values in the E_varying experiment reflect the importance of increased precipitation amounts during the African humid period for estimating lake status changes (Pausata et al., 2020; Specht et al., 2022). Elsewhere in the tropics, lower evaporative demand during the LGM are counter balanced with low precipitation anomalies which result in low-lake-status anomalies (Fig. 8a and d).

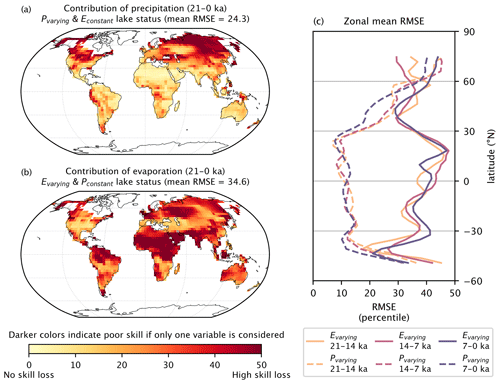
Figure 8 Lake status PSM sensitivity tests. Lake status values used in the assimilation were compared to similar values calculated using constant runoff and potential evaporation (a) or constant runoff and precipitation (b). Low RMSE values indicate areas where lake status can be accurately predicted using only the single variable. Panels (a) and (b) show values calculated for the entire time series. Panel (c) shows zonal mean RMSE values for sensitivity tests performed for three time periods.

Outside of the tropics, the role of evaporation increases so that both variables become important for quantifying lake status variability. In the midlatitudes, RMSE values decrease for the E_varying and increase for the P_varying experiments, which is consistent with previous lake status modeling of the LGM (Lowry and Morrill, 2019) and mid-Holocene (Li and Morrill, 2010). At high latitudes, high RMSE values are observed for both experiments, which could reflect the positive correlation between precipitation and temperature (Badgeley et al., 2020; Hancock et al., 2023; Thomas et al., 2018). As evaporation and precipitation both increase, the water balance equation integrates these counterbalancing forces, but by only including one variable, errors increase by assuming a more significant decrease or increase in lake status.

The spatial patterns of lake status sensitivity remain relatively stable between the Holocene, deglacial, and LGM segments. However, several notable features are evident. A subtle poleward shift in RMSE values for the 7–0 ka experiments appears to have occurred in the midlatitudes (30–50°) relative to the earlier time periods. In the Arctic (>60° N), lower E_varying RMSE values during the deglacial period also represent the emphasized role of lake evaporation during a time of increased temperature variability relative to precipitation (Badgeley et al., 2020). Overall, these results demonstrate that the simple PSM used for DAMP-21ka can account for the competing influence of temperature-driven PET and precipitation, as these variables change spatially and throughout the duration of the reconstruction.

Using a multivariate PSM, the effects of both evaporation and precipitation are quantified by the Kalman gain. This may explain the spatially varied precipitation update for eastern North America during the LGM (Fig. 6f). Lower proxy lake status values are expressed in the reconstruction through temperature dependence on lake status at this time, and the precipitation relationship is less meaningful. Accordingly, the LGM lake status innovation in eastern North America is reconstructed with warmer (less cold) temperature anomalies in central and eastern United States than those simulated by the model prior (Fig. S7), and the resulting positive precipitation innovation reflects the positive covariance between precipitation and temperature.

3.6 Reconstructed PC1 and PC2

To examine spatiotemporal patterns of terrestrial precipitation, we use PCA to identify common modes of variability within the data without predefining geographic boundaries. Overall, the reconstruction and prior PCA results broadly agree as expected, given the role of the model's covariance structure in the assimilation process. Nonetheless, the spatiotemporal patterns revealed by the PCA, as well as several notable differences between the prior and reconstruction, provide insight into global hydroclimate evolution over the past 21 kyr (Fig. 9).

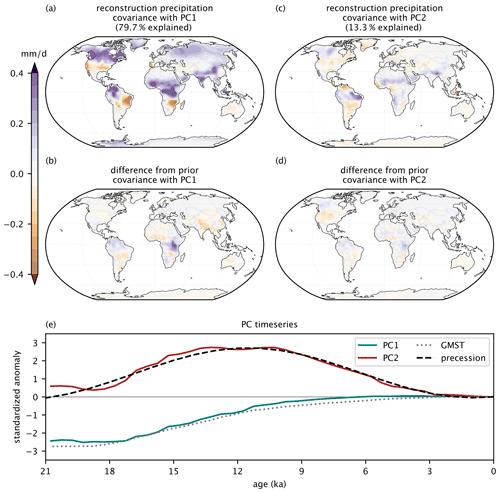
Figure 9 PCA of terrestrial annual precipitation (21–0 ka) in the reconstruction. The covariance between each grid cell and PC1 (a) and PC2 (c) is shown for the reconstruction. (b, d) The difference between panels (a) and (c) compared to the covariance calculated from the precipitation model prior with the reconstruction PC time series. (e) The PC time series are plotted (solid lines), along with the global mean surface temperature (GMST) of the reconstruction (black) and the precessional forcing (grey) (Berger and Loutre, 1991). The global mean time series are similar to those calculated for the model prior (Fig. S10). The time series values are standardized (z scores) to allow for plotting on a common y axis.

PC1, which explains 80 % of the variance in terrestrial precipitation (Fig. S8), characterizes the LGM-to-Holocene transition and integrates the thermodynamic and dynamical impacts of GMST warming and ice sheet retreat. Positive loadings at high latitudes are strongest over the Laurentide, Cordilleran, and Fennoscandian ice sheets, signifying the substantial increase in precipitation during the LGM-to-Holocene transition across these regions. Conversely, negative loadings in the midlatitudes, particularly in North America, correspond to diminishing precipitation amounts as circulation patterns adjust to the retreating ice sheets (McGee et al., 2018; Oster et al., 2015). Although noteworthy, these patterns are not meaningfully distinct from those of the model prior (Figs. 9b and S9).

In tropical regions, the covariance of PC1 is consistent with a suppressed hydrological cycle and southward position of the ITCZ during the LGM (Gasse et al., 2008; Wang et al., 2023). The reconstruction differs from the prior, most notably in east Africa where drier LGM anomalies for the reconstruction extend throughout both northern and eastern Africa. This regional change is also apparent in the 21 ka (Fig. 6) and, to a lesser extent, the 6 ka (Fig. 7) time slices and is possibly attributable to the absence of vegetation feedback in the model prior (Dallmeyer et al., 2021).

Positive loadings for both PC1 and PC2 suggest overall wetting trends during the deglacial period throughout the Northern Hemisphere tropics, but PC2 also incorporates a drying trend from the mid-Holocene to the present which is strongly correlated with orbital precession. Differing PC2 loadings in North America suggest that regional disagreement is related to the climate's response to orbital forcing. Negative covariance in the reconstruction may indicate that the model prior, which shows greater precipitation amounts during the mid-Holocene, overestimates the role of precession for the North American midlatitudes. Therefore, long-term trends in annual insolation and the strengthening of the annual latitudinal insolation gradient (Davis and Brewer, 2009; Routson et al., 2019) could be more significant than the seasonality suggested by precession alone.

3.7 Holocene hydroclimate in North America

Mid-Holocene hydroclimate anomalies in the North America midlatitudes reflect a well-established disagreement between generally dry proxies and wet models (Hermann et al., 2018; de Wet et al., 2023). In the DAMP-21ka precipitation reconstruction, the update results in dry annual precipitation outside of the monsoonal US southwest. To investigate potential mechanisms for this divergence from the model prior, mid-Holocene climate anomalies in the TraCE and HadCM simulations are explored in this section.

When the latitudinal temperature gradient (LTG) is greater, zonal winds strengthen, and more moisture is transported across the midlatitudes (Shaw et al., 2016). During the early and mid-Holocene, amplified warming in the Arctic reduced the Northern Hemisphere LTG, which shifted the position and strength of the midlatitude jet stream and associated storm tracks impacting North America hydroclimate (Routson et al., 2019; C. Xu et al., 2020). Previous multi-model evaluations of the mid-Holocene show weaker westerly winds during summer months when the insolation anomalies were greatest (Routson et al., 2022). However, a more varied annual zonal wind strength response is noteworthy because the position and strength of the westerly jet during winter is the more significant control on annual precipitation anomalies for much of western North America (Hermann et al., 2018). Furthermore, a recent study exploring winter sea level pressure (SLP) gradients during the last interglacial (∼120 ka) indicates that a subset of models with the greatest proxy agreement simulates weaker winter SLP gradients across the Pacific (de Wet et al., 2023).

In the HadCM and TraCE simulations, mid-Holocene SLP anomalies show an intensified Aleutian Low and steeper gradient during winter and spring relative to preindustrial conditions (Fig. 10). Correspondingly, the models also simulate strengthening westerly circulation in the upper atmosphere and increased precipitation amounts along the US West Coast. Because a majority of the region's precipitation occurs during winter, these changes represent substantial alteration to annual hydroclimate (Fig. S10; Hermann et al., 2018). Consequently, this covariance structure causes the dry western North America anomalies in DAMP-21ka during the mid-Holocene to suggest the opposite pattern, with weaker winter midlatitude westerly flow and a shallower SLP gradient in the mid-Holocene. In support of this hypothesis, independent δ¹⁸O (Anderson et al., 2005; Broadman et al., 2020; Jones et al., 2014; Nagashima et al., 2022), paleoenvironmental (Heusser et al., 1985; Nazarova et al., 2021), and marine (Barron and Anderson, 2011; Katsuki et al., 2009; Sun et al., 2021a) proxy records are interpreted to signify an intensification of the Aleutian Low throughout the Holocene.

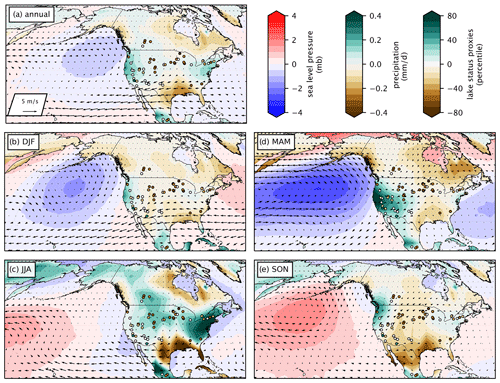
Figure 10 Simulated mid-Holocene climate anomalies for North America. Gridded values are representative of the model prior. Precipitation (green–brown) is shown for terrestrial regions, and SLP (red–blue) is mapped over oceans. Wind vector anomalies for the 200 mb geopotential height are plotted with arrows. The proxy lake values used in the assimilation are plotted with circles and are the same for each panel. Anomalies are calculated as the mean of 6.5–5.5 ka minus 1–0 ka values for both the HadCM and TraCE simulations.

A weaker winter SLP gradient during the mid-Holocene is also consistent with proxy–model comparisons for the last interglacial (de Wet et al., 2023), indicating a robust North Pacific and western North America response to amplified warming in the Arctic (Turney et al., 2020). Notably, simulations of modern climate change project an intensification of the wintertime Aleutian Low in response to future sea ice loss (Screen et al., 2018), and further research could provide additional insight into the precise mechanisms controlling the strength of the Aleutian Low in climate models during different time periods.

Mid-Holocene proxy–model disagreement in North America cannot be resolved by examining winter anomalies alone. In the central and eastern United States, simulated wet summer anomalies offset dry winter precipitation values to result in wet annual precipitation anomalies in the model prior. Accordingly, proxy–model disagreement may reflect winter sensitivity in the lake status proxies (Morrill et al., 2019) which are assumed to have annual seasonality for the PSM. Alternatively, the transient model prior, which simulates wetter conditions than the PMIP4 multi-model mean (Brierley et al., 2020; Hancock et al., 2023), could misrepresent the hydroclimate response of this region to mid-Holocene boundary conditions by incorrectly simulating the seasonality of precipitation anomalies so that dry winter and wet summer anomalies are not properly weighted in the annual mean.

Overall, the DAMP-21ka reanalysis reconstructs dry mid-Holocene precipitation anomalies throughout the North American midlatitudes, aligning the results with the coherent dry conditions inferred from both the assimilated and independent proxy data. This represents a key strength of the data assimilation methodology which incorporates the dynamics simulated by the model prior into a multivariate reconstruction constrained by the proxy observations. The reconstruction provides an improved understanding of past hydroclimate variability which can be used to benchmark future research and evaluate both proxy records and model simulations.

4 Conclusions

Data assimilation integrates the information from proxy observations and model simulations into a single gridded reconstruction of annual precipitation and lake status for the past 21 000 years, which is the first global application of the DA methodology to hydroclimate on both Holocene and LGM timescales. A mechanistic lake level PSM was developed to quantitatively compare model simulations with proxy records using runoff, precipitation, and potential evaporation. The multivariate PSM is capable of incorporating changing sensitivities to these variables across space and time and is a critical component for midlatitude and Arctic regions, where both precipitation amount and evaporative demand are needed to properly estimate water balance variability.

The DAMP-21ka reanalysis more skillfully estimates hydroclimate patterns than the model simulations alone, particularly in North America and east Africa, where data density is high and proxy–model disagreement is substantial. Several notable changes are observed for the reconstruction compared to the model prior. During the LGM, tropical aridity intensified and was more geographically widespread than in either simulation alone. For the mid-Holocene, increased precipitation is reconstructed for monsoon regions across North Africa, east Africa, and Asia. Outside of the tropics, dry precipitation anomalies are reconstructed throughout the midlatitudes in North America and Eurasia, which suggests a uniform response to orbital forcing in the midlatitudes. As a result, positive covariance in the model prior between North America and North Africa becomes negative in the DAMP-21ka reanalysis as it is constrained by the lake status proxies.

The reconstruction also reconciles the described proxy–model disagreement in North America for the mid-Holocene well. Investigation into the climate dynamics of the model prior identifies stronger SLP gradients in the North Pacific as a potential source of simulated wet anomalies in western North America. Consequently, dry mid-Holocene anomalies for DAMP-21ka are consistent with the weaker Aleutian Low recorded by marine and terrestrial proxies throughout the region and aligns the results mid-Holocene with data–model comparisons for the last interglacial, indicating a robust response in the North Pacific across two periods used as partial analogues for modern climate change.

Discrepancies between the model prior and reconstruction about the magnitude of change in the Northern Hemisphere tropics, direction of change in North America, and covariance between regions have implications for future climate change projections simulated by GCMs. Although neither the LGM nor mid-Holocene is a perfect analogue for modern climate change, these results demonstrate the importance of the spatial structure of temperature anomalies and boundary conditions on regional precipitation and water budgets. Therefore, accurate understanding of the patterns of temperature anomalies and the resulting dynamic and thermodynamic processes on regional circulation changes and evaporative demand is necessary for predicting the hydroclimate response to warming temperatures.