Precise dating of deglacial Laptev Sea sediments via ¹⁴C and authigenic ¹⁰Be∕⁹Be – assessing local ¹⁴C reservoir ages

Establishing accurate chronological frameworks is imperative for reliably identifying lead–lag dynamics within the climate system and enabling meaningful intercomparisons across diverse paleoclimate proxy records over long time periods. Robust age models provide a solid temporal foundation for establishing correlations between paleoclimate records. One of the primary challenges in constructing reliable radiocarbon-based chronologies in the marine environment is to determine the regional marine radiocarbon reservoir age correction. Calculations of the local marine reservoir effect (ΔR) can be acquired using independent ¹⁴C dating methods, such as synchronization with other well-dated archives. The cosmogenic radionuclide ¹⁰Be offers such a synchronization tool. Its atmospheric production rate is controlled by the global changes in the cosmic ray influx, caused by variations in solar activity and geomagnetic field strength. The resulting fluctuations in the meteoric deposition of ¹⁰Be are preserved in sediments and ice cores and can thus be utilized for their synchronization. In this study, for the first time, we use the authigenic ${}^{\mathrm{10}}\mathrm{Be}/{}^{\mathrm{9}}\mathrm{Be}$ record of a Laptev Sea sediment core for the period 8–14 kyr BP and synchronize it with the ¹⁰Be records from absolutely dated ice cores. Based on the resulting absolute chronology, a benthic ΔR value of +345 ± 60 ¹⁴C years was estimated for the Laptev Sea, which corresponds to a marine reservoir age of 848 ± 90 ¹⁴C years. The ΔR value was used to refine the age–depth model for core PS2458-4, establishing it as a potential reference chronology for the Laptev Sea. We also compare the calculated ΔR value with modern estimates from the literature and discuss its implications for the age–depth model.

1 Introduction

Paleoclimate reconstructions can provide useful information about the dynamics of the climate system under different boundary conditions. Investigating how the climate variations propagate in space and time can provide important information about the underlying driving mechanisms (Adolphi et al., 2018; Czymzik et al., 2016b, a; Reinig et al., 2021). To correctly assess regional variations and spatio-temporal patterns in climate fluctuations, it is crucial to construct precise chronological frameworks. These frameworks serve as the temporal backbone for establishing correlations between paleoclimate records derived from marine, terrestrial, and ice core archives. However, uncertainties in chronologies across different paleoclimate records often hinder the precise assessment of paleoclimate dynamics involving multiple records from different sites and archives (Southon, 2002).

One of the key challenges for constructing precise chronologies in the marine realm is to estimate the regional marine radiocarbon reservoir age correction, especially in polar regions (Alves et al., 2018; Heaton et al., 2023). For constructing an age–depth model using ¹⁴C dates of marine samples, it is crucial to include a precise marine reservoir age (MRA). The MRA is the radiocarbon age difference between a marine sample and its contemporary atmosphere (Stuiver et al., 1986). According to the most recent radiocarbon calibration curve, Marine20, the global average marine reservoir age is approximately 500 ¹⁴C years during the Holocene period (0–11.6 kilo-calendar years before present – kyr BP) (Heaton et al., 2020). However, regional differences in ocean–atmosphere exchange and internal ocean mixing can result in large regional deviations from this global mean (Heaton et al., 2023). Therefore, the local marine reservoir effect, ΔR, was introduced and is defined as the difference between the regional and the modelled global marine reservoir ages (Reimer and Reimer, 2001; Stuiver et al., 1986).

There is only one study that has provided modern MRA estimates for the Laptev Sea (Bauch et al., 2001). In this study, the MRAs range from 295 ± 45 to 860 ± 55 ¹⁴C years, with a mean value of 451 ± 72 ¹⁴C years. Estimates for MRA from the early deglaciation (∼ 15 kyr BP) to the Holocene period for creating reliable deglacial chronologies in the Laptev Sea have not been available so far.

In order to provide estimates of the local ΔR back in time the samples must be independently dated by other means than ¹⁴C. This can, for example, be achieved by synchronization to other well-dated archives. Cosmogenic radionuclides such as ¹⁰Be provide such a synchronization tool (Adolphi et al., 2018; Adolphi and Muscheler, 2016; Czymzik et al., 2018, 2020; Muscheler et al., 2014; Southon, 2002).

The cosmogenic radionuclides beryllium-10 (¹⁰Be, half-life 1.387 ± 0.012 Myr) (Chmeleff et al., 2010; Korschinek et al., 2010) and carbon-14 (¹⁴C, half-life 5.700 ± 0.03 kyr) (Audi et al., 2003) are mainly produced in Earth's upper atmosphere in a particle cascade that is triggered when galactic cosmic rays interact with atoms in the atmosphere (Lal and Peters, 1967; Dunai and Lifton, 2014). The flux of these cosmic rays reaching Earth is controlled by variations in the heliomagnetic and geomagnetic shielding (Lal and Peters, 1967; Masarik and Beer, 1999). During periods of higher solar activity and/or geomagnetic field strength, production rates of ¹⁰Be and ¹⁴C are decreased, whereas the production rates are higher during reduced solar activity and/or lower magnetic field strength. The production rates of both cosmogenic radionuclide isotopes covary globally due to these external processes.

Following production in the atmosphere, ¹⁴C oxidizes to ¹⁴CO₂, enters the global carbon cycle, and is incorporated in environmental archives such as tree rings, foraminifera, or speleothems. Annually, gigatons of carbon are exchanged between the Earth's active reservoirs of the atmosphere, biosphere, and ocean within the global carbon cycle. Carbon is recycled and reused within these reservoirs and some reservoirs such as the deep ocean can take hundreds of years to recycle carbon back to the atmosphere. The resulting heterogenous distribution of radiocarbon among the different reservoirs stresses the importance of understanding and determining precise reservoir ages.

In the atmosphere, the production of ¹⁰Be in the more stably layered stratosphere is higher than in the troposphere. About 63 % of ¹⁰Be is produced in the stratosphere, 30 % in the tropical and subtropical troposphere together, and 7 % in the polar troposphere (Adolphi et al., 2023; Poluianov et al., 2016). ¹⁰Be is adsorbed onto aerosol particles, mixed during about a 1-year residence time in the stratosphere, and then transported and deposited on Earth's surfaces through wet and dry deposition (Raisbeck et al., 1981; Zheng et al., 2023). The ¹⁰Be production rates are highest in the high-latitude stratosphere due to the weaker shielding of the cosmic ray flux by the Earth's magnetic field. However, the highest ¹⁰Be fluxes to Earth's surface are recorded in midlatitudes because of the strong regional exchange between the stratosphere and troposphere and high precipitation rates, leading to strong aerosol scavenging (Heikkilä et al., 2013). Non-production processes such as variations in mixing, transport, and deposition of ¹⁰Be and ¹⁴C can complicate the reconstruction of cosmogenic radionuclide production rates from paleoenvironmental archives. However, common variations in cosmogenic radionuclide records are considered to represent the cosmogenic radionuclide production signal due to their common production mechanism and different chemical behaviour (Lal and Peters, 1967; Muscheler et al., 2008). ¹⁰Be production rate changes are relatively well-known from independently dated ice core records (Finkel and Nishiizumi, 1997; Yiou et al., 1997), and this can serve as a synchronization target for other records of ¹⁰Be production rate changes.

In order to obtain reliable records of ¹⁰Be production rate changes from marine sediments, the effects of variable sedimentation rates and particle scavenging must be accounted for, which can be efficiently achieved by measuring authigenic ${}^{\mathrm{10}}\mathrm{Be}/{}^{\mathrm{9}}\mathrm{Be}$ (Bourles et al. 1989). The stable isotope ⁹Be is a trace component in all continental rocks. It is released by weathering of silicate rocks and transported to the ocean mainly by rivers (von Blanckenburg et al., 2015). ⁹Be (and to a lesser extent meteoric ¹⁰Be) is introduced into the ocean in its dissolved form where it is mixed with dissolved ¹⁰Be of ocean water (mainly derived from atmospheric fallout; see above). Since Be is particle-reactive in seawater, dissolved ${}^{\mathrm{10}}\mathrm{Be}/{}^{\mathrm{9}}\mathrm{Be}$ is incorporated in marine authigenic phases as amorphous coating on sediment or it can be preserved in authigenic Fe–Mn oxyhydroxides (von Blanckenburg and Bouchez, 2014). Therefore, in marine sediment the authigenic ${}^{\mathrm{10}}\mathrm{Be}/{}^{\mathrm{9}}\mathrm{Be}$ ratio reflects the isotope ratio of dissolved Be of the overlying water column at the time of sediment deposition (Bourles et al., 1989; von Blanckenburg and Bouchez, 2014).

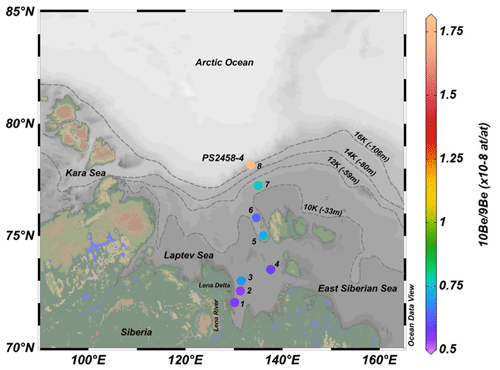
Figure 1 Map of the Laptev Sea shelf showing the location of core PS2458-4 with core-top ${}^{\mathrm{10}}\mathrm{Be}/{}^{\mathrm{9}}\mathrm{Be}$ concentration (numbered coloured circle 8) and ${}^{\mathrm{10}}\mathrm{Be}/{}^{\mathrm{9}}\mathrm{Be}$ concentrations of modern surface sediments (numbered coloured circles 1–7). The dashed lines represent the reconstructed coastline extent at four different time periods (where 16 K is 16 kyr BP), with corresponding water depth values in metres shown in brackets (Klemann et al., 2015). The map was created using Ocean Data View (Schlitzer, 2016).

If the riverine input of ⁹Be remains relatively constant, ⁹Be and ¹⁰Be are well-mixed (i.e., at sites > 200 km from the coast) (Wittmann et al., 2017) and the mixing of prevalent water masses does not change, then authigenic ${}^{\mathrm{10}}\mathrm{Be}/{}^{\mathrm{9}}\mathrm{Be}$ should primarily reflect changes in the cosmogenic production rates of ¹⁰Be. In the Arctic Ocean, the spatial patterns of ${}^{\mathrm{10}}\mathrm{Be}/{}^{\mathrm{9}}\mathrm{Be}$ in the water column are more heterogeneous than most other open-ocean settings because of the mixing of Atlantic waters with ${}^{\mathrm{10}}\mathrm{Be}/{}^{\mathrm{9}}\mathrm{Be}$ values of 5–10 × 10⁻⁸ and Arctic rivers with ${}^{\mathrm{10}}\mathrm{Be}/{}^{\mathrm{9}}\mathrm{Be}$ values of 0.3–1.5 × 10⁻⁸ (Frank et al., 2009).

The aim of this study is to explore the use of an authigenic ${}^{\mathrm{10}}\mathrm{Be}/{}^{\mathrm{9}}\mathrm{Be}$ ratio of a Laptev Sea sediment core for its synchronization to ¹⁰Be records from absolutely dated ice cores. Using this result, we aim to infer the local marine reservoir effect, ΔR, for the Laptev Sea during the deglaciation. This is the first study to exploit variations in ¹⁰Be production rates from Arctic marine sediments for stratigraphic purposes.

Table 1 Information about the location, water depth, distance from the Lena Delta, and concentration of authigenic¹⁰Be (atoms per gram, at g⁻¹), ⁹Be (atoms per gram, at g⁻¹), and ${}^{\mathrm{10}}\mathrm{Be}/{}^{\mathrm{9}}\mathrm{Be}$ (atoms per atom, at at⁻¹) ratio leached from the modern surface sediment samples.

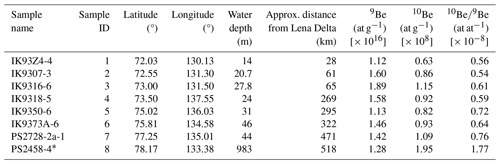
^∗ For core PS2458-4, the ⁹Be, ¹⁰Be, and ¹⁰Be/⁹Be results from the 30 cm sample are used as the core-top values.

Table 2 Radiocarbon and modelled ages from foraminifera and bivalve samples from core PS2458-4.

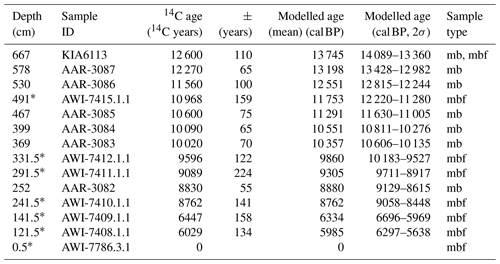
Modelled ages were calculated using OxCal4.4 (Ramsey, 2009) with a ΔR value of 345 ± 60 ¹⁴C years, as calculated in this study. Marine ¹⁴C dates were calibrated with the Marine20 curve (Heaton et al., 2020). The depth values with asterisks represent the new benthic foraminifera samples measured for ¹⁴C dates. The depth values without asterisks show the published ¹⁴C dates from Spielhagen et al. (2005). The Libby (1952) half-life (5568 ± 30 years) was used to calculate the ¹⁴C age of foraminifera samples. Sample type: mb – mixed bivalves, mbf – mixed benthic foraminifera.

2 Materials and methods

2.1 Sediment core location and initial chronology

The sediment core PS2458-4 measured for ⁹Be and ¹⁰Be in this study was retrieved in 1994 from the eastern Laptev Sea continental margin (78°10.0^′ N, 133°23.9^′ E) at a water depth of 983 m (Fütterer, 1994) and approximately 518 km from the Lena Delta (Fig. 1). The 8 m long core consists of very dark olive-grey silty clay of dominantly terrigenous origin (Fütterer, 1994). This core consists of a continuous high-sedimentation-rate (77 cm kyr⁻¹) sequence representing the deglaciation period between approximately 16.5 and 9.3 kyr BP, followed by a lower-sedimentation-rate (27 cm kyr⁻¹) early Holocene sequence (Fahl and Stein, 2012). The first chronology of core PS2458-4 was established by accelerator mass spectrometry (AMS) ¹⁴C dating of calcareous foraminifera, bivalves, and wood samples for the sediment interval between 201 and 667 cm, corresponding to a time interval between approximately 8.8 and 14.3 kyr BP (Spielhagen et al., 2005). To improve the existing age–depth model, seven new AMS ¹⁴C dates from mixed benthic foraminifera were used in combination with seven ¹⁴C dates from mixed benthic foraminifera and bivalves from Spielhagen et al. (2005), and an initial age model was derived using OxCal4.4 (Ramsey, 2009) (see Table 2). The mixed bivalve species used in Spielhagen et al. (2005) were described as Thyasira sp. and Yoldiella sp. (Table S1 in the Supplement). Both bivalve species typically occur in cold-water environments at continental margins and in areas of limited food supply, as is the Laptev Sea continental margin. Concerning the mixed benthic foraminifera species, usually epibenthic species such as Lobatula lobatula are preferred. Since this latter species is rare in our sediment samples, other species such as Cassidulina neoteretis, Islandiella helenae, and Islandiella norcrossi were selected for radiocarbon dating. In the Arctic Ocean all these species live close to the sediment surface (Wollenburg and Kuhnt, 2000; Wollenburg and Mackensen, 1998) and reflect the carbon and oxygen isotope record of the bottom water in their shells. The marine ¹⁴C dates were calibrated with the Marine20 curve (Heaton et al., 2020). An average local marine reservoir effect (ΔR) value of −110 ± 28 ¹⁴C years was used based on the nearest modern values from Bauch et al. (2001) available from the online database at http://calib.org/marine/ (last access: 26 May 2023). This chronology provides the initial basis for the stratigraphic fine-tuning using ${}^{\mathrm{10}}\mathrm{Be}/{}^{\mathrm{9}}\mathrm{Be}$ as described below.

2.2 Modern surface sediment samples from the Laptev Sea

Seven modern surface sediment samples collected in the Laptev Sea were also included in the analysis (Fig. 1, Table 1). Surface sediments with sample IDs 1 to 6 were collected during the TRANSDRIFT expeditions I and II in 1993 and 1994 using Van Veen grabs and a large spade box corer (Kassens and Dmitrenko, 1995; Kassens and Karpiy, 1994). A sediment sample from core PS2728-2 with ID number 7 was recovered in 1995 with a large rectangular box sampler during the Arctic Expedition ARK-XI/1 (Rachor, 1997). The sediment samples used in this study are distributed along a transect from near the Lena Delta towards the open ocean near the shelf break, close to where core PS2458-4 was retrieved.

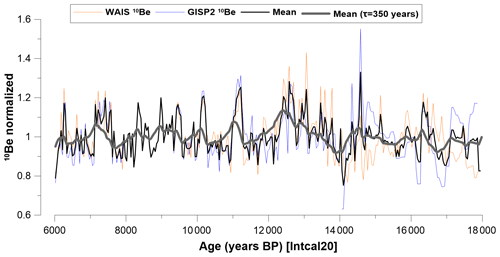
Figure 2 WAIS (orange) (Muschitiello et al., 2019; Sigl et al., 2016; Sinnl et al., 2023) and GISP2 (blue) (Finkel and Nishiizumi, 1997) ¹⁰Be fluxes corrected for correlation with ice core accumulation rates and δ¹⁸O, plotted on the IntCal20 timescale. The thick black line shows the mean of both datasets, and the bold grey line depicts the modelled oceanic ¹⁰Be signal assuming a residence time (τ) of 350 years for ¹⁰Be in the water column.

2.3 Sample preparation and measurements

A total of 54 sediment samples were selected along core PS2458-4 and processed for Be isotope analysis at the Alfred Wegener Institute in Bremerhaven (Germany). According to the initial radiocarbon-based age model, the selected samples covered three large cosmogenic radionuclide production rate swings, as evidenced by ice core ¹⁰Be and tree ring ¹⁴C records (e.g., Adolphi and Muscheler, 2016), that occurred between 8.5 and 11.5 kyr BP. The leaching of the authigenic Fe–Mn oxyhydroxide phase followed Gutjahr et al. (2007) with minor modifications. Sediment samples were freeze-dried and homogenized, and ∼ 1 g of sediment was treated with 1 M NaOAc and adjusted with HOAc to pH 4 to dissolve carbonates, which were discarded. Subsequently, the sediments were leached using 0.04 M hydroxylamine (NH₂OH-HCl) in 15 % HOAc at 95 °C for 4 h. We did not leach the exchangeable fraction as proposed by Gutjahr et al. (2007) as this contained less than 1 % of the Be leached in the hydroxylamine fraction with a very similar ${}^{\mathrm{10}}\mathrm{Be}/{}^{\mathrm{9}}\mathrm{Be}$ ratio. An aliquot from the resulting leaching solution was sampled for stable ⁹Be measurements using an atomic emission spectrophotometer at the Alfred Wegener Institute in Bremerhaven, Germany (Thermo Fisher Scientific Inc., ICP-OES-iCAP7400), with an internal yttrium standard and standard addition. The remaining ¹⁰Be aliquot solution was spiked with a precisely weighed amount of ⁹Be carrier (200, 300, or 500 µL of 1000 mg L⁻¹ carrier solution; LGC 998969-73; ${}^{\mathrm{10}}\mathrm{Be}/{}^{\mathrm{9}}\mathrm{Be}$ = (3.74 ± 0.31) × 10⁻¹⁵ at at⁻¹) (Merchel et al., 2021). The purification of the samples largely followed the method outlined by Simon et al. (2016). The samples were evaporated and dissolved in distilled HCl, and NH₃ was added for Be oxy-hydroxide precipitation from the solution at pH 8–9. The precipitate was recovered by centrifugation and then dissolved in 1 mL distilled 10.2 M HCl before loading onto a column filled with 15 mL Dowex^® 1 × 8 (100–200 mesh) anion-exchange resin in order to remove Fe from the sample. Previously, the resin was rinsed with 20 mL MilliQ^® water and conditioned with 30 mL 10.2 M HCl. The sample was then loaded onto the column and eluted using 30 mL 10.2 M HCl. A column filled with 10 mL 50 × 8 (100–200 mesh) cation-exchange resin was used to separate Be from B and Al. The resin was treated with 20 mL MilliQ^® water followed by 20 mL 1 M HCl. The sample was loaded onto the column and the first 25 mL 1 M HCl eluent, which contain mainly B, was discarded. Be was eluted and collected with the next addition of 90 mL 1 M HCl. The resulting Be oxy-hydroxides were precipitated at pH 8–9 by addition of NH₃, then separated by centrifugation and washed three times by rinsing with MilliQ^® water to remove all chlorides. The purified Be oxy-hydroxides were transferred into quartz vials, dried at 80 °C overnight, and finally calcinated to BeO at 900 °C for 2 h. The BeO was mixed with Nb powder (Nb:BeO = 4:1 by weight) and pressed into a Cu cathode-holder for accelerator mass spectrometry (AMS) measurements. One blank and one replicate were measured with each batch of samples in order to assess reproducibility and background during the extraction procedure.

AMS measurements were performed at the DREAMS (DREsden AMS) facility (Lachner et al., 2023; Rugel et al., 2016). All measurements were done relative to the standard “SMD-Be-12” with a weighted mean value of (1.704 ± 0.030) × 10⁻¹² (Akhmadaliev et al., 2013). Authigenic ${}^{\mathrm{10}}\mathrm{Be}/{}^{\mathrm{9}}\mathrm{Be}$ was calculated from the AMS results, the known amount of carrier, and the measured authigenic ⁹Be concentration from inductively coupled plasma atomic emission spectroscopy (ICP-AES) (see Simon et al., 2016). Considering the recent age of the samples, we did not correct for decay of ¹⁰Be. The correction would be of the order of 0.5 % and is an order of magnitude lower than our combined measurement precision.

The preparation and measurement of the seven new benthic foraminifera samples were undertaken based on the standard operation procedures routinely used at the MICADAS ¹⁴C laboratory facility of the Alfred Wegener Institute (Mollenhauer et al., 2021). Prior to measurement, care was taken to critically select an appropriate and sufficient number of foraminifera shells without brownish discolouration or authigenic calcite overgrowth to reduce uncertainty in the radiocarbon dates (Wollenburg et al., 2023).

2.4 Ice core ¹⁰Be record

The ice core ¹⁰Be record used in this study (Fig. 2) consists of normalized, averaged values of two ice cores: the West Antarctic Ice Sheet (WAIS) Divide ice core ¹⁰Be (Muschitiello et al., 2019; Sigl et al., 2016; Sinnl et al., 2023) and the Greenland Ice Sheet Project 2 (GISP2) ¹⁰Be fluxes (Finkel and Nishiizumi, 1997). The ice core fluxes had been corrected for climate influences by performing a regression against δ¹⁸O and snow accumulation rates (Adolphi et al., 2018). Prior to averaging, each ice core had been transferred to the IntCal20 timescale using the timescale transfer functions described in several previous studies (Adolphi and Muscheler, 2016; Adolphi et al., 2018 and Sigl et al., 2016). The glacial section of WAIS had been synchronized to Greenland Ice-Core Chronology 2005 (GICC05) by using volcanic (Svensson et al., 2020) and cosmogenic (Sinnl et al., 2023) tie points. The data from each ice core were resampled (averaged) to 40-year resolution before stacking. In order to facilitate a comparison between ice core and marine ¹⁰Be changes, we modelled the expected marine signal from the ice core record following Christl (2007). We chose a 350-year residence time of beryllium in the water column prior to deposition as this leads to good agreement of amplitudes of the modelled centennial changes in ¹⁰Be with the measured ${}^{\mathrm{10}}\mathrm{Be}/{}^{\mathrm{9}}\mathrm{Be}$ changes seen in the sediment. This 350-year residence time is within the range of values (80 ± 5 to 500 ± 25 years) reported in Arctic Ocean calculated from sedimentary fluxes and inventories (Frank et al., 2009).

3 Results

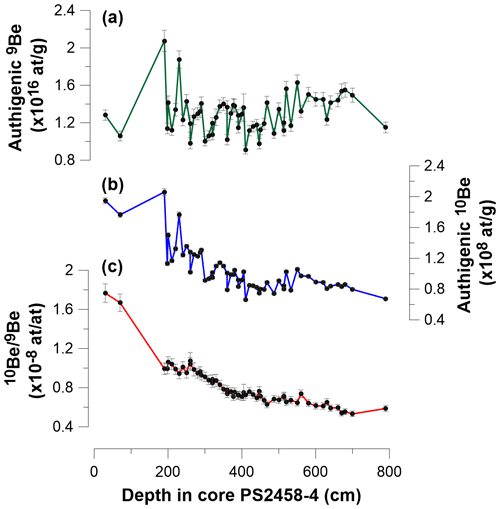
The concentrations of ⁹Be, ¹⁰Be, and ${}^{\mathrm{10}}\mathrm{Be}/{}^{\mathrm{9}}\mathrm{Be}$ atomic ratios from core PS2458-4 are displayed in Fig. 3 and the data are shown in Table S2. Five replicate samples of ${}^{\mathrm{10}}\mathrm{Be}/{}^{\mathrm{9}}\mathrm{Be}$ ratios are shown in Table S3 in the Supplement. The agreement between these replicate measurements was assessed using the coefficient of variation (CV) for each depth. We observe that the authigenic ${}^{\mathrm{10}}\mathrm{Be}/{}^{\mathrm{9}}\mathrm{Be}$ ratios demonstrated relatively low CV values, ranging from 0.98 % to 7.11 %, which is in agreement with the stated uncertainties of the ${}^{\mathrm{10}}\mathrm{Be}/{}^{\mathrm{9}}\mathrm{Be}$ ratio (Table S3). The dominant feature is an increasing trend of ${}^{\mathrm{10}}\mathrm{Be}/{}^{\mathrm{9}}\mathrm{Be}$ from the bottom to the top of the core. The modern surface sediment ${}^{\mathrm{10}}\mathrm{Be}/{}^{\mathrm{9}}\mathrm{Be}$ values ([0.54–0.76] × 10⁻⁸) from the offshore transect spanning from the Lena Delta to the core site (Table 1, Fig. 1) are consistent with ${}^{\mathrm{10}}\mathrm{Be}/{}^{\mathrm{9}}\mathrm{Be}$ of Lena water samples ([0.62 ± 0.07] × 10⁻⁸) (Frank et al., 2009) and within the same range as PS2458-4 ${}^{\mathrm{10}}\mathrm{Be}/{}^{\mathrm{9}}\mathrm{Be}$ ([0.53–1.77] × 10⁻⁸). They show an increasing trend from the Lena Delta to the open ocean (Fig. 1). The modern values close to the Lena are consistent with the lowest ${}^{\mathrm{10}}\mathrm{Be}/{}^{\mathrm{9}}\mathrm{Be}$ values of PS2458-4 during the deglaciation, when the core site was proximal to the paleo-river mouth of the Lena (see Fig. 1).

Figure 3 Concentrations of (a) ⁹Be, (b) ¹⁰Be, and (c) ${}^{\mathrm{10}}\mathrm{Be}/{}^{\mathrm{9}}\mathrm{Be}$ atomic ratios from core PS2458-4.

In order to use ${}^{\mathrm{10}}\mathrm{Be}/{}^{\mathrm{9}}\mathrm{Be}$ as a synchronization tool, we must remove the influence of mixing riverine and marine endmembers. It is nontrivial to derive a quantitative endmember mixing model solely from local sea level reconstructions because sea level only provides conceptual evidence of the variable proportions of open-ocean and riverine water masses bathing the core site. Hence, we chose a statistical model, assuming that the changes in the endmember mixing were gradual and could hence be removed by normalizing to the long-term trend in the ${}^{\mathrm{10}}\mathrm{Be}/{}^{\mathrm{9}}\mathrm{Be}$ record. The residual centennial variability in ${}^{\mathrm{10}}\mathrm{Be}/{}^{\mathrm{9}}\mathrm{Be}$ is hypothesized to be driven by ¹⁰Be production rate changes and therefore suitable for synchronization.

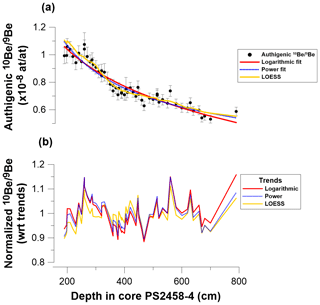
Figure 4 Sensitivity tests. (a) Three different trend fitting techniques (logarithmic, power, and LOESS). (b) Relative${}^{\mathrm{10}}\mathrm{Be}/{}^{\mathrm{9}}\mathrm{Be}$ residuals with respect to logarithmic, power, and LOESS trends.

Three different statistical models were used to test the sensitivity of our results to the choice of detrending techniques. Figure 4a illustrates the three different trend fitting techniques (logarithmic, power, and LOESS (locally estimated scatterplot smoothing) applied to the ${}^{\mathrm{10}}\mathrm{Be}/{}^{\mathrm{9}}\mathrm{Be}$ dataset. The relative ${}^{\mathrm{10}}\mathrm{Be}/{}^{\mathrm{9}}\mathrm{Be}$ residuals are plotted with respect to the logarithmic, power, and LOESS trends (Fig. 4b), and the differences fall within the measurement uncertainties of the individual data points, showing that variations of the ${}^{\mathrm{10}}\mathrm{Be}/{}^{\mathrm{9}}\mathrm{Be}$ ratio are robust against the choice of the detrending model.

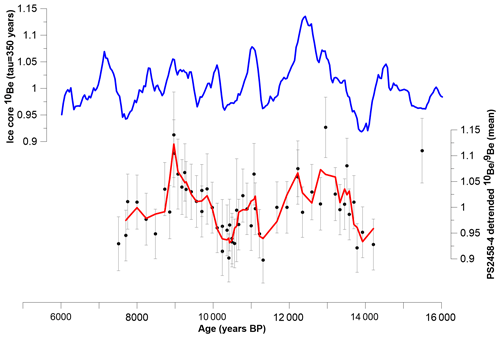
Figure 5 Ice core ¹⁰Be record with τ = 350 years (blue) and the PS2458-4 record calculated from the mean of the three detrended datasets with a three-point LOESS graph using a ΔR value of 345 ± 60 ¹⁴C years for the age model (red).

To check whether the detrended ${}^{\mathrm{10}}\mathrm{Be}/{}^{\mathrm{9}}\mathrm{Be}$ record is driven by cosmogenic ¹⁰Be production rate changes, we compare the detrended signal to the ice core ¹⁰Be record. Figure 5 shows the ice core ¹⁰Be record and PS2458-4 mean profile of the three detrended datasets with a three-point LOESS graph plotted on an initial ¹⁴C-based age scale (see the ΔR value used below). Note, however, that the following analyses have been performed on all three versions of the detrended dataset in order to test the robustness of our results against the choice of the detrending method. The variations observed in the sediment ${}^{\mathrm{10}}\mathrm{Be}/{}^{\mathrm{9}}\mathrm{Be}$ record closely follow the same pattern and relative amplitudes as the ice core ¹⁰Be record. Therefore, we suggest that the variations observed in the ${}^{\mathrm{10}}\mathrm{Be}/{}^{\mathrm{9}}\mathrm{Be}$ record indeed reflect the production rate changes in the centennial range.

In order to refine the initial ¹⁴C-based chronology and infer a regional deglacial ΔR estimate, we constructed ¹⁴C-based age–depth models for PS2458-4 using OxCal 4.4 (Ramsey, 2009) assuming a range of ΔR between −110 (Bauch et al., 2001) and +800 ¹⁴C years. Each age model was then evaluated by comparing the resulting PS2458-4 ${}^{\mathrm{10}}\mathrm{Be}/{}^{\mathrm{9}}\mathrm{Be}$ time series to the ice core ¹⁰Be record. For this purpose, we use the generalized likelihood function by Christen and Pérez, (2009) that is otherwise used for the calibration of ¹⁴C dates.

$$L_{\mathrm{\Delta }\mathrm{R}}\propto \prod _{j=\mathrm{1}}^n{\left[b+{\displaystyle \frac{(x_j-y(t_j){)}^{\mathrm{2}}}{\mathrm{2}({\mathit{\sigma }}_x^{\mathrm{2}}+{\mathit{\sigma }}_y^{\mathrm{2}})}}\right]}^{-(a+\frac{\mathrm{1}}{\mathrm{2}})}$$

In our case, the ice core provides the calibration that describes ¹⁰Be anomalies at each point in time (y(t)), which is compared to the sediment ${}^{\mathrm{10}}\mathrm{Be}/{}^{\mathrm{9}}\mathrm{Be}$ (x_j) of their modelled absolute age assuming a certain reservoir age. We use a = 3 and b = 4 based on the recommendation of Christen and Pérez (2009). This allows us to use ¹⁰Be to compare the likelihoods of different age models and thus ¹⁴C reservoir ages.

The likelihood values were calculated for each of the three different trend fitting techniques and are shown in Fig. 6. They result in a mean ΔR ± 1σ of 360 ± 75, 340 ± 50, and 335 ± 55 ¹⁴C years for the logarithmic, power, and LOESS trend fitting techniques, respectively. These values are statistically indistinguishable, and hence we opt for the arithmetic mean ΔR value of 345 ± 60 ¹⁴C years. By using a global average marine reservoir age of 503 ± 63 ¹⁴C years for the period 7.51–14.21 kyr BP (Heaton et al., 2020), we estimated a local MRA of 848 ± 90 ¹⁴C years for the Laptev Sea during the deglaciation. The age–depth model for core PS2458-4 was reconstructed using radiocarbon dates of mixed benthic bivalves and benthic foraminifera (Spielhagen et al., 2005). Therefore, our calculated ΔR and corresponding MRA reflect a benthic value.

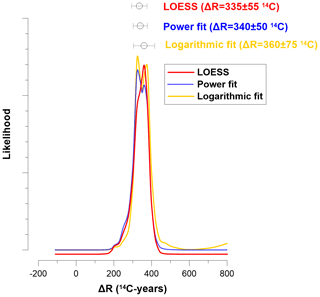
Figure 6 Likelihood results with mean ΔR ± 1σ values of 360 ± 75, 340 ± 50, and 335 ± 55 ¹⁴C years based on LOESS (red), power (blue dotted), and logarithmic (yellow) trend fitting techniques, respectively.

The depositional age–depth model with a ΔR value of 345 ± 60 ¹⁴C years for core PS2458-4 is shown in Fig. S2 in the Supplement accompanying this paper. Compared to the mean modelled ages calculated with a ΔR value of −110 ± 28 ¹⁴C years, the new modelled ages computed with a ΔR value of 345 ± 60 ¹⁴C years were observed to shift younger in the range of 429 to 707 years (Table S1 in the Supplement).

4 Discussion

We have been able to quantitatively compare the agreement between ice core ¹⁰Be and sediment ${}^{\mathrm{10}}\mathrm{Be}/{}^{\mathrm{9}}\mathrm{Be}$ for different ΔR values, and visually we can observe how the two records representing cosmogenic radionuclide production variations are in phase with each other. It is a more robust approach to compare whole time series by using a statistical method such as the likelihood function instead of matching single wiggles or shorter time periods with each other from both records. The latter method is more prone to noise in each dataset and complicates the correct identification of matching peaks. By using just one single ΔR value of 345 ± 60 ¹⁴C years, we found that there is strong agreement between the ice core ¹⁰Be and the sediment ${}^{\mathrm{10}}\mathrm{Be}/{}^{\mathrm{9}}\mathrm{Be}$ records. This indirectly supports our constant ΔR assumption, which implies a constant offset from Marine20 rather than a constant MRA (i.e., offset from IntCal20) throughout the studied period. Figure S2 in the Supplement illustrates the ¹⁴C ages of foraminifera samples plotted alongside the IntCal20 and Marine20 calibration curves. Figure S3 in the Supplement shows the non-polar global average MRA corresponding to Marine20 and the inferred MRA, calculated as the difference between the atmospheric ¹⁴C age (derived from IntCal20) and the ¹⁴C age of foraminifera and bivalve samples. The inferred MRA data points demonstrate close alignment with the Marine20 MRA + ΔR data, indicating a robust correlation. While this alignment is partially anticipated due to calibration with a constant ΔR, the agreement between the ¹⁴C-based age model and ¹⁰Be data from the ice core and sediment hence indicates that a time-variable ΔR is not required to bring the ¹⁰Be records into agreement.

When modelling the ice core data, we assumed a 350-year residence time of ¹⁰Be in the water column prior to deposition. We tested the influence of choosing different residence times of ¹⁰Be in the water column when modelling the ice core data and then synchronizing the modelled datasets with the PS2458-4 ${}^{\mathrm{10}}\mathrm{Be}/{}^{\mathrm{9}}\mathrm{Be}$ time series. Different τ values (τ = 200, 500, and 600 years) were used to model the ice core data, and the ΔR likelihood values from the LOESS-smoothed ¹⁰Be record were calculated. We observed that for all assumed τ values likelihood peaks occur at a ΔR value of 360 ¹⁴C years (Fig. 7). This indicates that the most likely ΔR value is not strongly dependent on the different assumed τ values. We found that only for the τ value of 200 years does another best likelihood estimate occur at a ΔR value of 300 ¹⁴C years, followed by the secondary likelihood maximum at a ΔR value of 360 ¹⁴C years. Figure S4 in the Supplement shows the modelled ice core time series with a τ value of 200 years; this indicates clearly larger ¹⁰Be amplitudes than what was calculated with a τ value of 350 years, which are larger than the ${}^{\mathrm{10}}\mathrm{Be}/{}^{\mathrm{9}}\mathrm{Be}$ changes seen in PS2458-4. Based on these results, it seems unlikely that the best likelihood estimate occurring at a ΔR value of 300 ¹⁴C years with τ = 200 years is real.

Figure 7 Likelihood results based on different ΔR for the LOESS-smoothed ice core ¹⁰Be using different τ values of 200, 350, 500, and 600 years.

Our calculated local benthic MRA value of 848 ± 90 ¹⁴C years is consistent with the modern values calculated by Bauch et al. (2001), which range from 295 ± 45 to 860 ± 55 ¹⁴C years. The largest modern reservoir age of 860 ± 55 ¹⁴C years is located closest to the Lena Delta, which is comparable to the setting of the location of core PS2458-4 during deglaciation around 14–12 kyr BP. Another study from the central Arctic Ocean reported MRA values of 1400 ¹⁴C years (ΔR = 1000) during the late glacial and 700 ¹⁴C years (ΔR = 300) during the Holocene (Hanslik et al., 2010).

The ΔR value was calculated during the deglaciation (14–8 kyr BP), and during this period the mean relative sea level rose by about 64 m (Klemann et al., 2015). The core was retrieved at a depth of 983 m in 1994, and at 14 and 8 kyr BP the depths were about 903 and 967 m, respectively. Moreover, as shown in Fig. 1, the modern surface ${}^{\mathrm{10}}\mathrm{Be}/{}^{\mathrm{9}}\mathrm{Be}$ values show an increasing trend from the Lena Delta to the open ocean (Fig. 1). Thus, we attribute the trend in PS2458-4 ${}^{\mathrm{10}}\mathrm{Be}/{}^{\mathrm{9}}\mathrm{Be}$ to deglacial sea level rise and the associated coastline retreat (Bauch et al., 2001; Klemann et al., 2015). During the glacial period, the core site was located close to the Lena River mouth and hence bathed in river water with low ${}^{\mathrm{10}}\mathrm{Be}/{}^{\mathrm{9}}\mathrm{Be}$. With increasing sea level and coastline retreat, open-ocean waters with higher ${}^{\mathrm{10}}\mathrm{Be}/{}^{\mathrm{9}}\mathrm{Be}$ became more dominant.

We compared our estimated ΔR value 345 ± 60 ¹⁴C years with the approach proposed by Heaton et al. (2023) to infer glacial ΔR values in polar regions. In the polar regions (outside 40° S–40° N), it is expected that during glacial episodes, there may have been regional differences in the amount of oceanic ¹⁴C depletion compared to the global non-polar ocean mean represented by Marine20. The increase in the volume and density of sea ice, limiting air–sea gas exchange, may have caused a significantly larger ΔR during the glacial era compared to the interglacial values. For glacial periods (55.0–11.5 kyr BP), Heaton et al. (2023) proposed a latitude-dependent method to infer upper bounds of the possible ΔR difference between the Holocene and the glacial period in polar regions. A lower-bound ΔR^Hol is based on samples from the Holocene and an upper-bound (glacial) ΔR^GS is calculated by increasing ΔR^Hol depending on the latitude.

The PS2458-4 record used in this study extends from about 7.5 to 14.2 kyr BP and therefore covers the early Holocene and parts of the deglacial period. Thus, from 11.5 to 14.2 kyr BP, the record extends into the glacial and samples from this period may require a glacial polar boost as proposed by Heaton et al. (2023). We calculated ΔR^Hol from ¹⁴C samples found in the online database at http://calib.org/marine/ (last access: 20 December 2023) (Reimer and Reimer, 2001). Using the weighed mean value of the five nearest ΔR values to the core location in the Laptev Sea from Bauch et al. (2001) yields a ΔR^Hol value of −95 ± 61 ¹⁴C years. ΔR^GS was calculated as ΔR^GS = ΔR^Hol + ΔR^Hol→GS, in agreement with the GS scenario as described in Heaton et al. (2023). The value ΔR^Hol→GS is dependent on the latitude of the sample, and at 78.75° N it amounts to 790 ¹⁴C years. The resulting ΔR^GS value is 695 ± 61 ¹⁴C years and is much larger than our inferred benthic ΔR value (345 ± 60 ¹⁴C years).

These differences are likely due to distinct regional changes in climate and hydrology. At the core location in the Laptev Sea, sea ice cover was less during the Younger Dryas and Heinrich Stadial 1 compared to the Holocene (Fahl and Stein, 2012), contrary to large-scale deglacial sea ice trends included in the model by Heaton et al. (2023). The expansion of regional sea ice cover during the recent past in the Laptev Sea could have further influenced the ΔR value, which then should have been larger during the Holocene compared to the early deglaciation. However, our calculated ΔR value of 345 ± 60 ¹⁴C years is larger than the modern average ΔR value of −95 ± 61 ¹⁴C years, making it unlikely that sea ice cover dynamics were the main driver of past changes in regional ΔR. Instead, as mentioned before, the local reservoir ages in the region are spatially highly variable and influenced by a hard-water effect (Bauch et al. 2001). These regional processes are thus site-specific and hence obviously cannot be covered by the approach of Heaton et al. (2023). Bauch et al. (2001) reported that the relatively old ¹⁴C age of bivalve shells collected in proximity to the Lena Delta near Tiksi Bay might be due to the influence of a local hard-water effect. This is consistent with the modern setting where the largest ΔR is found close to the Lena Delta and ΔR is lower towards the shelf edge (Bauch et al., 2001). Hence, the larger deglacial ΔR of PS2458-4 could be driven by its proximity to the Lena River during that time as evidenced by low ${}^{\mathrm{10}}\mathrm{Be}/{}^{\mathrm{9}}\mathrm{Be}$ as discussed earlier.

5 Conclusion

We present high-resolution ⁹Be and ¹⁰Be records reconstructed from core PS2458-4, which was retrieved from the continental slope of the eastern Laptev Sea in the Arctic Ocean. We demonstrate that these records are influenced by the distance of the core site to the Lena River, which changed depending on sea level. Centennial- to millennial-scale variability in the ${}^{\mathrm{10}}\mathrm{Be}/{}^{\mathrm{9}}\mathrm{Be}$ ratio can be attributed to variations in production rate and can hence be used to correlate our sediment record with ice core ¹⁰Be records.

This is the first study to reconstruct high-resolution ¹⁰Be production rate changes from ${}^{\mathrm{10}}\mathrm{Be}/{}^{\mathrm{9}}\mathrm{Be}$ records from Arctic marine sediments for correlation with ice cores, and this approach has been applied with success. We have correlated the ¹⁰Be from marine sediment core PS2458-4 with ¹⁰Be from the ice core and used a likelihood function to estimate ΔR values.

Our estimate for the deglacial benthic ΔR value for the Laptev Sea is 345 ± 60 ¹⁴C years, corresponding to an MRA of 848 ± 90 ¹⁴C years. The ΔR value will be used to refine the age–depth model for core PS2458-4 from the Laptev Sea, which could be used as a reference chronology for the Laptev Sea.