Multiproxy tree ring reconstruction of glacier mass balance: insights from Pinus cembra trees growing near Silvretta Glacier (Swiss Alps)

Glacier mass balance reconstructions provide a means of placing relatively short observational records into a longer-term context. Here, we use multiple proxies from Pinus cembra trees from God da Tamangur, combining tree ring anatomy and stable isotope chronologies to reconstruct seasonal glacier mass balance (i.e., winter, summer, and annual mass balance) for the nearby Silvretta Glacier over the last 2 centuries. The combination of tree ring width, radial diameter of earlywood cell lumina, and latewood radial cell wall thickness provides a highly significant reconstruction for summer mass balance, whereas for the winter mass balance, the correlation was less significant but still robust when radial cell lumina were combined with δ¹⁸O records. A combination of the reconstructed winter and summer mass balances allows the quantification of the annual mass balance of the Silvretta Glacier for which in situ measurements date back to 1919. Our reconstruction indicates a substantial increase in glacier mass during the first half of the 19th century and an abrupt termination of this phase after the end of the Little Ice Age. Since the 1860s, negative glacier mass balances have been dominant and mass losses accelerate as anthropogenic warming picks up in the Alps.

1 Introduction

One of the most iconic and noticeable consequences of anthropogenic climate change at high elevations is the decrease in the snow cover and the mass loss of glaciers (Zemp et al., 2019; Beaumet et al., 2021). In the European Alps, glaciers have been retreating since the end of the Little Ice Age (circa 1850) (Zemp et al., 2006), and future ice volumes are predicted to be largely reduced (Marzeion et al., 2018; Rounce et al., 2023), with the ice losses of alpine glaciers reaching up to 90 % by 2100 (Zekollari et al., 2019; Vincent et al., 2019). The ongoing reduction in the glacier volumes has very direct, negative implications for water resources, ecosystems, and livelihoods (IPCC, 2022; Huss and Hock, 2018; Immerzeel et al., 2020; Cauvy-Fraunié and Dangles, 2019; Bolibar et al., 2020).

Glaciers stand as one of the most important freshwater resources for societies and ecosystems. The recent increase in ice melt directly contributes to altered runoff patterns and rising sea levels (Anon, 2021). Recognizing their significance, the Global Climate Observing System (GCOS, https://gcos.wmo.int/en/home, last access: 4 June 2024) has designated glaciers as an essential climate variable (ECV). To reduce uncertainties in the quantification of future mass losses and their potential consequences, information on past glacier variability and changes is essential as it allows the improvement of simulations of glacier evolution (e.g., Brunner et al., 2019). In situ measurements of glacier mass balance constitute a key element in worldwide glacier monitoring. Open-access historical datasets – like those available from the World Glacier Monitoring Service (WGMS, 2024) – are crucial for an improved understanding of the glacier mass change and the calibration of models used for projections. The (net) mass balance of a glacier surface is defined as the difference between winter accumulation and summer ablation and is generally acknowledged to be the prime variable of interest to monitor and project the state of glaciers and their hydrological contribution under global warming scenarios (Hock and Huss, 2021). However, only few glaciers around the world have long-term, direct mass balance observations as these measurements require considerable human power, time, and economic resources to be sustained for a meaningful period of time (Kinnard et al., 2022). Despite recent monitoring efforts, the WGMS database – with more than 200 glacier mass balance series worldwide – contains only few records exceeding 20 years.

Various approaches have been used over the last few decades to estimate mass balance over multi-decadal timescales, often relying on remotely sensed data. Studies included the use of gravimetry (e.g., Wouters et al., 2019), the interpretation of series of multiple digital elevation models (e.g., Dussaillant et al., 2019), altimetry (e.g., Gardner et al., 2013), or glacier length change observations (e.g., Hoelzle et al., 2003). Where these approaches provided insights into past changes, the temporal resolution of the results does not provide information on the inter-annual variability and the drivers of change in glacier mass balance. Mass balance modeling based on meteorological series (Huss et al., 2008; Nemec et al., 2009) allows us to infer glacier mass balance over longer timescales at a high temporal resolution. However, accurate modeling requires long records of temperature and precipitation from high-elevation meteorological stations that are, in addition, located at the vicinity of the glaciers, but such datasets are scarce. To address this limitation, meteorological series are generally scaled to the glacier sites (Huss et al., 2021). While air temperatures often show strong a correlation over large distances (Begert et al., 2005), allowing for confident extrapolation, it is more difficult to estimate the distribution of precipitation in alpine environments, and larger uncertainties therefore persist in winter mass balance reconstructions (Sold et al., 2016).

High-elevation tree ring proxies portray past summer temperature fluctuations and changes and – to a lesser extent – winter precipitation signals, or, in other words, the main drivers of glacier fluctuations. Tree ring proxies located at high-elevation sites and at the vicinity of glaciers should thus hold the potential to extend glacier mass balance series farther back in time and offer an interesting alternative to meteorological series for mass balance reconstructions.

Several dendrochronological studies have been developed to test this hypothesis and have demonstrated the reliability of these proxies as reliable recorders of past mass balance variations. In the 2000s, seminal papers used tree ring width (TRW) series to reconstruct mass balance patterns for glaciers in Canada (Lewis and Smith, 2004; Larocque and Smith, 2005; Watson et al., 2006). Since 2007, multiproxy mass balance reconstructions combining TRW with maximum latewood density (MXD), stable isotopes, or blue intensity (BI) have been developed for glaciers in Pacific North America Wood et al., 2011; Malcomb and Wiles, 2013), Scandinavia (Linderholm et al., 2007; Hiemstra et al., 2022), or Central Asia (Zhang et al., 2019) (see Table 1 for a complete review).

Table 1 Synthesis of existing dendroclimatic studies, tree ring proxies, and meteorological data used for the reconstruction of winter (B_w), summer (B_s), and annual (B_a) glacier mass balance.

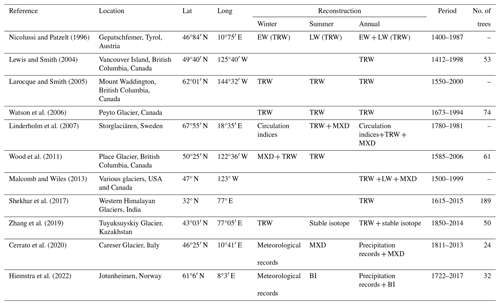
In the Alps, mass balance reconstructions are much scarcer. Nicolussi and Patzelt (1996) reconstructed 600 years of glacier mass balance for the Gepatschferner glacier using TRW records. More recently, both summer and winter mass balance dating back to 1811 have been reconstructed for the Careser glacier in the Italian Alps (Cerrato et al., 2020), with maximum latewood density (MXD) and long meteorological series available for the Alpine region (Brunetti et al., 2006, 2012, 2014; Crespi et al., 2018).

In Switzerland, GLAMOS (GLAcier Monitoring Switzerland; http://www.glamos.ch, last access: 4 June 2024) host a complete compilation of measured and re-analyzed mass balance data of Swiss glaciers, of which several span much of the 20th century (Huss et al., 2015). Despite the uniqueness of these records and their potential for validation and calibration of proxy-based reconstructions, no attempts have been undertaken so far to extend these datasets beyond the 20th century or even to preindustrial times.

In addition, recent developments in quantitative wood anatomy (QWA), relying on the analysis of dimensions of wood cells in tree rings, demonstrated that this approach offers an unparalleled measurement precision and substantial gain in temperature reconstructions (Lopez-Saez et al., 2023; Seftigen et al., 2022; Allen et al., 2022; Björklund et al., 2023). In this context, the aim of this study is to assess the reliability of a multiproxy approach, using only tree ring proxies, in extending historical winter and summer mass balance series farther into the past. To reach this goal, we employed stable isotope (δ¹⁸O; δ¹³C) and tree ring anatomy chronologies of P. cembra, which has recently been shown to be very sensitive to mean temperature over the ablation season (April–September; Lopez-Saez et al., 2023). We selected the Silvretta Glacier in the eastern Swiss Alps as our study site due to the availability of glacier mass balance data spanning from 1920 to the present, making it one of the longest continuous series in the Alps. Using increment cores from trees growing close to the Silvretta Glacier, we (i) construct TRW, anatomical, and isotope chronologies to (ii) derive annual time series of past summer temperature and winter precipitation as proxies for the summer and winter glacier mass balance. Our reconstruction provides new insights into mass balance dynamics of an Alpine glacier during the maximum and the termination of the Little Ice Age, which is a phase of important dynamics in glacier evolution but with very limited direct evidence on the rates and the exact timing of changes.

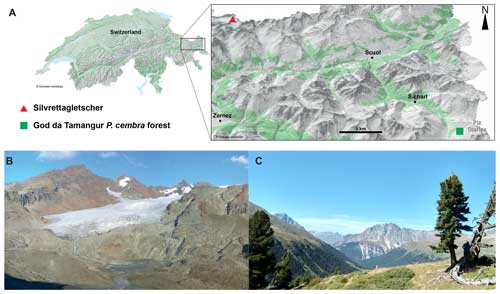
Figure 1 (a) The study site is in the eastern part of Switzerland, close to the municipality of Scuol. (b) Overview of the Silvretta Glacier (http://www.glamos.ch, last access: 4 June 2024) and (c) detailed view of a century-old P. cembra tree from God da Tamangur (Val S-charl, Scuol, Grisons, Switzerland) selected for analysis.

2 Materials and methods

2.1 Glacier and tree ring sites

The study focuses on the eastern Swiss Alps close to the borders with Austria and Italy (Fig. 1a). Silvretta (46.85° N, 10.08° E) is a small, temperate mountain glacier with a surface area of presently 2.7 km², extending from 3070 down to 2470 $\mathrm{m}\mathrm{a}.\mathrm{s}.\mathrm{l}.$ (above sea level) (Fig. 1a and b). The mean equilibrium line altitude of Silvretta was 2775 $\mathrm{m}\mathrm{a}.\mathrm{s}.\mathrm{l}.$ between 1960 and 1990, with a standard deviation of 140 m, and its first mass balance measurements date back to 1919. Seasonal observations at two stakes were conducted until 1959, which is when the stake network was increased to 40 stakes. Today, 18 stakes are surveyed seasonally. Huss et al. (2009) re-analyzed and homogenized the seasonal stake data back to 1959.

Silvretta is a global reference glacier of the WGMS, and the monitoring is maintained in the frame of GLAMOS. The tree ring site is located ca. 30 km to the southeast of Silvretta Glacier and known locally as God da Tamangur (46.68° N, 10.36° E), meaning the “forest back there” in Vallader Romansh. It is the highest, purest, and most continuous P. cembra forest in Europe (Fig. 1a and c). The forest is located at an elevation of up to 2300 $\mathrm{m}\mathrm{a}.\mathrm{s}.\mathrm{l}.$ at the end of Val S-charl (Grisons, Switzerland) on the NW-facing slope of Piz Starlex (3075 $\mathrm{m}\mathrm{a}.\mathrm{s}.\mathrm{l}.$). Lopez-Saez et al. (2023) recently showed that various wood anatomical parameters extracted from this forest allow a robust reconstruction of past temperature variability at annual to multi-decadal timescales.

2.2 Sample collection and wood processing

Tree cores were collected during a field campaign in summer 2018. To perform TRW analyses, 46 trees were sampled using a 12 mm increment borer. From each tree, we extracted two increment cores at breast height (ca. 130 cm above ground). Ring widths were measured to the nearest 0.01 mm using TSAP-Win (Rinntech, Germany), cross-dated using standard dendrochronological procedures (Stokes and Smiley, 1996), and checked for dating and measurement errors with the COFECHA software (Holmes, 1983). Ring widths from single radii were summarized to mean widths per tree. Values from 20 individual trees showing the best TRW inter-series correlation and covering the period 1802–2017 were averaged into a master TRW chronology to ensure a consistent sample depth across time.

2.3 Wood anatomical analyses

To perform wood anatomical analyses, the first of the two sampled cores from each of the 20 individuals included in the master TRW chronology was split into 4–5 cm long pieces to obtain 15 µm thick cross sections with a rotary microtome (Leica RM2255/2245). The sections were stained with safranin and astra blue to increase contrast and fixed with Canada balsam, following standard protocols (Gärtner and Schweingruber, 2013; von Arx et al., 2016). Digital images of the microsections – at a resolution of 2.27 pixels µm⁻¹ – were produced at the Swiss Federal Research Institute WSL (Birmensdorf, Switzerland) using a Zeiss AxioScan Z1 (Carl Zeiss AG, Germany). For the 20 trees, we used the ROXAS (v3.1) image analysis software (von Arx and Carrer, 2014) to automatically detect the anatomical structures for all tracheid cells and annual ring boundaries for the period 1800–2017. We excluded measurements of samples with cell walls damaged during sampling or preparation and focused on two parameters in quantitative wood anatomy analyses, namely the radial cell lumen diameter (D_rad) and radial cell wall thickness (CWT_rad) (Prendin et al., 2017; von Arx and Carrer, 2014).

Following Lopez-Saez et al. (2023), we assigned each cell to tangential bands of 40 µm in radial width (with distances measured parallel to ring boundaries). In addition, we determined the transition from earlywood to latewood cells for each ring using Mork's index = 1, at a 10 µm radial resolution (Denne, 1989; see Lopez-Saez et al., 2023, for more details). For each ring, maximum values of D_rad and CWT_rad were extracted from the bands identified as belonging to the ring. For D_rad, maximum values were extracted from each ring in the earlywood. For CWT_rad, maximum values were extracted from the latewood.

2.4 Isotopic analyses

For the isotopic analyses (δ¹⁸O and δ¹³C), we selected 10 trees showing the best inter-series correlation out of the 20 trees used for TRW and QWA analyses. Selected samples were between 242 and 634 years old at the time of sampling. Cores were cut, ring by ring, with a scalpel at the Laboratoire des Sciences du Climat et de l'Environnement (LSCE, Gif-sur-Yvette, France). The wood from each ring was processed separately between 1968 and 2017 and every fifth year between 1802 and 1967, so that, in total, 83 years were measured on each individual core. For all other years between 1802 and 1965, material from the 10 trees of the same year was pooled prior to analysis. The wood samples were grounded and α-cellulose was extracted according to the Soxhlet chemical method (Leavitt and Danzer, 1993) and homogenized ultrasonically. The oxygen and carbon isotopic composition was obtained by high-temperature pyrolysis in a high-temperature conversion elemental analyzer (Thermo Scientific) coupled to an IsoPrime mass spectrometer (see Penchenat et al., 2022, for details). The measured sample values were corrected based on an internal laboratory reference of cellulose (Whatman^® CC31) analyzed every three samples in each sequence of analysis. The analytical precisions of the instruments were within ± 0.20 ‰ for δ¹⁸O and ± 0.10 ‰ for δ¹³C, respectively, based on the standard uncertainty of the mean. A correction to the δ¹³C raw series was applied by means of linear interpolation to compensate for decreasing δ¹³C in organic matter related to fossil fuel combustion and increasing atmospheric concentration. The oxygen and carbon isotopic composition were expressed as δ as follows (Francey et al., 1999; McCarroll and Loader, 2004):

$$\mathit{\delta }=(R_{\text{samp}}-R_{\text{VSMOW}}-\mathrm{1})\times \mathrm{1000},$$

where R_samp is the isotopic ratio in the sample, and R_VSMOW the isotopic ratio in the Vienna Standard Mean Ocean Water (for oxygen) or the Vienna Pee Dee Belemnite (for carbon) (Coplen, 1996).

2.5 Establishment of wood proxy chronologies

The conventional TRW measurements were detrended with a negative exponential function to eliminate non-climatic (e.g., age-related growth trends and other biological disturbances) effects from the series (Fritts, 1976; Cook and Kairiukstis, 1990). The detrended series were then aggregated into a TRW chronology using a biweight robust mean which reduces the influence of outliers (Cook and Peters, 1981). Given the absence of any evident long-term ontogenetic trend in the anatomical series, detrending is not normally considered necessary (Carrer et al., 2018; Lopez-Saez et al., 2023) in QWA studies. As isotope chronologies were pooled prior to analysis, we did not detrend the data further. This absence of detrending has little influence on subsequent analyses as δ¹⁸O only contains minor changes related to age (Torbenson et al., 2022), while the presence of age-related trends remains debated for δ¹³C for which studies show age trends throughout the lifespan (Helama et al., 2015) – but also the lack thereof (Büntgen et al., 2021).

In a next step, empirical measures of dendroclimatic signals (Hughes et al., 2011) were computed to test the strength of the environmental information embedded in each wood proxy chronology using the maximum overlap of pairwise correlations (Bunn et al., 2013). These included the average inter-series correlation (RBAR_EFF) and expressed population signal (EPS) (Wigley et al., 1984). All analyses were performed in R Studio (R Studio Team, 2023) using the R package dplR (Bunn, 2008; Bunn et al., 2013).

2.6 Meteorological series

In this study, the gridded (1 km × 1 km) daily mean temperature and precipitation time series available from Imfeld et al. (2023), hereafter referred to as Imfeld23, were used to both identify the main drivers of radial growth and to reconstruct glacier mass balance fluctuations. The dataset (1763–2020) includes meteorological data rescued by various initiatives (Brugnara et al., 2020; Pfister et al., 2019; Brugnara et al., 2022) for the late 18th and early 19th centuries and systematic measurements available in Switzerland since 1864. Time series were initially checked and homogenized on a subdaily basis (following Brugnara et al., 2020). The dataset was then reconstructed at a 1 km × 1 km resolution using an analogue method which resamples meteorological fields for a historical period based on the most similar day in a reference period. The fields were improved with data assimilation for temperature and bias correction with quantile mapping for precipitation (Imfeld et al., 2023). Several limitations must be considered when working with this exceptional dataset: (1) the reconstruction skills decrease prior to 1864 as fewer stations provide direct observations, (2) larger reconstruction errors are observed for precipitation than for temperature due to the heterogeneous nature of precipitation, and (3) the quality of the dataset is spatially heterogeneous and considerably reduced in the Alps and the southern side of the Alps due to both the scarcity of observations and more complex topo-climatic conditions.

2.7 Climate–growth relationships

In a first step, we correlated wood proxy data with Imfeld23 by selecting the grid point centered over the God da Tamangur study site. To test for the robustness of the mixed proxies series for climate–growth relationship, we calibrated regression models on temperature and precipitation averaged over 30 to 365 d windows, starting on 1 October of the year preceding ring formation (n−1) and ending on 30 September of the year in which the ring was formed (n) using the R package dendroTools (Jevšenak and Levanič, 2018). This time window was chosen according to the growing season of P. cembra trees in the Alps (Saulnier et al., 2011). The selected time window encompasses both the accumulation and ablation periods which are used to derive the winter (1 October–30 April) and summer (1 May–30 September) mass balance series. Correlations were computed over the 1802–2017 period covered by the tree ring proxy series.

2.8 Glacier mass balance multiproxy reconstructions

In a next step, wood proxies correlated with precipitation totals and average air temperature during the ablation and accumulation periods were used as predictors to reconstruct winter (B_w) and summer (B_s) mass balance of the Silvretta Glacier, respectively. The glacier-wide time series of winter and summer mass balance available for the Silvretta Glacier (1919–2022) from the WGMS (Huss et al., 2015; WGMS, 2024) were used as predictands. Seasonal point measurements acquired in early May and September, respectively, were extrapolated to unmeasured areas of the glacier using a model-based extrapolation technique (Huss et al., 2015). Changes in the glacier geometry due to advance or retreat have a direct impact on the overall mass balance, mainly due to changes in the elevation range. These effects are included in the observational dataset of glacier-wide mass balances, as the latter always refer to the instantaneous glacier geometry. For the period before 1920, however, we do not explicitly adapt glacier geometry but assume the relations derived and tested over a 100-year period with significant changes to be representative.

A multiple linear regression model was selected for the reconstruction of winter and summer mass balances. When more than two proxies were included in the model, the number of predictors was lowered using principal component analysis. The first n principal components with eigenvalues exceeding 1 were retained in the principal component regression. We computed 10 000 summer and winter mass balance reconstructions using a split calibration–verification procedure coupled with a bootstrap approach in which 50 % of the years covered by both the mass balance observation and wood proxy datasets were randomly extracted for calibration, while the remaining years were used for validation over the 1920–2017 period. For each sampling, the root mean square error (RMSE), coefficient of determination (r² for the calibration and R² for the verification periods), reduction in the error (RE), and coefficient of efficiency (CE) statistics (Cook et al., 1995) were applied to test the predictive capacity of the transfer function. Calibration and validation statistics are illustrated for each of the TRW, wood anatomical, and isotope parameters with their 5th, 50th, and 95th percentiles. In a final step, annual mass balance (B_a) was reconstructed using the sum of the final winter and summer mass balance reconstructions.

In parallel, we reconstructed winter and summer mass balances over the 1763–2020 period using the gridded temperature and precipitation field records from Imfeld23. With the purpose to identify the optimal time window for the reconstruction, we selected the grid point closest to the Silvretta Glacier and calibrated regression models between daily temperature series computed over 1–365 d windows starting on 1 January of the year preceding observations of summer mass balance and ending on 31 December of the year in which the mass balance measurement was acquired. In addition, daily precipitation–temperature series were used as regressors for observed winter–summer mass balances. For each optimal precipitation and temperature time window identified, we computed 10 000 reconstructions following the calibration/verification procedure described for tree rings.

3 Results and discussion

3.1 Isotope and wood anatomical features chronology characteristics

We measured wood anatomical features for the period 1802–2017 on the 20 sampled trees for a total of 75–100 radial files per ring, with anatomical information catalogued by its position in each dated tree ring. After the exclusion of cells with walls damaged during sampling or preparation, a total of 2 277 779 tracheid cells were used for analysis.

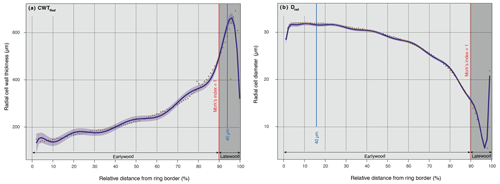
Figure 2 Profiles of (a) radial cell wall thickness (CWT_rad) and (b) radial cell diameters (D_rad) along P. cembra tree rings. Purple dots represent the mean values of 20 trees over 217 years (1800–2017) smoothed with a polynomial regression (black line) represented with its 95th confidence interval (shadowed purple areas). The blue line represents maximum values for each of the wood parameters analyzed for 40 µm wide radial bands. The red line shows the mean relative position of the transition between earlywood (light grey area) and latewood (dark grey area) according to Mork's index = 1.

Figure 2 showcases the evolution of wood anatomical parameters as a function of relative distance to ring border. It also shows that, based on Mork's index, latewood represents roughly 10 % of total ring width on average. P. cembra trees feature the classical ring structure of conifers growing in cold, temperate environments, with an increase in radial cell wall thickness (CWT_rad; Fig. 2a) and a monotonic reduction in radial diameter (D_rad; Fig. 2b) from earlywood to latewood. Statistical characteristics of the Tamangur chronologies are summarized in Table 2.

Table 2 Statistics of chronologies based on TRW, D_rad, CWT_rad, and δ¹³C, δ¹⁸O. EPS is the expressed population signal, and Rbar is the average inter-series correlation.

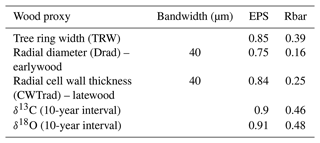
The EPS and Rbar values show that TRW has a stronger common signal (Rbar = 0.39; EPS = 0.85) than the wood anatomical chronologies (D_rad; CWT_rad), with the Rbar for the latter ranging between 0.16 (for D_rad at 40 µm radial band width) and 0.25 (for a CWT_rad at 40 µm radial band width). Several studies report lower common signals in wood anatomical parameters than in the TRW series from deciduous (Fonti and García-González, 2004) and conifer trees (Seftigen et al., 2022).

This weaker signal is generally attributed to inter-annual variability in microscopic wood features (Olano et al., 2012; Liang et al., 2013; Pritzkow et al., 2014), heterogeneous intra-annual internal physiological processes which regulate carbon assimilation and allocation in tree rings, or to relationships with intra-annual environmental variables (Yasue et al., 2000; Ziaco et al., 2016) rather than to limiting factors exerted over the entire growing season (Eckstein, 2004; Ziaco et al., 2016). Regarding isotope parameters, Rbar values computed for 10-year windows are 0.46 (δ¹³C) and 0.48 (δ¹⁸O).

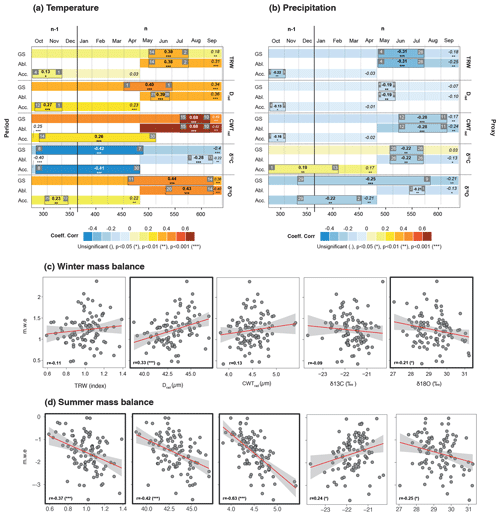
Figure 3 Correlations between the TRW, D_rad, CWT_rad, δ¹³C, and δ¹⁸O chronologies from God da Tamangur, gridded temperature (a) and precipitation (b) fields from Imfeld23, as well as winter (c) and summer (d) mass balance series from the Silvretta Glacier. In panels (a) and (b), correlation coefficients and their associated p values are presented in italics for the growing (GS; 1 October (n−1)–30 September (n)), ablation (Abl; 1 May (n)–30 September (n)), and accumulation (Acc; 1 October (n−1)–30 April (n)) seasons. Time periods with the highest coefficients (highlighted in bold) are delineated by black rectangles. The beginning and end of these optimal periods are denoted by white numbers on a grey background.

3.2 Climate–growth relationships

Correlation coefficients between the TRW chronology from God da Tamangur and the gridded temperature and precipitation fields from Imfeld23 show that the spring to summer temperature increase is the main driver of radial growth (r_max = 0.38; p < 0.001; 14 May–2 August) between 1802 and 2017 (Fig. 3a). For wood anatomical parameters, significant correlations exist between radial diameter (D_rad) and early-spring to early-summer temperatures (r = 0.40; p < 0.001; 1 April–1 July). This association spans a longer seasonal window than the ones reported by Carrer et al. (2017, 2018) for earlywood cell areas of P. cembra and P. abies trees in the Italian Alps. In these studies, correlations were restricted to mid-May/early June and mid-June/mid-July, respectively. At God da Tamangur, highest correlations were obtained between the CWT_rad chronology and temperatures over a 58 d time window extending from 15 July to 10 September (r = 0.68; p < 0.001; Fig. 2). R values computed between CWT_rad and summer temperatures agree with results reported by Carrer et al. (2018) for the Italian Dolomites (r > 0.6 with 15 July–15 August temperatures; 1926–2014) or Ştirbu et al. (2022) for the Carpathians (r = 0.65 with July–August temperatures; 1961–2013). The period overlaps with the wall-thickening phase observed in latewood during summer for high-elevation P. abies trees (Gindl et al., 2001; Rossi et al., 2008). Its duration also agrees with current knowledge on xylogenesis, which can last from 1 (mild environments) to 2 months (cold environments) in latewood cells (Rossi et al., 2008; Cuny et al., 2013; Castagneri et al., 2017).

The δ¹³C chronologies are negatively correlated with mean daily temperature from October (n−1) to September (n) (r = −0.4; p < 0.001) and especially from 8 October (n−1) to 7 May (n) (r = −0.42; p < 0.001) (Fig. 3a). Mean daily temperatures from October (n−1) to September (n) (r = 0.36; p < 0.001) and during the growing season (11 April–14 September; r = 0.44; p < 0.001) are the main drivers of δ¹⁸O variations. A negative correlation is also found between δ¹³C and 26 May–26 July (n) (r = −0.22; p < 0.01) and between δ¹⁸O and fall (n−1) to summer (n) precipitation totals (r = −0.25; p < 0.01) (Fig. 3b). Both chronologies also portray a significant association with winter precipitation (October (n−1)–April (n)) that is positive for δ¹³C (r = 0.17; p < 0.01) and negative for δ¹⁸O (r = −0.21; p < 0.01).

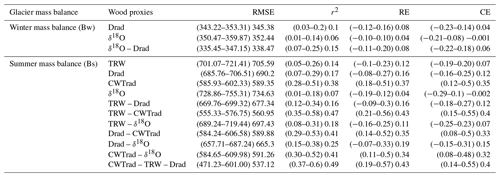
Table 3 Statistics of summer (B_s) and winter (B_w) mass balance reconstructions based on several combinations of tree ring proxies.

The analysis of δ¹³C and δ¹⁸O stable isotope signals in P. cembra trees has been initiated only recently in the Alps (Haupt et al., 2014; Arosio et al., 2020) and in the Carpathians (Nagavciuc et al., 2021, 2022; Kern et al., 2023). In the Alps, studies have focused on the detection of age-related trends in the series (Arosio et al., 2020) but did not provide correlation profiles with climatic variables. In the Carpathians, by contrast, positive correlations were reported with April–August temperatures δ¹⁸O (Nagavciuc et al., 2021), in line with our results. By contrast, no significant correlation was found between δ¹³C and temperature. Consistent results are also found with precipitation for δ¹³C in both Tamangur and Carpathian chronologies which show a negative correlation with June precipitation. The winter signal embedded in the δ¹⁸O chronologies of God da Tamangur echoes the significant associations observed between the isotope series and winter precipitation in the Arctic (Holzkämper et al., 2008), Kazakhstan (Qin et al., 2022), the Tibetan Plateau, northwestern China (Grießinger et al., 2017; Wernicke et al., 2017; Liu et al., 2013; Qin et al., 2015), Iran (Foroozan et al., 2020), or Pakistan (Treydte et al., 2006) and are thus interpreted as the result of the trees' use of precipitation from before the growing seasons stored in the soil or in groundwater reservoirs. In the Russian Arctic, Holzkämper and Kuhry (2009) suggested that the thickness of the snowpack and the timing of snowmelt has a strong impact on the δ¹⁸O composition of tree ring α-cellulose because moisture in the early summer is most critical for wood formation. Soil and atmospheric droughts caused by a deficit in previous winter alpine snowfall therefore lead to δ¹⁸O enrichment in tree ring α-cellulose.

3.3 Multiproxy glacier mass balance reconstruction

Based on the above climate–growth relation analyses, we tested several combinations of parameters to reconstruct winter (B_w) and summer (B_s) glacier mass balances. The isotopic parameter δ¹³C has been excluded from the combinations for B_w and B_s reconstruction because statistically, it is not significant. Statistics of these reconstructions are reported in Table 3.

For the winter mass balance B_w, the best combination includes D_rad and δ¹⁸O. Both proxies are sensitive to precipitation during the accumulation period and show a significant positive (D_rad; r = 0.33; p < 0.001) and negative (δ¹⁸O; r = -0.21; p < 0.05) correlation with the winter mass balance series recorded at Silvretta Glacier (Fig. 3c). Both parameters allow a statistically significant reconstruction (RE = 0.08; CE = 0.06) over the period 1920–2017 (Table 3; Fig. 4a) covered by glaciological measurements and tree proxy reconstructions. At decadal timescales, the 11-year spline-smoothed winter mass balance reconstructions correlate at 0.65 with observations and capture positive (i.e., from the late 1940s to the late 1950s) and negative (i.e., from the 1960s to 1980s) anomalies over the entire period (Fig. 4a).

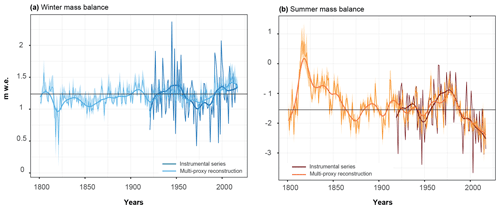
Figure 4 Winter (a) and summer (b) mass balance of the Silvretta Glacier reconstructed from tree ring proxies over the 1802–2017 period. The thin light blue and orange curves illustrate inter-annual variations in winter and summer mass balance, respectively, derived from δ¹⁸O and D_rad (winter) and TRW, CWT_rad, and D_rad (summer). The dark blue and dark brown curves represent the winter and summer mass balance records of Silvretta Glacier from 1919–2017. Thick lines indicate decadal variations smoothed with an 11-year spline. The black line represents the mean of the winter (a) and summer (b) mass balance reconstructed series.

The best combination of proxies for summer glacier mass balance B_s includes the TRW, D_rad, and CWT_rad chronologies (Table 3; Fig. 3d), each showing significant negative correlations with B_s at −0.37 (p < 0.001), −0.42 (p < 0.001), and −0.63 (p < 0.001), respectively. Based on these proxies, the two first principal components of the principal component regression allow a robust reconstruction of B_s (r² = 0.49) and significant RE (0.43 (0.19–0.57)) and CE (0.4, (0.14–0.55)) statistics (Table 3). These values exceed those computed by (Cerrato et al., 2020) using P. cembra MXD series for Careser glacier over the period 1967–2005 (r² = 0.45). The summer balance reconstruction also depicts the positive (1960s to early 1980s) and negative (i.e., 1950s and since the late 1980s) anomalies found in the measurements (Fig. 4b).

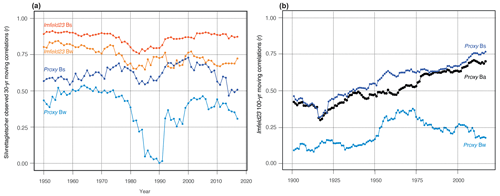
Figure 5 (a) 30-year moving correlations (r) of summer (B_s) and winter (B_w) mass balances estimated from gridded temperature and precipitation fields (Imfeld et al., 2023) and multiple wood proxy B_s and B_w mass balance reconstruction (this study) with the Silvretta Glacier B_w and B_s records (Huss et al., 2015). (b) 100-year moving correlations of proxy B_s, B_w, and annual (B_a) mass balance reconstruction (Imfeld et al., 2023).

Figure 5 shows the 30-year moving correlations computed between the reconstructed and observed glacier mass balances. Specifically, for winter, it shows a lower correlation for time windows ending between 1981 and 2000 and the smallest correlations (r < 0.25) for time windows ending between 1983 and 1999 (Fig. 5a). As this period coincides with the last phase of positive annual mass balance in the (Southern) Alps (Huss et al., 2015), one can hypothesize that the limited correlations could be related to specific environmental conditions at the site and the complexity of capturing annual glacier mass balance adequately with the tree ring proxies selected for the B_w reconstruction. In addition, no in situ measurements of B_w exist between 1984 and 2003 (Huss and Bauder, 2009), and these gaps in winter mass balance series were filled with a calibrated mass balance model driven by data from nearby meteorological stations (Huss et al., 2015). Therefore, it is also possible that the decrease in correlation may be attributed in part to the quality of the mass balance time series and not the result from the tree proxy dataset.

For B_s, the 30-year correlations between observations and the multiproxy reconstructions consistently exceed r = 0.48 throughout the period covered by the reconstruction, with a limited standard deviation (0.06) between 1920 and 2017 (Fig. 5a). However, while correlation values show an increasing trend (from r = 0.52–0.74) for time windows ending before 2000, they significantly decrease to reach r = 0.50 by 2017. This reduction in prediction skills, from r = 0.74 to r = 0.50, starting in the 1970s, is comparatively less marked than the one documented by Cerrato et al. (2020) (from 0.45 to r = 0.2) for P. cembra, based on MXD records, despite occurring a decade earlier. These results confirm that our multiproxy reconstruction records only suffer from limited divergence and standardization issues which notoriously affect both TRW and MXD records but seem to be largely absent in wood anatomical series (Cook et al., 1995; Björklund et al., 2019; Cerrato et al., 2019).

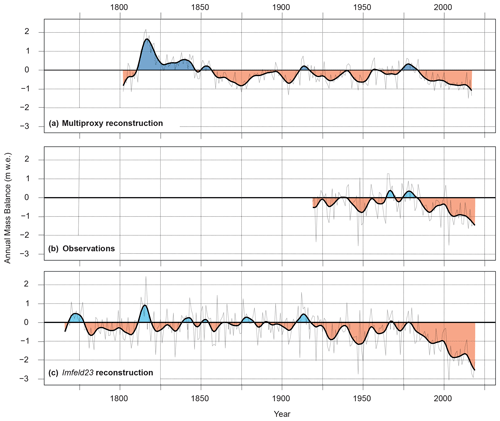
Figure 6 Comparison between annual (thin grey lines) and 11-year spline-smoothed (thick lines) variations in (a) the multiple wood proxy annual mass balance (Ba) reconstruction, (b) observed Ba, and (c) Ba reconstructed from gridded temperature and temperature fields (Imfeld et al., 2023). Periods with positive mass balance are shown in blue, and periods with negative mass balance are given in red.

Considering the annual glacier mass balance reconstruction (B_a), we finally combined proxy values for winter and summer balance (Fig. 6a), thus extending the GLAMOS record by 120 years. At inter-annual timescales, Pearson correlation coefficients between the wood proxy annual glacier mass balance and in situ measurements at the Silvretta Glacier (Fig. 6b) are highly significant at r = 0.62 (p < 0.05). When applying a 11-year spline to both the reconstructed and measured time series, correlations reach r = 0.87. The influence of proxy winter balance on proxy annual balance is limited, explaining only 8 % of the annual average variance. These results are consistent with Zemp et al. (2015) for glaciers in the European Alps, where winter mass balance explains 6 % of the annual mass balance variations on average.

3.4 Comparison with Imfeld23 records and reconstructions

For the mass balance of the Silvretta Glacier, correlations between the observed glacier mass balance and Imfeld23 are higher than those obtained with the wood proxies. Over the ablation period, lasting from 1 May to 30 September, the correlation is r = 0.85 (p < 0.001; 1920–2017) and reaches r = 0.87 (p < 0.001) for the optimal time window extending from 17 May to 19 September. Correlations between precipitation from Imfeld23 and B_w are r = 0.48 (r < 0.001) over the accumulation period sensu stricto from 1 October to 30 April and r = 0.49 for the optimal time window extending from 17 October to 9 March (r = 0.49; p < 0.001), respectively. At the annual scale, the Imfeld23 reconstruction explains 74 % of annual glacier mass balance variability observed over the period 1920–2017. Over the full period (1802–2017), the B_s, B_w, and B_a wood proxy reconstructions significantly correlate (r = 0.63, 0.15, and 0.61; p < 0.001) with the reconstruction based on Imfeld23 (Fig. 6c). Synchronous periods are characterized by positive anomalies in the 1810s, 1840s, 1910s, and the late 1970s, and likewise, negative anomalies are observed in the two time series in the 1870s, the early 20th century, the 1950s, and since the mid-1980s. This is well in line with contemporary and documentary sources, as well as information on dated moraines available for the Swiss Alps (e.g., Zumbühl et al., 2008; Nussbaumer and Zumbühl, 2012; Schimmelpfennig et al., 2014). More interestingly, the proxy reconstruction shows a strong glacier mass increase in the first part of the 19th century and confirms the abrupt mass loss previously reported in the Alps in the 1850s and 1860s considered to correspond to the end of the Little Ice Age (Holzhauser et al., 2005; Vincent, 2005; Zemp et al., 2006; Painter et al., 2013). Sigl et al. (2015, 2018) hypothesized that the mass gain in the Alps in the early 19th century could result from the strong negative radiative forcing induced by at least five large tropical eruptions between 1809 and 1835 (Sigl et al., 2015; Toohey and Sigl, 2017) in tandem with the Dalton solar minimum (Usoskin et al., 2013; Jungclaus et al., 2017).

By contrast to the wood proxy reconstruction, this positive annual mass balance pattern is not reproduced by the Imfeld23 reconstruction, and therefore, the moving correlations computed for 100-year time periods between both records thus decrease significantly before the 1960s (Fig. 5b). One could hypothesize that this divergence during preindustrial times between the two reconstructions could be attributed (i) to tree ring proxy, particularly with respect to their reduced explanatory power in colder periods as evidenced by time windows ending between 1983 and 1999 (see Sect. 3.3). The divergence could also stem (ii) from the optimal fixed-length window utilized in the Imfeld23 reconstruction and calibrated on recent environmental conditions. This methodology has assumed a constant length for the accumulation and ablation seasons since the early 19th century, despite significant variations in temperature, precipitation, and snowpack conditions compared to the present (Carrer et al., 2023). Such an assumption may introduce bias into the reconstruction (Cerrato et al., 2020). Finally, (iii) the complete absence of high-elevation records in the Imfeld23 dataset prior to 1864 (see Sect. 2) also raises questions about the robustness of the reconstruction prior to the mid-19th century. It is possible that the gridded temperature and precipitation fields may fail to accurately reproduce changes in winter precipitation distributions in the early stages of their reconstruction.

4 Conclusions

Mountain glaciers are reliable and unequivocal indicators of climate change due to their sensitivity to changes in temperature and precipitation (Zhang et al., 2019). The advance or retreat of a glacier is thereby related to the amount of snow accumulation, as well as snow and ice melt, commonly referred to as its mass balance. This study allowed developing of multiproxy chronologies from P. cembra wood traits based on the dynamic relationships between climate processes that jointly influence tree (cell) growth and glacier mass balance. The Silvretta Glacier has been monitored since 1919 and therefore forms a very robust baseline against which the wood proxy reconstruction presented here can be compared. The study also constitutes an important step in extending glacier mass balance records beyond the instrumental period for the Swiss Alps. By combining wood anatomical parameters and stable isotopes, we obtain very promising results for seasonal glacier mass balance reconstructions because some proxies are sensitive to mean temperatures over the entire ablation period, while others estimate winter precipitation during the accumulation period. Our results based on multiple wood proxies reveal that glacier mass gains during the final stages of the Little Ice Age were strongest between 1810 and 1820. Considering the synchronicity of increasing mass balance with a cluster of volcanic eruptions and diminished solar activity, we align with Sigl et al. (2015, 2018) in hypothesizing that these gains may partly result from the co-occurrence of volcanic forcing and the Dalton minimum. This period of positive mass balances and resulting glacier advances rapidly ended in the 1860s and 1870s when a first episode of substantial negative mass balances led to a first phase of “modern” glacier downwasting.