the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
A spectral approach to estimating the timescale-dependent uncertainty of paleoclimate records – Part 2: Application and interpretation
Torben Kunz
Jeroen Groeneveld
Thomas Laepple
Proxy climate records are an invaluable source of information about the earth's climate prior to the instrumental record. The temporal and spatial coverage of records continues to increase; however, these records of past climate are associated with significant uncertainties due to non-climate processes that influence the recorded and measured proxy values. Generally, these uncertainties are timescale dependent and correlated in time. Accounting for structure in the errors is essential for providing realistic error estimates for smoothed or stacked records, detecting anomalies, and identifying trends, but this structure is seldom accounted for. In the first of these companion articles, we outlined a theoretical framework for handling proxy uncertainties by deriving the power spectrum of proxy error components from which it is possible to obtain timescale-dependent error estimates. Here in Part 2, we demonstrate the practical application of this theoretical framework using the example of marine sediment cores. We consider how to obtain estimates for the required parameters and give examples of the application of this approach for typical marine sediment proxy records. Our new approach of estimating and providing timescale-dependent proxy errors overcomes the limitations of simplistic single-value error estimates. We aim to provide the conceptual basis for a more quantitative use of paleo-records for applications such as model–data comparison, regional and global synthesis of past climate states, and data assimilation.
- Article
(2115 KB) - Full-text XML
- Companion paper
-
Supplement
(211 KB) - BibTeX
- EndNote
Proxies of climate variables, such as geochemical indicators of temperature in marine sediments or ice cores, are a valuable source of information about the earth's climate prior to the instrumental record. However, these records are an imperfect representation of past climate as they are also influenced by non-climatic factors in addition to the climate signal. Errors in a proxy record mean that the past climate inferred from these proxy records is uncertain; understanding these associated uncertainties is important for all quantitative uses of climate proxies, such as data assimilation (Goosse et al., 2006), model–data comparisons (Lohmann et al., 2013), hypothesis testing (Hargreaves et al., 2011), and the optimal combination and synthesis of climate records (Marcott et al., 2013; Shakun et al., 2012). Finally, knowing the error as a function of environmental or proxy-specific parameters also allows for the optimization of the sampling and measurement strategy in order to obtain the information required to test specific hypotheses.
Errors in a proxy record, defined here as differences between the climate inferred from the proxy record and the true climate, are introduced at multiple stages between the true climate signal and final inferred past climate time series (see, for example, Evans et al., 2013; Dee et al., 2015; Dolman and Laepple, 2018). Importantly, the resulting errors are not all independent in time, rather they are often correlated and timescale dependent (Fig. 1). Currently the temporal covariance structure of proxy uncertainties is largely ignored in the literature (but see Moberg and Brattström, 2011). In many cases, a single number, perhaps derived from a calibration data set, is reported as the uncertainty for a given proxy. However, its utility is very limited without additional information about the structure of the error. For example, consider an error of 1.5 ∘C. If the error were due to an uncertainty in the temperature to proxy relationship, e.g., the error of the intercept of a linear calibration equation, the uncertainty of a time slice containing multiple observations would still be 1.5 ∘C as the error does not reduce by averaging more samples calibrated using the same equation (Fig. 1c), while the error from calibration on a difference between two time slices would be zero. On the other hand, if this error were independent in time and thus between samples, e.g., if it were related to the error of a measurement device, the uncertainty of a time slice based on nine samples would be just (1.5 ∘C ) = 0.5 ∘C, while the error in the difference between two time slices would be approximately 0.7 ∘C (). Indeed, a number of recent studies assume independence in time (and space) and thus arrive at unrealistic uncertainty estimates (e.g., Fedorov et al., 2013; Shakun et al., 2012; Marcott et al., 2013).
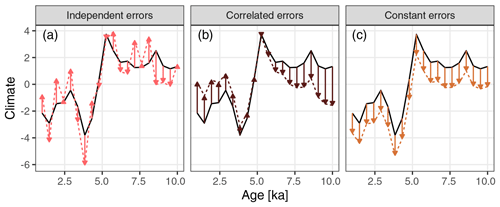
Figure 1Illustration of different timescale dependences of proxy errors. The independent and correlated errors both have standard deviations of 1.5 ∘C, while the constant error is 1.5 ∘C with zero standard deviation.
More difficult than either fully independent errors (Fig. 1a), or constant errors or “biases” (Fig. 1c), are correlated errors that manifest as slowly varying biases (Fig. 1b) for which we need to quantify both the magnitude and autocorrelation structure. The idea we introduce in Part 1 (Kunz et al., 2020) is to work in the spectral domain as this allows for an explicit representation of the timescale dependence of uncertainty. Assuming a stationary climate process, the power spectrum of a proxy error contains all the information required to derive timescale-dependent uncertainties, and working in the frequency domain further simplifies the estimation of the different error components. A number of additional useful quantities, such as the uncertainty in a time-slice mean, the uncertainty in the difference between two time slices, and the expected timescale-dependent correlation between replicates of proxy records and between proxy records and the true climate, can easily be derived from the error spectrum.
In Part 1, we discuss the theoretical basis for and give a full mathematical derivation of the Proxy Spectral Error Model (PSEM). Here in Part 2, we aim to facilitate the use of PSEM in paleoclimate applications. Thus, we (1) sketch the concepts behind the different error components in a more applied way, (2) provide heuristic approaches to parametrize the climate spectra and other parameters of the error model, (3) provide examples using virtual and actual sediment cores, and (4) provide an R package implementing the spectral error estimation method.
In this section, we illustrate the error spectrum framework for the specific example of temperature-related proxies in the shells of planktic foraminifera recovered from marine sediment cores. The major processes contributing uncertainty to these proxy records have been explored using physically motivated proxy forward models that simulate pseudo-proxies from an assumed true input climate (Laepple and Huybers, 2013; Dolman and Laepple, 2018). These processes include seasonality in the creation of proxy signal carriers (e.g., foraminiferal tests), aliasing due to under-sampling of the seasonal climate cycle, mixing and smoothing of the signal due to bioturbation, and independent measurement and processing error. One approach to estimating the uncertainty for a given metric and proxy record is to use such a forward model to simulate ensembles of pseudo-proxy records, calculate the metric for each, and then examine their statistical properties. In the approach we propose here, we do not simulate pseudo-proxies for a specific climate time series, rather we make some simplifying assumptions about the properties of the power spectrum of the climate and then estimate the uncertainty directly from expressions for the power spectra of the errors associated with proxy creation. The advantage of this analytical method over simulation is that it allows for very rapid assessments of proxy error, the relative contribution of different error sources, and the expected correlation between replicated proxy records and between proxy records and the true climate – and all of these at multiple timescales. This makes it possible to scan potential coring locations, to develop sampling and measurement strategies to optimize future data acquisition, and to help interpret existing records. Finally, PSEM also provides a basis for estimating the spectrum of climate variability from error-corrupted proxy records at a future stage.
2.1 A simple model for the power spectrum of the climate
The uncertainty from some proxy error sources depends on the strength of the variations in the climate. For example, the error from smoothing a time series is zero if the time series is constant and becomes larger the more the time series varies. We therefore need a model for the variability of the climate, and we describe this using the power spectrum of the climate S(ν) (see Sects. 2.1 and 3.1 of Part 1). While the developed approach allows for any choice of a climate spectrum, e.g., from complex climate models or estimated from observations, we here outline a heuristic method suitable for marine sea-surface temperature (SST) and surface δ18O calcite records. This method is implemented in the PSEM R package and requires only the core position and habitat depth range as input parameters.
A detailed, site-specific power spectrum of the climate can only easily be estimated empirically for timescales up to the length of the instrumental record. At longer timescales, the climate spectrum can be approximated by a power-law-type scaling, , where the exponent β characterizes the scaling behavior and is thought to lie between 0 and 2 (Lovejoy, 2015; Schmitt et al., 1995), and α scales the amplitude of climate variation. Here we take the pragmatic approach of splicing zonally averaged empirical climate spectra for frequencies above years with theoretical power-law spectra at lower frequencies (Laepple and Huybers, 2014b) (Fig. 2). As the empirical spectra were estimated from annual-resolution ocean temperature records, we set power to zero at frequencies above years.
For the power-law section of the climate spectra, α was chosen so that the low-frequency power-law spectra are continuous with the empirically estimated high-frequency regions of the spectra. We typically assume a value of 1 for β as this was found to be a good description of Holocene SST variability (Laepple and Huybers, 2014a), but this parameter can be freely specified, and we illustrate the affect of varying this parameter in Appendix A. To allow these spectra to also be used for δ18O records, we recalibrate them to δ18O calcite units using a standard calibration (Bemis et al., 1998), which in terms of variance is effectively just a division by a factor of 4.82, assuming that the δ18Ocalcite is generally dominated by temperature variations at these timescales. A function to generate these spliced empirical and power-law spectra is supplied as part of the PSEM R package.
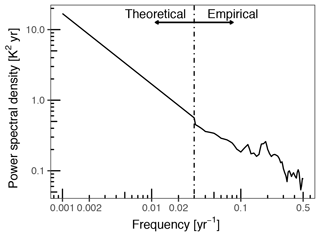
Figure 2An example spliced empirical and power-law power spectrum of ocean temperature (0–120 m water depth) for 20∘ N latitude. A small discontinuity at ν=0.03 is visible, since to increase the robustness of the intercept estimate, the splicing is implemented by matching the integrated spectra between ν=0.03 and ν=0.1.
To this stochastic climate, we add a deterministic seasonal cycle modeled as the power spectrum of a sine wave with a frequency of year (see Sect. 3.2 in Part 1). For a given location, we parametrize the amplitude of the seasonal cycle using a gridded data set of assimilated physically consistent δ18Osw and temperature (Breitkreuz et al., 2018). The δ18Ocalcite value was calculated on the Pee Dee belemnite (PDB) scale from δ18Osw and temperature using the equations of Shackleton (1974).
Additionally, the amplitude of earth's seasonal temperature cycle varies over a precessional orbital cycle with an approximate frequency of kyr. The magnitude of this amplitude modulation depends primarily on latitude, and we assume this is equal to the amplitude modulation of incoming solar radiation at a given latitude (Berger and Loutre, 1991). This introduces a low-frequency ( kyr) deterministic signal to the climate.
2.2 Proxy error processes as filters
During the creation of a climate proxy record, some of the processes that introduce errors, defined here as differences between the proxy record and the true climate, can be thought of as acting like filters on the true climate signal. Here we illustrate the concept of PSEM by considering the smoothing effects of bioturbation and the width of sediment slices from which signal carriers, e.g., foraminiferal shells, are extracted.
Bioturbation at the water–sediment interface mixes the upper few centimeters of sediment, thereby mixing together signal carriers of different ages. This acts like a smoothing filter on the climate signal, reducing the amplitude of climate variations in a frequency-dependent way. The magnitude of the reduction at each frequency depends on the filter characteristics; using the simple physical bioturbation model of Berger and Heath (Berger and Heath, 1968), the filter width, τb, is simply the bioturbation depth divided by the sedimentation rate. In the frequency domain, this is equivalent to multiplying the power spectrum of the climate with the transfer function of the filter and results in a power spectrum of the error, as described in Sects. 2.2 and 3.1 of Part 1.
Similarly, when a sediment core is sampled, the proxy signal carriers are picked from a series of slices of sediment, each with a finite width of typically 1–2 cm. This again acts as a filter, this time a running mean filter with width, τs, equal to the ratio of the slice thickness and sedimentation rate. As for the bioturbation filter, in the frequency domain the effect on the original signal is obtained by multiplying the power spectrum with the transfer function of the filter (see Sects. 2.3 and 3.1 in Part 1).
Error relative to the reference climate
So far we refer to a proxy error as a difference between the measured proxy value and the “true” climate signal. The bioturbation and slice thickness filters smooth the climate signal so that the proxy differs from the true climate. However, in practice, values of proxy variables from marine sediments are rarely interpreted as representing the instantaneous climate state; it is understood implicitly that some smoothing has taken place. The error therefore depends on the interpreted timescale of the proxy record, and so, in the spectral error model, we define error relative to the true climate at a specific timescale provided by the user (see Sect. 2.4 in Part 1). The power spectrum of this error is shown as the dashed brown line in Fig. 3a.
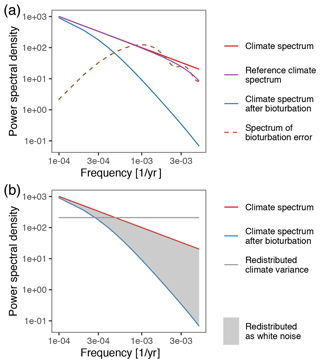
Figure 3A conceptual representation of PSEM. (a) The true climate signal is filtered (smoothed) by processes such as bioturbation. This modifies the power spectrum of the climate (red) in a frequency-dependent way, producing the power spectrum of the climate signal after bioturbation (blue). Proxy records are assumed to represent the climate at a particular timescale (e.g., centennial, millennial), and the reference climate spectrum (purple) is the power spectrum of the true climate smoothed to this timescale. The error that bioturbation and other smoothing produces (dashed brown) is a function of the reference and bioturbated climate spectra. (b) The power of the true climate signal that is removed by bioturbation and other smoothing processes (gray shaded region) can be redistributed as a white noise error component (gray horizontal line) if the time period over which individual signal carriers are created (e.g., foraminiferal tests calcify) is short relative to the timescale of the smoothing processes. This white noise term is reduced if multiple signal carriers are measured together or if their values are averaged together later.
2.3 Redistribution of climate power due to under-sampling
The proxy quantity (e.g., δ18O, Mg Ca, etc.) is often measured on a finite number, N, of discrete signal carriers such as foraminiferal tests, each of which calcifies and records or samples a short snapshot of the climate, typically 2–4 weeks for pelagic foraminifera (Bijma et al., 1990; Spero, 1998). The bioturbation and slice thickness filters can be thought of as probability density functions (PDFs) that describe the portion of time from which the climate signal is sampled by these N signal carriers. As this is a finite sample, the resulting proxy value is an estimate of the mean value and contains a stochastic noise component in addition to the deterministic error caused by the smoothing. The variance of this stochastic error term is equal to the integral of the difference between the climate spectrum and the spectrum of the smoothed climate signal divided by the number of individual signal carriers in a sample, shown as the gray line and shaded area in Fig. 3b (see Sects. 2.3 and 3.1 in Part 1). As N tends to infinity, the error due to under-sampling tends toward zero. This may be the case for proxies such as Uk'37 whose measurements consist of many thousands of organic molecules.
2.4 The seasonal cycle
The often large cyclical variation in climate variables associated with the seasonal cycle can also add noise to a proxy record if the seasonal cycle is not adequately sampled by individual signal carriers, each of which records a short portion of the cycle (Laepple and Huybers, 2013; Schiffelbein and Hills, 1984). Additionally, a bias can be introduced in the record if the signal carriers are produced in greater numbers during a particular part of the year (Jonkers and Kučera, 2015; Leduc et al., 2010). In the case of the orbital modulation of the amplitude of the seasonal cycle, this bias becomes a slowly varying error, and the variance of the noise process also varies over the course of an orbital cycle (see Sect. 3.2 of Part 1).
In the spectral error model, the seasonal cycle is represented by the discrete power spectrum of a deterministic sine wave (Eq. 1 in Part 1). The interaction between this signal and seasonality in the production of signal recorders determines the magnitude of two errors: a white noise error generated by the under-sampling of the seasonal cycle and a bias due to only sampling a portion of the seasonal cycle.
We represent seasonality in the production of signal carriers here by saying that production occurs continuously over a set fraction of the year, τp (see Sect. 2.2 in Part 1). This can also be viewed as a kind of filter, this time on the discrete spectrum of the deterministic sine wave seasonal cycle. The transfer function of this filter can be constructed in an analogous way to those for bioturbation and slice thickness, and the difference between the filtered and unfiltered spectra gives the error due to sampling only part of the seasonal cycle (see Sect. 3.2 in Part 1). Again, the finite time period each carrier records means that the portion of the seasonal cycle during which signal carriers are created is sampled by the individuals, and this generates additional redistributed white noise in the proxy signal.
In the absence of orbital modulation, four parameters determine the errors generated by filtering and sampling the seasonal cycle: , the variance of the full seasonal cycle; τp, the proportion of the seasonal cycle during which signal carriers are produced; 〈ϕc〉, the expected midpoint (phase) of the signal carrier production; and Δϕc, which represents uncertainty in the phase of the carrier production (Sect. 2.5 in Part 1).
If the signal carriers are produced all year round, τp=1, there is no bias, and the white noise component has a variance equal to the variance of the full seasonal cycle divided by the number of signal carriers per sample, N.
If the signal carriers are produced for only part of the year, τp<1, but with completely unknown timing (we do not know which months, Δϕc=2π), then the expected variance of this white noise is equal to the difference between the variance of the full seasonal cycle and the variance of the seasonal cycle filtered with a running mean filter of width, τp. In the spectral domain, this is analogous to the gray shaded area in Fig. 3a but this time for the discrete spectrum of the deterministic sine wave seasonal cycle. In this situation, the sign of the seasonal bias is unknown. It appears in the error spectrum as power at frequency zero.
If the timing of the production phase of the signal carriers is known precisely, Δϕc=0, then the white noise variance is equal to the variance of the piece of the sine wave that describes the portion of the year in which the carriers are produced. In this case, the sign and value of the bias are completely “known” given the parameters of the model, or, put another way, the proxy record can be attributed to the correct season.
PSEM can handle intermediate situations when, for example, we can parametrize with a proxy season length, τp, an expected phase, 〈ϕc〉, which is the midpoint of the proxy production season, and an uncertainty in this phase, . In this situation, there is both a bias with an expected value and sign and an uncertainty around this expected value that comes from the phase uncertainty.
Finally, if we include the amplitude modulation of the seasonal cycle over the course of a precessional cycle, , the size of any seasonal bias and bias uncertainty will vary over time. In the spectral domain, this manifests as leakage of power from frequencies lower than to higher frequencies and creates additional timescale-dependent errors corresponding to uncertain changes in the magnitude of seasonal biases between time periods. Additionally, the magnitude of aliased seasonal cycle variation will vary over a precessional period (see Sect. 3.2 of Part 1).
2.5 Measurement error and individual variation
As a first order, the measurement error can be assumed to be independent between measurements, and we simply add the power spectrum of a white noise error term σmeas. More complex measurement errors such as machine drift or memory between measurements could be integrated by adding a power spectrum characterizing these machine characteristics. We add an additional error term, σind, to account for inter-individual variation in the encoded signal. This is a catch-all term to include things like differences in depth habitat occupied by individuals and variation in the encoding of the signal, i.e., “vital effects” (Haarmann et al., 2011; Schiffelbein and Hills, 1984; Sadekov et al., 2008; Duplessy et al., 1970). For a given proxy measurement, the variance of this term is scaled by the number of individual signal carriers in the sample, N.
2.6 Calibration error
Finally, we add uncertainty in the proxy's calibration to temperature as a constant error, applying to all values in a given record for which we do not know the sign but do have some idea of the magnitude, σcal. This could, for example, be the standard error of the intercept term in a linear calibration model. This is implemented as additional power at frequency zero.
2.7 Power spectrum of the total error
As the individual error components are independent, their power spectra can be added together to get the spectrum of the total error. Once the spectral error model has been parameterized for a given core, proxy, and sampling scheme, the resulting empirical power spectrum provides the magnitude and full temporal correlation structure of the error components. From this, a number of useful quantities can be obtained. These include the error in individual proxy measurements, the error after smoothing a record to a lower resolution, the error in a time slice and in the difference between two time slices, and the expected correlation between replicated proxy records. We illustrate these applications in the following two sections.
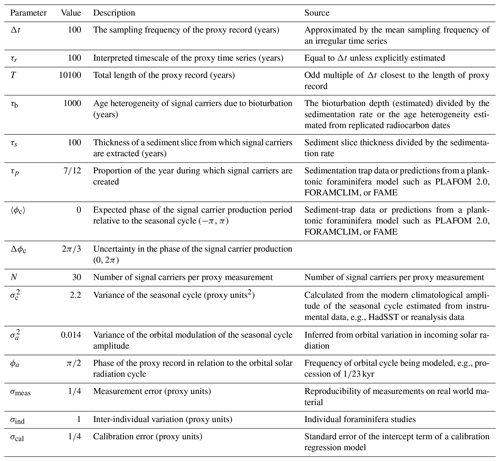
We first illustrate the error spectrum approach for a hypothetical 10 kyr foraminiferal Mg Ca record. Parameter values have been chosen to be realistic while ensuring that all components of the error model are presented. We parametrize the climate spectrum as described in Sect. 2.1, assuming a surface dwelling foraminifera at a virtual core position of 20∘ N, 18∘ W calcifying between the surface down to 120 m (Fig. 2). We further assume that this taxon forms tests for a 7 month period of the year, centered around the peak of the seasonal cycle but with an uncertainty in this phase of 2 months in either direction. A bioturbation depth of 10 cm and sedimentation rate of 10 cm kyr−1 are assumed. Thirty foraminifera are picked from contiguous 1 cm thick sediment slices so that the resulting record has a sampling interval, Δt, of 100 years. We assume a measurement error of 0.25 ∘C and inter-individual variation of 1 ∘C. All parameters are given in Table 1.
Table 1Parameters required for the spectral error model with their values in example 1 plus possible sources.
The power spectra of the individual error components, together with their sum and the assumed power spectrum of the climate, are shown for this example parameter set in Fig. 4. Power at ν=0 corresponds to errors that are constant for a given proxy time series and thus do not shrink as additional measurements are averaged together. Here it is composed of those parts of the seasonal bias and bias uncertainty that are constant over time (i.e., not orbitally modulated) and the calibration uncertainty.
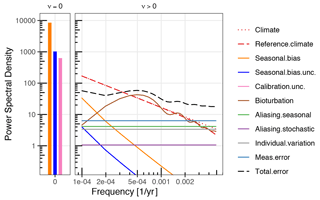
Figure 4Power spectra of error components of a climate proxy record. As the proxy record was sampled at 100-year resolution, only the power-law portion of the climate power spectrum is visible. The error spectra are plotted on log–log axes with a broken frequency axis so that power at the zeroth frequency (ν=0) can be shown.
The power spectral densities of the measurement error and individual variation components are horizontal lines, indicating that their power is independent of frequency, i.e., that these error components have the property of white noise. This applies also to the two components of aliased/redistributed seasonal cycle and stochastic climate variation.
In contrast, the component due to bioturbation and sediment slice thickness smoothing shows strong frequency dependence. The error due to smoothing is proportional to the variation in the climate signal; therefore, as variation in the climate is larger at lower frequencies, the error due to smoothing also increases towards lower frequencies. This is true up until the point at which the frequency examined exceeds the width of the smoothing filter, at which point the error due to smoothing declines towards lower frequencies.
The individual values in the record are most likely interpreted as a kind of mean of the time interval between observations, and so we set the implicit reference timescale to be the same as the sampling resolution (Δt=100). For this example, the timescale of the bioturbation smoothing, τb, is 1000 years. The large difference between these timescales implies a large error due to bioturbation smoothing. At frequencies above about 2 times the bioturbation filter width, the power of the bioturbation error is equal to the power of the reference climate.
The timescale-dependent portions of the seasonal bias and seasonal bias uncertainty are due to the orbital modulation of the amplitude of the seasonal cycle. As this is an approximately 23 kyr cycle, these errors only become large at timescales approaching 23 kyr.
3.1 Timescale-dependent proxy error
The error for the individual proxy values at their original sample resolution can be obtained by integrating the error spectrum. When the record is smoothed before its interpretation, the timescale represented by each point changes, as does the error. The error for a given timescale can be obtained by integrating the error spectra after first multiplying them by the transfer function of the smoothing filter (see Sect. 4, Eq. 110 of Part 1).
Timescale-dependent error for the example parameter set is shown in Fig. 5 for timescales from 100 years (the original sampling resolution of the record) to 10 000 years (a mean or time slice of the entire length of the record), assuming a running mean smoothing filter. The errors are shown on the variance scale so that they are additive and can be plotted stacked together. The error(s) associated with the individual proxy measurements corresponds to the rightmost edge of each subplot.
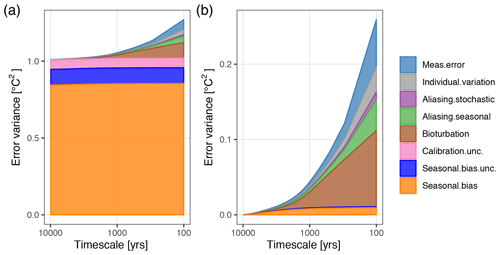
Figure 5Timescale-dependent proxy error for an example parameter set. (a) Timescale-dependent error variance for all components of the spectral error model. (b) Timescale-dependent error variance for all components excluding those that manifest as constant errors that do not change with timescale, i.e., those originating as power at frequency zero.
Figure 5a includes error components that are constant for a given record and do not shrink as a record is smoothed. For example, a seasonal bias in a record due to signal carriers (e.g., Foraminifera) preferentially recording a particular part of the seasonal cycle will not disappear as additional proxy measurements are averaged together. For this example here, the total error is dominated by the constant part of the seasonal bias component and to a lesser extent the bias uncertainty and calibration uncertainty.
Figure 5b includes only those error components that are at least partly independent between time points and therefore vary with timescale; i.e., it excludes errors that originate from power at frequency zero. The component measurement error, individual variation, and the aliased components of the stochastic climate and seasonal cycle all decline rapidly with timescale (i.e., as a record is smoothed with a running mean to lower resolutions) as the errors are independent between samples and so decline inversely with the number of samples being averaged together. The bioturbation component declines more slowly as errors are positively autocorrelated up until timescales of approximately 2τb. A portion of each of the seasonal bias and bias uncertainty components does vary with timescale due to the orbital modulation of the amplitude of the seasonal cycle. They may become important when comparing proxy values from two time slices that are far enough apart in time that any seasonal bias may differ between the two time periods.
3.2 Error in a time-slice mean and the difference between two time slices
The information contained in the power spectra also allows us to estimate the uncertainty in the difference in the climate between two time points or between two time slices. A time slice refers to an average taken over a set of proxy values within a certain time period of interest. For example, using the parametrization from Table 1, if we wanted to compare the mean climate over the first and last 1000 years of the proxy record, the error variance of each individual time slice would be the value at timescale = 1000 years in Fig. 5. If all the errors were independent in time, then the error variance of the difference between these two time slices would simply be the sum of the two variances. However, as some of these error components are autocorrelated (or even constant over the entire time series), the covariance in the errors for the two time slices needs to be accounted for. The information to do this is contained in the power spectrum of the error (see Sect. 4; Eqs. 111–112 of Part 1). The uncertainty, or error, in the estimate of the difference between two time slices is much smaller than the errors in the time slices themselves (Fig. 6).
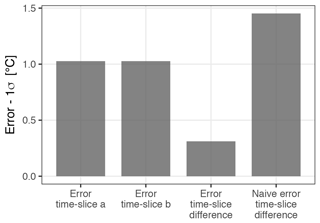
Figure 6The uncertainty or error in the estimate of the mean climate over two time slices covering the first and last 1000 years of the pseudo-proxy record and the error in the estimate of the difference between these two time slices. The realistic error estimate using PSEM (third column) is much smaller than the naive error estimate that one would obtain by just adding up the variances.
Here we illustrate the use of the error spectrum model on a real proxy record by applying it to replicated foraminiferal δ18O records taken from core GeoB 10054-4 off southern Java in the Indian Ocean collected during the R/V SONNE 184 expedition (8∘40.90′ S, 112∘40.10’ E; 1076 m water depth; Hebbeln and cruise participants, 2006). Replicated δ18O records were created using two different sampling schemes. In record 1 (Rep1), measurements were made on samples consisting of five Globigerinoides ruber (s.s.) tests each at a mean interval of 83 years; in Rep2, 30 tests of G. ruber (s.s.) were used per sample at a mean interval of 246 years. An age model was constructed using nine AMS-14C dates on mono-specific samples of Trilobatus sacculifer (see Supplement Table S1). The Marine13 radiocarbon calibration curve was used to calibrate the ages and construct a linear age model (Reimer et al., 2013). As both records come from the same core, more advanced age–depth modeling is not required here.
A replicated set of radiocarbon dates taken from 10 samples each of 10 foraminifera indicated an inter-individual standard deviation in age of 720 years (Dolman et al., 2020), which we use for τb, corresponding to a bioturbation depth of about 14 cm.
4.1 Parametrization
To assist potential users of PSEM, here we describe the parameter choices step by step.
Formally, the spectral error model describes only regularly sampled time series whose total length, T, is an odd multiple of the sampling interval, Δt. When applying the spectral error model to real proxy time series, we have to make some additional approximations to accommodate their inevitably irregular (in time) sampling intervals. Hence, we approximate the sampling interval for each record, Δt, by .
For the climate spectrum, we again used a spliced empirical and theoretical spectrum and estimated the amplitude of the seasonal cycle, as described in Sect. 2.1, but this time for the surface down to 50 m, resulting in an amplitude of 0.53 ‰.
At this location, G. ruber is thought to produce tests at an approximately equal rate throughout the year and represent the annual mean surface temperature in this region (Mohtadi et al., 2011). We therefore set τp=1, which implies year-round production of signal carriers. As τp=1, the parameters 〈ϕc〉 and Δϕc, which control the phase of signal carrier production relative to the seasonal cycle, have no effect on the error spectrum. Similarly, orbital modulation of the amplitude of the seasonal cycle will have only a small effect and is ignored here.
The sediment accumulation rate estimated from the calibrated radiocarbon dates and retrieval depths is approximately 20 cm kyr−1. The sediment slices were 1 cm thick, so τs was set to 50 years. A replicated set of radiocarbon dates taken from 10 samples each of 10 foraminifera indicated an inter-individual standard deviation in age of 720 years (unpublished data) which we use for τb, corresponding to a bioturbation depth of about 14 cm.
For σmeas, we use the analytic replicability of 0.1 ‰, but σind is more difficult to parametrize; we use 0.32 ‰, which was estimated by Sadekov et al. (2008) as the contribution of vital effects to replicability estimates for G. ruber.
4.2 Timescale-dependent uncertainty
Total error variance at the highest frequency resolved () is much higher for Rep1 than Rep2 as there are fewer foraminifera per sample so that the individual variation, aliased seasonal cycle, and aliased stochastic climate components are all larger for Rep1 than for Rep2 (Fig. 7). The effect of this can be seen clearly in Fig. 8a which shows Rep1 and Rep2 at their original, irregularly sampled time points, together with their PSEM estimated uncertainties. Rep1 shows much higher variance despite the fact that Rep1 and Rep2 come from the same sediment core and therefore both experienced the same climate signal and the same degree of bioturbation smoothing.
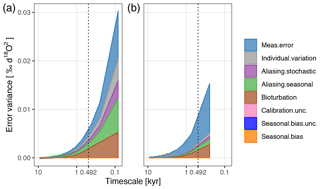
Figure 7Timescale-dependent error variance for two different δ18O sampling strategies at GeoB 10054-4. (a) Five foraminifera per measured sample with a mean time interval of 83 years between samples. (b) Thirty foraminifera per measured sample with a mean time interval of 246 years between samples. The vertical line at 0.492 kyr indicates the timescale to which the proxy records are smoothed in Fig. 8b.
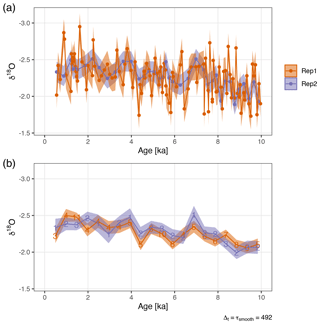
Figure 8The δ18O records from GeoB 10054-4 (a) at their original temporal resolutions and (b) interpolated to a regular time series and smoothed to 492-year resolution. Shaded regions show 1σ error estimated using the PSEM. The error due to smoothing by bioturbation is excluded as it is deterministic and thus the same for each record. Numbers indicate the number of original data points contained in each averaged proxy value.
In Fig. 8b, Rep1 and Rep2 have both been interpolated and smoothed to a regular 492-year resolution ( for Rep2). As the original time series were irregular, a different number of proxy measurement now contribute to each mean value. To account for this, we evaluate PSEM separately for each point, setting () to the timescale, τsmooth, divided by the number of original proxy measurements. After this smoothing, the two series are in much closer agreement. The error for Rep1 has shrunk much more than that for Rep2. In fact, smoothed to a timescale of 492 years, the error in Rep1 is now smaller than that in Rep2 due to the larger number of proxy measurements contributing on average to each point in the smoothed series (dotted vertical line in Fig. 7).
Expected correlation with the true climate
Finally, for the property of a proxy record, we are perhaps most interested in is its correlation with the true climate. The proxy and climate can have low correlation due to a combination of non-climate variation (noise) in the proxy record and because variation in the climate has been smoothed out in the proxy record. As the noise and degree of smoothing are timescale dependent, so too is the proxy–climate correlation. Using the power spectra of the errors and the assumed power spectrum of the climate signal, we can calculate the expected timescale-dependent correlation between the proxy and climate. We do not in general know the true climate and so cannot test the accuracy of the climate–proxy correlation estimate; however, we can also calculate the expected correlation between replicate proxy records and use this as a partial test of the model under the assumption that only the processes considered in PSEM affect the proxy record. The results (Fig. 9) indicate an increasing expected correlation from around 0 at centennial timescales to around 0.5 at millennial timescales. This is an upper bound estimate as the chronological uncertainty and other effects not considered here will further decrease the climate-to-proxy relationship.
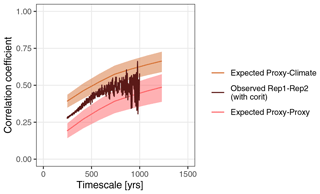
Figure 9Timescale-dependent correlation between replicated δ18O records at GeoB 10054-4 and their expected correlation with each other and with the true climate. The dark brown curve shows the observed timescale-dependent correlation between the replicate proxy records Rep1 and Rep2. The light brown and pink curves show the expected correlation between the two proxy records and between the proxy records and the true climate as calculated from the error spectra. The shaded areas indicate plus or minus the expected standard deviation in the correlation coefficients.
We estimated the timescale-dependent correlation between Rep1 and Rep2 using the R package corit (Reschke et al., 2019). The irregular time series were first interpolated to high-resolution regular time series and then smoothed with a set of increasingly wide running mean filters before calculating the correlation between them. The observed correlation between Rep1 and Rep2 is somewhat higher than that estimated from the error spectra (Fig. 9), perhaps indicating that we have assumed, for example, a measurement error that is slightly too high, although it is unclear if this difference is statistically significant. At timescales above 1000 years, estimates of the observed correlation become very variable due to there being very few effective data points left after smoothing.
Understanding the errors associated with climate proxies is an important task for paleoclimate research. Proxy errors, defined here as differences between the inferred climate and the unknown true climate, can be large and can thus strongly influence our understanding of past climate history and the functioning of the climate system. Many components of proxy error have a complex temporal autocorrelation structure, making them timescale dependent and a challenge to properly quantify and account for. The model introduced here (PSEM) and in the companion paper (Kunz et al., 2020) offers a rigorous and compact way to calculate and express this structure as error spectra, specifically here in this first version for marine sediment cores. Once defined, the error spectra can be used to calculate many quantities that will be useful to paleoclimate research. In addition to the error in individual measurements, these include the error after smoothing the record, the error in time slices, differences between time slices, and the expected correlation between replicates of a proxy record and between a record and the true climate. As with every model, some challenges remain, in particular how to deal rigorously with the irregularity of real proxy time series, the climate dependency of the habitat of the organisms recording the climate signal, and the error associated with the age uncertainty. Nevertheless, we argue that the spectral error approach represents a significant advance towards obtaining reliable uncertainty estimates for all quantities of interest rather than single estimates applied uniformly to the record.
Although we have restricted the examples given here to the Holocene, PSEM can be applied to other periods, albeit with greater uncertainty in its parametrization. Many of the error components, such as the bioturbation smoothing and seasonal aliasing, should remain approximately correct; however, if we include glacial–interglacial cycles, there will be larger variations in the sedimentation rate, and the seasonality of the signal carriers (e.g., foraminifera) may change in unexpected ways. The amplitude of the seasonal temperature cycle and the precession-driven modulation of the seasonal cycle will vary with the longer inclination and eccentricity orbital cycles, although these changes are proportionally relatively small and deterministic. For the assumed stochastic climate spectrum, the key issue is the assumption of stationarity. If multiple glacial cycles are included, then one could argue that the spectrum is again stationary and still dominated by a power-law type variation. It becomes more difficult to justify if only one glacial–interglacial is included. Nonetheless, the PSEM approach should be a significant improvement over assuming independent errors.
Simulation-based forward modeling approaches such as sedproxy (Dolman and Laepple, 2018) and PRYSM (Dee et al., 2015) could also be used to estimate these quantities by generating and summarizing over many simulated pseudo-proxy records. The advantages of PSEM are that it provides an analytic understanding of the timescale dependence of error components while retaining the mechanistic understanding of the proxy generating process and can make these uncertainty estimates rapidly for large sets of parameters, for example, to directly model the error for a wide range of potential sediment core characteristics (sedimentation rate and bioturbation depth) with different sampling schemes and at different locations with differing climate properties such as seasonal cycle amplitude. This allows us to both better interpret the existing proxy record and to optimize future field work to answer specific questions.
Beyond modeling errors, PSEM also facilitates the use of the proxy variability itself to make inferences about the climate system. It allows us to predict the variability observed in individual foraminifera assemblages (IFAs) (e.g., Groeneveld et al., 2019; Thirumalai et al., 2019) and thus to directly test the sensitivity of IFA statistics on the sedimentation rate, seasonality, or the spectrum of climate variability. Finally, PSEM provides the basis to develop spectral correction approaches that infer the climate spectrum from the corrupted and distorted proxy spectrum, building on the approaches previously proposed for simpler sediment models (Laepple and Huybers, 2013) or for aliasing only (Kirchner, 2005).
The PSEM version proposed here includes the sediment proxy processes described earlier for the proxy forward model sedproxy (Dolman and Laepple, 2018) and represents a trade-off between complexity and completeness. For example, the interaction of seasonality in the recording and climate signal is the only slowly varying process so far included. However, the general formulation of the PSEM allows other processes to be added. For example, depending on the timescale of interest and the proxy type, other slowly varying processes, such as long-term changes in seawater Mg Ca (Medina-Elizalde et al., 2008) or long-term instrumental drift and memory effects of the measurement process, could be included by specifying the power spectra. When accounting for these processes, the use of PSEM vs. the classical single-value uncertainty approach becomes even more important.
Here, and in Part 1, we have defined analytical expressions specifically for sediment-archived climate proxies; however, the approach is applicable to other proxy types as most proxy types experience similar error generation and distortion processes. For example, smoothing also affects water isotopes measured in ice cores via water vapor diffusion (Johnsen et al., 2000) and geochemical indices measured in coral records (Gagan et al., 2012) via successive incremental calcification in corals. These processes can also be expressed as filters acting on the climate signal, and the power spectra of the errors they produce are derived in a similar way. Thus, we hope that PSEM presents an important step towards providing more realistic error estimates for paleoclimate research.
An advantage of the spectral error method is that it does not require a specific realization of a climate model; we do, however, need to make some assumptions about the statistical properties of the true climate trajectory, which we encode via an assumed power spectrum of the climate. Our approach is to use a composite spectrum in which we splice an empirical spectrum derived from observations for frequencies above years with a theoretical power-law spectrum for lower frequencies. In the examples presented in the main body of the paper, we have assumed a slope of 1 for the power-law portion of the spectrum. Here we test the sensitivity of the method to the slope assumption by re-evaluating the error spectra for the example in Sect. 3 using slopes of 0.5 and 1.5 in addition to 1 (Fig. A1). As changing the climate spectrum slope primarily influences the power at low frequencies, the effect of this on proxy error depends on the scale of the bioturbation; if bioturbation is so low that it integrates only short-timescale climate fluctuations, then the influence of the climate slope will be low. To illustrate this, we additionally use values of 20, 200, and 2000 for the parameter τb, corresponding to sedimentation rates of 5, 50, and 500 cm kyr−1 for sediment with a 10 cm bioturbation depth.
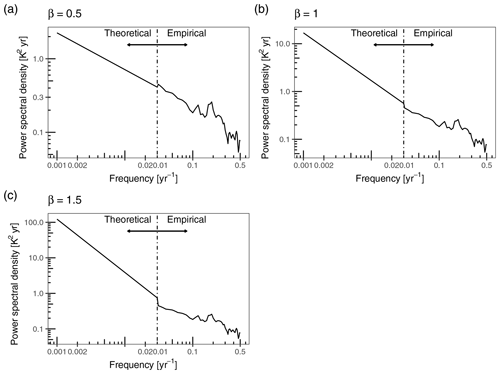
Figure A1Spliced empirical and power-law power spectrum of ocean temperature (0–120 m water depth) for 20∘ N latitude with slopes of 0.5, 1, and 1.5 for the low-frequency power-law region of the spectrum.
Increasing the slope of the stochastic climate spectrum increases the error components due to the smoothing of the climate signal by bioturbation and the aliasing of this filtered climate variation as a white noise error term (see Fig. A2). However, the magnitude of these effects depends additionally on the parameter τb controlling the timescale of the smoothing filter. If τb is small, e.g., 20 years (Fig. A2a, b, c), the increase in error is minimal as the change in climate power only starts at frequencies below years which are barely influenced by the smoothing filter. The result of this is that increasing the climate spectrum slope shifts the point at which the power of the climate signal exceeds the total error spectrum to higher frequencies. For τb=20 years, this point shifts from approximately years with β=1 to years for β=1.5. When β=0.5, climate power remains below the total error at all shown frequencies even with very low bioturbation.
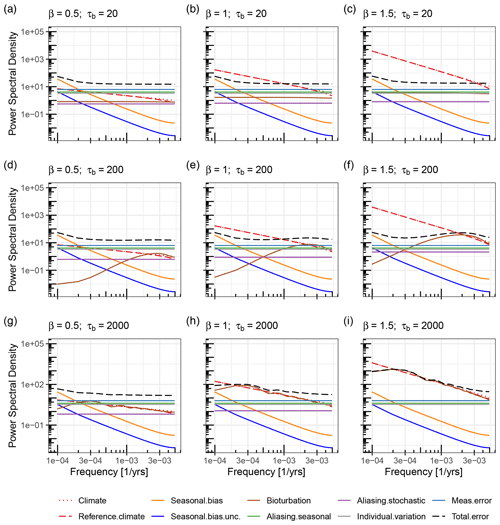
Figure A2A comparison of error spectra using different slopes for the power-law portion of the stochastic climate spectrum. Comparisons are made for slopes, β, of 0.5, 1, and 1.5 and for different amounts of bioturbation smoothing with values for τb of 20, 200, and 2000 years.
For larger values of τb, the bioturbation filter smooths the additional climate variation down to lower frequencies such that the increase in bioturbation and aliasing error is larger, offsetting the increase in climate power. For τb=200, shifting beta from 1 to 1.5 moves this from approximately to years (Fig. A2d, e, f). For very large values of τb corresponding to a sedimentation rate of 5 cm kyr−1 and bioturbation depth of 10 cm (τb=2000), increased climate variation is almost completely offset by increased bioturbation, smoothing error down to frequencies of years (Fig. A2g, h, i).
The Proxy Spectral Error Model (PSEM) is implemented as an R package. Its source code is available from the public Git repository https://github.com/EarthSystemDiagnostics/psem (last access: 24 March 2021). A snapshot of the R package at the time these analyses were performed is archived at Zenodo (https://doi.org/10.5281/zenodo.4271300, Dolman, 2020). Down-core radiocarbon dates and δ18O isotope data for GeoB 10054-4 are provided in Supplement Table S1.
The supplement related to this article is available online at: https://doi.org/10.5194/cp-17-825-2021-supplement.
TK, AMD, and TL designed the conceptual outline of the research. AMD coded the PSEM R package and produced the figures. AMD and TL wrote the paper with contributions from TK and JG.
The authors declare that they have no conflict of interest.
This article is part of the special issue “Paleoclimate data synthesis and analysis of associated uncertainty (BG/CP/ESSD inter-journal SI)”. It is not associated with a conference.
This work was supported by the German Federal Ministry of Education and Research (BMBF) as a Research for Sustainability initiative (FONA); through the PALMOD project (FKZ: 01LP1509C). Thomas Laepple and Torben Kunz have received funding from the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation programme (grant agreement no. 716092). The work profited from discussions at the CVAS working group of the Past Global Changes (PAGES) programme. We thank Henning Kuhnert for isotope analyses, Mahyar Mohtadi for providing the sediment core GeoB 10054-4, Nele Behrendt and Lena Kafemann for processing samples, and Gesine Mollenhauer and Torben Gentz for radiocarbon dating.
This research has been supported by the Bundesministerium für Bildung und Forschung (grant no. 01LP1509C) and the European Research Council (SPACE; grant no. 716092).
The article processing charges for this open-access publication were covered by a Research Centre of the Helmholtz Association.
This paper was edited by Denis-Didier Rousseau and reviewed by two anonymous referees.
Bemis, B. E., Spero, H. J., Bijma, J., and Lea, D. W.: Reevaluation of the Oxygen Isotopic Composition of Planktonic Foraminifera: Experimental Results and Revised Paleotemperature Equations, Paleoceanography, 13, 150–160, https://doi.org/10.1029/98PA00070, 1998. a
Berger, A. and Loutre, M.: Insolation Values for the Climate of the Last 10 Million Years, Quaternary Sci. Rev., 10, 297–317, https://doi.org/10.1016/0277-3791(91)90033-Q, 1991. a
Berger, W. H. and Heath, G. R.: Vertical Mixing in Pelagic Sediments, J. Mar. Res., 26, 134–143, 1968. a
Bijma, J., Erez, J., and Hemleben, C.: Lunar and Semi-Lunar Reproductive Cycles in Some Spinose Planktonic Foraminifers, J. Foramin. Res. 20, 117–127, 1990. a
Breitkreuz, C., Paul, A., Kurahashi-Nakamura, T., Losch, M., and Schulz, M.: A Dynamical Reconstruction of the Global Monthly Mean Oxygen Isotopic Composition of Seawater, J. Geophys. Res.-Oceans, 123, 7206–7219, https://doi.org/10.1029/2018JC014300, 2018. a
Dee, S., Emile-Geay, J., Evans, M. N., Allam, A., Steig, E. J., and Thompson, D.: PRYSM: An Open-Source Framework for PRoxY System Modeling, with Applications to Oxygen-Isotope Systems, J. Adv. Model. Earth Sy., 7, 1220–1247, https://doi.org/10.1002/2015MS000447, 2015. a, b
Dolman, A. M.: EarthSystemDiagnostics/Psem: Psem-Pub-Rev-1, Zenodo, https://doi.org/10.5281/zenodo.4271300, 2020 (data available at: https://github.com/EarthSystemDiagnostics/psem, last access: 24 March 2021). a
Dolman, A. M. and Laepple, T.: Sedproxy: a forward model for sediment-archived climate proxies, Clim. Past, 14, 1851–1868, https://doi.org/10.5194/cp-14-1851-2018, 2018. a, b, c, d
Dolman, A. M., Groeneveld, J., Mollenhauer, G., Ho, S. L., and Laepple, T.: Estimating Bioturbation from Replicated Small-Sample Radiocarbon Ages., Earth Space Sci. Open Arch., pp. 19, https://doi.org/10.1002/essoar.10504501.2, submitted, 2020. a
Duplessy, J. C., Lalou, C., and Vinot, A. C.: Differential Isotopic Fractionation in Benthic Foraminifera and Paleotemperatures Reassessed, Science, 168, 250–251, https://doi.org/10.1126/science.168.3928.250, 1970. a
Evans, M. N., Tolwinski-Ward, S. E., Thompson, D. M., and Anchukaitis, K. J.: Applications of Proxy System Modeling in High Resolution Paleoclimatology, Quaternary Sci. Rev., 76, 16–28, https://doi.org/10.1016/j.quascirev.2013.05.024, 2013. a
Fedorov, A. V., Brierley, C. M., Lawrence, K. T., Liu, Z., Dekens, P. S., and Ravelo, A. C.: Patterns and Mechanisms of Early Pliocene Warmth, Nature, 496, 43–49, https://doi.org/10.1038/nature12003, 2013. a
Gagan, M. K., Dunbar, G. B., and Suzuki, A.: The Effect of Skeletal Mass Accumulation in Porites on Coral Sr Ca and δ18O Paleothermometry, Paleoceanogr. Paleoclim. 27, PA1203, https://doi.org/10.1029/2011PA002215, 2012. a
Goosse, H., Renssen, H., Timmermann, A., Bradley, R. S., and Mann, M. E.: Using Paleoclimate Proxy-Data to Select Optimal Realisations in an Ensemble of Simulations of the Climate of the Past Millennium, Clim. Dyn., 27, 165–184, https://doi.org/10.1007/s00382-006-0128-6, 2006. a
Groeneveld, J., Ho, S. L., Mackensen, A., Mohtadi, M., and Laepple, T.: Deciphering the Variability in Mg/Ca and Stable Oxygen Isotopes of Individual Foraminifera, Paleoceanogr. Paleoclim., 34, 755–773, https://doi.org/10.1029/2018PA003533, 2019. a
Haarmann, T., Hathorne, E. C., Mohtadi, M., Groeneveld, J., Kölling, M., and Bickert, T.: Mg Ca Ratios of Single Planktonic Foraminifer Shells and the Potential to Reconstruct the Thermal Seasonality of the Water Column, Paleoceanogr. Paleoclim., 26, PA3218, https://doi.org/10.1029/2010PA002091, 2011. a
Hargreaves, J. C., Paul, A., Ohgaito, R., Abe-Ouchi, A., and Annan, J. D.: Are paleoclimate model ensembles consistent with the MARGO data synthesis?, Clim. Past, 7, 917–933, https://doi.org/10.5194/cp-7-917-2011, 2011. a
Hebbeln, D. and cruise participants: Report and Preliminary Results of RV Sonne Cruise SO-184, Pabesia, Durban (South Africa) - Cilacap (Indonesia) - Darwin (Australia), July 8th - September 13th, 2005, vol. 246, Department of Geosciences, Bremen University, 2006. a
Johnsen, S. J., Clausen, H. B., Cuffey, K. M., Hoffmann, G., Schwander, J., and Creyts, T.: Diffusion of Stable Isotopes in Polar Firn and Ice: The Isotope Effect in Firn Diffusion, in: Physics of Ice Core Records, vol. 159, edited by: Hondoh, T., Hokkaido University Press, Sapporo, Japan, 121–140, 2000. a
Jonkers, L. and Kučera, M.: Global analysis of seasonality in the shell flux of extant planktonic Foraminifera, Biogeosciences, 12, 2207–2226, https://doi.org/10.5194/bg-12-2207-2015, 2015. a
Kirchner, J. W.: Aliasing in Noise Spectra: Origins, Consequences, and Remedies, Phys. Rev. E 71, 066110, https://doi.org/10.1103/PhysRevE.71.066110, 2005. a
Kunz, T., Dolman, A. M., and Laepple, T.: A spectral approach to estimating the timescale-dependent uncertainty of paleoclimate records – Part 1: Theoretical concept, Clim. Past, 16, 1469–1492, https://doi.org/10.5194/cp-16-1469-2020, 2020. a, b
Laepple, T. and Huybers, P.: Reconciling Discrepancies between Uk37 and Mg Ca Reconstructions of Holocene Marine Temperature Variability, Earth Planet. Sci. Lett., 375, 418–429, https://doi.org/10.1016/j.epsl.2013.06.006, 2013. a, b, c
Laepple, T. and Huybers, P.: Global and Regional Variability in Marine Surface Temperatures, Geophys. Res. Lett., 41, 2528–2534, https://doi.org/10.1002/2014GL059345, 2014a. a
Laepple, T. and Huybers, P.: Ocean Surface Temperature Variability: Large Model – Data Differences at Decadal and Longer Periods, P. Natl. Acad. Sci., 111, 16682–16687, https://doi.org/10.1073/pnas.1412077111, 2014b. a
Leduc, G., Schneider, R., Kim, J.-H., and Lohmann, G.: Holocene and Eemian Sea Surface Temperature Trends as Revealed by Alkenone and Mg Ca Paleothermometry, Quaternary Sci. Rev., 29, 989–1004, https://doi.org/10.1016/j.quascirev.2010.01.004, 2010. a
Lohmann, G., Pfeiffer, M., Laepple, T., Leduc, G., and Kim, J.-H.: A model–data comparison of the Holocene global sea surface temperature evolution, Clim. Past, 9, 1807–1839, https://doi.org/10.5194/cp-9-1807-2013, 2013. a
Lovejoy, S.: A Voyage through Scales, a Missing Quadrillion and Why the Climate Is Not What You Expect, Clim. Dyn., 44, 3187–3210, 2015. a
Marcott, S. A., Shakun, J. D., Clark, P. U., and Mix, A. C.: A Reconstruction of Regional and Global Temperature for the Past 11,300 Years, Science, 339, 1198–1201, https://doi.org/10.1126/science.1228026, 2013. a, b
Medina-Elizalde, M., Lea, D. W., and Fantle, M. S.: Implications of Seawater Mg Ca Variability for Plio-Pleistocene Tropical Climate Reconstruction, Earth Planet. Sci. Lett., 269, 585–595, https://doi.org/10.1016/j.epsl.2008.03.014, 2008. a
Moberg, A. and Brattström, G.: Prediction Intervals for Climate Reconstructions with Autocorrelated Noise – An Analysis of Ordinary Least Squares and Measurement Error Methods, Palaeogeogr. Palaeoclimatol. Palaeoecol., 308, 313–329, https://doi.org/10.1016/j.palaeo.2011.05.035, 2011. a
Mohtadi, M., Oppo, D. W., Steinke, S., Stuut, J.-B. W., De Pol-Holz, R., Hebbeln, D., and Lückge, A.: Glacial to Holocene Swings of the Australian-Indonesian Monsoon, Nat. Geosci., 4, 540–544, https://doi.org/10.1038/ngeo1209, 2011. a
Reimer, P. J., Bard, E., Bayliss, A., Beck, J. W., Blackwell, P. G., Ramsey, C. B., Buck, C. E., Cheng, H., Edwards, R. L., Friedrich, M., Grootes, P. M., Guilderson, T. P., Haflidason, H., Hajdas, I., Hatté, C., Heaton, T. J., Hoffmann, D. L., Hogg, A. G., Hughen, K. A., Kaiser, K. F., Kromer, B., Manning, S. W., Niu, M., Reimer, R. W., Richards, D. A., Scott, E. M., Southon, J. R., Staff, R. A., Turney, C. S. M., and van der Plicht, J.: IntCal13 and Marine13 Radiocarbon Age Calibration Curves 0–50,000 Years Cal BP, Radiocarbon, 55, 1869–1887, https://doi.org/10.2458/azu_js_rc.55.16947, 2013. a
Reschke, M., Kunz, T., and Laepple, T.: Comparing Methods for Analysing Time Scale Dependent Correlations in Irregularly Sampled Time Series Data, Comput. Geosci., 123, 65–72, https://doi.org/10.1016/j.cageo.2018.11.009, 2019. a
Sadekov, A., Eggins, S. M., De Deckker, P., and Kroon, D.: Uncertainties in Seawater Thermometry Deriving from Intratest and Intertest Mg Ca Variability in Globigerinoides Ruber, Paleoceanography, 23, 1–12, https://doi.org/10.1029/2007PA001452, 2008. a, b
Schiffelbein, P. and Hills, S.: Direct Assessment of Stable Isotope Variability in Planktonic Foraminifera Populations, Palaeogeogr. Palaeoclimatol. Palaeoecol., 48, 197–213, https://doi.org/10.1016/0031-0182(84)90044-0, 1984. a, b
Schmitt, F., Lovejoy, S., and Schertzer, D.: Multifractal Analysis of the Greenland Ice-Core Project Climate Data, Geophys. Res. Lett., 22, 1689–1692, https://doi.org/10.1029/95GL01522, 1995. a
Shackleton, N. J.: Attainment of Isotopic Equilibrium between Ocean Water and the Benthonic Foraminifera Genus Uvigerina, in: Isotopic Changes in the Ocean during the Last Glacial, Cent. Nat. Rech. Sci. Colloq. Int., 219, 203–209, 1974. a
Shakun, J. D., Clark, P. U., He, F., Marcott, S. A., Mix, A. C., Liu, Z., Otto-Bliesner, B., Schmittner, A., and Bard, E.: Global Warming Preceded by Increasing Carbon Dioxide Concentrations during the Last Deglaciation, Nature, 484, 49–54, https://doi.org/10.1038/nature10915, 2012. a, b
Spero, H. J.: Life History and Stable Isotope Geochemistry of Planktonic Foraminifera, Paleontol. Soc. Papers, 4, 7–36, https://doi.org/10.1017/S1089332600000383, 1998. a
Thirumalai, K., DiNezio, P. N., Tierney, J. E., Puy, M., and Mohtadi, M.: An El Niño Mode in the Glacial Indian Ocean?, Paleoceanogr. Paleoclimatol., 34, 1316–1327, https://doi.org/10.1029/2019PA003669, 2019. a
- Abstract
- Introduction
- Error spectra as a framework for timescale-dependent proxy uncertainty
- Illustration of the error spectrum approach for a hypothetical proxy record
- A working example: replicated Holocene δ18O records from southern Java
- Discussion and conclusions
- Appendix A: The influence of the assumed climate spectrum on estimates of proxy error
- Code and data availability
- Author contributions
- Competing interests
- Special issue statement
- Acknowledgements
- Financial support
- Review statement
- References
- Supplement
- Abstract
- Introduction
- Error spectra as a framework for timescale-dependent proxy uncertainty
- Illustration of the error spectrum approach for a hypothetical proxy record
- A working example: replicated Holocene δ18O records from southern Java
- Discussion and conclusions
- Appendix A: The influence of the assumed climate spectrum on estimates of proxy error
- Code and data availability
- Author contributions
- Competing interests
- Special issue statement
- Acknowledgements
- Financial support
- Review statement
- References
- Supplement





