the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Milankovitch, the father of paleoclimate modeling
Andre Berger
The history of the long-term variations in the astronomical elements used in paleoclimate research shows that, contrary to what might be thought, Milutin Milankovitch is not the father of the astronomical theory but he is definitely the father of paleoclimate modeling. He did not calculate these long-term variations himself but used them extensively for calculating the “secular march” of incoming solar radiation. He advanced our understanding of Quaternary climate variations by two important and original contributions fully described in his Canon of insolation. These are the definition and use of caloric seasons and the concept of the “mathematical climate”. How his mathematical model allowed him to give the caloric summer and winter insolation a climatological meaning is illustrated.
- Article
(397 KB) - Full-text XML
- BibTeX
- EndNote
Paleoclimatology is primarily a reconstruction of past climatic variations on the basis of proxy records. It aims also to explain these variations from principles of climatic behavior using climate models. Milankovitch has contributed significantly to this second objective by using the astronomical parameters to compute the long-term variations in his caloric insolation which he used in a climate model (although very simple) to reconstruct the past climates. This paper intends to underline the fundamental and original contributions of Milankovitch to the understanding of the long-term climatic variations over the last 1 million years.
The two remarkable books of Milutin Milankovitch, his 1920 Théorie mathématique written in French and his 1941 Kanon der Erdbestrahlung written in German and translated into English in 1969, have largely contributed to his reputation. The celebration of the 100th anniversary of his 1920 French book is a good opportunity to stress what his main contributions were and to “rendre à César ce qui appartient à César (give back to Caesar what belongs to Caesar)” (Marc, XII, 13-17; Matthieu, XXI, 21; Luc, XX, 25). There is indeed a tendency to overinflate one's work for reasons that have nothing to do with the scientist, but for reasons that have to do with corporative or national politics of the history of science. It is important to stress here that Milankovitch was always very careful through all his publications, referring properly to the publications of others when he was using their results.
Contrary to what might be thought, Milankovitch did not calculate the long-term variations in the astronomical elements. He used them extensively for calculating the “secular march” of the incoming solar radiation.
The first to calculate these astronomical elements was the French astronomer Joseph-Louis Lagrange (1736–1813). He made the calculation for the six great planets (Lagrange, 1781–1782). At that time, Uranus had not been discovered and the mass of the planets could only be roughly estimated. Aware of this uncertainty of the masses, Lagrange investigated its possible influence on his calculations, a formulation that was going to be used more than 1 century later by Prof. Vojislav Miskovitch (1892–1976), a colleague whose collaboration Milankovitch solicited.
During the early 19th century, Pierre-Simon Laplace (1749–1827) wrote his five-volume Celestial mechanics between 1799 and 1825 (Laplace, 1799–1825). Philippe Gustave le Doulcet, Comte de Pontécoulant (1795–1874), carried out the computation of the long-term variations in the elements of the great planets but with a few decimals only (Pontécoulant, 1834).
It is during the second part of the 19th century that Urbain Le Verrier (1811–1877) introduced a new theory of the planetary motion (1855) and the calculation of the secular perturbations (1856; Le Verrier, 1855–1856). He published the numerical values of eccentricity (with a precision of 10−4), longitude of the perihelion (in arcmin), inclination (in arcsec) and longitude of the node over 100 000 years before and after 1800 CE each 10th millennium. His calculations were carried out before he discovered the planet Neptune. As this planet could not therefore be included in the Le Verrier calculations, John Nelson Stockwell (1832–1920) computed the secular perturbations by considering all the eight planets known at his time (Stockwell, 1873): Mercury, Venus, the Earth, Mars, Jupiter, Saturn, Uranus and Neptune. Stockwell, like Le Verrier, had the possibility of correcting their computations by using better values of masses. This work completed the calculations of the secular perturbations of the great planets, but an error was discovered by Harzer (1895) 22 years later. Finally, it is the German Ludwig Pilgrim (1879–1935) (known mostly as a pioneer in colorimetry), who, at a time when Milankovitch was completing his doctoral degree thesis in 1904, computed the astronomical elements required for the computation of insolation. Pilgrim (1904) extended the numerical computations of eccentricity, obliquity and longitude of the moving perihelion, using the Stockwell integrals for every fifth millennium over 1 010 000 before and 40 000 years after 1850 CE (part of these values are in Milankovitch, 1920, pp. 223–225, and Köppen and Wegener, 1924, pp. 254–255; a more complete list is found in Milankovitch, 1941, Table VIII, pp. 254–258) and also for dates where the longitude of the perihelion was either 90 or 270∘ (Northern Hemisphere summer at perihelion or at aphelion). In Milankovitch's own words (Milankovitch, 1920, p. 222; 1941, p. 372), Pilgrim was the first to compute adequately the elements affecting the long-term variations in insolation, so that Milankovitch could use them for his research. Pilgrim tried also to treat the Ice Age mathematically, but according to Milankovitch, this treatment of the climatological part by Pilgrim was a failure.
Milankovitch clearly indicates that for the calculation of his incoming solar radiation (insolation for short), he first used the Stockwell–Pilgrim values of the eccentricity, obliquity and precession for the last 1 000 000 years before 1850 CE. The insolation values for 55, 60 and 65∘ N were published in Köppen and Wegener (1924, p. 214) before the calculation was extended to other geographical latitudes and the new values published in his “Mathematische Klimalehre” in 1930 (Milankovitch, 1930; also cited in Milankovitch, 1941, p. 253).
Because of some errors in Stockwell (already detected by Harzer) and because he wanted to use the astronomical parameters based on the most reliable values of the planetary masses, Milankovitch decided to use the Le Verrier calculation including his corrections for the masses. In order to complete this work, he asked the collaboration of his colleague, Miskovitch. Miskovitch made the necessary corrections of the masses following Le Verrier's procedure and computed the long-term variations in eccentricity e, obliquity ε and climatic precession esin Πγ (Πγ the longitude of the perihelion) for the past 600 000 years before 1800 CE with the following initial values (Miskovitch, 1931):
All these values were published in “Mathematische Klimalehre” in 1930 and in “Astronomische Mittel” in 1938 and reproduced in Table IX of his Canon (Milankovitch, 1941, pp. 260–262). Milankovitch carefully noted that the Hungarian scientist von Bacsàk (1870–1970) drew his attention to two calculation errors, both related to Δ(esin Πγ) – one at 500 kyr BP and the other at 465 kyr BP – errors that Milankovitch took care to eliminate from his tables.
This use of two different astronomical solutions explains why, in the early work of Milankovitch, we find the astronomical values of Stockwell–Pilgrim and in his later work the values of Le Verrier–Miskovitch. The comparison of the insolation values that Milankovitch calculated from these solutions shows a good agreement. Milankovitch concluded that a further improvement of the planetary masses using the formulation by Le Verrier would not change “the essential features of the secular course of insolation as I have calculated”.
Milankovitch was however well aware that the solution by Le Verrier could not be extended over millions of years because of the limited accuracy of the perturbation calculation that was based upon classical mechanics, missing the Einstein relativistic displacement of the perihelion of the planets.
Milankovitch calculated the incoming solar radiation on the Earth in great detail but seemed to have not been much interested in the astronomical periodicities themselves. From his table (based on Stockwell–Pilgrim), he simply deduced the average period of the oscillations of eccentricity as being 92 kyr, varying between 77 and 103 kyr. For precession, he found an average period of 21 kyr, varying between 16.3 and 25.8 kyr. For the longitude of the moving perihelion, he explained that its irregularities are due to the longitude of the fixed perihelion, but whether the perihelion has a mean motion remains an open question. For obliquity, he noted that it “oscillates between extremely narrow limits” with a relatively stable period of 40 kyr varying between 38 and 45 kyr (Milankovitch, 1941, pp. 264, 269, 270). It was actually the French mathematician Joseph Alphonse Adhémar (1797–1862), who was the first in 1842 to deduce the value of 21 000 years for precession by combining the astronomical precession calculated from the value of 50.1′′ yr−1 of the French astronomer Jean-Baptiste Joseph Delambre (1749–1822) and the rotation of the terrestrial orbit calculated from the value of 11.83′′ yr−1 of the French mathematician Louis Benjamin Francoeur (1773–1849).
The harmonics of precession, in particular those with a period of 19 000 and of 23 000 years – also found by Hays et al. (1976) in their geological data – and the 400 000 years of eccentricity were discovered by Berger (1973, 1976, 1977, 1978a), who calculated all the periods in the expansion of the long-term variations in the astronomical variables used in the calculation of insolation.
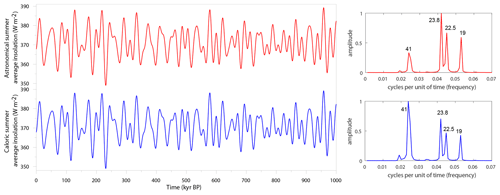
Figure 1Average insolation of the half-year astronomical (red) and caloric (blue) summer seasons and their spectra (based on Berger and Loutre, 1991; Berger et al., 2010). The major periodicities are indicated in thousands of years.
It is worth noting that Milankovitch was very much interested in obliquity probably because of the strong obliquity signal in his caloric half-year insolation (see Fig. 1). Milankovitch mentioned many times that the authors who were mainly stressing precession were not sufficiently or not properly taking into account obliquity. Tables XII and XIII of his Canon give the change in the radiation of his Table XI for an increase in the obliquity by 1∘ (respectively in canonic units and in percent). These three tables were first published in his “The problem of the astronomical theories of the ice ages” (Milankovitch, 1914), showing in detail for the first time the influence of obliquity upon insolation. To put it briefly, an increase in obliquity reduces the latitudinal contrast between the Equator and the poles mainly in the annual irradiation and increases the seasonal one (with an augmentation of the summer irradiation and a reduction of the winter one), with a similar effect in both hemispheres.
In fact, it is not widely known that similar insolation computations were actually already done in the 19th century by the Englishman Sir John Frederick William Herschel (1792–1871) (published in 1832 for the total irradiation; Herschel, 1832), by the American scientist Levi Witter Meech (1821–1912) (published in 1856 for the daily and seasonal irradiation at any latitude based on elliptical integrals; Meech, 1856), by the German mathematician Ludwig Christian Wiener (1826–1896) (published in 1876, he did the same as Meech with, in addition, the total irradiation over different parts of the Earth; Wiener, 1876) and by the Irish intellectual Joseph John Murphy (1827–1894). It is actually Murphy who was the first in 1869 (Murphy, 1869) to put forward the idea that a long, cool summer and a short, mild winter are the most favorable conditions for glaciations (a hypothesis totally the opposite of that of Croll, 1864). This idea was taken up by the Austrian climatologist Rudolf Spitaler (1859–1946) half a century later (Spitaler, 1921). It therefore follows that it is not Milankovitch who originated this principle, as some authors have claimed and still claim, calling it the “Milankovitch model”. Milankovitch actually popularized and spread the idea under the advice of Köppen (1940), who claimed that “the diminution of heat during the summer half-year is the decisive factor in glaciation” and also following the comments made earlier by Penck and Brückner (1909) and Brückner et al. (1925): “From the climatological point of view, glaciers are not favoured by severe winter … but by a mild winter and a cool summer”. It must also be noted that in Köppen and Wegener (1924, p. 184, English edition) we find that the “two causes responsible for the growth of a glacier are huge amounts of snow and low temperature, especially in summer”.
When dealing with the astronomical seasons, the long-term variations in both their total irradiation and their length must be taken into account. To accommodate this duality, Milankovitch introduced the caloric seasons. This concept of caloric seasons (Berger, 1978b) is one of the two most important and original contributions of Milankovitch. These divide the year into two equally long seasons, one of which – the caloric summer – comprises all days during which the irradiation at the given latitude is stronger than on any day of the other half-year – the caloric winter. Because the semi-major axis of the Earth's orbit, the sidereal period of revolution of the Earth around the Sun and, to an excellent approximation, the tropical year do not change with time, the length of these caloric seasons is exactly 182.6211 mean solar days when the tropical year is used. This, however, does not solve the problem completely because the start and end of these half-year seasons change with time and because of the double maximum and minimum characterizing the insolation in the intertropical regions.
Milankovitch noted that he discovered these caloric seasons after his 1920 book on a Théorie mathématique was published, and he used them for the first time in Köppen and Wegener (1924, p. 194, English edition) and in his contribution (“Mathematische Klimalehre”) to the 1930 Köppen-Geiger Handbook. Actually, Köppen and Wegener invited Milankovitch to contribute a text (Köppen and Wegener, 1924, p. 193ff, English edition) in which Milankovitch referred to his 1923 paper (Milankovitch, 1923; Köppen and Wegener,1924, p. 194, English edition).
In his Canon (Milankovitch, 1941), Milankovitch devoted 20 pages to the “quantities of heat received by a latitude during a caloric summer and winter half-year”. From the formulas that he developed, it is clear that, during their local season, the impact of the variations in obliquity is the same in both hemispheres and at a maximum in the high latitudes, whereas the impact of climatic precession is opposite in the two hemispheres and at a maximum in the low latitudes.
In chap. XX of his Canon, Milankovitch gave the numerical values of the caloric Northern and Southern Hemisphere summer half-years for 1800 (Table XXIII) and over the last 600 000 years (Table XXV) in canonic units (the canonic units introduced by Milankovitch are the units obtained if the solar constant is the unit of solar radiation and if the unit of time is 100 000 instead of seconds). Since no hypotheses were introduced for these calculations, Milankovitch, who was convinced of the perennity of his work, decided to call his results Kanon der Erdbestrahlung (Canon of insolation).
With Köppen's approval, Milankovitch preferred not to continue reproducing the numerical values of insolation themselves but rather to transform them into fictitious latitudes, called the 65∘ N equivalent latitudes; these values and figures were first published in Köppen and Wegener (1924, pp. 240–241, English edition) and in his “Mathematische Klimalehre” but the definition was already given in Milankovitch (1920, p. 73). These latitudes are actually the present-day latitudes which received the same irradiation during the Northern Hemisphere caloric summer half-year as 65∘ N in the past. A fictitious motion of these latitudes to the south corresponds therefore to an increase in the summer irradiation and in the north to a decrease in insolation leading possibly to a glaciation.
It must be stressed that the main contributions of Milankovitch were not only based on his insolation and radiation curves, but also on his mathematical computation of the thermal effects of the secular march of insolation, his so-called mathematical climate. The direct effect calculated if insolation only varied was published in his 1930 “Mathematische Klimalehre”. From the Stefan–Boltzmann law and a grey body model with the reflective power of the surface and the absorption coefficient in infrared kept invariable, Milankovitch calculated the long-term variations in the mean temperatures of the caloric summer and winter half-years (, ΔQ in canonic units).
If the ice cover and other feedbacks are taken into account, the indirect effects can be estimated. This was published in 1938 in “Astronomische Mittel”, where Milankovitch first calculated the altitude of the snow line (called snow limit by Köppen and Milankovitch; Milankovitch, 1941, p. 437), Hi, as a function of the caloric summer insolation. This calculation was based on the correlation between these variables according to Köppen snow limit data for different latitudes. According to his relationship, any variation in the summer irradiation by 1 canonic unit produces a shift in the snow limit altitude by 1 m (ΔHi=1.09ΔQS).
These relationships allowed Milankovitch to give the caloric summer and winter insolation a climatological meaning. This shows how much he was concerned with climate and its variations. As these relationships are simple and straightforward, Milankovitch did not publish any additional tables and referred only to his tables providing the long-term variations in the caloric summer and winter half-year insolation. From his Table XXV, we can see that the deficit in summer radiation reached 573 canonic units at 75∘ N 22 100 years ago, which according to his formula means a drop in the altitude of the snow line of more than 500 m. Following the Köppen table of the altitude of the snow limit for different latitudes (Milankovitch, 1941, Fig. 53, p. 435 and Table XXVII, p. 437), the polar cap can then have extended from 75 up to 65∘ N, which means it covered an area 2.75 times greater. This kind of deficit can also be reached in the tropical latitudes with an accompanying lowering of the snow limit altitude, which, as noted by Milankovitch (1941, p. 471) “refutes the opinion expressed by some geologists that insolation cannot explain such displacement”. Milankovitch also pointed out that “owing to such variations in the summer irradiation, the mean summer temperature dropped from time to time by more than 5∘ in the high and temperate latitudes of both hemispheres and even in the tropical latitudes”.
The most important point is that such an increase in the size of the polar snow cover changes the reflective power of the Earth. This is why to complete his Canon, Milankovitch decided to compute the long-term variations in the mean summer and winter insolation per unit surface area of the northern and southern polar snow caps over the last 600 000 years (Table XXVIII). The extent of these polar caps was deduced from the treatise by Wundt (1933). In this treatise, the northern cap extends presently to 75∘ N and reached 55∘ N at the maximum of the Ice Age. From these values, Milankovitch could compute the long-term variations in the insolation over such polar caps delimited by the parallel 55∘ assuming that the extension of the snow cap was always proportional to the corresponding deficit in summer radiation. If the albedo is kept constant, it can be seen that the minimum summer radiation over the northern cap reaching 55∘ N occurred 230 000 years ago, with a radiation deficit , compared to the present, amounting to 660 canonic units (ε is the obliquity, e the eccentricity and Πγ the longitude of the perihelion). As this deficit caused a southward extension of the cap of 20∘, Milankovitch concluded that a change by 1 canonic unit corresponds to a meridional change in the extent of the northern polar cap by about 1′82, which is equivalent to 3.37 km. This means also that the northern snow cap totally disappears for an increase in the summer insolation by 495 canonic units. This occurred quite a few times over the last 600 000 years, as for example 10 000 and 127 000 years ago.
Taking into account the reflective power of snow at the Earth's surface, for the cap reaching 55∘ N, shows that large negative amplitudes occurred several times over the last 600 000 years. At 230 kyr BP, the total deficit now amounts to 2180 canonic units. This is far more than the deficit of 660 units calculated if the reflective power of snow is not taken into account. It corresponds to a displacement downward of the snow limit of 2180 m, which is about the present altitude of the snow limit at 55∘ N. This implies that the polar cap must have reached this latitude at that time, which according to Milankovitch was actually observed in the geological reconstruction. It is also interesting to note with Milankovitch that the deficit of the annual radiation at 230 kyr BP amounted to 1920 canonic units, which means a decrease in the annual temperature by 6.4 ∘C , contradicting those who claims that the long-term variations in insolation cannot cause any important drop in the annual temperature.
Using the data for the cap reaching 45∘ N, nine large deficits can be observed at 590.3, 550, 475.6, 435, 230, 187.5, 115, 71.9 and 25 kyr BP. These can be assembled into groups corresponding to the four glacial periods of the Penck–Brückner scheme recognized by Köppen in the Milankovitch 65∘ N equivalent latitude.
These new results considering the reflective power of the polar caps in addition to the long-term variations in insolation were published in “Neue Ergebnisse” (Milankovitch, 1937, 1938) and, according to Milankovitch, are “absolutely sufficient to explain the full extent of even the greatest climatic events of the Quaternary and to clearly show their causes” refuting Penck (1940)'s opinion (see Milankovitch, 1941, p. 477).
All these calculations show clearly that Milankovitch can be named the “father of paleoclimate modeling”, certainly more specifically than the father of the astronomical theory in general (the first to propose the variations in the Earth's orbit as the causes of climate changes was Jens Esmark (1763–1839), 100 years before Milankovitch (Hestmark, 2018). Milankovitch was the first to demonstrate mathematically that the long-term variations in insolation are responsible for the climatic variations over the last hundreds of thousands of years. With his contemporary colleagues, Penck, Brückner, Köppen and Wegener (see also Thiede, 2018), to cite only a few of the best known, he could show that his mathematical climate fits well the geological reconstruction of climate available at that time.
Milankovitch deserves this title of father of paleoclimate modeling because it is hard to find any scientist before him with so many papers stressing a mathematical climate and the calculation of the incoming solar radiation. He wrote about 100 papers (in Serbo-Croatian, German or French, most of them having more than 20 pages) as a single author. His mathematical climate and his caloric incoming solar radiation are fully original, as well as his dating and interpretation of the paleoclimate data. To cite only his best known 1941 book, besides eight chapters on fundamental celestial mechanics (150 pp.) and four on polar wandering (61 pp.), there are three chapters (80 pp.) on terrestrial insolation, three (70 pp.) on the connection between insolation and atmospheric temperature (his mathematical climate), and five (117 pp.) on ice ages, mechanisms and chronology. This is about 270 pages on what may be called paleoclimate modeling. Written in the first part of the 20th century, about 100 years ago, his work had a profound influence on the geologists and geophysicists of these early times (Penck, Brückner, Köppen and Wegener, in particular) but also continues to have one since the revival by Hays, Imbrie, Shackleton and Berger in the 1970s. The early part of the 20th century actually saw two exceptional geophysicists: Wegener and Milankovitch. Not only did they work together, but both of them also “had the imagination to bridge the confines of one discipline to make a major contribution to another” (Ledley, 1987).
Finally, it must be stressed that paleoclimate modeling is a subject more fundamentally related to astronomy (a forcing) than to CO2 (a feedback). The title of father of paleoclimate modeling given to Milankovitch does not therefore do injustice to scientists like Joseph Fourier (1768–1830), John Tyndall (1820–1893), Svante Arrhenius (1859–1927), Guy Steward Callendar (1898–1964) and others. Their individual contributions to CO2 must also be stressed. For example, the book on the Théorie de la chaleur (Fourier, 1822, 648 pp.) by Fourier dates back to 1822 and his paper on the “Températures du globe terrestre” (Fourier, 1824) was published in 1824; the greenhouse effect by Tyndall dates back 1859, the year Arrhenius was born and 37 years before the paper by Arrhenius. Such a paper on the history of CO2 and the ice ages is certainly welcome to underline this other important aspect of paleoclimate (Bard, 2004) as is a book on the full history of paleoclimates (Krüger, 2013).
The insolation data used in Fig. 1 can be calculated by using the code at https://www.elic.ucl.ac.be/modx/index.php?id=83 (Berger, 2021; Berger and Loutre, 1991; Berger et al., 2010).
The author declares that there is no conflict of interest.
Publisher’s note: Copernicus Publications remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This article is part of the special issue “A century of Milankovic's theory of climate changes: achievements and challenges (NPG/CP inter-journal SI)”. It is a result of the conference “One Hundred Years of Milankovic's Theory of Climate Changes: synergy of the achievements and challenges of the next century”, 17–18 November 2020.
Thanks to Vladimir Jankovic from the Center for the History of Science, Technology and Medicine at the University of Manchester for his thoughtful comments. Thanks to James Hays from the Lamont Doherty Earth Observatory, Columbia University, to Martin Claussen from the Max Planck Institute for Meteorology Hamburg and to another anonymous reviewer for their helpful comments and proof-reading suggestions. Thanks also to Qiuzhen Yin from Université catholique de Louvain for reading the paper and for providing Fig. 1.
This paper was edited by Denis-Didier Rousseau and reviewed by Martin Claussen and two anonymous referees.
Bard, E.: Greenhouse effect and ice ages: historical perspective, External Geophysics, Climate and Environment (Climate), 336, 603–638, https://doi.org/10.1016/j.crte.2004.02.005, 2004.
Berger, A.: Théorie Astronomique des Paléoclimats, Dissertation doctorale, 2 volumes, Université catholique de Louvain, Louvain-la-Neuve, Belgium, 1973.
Berger, A.: Obliquity and general precession for the last 5 000 000 years, Astron. Astrophys., 51, 127–135, 1976.
Berger, A.: Long-term variations of the Earth's orbital elements, Celestial Mech., 15, 53–74, 1977.
Berger, A.: Long-term variations of daily insolation and Quaternary climatic changes, J. Atmos. Sci., 35, 2362–2367, 1978a.
Berger, A.: Long-term variations of caloric insolation resulting from the Earth's orbital elements, Quaternary Res., 9, 139–167, 1978b.
Berger, A.: Astronomical insolation forcing, Earth and Life Institute [code], available at: https://www.elic.ucl.ac.be/modx/index.php?id=83, last access: 15 August 2021.
Berger, A. and Loutre, M. F.: Insolation values for the climate of the last 10 million years, Quaternary Sci. Rev., 10, 297–317, 1991.
Berger, A., Loutre, M. F., and Yin, Q. Z.: Total irradiation during the interval of the year using elliptical integrals, Quaternary Sci. Rev., 29, 1968–1982, https://doi.org/10.1016/j.quascirev.2010.05.007, 2010.
Brückner, E., Köppen, W., and Wegener, A.: Über die Klimate der geologischen Vorzeit, Zeitschrift für Gletscherkunde, 14, 149–169, 1925.
Croll, J.: On the physical cause of the change of climate during geological epochs, Philos. Mag., 28, 121–137, 1864.
Fourier, J.: Théorie de la chaleur, Chez Firmin Didot, Père et Fils, Paris, France, 1822.
Fourier, J.: Remarques générales sur les Températures du Globe Terrestre et des Espaces Planétaires, Annales de Chimie et de Physique, 27, 136–167, 1824.
Harzer, P.: Die säkularen Veränderungen der Bahnen der grosse Planeten, Preisschriften/Fürstlich-Jablonowskische Gesellschaft der Wissenschaften, no. 31: Mathematisch- naturwissenschaftliche Sektion, Band 12; 280 pp., S. Hirzel, Leipzig, Germany, 1895.
Hays, J., Imbrie, J., and Shackleton, N.: Variations in the earth's orbit: pacemaker of the ice ages, Science, 194, 1121–1132, 1976.
Herschell, J. W.: On the astronomical causes which may influence geological phenomena, Trans. Geological Society of London, 3, 293–300, 1832.
Hestmark, G.: Jens Esmark's mountain glacier traverse 1823 – the key to his discoveryof Ice Ages, Boreas, 47, 1–10, https://doi.org/10.1111/bor.12260, 2018.
Köppen, W.: Ergänzungen und Berichtigungen zu W. Köppen und A. Wegener: Die Klimate der geologischen Vorzeit, Gebrüder Borntraeger, Berlin, Germany, 1940.
Köppen, W. and Wegener, A.: Die Klimate der geologischen Vorzeit. Verlag von Gebrüder Bornträger, Berlin, Germany, 256 pp., Reproduction of the original German edition and complete English translation (The Climates of the Geological past) by: Thiede, J., Lochte, K., and Dummermuth, A., translated by: Oelkers, B., Borntraeger, Stuttgart, Germany, 2015, 1924.
Krüger, T.: Discovering the Ice Ages, International Reception and Consequeences for a historical understanding of Climate, translated by: Hentschel, A. M., Brill, Leiden, the Netherlands, Boston, USA, 533 pp., 2013.
Lagrange, J. L.: Théorie des variations séculaires des éléments des planètes. Nouveau Mémoire de l'Académie royale des Sciences et des Belles Lettres de Berlin, printed in Oeuvres de Lagrange, Volume 5, Paris, France, 1870, 1781–1782.
Laplace, P. S.: Traité de Mécanique Céleste, J. B. M. Duprat, Paris, France, 1799–1825.
Ledley, T. S.: Wegener, the father of continental drift, EOS-Transactions of AGU, 68, p. 516, 1987.
Le Verrier, U. J. J.: Recherches astronomiques, Annales Observatoire Impérial de Paris, volumes I and II, Mallet-Bachelier, Paris, France, 1855–1856.
Meech, L. W.: On the relative intensity of the heat and light of the Sun upon different latitudes of the Earth, Smithsonian Contribution to Knowledge IX, Washington, D.C., USA, 64 pp., 1856 (accepted for publication 1855).
Milankovitch, M.: O pitanju astronomskih teorija ledenih doba. Rad Jukoslovenske akademije znanosti i umjetnosti, vol. 204, Zagreb. Über die Frage der astronomischen theorien der Eiszeiten. This German translation was published by V. Vari'cak in the Bulletin des Travaux de l'Académie des Sciences de Zagreb in 1915, 1914.
Milankovitch, M.: Théorie Mathématique des Phénomènes Thermiques Produits par la Radiation Solaire. Académie Yougoslave des Sciences et des Arts de Zagreb, Gauthier Villars, Paris, France, 1920.
Milankovitch, M.: Kaloric̆na godis̆nja doba i njihov primena u paleoklimaskom problemu (in Cyrillic). Separat iz., Glas Sprske kraljevske akademje, vol. CIX, 1–30, 1923 (Kalorische Jahreszeiten und deren Anwendung im paläoklimalen Problem; Caloric seasons and their application in paleoclimate problem; Les saisons caloriques et leurs applications au problème paléoclimatique).
Milankovitch, M.: Mathematische Klimalehre und Astronomische Theorie der Klimaschwankungen. (Mathematical Climatology and the Astronomical theory of the Climatic changes). Köppen Geigersches Handbuch der Klimatologie, edited by: Köppen, W. and Geiger, R., Borntraeger, Berlin, Germany, Band I Teil A, 176 pp., 1930.
Milankovitch, M.: Neue Ergebnisse der astronomische Theorie der Klimaschwankungen. Bulletin de l'Académie des Sciences Mathématiques et Naturelles, A. Sciences Mathématiques et Physiques, no. 4, Académie Royale Serbe, Belgrade, Serbia, 41 pp., 1938. This paper on “New results of the astronomical theory of climatic oscillations ” was originally “Novi rezultati astronomske teorije klimatskih promena” published in Separat iz “Glas Srpske kraljevske iakademije, vol. 175, Belgrade, Serbia, 1937.
Milankovitch, M.: Astronomische Mittel zur Erforschung der erdgeschichtlichen Klimate (Astronomical Means for Investigating the Earth's Historical Climates), Handbuch der Geophysik, vol. 9, Sect. 8, Berlin, Germany, 1938.
Milankovitch, M.: Kanon der Erdbestrahlung und seine Anwendung auf des Eiszeitenproblem. Special Publication 132, Section of Mathematical and Natural Sciences, vol. 33, p. 633, Royal Serbian Academy of Sciences, Belgrade, Serbia (“Canon of Insolation and the Ice Age Problem”) (trans. Israel Program for the US Department of Commerce and the National Science Foundation, Washington, D.C., USA, 1969, and by Zavod za udzbenike i nastavna sredstva in cooperation with Muzej nauke i tehnike Srpske akademije nauka i umetnosti, Belgrade, Serbia, 1998), 1941.
Miskovitch, V. V.: Variations séculaires des éléments astronomiques de l'orbite terrestre, Glas Srp. kraljevske akad., 143, Première Classe no. 70, Belgrade, Serbia, 1931.
Murphy, J. J.: On the nature and cause of the glacial climate, Quaterly J. of Geological Society, 25, 350–356, 1869.
Penck, A.: Glacial Period and radiation Curve. Research and Progress, Bi-monthly review of German science, vol. VI, 11–16, Müller and Sohn, Berlin, Germany, 1940.
Penck, A. and Brückner, E.: Die Alpen in Eiszeitalter, Tauchnitz, Leipzig, Germany, 1042 pp., 1909.
Pilgrim, L.: Versuch einer rechnerischen Behandlung der Eiszeitalters, Jahresshefte des Vereins für Vaterl. Naturkunde in Württemberg, Bd. 60, 1904.
Pontécoulant, P. G.: Théorie analytique du Système du Monde, Livre VI, Bachelier, Imprimeur-Libraire pour les Mathématiques, Paris, France, 563 pp., 1834 (1829–1846).
Spitaler, R.: Das Klima des Eiszeitalters, Selbstverlag, Prag (lithographed), 138 pp., 1921.
Stockwell, J. N.: Memoir on the Secular Variations of the Elements of the Eight Principal Planets, Smiths Contr. Knowledge, Washington, 18, 199 pp., 1873 (accepted for publication in 1870).
Thiede, J.: Wladimir Köppen, Alfred Wegener, and Milutin Milankovitch: their impact on modern paleoclimate research and the revival of the Milankovitch hypothesis, Vestnik of Saint Petersburg University, Earth Sciences, 63, 230–250, https://doi.org/10.21638/11701/spbu07.2018.207, 2018.
Wiener, C.: Ueber die Stärke der Bestrahlung der Erde duch die Sonne in ihren verschiedenen Breiten und Jahreszeiten, Zeitschrift f. Mathematik u. Physik, XXII, 341–368, 1876.
Wundt, W.: Aenderungen der Erdalbedo wahrend der Eiszeit, Meteorol. Zeit., 50, 241–250, 1933.
- Abstract
- Introduction
- Long-term variations in the astronomical parameters
- Periods of astronomical parameters
- Caloric seasons
- The mathematical climate
- Irradiation over the polar caps
- Milankovitch, father of paleoclimate modeling
- Code and data availability
- Competing interests
- Disclaimer
- Special issue statement
- Acknowledgements
- Review statement
- References
- Abstract
- Introduction
- Long-term variations in the astronomical parameters
- Periods of astronomical parameters
- Caloric seasons
- The mathematical climate
- Irradiation over the polar caps
- Milankovitch, father of paleoclimate modeling
- Code and data availability
- Competing interests
- Disclaimer
- Special issue statement
- Acknowledgements
- Review statement
- References





