the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Modeling the evolution of pulse-like perturbations in atmospheric carbon and carbon isotopes: the role of weathering–sedimentation imbalances
Aurich Jeltsch-Thömmes
Fortunat Joos
Measurements of carbon isotope variations in climate archives and isotope-enabled climate modeling advance the understanding of the carbon cycle. Perturbations in atmospheric CO2 and in its isotopic ratios (δ13C, Δ14C) are removed by different processes acting on different timescales. We investigate these differences on timescales of up to 100 000 years in pulse-release experiments with the Bern3D-LPX Earth system model of intermediate complexity and by analytical solutions from a box model. On timescales from years to many centuries, the atmospheric perturbations in CO2 and δ13CO2 are reduced by air–sea gas exchange, physical transport from the surface to the deep ocean, and by the land biosphere. Isotopic perturbations are initially removed much faster from the atmosphere than perturbations in CO2 as explained by aquatic carbonate chemistry. On multimillennial timescales, the CO2 perturbation is removed by carbonate compensation and silicate rock weathering. In contrast, the δ13C perturbation is removed by the relentless flux of organic and calcium carbonate particles buried in sediments. The associated removal rate is significantly modified by spatial δ13C gradients within the ocean, influencing the isotopic perturbation of the burial flux. Space-time variations in ocean δ13C perturbations are captured by principal components and empirical orthogonal functions. Analytical impulse response functions for atmospheric CO2 and δ13CO2 are provided.
Results suggest that changes in terrestrial carbon storage were not the sole cause for the abrupt, centennial-scale CO2 and δ13CO2 variations recorded in ice during Heinrich stadials HS1 and HS4, though model and data uncertainties prevent a firm conclusion. The δ13C offset between the Penultimate Glacial Maximum and Last Glacial Maximum reconstructed for the ocean and atmosphere is most likely caused by imbalances between weathering, volcanism, and burial fluxes. Our study highlights the importance of isotopic fluxes connected to weathering–sedimentation imbalances, which so far have been often neglected on glacial–interglacial timescales.
- Article
(5578 KB) - Full-text XML
- BibTeX
- EndNote
Research efforts to understand the past and future evolution of atmospheric CO2 and of its isotopic signature have been ongoing for many decades. Yet, many open questions remain, including, for example, the offsets in the stable isotope signature of CO2 (δ13Catm) and of dissolved inorganic carbon (δ13CDIC) between the Penultimate Glacial Maximum (PGM) and Last Glacial Maximum (LGM), as well as between the last (Eem) and current (Holocene)interglacials (Schneider et al., 2013; Eggleston et al., 2016; Hoogakker et al., 2006; Oliver et al., 2010). Could this PGM–LGM δ13C offset result from a change in terrestrial carbon storage or rather from changes in carbon and carbon isotope fluxes connected to the sedimentary weathering–burial cycle? Further questions remain regarding CO2 and δ13Catm variations on centennial and millennial timescales and a possible role of changes in the land biosphere carbon inventory (e.g., Köhler et al., 2010; Skinner et al., 2010, 2017; Schmitt et al., 2012; Bauska et al., 2018). Reconstructed variations in CO2 and δ13Catm during Heinrich stadials 4 and 1 (HS4 and HS1), two Northern Hemisphere cold periods during the last glacial, have been attributed to changes in terrestrial carbon storage (e.g., Bauska et al., 2016, 2018); however, other scenarios might be possible.
The perturbations in CO2 and δ13CO2 due to a carbon input (or removal) from the land biosphere or from fossil fuel burning are eventually removed by a few principal processes. In the case of CO2, over the first decades and centuries, this removal is because of ocean and land uptake; on millennial timescales, it is CaCO3 compensation; finally, on timescales of hundreds of thousands of years, the remaining atmospheric CO2 perturbation is removed by enhanced silicate rock weathering (e.g., Archer et al., 1998; Joos et al., 2001, 2013; Colbourn et al., 2015; Lord et al., 2016). In the case of δ13C, the perturbation is mixed rather quickly throughout the atmosphere–land–ocean reservoir and is removed on multimillennial timescales by changes in the isotopic signature of burial fluxes to the lithosphere.
The simulation of climate and CO2 over thousands of years with dynamic three-dimensional models remains challenging. Over the last decades, computational power has continuously increased and first results from simulations with Earth system models of intermediate complexity (EMICs) covering glacial–interglacial cycles have been published (e.g., Brovkin et al., 2012; Menviel et al., 2012; Ganopolski and Brovkin, 2017). However, to date these long timescales prevented large ensemble simulations with spatially resolved models as well as glacial–interglacial simulations using state-of-the-art Earth system models. A possible tool to overcome these computational obstacles is the use of reduced-form models invoking impulse response functions (IRFs) and principal component and empirical orthogonal function (PC-EOF) analysis. IRFs and PC-EOF analysis are instrumental to characterize the fundamental time and spatial scales of model response to a perturbation.
The response of a linear system to a perturbation such as carbon emissions to the atmosphere can be fully characterized by its IRF. The atmosphere–ocean CO2 cycle can be approximated as a nearly linear system, as long as concentrations do not vary much, i.e., less than a doubling of preindustrial CO2 concentrations (Hooss et al., 2001). The perturbation in the atmosphere or ocean is then given by the convolution integral of the emission history and the corresponding IRF (e.g., Joos and Bruno, 1996; Joos et al., 1996). IRFs can easily be described by a sum of exponentials, yielding a cost-efficient substitute model for describing the temporal evolution of an atmospheric CO2 perturbation. IRFs have been widely used to calculate remaining atmospheric fractions of anthropogenic CO2 emissions on different timescales and to characterize model behavior and their characteristic response timescales (e.g., Siegenthaler and Oeschger, 1978; Maier-Reimer and Hasselmann, 1987; Sarmiento et al., 1992; Siegenthaler and Joos, 1992; Enting et al., 1994; Joos and Bruno, 1996; Archer et al., 1997, 1998, 2009; Ridgwell and Hargreaves, 2007; Archer and Brovkin, 2008; Joos et al., 2013; Colbourn et al., 2015; Lord et al., 2016). However, peer-reviewed studies that quantify the IRF for carbon isotopes of CO2 are scarce (Schimel et al., 1996; Joos and Bruno, 1996) and, to our knowledge, not available for multimillennial timescales.
Principal component analysis is widely used to capture the information of multidimensional data. The atmospheric perturbation in CO2 and its isotopes in response to carbon input external to the ocean–atmosphere system is propagated to the ocean. The resulting spatiotemporal (4-D) evolution of marine tracers may be conveniently approximated using PC-EOF analysis. The perturbation is described as a superposition of spatial empirical orthogonal functions (EOF(x)) multiplied with the corresponding time-dependent principal component (PC(t)). Combining IRF and PC-EOF then allows one to compute the perturbation in space and time with minimal computational resources (Hooss et al., 2001; Joos et al., 2001)
The main goal of this study is to investigate the timescales and underlying processes for the removal of an atmospheric perturbation in CO2 and its δ13C signature in response to an external carbon input. To this end, we performed pulse-release (uptake) experiments over 100 000 years with the Bern3D-LPX EMIC. We determine characteristic impulse response (or Green's) functions (IRF) and describe marine spatiotemporal variations using PC-EOF analysis. Responses of the atmospheric radiocarbon signature (Δ14C) are briefly addressed. Implications of our results for the PGM–LGM δ13C difference and for past centennial CO2 variations are discussed. Simple expressions that illuminate the fundamental differences in the removal timescales for an atmospheric perturbation in CO2 versus the associated perturbation in δ13CO2 are developed in the Appendix. The pulse experiments represent (i) the sudden carbon uptake from or release to the atmosphere by the land biosphere, (ii) the release of old organic carbon, e.g., from ancient peat or permafrost material, (iii) the burning of all conventional fossil fuel resources, and (iv) a variation in 14C production by cosmic radiation or atomic bomb tests.
2.1 The Bern3D-LPX model
For this study, the Bern3D v2.0s Earth system model of intermediate complexity (EMIC) is used coupled to the dynamic vegetation model LPX-Bern v1.4. The Bern3D model consists of a three-dimensional geostrophic ocean (Edwards et al., 1998; Müller et al., 2006) with an isopycnal diffusion scheme and Gent–McWilliams parameterization for eddy-induced transport (Griffies, 1998) and a single-layer energy-moisture balance atmosphere to which a thermodynamic sea-ice component is coupled (Ritz et al., 2011). We use the ocean model coupled to a 10 layer sediment module (Tschumi et al., 2011; Heinze et al., 1999) with updated sediment parameters (Jeltsch-Thömmes et al., 2019) and to a global representation of rock weathering (Colbourn et al., 2013). The resolution of the Bern3D model components is 41×40 horizontal grid cells with 32 logarithmically spaced depth layers in the ocean. Wind stress at the ocean surface is prescribed from the NCEP/NCAR monthly wind stress climatology (Kalnay et al., 1996), and air–sea gas exchange and carbonate chemistry follow OCMIP-2 protocols (Najjar and Orr, 1999; Orr et al., 1999, 2017; Wanninkhof, 2014; Orr and Epitalon, 2015). The global-mean air–sea gas transfer rate is reduced by 19 % to match observational radiocarbon estimates (Müller et al., 2006), and gas transfer velocity scales linearly with wind speed (Krakauer et al., 2006).
Marine productivity is calculated as a function of light availability, temperature, and nutrient concentrations (P, Fe, Si), and it is restricted to the euphotic zone in the uppermost 75 m. Tracers, including dissolved inorganic carbon (DIC) and semilabile dissolved organic carbon (DOC); the corresponding isotopic forms; and alkalinity (Alk), phosphate (PO4), oxygen (O2), iron (Fe), silicon (Si), and an ideal age tracer are transported by advection, diffusion, and convection. Biogeochemical cycling is described in detail in Tschumi et al. (2011), Parekh et al. (2008), and subsequent studies (e.g., Menviel and Joos, 2012; Menviel et al., 2012; Roth and Joos, 2012; Roth et al., 2014; Menviel et al., 2015; Battaglia et al., 2016; Battaglia and Joos, 2018a, b; Jeltsch-Thömmes et al., 2019). Isotopic fractionation between model components is documented in Jeltsch-Thömmes et al. (2019).
The sediment module dynamically calculates the transport, redissolution or remineralization, and bioturbation of solid material, the porewater chemistry, and diffusion in the top 10 cm of the sediment. The governing equations of the sediment model are given in Appendix A of Tschumi et al. (2011). A comparison of simulated versus observation-based sediment composition for the setup used in this study is given in Appendix B of Jeltsch-Thömmes et al. (2019). A table with all parameters applied here and by Jeltsch-Thömmes et al. (2019) is given in the Appendix (Table B1). Four solid tracers (CaCO3, opal, particulate organic carbon (POC), clay) and seven tracers in the porewater (DIC, DI13C, DI14C, alkalinity, phosphate, oxygen, and silicic acid) are modeled. The dissolution of CaCO3 and POC depends on the respective weight fraction of CaCO3 and POC in the solid phase of the sediment and the porewater and O2 concentrations, respectively. Denitrification is not considered in this model version, but O2 is not consumed below a threshold, somewhat reflecting the process of denitrification without modeling . The respective reaction rate parameters for CaCO3 dissolution and POC oxidation are global constants (see Roth et al., 2014; Jeltsch-Thömmes et al., 2019). The model assumes conservation of volume, i.e., the entire column of the sediments is pushed downward if deposition exceeds redissolution into porewaters. Any solid material that is pushed out of the diagenetic zone (top 10 cm) disappears into the subjacent diagenetically consolidated zone (burial or loss flux) (see Tschumi et al., 2011, for more details). The burial flux at preindustrial steady state is 0.22 GtC yr−1 in the form of CaCO3, 0.24 GtC yr−1 in the form of POC, and 6.96 Tmol Si yr−1 in the form of opal, all within the observational range. The global inventories in the interactive sediment layers amount to 916 GtC for CaCO3, to 510 GtC for POC, and to 21 460 Tmol Si for opal. Carbonate chemistry within sediment porewaters is calculated as in the ocean by using the MOCSY routine of Orr and Epitalon (2015).
Input fluxes by “weathering” of P, ALK, DIC, DI13C, and Si are added uniformly to the coastal surface ocean. At the beginning of transient simulations, the global input fluxes of these compounds are set equal to the burial fluxes diagnosed at the end of the model spin-up. These input fluxes are jointly denoted as “weathering flux”. These fluxes are further attributed to weathering of organic material, of CaCO3, of CaSiO3, and to volcanic CO2 outgassing. The flux of phosphorus (P) is assigned to weathering of organic material, and related carbon (C) and ALK fluxes are computed by multiplication of the P flux with the Redfield ratios where P : C : Alk is equal to for organic material. Similarly, the silicon (Si) flux is assigned to CaSiO3 weathering, and the related ALK flux is computed using Si : ALK is equal to 1:2 based on the simplified equation for CaSiO3 weathering: 2CO2 + H2O + CaSiO3 → Ca2+ + + SiO2 (Colbourn et al., 2013). The remaining ALK flux is attributed to CaCO3 weathering with the stoichiometric ratio C : ALK equal to 1:2 following from CO2 + H2O + CaCO3 → Ca2+ + . The volcanic flux is the remaining flux needed to balance the C input flux. The diagnosed fluxes at the end of the spin-up are 0.24 GtC yr−1 for weathering of organic material, 0.14 GtC yr−1 for CaCO3 weathering, 0.08 GtC yr−1 for volcanic CO2 outgassing, and 6.96 Tmol Si yr−1 for CaSiO3 weathering. The isotopic signature of the weathering carbon corresponds to the respective signature of the burial fluxes and amounts to δ13C = −9.2 ‰, intermediate between isotopically light organic carbon (δ13C = −20.5 ‰) and heavier CaCO3 (δ13C = 2.9 ‰). During experiments, weathering fluxes of CaCO3 and CaSiO3, and accordingly DIC, DI13C, and alkalinity, are allowed to vary as a function of surface air temperature, runoff, and net primary productivity (NPP). The parameterization of this weathering feedback follows equations described in detail in Colbourn et al. (2013). The runoff dependence is parameterized as a function of temperature, and for the productivity feedback the NPP from the coupled LPX-Bern model is used. We apply weathering feedbacks in the global average 0-D version (Colbourn et al., 2013, 2015); the equations are given in Appendix B.
The Bern3D model is coupled to the Land surface Processes and eXchanges (LPX) model v1.4 (Lienert and Joos, 2018), which is based on the Lund-Potsdam-Jena (LPJ) model (Sitch et al., 2003). In LPX, coupled nitrogen, water, and carbon cycles are simulated and vegetation composition is determined dynamically and represented with 20 (15 on natural and 5 on anthropogenically used land) plant functional types (PFTs). The PFTs compete within their bioclimatic limits for resources. CO2 assimilation of plants is implemented following Farquhar et al. (1980) and Haxeltine and Prentice (1996a, b), and isotopic discrimination during photosynthesis is calculated according to Lloyd and Farquhar (1994). The carbon cycles of Bern3D and LPX-Bern are coupled through carbon and isotope exchange fluxes between the land and atmosphere and between the ocean and atmosphere. Climate change information from the Bern3D model is passed on to LPX-Bern via a pattern-scaling approach (Stocker et al., 2013). Spatial anomaly patterns in monthly temperature and precipitation, derived from a 21st century simulation with the Community Climate System Model (CCSM4), are scaled by the anomaly in global monthly mean surface air temperature as computed interactively by the Bern3D. These anomaly fields are added to the monthly baseline (1901 to 1931 CE) climatology of the Climate Research Unit (CRU) (Harris et al., 2014). A more detailed description of the LPX-Bern model can be found in Keller et al. (2017) and Lienert and Joos (2018).
2.2 Experimental protocol
The Bern3D model is spun-up over 60 000 years (1000 years is represented by “kyr”) to a preindustrial steady state with 1850 CE boundary conditions. Atmospheric CO2 is prescribed to 284.7 ppm, δ13C to −6.305 ‰, and Δ14C to 0 ‰. For LPX, the land area under anthropogenic use is fixed to its 1850 CE extent and kept constant in all simulations. The LPX-Bern model had an uncoupled spin-up under identical 1850 CE boundary conditions over 2500 years. Bern3D and LPX-Bern are then coupled and equilibrated for 500 years, again under fixed 1850 CE boundary conditions. After the spin-up, atmospheric CO2 and its isotopic ratio are calculated interactively, with enabled carbon–climate feedbacks. Pulse experiments are started from the 1850 CE equilibrium state at nominal year −100. After 100 years, i.e., during nominal year 0 of the simulations, an external flux of carbon with characteristic isotopic signatures is removed from or added to the model atmosphere at a constant rate over the year. Runs are continued for 100 kyr to simulate the redistribution of the added carbon and isotopes in the Earth system.
Table 1Overview of simulations.
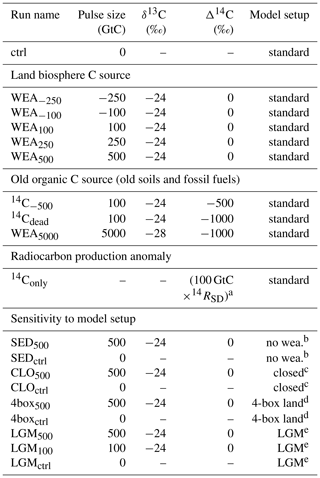
a The number of 14C atoms corresponding to 100 GtC with Δ14C = 0 ‰ is added. b Setup without CaCO3 and CaSiO3 weathering feedbacks. c “Closed system”: atmosphere–ocean–land without ocean sediment module and CaCO3 and CaSiO3 weathering feedbacks. d Setup with four-box land biosphere instead of LPX. e Setup with four-box land biosphere instead of LPX under LGM conditions.
Table 1 summarizes run names and key characteristics of all simulations. Pulse sizes are varied between −250 GtC (removal) to +500 GtC (addition) with δ13C of −24 ‰ and Δ14C of 0 ‰. This corresponds to a hypothetical, sudden uptake or release of carbon from the land biosphere with a typical C3-like δ13C signature. For simplicity, and to ease interpretation, we set the Δ14C of these land biosphere carbon pulses to the atmospheric signature; thus, we assume that the released material has been recently assimilated and neglect the small depletion in 14C of “young” plant, litter, and soil material. In sensitivity experiments, Δ14C is set to −500 ‰ and −1000 ‰ to mimic the release of old, dead, organic carbon, e.g., from buried peat or permafrost soils instead of young plant-derived material. In another simulation, the isotopic signatures are set to the signature for the modern mix of fossil fuels. Finally, we also performed a run where only 14C, but no 12C or 13C, is added to represent a change in radiocarbon production in the atmosphere. All these simulations were performed with fully interactive ocean sediments and enabled CaCO3 and CaSiO3 weathering feedbacks. The influence of the weathering feedback and of ocean–sediment interactions is quantified using two additional simulations. First, the weathering input flux is kept time invariant (“no weathering feedback”), Second, the sediment module is, in addition, not included in a so-called “closed” atmosphere–ocean–land model setup.
We also assess the influence of glacial climate boundary conditions and of a different land biosphere model in two additional simulations: LGM500 and 4box500. In 4box500 the Bern3D setup and spin-up is as in WEA500, except that an atmospheric CO2 concentration of 278 ppm is used instead of 284.7 ppm, and the pulse is released in the first time step of simulation year 100, rather than being distributed over year 100. The model configuration includes reactive sediments and weathering feedbacks. A four-box terrestrial biosphere model (Siegenthaler and Oeschger, 1987), that allows for CO2 fertilization, instead of LPX-Bern is coupled to the Bern3D in these runs. In LGM500 the model is forced by glacial boundary conditions instead of preindustrial conditions as in 4box500 and in WEA500. CO2 is set to 180 ppm and Northern Hemisphere ice sheets are set to Last Glacial Maximum coverage (Peltier, 1994). It has to be noted, however, that forcing the model with 180 ppm during spin-up leads to less carbon stored in the ocean under LGM compared to preindustrial (PI) conditions, and results from LGM500 should be treated with some caution. Differences in results between WEA500 and 4box500 are due to differences in the two land biosphere models. Differences between 4box500 and LGM500 are exclusively due to differences in climatic boundary conditions.
2.3 Data reduction
The remaining fraction of a pulse-like perturbation or IRF at time t after the pulse release is defined for atmospheric CO2 as
Δ indicates a perturbation, here evaluated as the difference between a simulation with pulse release and a corresponding control simulation. P indicates the pulse size in gigatonnes of carbon (GtC), which yields the initial atmospheric CO2 perturbation in parts per million (ppm) when divided by 2.12 GtC ppm−1. The superscript “ctrl” refers to the control simulation without pulse, “ini” to the (maximum) initial perturbation assuming an instantaneous carbon release, and subscript “a” to the atmosphere. The IRF for δ13Ca is
denotes the initial isotopic perturbation in the atmosphere and equals:
δ13CP indicates the isotopic signature of the pulse, the subscript 0 the value prior to the pulse, and Na the atmospheric carbon inventory. Analogous equations to Eqs. (2) and (3) hold for Δ14C.
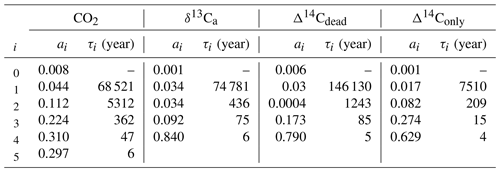
An analytical expression for the IRF is calculated from experiment WEA500. The IRF is fitted by the sum of five exponential terms to
using a least-squares optimization routine in Python. The coefficients ai are fractions of the perturbation, each associated with a timescale τi, and a0 is the fraction of the perturbation remaining constant in the atmosphere (τ0=∞). The sum over all six coefficients, ai, equals 1. Modeled values are well reproduced with n=5 exponents. Differences between the original model output and the fit are insignificant for practical applications. Finally, we note that the IRF or remaining atmospheric fraction is in our experimental setup always smaller than one: the carbon is added at a constant rate during year 0 in the pulse simulations, and part of this carbon is already taken up by the ocean during this initial year. Similarly, the IRF for δ13Ca and Δ14Ca is fitted with n=4 exponents.
Principal component empirical orthogonal function (PC-EOF) analysis is used to fit the 13C isotopic perturbations of dissolved inorganic carbon (DIC) in the ocean (). To this end, the Python package eofs (Dawson, 2016) is used to calculate principal component time series (PC(t)) and the spatial empirical orthogonal functions (EOF(x)) from the volume-weighted 4-D field of (t, x). PCs and EOFs are then used to build a cost-efficient substitute model of the spatiotemporal evolution of in response to an atmospheric pulse perturbation. The output frequency for marine 3-D tracer fields after the perturbation is every 10 years during the first 1 kyr, every 200 years until 10 kyr, and every 1 kyr thereafter. In the PC-EOF calculation this gives more weight to the first part of the simulation, where changes in the perturbation are larger.
3.1 Earth system response to a pulse release of carbon
Impulse response functions for atmospheric CO2 and δ13C
We first describe the IRF for the atmospheric CO2 perturbation using experiment WEA250 (Fig. 1a). The initial spike in response to the carbon release is followed by a substantial decline over the first decades due to carbon uptake by the upper ocean and land biosphere. The IRF is reduced to less than 40 % within the first century and decreases further on the timescale of ocean mixing to less than 16 % by year 2000. The fit by exponentials (Table 2) yields timescales of 6, 47, and 362 years for this initial decline. They represent the continuum of carbon overturning timescales within the ocean and the land biosphere as well as timescales governing air–sea and air–land carbon exchanges.
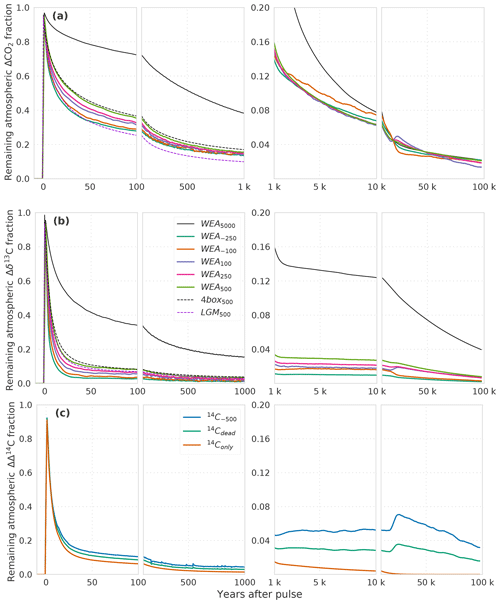
Figure 1(a) CO2, (b) δ13C, and (c) Δ14C perturbations in the atmosphere for different simulations with different pulse sizes and model configurations. The isotopic signature is δ13C = −24 ‰ for all pulse sizes except the 5000 GtC pulse with δ13C = −28 ‰. See Table 1 and Sect. 2.2 for details of the experimental setup of the runs. Data are filtered with a moving average of 1000 years in the interval 1–10 kyr and 5000 years in the interval 10–100 kyr for better visibility. Factorial simulations (WEA500, SED500, CLO500, 4box500, and LGM500) for the time interval 1 to 100 kyr are shown in Fig. 2 for better visibility.
CaCO3 compensation and weathering–burial imbalances remove the atmospheric perturbation on multimillennial timescales such that after 10 kyr less than 8 % and after 100 kyr less than 2 % of the CO2 perturbation remain airborne (Fig. 1a). The fit by exponentials shows that a fraction of 11.2 % of the initial perturbation is removed with a timescale of 5.5 kyr. We associate these values with the process of CaCO3 compensation. A remaining fraction of 4 % to 5 % is removed with a timescale of 69 kyr (Table 2), linked to enhanced silicate rock weathering. The jumps visible at around 20 kyr in Fig. 1 arise from a sea-ice–albedo feedback in the control run. They appear most pronounced in the experiments with small perturbations. The change in the control run in CO2 is less than 1 ppm and less than 0.03 ‰ in δ13CO2. These jumps are not of further relevance for our discussion. In comparison to others, our results show, up to a few percent, lower remaining fractions for the 5000 GtC pulse (WEA5000) than results presented by Colbourn et al. (2015) and Lord et al. (2016). The remaining airborne fraction of the CO2 perturbation is 5 % and less after 100 kyr in all studies.
Compared to CO2, the atmospheric δ13C perturbation is initially removed much faster (Fig. 1b). Within the first decades, IRF(δ13Ca) is reduced to below 10 %. The further decline is slower, and 1 kyr after the pulse less than 3 % of the initial perturbation remains airborne. The remaining atmospheric perturbation is finally reduced to ≤1 % of the initial perturbation at the end of the simulation (Fig. 1b). The fit by exponentials for IRF() (Table 2) shows that 84 % of the perturbation are removed with a timescale of 6 years, reflecting the initial fast decline seen in Fig. 1b when the perturbation is taken up by the upper ocean and living vegetation. About 9 % and 3 % are removed on timescales of 75 and 436 years, respectively, reflecting the decadal and centennial uptake of the perturbation by the land biosphere and deeper ocean. Approximately 3 % of the perturbations are finally removed with a timescale of ∼74 kyr by weathering–sedimentation processes, in agreement with the e-folding timescale of the decline (∼70 kyr; see further below). However, it has to be kept in mind that these removal timescales result from a fit, and thus other equally accurate solutions are possible to approximate the continuum of removal timescales.
Table 2Fit parameters for IRF(ΔCO2(t)) and IRF(Δδ13Ca(t)) of WEA500, IRF(ΔΔ14Ca,dead(t)), and IRF(ΔΔ14Ca,only(t)). Note that in the case of IRF(ΔΔ14Ca,dead(t)) the actual fitting was done only with data until simulation year 15 000 to avoid complications from the sea-ice feedback in the control run (see main text and Fig. 1c).
Processes
Next, we address the processes behind the different temporal evolution of CO2,a and δ13Ca. We focus on the ocean as ocean uptake is thought to dominate on long timescales. A perturbation in atmospheric CO2 or in 13CO2 is communicated by air–sea gas exchange to the surface ocean and further transported, mainly by physical processes, to the deep ocean. The fundamental difference between the IRF for CO2,a and δ13Ca is linked to the aquatic carbonate chemistry and the associated equilibrium between dissolved CO2 and bicarbonate and carbonate ions (CO2 + H2O ⇔ + H+ ⇔ + 2H+) (Dickson et al., 2007). The removal of an atmospheric CO2 perturbation is co-controlled by this acid–base carbonate chemistry (Revelle and Suess, 1957). In contrast, the removal of a perturbation in the isotopic ratio 13CO2∕12CO2 is hardly affected by this chemical buffering, because 13CO2 and 12CO2 are affected approximately equally by the acid–base chemical reactions. The chemical buffering diminishes the uptake capacity of the ocean for CO2 but not for the isotopic ratio. Correspondingly, the IRF for CO2,a decreases less rapidly than the IRF for δ13Ca, and IRF(δ13Ca) is smaller than IRF(CO2,a) over the simulation period.
For an illustrative, semiquantitative analysis, we developed approximate expressions for the IRF for CO2,a and δ13Ca for timescales up to 2 kyr as explained in the Appendix. Simplifying assumptions are that equilibrium between the atmosphere and a fraction of the ocean with the initial carbon inventory No,0 is assumed, while land biosphere carbon uptake and other climate–carbon-cycle feedbacks are neglected. Changes in land biosphere carbon storage can be considerable, in particular during the first century (see Fig. 3a). However, the role of the changes in land carbon stock becomes smaller when more carbon is taken up by the ocean, and thus for simplicity it is not considered in the analytical expression for CO2. For CO2, the expression reads as
The subscripts “a” and “o” indicate the atmosphere and ocean, respectively; 0 represents the time prior to the pulse; and ∞ represents the time when an effective ocean volume with the initial carbon inventory of No,0 is equilibrated with the atmosphere. ξ describes the influence of the acid–base carbonate chemistry on the relationship between the relative perturbation in the CO2 partial pressure and in dissolved inorganic carbon (DIC) (Revelle and Suess, 1957). ξ varies with environmental conditions and increases with the size of the CO2 perturbation. ξ is on the order of 10 for small pulse sizes (here −250 to 500 GtC). The dependency of IRF(CO2) on the size of the carbon pulse is implicitly captured in the variable ξ. The key information of Eq. (5) is that the magnitude of the IRF is determined by the ratio of the (equilibrated) ocean carbon inventory and the buffer factor (). The smaller this ratio, the larger IRF(CO2,a) is.
For δ13Ca, we also consider the initial carbon inventory of the land biosphere (Nb,0), as a substantial amount of the isotopic perturbation is contained in the land biosphere on multicentennial-to-millennial timescales (Fig. 3b). The corresponding expression reads as follows (for the derivation, see the Appendix):
Equation (6) shows that IRF(δ13Ca) is described by the product of two ratios. The first ratio corresponds to the ratio of the carbon inventory in the atmosphere immediately after the pulse release to the total carbon inventory in the (“equilibrated”) atmosphere–ocean–land-biosphere system. It tells us that the pulse perturbation is mixed uniformly (see also Appendix Eq. A20) and in proportion to the carbon inventories of the different reservoirs (atmosphere, ocean, land biosphere). The second fraction is about 1.2 and is thus a correction term of order 20 % for small pulse sizes, as typically applied in this study. It arises as the isotopic signature of the ocean and land biosphere is different from that of the atmosphere. δ13Cmean corresponds to the weighted mean signature of the atmosphere, ocean, and land biosphere, with the fraction of the pulse found in each of these reservoirs as weights (Appendix Eq. A27). Remarkably, the buffer factor ξ does not directly show up in Eq. (6). The reason is, as noted already above, that CO2 and 13CO2 are both about equally affected by the aquatic chemistry. In turn, their ratio, i.e., δ13C, is hardly affected by this acid–base buffering.
Equations (5) and (6) reveal the fundamental difference between a perturbation in CO2 (and 13CO2) and in the isotopic ratio (δ13CO2). For small pulse sizes (P→0), neglecting the influence of the land biosphere and the correction term in Eq. (6) for δ13C, Eqs. (6) and (5) are formally equal, except that a buffer factor ξ of 1, instead of ∼12, applies for δ13Ca. Equations (6) and (5) show that the pulse perturbation is distributed between the atmosphere and ocean proportionally to their initial carbon inventories Na,0 and No,0 in the case of δ13Ca but proportionally to Na,0 and in the case of CO2. As a consequence, the perturbation in the ratio δ13Ca is apparently removed much faster than the perturbation in the concentration CO2,a, despite the fact that the timescales to transport a perturbation from the surface ocean to the deep ocean by advection, convection, or diffusion are the same.
We may illustrate this difference in the removal rate numerically. ξ is about 12 for a small pulse, Na,0 is 600 GtC, and No,0 is 37 400 GtC for the whole ocean. Further, the top 300 m with a carbon inventory of 2600 GtC is ventilated within approximately a decade through air–sea gas exchange and upper-ocean physical transport processes (circulation, mixing). Then, the evaluation of Eq. (5) means, for a small pulse, that around 73 % and 16 % of the initial CO2 perturbation are still found in the atmosphere after about 10 years and 2 kyr, respectively. It has to be noted here that we assume ξ to be constant for small perturbations. With increasing pulse sizes, ξ also increases, leaving larger airborne fractions (cf. WEA500 versus WEA5000 in Fig. 1a after 1–2 kyr). Regarding δ13C, the corresponding fractions (Eq. 6) are much smaller (12 % to 31 % and 1 % to 3 %) for small pulse sizes (−250 to 500 GtC; see Appendix text after Eq. A14 for more details). We assume the perturbation to have mixed with 500 and 2700 GtC on land after 10 yr and 2 kyr, respectively. These values are roughly in agreement with the values shown in Fig. 1a for pulse sizes of up to 500 GtC.
Turning to intermediate timescales (2 kyr 20 kyr), CaCO3 compensation further reduces the atmospheric CO2 perturbation and removes the differences in IRF(CO2,a) arising from different pulse sizes (Fig. 1a). The process of CaCO3 compensation is briefly explained as follows. CO2 is taken up by the ocean and partly reacts to form bicarbonate () and hydrogen (H+) ions. This makes the water more acidic; the carbonate ion concentration ([]) is reduced and the water becomes corrosive to CaCO3. In turn, sedimentary CaCO3 dissolves to and Ca2+ ions, partly removing the perturbations in [] and [H+], a so-called seafloor neutralization. Under more acidic conditions, less alkalinity and carbon, in the form of CaCO3, is buried in the lithosphere than delivered by weathering input; this excess input leads to an increase in alkalinity and DIC, further removing the perturbations in [] and [H+] , a so-called terrestrial neutralization, and a new equilibrium between weathering and burial fluxes is established. This chain of processes raises the alkalinity twice as much as the DIC concentration in the ocean, and additional CO2 is taken up from the atmosphere.
Again, an approximate expression for the IRF(CO2,a) is developed. This applies for the time when CaCO3 compensation for the pulse perturbation is completed (see Appendix):
The factor 2 in Eq. (7) arises from the acid–base carbonate chemistry and the factor 1.5 from the change in the ocean carbon inventory due to excess dissolution (or burial) of CaCO3, equivalent to . The factor 1.5 is model dependent (see Archer et al., 1998) and also slightly different from previous Bern3D model versions. This equation shows that the airborne fraction after CaCO3 compensation depends on the ratio of the initial atmosphere-to-ocean carbon inventory (Na,0 to No,0). Therefore, IRF is (approximately) independent of the pulse size. Equation (7) successfully explains why IRF(CO2,a) for pulse sizes from −250 to +5000 GtC take on a nearly identical value of 5 % around 20 kyr after the pulse.
IRF(δ13Ca) stays nearly constant between 1 and 10 kyr (Fig. 1b). This implies that CaCO3 compensation has little influence on the removal of the δ13C perturbation. Reasons are that the change in ocean carbon inventory due to CaCO3 dissolution (burial) is small compared to the total ocean inventory, and that the isotopic signature of CaCO3 is similar to that of DIC.
On even longer timescales, the CaSiO3 weathering feedback further removes the remaining perturbation in CO2,a with an e-folding timescale on the order of 70 kyr. The perturbation in δ13Ca is removed by the burial flux of organic carbon and CaCO3. This burial flux removes the isotopic perturbation to the lithosphere. Surprisingly, the removal rate is substantially faster than expected from the residence time of carbon, and it is highly sensitive to the gradients in the perturbation of δ13C (Δδ13C) within the ocean as further discussed below in the context of the factorial simulations and in the Appendix.
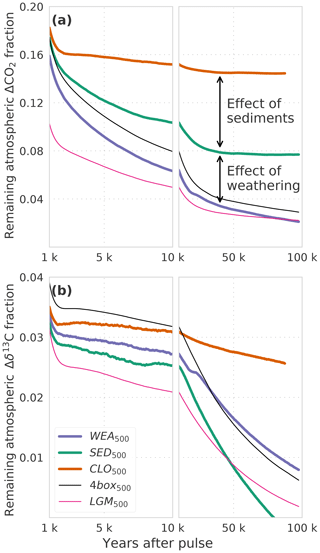
Figure 2(a) CO2 and (b) δ13C perturbations in the atmosphere for the factorial simulations WEA500, SED500, CLO500, 4box500, and LGM500. Shown is the time interval 1 to 100 kyr. Data are filtered with a moving average of 1000 years in the interval 1–10 kyr and 5000 years in the interval 10–100 kyr for better visibility. Note that experiment CLO500 was run for 90 kyr instead of 100 kyr.
Factorial simulations
We now turn to the factorial simulations to further quantify the effect of CaCO3 compensation, burial fluxes, and CaCO3 and CaSiO3 weathering feedbacks on the CO2 and δ13C perturbations. The evolution of IRF(CO2,a) for experiment SED500 (no terrestrial weathering feedback but with marine sediments) is comparable to WEA500 until simulation year 1000 and, it differs thereafter due to varying weathering rates in WEA500 (Figs. 1a and 2a). There is no addition of alkalinity to the ocean from enhanced terrestrial weathering in SED500, and ΔCO2,a levels out at a higher value than in WEA500, with about 8 % of the perturbation remaining constantly airborne in SED500. This value is in agreement with previous studies (e.g., Archer et al., 1998). It is somewhat higher than suggested by Eq. (7) as this equation represents a simplification.
CaCO3 compensation leads, in both WEA500 and SED500, to a further removal of ΔCO2,a on multimillennial timescales as seen between 1 and 10 kyr in Fig. 2a. After 10 kyr, IRF(CO2,a) decreases further as a result of weathering–burial imbalances in the CaCO3 flux, also referred to as terrestrial neutralization (e.g., Archer et al., 1998; Colbourn et al., 2015). The e-folding timescale for this terrestrial neutralization from SED500 is about 11 kyr, which is higher than the value provided by Archer et al. (1998) (8.5 kyr) but in the range (8 to 12 kyr) provided by Colbourn et al. (2015).
Comparing of SED500 and WEA500, the evolution is initially comparable, but on multimillennial timescales the isotopic perturbation is, somewhat surprisingly and in contrast to the CO2 perturbation, removed slower in WEA500 compared to SED500 (Fig. 2b). In the case of SED500 the e-folding timescale is on the order of 20 to 30 kyr. This is much shorter than expected from the mean residence time of carbon in the atmosphere–ocean–land-biosphere system of about 90 kyr (carbon inventory: ∼40 000 GtC; burial flux: 0.46 GtC yr−1). In simulation WEA500, with weathering feedbacks enabled, the long-term removal timescale of (∼70 kyr) is also shorter than the residence time of carbon in the atmosphere–ocean–land-biosphere system. The isotopic perturbation is larger in the surface ocean than in the ocean mean. In turn, the perturbation is removed more efficiently than expected from the residence time of carbon (see Fig. A1). The isotopic signature of the carbon burial flux is mainly determined by the upper-ocean isotopic signature, which is more depleted than the ocean mean for WEA500. In the case of SED500 this gradient is even stronger and lasts longer (Fig. A1; see Sect. 3.2 for further explanation). These results highlight the importance of spatial patterns within the ocean for the removal of an isotopic perturbation even for these very long timescales. However, the absolute perturbation in δ13Ca for these small pulse sizes and with δ13C = −24 ‰ is rather small after a few thousand years. For example, in the case of SED500, decreases to below 0.05 ‰ after ∼60 kyr. The interannual variability from the LPX-Bern model is of the same magnitude, and model drift also starts to play a role.
In scenario CLO500, we exclude the effect of ocean sediment interactions, and we treat the atmosphere, ocean, and land biosphere as a closed system. Considering ocean mixing times of 1–2 kyr, we would expect the CO2 perturbation for experiment CLO500 to reach a steady state within 2 kyr. The slow response timescale of peat carbon in the LPX-Bern model, however, leads to a further decline of ΔCO2,a over multiple millennia (Fig. 2a). About 15 % of the initial perturbation remains constantly airborne in the closed system model setting as expected from Eq. (5). δ13Ca levels out around 2 kyr at around 3 %, which is as expected from Eq. (6). The further decrease on multimillennial timescales results from model drift in the LPX-Bern model.
Next we compare WEA500, where LPX-Bern is used as land model, with 4box500, where a four-box land biosphere is used. Differences in IRF(CO2,a) between WEA500 and 4box500 are due to the different land biosphere models. The four-box land biosphere model takes up less of the CO2 perturbation than LPX-Bern. The root-mean-square deviation in IRF(CO2,a) from the two simulations is less than 1 % of the perturbation. Differences are most pronounced between simulation year 1 and 10 000 (Fig. 2a). Differences in IRF(δ13Ca) (Fig. 2b) are largest in the first decades after the pulse, and the root-mean-square deviation in IRF(δ13Ca) amounts to less than 1 % between the two simulations.
Finally, we compare the simulations LGM500, forced by glacial boundary conditions, and 4box500, forced by preindustrial conditions. Differences between the two simulations are solely due to the difference in climate and CO2 forcing. IRF(CO2,a) is lower by a few percent in LGM500 compared to 4box500 (Fig. 2a). The difference is largest in the first 10 kyr, and it is up to 12 % of the perturbation. The root-mean-square deviation between the two simulations amounts to ∼2 %. The larger oceanic carbon uptake in LGM500 compared to 4box500 can be explained by the higher alkalinity simulated for LGM than for preindustrial conditions. A higher alkalinity implies lower values of the Revelle factor ξ and a larger carbon uptake capacity of the ocean. IRF(δ13Ca) shows a similar pattern with lower values for the LGM background compared to the preindustrial background (cf. dotted black and dotted dark-violet lines in Fig. 1b). The difference can be understood with the help of Eq. (6); inserting the small glacial value for the atmospheric carbon inventory (381.6 GtC) in the first term yields IRF∞(δ13Ca) = 0.027 compared to IRF∞(δ13Ca) = 0.032 when using the preindustrial value (589.4 GtC) in the equation. These estimates of IRF(δ13Ca) are in good agreement with the results from LGM500 and 4box500 (Fig. 2b). In summary, the influence of glacial compared to preindustrial boundary conditions on IRF(δ13Ca) appears modest in our model.
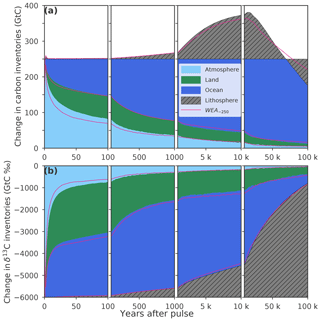
Figure 3Inventories of the (a) carbon and (b) δ13C perturbations for experiment WEA250. Shown are inventories of the perturbations in the atmosphere (light blue), the land biosphere (green), and the ocean (blue). Hatching indicates the influence of changes in the lithosphere (including sediments) due to CaCO3 compensation and imbalances in the weathering and burial fluxes on the carbon and isotopic inventories of the ocean–atmosphere–land system. For carbon, this inventory is elevated above the pulse perturbation of 250 GtC until about 70 kyr and depleted thereafter. For δ13C, the atmosphere–ocean–land inventory is continuously reduced over the course of the simulation. Magenta lines show results for experiment WEA−250 multiplied by −1.
The budgets of the carbon and carbon isotope perturbations
Next, we discuss the budgets of the carbon and 13C perturbations. Figure 3 shows results for simulation WEA250, with a pulse release of 250 GtC, and for simulation WEA−250, with a pulse removal of 250 GtC. Differences between these two runs are clearly visible in Fig. 3, but the general evolution of the budgets is similar. In the following, we give numerical results for simulation WEA250. After 100 years, about 82 GtC is still airborne, and the land and the ocean carbon inventories have increased by about 65 and 105 GtC, respectively (Fig. 3a). As time evolves, the oceanic carbon perturbation grows at the cost of the atmosphere and land. On multimillennial timescales, carbonate compensation and enhanced terrestrial carbonate and silicate weathering increase ocean alkalinity, and thereby the uptake capacity for atmospheric CO2 and the remaining atmospheric CO2 fraction decreases. Nevertheless, the carbon perturbation in the atmosphere–ocean–land system exceeds the 250 GtC of the pulse as more carbon is added to the ocean through increased CaCO3 weathering and redissolution or reduced burial of marine sediments (hatching in Fig. 3a). The maximum perturbation is reached after ∼16 kyr with a total of about 381 GtC in the atmosphere–ocean–land system. Thereafter, this inventory decreases due to weathering–burial imbalances. After 100 kyr, about 5 GtC of the perturbation remains airborne, 8 GtC is stored in the land biosphere, and the ocean contains 163 GtC more carbon than before the perturbation. Accordingly, 74 GtC of the initial perturbation is lost from the atmosphere–ocean–land system through increased marine burial compared to terrestrial weathering input (hatching extends below the 250 GtC line in Fig. 3a).
The isotopic perturbation budget is established in units of gigatonnes of carbon per mill (GtC ‰). Any isotopic inventory is defined as the product of the corresponding carbon inventory in gigatonnes of carbon (GtC) multiplied by its isotopic signature in ‰. The role of the land biosphere in removing the δ13Ca perturbation is clearly visible (Fig. 3b). After 100 years, the ocean contains ∼50 % of the isotopic perturbation (in GtC ‰), the land biosphere about 35 %, and the atmosphere less than 15 %. On millennial timescales, the perturbation is slowly removed from the atmosphere–ocean–land system. The δ13C perturbation of the burial flux (combined POC and CaCO3) follows the negative δ13C perturbation in surface DIC. Therefore, the burial flux is what ultimately removes the δ13C perturbation from the atmosphere–ocean–land-biosphere system (Fig. 3b).
We further illustrate the contribution of the burial and weathering fluxes to the carbon and isotope budgets for the simulation with (WEA500) and without weathering feedbacks (SED500) in Fig. 4. The inventory in the relatively fast-exchanging pools – atmosphere, ocean, reactive sediments, land biosphere – increases by ∼350 GtC in addition to the pulse input of 500 GtC over the course of simulation SED500, leading to a total increase of 850 GtC. The increase, in addition to the pulse, is mainly due to a reduction in the burial of CaCO3. In contrast, CaCO3 burial is enhanced in simulation WEA500, and ∼430 Gt of carbon is removed from the fast-exchanging reservoirs. This removal is only partly compensated by enhanced weathering (∼380 GtC), leading to a reduction in the inventory of the fast-exchanging pools from 500 GtC immediately after the pulse to 453 GtC at 100 kyr. Changes in POC burial fluxes are negligible for the carbon budget.
Turning to the isotopic perturbation budget, the initial perturbation due to the pulse input of −12 000 GtC ‰ is mainly removed by anomalies in the POC burial flux both in SED500 (∼10 000 GtC ‰) and WEA500 (∼7000 GtC ‰). Changes in CaCO3 burial and weathering mitigate about a quarter (∼2900 GtC ‰) of the initial isotopic perturbation in the two simulations. This leaves a relatively small isotopic inventory perturbation of about +1100 and −1600 GtC ‰ in the fast-exchanging reservoirs at 100 kyr in simulations SED500 and WEA500.
The contributions of the anomalies in the POC and CaCO3 burial fluxes may be approximately attributed to changes in the signature (Δδ) and to changes in flux (ΔF) relative to the initial flux, F0, and signature, δ0, before the perturbation:
The isotopic perturbation of the POC burial flux is mainly mediated by a change in the signature of the organic carbon buried (Δδ13C(POC)). For example, the signature of the total POC burial flux is on average 0.29 ‰ more negative than the corresponding input from weathering in simulation WEA500. This change in signature of the total POC burial flux leads to an effective reduction of the isotopic perturbation. The change in POC burial flux (ΔF(POC)) is, as mentioned above, negligible. Both changes in the signature of the total CaCO3 burial flux and changes in CaCO3 burial contribute significantly to the isotopic perturbation. At the end of simulation WEA500, the mean δ13C signature of CaCO3 burial is on average 0.14 ‰ more negative than the input from weathering. In turn, the term F0⋅Δδ for CaCO3 burial contributes GtC ‰ to the mitigation of the initial isotopic perturbation. This is partly counteracted by excess burial of CaCO3, with ΔF⋅δ0 equal to ∼1300 GtC ‰. This yields an overall burial contribution of GtC ‰. The δ13C perturbation is further removed by increased weathering input of CaCO3 (see “Model and experimental setup”), contributing about 1100 GtC ‰ over 100 years in WEA500.
In summary, the isotopic perturbation is mainly mitigated by a change in the signature of the mean POC burial flux. The smaller contributions from the CaCO3 cycle to the isotopic budget are related to both a change in the signature of the mean CaCO3 burial flux and to changes in burial and weathering carbon fluxes.
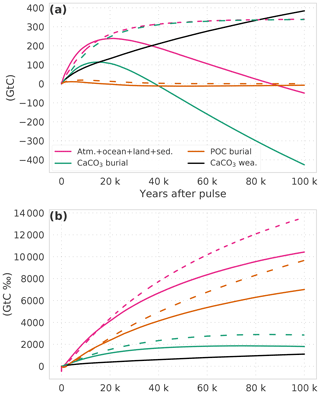
Figure 4The perturbation budget for (a) carbon and (b) carbon isotopes. Solid lines show results from experiment WEA500; dashed lines are from experiment SED500. (a, b) The pulse (500, −12 000 GtC ‰) is subtracted from the combined atmosphere–ocean–land-reactive sediment inventory. Burial fluxes are plotted inversely, and the sum of burial (green, orange lines) and weathering (black) fluxes yields the combined inventory (pink).
Influence of pulse size
The IRF for atmospheric CO2 and δ13C is sensitive to the magnitude of the pulse size (Fig. 1a, b), and we next address related differences between simulations. For CO2, the remaining atmospheric fraction is higher for larger pulse sizes than for smaller pulse sizes. Differences between different small pulses (−250 to 500 GtC) are most significant in the first decades; differences between the large (WEA5000) and any small pulse (Fig. 1a) are most significant in the first millennium. Several processes contribute to these differences.
First, nonlinearities in the carbonate chemistry contribute to differences in IRF(CO2,a) in the first centuries to millennia, where the perturbation is largely contained in the atmosphere–ocean–land-biosphere system. We see from Eq. (5) that a controlling factor is the oceanic buffer factor. As pulse size increases, so does the buffer factor, leading to higher values of IRF(CO2,a) for WEA5000 compared to smaller pulse sizes (Fig. 1a).
Second, productivity on land depends nonlinearly on CO2 (Farquhar et al., 1980), and the loss of carbon from the land biosphere in response to a negative pulse is larger than the uptake in response to a positive pulse of the same size. This contributes to the initially smaller remaining atmospheric fraction for negative pulses (see WEA250 and WEA−250 in Figs. 1a and 3a). The difference is most strongly pronounced in the first centuries and millennia, but it prevails until the end of the simulation.
Third, the response in marine export production is also nonlinear for pulses of same absolute size but different sign. The initial decrease in export production after a positive pulse is smaller than the increase after a negative pulse of the same size, thereby affecting surface ocean CO2 concentrations, and thus air–sea gas exchange, and partly leveling out the effect from the land biosphere.
For δ13Ca, the perturbation is smaller for negative compared to positive pulses of the same magnitude (Fig. 1). The difference can be understood with the help of Eq. (6). Evaluation of Eq. (6, see Appendix) yields an IRF(δ13Ca) of ∼2 % for the pulse addition of 250 GtC (WEA250) but of only ∼1 % for a corresponding removal (WEA−250).
Radiocarbon
Finally, we discuss the Δ14C perturbation experiments. In experiment 14Conly, a positive pulse of 14C is added to the atmosphere, but there is no perturbation in CO2, analogous to a radiocarbon production pulse by atomic bomb tests or cosmic rays. The initial evolution of the IRF(Δ14Ca) is very similar to the one of IRF(δ13Ca) (Fig. 1b, c). On longer timescales, radioactive decay additionally removes the perturbation, so that after ∼20 kyr less than 0.1 % of the perturbation is left airborne. In simulations 14C−500 and 14Cdead, a radiocarbon-depleted carbon source of 100 GtC is added to the atmosphere causing a negative perturbation in Δ14C and a positive perturbation in CO2 in the atmosphere. As visible from Fig. 1a for WEA100, a small percentage of the CO2 perturbation remains airborne even after 100 kyr. This explains the persistence of a small atmospheric perturbation in Δ14C, well beyond the lifetime of the initially added 14C. IRF(Δ14Ca) is larger for 14C−500 than for 14Cdead on these very long timescales. This is because the perturbation in CO2, and in turn the long-term perturbation in Δ14Ca, is the same for both experiments. However, the initial perturbation in Δ14C – the denominator of the response function (see Eq. 2) – is smaller in 14C−500 than in 14Cdead.
3.2 The δ13C perturbation of marine dissolved inorganic carbon and its approximation by PC-EOF
The ocean mean perturbation in δ13C of DIC () increases in absolute magnitude during the first millennium, as the atmospheric perturbation is propagated to the ocean (Fig. 5, thick gray line). The most negative mean perturbation (−0.23 ‰ for experiment WEA500) occurs ∼1500 years after the pulse release (Fig. 5), reflecting ocean mixing timescales. Thereafter, the δ13CDIC perturbation decreases in magnitude as a result of weathering–burial imbalances (see Sect. 3.1, Figs. 3 and 5). At the end of the simulation, less than 15 % of the maximum perturbation (−0.03 ‰) remains in the ocean.
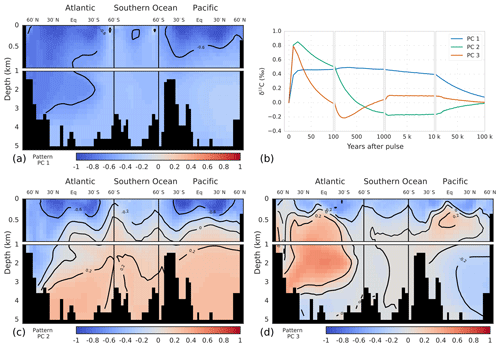
Deep ocean invasion of the δ13CDIC perturbation is first accomplished in the North Atlantic Deep Water (NADW) region. After 100 years, the signal has already propagated to a depth of ∼3.5 km in the North Atlantic, whereas it is confined to the upper ocean (>1 km) in the rest of the ocean (Fig. 6a). At year 1000, the δ13CDIC perturbation is rather uniformly distributed in the ocean. Only the deep North Pacific (region of oldest waters; ideal age >1 kyr in Bern3D) and waters at intermediate depths in the Southern Ocean show a smaller perturbation (Fig. 6c). On multimillennial timescales, decreases throughout the ocean. The perturbation, however, is not entirely uniformly distributed as expected from a completed ocean mixing by physical transport. More negative values are present in the upper ocean and in North Atlantic Deep Water compared to the intermediate and deep Southern Ocean, in Antarctic Bottom Water in the Atlantic, and in the deep Pacific (Fig. 6e, g). This may be due to changes in the fractionation during air–sea gas exchange at higher temperatures, leading to more negative δ13C signatures in the surface ocean. Additionally, gross air–sea fluxes are increased as a result of the higher CO2 concentrations, decreasing the air–sea disequilibrium. This leads to more negative δ13C signatures in mid- and low-latitude surface waters and less negative signatures in cold high-latitude waters (see Menviel et al., 2015). This surface-to-deep gradient is dampened in the case of experiment WEA500 by enhanced weathering of CaCO3 on land, adding carbon with a positive δ13C signature (∼2.9 ‰) to the surface ocean. As discussed above, these spatial Δδ13C gradients are important and co-govern the removal rate of the δ13C perturbation. The larger-than-average δ13C perturbation in the surface is imparted to phytoplankton and zooplankton, feeding the burial flux of biogenic material. Further, fractionation during phytoplankton growth at elevated CO2 concentrations is higher, leading to lower δ13C values of the POC export flux. This accelerates the removal of the δ13C perturbation in comparison to a uniformly mixed ocean.
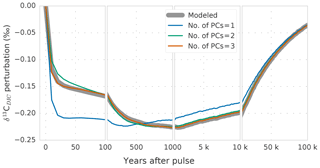
Figure 5Modeled global-average perturbation of the isotopic signature of dissolved inorganic carbon in the ocean (δ13CDIC; thick gray line) in response to a carbon pulse to the atmosphere of 500 GtC with a δ13C signature of −24 ‰. The thin colored lines show the perturbation as reconstructed with one (blue), two (green), and three (orange) principal components.
Next, the temporal evolution of the δ13CDIC perturbation and its spatial pattern are described by PC-EOF (Fig. 7). The first PC-EOF pair captures approximately the δ13CDIC evolution after 1 kyr, while the second and third PC-EOF pairs capture, together with the first pair, the decadal-to-centennial-scale penetration of the perturbation into the ocean (Fig. 5). The first EOF pattern (Fig. 7a) shows negative values throughout the ocean, with a pattern similar to that modeled for year 50 000 (Fig. 6g). The corresponding PC time series increases during the first decades after the pulse, followed by a slow decline on multimillennial timescales (Fig. 7b). This first PC captures the evolution of ocean mean well after 1 kyr (Fig. 5, blue versus gray lines). In contrast to the first EOF, the second EOF has a clear dipole pattern with negative values in surface and intermediate waters and in the NADW region and positive values below ∼1 km depth (Fig. 7c). The corresponding PC time series has high positive values in the first decades of the simulation, declining over the next centuries, becoming negative around year 500, and approaching zero on multimillennial timescales. In combination with the first PC-EOF pair this leads to strongly negative δ13C values in surface and intermediate waters in the first centuries of the simulation, whereas on longer timescales the depth gradient in disappears. The third PC-EOF, finally, is of importance during the first century (Fig. 7b), and it captures regional features, e.g., related to North Atlantic Deep Water or intermediate waters (Fig. 7d).
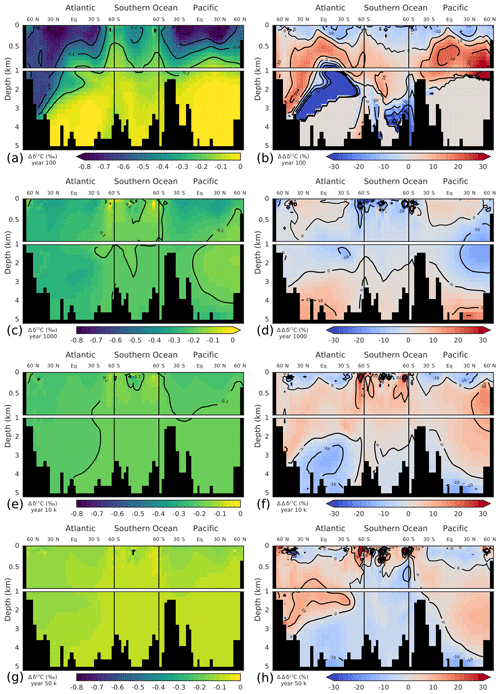
Figure 6Modeled δ13CDIC perturbations (‰) (a, c, e, g) and difference between modeled and reconstructed δ13CDIC perturbation using the first three principal components. These differences are shown in percent of the modeled perturbation (b, d, f, h). Shown are time slices at 100 years (a, b), 1 kyr (c, d), 10 kyr (e, f), and 50 kyr (g, h) after the pulse release of carbon. Note that in panel (b) perturbation values smaller than ‰ (abyssal Atlantic and Pacific) were masked for better visibility as the perturbation has not yet propagated into these regions (see panel a).
The global-mean is well described by the first two PCs (Fig. 5, green vs. gray line). The third PC-EOF pair mostly adds performance during the first century (cf. green and orange lines in Fig. 5), and it reduces the root-mean-square error (RMSE) between reconstructed and modeled global-mean from 0.003 ‰ with two PC-EOF pairs to 0.001 ‰ with three PC-EOF pairs used in the reconstruction.
For the reconstruction of the spatiotemporal evolution of , we will now use the first three PC-EOF pairs. The RMSE between the modeled and reconstructed 3-D field is highest (0.1 ‰) for the first 3-D output at year 10, after the pulse, and decreases to 0.03 ‰ at year 100. As visible from Fig. 6a and b, largest deviations between modeled and reconstructed are found in the thermocline of the Pacific and in the deep North Atlantic. Further, the modeled perturbation has not yet propagated to the deep Pacific and Atlantic by year 100 (Fig. 6a), whereas the PC-EOF reconstruction displays a signal in these water masses. The performance of the reconstruction increases over the course of the simulation. The RMSE of the fields amounts to 0.01 ‰ at 1 and 10 kyr, and it decreases to 0.007 ‰ at 50 kyr after the pulse. Overall, reconstructing with three PC-EOF pairs shows good results, and deviations from the modeled are of the order of 10 % of the perturbation and smaller on centennial-to-millennial timescales (Fig. 6d, f, h). To reconstruct the modeled evolution of precisely during the first few centuries after a perturbation, more than three PC-EOF pairs are necessary. In summary, the spatiotemporal evolution of over ∼1000 years to 100 kyr after a pulse input of carbon into the atmosphere is described accurately and conveniently by three PC-EOFs pairs.
The aim of this study is to investigate the evolution of a δ13C perturbation in the Earth system in response to a carbon input to the atmosphere on timescales from centuries to 100 kyr. To this end, the response of the Bern3D-LPX model was probed by pulse-like emissions of carbon to the atmosphere from an external source such as land biosphere carbon release or fossil fuel burning. The δ13C response is compared to that of atmospheric CO2 and radiocarbon.
The impulse response (or Green's) functions (IRF) for atmospheric CO2 and its δ13C signature are fitted by a sum of exponential functions. Additionally, we show that the spatiotemporal evolution of a δ13CDIC perturbation is reasonably represented with three PC-EOF pairs. Deviations between the PC-EOF reconstruction and modeled δ13CDIC results are largest in the first decades after the pulse, and they are on the order of 10 % of the perturbation on millennial timescales. This allows for the construction of a computationally efficient substitute model, which can be applied to investigate, for example, reconstructed δ13CDIC variations from marine sediments in future studies. The evolution of the atmospheric CO2 perturbation in the coupled Bern3D-LPX model is comparable to results from earlier studies addressing the pulse-like input of carbon into the atmosphere (e.g., Maier-Reimer and Hasselmann, 1987; Siegenthaler and Joos, 1992; Archer et al., 1998, 2009; Ridgwell and Hargreaves, 2007; Colbourn et al., 2015; Lord et al., 2016). The inclusion of peat lands in the LPX-Bern model adds a (small) additional sink on multimillennial timescales, previously not considered in such simulations. For the carbon isotopes, corresponding long-term pulse response simulations that consider ocean-sediment and weathering feedbacks are lacking in the literature. The “short-term” response from years to one or two millennia is consistent with earlier results (Joos et al., 1996).
We quantify the processes leading to the different removal timescales of atmospheric CO2 and δ13Catm perturbations with the help of factorial experiments. The role of different processes is further illustrated by analytical descriptions derived from a two-box atmosphere–ocean model and three-box atmosphere–ocean–land model provided in the Appendix. The removal of an atmospheric perturbation in the isotopic ratio 13C∕12C is not buffered by marine carbonate chemistry, unlike CO2. The atmospheric δ13C perturbation is partitioned among the ocean, land biosphere, and atmosphere roughly in proportion to their carbon inventories over about 2 kyr. This leaves only a very small fraction airborne (1 % to 3 % for pulses of a few hundred gigatonnes of carbon, GtC) after the signal is mixed within these three reservoirs. In contrast, a substantial fraction of carbon emissions and the CO2 perturbation remain airborne for millennia. On timescales of a few millennia to 20 kyr, the initial atmospheric CO2 perturbation is lowered by carbonate compensation to a fraction of about 8 %. In contrast, this chemical buffering hardly affects the atmospheric δ13C perturbation. On even longer timescales, the CO2 and the isotopic perturbation are removed by different, though related, processes. For δ13C, the continuous flux of biogenic calcium carbonate and organic carbon particles carries the isotopic perturbation from the surface ocean to the lithosphere. For CO2, the excess weathering of silicate rocks in response to the CO2 and climate perturbation adds alkalinity to the ocean, which leads to a complete removal of the atmospheric CO2 perturbation.
Gradients in the δ13CDIC perturbation strongly influence the long-term removal timescale of the isotopic perturbation. In the pulse experiments, Δδ13C is enlarged in the surface relative to the deep ocean by temperature-dependent fractionation during air–sea gas exchange (Mook, 1986) and altered air–sea disequilibrium resulting from changes in gross exchange fluxes due to altered CO2. Changes in CaCO3 weathering, on the other hand, diminish the surface perturbation (e.g., experiment WEA500 vs. SED500 in Fig. 1a). All these processes lead to spatial gradients in the δ13C perturbation in the ocean. As a result of these gradients in Δδ13C, the isotopic perturbation is removed faster by particle burial than expected from a uniformly mixed ocean. This highlights the importance of resolving spatial structures in the perturbation to represent its removal timescales. More generally and beyond pulse-release experiments, any process that changes the δ13C signature of the relentless flux of organic and calcium carbonate particles will influence the δ13C loss flux from the ocean–atmosphere–land-biosphere system to the lithosphere (for examples, see Jeltsch-Thömmes et al., 2019; Roth et al., 2014; Tschumi et al., 2011).
Our results have consequences for the interpretation of the difference in δ13C between similar climate states such as the Penultimate Glacial Maximum (PGM) and the Last Glacial Maximum (LGM). Substantial temporal δ13C differences between these periods are recorded in ice cores (Schneider et al., 2013; Eggleston et al., 2016) and in marine sediments (Hoogakker et al., 2006; Oliver et al., 2010). Different mechanisms – such as changes in the δ13C signature of weathering and burial fluxes, varying contribution of volcanic outgassing of CO2, and changes in the amount of carbon stored in the land biosphere, especially in yedoma and permafrost soils – have been discussed for the PGM–LGM δ13C offset (e.g., Lourantou et al., 2010; Schneider et al., 2013). An internal reorganization of the marine carbon cycle without considering changes in burial may not explain the offset. With no changes in the weathering–burial balance, the mass in the atmosphere–ocean–land system remains constant. Then, a change in atmospheric δ13C would require an opposing δ13C change in the ocean. This appears to be in conflict with marine and ice core records, which suggest that δ13C increased both in the ocean and in atmosphere by about 0.3 ‰ between the PGM and LGM (Hoogakker et al., 2006; Oliver et al., 2010; Schneider et al., 2013; Eggleston et al., 2016). However, internal marine carbon-cycle reorganizations, e.g., due to changes in circulation, may have altered δ13C in the surface ocean, and in turn δ13C of the burial flux, and thereby the balance between weathering input and burial.
The Bern3D results suggest that changes in organic carbon storage on land (or in the ocean) are not a likely explanation of the isotopic offset between the PGM and LGM. The δ13C signal of a transfer of organic carbon of plausible magnitude to the atmosphere and ocean would have been attenuated too much over time to cause the observed PGM–LGM δ13C difference. Schneider et al. (2013) estimated required changes in land carbon storage to match the ice core and marine temporal offsets in δ13C using preliminary Bern3D results for pulse-release simulations. Our results show, in agreement with these earlier results, that the isotopic perturbation associated with a terrestrial carbon release is attenuated to less than 15 % within two millennia for pulse sizes of up to 5000 GtC and declines thereafter (see black line in Fig. 1b). This would require several thousand GtC to have been stored additionally in the land biosphere during the LGM compared to the PGM in order to explain the δ13C offset (see also Schneider et al., 2013). This amount seems large in light of estimated total carbon stocks of ∼1500 GtC in perennially frozen soils in Northern Hemisphere permafrost regions today (Tarnocai et al., 2009) and an even smaller inventory at the LGM (Lindgren et al., 2018).
Taken together, these ad hoc considerations suggest that long-term imbalances in the weathering (including volcanic emissions) and burial fluxes appear to be a plausible cause for the δ13C differences between PGM and LGM. However, further work, which considers the transient evolution of CO2, δ13C, and other proxies, is required to gain further insight into the contributions of individual mechanisms to long-term δ13C changes recorded in ice and marine cores.
Further, the different behavior of CO2 and δ13Catm perturbations also has consequences for centennial-scale CO2 and δ13Catm variations such as during Heinrich stadials 4 and 1 (HS4 and HS1). Variations in CO2 and δ13Catm during HS4 and HS1 have been measured on Antarctic ice cores. The data show an increase in CO2 on the order of ∼10 ppm over 200–300 years, accompanied by a decrease in δ13Catm of ∼0.2 ‰. This results in a value of roughly −0.02 ‰ ppm−1 for the ratio of the change in δ13C to the change in CO2 (). A release of terrestrial carbon has been discussed as a possible cause of these events (Bauska et al., 2016, 2018).
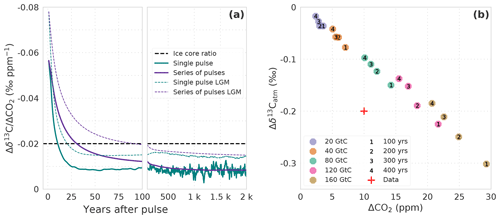
Figure 8(a) Temporal evolution of the ratio of Δδ13C to ΔCO2 in the atmosphere. Results are from simulations WEA100 forced by preindustrial boundary conditions (solid lines) and LGM100 forced by Last Glacial Maximum boundary conditions (thin dashed lines). Carbon is released as a single pulse at year 0 (green lines) or assumed to be released at a uniform rate from year 0 to the year plotted (purple lines; see main text). The dashed horizontal line indicates a Δδ13C-to-ΔCO2 ratio of −0.2 ‰ to 10 ppm as seen in ice core records for HS1 and HS4. (b) Response in ΔCO2 and to a uniform release of 20, 40, 80, 120, and 160 GtC (colors) of isotopically light carbon (δ13C = −24 ‰) to the atmosphere over 100, 200, 300, and 400 years (numbers). Shown is the mean over 30 years starting in the last year of the release. The red cross indicates the approx. Δδ13C-to-ΔCO2 change as seen in ice core records for HS1 and HS4 (Bauska et al., 2016, 2018).
We utilize our pulse response simulations under PI and LGM boundary conditions to estimate the changes in r in response to a transient terrestrial carbon input with an isotopic signature of −24 ‰. The results for r will depend on the evolution of the emissions into the atmosphere. For a pulse-like input at time zero, the evolution of r after the pulse is shown in Fig. 8a for the first 2000 years. r is about −0.08 (−0.06) ‰ ppm−1 immediately after the release under LGM (PI) boundary conditions. The difference between LGM and PI values of r comes from the difference in the atmospheric C and 13C inventory to which the pulse is added. The magnitude of r is reduced rapidly within the first 25 years and remains approximately constant at −0.015 (−0.01) ‰ ppm−1 thereafter. Thus, r recorded in ice after a hypothetical pulse release of carbon would be above −0.02 ‰ ppm−1 if the age distribution of the ice core samples is wider than a few decades. However, emissions may occur more gradually. For simplicity, we assume an emission pulse sustained over period T according to a two-sided Heaviside function; terrestrial emissions, e(t), suddenly increase to unity, remain elevated for a period T, and are then immediately reduced again to zero. r is then readily calculated from the IRFs ( IRF(δ13C) IRF(CO2)(T−t)). The results for r are again plotted in Fig. 8a. r is decreasing with the duration T of sustained emissions and falls below −0.02 ‰ ppm−1 for T larger than about 90 (30) years for LGM (PI) boundary conditions. Finally, we also performed simulations with the Bern3D-LPX under PI boundary conditions to account for nonlinearity that may not be captured in the IRF representation. The releases of varying amounts of terrestrial carbon with δ13C ‰ over 100 to 400 years yield a linear response in ΔCO2 and (Fig. 8b) with a slope r of about −0.01 ‰ ppm−1, in agreement with the IRF results.
There are uncertainties in these estimates of r. We assumed that the emitted carbon was about −18 ‰ depleted with respect to the atmosphere. The relative uncertainty in this value translates directly to the relative uncertainty in r. The release of material that is isotopically even more depleted would bring our model results into better agreement with the ice core estimate of r. Observations and land model simulations suggest that the δ13C depletion in vegetation and soils may vary between −24 ‰ for heavily discriminated C3 plant material and to −5 ‰, which is indicative of C4 plant material (Keller et al., 2017). C4 plants were likely more abundant during glacials than interglacials (Collatz et al., 1998). Also, the values shown in Fig. 8b for century-scale emissions are 30-year means. A wider gas age distribution would reduce the perturbation in δ13Catm more than in CO2 (see Köhler et al., 2011). On the other hand, the CO2 increase may have occurred in less than 100 years (Bauska et al., 2018); correspondingly, a more negative value of r is expected for such a fast (<100 years) increase. Given these uncertainties in our model estimates, as well as in the determination of r from the ice core measurements, we are not in a position to firmly conclude on whether a terrestrial carbon release was the sole mechanism for the HS1 and HS4 CO2 events or not. Other mechanisms in addition to a terrestrial release may have contributed to the CO2 and δ13Catm excursions during HS4 and HS1.
We acknowledge that most of the idealized simulations presented in this study were run under preindustrial boundary conditions. A limited set of sensitivity simulations suggests that the IRFs for CO2 and δ13C are similar under preindustrial and glacial CO2 in our model. The direct influence of lower atmospheric CO2 on IRF(δ13C) appears limited. Further work is needed to better quantify the dependency of IRFs on the climate state.
In conclusion, the responses of atmospheric CO2 and of δ13Catm to a carbon input (or removal) are different, with implications for the interpretation of paleoproxy data. The difference in response is related to the aquatic carbonate chemistry and, on millennial-to-multimillennial timescales, to the burial weathering cycle, which affect CO2,a and its isotopic ratio differently. Our study highlights the importance of carbon isotope fluxes to and from the lithosphere on timescales when the ocean–atmosphere–land-biosphere system has so far often been assumed to represent a closed system. Perturbations in δ13C are removed from or modified within the atmosphere–ocean–land-biosphere system by the continuous flux of biogenic organic and calcium carbonate particles buried in marine sediments. This isotopic burial flux is substantially influenced by spatial gradients in δ13C within the ocean, calling for a spatially resolved representation of the marine carbon cycle to address isotopic change. Carbon isotope fluxes to and from the lithosphere need to be considered for the interpretation of changes in atmospheric and marine δ13C during glacial–interglacial, and longer, periods.
Ocean invasion of an atmospheric CO2 perturbation
The difference in the IRF for carbon and the isotopic ratios can be understood in terms of the aquatic carbonate chemistry. We develop approximate expressions for the IRF of atmospheric CO2 (Eq. A7) and δ13C (Eq. A29), starting in this section with IRF(CO2).
For small pulses, changes in sea surface temperature, in CO2 solubility, in ocean circulation, and in the marine biological cycle are small and neglected in the following. Changes in land biosphere carbon storage can be considerable, in particular during the first century. However, the role of changes in land carbon stock becomes smaller when more carbon is taken up by the ocean, and thus it is neglected for simplicity.
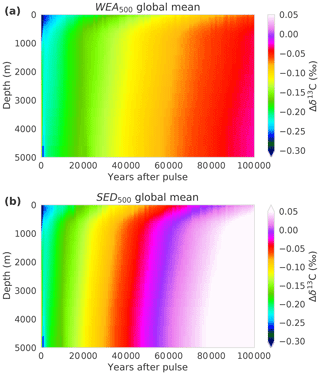
Figure A1Hovmöller-type diagram showing the temporal evolution of the global-mean vertical profile of for experiments (a) WEA500 and (b) SED500.
We consider a two-box model of the atmosphere (index: a) and ocean (index: o) with area and heights ha and ho. All boxes are assumed to be well mixed. Before the pulse addition, the model is in equilibrium and the initial CO2 partial pressure is . The initial concentration of dissolved inorganic carbon (DIC) in the ocean is DIC0, and the carbon inventory in the ocean is given by . We relate the atmospheric carbon inventory, Na, to a time-varying atmospheric concentration Ca and to the fixed volume of the model atmosphere: . We are free to select the units of the model-specific concentration Ca. Here, we express Ca in units of DIC0 and set the initial atmospheric concentration Ca,0 equal to DIC0. The atmospheric inventory is proportional to the atmospheric partial pressure, pCO2,a, and, correspondingly, Ca has to be proportional to pCO2,a. This leads to the following definition of Ca:
where Ca is specifically defined for our box model and should not be confused with the concentration or mixing ratio of CO2 in the real-world atmosphere. The atmospheric scale-height ha is given by the requirement that volume times concentration equals inventory:
The perturbation (Δ) from the initial equilibrium in pCO2, and similarly for other quantities, is defined by ΔpCO2(t) = pCO2(t) − pCO2(t0). The perturbation in pCO2,o is related to that in DIC by the Revelle factor ξ (Revelle and Suess, 1957):
We note that the carbonate chemistry is nonlinear, and ξ varies with environmental conditions (DIC, alkalinity, temperature, salinity). Assuming a constant Revelle factor, ξ is therefore an approximation. In particular, ξ increases with increasing DIC. As a consequence, the “effective” value of ξ increases with increasing carbon emission, and thus it is larger when the magnitude of the carbon pulses is larger. This yields, for the perturbation in the net air-to-sea carbon flux per unit area, :
where ΔpCO2,a and ΔpCO2,o were replaced with the help of Eqs. (A1) and (A3) to obtain the right-hand side of Eq. (A4). kg is the gas transfer rate relative to the partial pressure (Wanninkhof, 1992), and g is the rate relative to DIC:
The IRF, or equivalent airborne fraction, is defined by
P is the magnitude of the initial carbon pulse at time t0, and this released carbon is conserved within the model atmosphere and ocean. The net air-to-sea flux becomes zero when a new equilibrium at time t∞ is reached; it follows from Eq. (A1) that and from Eq. (A4) that . Finally, using this, as well as and , yields the following for the IRF in an ocean–atmosphere system at equilibrium:
Distribution of a δ13C perturbation within the atmosphere–ocean–land-biosphere system
We now turn to the isotope 13C. The isotopic ratio is given by the following (see Mook, 1986):
And the isotopic signature in per mill is given by
13RSD is the standard ratio. Isotopic discrimination is described by factors using the symbol α or by additive terms in δ notation using symbol ε in per mill. It holds true that
In the following, we neglect for simplicity the approximately 1 % difference between the concentration of 12C and total C. (This difference may be accounted for in the definition and values of the isotopic discrimination factors.)
We address first the response during the first two millennia after the pulse. In the following paragraphs, we will develop a simple analytical expression for the IRF (δ13Ca) after a new equilibrium for the atmosphere–ocean–land-biosphere system is reached. Thus, we neglect carbonate compensation and weathering and burial fluxes. We consider exchange between the atmosphere and ocean and between the atmosphere and land biosphere reservoirs, and we assume that these three reservoirs are well mixed.
The box model
The carbon and 13C budgets for the three-box model are described by
where N is the reservoir size (e.g., in GtC) and indices a, o, and b denote the atmosphere, ocean, and land biosphere boxes, respectively. Index i refers either to carbon or 13C. F denotes fluxes between reservoirs. δ is the Kronecker symbol, and Pi is the pulse released to the atmosphere at time .
The initial atmospheric δ13C perturbation
The IRF(t) for is given by the perturbation in the isotopic signature, , divided by the initial (ini) perturbation, ; is the perturbation immediately after a carbon input of amount P and with signature ). Mass balance implies that the amount of 13C before and after the pulse release is equal:
We convert the ratios to δ units and subtract on both sides Ca,0 to get the initial perturbation:
is proportional to the difference between the signature of the pulse and the initial atmospheric signature. Thus, the initial perturbation is relative to the atmospheric δ13C signature.
The relationship between δ13Ca, δ13Co, and δ13Cb at equilibrium
In this subsection, relationships between the isotopic signatures are developed by considering equilibrium between the three boxes. This will allow us to simplify the isotopic mass balance equations further below.
The gross air-to-sea flux per unit area is
where is the discrimination factor for the gross air-to-sea transfer. The gross sea-to-air flux is
The term in parentheses is the discrimination factor for the transfer of carbon from the DIC pool to the atmosphere (13αo→a). At equilibrium (eq), the two gross fluxes cancel each other out. It follows with p = p and 13p = 13p that
This equation gives the equilibrium relationship between the atmospheric and oceanic signature. αa,o denotes the equilibrium discrimination factor between pCO2,a and DIC. αa,o depends on temperature and somewhat on carbonate chemistry (Mook, 1986), and it is about 1.008 and thus close to 1.
A similar relationship is readily developed for the isotopic ratio of the total carbon in the land biosphere. The gross fluxes between the land and atmosphere are
This yields at equilibrium
Equations (A16) and (A18) are readily converted into δ notation:
Equations (A16), (A18), and (A19) allow us to express the isotopic signature of the land biosphere and the ocean by the isotopic signature of the atmosphere at equilibrium. These equations hold true both for the initial equilibrium (t0) before the pulse release and when a new equilibrium is reached at t∞. In practice t∞ is about 2 kyr. It follows immediately from Eq. (A19) that the isotopic signatures at the new equilibrium are about equal for the three reservoirs:
In other words, the isotopic signal is mixed uniformly through the atmosphere, ocean, and land biosphere when assuming that these three reservoirs are well mixed as in this appendix section.
Solving the mass balance equations of the isotopic perturbation for Δδ13C
The mass balance equations for the ocean–land-biosphere–atmosphere system are given for carbon by
The second equation describes the perturbation only. We use Eqs. (A16) and (A18) to replace No⋅13Ro with , similarly for the land reservoir, and write the mass balance for 13C.
Now we convert to δ units:
We subtract on both side the mass balance equation for carbon (Eq. A21) multiplied by a factor of 1000. Note that αa,o and αa,b are present in the carbon terms in Eq. (A23) but not in the mass balance for carbon (Eq. A21). This difference results in the first two terms in Eq. (A24) below.
Next, we subtract on both sides the third left-hand side term, Ca,0, as well as the term . We rearrange and use again the mass balance for carbon to get
The terms with ε∕1000 represent a small correction (<0.02) and can be safely neglected. We replace P with in the above equation and exchange the left and right side to get the following mass balance for the δ13C perturbation:
with
Equation (A26) represents the mass balance for the isotopic perturbation and its interpretation is as follows. The term on the left-hand side equals the carbon mass in the system times the perturbation in the signature, and it therefore equals the total isotopic perturbation (GtC ‰). In equilibrium, the δ13C perturbation, Δδ13C∞, is well mixed (Eq., A20) within the total ocean–atmosphere carbon reservoir . The terms after the first equal sign provide a different view of the total isotopic perturbation. In this picture, a fraction ΔNl,∞ of the pulse is added to each reservoir (index l) with the perturbation in signature given by (δ13CP−δ13Cl). This is then summarized after the second equal sign by the product of the carbon input P times the isotopic perturbation of the pulse relative to the mean signature of the reservoirs absorbing this additional carbon (δ13CP−δ13Cmean).
By rearranging Eq. (A26) we get the perturbation in the isotopic signature of the atmosphere–ocean–land system:
In other words, the perturbation in the signature scales with the carbon mass ratio of the pulse input to the total mass in the system. This perturbation is also proportional to the difference between the signature of the pulse and the “mean” signature of the system as defined by Eq. (A27).
IRF(δ13Ca) at equilibrium (t∼2 kyr)
Finally, we use the definition for the IRF and Eqs. (A13) and (A28) to obtain the following expression for the IRF at a new equilibrium for the ocean–atmosphere–land-biosphere system:
The fraction of the initial perturbation in the atmosphere that remains airborne corresponds roughly to the ratio of the carbon in the atmosphere immediately after the pulse release to the total carbon in the system. The second fraction on the right-hand side modifies this ratio by about +20 % for a typical negative isotopic pulse perturbation applied in this study, because the mean signature is slightly heavier than the atmospheric signature. The numerator of this modifier reflects that the pulse perturbation is distributed within the system at the new equilibrium, while the denominator reflects that the pulse is initially added to the atmosphere.
Ocean invasion: numerical examples
Equations (A7) and (A29) provide simple expressions to approximate the IRF for the perturbation in atmospheric CO2 and its isotopic signature after a pulse-like carbon input. These equations illustrate the fundamental difference in the IRF for CO2,a and for δ13Ca. To ease interpretation, we neglect the land biosphere for the moment. Then, in the limit of P→0, Eqs. (A7) and Eq. (A29) are formally identical for carbon and 13C (index: i):
However, for δ13Ca, a Revelle factor of 1 instead of about 12 applies, while the modifier M is exactly 1 for CO2,a and around 1 for δ13Ca. The perturbation in the isotopic signature is diluted by the entire carbon inventory in the system, whereas the “available” ocean inventory is reduced by the Revelle factor for the dilution of an atmospheric CO2 perturbation.
Numerically, the preindustrial carbon inventory is 600 GtC in the atmosphere and 37 400 GtC in the ocean. These values are equivalent to a scale height of 69 m for the atmosphere and of 4300 m for the ocean, when assuming a preindustrial (surface) concentration of DIC of 24 g m−3 and an ocean area of 3.6×1014 m2. The buffer factor is about 12 for small perturbations. This yields for IRF∞(CO2,a) a value of about 0.16. In other words, a fraction of about 16 % of a (small) carbon input into the atmosphere is still airborne after about 1 to 2 kyr, when the ocean and atmosphere have approached a new equilibrium. The observed penetration of chlorofluorocarbons and bomb-produced radiocarbon suggests that an atmospheric perturbation penetrates about the top 300 m of the ocean within a decade. Thus, we expect that about 70 % of the initial perturbation is still found in the atmosphere after a decade. These numbers are comparable in magnitude to the IRF of CO2 shown in Fig. 1a for 10 years and 2 kyr after the pulse input. The buffer factor increases with the magnitude of the perturbation in DIC and pCO2 and thus with pulse size P. Hence, IRF increases with increasing pulse size, as again shown in Fig. 1a. We note that any carbon uptake or release by the land biosphere is not taken into account in Eq. (A7) or in this discussion, in contrast to the results discussed in the main text.
To determine the IRF for δ13Ca, we take into account that the isotopic signal is also entering the land biosphere, and we assume a total inventory in the atmosphere–ocean–land system of 40 000 GtC. This yields an IRF∞ of 1 % to 3.2 % for P varying between −250 and +500 GtC and of about 18 % for P equal to 5000 GtC and using δ13Cmean=4 ‰ (calculated with Eq. A27). These values are in agreement with the estimates shown in Fig. 1b for year 2000. Assuming that the isotopic perturbation has mixed within a layer of 300 m in the ocean (∼2600 GtC) and with the living vegetation on land (500 GtC) yields a “decadal” IRF of about 12 %–31 % for small pulse sizes (−250 to 500 GtC), again in agreement with the Bern3D-LPX results.
Carbonate compensation and terrestrial neutralization of the CO2 perturbation
Next, we address CaCO3 compensation of the carbon added by the pulse. We derive an expression for the IRF(CO2,a) at the time when CaCO3 compensation of the pulse is completed – about 10–20 kyr after the pulse input. The following calculations are based on Archer et al. (1998). As above, we assume the ocean to consist of a single well-mixed box which is, after CaCO3 compensation, again in equilibrium with the atmosphere. Concentrations of CO2, , and in seawater are related by
and are the apparent dissociation constants for carbonic acid and KH is the Henry's law solubility product for CO2. For simplicity, we assume the ratio of , , and KH, which are temperature and salinity dependent, to be constant over the course of the experiments. With the above assumption and by taking the ratio of initial and final states, we rearrange to get
Sedimentary dissolution of CaCO3 in response to the carbon pulse tends to keep the carbonate ion concentration constant over the course of the simulations, yielding
is by far the dominant form of DIC. This allows one to approximate by DIC in Eq. (A33) to get
Δ refers here to the difference between the final and initial state. With pulse sizes substantially smaller than the oceanic DIC inventory, , we approximate
From Fig. 3a we see that on multimillennial timescales the majority of the pulse is taken up by the ocean. Further, CaCO3 compensation and weathering–burial imbalances in the CaCO3 cycle (terrestrial neutralization) add (or remove) additional carbon to (from) the ocean. We thus assume that ; P is the pulse size in GtC. The factor 1.5 is model dependent and slightly different here from the value provided by Archer et al. (1998) or in previous versions of the Bern3D model. This yields for the relative increase in pCO2
We recall the definition of the airborne fraction:
Finally, with Eqs. (A36) and (A37), we express the IRF at the time when CaCO3 compensation is completed by
The remaining atmospheric fraction is thus independent of the pulse size for . Its magnitude results directly from the carbonate chemistry (Archer et al., 1998). With a preindustrial ocean DIC inventory of 37 400 GtC and surface ocean pCO2 of 284 µatm, we get a remaining airborne perturbation of ∼5 %. This is in agreement with results from the Bern3D-LPX model after about 10–20 kyr (Fig. 1a).
Carbonate compensation of the δ13C perturbation
Carbonate compensation has almost a negligible influence on the δ13C perturbation. The carbonate compensation process acts, aside from small isotopic discrimination, equally on the different isotopes. Therefore, 12CO2,a and 13CO2,a both decrease according to Eq. (A38), leaving the isotopic ratio, to first-order approximation, unchanged. Additional effects are, here formulated for a positive pulse, as follows. The dissolution of CaCO3 adds an isotopic perturbation to the ocean–atmosphere–land system. The amount of carbon added corresponds to about half of the pulse size (P). CaCO3 has a δ13C signature of about +2.9 ‰ compared to −24 ‰ of the pulse. We reference the CaCO3 isotopic perturbation relative to the mean signature of the ocean in the model (∼0.8 ‰) as this additional carbon remains mainly in the ocean, while the mean signature that applies for the pulse is, according to Eq. (A27), about −3 ‰ for pulse sizes between −250 GtC and 500 GtC. Thus the isotopic perturbation by CaCO3 dissolution is about 20 times smaller than that of the pulse . The dissolution of CaCO3 enlarges the carbon reservoir by which the initial atmospheric δ13C is diluted. However, the amount of added carbon is, except for the 5000 GtC pulse, small compared the total inventory of the system of about 40 000 GtC. In summary, the influence of CaCO3 compensation on δ13Ca is small, and Eq. (A29) is still approximately valid for the timescale of CaCO3 compensation.
Removal of the remaining CO2 perturbation by silicate weathering
Finally, on timescales of hundreds of thousands of years, imbalances in the weathering and burial fluxes remove any remaining perturbation in carbon from the atmosphere–ocean–land system. Silicate rock weathering leads to a net removal of carbon from the atmosphere by the following simplified reaction (see Colbourn et al., 2013, for more details):
The timescale for this silicate weathering feedback has been determined to be on the order of 240 kyr (Colbourn et al., 2015) or 270 kyr (Lord et al., 2016) but with a large spread. Silicate rock weathering removes the remaining atmospheric perturbation (∼8 %). Further, the additional alkalinity added to the ocean deepens the saturation horizon, resulting in higher carbon burial in marine sediments, and thus it also removes the DIC perturbation (see Fig. 3a).
Removal of the remaining δ13C perturbation by burial of organic matter and CaCO3
In the case of δ13C, silicate rock weathering has no direct effect on the δ13C signature. The perturbation is removed on these long timescales by the replacement of carbon through burial of organic matter and CaCO3 and weathering inputs:
with NS and equal to the total mass and mean isotopic perturbation in the atmosphere–ocean–land system; Fburial being the burial flux of carbon leaving the system; and being its isotopic signature. In simulations with constant weathering rates, the residence time of carbon in the atmosphere–ocean–land system is on the order of kyr) (burial or weathering input is 0.46 GtC yr−1; total amount: ∼40 000 GtC). Surprisingly, in the factorial simulation with sediments and constant weathering fluxes (SED500), the perturbation is removed much faster than expected from the mean residence time (Fig. 1b, dotted line), because the isotopic perturbation of the burial flux is larger than that of the ocean–atmosphere–land system.
The long-term removal rate of the δ13C perturbation is sensitive to Δδ13C gradients in the ocean. The isotopic signature of the burial flux is mainly determined by the upper-ocean signature. Changes in the gross exchange fluxes of carbon between the atmosphere and the ocean in response to perturbed CO2 and changes in the isotopic fractionation of air–sea fluxes in response to perturbed temperatures increase the Δδ13C perturbation in the upper ocean relative to the deep (Fig. A1). In the case of enabled weathering feedbacks, the additional flux of isotopically heavy carbon from excess weathering partly mitigates surface-to-deep Δδ13C gradients. In turn, the perturbation is removed faster in simulations with constant weathering compared to simulations with enabled weathering feedbacks. Taken together, this highlights the role of spatial patterns of the δ13C perturbation even on these very long timescales.
Parameterization of weathering feedbacks on land
We use the 0-D version of the Rock Geochemical Model v0.9 (Colbourn et al., 2013). Weathering of CaCO3 and CaSiO3 is parameterized as functions of temperature (T), runoff (R), and productivity (P) in the following form for CaCO3:
and for CaSiO3
Subscript “0” indicates the initial value diagnosed prior to the pulse; kCa stems from a correlation between temperature and ion concentration of groundwater with a value of 0.049; Ea is the activation energy for silicate weathering (63 kJ mol−1); β is taken as 0.65; and R indicates runoff and is parameterized as a function of temperature:
with krun=0.025. In the case of experiments 4box500 and LGM500, LPX-Bern was not coupled and instead productivity was parameterized, again following equations given in Colbourn et al. (2013):
with C being atmospheric CO2 in parts per million (ppm). Reference values (0) for temperature, runoff, and productivity are diagnosed in the 100 years prior to the pulse. For further details and discussion of parameter value choices, the reader is referred to Colbourn et al. (2013).
Roth et al. (2014)Heinze et al. (1999)Heinze et al. (1999)Heinze et al. (1999)Heinze et al. (1999)Heinze et al. (1999)Roth et al. (2014)Jeltsch-Thömmes et al. (2019)Tschumi et al. (2011)Roth et al. (2014)Heinze et al. (1999)Jeltsch-Thömmes et al. (2019)Heinze et al. (1999)Anderson and Sarmiento (1994)Anderson and Sarmiento (1994)Anderson and Sarmiento (1994)Anderson and Sarmiento (1994)Roth et al. (2014)Table B1Parameters used for the sediment module, similar to what is shown in Appendix A of Tschumi et al. (2011) and with updates from Roth et al. (2014) and Jeltsch-Thömmes et al. (2019).
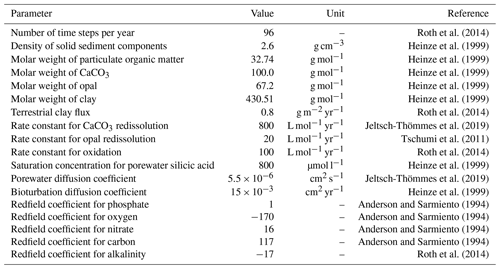
Pulse response data and EOF patterns and PC time series are available in the Supplement to this paper.
The supplement related to this article is available online at: https://doi.org/10.5194/cp-16-423-2020-supplement.
The study was designed by both authors, AJT performed model simulations and analyzed results, both authors contributed to the writing of the manuscript.
The authors declare that they have no conflict of interest.
We thank Sebastian Lienert, Daniel Baggenstos, and James Menking for helpful comments on the paper.
This research has been supported by the Swiss National Science Foundation (grant no. 200020_172476) and the Oeschger Centre for Climate Change Research
This paper was edited by Luke Skinner and reviewed by two anonymous referees.
Anderson, L. A. and Sarmiento, J. L.: Redfield ratios of remineralization determined by nutrient data analysis, Global Biogeochem. Cy., 8, 65–80, https://doi.org/10.1029/93GB03318, 1994. a, b, c, d
Archer, D. and Brovkin, V.: The millennial atmospheric lifetime of anthropogenic CO2, Climatic Change, 90, 283–297, https://doi.org/10.1007/s10584-008-9413-1, 2008. a
Archer, D., Kheshgi, H., and Maier-Reimer, E.: Multiple timescales for neutralization of fossil fuel CO2, Geophys. Res. Lett., 24, 405–408, https://doi.org/10.1029/97GL00168, 1997. a
Archer, D., Kheshgi, H., and Maier-Reimer, E.: Dynamics of fossil fuel CO2 neutralization by marine CaCO3, Global Biogeochem. Cy., 12, 259–276, https://doi.org/10.1029/98GB00744, 1998. a, b, c, d, e, f, g, h, i, j
Archer, D., Eby, M., Brovkin, V., Ridgwell, A., Cao, L., Mikolajewicz, U., Caldeira, K., Matsumoto, K., Munhoven, G., Montenegro, A., and Tokos, K.: Atmospheric Lifetime of Fossil Fuel Carbon Dioxide, Annu. Rev. Earth Pl. Sc., 37, 117–134, https://doi.org/10.1146/annurev.earth.031208.100206, 2009. a, b
Battaglia, G. and Joos, F.: Marine N2O Emissions From Nitrification and Denitrification Constrained by Modern Observations and Projected in Multimillennial Global Warming Simulations, Global Biogeochem. Cy., 32, 92–121, https://doi.org/10.1002/2017GB005671, 2018a. a
Battaglia, G. and Joos, F.: Hazards of decreasing marine oxygen: the near-term and millennial-scale benefits of meeting the Paris climate targets, Earth Syst. Dynam., 9, 797–816, https://doi.org/10.5194/esd-2017-90, 2018b. a
Battaglia, G., Steinacher, M., and Joos, F.: A probabilistic assessment of calcium carbonate export and dissolution in the modern ocean, Biogeosciences, 13, 2823–2848, https://doi.org/10.5194/bg-13-2823-2016, 2016. a
Bauska, T. K., Baggenstos, D., Brook, E. J., Mix, A. C., Marcott, S. A., Petrenko, V. V., Schaefer, H., Severinghaus, J. P., and Lee, J. E.: Carbon isotopes characterize rapid changes in atmospheric carbon dioxide during the last deglaciation, P. Natl. Acad. Sci. USA, 113, 3465–3470, https://doi.org/10.1073/pnas.1513868113, 2016. a, b, c
Bauska, T. K., Brook, E. J., Marcott, S. A., Baggenstos, D., Shackleton, S., Severinghaus, J. P., and Petrenko, V. V.: Controls on Millennial-Scale Atmospheric CO2 Variability During the Last Glacial Period, Geophys. Res. Lett., 45, 7731–7740, https://doi.org/10.1029/2018GL077881, 2018. a, b, c, d, e
Brovkin, V., Ganopolski, A., Archer, D., and Munhoven, G.: Glacial CO2 cycle as a succession of key physical and biogeochemical processes, Clim. Past, 8, 251–264, https://doi.org/10.5194/cp-8-251-2012, 2012. a
Colbourn, G., Ridgwell, A., and Lenton, T. M.: The Rock Geochemical Model (RokGeM) v0.9, Geosci. Model Dev., 6, 1543–1573, https://doi.org/10.5194/gmd-6-1543-2013, 2013. a, b, c, d, e, f, g, h
Colbourn, G., Ridgwell, A., and Lenton, T. M.: The time scale of the silicate weathering negative feedback on atmospheric CO2, Global Biogeochem. Cy., 29, 583–596, https://doi.org/10.1002/2014GB005054, 2015. a, b, c, d, e, f, g, h
Collatz, G. J., Berry, J. A., and Clark, J. S.: Effects of climate and atmospheric CO2 partial pressure on the global distribution of C4 grasses: present, past, and future, Oecologia, 114, 441–454, https://doi.org/10.1007/s004420050468, 1998. a
Dawson, A.: eofs: A Library for EOF Analysis of Meteorological, Oceanographic, and Climate Data, Journal of Open Research Software, 4, 4–7, https://doi.org/10.5334/jors.122, 2016. a
Dickson, A. G., Sabine, C. L., and Christian, J. R. (Eds.): Guide to Best Practices for Ocean CO2 Measurements, PICES Special Publication 3, 191 pp., 2007. a
Edwards, N. R., Willmott, A. J., and Killworth, P. D.: On the Role of Topography and Wind Stress on the Stability of the Thermohaline Circulation, J. Phys. Ocean., 28, 756–778, https://doi.org/10.1175/1520-0485(1998)028<0756:OTROTA>2.0.CO;2, 1998. a
Eggleston, S., Schmitt, J., Bereiter, B., Schneider, R., and Fischer, H.: Evolution of the stable carbon isotope composition of atmospheric CO2 over the last glacial cycle, Paleoceanography, 31, 434–452, https://doi.org/10.1002/2015PA002874, 2016. a, b, c
Enting, I. G., Wigley, T. M. L., and Heimann, M.: Future Emissions and Concentrations of Carbon Dioxide: Key Ocean/Atmosphere/Land Analyses, CSIRO, Division of Atmospheric Research Technical Paper, 31, 1–133, 1994. a
Farquhar, G. D., von Caemmerer, S., and Berry, J. A.: A biochemical model of photosynthetic CO2 assimilation in leaves of C3 species, Planta, 149, 78–90, https://doi.org/10.1007/BF00386231, 1980. a, b
Freeman, K. H. and Hayes, J. M.: Fractionation of carbon isotopes by phytoplankton and estimates of ancient CO2 levels, Global Biogeochem. Cy., 6, 185–198, https://doi.org/10.1029/92GB00190, 1992.
Ganopolski, A. and Brovkin, V.: Simulation of climate, ice sheets and CO2 evolution during the last four glacial cycles with an Earth system model of intermediate complexity, Clim. Past, 13, 1695–1716, https://doi.org/10.5194/cp-13-1695-2017, 2017. a
Griffies, S. M.: The Gent-McWilliams Skew Flux, J. Phys. Oceanogr., 28, 831–841, https://doi.org/10.1175/1520-0485(1998)028<0831:TGMSF>2.0.CO;2, 1998. a
Harris, I., Jones, P. D., Osborn, T. J., and Lister, D. H.: Updated high-resolution grids of monthly climatic observations – the CRU TS3.10 Dataset, Int. J. Climatol., 34, 623–642, https://doi.org/10.1002/joc.3711, 2014. a
Haxeltine, A. and Prentice, I. C.: BIOME3: An equilibrium terrestrial biosphere model based on ecophysiological constraints, resource availability, and competition among plant functional types, Global Biogeochem. Cy., 10, 693–709, https://doi.org/10.1029/96GB02344, 1996a. a
Haxeltine, A. and Prentice, I. C.: A General Model for the Light-Use Efficiency of Primary Production, Funct. Ecol., 10, 551, https://doi.org/10.2307/2390165, 1996b. a
Heinze, C., Maier-Reimer, E., Winguth, A. M. E., and Archer, D.: A global oceanic sediment model for long-term climate studies, Global Biogeochem. Cy., 13, 221–250, https://doi.org/10.1029/98GB02812, 1999. a, b, c, d, e, f, g, h
Hoogakker, B. A., Rohling, E. J., Palmer, M. R., Tyrrell, T., and Rothwell, R. G.: Underlying causes for long-term global ocean δ13C fluctuations over the last 1.20 Myr, Earth Planet. Sc. Lett., 248, 15–29, https://doi.org/10.1016/j.epsl.2006.05.007, 2006. a, b, c
Hooss, G., Voss, R., Hasselmann, K., Maier-Reimer, E., and Joos, F.: A nonlinear impulse response model of the coupled carbon cycle-climate system (NICCS), Clim. Dynam., 18, 189–202, https://doi.org/10.1007/s003820100170, 2001. a, b
Jeltsch-Thömmes, A., Battaglia, G., Cartapanis, O., Jaccard, S. L., and Joos, F.: Low terrestrial carbon storage at the Last Glacial Maximum: constraints from multi-proxy data, Clim. Past, 15, 849–879, https://doi.org/10.5194/cp-15-849-2019, 2019. a, b, c, d, e, f, g, h, i, j
Joos, F. and Bruno, M.: Pulse response functions are cost-efficient tools to model the link between carbon emissions, atmospheric CO2 and global warming, Phys. Chem. Earth, 21, 471–476, https://doi.org/10.1016/S0079-1946(97)81144-5, 1996. a, b, c
Joos, F., Bruno, M., Fink, R., Siegenthaler, U., Stocker, T. F., and LeQuere, C.: An efficient and accurate representation of complex oceanic and biospheric models of anthropogenic carbon uptake, Tellus B, 48, 397–417, https://doi.org/10.1034/j.1600-0889.1996.t01-2-00006.x, 1996. a, b
Joos, F., Prentice, I. C., Sitch, S., Meyer, R., Hooss, G., Plattner, G.-K., Gerber, S., and Hasselmann, K.: Global warming feedbacks on terrestrial carbon uptake under the Intergovernmental Panel on Climate Change (IPCC) Emission Scenarios, Global Biogeochem. Cy., 15, 891–907, https://doi.org/10.1029/2000GB001375, 2001. a, b
Joos, F., Roth, R., Fuglestvedt, J. S., Peters, G. P., Enting, I. G., von Bloh, W., Brovkin, V., Burke, E. J., Eby, M., Edwards, N. R., Friedrich, T., Frölicher, T. L., Halloran, P. R., Holden, P. B., Jones, C., Kleinen, T., Mackenzie, F. T., Matsumoto, K., Meinshausen, M., Plattner, G.-K., Reisinger, A., Segschneider, J., Shaffer, G., Steinacher, M., Strassmann, K., Tanaka, K., Timmermann, A., and Weaver, A. J.: Carbon dioxide and climate impulse response functions for the computation of greenhouse gas metrics: a multi-model analysis, Atmos. Chem. Phys., 13, 2793–2825, https://doi.org/10.5194/acp-13-2793-2013, 2013. a, b
Kalnay, E., Kanamitsu, M., Kistler, R., Collins, W., Deaven, D., Gandin, L., Iredell, M., Saha, S., White, G., Woollen, J., Zhu, Y., Chelliah, M., Ebisuzaki, W., Higgins, W., Janowiak, J., Mo, K. C., Ropelewski, C., Wang, J., Leetmaa, A., Reynolds, R., Jenne, R., and Joseph, D.: The NCEP/NCAR 40-year reanalysis project, B. Am. Meteorol. Soc., 77, 437–472, https://doi.org/10.1175/1520-0477(1996)077<0437:TNYRP>2.0.CO;2, 1996. a
Keller, K. M., Lienert, S., Bozbiyik, A., Stocker, T. F., Churakova (Sidorova), O. V., Frank, D. C., Klesse, S., Koven, C. D., Leuenberger, M., Riley, W. J., Saurer, M., Siegwolf, R., Weigt, R. B., and Joos, F.: 20th century changes in carbon isotopes and water-use efficiency: tree-ring-based evaluation of the CLM4.5 and LPX-Bern models, Biogeosciences, 14, 2641–2673, https://doi.org/10.5194/bg-14-2641-2017, 2017. a, b
Köhler, P., Fischer, H., and Schmitt, J.: Atmospheric δ13CO2 and its relation to pCO2 and deep ocean δ13C during the late Pleistocene, Paleoceanography, 25, PA1213, https://doi.org/10.1029/2008PA001703, 2010. a
Köhler, P., Knorr, G., Buiron, D., Lourantou, A., and Chappellaz, J.: Abrupt rise in atmospheric CO2 at the onset of the Bølling/Allerød: in-situ ice core data versus true atmospheric signals, Clim. Past, 7, 473–486, https://doi.org/10.5194/cp-7-473-2011, 2011. a
Krakauer, N. Y., Randerson, J. T., Primeau, F. W., Gruber, N., and Menemenlis, D.: Carbon isotope evidence for the latitudinal distribution and wind speed dependence of the air-sea gas transfer velocity, Tellus B, 58, 390–417, https://doi.org/10.1111/j.1600-0889.2006.00223.x, 2006. a
Lienert, S. and Joos, F.: A Bayesian ensemble data assimilation to constrain model parameters and land-use carbon emissions, Biogeosciences, 15, 2909–2930, https://doi.org/10.5194/bg-15-2909-2018, 2018. a, b
Lindgren, A., Hugelius, G., and Kuhry, P.: Extensive loss of past permafrost carbon but a net accumulation into present-day soils, Nature, 560, 219–222, https://doi.org/10.1038/s41586-018-0371-0, 2018. a
Lloyd, J. and Farquhar, G. D.: 13C discrimination during CO2 assimilation by the terrestrial biosphere, Oecologia, 99, 201–215, https://doi.org/10.1007/BF00627732, 1994. a
Lord, N. S., Ridgwell, A., Thorne, M. C., and Lunt, D. J.: An impulse response function for the long tail of excess atmospheric CO2 in an Earth system model, Global Biogeochem. Cy., 30, 2–17, https://doi.org/10.1002/2014GB005074, 2016. a, b, c, d, e
Lourantou, A., Chappellaz, J., Barnola, J. M., Masson-Delmotte, V., and Raynaud, D.: Changes in atmospheric CO2 and its carbon isotopic ratio during the penultimate deglaciation, Quaternary Sci. Rev., 29, 1983–1992, https://doi.org/10.1016/j.quascirev.2010.05.002, 2010. a
Maier-Reimer, E. and Hasselmann, K.: Transport and storage of CO2 in the ocean – an inorganic ocean-circulation carbon cycle model, Clim. Dynam., 2, 63–90, https://doi.org/10.1007/BF01054491, 1987. a, b
Menviel, L. and Joos, F.: Toward explaining the Holocene carbon dioxide and carbon isotope records: Results from transient ocean carbon cycle-climate simulations, Paleoceanography, 27, PA1207, https://doi.org/10.1029/2011PA002224, 2012. a
Menviel, L., Joos, F., and Ritz, S. P.: Simulating atmospheric CO2, 13C and the marine carbon cycle during the Last Glacial-Interglacial cycle: Possible role for a deepening of the mean remineralization depth and an increase in the oceanic nutrient inventory, Quaternary Sci. Rev., 56, 46–68, https://doi.org/10.1016/j.quascirev.2012.09.012, 2012. a, b
Menviel, L., Mouchet, A., Meissner, K. J., Joos, F., and England, M. H.: Impact of oceanic circulation changes on atmospheric δ13CO2, Global Biogeochem. Cy., 29, 1944–1961, https://doi.org/10.1002/2015GB005207, 2015. a, b
Mook, W.: 13C in atmospheric CO2, Neth. J. Sea Res., 20, 211–223, https://doi.org/10.1016/0077-7579(86)90043-8, 1986. a, b, c
Müller, S. A., Joos, F., Edwards, N. R., and Stocker, T. F.: Water Mass Distribution and Ventilation Time Scales in a Cost-Efficient, Three-Dimensional Ocean Model, J. Climate, 19, 5479–5499, https://doi.org/10.1175/JCLI3911.1, 2006. a, b
Najjar, R. G. and Orr, J. C.: Biotic-HOWTO. Internal OCMIP, Tech. Rep., LSCE/CEA, Saclay, Gif-sur-Yvette, France, 15 pp., 1999. a
Oliver, K. I. C., Hoogakker, B. A. A., Crowhurst, S., Henderson, G. M., Rickaby, R. E. M., Edwards, N. R., and Elderfield, H.: A synthesis of marine sediment core δ13C data over the last 150 000 years, Clim. Past, 6, 645–673, https://doi.org/10.5194/cp-6-645-2010, 2010. a, b, c
Orr, J. C. and Epitalon, J.-M.: Improved routines to model the ocean carbonate system: mocsy 2.0, Geosci. Model Dev., 8, 485–499, https://doi.org/10.5194/gmd-8-485-2015, 2015. a, b
Orr, J. C., Najjar, R., Sabine, C. L., and Joos, F.: Abiotic-HOWTO. Internal OCMIP, Tech. rep., LSCE/CEA, Saclay, Gif-sur-Yvette, France, 25 pp., 1999. a
Orr, J. C., Najjar, R. G., Aumont, O., Bopp, L., Bullister, J. L., Danabasoglu, G., Doney, S. C., Dunne, J. P., Dutay, J.-C., Graven, H., Griffies, S. M., John, J. G., Joos, F., Levin, I., Lindsay, K., Matear, R. J., McKinley, G. A., Mouchet, A., Oschlies, A., Romanou, A., Schlitzer, R., Tagliabue, A., Tanhua, T., and Yool, A.: Biogeochemical protocols and diagnostics for the CMIP6 Ocean Model Intercomparison Project (OMIP), Geosci. Model Dev., 10, 2169–2199, https://doi.org/10.5194/gmd-10-2169-2017, 2017. a
Parekh, P., Joos, F., and Müller, S. A.: A modeling assessment of the interplay between aeolian iron fluxes and iron-binding ligands in controlling carbon dioxide fluctuations during Antarctic warm events, Paleoceanography, 23, PA4202, https://doi.org/10.1029/2007PA001531, 2008. a
Peltier, W. R.: Ice Age Paleotopography, Science, 265, 195–201, 1994. a
Revelle, R. and Suess, H. E.: Carbon Dioxide Exchange Between Atmosphere and Ocean and the Question of an Increase of Atmospheric CO2 during the Past Decades, Tellus, 9, 18–27, https://doi.org/10.1111/j.2153-3490.1957.tb01849.x, 1957. a, b, c
Ridgwell, A. and Hargreaves, J. C.: Regulation of atmospheric CO2 by deep-sea sediments in an Earth system model, Global Biogeochem. Cy., 21, GB2008, https://doi.org/10.1029/2006GB002764, 2007. a, b
Ritz, S., Stocker, T., and Joos, F.: A Coupled Dynamical Ocean-Energy Balance Atmosphere Model for Paleoclimate Studies, J. Climate, 24, 349–375, https://doi.org/10.1175/2010JCLI3351.1, 2011. a
Roth, R. and Joos, F.: Model limits on the role of volcanic carbon emissions in regulating glacial-interglacial CO2 variations, Earth Planet. Sc. Lett., 329, 141–149, https://doi.org/10.1016/j.epsl.2012.02.019, 2012. a
Roth, R., Ritz, S. P., and Joos, F.: Burial-nutrient feedbacks amplify the sensitivity of atmospheric carbon dioxide to changes in organic matter remineralisation, Earth Syst. Dynam., 5, 321–343, https://doi.org/10.5194/esd-5-321-2014, 2014. a, b, c, d, e, f, g, h
Sarmiento, J. L., Orr, J. C., and Siegenthaler, U.: A perturbation simulation of CO2 uptake in an ocean general circulation model, J. Geophys. Res.-Oceans, 97, 3621–3645, https://doi.org/10.1029/91JC02849, 1992. a
Schimel, D., Alves, D., Enting, I. G., Heimann, M., Joos, F., Raynaud, D., and Wigley, T. M. L.: CO2 and the carbon cycle, in: Climate Change 1995 The Science of Climate Change Contribution of Working Group I to the Second Assessment Report of the Intergovernmental Panel on Climate Change, edited by: Houghton, J. T., Meira Filho, L. G., Callander, B. A., Harris, N., Kattenberg, A., and Maskell, K., Cambridge University Press, 76–86, 1996. a
Schmitt, J., Schneider, R., Elsig, J., Leuenberger, D., Lourantou, a., Chappellaz, J., Kohler, P., Joos, F., Stocker, T. F., Leuenberger, M., and Fischer, H.: Carbon Isotope Constraints on the Deglacial CO2 Rise from Ice Cores, Science, 336, 711–714, https://doi.org/10.1126/science.1217161, 2012. a
Schneider, R., Schmitt, J., Köhler, P., Joos, F., and Fischer, H.: A reconstruction of atmospheric carbon dioxide and its stable carbon isotopic composition from the penultimate glacial maximum to the last glacial inception, Clim. Past, 9, 2507–2523, https://doi.org/10.5194/cp-9-2507-2013, 2013. a, b, c, d, e, f
Siegenthaler, U. and Joos, F.: Use of a simple model for studying oceanic tracer distributions and the global carbon cycle, Tellus B, 44, 186–207, https://doi.org/10.1034/j.1600-0889.1992.t01-2-00003.x, 1992. a, b
Siegenthaler, U. and Oeschger, H.: Predicting future atmospheric carbon dioxide levels, Science, 199, 388–395, https://doi.org/10.1126/science.199.4327.388, 1978. a
Siegenthaler, U. and Oeschger, H.: Biospheric CO2 emissions during the past 200 years reconstructed by deconvolution of ice core data, Tellus B, 39, 140–154, https://doi.org/10.3402/tellusb.v39i1-2.15331, 1987. a
Sitch, S., Smith, B., Prentice, I. C., Arneth, A., Bondeau, A., Cramer, W., Kaplan, J. O., Levis, S., Lucht, W., Sykes, M. T., Thonicke, K., and Venevsky, S.: Evaluation of ecosystem dynamics, plant geography and terrestrial carbon cycling in the LPJ dynamic global vegetation model, Global Change Biol., 9, 161–185, https://doi.org/10.1046/j.1365-2486.2003.00569.x, 2003. a
Skinner, L. C., Fallon, S., Waelbroeck, C., Michel, E., Barker, S., Klug, A., Stark, A., Peters, K., Schnering, H. G., Umemoto, K., Yamaguchi, K., Fujita, M., Powers, R. E., Parac, T. N., Raymond, K. N., Olenyuk, B., Muddiman, D. C., Smith, R. D., Whiteford, J. A., Stang, P. J., Levin, M. D., Shield, J. E., Egan, S. J., Robson, R., Dress, A. W. M., Roy, S., Ni, Z., Yaghi, O. M., Lu, J., Mondal, A., Zaworotko, M. J., Atwood, J. L., Tominaga, M., Kawano, M., Tang, C., Wiesenfeld, K., Gustafson, S., Pelta, D. A., Verdegay, J. L., Systems, B., Pelzing, M., Skinner, L. C., Fallon, S., Waelbroeck, C., Michel, E., and Barker, S.: Ventilation of the Deep Southern Ocean and Deglacial CO2 Rise, Science, 328, 1147–1151, https://doi.org/10.1126/science.1183627, 2010. a
Skinner, L. C., Primeau, F., Freeman, E., de la Fuente, M., Goodwin, P. A., Gottschalk, J., Huang, E., McCave, I. N., Noble, T. L., and Scrivner, A. E.: Radiocarbon constraints on the glacial ocean circulation and its impact on atmospheric CO2, Nat. Commun., 8, 16010, https://doi.org/10.1038/ncomms16010, 2017. a
Stocker, B. D., Roth, R., Joos, F., Spahni, R., Steinacher, M., Zaehle, S., Bouwman, L., Xu-Ri, and Prentice, I. C.: Multiple greenhouse-gas feedbacks from the land biosphere under future climate change scenarios, Nat. Clim. Change, 3, 666–672, https://doi.org/10.1038/nclimate1864, 2013. a
Tarnocai, C., Canadell, J. G., Schuur, E. A. G., Kuhry, P., Mazhitova, G., and Zimov, S.: Soil organic carbon pools in the northern circumpolar permafrost region, Global Biogeochem. Cy., 23, GB2023, https://doi.org/10.1029/2008GB003327, 2009. a
Tschumi, T., Joos, F., Gehlen, M., and Heinze, C.: Deep ocean ventilation, carbon isotopes, marine sedimentation and the deglacial CO2 rise, Clim. Past, 7, 771–800, https://doi.org/10.5194/cp-7-771-2011, 2011. a, b, c, d, e, f, g
Wanninkhof, R.: Relationship between wind speed and gas exchange over the ocean, J. Geophys. Res., 97, 7373–7382, https://doi.org/10.1029/92JC00188, 1992. a
Wanninkhof, R.: Relationship between wind speed and gas exchange over the ocean revisited, Limnol. Oceanogr.-Meth., 12, 351–362, https://doi.org/10.4319/lom.2014.12.351, 2014. a
- Abstract
- Introduction
- Model and experimental setup
- Results
- Discussion and conclusion
- Appendix A: Analytical expressions for the impulse response functions of CO2,a and δ13Ca
- Appendix B: Sediment module and weathering feedback
- Data availability
- Author contributions
- Competing interests
- Acknowledgements
- Financial support
- Review statement
- References
- Abstract
- Introduction
- Model and experimental setup
- Results
- Discussion and conclusion
- Appendix A: Analytical expressions for the impulse response functions of CO2,a and δ13Ca
- Appendix B: Sediment module and weathering feedback
- Data availability
- Author contributions
- Competing interests
- Acknowledgements
- Financial support
- Review statement
- References