the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Varying regional δ18O–temperature relationship in high-resolution stable water isotopes from east Greenland
Christian Holme
Vasileios Gkinis
Mika Lanzky
Valerie Morris
Martin Olesen
Abigail Thayer
Bruce H. Vaughn
Bo M. Vinther
This study examines the stable water isotope signal (δ18O) of three ice cores drilled on the Renland peninsula (east Greenland coast). While ice core δ18O measurements qualitatively are a measure of the local temperature history, the δ18O variability in precipitation actually reflects the integrated hydrological activity that the deposited ice experienced from the evaporation source to the condensation site. Thus, as Renland is located next to fluctuating sea ice cover, the transfer function used to infer past temperatures from the δ18O variability is potentially influenced by variations in the local moisture conditions. The objective of this study is therefore to evaluate the δ18O variability of ice cores drilled on Renland and examine the amount of the signal that can be attributed to regional temperature variations. In the analysis, three ice cores are utilized to create stacked summer, winter and annually averaged δ18O signals (1801–2014 CE). The imprint of temperature on δ18O is first examined by correlating the δ18O stacks with instrumental temperature records from east Greenland (1895–2014 CE) and Iceland (1830–2014 CE) and with the regional climate model HIRHAM5 (1980–2014 CE). The results show that the δ18O variability correlates with regional temperatures on both a seasonal and an annual scale between 1910 and 2014, while δ18O is uncorrelated with Iceland temperatures between 1830 and 1909. Our analysis indicates that the unstable regional δ18O–temperature correlation does not result from changes in weather patterns through strengthening and weakening of the North Atlantic Oscillation. Instead, the results imply that the varying δ18O–temperature relation is connected with the volume flux of sea ice exported through Fram Strait (and south along the coast of east Greenland). Notably, the δ18O variability only reflects the variations in regional temperature when the temperature anomaly is positive and the sea ice export anomaly is negative. It is hypothesized that this could be caused by a larger sea ice volume flux during cold years which suppresses the Iceland temperature signature in the Renland δ18O signal. However, more isotope-enabled modeling studies with emphasis on coastal ice caps are needed in order to quantify the mechanisms behind this observation. As the amount of Renland δ18O variability that reflects regional temperature varies with time, the results have implications for studies performing regression-based δ18O–temperature reconstructions based on ice cores drilled in the vicinity of a fluctuating sea ice cover.
- Article
(15071 KB) - Full-text XML
- BibTeX
- EndNote
Polar ice sheets store deposited precipitation as stratified ice layers thousands of years back in time. This precipitation consists of stable water isotopes (δ18O, δD) that work as a direct proxy of the relative depletion of a water vapor mass in its transport from the evaporation source to the site where condensation takes place (Epstein et al., 1951; Mook, 2000). This traceability manifests as a correlation between δ18O and the temperature in the cloud at the time of condensation (Dansgaard, 1954, 1964). Thus, a relationship between δ18O and temperature is preserved in annual layers of precipitation on an ice cap. Hence, by drilling ice cores at polar sites such as Antarctica and Greenland, it is possible to access past temperatures imprinted on the δ18O signal. Several studies have examined the relation between temperature and ice core δ18O, and its linear or quadratic relationship has regularly been used as a transfer function to infer past temperature (Jouzel and Merlivat, 1984; Johnsen et al., 1989, 2001; Jouzel et al., 1997; Ekaykin et al., 2017). While it is evident that δ18O and temperature covary, the δ18O signal is also affected by changes in sea ice and atmospheric circulation (Noone and Simmonds, 2004; Steig et al., 2013). Changes in regional quasi-stationary modes of climate variability such as the North Atlantic Oscillation can modulate global atmospheric circulation patterns (e.g., precipitation patterns) which affect the δ18O variability. Additionally, changes in sea ice extent affect the local moisture conditions, which particularly influence the coastal precipitated δ18O variability (Bromwich and Weaver, 1983; Noone and Simmonds, 2004). Such variations have implications for a simple regression-based reconstruction of temperature from δ18O as the variability patterns between the ice core isotope signal and the oscillation modes and sea ice extent can have varied in strength back in time. Furthermore, in studies that analyze the relationship between polar precipitated δ18O and temperature, the temperature record is often substantially shorter than the δ18O series. While this is inevitable when performing temperature reconstructions, utilizing a short temperature record complicates the possibility of verifying whether the estimated δ18O–temperature relation is stable with time.
The aim of this study is to examine how much of the δ18O variability (1801–2014 CE) from a stack of ice cores drilled on the Renland peninsula, eastern Greenland, can be attributed to temperature variations (map in Fig. 1). In the analysis, seasonally averaged δ18O time series have been compared with regional temperatures through instrumental temperature records from the coasts of east Greenland (1895–2014 CE) and Iceland (1830–2014 CE) and the regional atmospheric climate model HIRHAM5 2 m temperature output (1980–2014 CE). The δ18O signal is divided into its seasonal components as it potentially improves the reconstruction of variability in weather regimes and past temperatures (Vinther et al., 2003b, 2010; Zheng et al., 2018). As Renland is located on the coast, its hydrological conditions are connected with the sea ice that is transported south annually along the coast of east Greenland. A relatively small loss in regional sea ice extent (≈ 10 % or less) has previously been found to influence local Greenland moisture source water vapor, which is traceable in the corresponding ice core deuterium excess values (Klein and Welker, 2016). The deuterium excess signal (; Dansgaard, 1964) contains information about the kinetic fractionation occurring when moisture evaporates from the ocean surface and the ice core dxs has been found to correlate with relative humidity and sea surface temperature at the source region (Jouzel and Merlivat, 1984; Johnsen et al., 1989). Thus, besides investigating the regional δ18O–temperature relationship, this study examines if changes in the Arctic sea ice extent can be detected in the Renland stable water isotopes.
The Renland ice cap has an area of 1200 km2 with an average ice thickness of a few hundred meters. It is separated from the main Greenlandic ice sheet as a small peninsula on the east coast of Greenland (map in Fig. 1). The ice cap experiences a high annual accumulation rate of around 0.47 m ice yr−1 with an annual surface temperature of −18 ∘C. Renland has probably never been overridden by the inland ice as it is surrounded by deep branches of the Scoresbysund Fjord which effectively drains the inland ice (Johnsen et al., 1992). Additionally, the small width of the ice cap, which is constrained by the surrounding mountains, prevents the ice elevation from significantly increasing from present-day height. As a result, the ice cap has not experienced any ice sheet elevation changes for the past 8000 years (except for slight uplift due to isostatic rebound) (Vinther et al., 2009). This implies that lapse-rate-controlled temperature variations resulting from a varying ice sheet thickness will be negligible.
This study utilizes three ice cores drilled on Renland in the analyses (Table 1). Two cores were drilled next to each other in the year 1988 (main (M) and shallow (S) cores), while the third was drilled approximately 2 km away in 2015 as part of the REnland ice CAP project (RECAP). The 1988 M and RECAP cores extend over the past 120 ka, while the 1988 S core only covers the time back to the year 1801. Despite two cores covering the past interglacial and glacial period, the study focuses on the period 1801–2014 CE where three overlapping ice core records and instrumental temperature recordings are available. Moreover, the separation of the summer and winter signals is better facilitated when the annual layers are not obliterated due to diffusion and ice thinning.
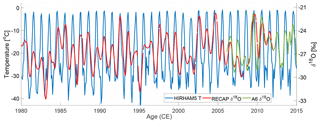
The records from 1988 were measured with an isotope ratio mass spectroscopy (IRMS) with a discrete resolution of 5.0 cm, while the RECAP core was measured using cavity ringdown spectroscopy (Picarro L2130) on a continuous flow analysis (CFA) system with a nominal resolution of 0.5 cm. For the RECAP core, the years 2011–2014 are covered by the snow pit core A6 drilled next to the drill site. The A6 core was measured discretely with a sample size of 5.0 cm on a Picarro L2130. This was done as the porous snow in the upper firn column easily inhibits a stable measurement flow in the CFA analysis, which complicates precise water isotope measurements.
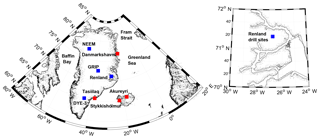
Figure 1Locations of ice core drill sites (blue squares) and the instrumental temperature records (red squares).
Firn diffusion dampens the annual oscillations in the δ18O data. This takes place while firn (snow that survived a season) is transformed into ice in the top 60–80 m of the ice sheet. During this densification process, air in the open porous firn is interconnnected, which enables the stable water isotopes in the firn air to mix with the snow grains (Johnsen, 1977). This molecular diffusion process makes the δ18O signal become increasingly more smooth with depth until pore close-off. The firn diffusion of stable water isotopes imposes two challenges on the analysis presented in this study. First, the diffusion of the annual oscillations creates artificial trends in summer and winter season time series of δ18O (Vinther et al., 2010). Secondly, it introduces a bias when comparing the ice cores drilled in 1988 with the ice core drilled in 2015. For instance, the δ18O signal representing the year 1987 has only experienced 1 year of firn diffusion in the 1988 ice cores, while it has experienced 28 years of firn diffusion in the 2015 core. The δ18O signal for overlapping years will therefore be more attenuated in the 2015 core.
As this study compares the seasonally averaged δ18O signals of three ice cores drilled in different years, it is necessary to ensure that each δ18O record has the same firn diffusive properties with depth. This is typically achieved by correcting each δ18O record such that the effect of increasing smoothing with depth is removed by deconvolving the measured δ18O signal to restore the originally deposited signal. However, Renland frequently experiences summer melting which causes steep isotopic gradients in the firn. Such high-frequency gradients complicate a deconvolution of the measured δ18O signal (Cuffey and Steig, 1998; Vinther et al., 2010). Instead, this study forward-diffuses the three δ18O records with depth such that each δ18O series has been influenced by the same amount of firn diffusion. Diffusion of stable water isotopes is typically described by the diffusion length (σ), which is the average vertical displacement of a water molecule (units in meters). Thus, the δ18O series are forward-diffused () such that each record has the same σ with depth. Despite such a smoothing procedure slightly mixing the summer and winter signals, a distinction of the seasonal components is still possible due to Renland's thick annual layers greatly exceeding the diffusion length.
The procedure below outlines in three steps how this was done separately for the 2015, 1988 M and 1988 S cores.
Step 1. First, the amount of diffusion that the measured δ18O signal already has experienced with depth is computed through the diffusion length's density dependence (for origin, see Gkinis et al., 2014; Holme et al., 2018):
where D(ρ) is the firn diffusivity and dρ∕dt is the densification rate. This study uses the firn diffusivity parameterization of Johnsen et al. (2000) (described in Appendix A) that employs the site-dependent parameters of temperature (C), accumulation rate (0.47 m ice yr−1), surface pressure (0.75 atm) and density. Density is here modeled with depth by fitting a Herron and Langway (1980) densification model to density measurements from the drill sites. From Eq. (1), it is possible to calculate the diffusion length that each layer has experienced (σ2(ρ)) (Fig. C1a).
Step 2. Eq. (1) can be used to calculate the auxiliary diffusion needed to transform a δ18O record into having a uniform diffusion length independent of depth. An auxiliary diffusion (σ2(ρ)aux) is calculated as the difference between the final diffusion length at the pore close-off density (σ2(ρpc=804.3 kg m−3)) and the diffusion length at a given layer in meters of ice-equivalent depth:
where the fraction ρi∕ρ(z) ultimately is multiplied onto the auxiliary diffusion length in order to transform the σ2(ρ)aux from representing ice-equivalent depth to density-equivalent depth (as the annual oscillations are squeezed during firn compaction). Using Eq. (2), an auxiliary diffusion profile with respect to density (and thus depth) is calculated for an ice core (Fig. C1a).
Step 3. Forward diffusion is then simulated through a convolution of the measured data () with a Gaussian filter (𝒢) with a standard deviation equal the auxiliary diffusion length as this is mathematically equivalent to firn diffusion (Johnsen, 1977):
where
As the auxiliary diffusion length decreases with depth, the width of the Gaussian filter changes accordingly. Thus, the convolution (using the σaux for the corresponding depth) is applied to a moving 2 m section which is shifted in small steps equal to the sampling interval. For each convolved data section, only the midpoint of the sliding window is retained as the new forward-diffused δ18Ofd value. In order to avoid tail problems when diffusing the top 2 m measurements, the data were extended by using its prediction filter coefficients estimated from a maximum entropy method algorithm by Andersen (1974). This assumes that the extended series has the same spectral properties as the original series. After applying this smoothing routine to the entire record, a δ18Ofd series with constant σ is obtained. A comparison between δ18Ofd and δ18Omeas is shown in Fig. C1.
It is important to ensure that the chronologies of the three ice cores are synchronous before comparing the δ18O variability. The two cores drilled in 1988 were manually dated by counting the summer maxima and winter minima in the δ18O series and verified by identifying signals of volcanic eruptions in the electrical conductivity measurements (Vinther et al., 2003b, 2010). For the 2015 RECAP core, the period 1801–2007 was dated with the annual layer algorithm (StratiCounter) presented in Winstrup et al. (2012) and the years 2007–2014 were manually counted similar to the 1988 cores (the RECAP chronology is presented in Simonsen et al., 2018). The annual layer algorithm uses signals in the ice core that all have annual oscillations or peaks such as the chemical impurities (Na+, Ca, and ), electrical conductivity and stable water isotopes. Even though the model automatically counts years, the chronology is still restricted by the same volcanic eruptions as in the 1988 cores. The model marks a year when Na+ has a peak, which indicates winter. Na+ is a result of the transport of salt from the ocean, and it peaks during winter due to the strong winds during the fall. As the timing of this winter peak might not be similar to the timing of the δ18O series' winter minima (used for the 1988 cores), this study has tuned the RECAP dating presented Simonsen et al. (2018) slightly. For each year, this is done by tuning the timing of the summer and winter in the dated RECAP record to match the maximum and minimum of the δ18O series. The chronology is only shifted a maximum of a few months, and it is only changed within a given year. This ensures that the modified dating profile remains consistent with the original chronology, while it facilitates an optimal comparison between the manually dated and the automatically dated stable water isotopes profiles.
In order to analyze the seasonal signals of the δ18O series, we need to distinguish between snow deposited during summer and winter. Under the assumption that δ18O and temperature extremes in the Greenland region occur simultaneously, Vinther et al. (2010) found it best to define the summer and winter seasons such that they each contain 50 % of the annual accumulation. Besides maximizing the amount of utilized data, this definition ensures that the winter and summer signals contain no overlapping data. This study has therefore defined the summer and winter seasons similarly to Vinther et al. (2010). The summer, winter and annually averaged δ18O data used in this study are thus seasonal or annual averages of the forward-diffused δ18O series.
The three ice cores' δ18O data as representative of the isotope hydrology on Renland are first evaluated by calculating Pearson correlation coefficients and signal-to-noise variance ratios (SNRs) on the forward-diffused δ18O records in the overlapping period 1801–1987. The correlation coefficient is a metric that describes the linear relation between two signals and it has been calculated for different combinations of the presented ice cores (Table 2). For all correlation coefficient calculations throughout this study, the level of significance is estimated based on a Monte Carlo routine described in Appendix B. From the results displayed in Table 2, it is evident that the lowest correlation coefficients are found for the winter-averaged data with values ranging from 0.60 to 0.78, while the summer- and annually averaged signals have higher values ranging from approximately 0.64 to 0.84. The high correlation coefficients indicate that there is a strong linear relationship between the δ18O records. This is further illustrated by the visual covariation of the annually averaged δ18O records in Fig. 2. In all instances, the highest correlations are found when correlating the two ice cores drilled in 1988. This might be attributed to the use of a similar dating method and their close proximity. Nonetheless, all the presented ice cores correlated significantly during the 1801–1987 period.
Table 2Correlation coefficients (r) calculated for different combinations of δ18O records for the period 1801–1987 (p<0.05).
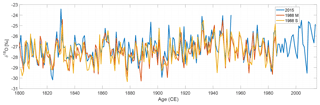
Figure 2Annually averaged δ18O for the RECAP 2015 (blue), 1988 M (red) and 1988 S (yellow) cores with age.
The δ18O variability can be further analyzed by examining the mean single series SNR which provides an insight into the amount of signal and noise in the δ18O series (Fisher et al., 1985). Noise can originate from depositional effects such as wind shuffling of snow and melt layers and from dating uncertainties (±1 year) in between the three cores. By averaging n (3) overlapping ice core data records, the mean single series SNR is calculated by comparing the variance of an averaged record (VARs) with the mean of the variances () for the n individual records (Johnsen et al., 1997; Vinther et al., 2006):
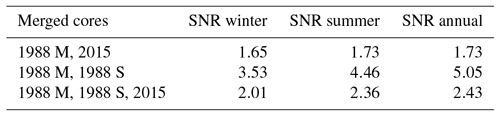
Alternatively, a recent study by Münch and Laepple (2018) introduced a new way of calculating timescale-dependent SNR values, which provides a basis for interpreting noise across timescales. The SNR results are shown in Table 3. Similar to the high correlation, it is evident that merging the two 1988 records results in the highest SNR values. Moreover, the summer-averaged signal has a higher SNR compared to the winter-averaged signal, which probably is a consequence of winters having more windy conditions that generate the redeposition of snow. A similar pattern has previously been found for the seasonal isotopes of GRIP ice core (n=5; SNR summer: 0.70; winter: 0.51), Dye-3 ice core (n=2; SNR summer: 1.73; winter: 1.56) and NEEM ice core (n=4; SNR summer: 1.28; winter: 0.64) (map in Fig. 1) (Vinther, 2003a; Zheng et al., 2018). This comparison also shows that the SNR values of the three Renland ice cores are high compared to GRIP, Dye-3 and NEEM which likely can be attributed to a combination of a high accumulation rate and a good cross-dating between the compared cores.
From this analysis, the study can comment on two things. First, the two 1988 cores have the most robust common signal of all the tested combinations. As this was for two adjacently drilled ice cores, utilizing all three records still results in a larger spatial atmospheric representativeness of the region. Secondly, the high SNR and correlation coefficients imply that the chronologies from the annual layer detection algorithm and the manual counting are consistent. This has implications for future ice core science as manual layer counting can be a slow and inefficient procedure. Thus, manual counting can effectively be replaced with the StratiCounter software by Winstrup et al. (2012) for ice cores, where several datasets that contain observable annual peaks or oscillations are available.
Table 3Mean signal-to-noise variance ratios calculated for the summer, winter and annually averaged data using two and three cores in the period 1801–1987.
The high combined SNR values and correlation coefficients indicate that it is beneficial to combine the time series into a stacked δ18O record. We choose to employ all three ice cores as that increases the spatial representativeness of δ18O, while it provides water isotopic variability for the years 1988–2014. A stacked record is typically created by averaging the time series but the time span 1801–2014 consists of an inhomogeneous amount of data records as only the RECAP core contains data in the 1988–2014 period, while it also has a gap between 1954 and 1961 due to missing ice samples. Thus, it is important to implement a variance correction in order to avoid bias issues when averaging time series with nonuniform length (Osborn et al., 1997; Jones et al., 2001). This variance correction (c) can be expressed directly through the SNR values in Table 3 and the number of records (m) used in the averaging for the given year (derivation can be found in Vinther et al., 2006):
Before stacking, the three time series are standardized based on the period of overlap (1801–1987) ( has mean = 0 and standard deviation = 1). An average value is then calculated by multiplying c onto the mean for each year:
The amplitude and variability of the original δ18O series are then restored by using the average variance () and the average () of the three time series (from the period where the time series were standardized):
Figure 3 shows the summer, winter and annual series for the period 1801–2014. In the figure, a 5-year moving average has been applied to the stacked records in order to filter out any remaining high-frequency noise variability. From the figure, it is evident that the summer-averaged signal is less depleted than the annual and winter-averaged signals. Moreover, the summer signal has the largest trend in δ18O with an increase of 0.54 ‰ per century, while the winter and annually averaged data show lower increases of, respectively, 0.24 ‰ per century and 0.37 ‰ per century. The amount of variability that correlates with temperature will be examined in Sect. 6.
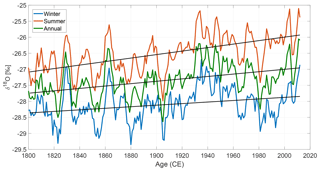
Figure 3Summer (red), winter (blue) and annually averaged (green) δ18O stacks together with their corresponding linear trends (black lines) for the period 1801–2014. A moving average of 5 years has been applied to all the time series. For the unfiltered series, the reader is referred to Figs. 4, C2 and C3.
6.1 Correlation with instrumental temperature records
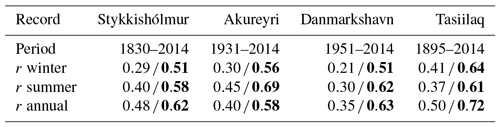
The relationship between Renland δ18O variability and temperature is first investigated by comparing the stacked δ18O series with instrumental temperature records. This study uses the nearest and longest temperature recordings from Greenland (Tasiilaq and Danmarkshavn) and Iceland (Akureyri and Stykkishólmur) – locations are shown in Fig. 1. The Greenland temperature records are available from the Danish Meteorological Institute (2018) and the Iceland temperatures are available from the Icelandic Met Office (2018). For the temperature measurements, the seasons have been defined similarly to Vinther et al. (2010) with summer extending from May to October and winter from November to April. Figure 4 shows the annually averaged δ18O stack together with the annually averaged temperature measurements (winter and summer averages are shown in Figs. C2 and C3). Visually, the past 100 years of summer, winter and annually averaged δ18O signals of Renland covary with the regional temperature. However, the years 1830–1910 show periods with both anticorrelation and correlation. Besides the visual covariation, correlation coefficients between the temperature recordings and the δ18O stacks are calculated and shown in Table 4. The correlations with the winter-averaged data are in general the lowest, while annual and summer signals have similar high correlations at all the sites. The best correlation with the Renland δ18O signal is found for the annual averages at Tasiilaq (r=0.50). Additionally, applying a 5-year moving mean on the δ18O and temperature series increases all the correlations (i.e., the Tasiilaq correlation coefficient increases to r=0.72).
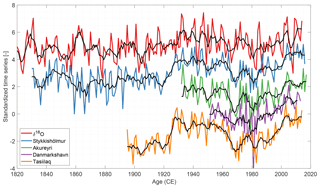
Figure 4Annually averaged δ18O and temperature series. For visualization, the time series have been standardized and shifted vertically. The black curves represent a moving average of 5 years.
Table 4Correlation coefficients between the δ18O stack and instrumental temperature records (p <0.05) both at a 1-year resolution and with a 5-year moving mean applied (in bold).
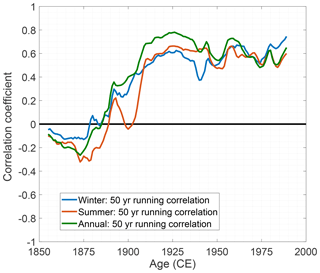
The high correlation between δ18O and temperature implies that the region's temperature variability is imprinted in the Renland δ18O stack. Conventionally, a simple interpretation in terms of local temperature can then be achieved by using the linear relation between δ18O and temperature. However, this requires that the linear relationship between temperature and δ18O is stable throughout time. In order to examine this, correlation coefficients between Stykkishólmur temperature and δ18O have been calculated on a 50-year running window and shown in Fig. 5. Here Stykkishólmur is chosen as it has the longest temperature record, while we selected a window size of 50 years in order to include enough independent data as the time series have been smoothed with a 5-year moving mean. This analysis indicates that the Stykkishólmur temperature and the δ18O stack only correlates in the period 1910–2014. For winter, summer and annual averages, the average correlation in the period 1910–2014 is 0.56, 0.65 and 0.66, while it severely reduces to −0.02, −0.02 and 0.004 in the 1830–1909 period. Thus, the high correlation coefficients presented in Table 4 is only a result of the high correlations in the 1910–2014 period. This could explain why the highest δ18O–temperature correlation was found at Tasiilaq as it only extended back to 1895. Consequently, the regional δ18O–temperature relationship between Renland isotopes and the Iceland temperature record is not constant through time. While it remains unknown if the temperature on Iceland and Renland was similar between 1830 and 1909, it is certain that the Renland δ18O variability does not represent the temperature variability in Iceland in the studied period. Thus, even though the δ18O variability probably reflects the local temperature on Renland, the results show that the spatial extent of this δ18O–temperature relationship was different in the 1830–1909 period.
6.2 Correlation with the HIRHAM5 2 m temperature output
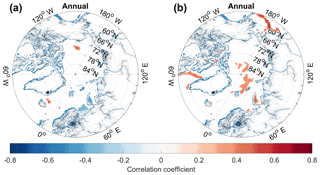
The spatial extent of the correlation between the δ18O signal and temperature is further investigated by using 2 m temperature output from the regional climate model, HIRHAM5 (Christensen et al., 2007). This particular HIRHAM5 simulation (Langen et al., 2017) covers the entire Greenlandic region including Iceland. At the lateral boundaries and over the ocean, the model is driven with the European Re-Analysis dataset ERA-Interim (Dee et al., 2011). This study uses monthly averaged data (1980–2014 CE) on a horizontal resolution of 0.05∘ (∼5.5 km) converted to summer and winter temperatures by averaging May–October and November–April, respectively. The RECAP core is used instead of the stacked record as the analysis is on data from the satellite era, which is minimally available in the 1988 cores. The correlation maps are shown in Fig. 6. The results show significant positive correlations between the winter signals of HIRHAM5 2 m temperature and the RECAP δ18O. Moreover, the high correlations (r>0.5) that extend over most of Greenland, irrespectively of the ice divide, indicate that the winter temperature variability over Greenland is imprinted in the Renland δ18O signal. Results furthermore show that there is no statistically significant correlation between δ18O and temperature east of Renland in areas regularly covered by sea ice. For the summer and annually averaged signals, the correlations are lower (r∼0.4–0.5) and they only cover the east coast region. This local spatial pattern is consistent with Vinther et al. (2010), who found that the summer-averaged δ18O data from different Greenlandic ice cores were less internally coherent than the corresponding winter data. This could explain why the summer δ18O variability of the RECAP core only correlates with the local temperatures on the coast of east Greenland. Moreover, the variance in summer-averaged temperatures over Greenland is very low, as shown in Fig. 7. The low variance is due to the HIRHAM5 summer temperatures reaching a maxima just below 0∘C at places with constant ice cover. For instance, Fig. 8 shows the monthly averaged HIRHAM5 temperature from a grid point on Renland where it is evident that the monthly averaged temperature fluctuations during summer are very small. Thus, the small temperature fluctuations can limit the possibility of interpreting the spatial extent of summer and annual temperature variability imprinted in the δ18O signal.
All in all, these results support the correlations from Sect. 6.1 that were high between δ18O and temperature in the 1910–2014 period.
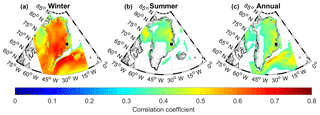
Figure 6Figures showing the correlation between winter (a), summer (b) and annually (c) averaged RECAP δ18O and HIRHAM5 temperatures. Only correlations with p<0.05 are shown.
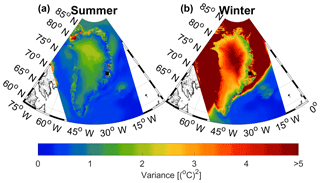
Figure 7Variances of the summer (a) and winter-averaged temperatures (b). A maximum variance of 5 (∘C)2 is displayed in order to emphasize the small variance in the summer-averaged signal.
A strengthening and weakening of, respectively, the low-pressure system over Iceland and high-pressure system over the Azores control both the direction and strength of westerly winds and storm tracks over the North Atlantic. Fluctuations in the difference in atmospheric pressure at sea level between Iceland and the Azores is described by the North Atlantic Oscillation (NAO). Changes in the NAO has previously been found to have an imprint on precipitation in western Greenland (Appenzeller et al., 1999). Correspondingly, the winter isotope signal of west and south Greenland ice cores have previously been found to anticorrelate with the atmospheric circulation changes from the NAO (Vinther et al., 2003b, 2010). Despite Vinther et al. (2010) showing that ice cores drilled on the Greenland east coast revealed no connection with the NAO, this study examines potential correlation in order to determine if changes in the NAO can be linked to the varying δ18O–temperature relationship.
While the NAO is best described through a principal component analysis of multiple sea level pressure records or gridded datasets of sea level pressure in the North Atlantic region, this study uses an approximation where the NAO index is based on pressure observations only near the two centers of action of the surface pressure field (the Azores and Iberian Peninsula and Iceland). Such an approximation was carried out by Jones et al. (1997), who reconstructed the NAO variation back to 1821 (and have since extended it up to present time). This study uses a slightly modified version of this NAO index by Vinther et al. (2003c), who improved the NAO record in the period 1821–1856 by using extra pressure series.
The connection between the NAO index and seasonally (and annually) averaged δ18O stacks is examined by estimating their correlation. Correlation coefficients have been calculated on 5-year moving averages of the NAO and δ18O stacks and shown in Table 5 (the annual NAO record is plotted in Fig. 9). The level of significance is estimated based on a Monte Carlo routine described in Appendix B. In the complete 1821–2014 period, the summer, winter and annually averaged NAO and δ18O data are uncorrelated with coefficients of 0.01, −0.05 and 0.02, respectively. If we instead examine the time before and after the δ18O–temperature correlation terminated (the year 1909), the summer and annually averaged data yield positive correlations of 0.29 and 0.30 between 1821 and 1909, while the winter and annually averaged data yield negative correlations of −0.25 and −0.22 between 1910 and 2014. Thus, there is a varying relation between the NAO and the δ18O data, and the weak δ18O–NAO anticorrelation coincides with a covarying δ18O–temperature relation. However, the weak correlations during 1821–1909 imply that the NAO only can account for around 8 %–9 % of the corresponding δ18O variability. It therefore seems unlikely that strengthening and weakening of the NAO causes changes in the δ18O–temperature relation.
8.1 Fram Strait sea ice export
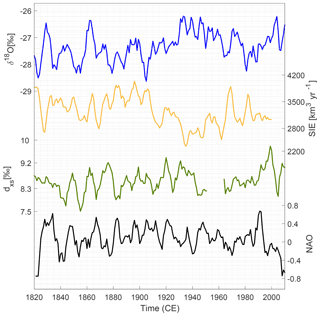
In this section, it is investigated whether there is a connection between the Renland δ18O variability and the sea ice export (SIE) through the Fram Strait (map in Fig. 1). Sea ice from the Arctic Ocean is exported southward through Fram Strait along the eastern coast of Greenland into the Greenland Sea. Fluctuations in this sea ice volume flux have a direct effect on the amount of open water located east and northeast of Renland. As δ18O is an integrated signal of the hydrological activity along the moisture transport pathway from evaporation source to deposition, the open water which facilitates moist and mild climatic conditions will likely affect the isotopic composition of the precipitation deposited on Renland. Essentially, besides the temperature dependence of isotopic fractionation during local condensation, δ18O contains information about the amount of water mass that is removed from the air during the poleward transport and the continuous contribution of local water mixing with the transported water mass (Noone and Simmonds, 2004).
This analysis uses a Fram Strait SIE record covering the period 1820–2000 reconstructed by Schmith and Hansen (2002). It is an ice volume flux record (km3 yr−1) based on historical observations of sea ice obtained from ship logbooks and ice charts. As the record represents the annual SIE, only the annually averaged δ18O stack is used in the analysis. Figure 9 shows the SIE together with the annually averaged δ18O stack and the RECAP dxs record (dxs is only available for the RECAP core). A correlation analysis is carried out in order to quantify any covariation of the records. For a moving average of 5 years applied to the time series, there is an anticorrelation of −0.54 (p<0.01) between the annual SIE and δ18O, while there is no significant correlation between dxs and the SIE (). From the correlation analyses, it is clear that δ18O anticorrelates with SIE, while it correlates with temperature (Sect. 6.1). In order to examine if these correlations apply simultaneously, correlation coefficients have been calculated on a 50-year running window. The level of significance is estimated based on a Monte Carlo routine described in Appendix B. The results are plotted in Fig. 10. In the past 100 years, the Stykkishólmur temperature record is found to correlate with Renland δ18O, while it (like δ18O) anticorrelates with SIE through Fram Strait. This likely indicates that warm temperatures result in less sea ice that can be exported away from the Arctic Ocean (with less sea ice formation locally). However, this pattern ceases to exist prior to the early 1900s such that neither the δ18O signal or temperature share any correlation with the SIE. This synchronous decrease in correlation indicates that a lack of correlation between δ18O and temperature cannot be explained by dating errors in the ice core chronologies. In addition, while we acknowledge that part of the missing δ18O–SIE correlation might be a consequence of the progressively decreasing sea ice data quality prior to 1900, we do not expect similar uncertainty with the instrumental temperature data. Thus, this indicates that the varying relationships are not solely an artifact of poor data quality. Furthermore, as discussed in Sect. 7 and shown as running correlations in Fig. 10, the varying δ18O–temperature correlation cannot be a consequence of the NAO controlling the δ18O variability. Moreover, Fig. 10 also shows that changes in local moisture source regions are not traceable through the dxs–SIE correlation.
In order to examine the lacking δ18O–temperature correlation, the connection between the SIE anomaly and the δ18O–temperature relation is plotted in Fig. 11 (SIE anomaly is here defined as the deviation from the mean flux). As a 5-year moving mean has been applied to the time series, only every 5 points are used in the analysis. From the figure, it is clear that in years when the temperature anomaly is positive (), there is always a negative SIE anomaly and a high δ18O–temperature correlation of 0.83, whereas for Tanom<0 there is no δ18O–temperature correlation (r=0.02) which coincides with a combination of both positive and negative SIE anomalies. Besides showing that higher temperatures coincide with less sea ice being transported south (likely due to an already lower extent of sea ice), it appears that lower temperatures coincide with more fluctuations in the SIE, which possibly reduce the δ18O–temperature correlation. These results imply that the δ18O variability can be dominated by other climatic conditions such as SIE and does not only represent variations in regional temperature for an extended period of time.
8.2 The sea ice edge in the Greenland Sea
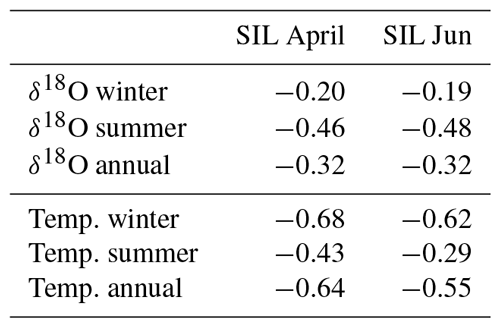
The position of the sea ice edge or line (SIL) is another way of characterizing the local sea ice extent. Here, we use a record of seasonal SIL anomalies in the Greenland Sea from Divine and Dick (2006) to further examine the relation between δ18O and sea ice. The SIL anomaly (km) describes the advance and retreat of the ice edge position in the Greenland Sea (defined as the perpendicular distance from the mean edge to a given point). The SIL separates close pack ice (defined as concentrations greater than 30 %) from loose ice drift. Here, we only use data from the period 1850–2002 as it is has the highest density of data (we fill the gaps by linear interpolation). The record is based on historical observations of the ice edge and presents monthly averages for April, June and August where the sea ice extent are expected to experience both its maximum (April) and its minimum (August). Only April and June data are used in this analysis as the data are too sparse for August.
This study compares the winter-averaged δ18O signal with the SIL data from April (maximum extent), the annually averaged δ18O with SIL data from June (intermediate extent) and the summer-averaged δ18O with the SIL data from June as they have approximately the same timing (all combinations are tested and the correlations are displayed in Table C1). Similar to Sect. 8.1, correlations are calculated on a 50-year running window and displayed in Fig. 12. Except from a period of anticorrelation between δ18O and SIL (1890–1940), there exists no clear correlation pattern between the Greenland Sea's SIL and the Renland δ18O signal. This is in contrast with the stronger connection between the Renland δ18O signal and the SIE through Fram Strait. From Fig. 12, it is seen that the SIL and SIE data are uncorrelated (r=0.15 for a moving average of 5 years and detrended time series). Furthermore, the SIL has been linearly decreasing (retreating), while the SIE has remained more constant in the period 1850–2000 CE. This is because the SIE through Fram Strait reflects the net production of sea ice in the Arctic Ocean (Vinje et al., 1998) compared to the SIL presumably documenting more local sea ice extent. For instance, April SIL has a strong anticorrelation (r=0.68) with Stykkishólmur winter temperature (Table C1) which could indicate that the retreat and advance of the SIL is connected with local Icelandic temperatures. Aside from the SIL recording a position and the SIE recording a volume flux of sea ice, it is possible that the δ18O–SIE correlation is strengthened through the SIE's dependence on its drifting velocity. For instance, winters exert stronger northerly winds (Steffen and Box, 2001), which increases the southward ice drifting velocity. This feature will increase the SIE additionally, independently of the actual amount of sea ice. While this could enhance the correlation, it does not explain why both the δ18O and the SIE become uncorrelated synchronously with their correlation with the Iceland temperature (Sect. 8.1). This indicates that the δ18O–SIE connection is more complex than a wind influence. From this, it is evident that the Renland δ18O signal has a stronger linear resemblance with the SIE through Fram Strait than with the Greenland Sea's seasonal SIL.
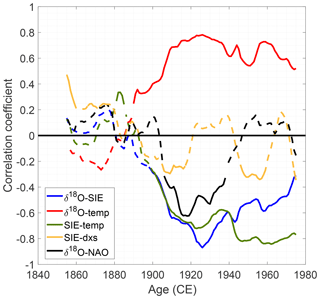
Figure 10Running correlations of 50 years between Stykkishólmur temperature and the δ18O stack (red), SIE and the δ18O stack (blue), SIE and Stykkishólmur temperature (green), the δ18O stack, and the NAO index (black) and dxs with SIE (yellow). The solid lines represent significant correlation (p<0.05), while the dashed lines are insignificant p>0.05. Each year represents the midpoint of the running window.
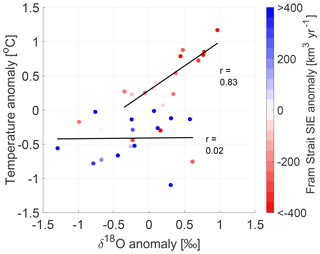
Figure 11Annual temperature anomaly plotted with respect to annual δ18O anomaly, where colors indicate the strength of the Fram Strait sea ice export anomaly. A 5-year moving average has been applied to all the time series but only every 5 points are displayed and used in the analysis. The solid black lines represents linear fits between δ18O and temperature for positive and negative temperature anomalies.
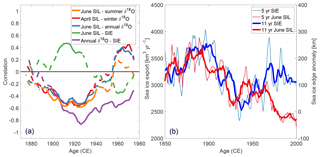
Figure 12(a) Running correlations of 50 years between June SIL and summer δ18O (orange), April SIL and winter δ18O (red), June SIL and annual δ18O (blue), June SIL and Fram Strait SIE (green), and annual δ18O with Fram Strait SIE (purple). (b) Fram Strait SIE (blue) and Greenland Sea SIL (red) with 5- and 11-year moving means applied.
8.3 Sea ice concentration and sea surface temperature
The Arctic sea ice concentration (SIC) data (fractional ice cover in percentage) from the ERA-Interim reanalysis (Dee et al., 2011) has been correlated with the RECAP δ18O and dxs series, and the results are shown in Figs. 13 and 14 (1980–2014). In the case of sea ice extent, summer refers to June-November and winter refers to December–May, while the seasonally averaged δ18O is defined similarly to Sect. 6.2 (summer: May–October; winter: November–April). In the case of dxs, only the annually averaged data are used as its seasonal components are smeared out after the δ18O and δD data have been forward-diffused. The results show a large patch of anticorrelation between δ18O and SIC in the Baffin Bay area () outside west Greenland for both winter and annually averaged data. Presumably, this indicates that the climate at Renland is similar to the climate at Baffin Bay which controls the advance and retreat of the sea ice extent. A similar connection was found in Sect. 6.2, which showed that the winter-averaged δ18O signal correlated with temperatures all over Greenland, resembling the anticorrelations between NEEM δ18O and Baffin Bay SIC that have previously been found (Steen-Larsen et al., 2011; Zheng et al., 2018). Moreover, the results are consistent with Faber et al. (2017), who found that changes in the Baffin Bay sea ice coverage can impact the δ18O precipitation over Greenland (by using an atmospheric general circulation model coupled with water isotopologue tracing (isoCAM3)). Furthermore, the analysis shows only a small patch of correlation between the δ18O series and the SIC south of Fram Strait. However, this is not necessarily inconsistent with the significant anticorrelation presented in Sect. 8.1. Possibly, this nuance can be explained by the SIE representing the annual discharge of sea ice (ice volume flux), while the SIC represents the fractional ice cover in percentage (area).
The connection between the Renland stable water isotopes and the local climate conditions is further investigated by correlating the RECAP dxs signal with the Arctic SIC and sea surface temperature (SST). Figure 14 shows that there exist small patches of positive correlation patterns between the dxs signal and the SIC in the Arctic Ocean and south of Baffin Bay. As these areas are very small, it is difficult to evaluate the connection between the extent of SIC and dxs at Renland. The dxs signal is further examined by checking if it reflects the local SST variability. This has been done by correlating the dxs signal with the SST data in the Arctic region from ERA-Interim data (1980–2014). From Fig. 14, it is evident that there barely exist patches with significant correlation. Thus, it is difficult to assess whether the RECAP dxs record directly reflects the local SST or SIC variability during the 1980–2014 period. More analysis on what controls the Renland dxs signal is needed in future research.
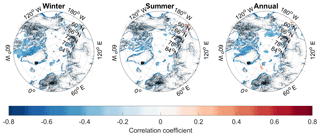
Figure 13Maps showing the correlation coefficients between the ERA-Interim sea ice concentration and the RECAP δ18O data for the 1980–2014 period (p<0.05).
The analysis showed no constant linear coupling between the Renland δ18O signal and the advance and retreat of the Greenland Sea's SIL. However, the SIL record documented a great sea ice extent in the Greenland Sea prior to the 1910s. Hence, despite the two datasets not being linearly connected, a large sea ice extent still coincides with the weakened δ18O–temperature correlation. Furthermore, the analysis showed that fluctuations in Fram Strait SIE could be connected with the regional δ18O–temperature relationship. Despite the apparent connection, this study has not proved any causality between the δ18O–temperature relation and the SIE. Still, a proposed hypothesis for this connection is that the fluctuating SIE conditions during cold years impose changes in the location of the local moisture sources, which suppress the imprint of Iceland temperature variability in Renland δ18O. It is likely that this connection has its strongest impact on ice cores drilled in the coastal regions near sea ice as Vinther et al. (2010) found that the δ18O records of Greenlandic ice cores drilled in south and central Greenland correlated well with a southwest Greenland instrumental temperature series in the period 1785–1980 (Vinther et al., 2006). With reference to this temperature series, Fig. C4 shows that these temperatures do not have a stable linear covariation with the Renland δ18O stack (winter averages are here chosen as they constitute the longest and most homogeneous record). Besides Renland obviously being located far away from the southwest Greenland instrumental temperature stations, this contrariety might result from the isotope distillation process being more manifest as a temperature variability in the δ18O signal when the precipitation has had a longer distillation path and has risen in more altitude than that of the coastal region, further depleting the δ18O signal. In order to evaluate this hypothesis, more studies using isotope-enabled modeling are needed. The impact of changes in sea ice on the Arctic δ18O precipitation has previously been investigated by Faber et al. (2017), who found that the δ18O precipitation on Greenland only responded to perturbations of the Baffin Bay sea ice coverage. However, they used a horizontal resolution of which barely resolved the Renland Ice Cap of ∼1200 km2. Thus, a further examination of how changes in sea ice extent is connected with the coastal Greenlandic precipitation on a higher spatial resolution grid is essential in order to evaluate this hypothesis.
Alternatively, if the seasonal distribution of precipitation on Renland changed significantly prior to the 1910s, it could lead to a change in the relationship between the δ18O signals and temperature. While the dating resolution does not permit a direct assessment of such changes, we do observe that the difference between the summer and winter δ18O have in fact changed over the 1801–2014 period (Fig. 3).
Moreover, while this study found that the Renland δ18O signal anticorrelated with variations in the sea ice extent outside west Greenland (Sect. 8.3), a similar pattern was found with the HIRHAM5 temperature correlations presented in Sect. 6.2. It is therefore likely that the connection represents a reduced sea ice coverage due to increasing temperatures rather than an actual interconnection between Renland δ18O and Baffin Bay sea ice.
This study found that by quantifying the mean signal-to-noise variance ratios, a robust seasonal δ18O signal (1801–2014) could be extracted by stacking three ice cores from Renland. This δ18O stack was correlated with instrumental temperature records from east Greenland and Iceland and with the HIRHAM5 2 m temperature output. Results showed that there were high correlations between δ18O and regional temperatures on both a seasonal and annual scale between 1910 and 2014. A similar anticorrelation was found between the δ18O stack and the amount of sea ice exported through Fram Strait. However, both correlations diminished in the 1830–1909 period. The results indicated that the varying regional temperature variability in the δ18O signal could not be explained by the North Atlantic Oscillation. Instead, the linear δ18O–temperature relation depended on whether the temperatures were warmer or colder than the temperature anomaly. Warm years were associated with a high correlation and accompanied by less sea ice transported south along the coast, while cold years were associated with zero correlation that accompanied a fluctuating amount of sea ice along the coast. These results implied that changes in the extent of open water outside Renland might affect the local moisture conditions. Hence, greater sea ice flux along the coast of Greenland may suppress the Iceland temperature signature in the δ18O signal; however, this was not confirmed by correlations between dxs and sea surface temperature in the Arctic region. Thus, more high-resolution isotope-enabled modeling focused on the effect of Arctic sea ice on coastal precipitation are needed in order to quantify this process.
These results have implications for ice core temperature reconstructions based on the linear relationship between δ18O variability and local temperature records. For Renland, the linear δ18O–temperature relationship was unstable with time which implied that the annual-to-decadal variability of δ18O measured in an ice core could not be directly attributed to temperature variability. Similar conditions might apply for other ice cores drilled in the vicinity of a fluctuating sea ice cover. This reinforces the interpretation that δ18O is an integrated signal of all the hydrological activity that a vapor mass experiences en route from the evaporation at the source to its condensation at the drill site.
The annualized δ18O data will be available on http://www.iceandclimate.nbi.ku.dk/data/ (Holme, 2019).
This study uses the firn diffusivity parameterization of Johnsen et al. (2000):
which depends on the molar weight of water (m), the saturation vapor pressure (p), diffusivity of water vapor (Dai), the molar gas constant (R), the site temperature (T), the ice–vapor fractionation factor (αi) and the firn air tortuosity (τ). Similar to Johnsen et al. (2000) and subsequently used in Simonsen et al. (2011), Gkinis et al. (2014) and Holme et al. (2018), we used the following definitions which can be parameterized through annual mean surface temperature, annual accumulation rate, surface pressure and density (ρ):
-
saturation vapor pressure over ice (Pa) (Murphy and Koop, 2006):
-
Dai – diffusivity of water vapor (for isotopologue i) in air (m2s−1). For the diffusivity of the abundant isotopologue water vapor Da (Hall and Pruppacher, 1976),
with P0=1 atm, To=273.15 K, and P and T the ambient pressure (atm) and temperature (K). Additionally from Merlivat and Jouzel (1979), and ;
-
R – molar gas constant R=8.3144 m3 PaK−1 mol−1;
-
αi – ice–vapor fractionation factor. we use the formulations by Majoube (1970) and Merlivat and Nief (1967) for and , respectively.
-
τ – the firn tortuosity (Schwander et al., 1988):
based on Eq. (A7), τ→∞ for ρ>804.3 kg m−3
In this study, time series have often been smoothed with a 5-year moving mean before estimating their correlation. Potentially, this results in artificially improved correlation coefficients as a moving mean is a low-pass filter. It is therefore necessary to quantify the significance of the linear relationship (p value) by running a Monte Carlo simulation. This study tested significance by examining what correlation coefficients we would estimate if we had randomly generated data instead of the δ18O signal (following the procedure proposed by Macias-Fauria et al., 2011). For simplicity, this section refers to the correlation between δ18O and temperature, while it applies equally for all types of time series.
Synthetic data are created by generating time series with the same power spectrum as the δ18O signal. This study uses a method outlined in Ebisuzaki (1977) that is based on a random resampling of the δ18O signal in the frequency domain. The synthetic time series is then found by taking the inverse fast Fourier transform of the shuffled signal. This procedure retains the same autocorrelation as the input time series hereby mimicking the influence of a 5-year moving mean applied to data.
This procedure is simulated 1000 times. For each iteration, the correlation coefficient between the synthetic δ18O series and the temperature series is calculated. From this Monte Carlo routine, an empirical probability distribution function that describes the relation between synthetic generated data and the temperature series is obtained. From this distribution, it is possible to compute the p value, which describes how probable it is that the correlation between δ18O and temperature is significantly different from that of the synthetic δ18O and temperature. In this study, p values below 0.05 are considered statistically significant.
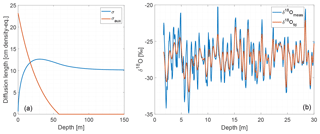
Figure C1(a) Modeled firn diffusion with depth (σ; blue) and calculated auxiliary diffusion length that should be applied to the measured δ18O data (σaux; red). After the pore close-off (ρpc=804.3 kg m−3), σaux=0 as σ just changes due to the compaction of firn. (b) The measured δ18O data (blue) and the forward-diffused δ18O data (red) for the 1988 M core.
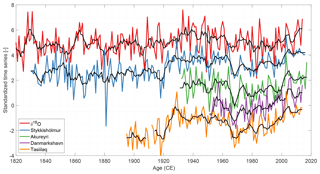
Figure C2Winter-averaged δ18O and temperature series. For visualization, the time series have been standardized and shifted vertically. The black curves represent a moving average of 5 years.
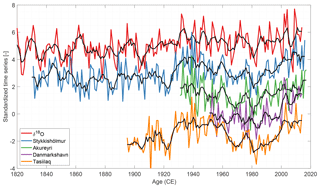
Figure C3Summer-averaged δ18O and temperature series. For visualization, the time series have been standardized and shifted vertically. The black curves represent a moving average of 5 years.
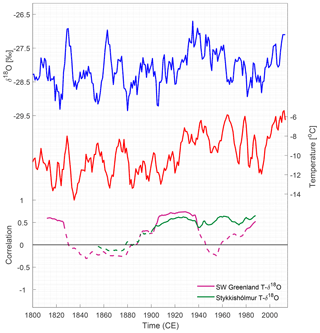
Figure C4(a) Five-year moving average of the winter-averaged δ18O stack. (b) Five-year moving average of the December–January–February averaged southwest Greenland temperatures from Vinther et al. (2006). (c) 50-year running correlations between δ18O and southwest Greenland (magenta) and δ18O and Stykkishólmur (green). Each year represents the midpoint of the running window. Solid lines are significant correlations and dashed lines are insignificant (p>0.05).
The authors declare that they have no conflict of interest.
The RECAP ice coring effort was financed by the Danish Research Council through a Sapere Aude grant, the NSF through the Division of Polar Programs, the Alfred Wegener Institute, and the European Research Council under the European Community's Seventh Framework Programme (FP7/2007–2013)/through the Ice2Ice project and the Early Human Impact project (267696). The authors acknowledge the support of the Danish National Research Foundation through the Centre for Ice and Climate at the Niels Bohr Institute (Copenhagen, Denmark). We kindly thank Dmitry Divine and one anonymous reviewer whose thoughtful comments helped improve and clarify this paper.
This research has been supported by the FP7 Ideas: European Research Council (grant no. ICE2ICE (610055)).
This paper was edited by Elizabeth Thomas and reviewed by Dmitry Divine and one anonymous referee.
Andersen, N.: On the calculation of filter coefficients for maximum entropy spectral analysis, Geophysics, 39, 69–72, 1974. a
Appenzeller, C., Schwander, J., Sommer, S., and Stocker, T. F.: The North Atlantic Oscillation and its imprint on precipitation and ice accumulation in Greenland, Geophys. Res. Lett., 25, 1939–1942, 1999. a
Bromwich, D. H. and Weaver, C. J.: Latitudinal displacement from main moisture source controls δ18O of snow in coastal Antarctica, Nature, 301, 145–147, 1983. a
Christensen, O. B., Drews, M., Christensen, J. H., Dethloff, K., Ketelsen, K., Hebestadt, I., and Rinke, A.: The HIRHAM Regional Climate Model Version 5, Technical report 06–17, Danish Climate Centre, DMI, 2007. a
Cuffey, K. M. and Steig, E. J.: Isotopic diffusion in polar firn: implications for interpretation of seasonal climate parameters in ice-core records, with emphasis on central Greenland, J. Glaciol., 44, 273–284, 1998. a
Danish Meteorological Institute: Greenland temperature records, available at: http://www.dmi.dk/laer-om/generelt/dmi-publikationer/tekniske-rapporter/, last access: 1 December 2018. a
Dansgaard, W.: The 18O-abundance in fresh water, Geochim. Cosmochim. Ac., 6, 241–260, 1954. a
Dansgaard, W.: Stable isotopes in precipitation, Tellus B, 16, 436–468, 1964. a, b
Dee, D. P., Uppala, S. M., Simmons, A., Berrisford, P., Poli, P., Kobayashi, S., Andrae, U., Balmaseda, M., Balsamo, G., Bauer, P., Bechtold P., Beljaars, A. C. M., van de Berg, L., Bidlot, J., Bormann, N., Delsol, C., Dragani, R., Fuentes, M., Geer, A. J., Haimberger, L., Healy, S. B., Hersbach, H., Hólm, E. V., Isaksen, L., Kållberg, P., Köhler, M., Matricardi, M., McNally, A. P., Monge-Sanz, B. M., Morcrette, J.-J., Park, B.-K., Peubey, C., de Rosnay, P., Tavolato, C., Thépaut, J.-N., and Vitart, F.: The ERA-Interim reanalysis: Configuration and performance of the data assimilation system, Q. J. Roy. Meteorol. Soc., 137, 553–597, 2011. a, b
Divine, D. V. and Dick, C.: Historical variability of sea ice edge position in the Nordic Seas, J. Geophys. Res.-Ocean., 111, 1–14, 2006. a
Ebisuzaki, W.: A method to estimate the statistical significance of a correlation when the data are serially correlated, J. Clim., 10, 2147–2153, 1977. a
Ekaykin, A. A., Vladimirova, D. O., Lipenkov, V. Y., and Masson-Delmotte, V.: Climatic variability in Princess Elizabeth Land (East Antarctica) over the last 350 years, Clim. Past, 13, 61–71, https://doi.org/10.5194/cp-13-61-2017, 2017. a
Epstein, S., Buchsbaum, R., Lowenstam, H., and Urey, H.: Carbonate-water isotopic temperature scale, Geol. Soc. Am. Bull., 62, 417–426, 1951. a
Faber, A.-K., Møllesøe Vinther, B., Sjolte, J., and Anker Pedersen, R.: How does sea ice influence d18O of Arctic precipitation?, Atmos. Chem. Phys., 17, 5865–5876, https://doi.org/10.5194/acp-17-5865-2017, 2017. a, b
Fisher, D. A., Reeh, N., and Clausen, H.: Stratigraphic noise in time series derived from ice cores, Ann. Glaciol., 7, 76–83, 1985. a
Gkinis, V., Simonsen, S. B., Buchardt, S. L., White, J. W. C., and Vinther, B. M.: Water isotope diffusion rates from the NorthGRIP ice core for the last 16,000 years – glaciological and paleoclimatic implications, Earth Planet. Sc. Lett., 405, 132–141, 2014. a, b
Hall, W. D. and Pruppacher, H. R.: The Survival of Ice Particles Falling from Cirrus Clouds in Subsaturated Air, J. Atmos. Sci., 33, 1995–2006, 1976. a
Herron, M. M. and Langway, C. C.: Firn Densification: An Empiricial Model, J. Glaciol., 25, 373–385, 1980. a
Holme, C., Gkinis, V., and Vinther, B. M.: Molecular diffusion of stable water isotopes in polar firn as a proxy for past temperatures, Geochem. Cosmochim. Ac., 225, 128–145, 2018. a, b
Holme, C.: Seasonally averaged δ18O ice core data (1801–2015 CE) for Renland, Greenland, available at: http://www.iceandclimate.nbi.ku.dk/data/, last access: 15 May 2019.
Icelandic Met Office: Icelandic temperature records, available at: http://en.vedur.is/climatology/data/\#a, last access: 1 December 2018. a
Johnsen, S., Clausen, H. B., Cuffey, K. M., Hoffmann, G., Schwander, J., and Creyts, T.: Diffusion of stable isotopes in polar firn and ice: the isotope effect in firn diffusion, Physics of Ice Core Records, 121–140, 2000. a, b, c
Johnsen, S. J.: Stable Isotope Homogenization of Polar Firn and Ice, Isotopes and Impurities in Snow and Ice, 118, 210–219, 1977. a, b
Johnsen, S. J., Dansgaard, W., and White, J.: The origin of Arctic precipitation under present and glacial conditions, Tellus B, 41, 452–468, 1989. a, b
Johnsen, S. J., Clausen, H. B., Dansgaard, W., Gundestrup, N. S., Hansson, M., Jonsson, P., Steffensen, J. P., and Sveinbjornsdottir, A. E.: A “deep” ice core from East Greenland, Meddelelser om Groenland, Geoscience, 29, 3–22, 1992. a
Johnsen, S. J., Clausen, H. B., Dansgaard, W., Gundestrup, N. S., Hammer, C. U., Andersen, U., Andersen, K. K., Hvidberg, C. S., Dahl-Jensen, D., Steffensen, J. P., Shoji, H., Sveinbjornsdottir, A. E., White, J., Jouzel, J., and Fisher, D.: The δ18O record along the Greenland Ice Core Project deep ice core and the problem of possible Eemian climatic instability, J. Geophys. Res., 102, 26397–26410, https://doi.org/10.1029/97JC00167, 1997. a
Johnsen, S. J., Dahl-Jensen, D., Gundestrup, N., Steffensen, J. P., Clausen, H. B., Miller, H., Masson-Delmotte, V., Sveinbjornsdottir, A. E., and White, J.: Oxygen isotope and palaeotemperature records from six Greenland ice-core stations: Camp Century, Dye-3, GRIP, GISP2, Renland and NorthGRIP, J. Quaternary Sci., 16, 299–307, 2001. a
Jones, P. D., Jonsson, T., and Wheeler, D.: Extension to the North Atlantic oscillation using early instrumental pressure observations from Gibraltar and south-west Iceland, Int. J. Climatol., 17, 1433–1450, 1997. a
Jones, P. D., Osborn, T. J., Briffa, K. R., Folland, C. K., Horton, E. B., Alexander, L. V., Parker, D. E., and Rayner, N. A.: Adjusting for sampling density in grid box land and ocean surface temperature time series, J. Geophys. Res., 106, 3371–3380, 2001. a
Jouzel, J. and Merlivat, L.: Deuterium and oxygen 18 in precipitation: modeling of the isotopic effects during snow formation, J. Geophys. Res.-Atmos., 89, 11749–11759, 1984. a, b
Jouzel, J., Alley, R. B., Cuffey, K. M., Dansgaard, W., Grootes, P., Hoffmann, G., Johnsen, S. J., Koster, R. D., Peel, D., Shuman, C. A., Stievenard, M., Stuiver, M., and White, J.: Validity of the temperature reconstruction from water isotopes in ice cores, J. Geophys. Res.-Ocean., 102, 26471–26487, 1997. a
Klein, E. S. and Welker, J. M.: Influence of sea ice on ocean water vapor isotopes and Greenland ice core records, Geophys. Res. Lett., 43, 12475–12,483, 2016. a
Langen, P. L., Fausto, R. S., Vandecrux, B., Mottram, R. H., and Box, J. E.: Liquid Water Flow and Retention on the Greenland Ice Sheet in the Regional Climate Model HIRHAM5: Local and Large-Scale Impacts, Front. Earth Sci., 4, 1–18, 2017. a
Macias-Fauria, M., Grinsted, A., Helama, S., and Holopainen, J.: Persistence matters: Estimation of the statistical significance of paleoclimatic reconstruction statistics from autocorrelated time series, Dendrochronologia, 30, 179–187, 2011. a
Majoube, M.: Fractionation factor of 18O between water vapour and ice, Nature, 226, p. 1242, 1970. a
Merlivat, L. and Jouzel, J.: Global Climatic Interpretation of the Deuterium-Oxygen 18 Relationship for Precipitation, J. Geophys. Res., 84, 5029–5033, 1979. a
Merlivat, L. and Nief, G.: Fractionnement Isotopique Lors Des Changements Detat Solide-Vapeur Et Liquide-Vapeur De Leau A Des Temperatures Inferieures A 0 ∘C, Tellus, 19, 122–127, 1967. a
Mook, J.: Environmental Isotopes in the Hydrological Cycle Principles and Applications, International Atomic Energy Agency, 1, 1–185, 2000. a
Münch, T. and Laepple, T.: What climate signal is contained in decadal- to centennial-scale isotope variations from Antarctic ice cores?, Clim. Past, 14, 2053–2070, https://doi.org/10.5194/cp-14-2053-2018, 2018. a
Murphy, D. M. and Koop, T.: Review of the vapour pressures of ice and supercooled water for atmospheric applications, Q. J. R. Meteorol. Soc., 131, 1539–1565, 2006. a
Noone, D. and Simmonds, I.: Sea ice control of water isotope transport to Antarctica and implications for ice core interpretation, J. Geophys. Res., 109, 1–13, 2004. a, b, c
Osborn, T., Briffa, K. R., and Jones, P. D.: Adjusting Variance for sample-size in tree-ring chronologies and other regional mean time series, Dendrochronologies, 15, 89–99, 1997. a
Schmith, T. and Hansen, C.: Fram Strait Ice Export during the Nineteenth and Twentieth Centuries Reconstructed from a Multiyear Sea Ice Index from Southwestern Greenland, J. Clim., 16, 2782–2791, 2002. a
Schwander, J., Stauffer, B., and Sigg, A.: Air mixing in firn and the age of the air at pore close-off, Ann. Glaciol., 10, 141–145, 1988. a
Simonsen, M. F., Baccolo, G., Blunier, T., Borunda, A., Delmonte, B., Frei, R., Goldstein, S., Grindsted, A., Kjaer, H. A., Sowers, T., Svensson, A., Vinther, B. M., Vladimirova, V., Winckler, G., Winstrup, M., and Vallelonga, P.: Ice core dust particle size reveals past glacier extent in East Greenland, Nat. Commun., in review, 2018. a, b
Simonsen, S. B., Johnsen, S. J., Popp, T. J., Vinther, B. M., Gkinis, V., and Steen-Larsen, H. C.: Past surface temperatures at the NorthGRIP drill site from the difference in firn diffusion of water isotopes, Clim. Past, 7, 1327–1335, https://doi.org/10.5194/cp-7-1327-2011, 2011. a
Steen-Larsen, H. C., Masson-Delmotte, V., Sjolte, J., Johnsen, S. J., Vinther, B. M., Bréon, F., Clausen, H. B., Dahl-Jensen, D., Falourd, S., Fettweis, X., Gallée, H., Jouzel, J., Kageyama, M., Lerche, H., Minster, B., Picard, G., Punge, H. J., Risi, C., Salas, D., Schwander, J., Steffen, K., Sveinbjornsdottir, A. E., Svensson, A., and White, J.: Understanding the climatic signal in the water stable isotope records from the NEEM shallow firn/ice cores in northwest Greenland, J. Geophys. Res., 116, 1–20, 2011. a
Steffen, K. and Box, J.: Surface climatology of the Greenland ice sheet: Greenland Climate Network 1995–1999, J. Geophys. Res.-Atmos., 106, 33951–33964, 2001. a
Steig, E. J., Ding, Q., White, J. W. C., Kuttel, M., Rupper, S. B., Neumann, T. A., Neff, P. D., Gallant, A. J. E., Mayewski, P. A., Taylor, K. C., Hoffmann, G., Dixon, D. A., Schoenemann, S., M., M. B., Schneider, D. P., Fudge, T. J., Schauer, A. J., Teel, R. P., Vaughn, B., Burgener, L., Williams, J., and Korotkikh, E.: Recent climate and ice-sheet change in West Antarctica compared to the past 2000 years, Nat. Geosci., 6, 372–375, 2013. a
Vinje, T., Nordlund, N., and Kvambekk, Å.: Monitoring ice thickness in Fram Strait, J. Geophys. Res.-Ocean., 103, 10437–10449, 1998. a
Vinther, B. M.: Seasonal δ18O Signals in Greenland Ice Cores, Master's thesis, University of Copenhagen, Denmark, 2003a. a
Vinther, B. M., Johnsen, S. J., Andersen, K. K., Clausen, H. B., and Hansen, A. W.: NAO signal recorded in the stable isotopes of Greenland ice cores, Geoph. Res. Lett., 30, 1–4, 2003b. a, b, c
Vinther, B. M., Andersen, K. K., Hansen, A. W., Schmidth, T., and Jones, P. D.: Improving the Gibraltar/Reykjavik NAO Index, Geoph. Res. Lett., 30, 1–4, 2003c. a
Vinther, B. M., Andersen, K. K., Jones, P. D., Briffa, K. R., and Cappelen, J.: Extending Greenland temperature records into the late eighteenth century, J. Geophys. Res., 111, 1–13, 2006. a, b, c, d
Vinther, B. M., Buchardt, S. L., Clausen, H. B., Dahl-Jensen, D., Johnsen, S. J., Fisher, D. A., Koerner, R. M., Raynaud, D., Lipenkov, V., Andersen, K. K., Blunier, T., Rasmussen, S. O., Steffensen, J. P., and Svensson, A. M.: Holocene thinning of the Greenland ice sheet, Nature, 461, 385–388, 2009. a
Vinther, B. M., Jones, P. D., Briffa, K. R. and. Clausen, H. B., Andersen, K. K., Dahl-Jensen, D., Johnsen, S. J., and Clausen, H. B.: Climatic signals in multiple highly resolved stable isotope records from Greenland, Quaternary Sci. Rev., 29, 522–538, 2010. a, b, c, d, e, f, g, h, i, j, k
Winstrup, M., Svensson, A. M., Rasmussen, S. O., Winther, O., Steig, E. J., and Axelrod, A. E.: An automated approach for annual layer counting in ice cores, Clim. Past, 8, 1881–1895, https://doi.org/10.5194/cp-8-1881-2012, 2012. a, b
Zheng, M., Sjolte, J., Adolphi, F., Vinther, B. M., Steen-Larsen, H. C., Popp, T. J., and Muscheler, R.: Climate information preserved in seasonal water isotope at NEEM: relationships with temperature, circulation and sea ice, Clim. Past, 14, 1067–1078, https://doi.org/10.5194/cp-14-1067-2018, 2018. a, b, c
- Abstract
- Introduction
- The ice cores
- Diffusion correction
- Chronology
- δ18O variability on Renland
- The temperature signature in δ18O
- The North Atlantic Oscillation's imprint on δ18O
- The impact of sea ice fluctuations on the stable water isotopes
- Discussion
- Conclusions
- Data availability
- Appendix A: Firn diffusivity
- Appendix B: Significance analysis
- Appendix C: Figures and tables
- Competing interests
- Acknowledgements
- Financial support
- Review statement
- References
- Abstract
- Introduction
- The ice cores
- Diffusion correction
- Chronology
- δ18O variability on Renland
- The temperature signature in δ18O
- The North Atlantic Oscillation's imprint on δ18O
- The impact of sea ice fluctuations on the stable water isotopes
- Discussion
- Conclusions
- Data availability
- Appendix A: Firn diffusivity
- Appendix B: Significance analysis
- Appendix C: Figures and tables
- Competing interests
- Acknowledgements
- Financial support
- Review statement
- References