the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Objective extraction and analysis of statistical features of Dansgaard–Oeschger events
Johannes Lohmann
Peter D. Ditlevsen
The strongest mode of centennial to millennial climate variability in the paleoclimatic record is represented by Dansgaard–Oeschger (DO) cycles. Despite decades of research, their dynamics and physical mechanisms remain poorly understood. Valuable insights can be obtained by studying high-resolution Greenland ice core proxies, such as the NGRIP δ18O record. However, conventional statistical analysis is complicated by the high noise level, the cause of which is partly due to glaciological effects unrelated to climate and which is furthermore changing over time. We remove the high-frequency noise and extract the most robust features of the DO cycles, such as rapid warming and interstadial cooling rates, by fitting a consistent piecewise linear model to Greenland ice core records. With statistical hypothesis tests we aim to obtain an empirical understanding of what controls the amplitudes and durations of the DO cycles. To this end, we investigate distributions and correlations between different features, as well as modulations in time by external climate factors, such as CO2 and insolation. Our analysis suggests different mechanisms underlying warming and cooling transitions due to contrasting distributions and external influences of the stadial and interstadial durations, as well as the fact that the interstadial durations can be predicted to some degree by linear cooling rates already shortly after interstadial onset.
- Article
(4514 KB) - Full-text XML
-
Supplement
(348 KB) - BibTeX
- EndNote
Different physical mechanism(s) underlying Dansgaard–Oeschger (DO) events have been proposed in the literature. Most of these are characterized by changes between different modes of operation of the Atlantic Meridional Overturning Circulation (AMOC) that accompany the warm and cold phases of a DO cycle. This is supported by marine sediment data evidence linking DO cycles and changes in the AMOC (Henry et al., 2016; Lynch-Stieglitz, 2017). Different drivers for these AMOC changes have been proposed, including North Atlantic freshwater forcing (Ganopolski and Rahmstorf, 2001; Timmermann et al., 2003; Kageyama et al., 2013), variations in ice sheet topography (Zhang et al., 2014), and atmospheric CO2 (Zhang et al., 2017). On the other hand, unforced millennial-scale oscillations involving the AMOC have been reported in comprehensive climate models (Vettoretti and Peltier, 2016; Klockmann et al., 2018). In these oscillations, sea ice variability in ocean convection areas plays an important role, which has been proposed previously (Li et al., 2010; Dokken et al., 2013; Petersen et al., 2013) and is supported by recent proxy records (Sadatzki et al., 2019). Another scenario underlying DO cycles might be spontaneous climate transitions due to extremes in the chaotic atmospheric dynamics (Drijfhout et al., 2013; Kleppin et al., 2015).
The modeling of DO events is guided by proxy records, among which stable water isotope records from Greenland ice cores are very prominent. DO-type transitions in models range in their dynamics from stochastic to excitable and oscillatory, and they are sensitive to different forcings. A statistical analysis of the DO cycles extracted from Greenland ice core records can thus be useful to evaluate the proposed models. The records are noisy, and since there are no established theories about how they should evolve, there is no obvious filter to extract the large-scale climate signal. A common characteristic of the DO cycles seems to be an abrupt temperature increase from cold stadial conditions to a maximum temperature in the warm interstadial state followed by a gradual cooling until there is another abrupt jump back into the stadial state. This is referred to as the sawtooth shape of the events.
Due to the high noise level in the record it is, however, difficult to discern this specific structure in all of the events. Some events do not seem to follow the generic shape. Furthermore, there are very short events during which it is difficult to speak of a gradual cooling episode. Other events are interrupted by shorter cooling episodes, referred to as sub-events (Capron et al., 2010). As interpretations of noisy time series are often biased, subjective, and prone to the recognition of patterns that can arise by chance, we seek a quantitative evaluation of the record. Assuming the sawtooth shape of the events, we develop an algorithm for fitting the sawtooth shape to the entire NGRIP δ18O record of the last glacial, similar to ramp-fitting a jump in a noisy record.
First, our method gives an objective basis of the validity of the generic sawtooth description of the DO cycles and identifies which individual cycles fall outside this description. Secondly, with a piecewise linear fit, we obtain estimates for the stadial and interstadial levels, the abruptness of the transitions, and the gradual cooling rate in the interstadial periods. By bootstrapping, we estimate the uncertainty in extracting these parameters from the noisy background. Finally, we perform a comprehensive statistical analysis of the fit parameters across the DO events and their relation to external forcings in order to obtain an empirical understanding of what controls the evolution of the amplitudes and durations of the DO cycles. This can potentially be used for identifying or excluding proposed mechanisms and for benchmarking model results.
Previous efforts to extract robust DO event features from the record were conducted on only part of the record and were focused on single or very few features. In Schulz (2002), linear fits to the interstadials were used to infer the cooling rates starting with Greenland interstadial 14 (GI-14). Estimates for the abruptness of warming transitions and the durations of interstadials have been derived by Rousseau et al. (2017), starting at GI-17.1. A comprehensive survey of the onset times of all interstadial and stadial periods is given in Rasmussen et al. (2014). Our work is different in that we derive all features that can be extracted from a sawtooth-shaped fit to all events at once by using a fit that is consistent and continuous throughout the record. Thus, our results are not sensitive to subjective choices of cutting the record at predefined times before and after a transition. We do, however, not define the DO events themselves from the NGRIP δ18O record but instead use the set of all previously classified events in Rasmussen et al. (2014), which have been derived from three ice cores and two proxy records each.
In this study, we show that a characteristic sawtooth waveform can be fit to all DO cycles. However, almost half of the cycles do not actually display a significant rapid cooling episode after the more gradual interstadial cooling. A subsequent statistical analysis of DO event features hints at different mechanisms underlying warming and cooling transitions. First, this follows from the distributions of the durations of the stadials as well as the rapid DO warmings, on the one hand, and of the interstadials on the other hand. Secondly, the influence of external forcing is contrasting, with stronger evidence for insolation influence on stadials and CO2 or ice volume influence on interstadials. Thirdly, the interstadial durations can be predicted to some degree by the linear cooling rates within a few hundred years after interstadial onset. In contrast, the stadial and rapid warming durations are consistent with the stadial–interstadial transitions as spontaneous, noise-induced escapes from a metastable state.
The paper is structured in the following way: in Sect. 2 we introduce the data used in the study and their preprocessing, the iterative fitting algorithm, the features we extract from the sawtooth-shaped fit to the events, and the statistical tools to analyze these features. In Sect. 3 we report the results of the fit. Section 3.1 discusses the appropriateness of the sawtooth fit to the events, and Sect. 3.2 and 3.3 treat the uncertainty in estimating the fit parameters and the derived features. In Sect. 4 we analyze in detail the features characterizing the stadial, interstadial, and abrupt warming periods. The results of the fit and the implications of the subsequent data analysis are discussed in Sect. 5. We conclude in Sect. 6.
2.1 Data
This study is based on the δ18O Greenland ice core record of the last glacial period (120–12 kyr BP; kyr BP is 1000 years before present). In the NGRIP ice core, δ18O has been measured in 5 cm samples (NGRIP Members, 2004; Gkinis et al., 2014; Rasmussen et al., 2014). The raw depth measurements are transferred to the GICC05 timescale (Svensson et al., 2006), resulting in an unevenly spaced time series with a resolution of ∼3 years at the end to 10 or more years at the beginning of the glacial. To simplify the analysis we transfer this to an evenly spaced time series by oversampling to 1-year resolution using nearest-neighbor interpolation. Thus, we do not alter the actually measured values and thus add or remove any variability. For subsequent comparison, the high-resolution δ18O record from the GRIP ice core on the GICC05 timescale is used (Johnsen et al., 1997; Rasmussen et al., 2014) and processed in the same way.
Our method uses a previously classified set of events from Greenland, which has been reported by Rasmussen et al. (2014) together with the time stamps. These time stamps are used to initialize our iterative routine and are subsequently refined during the process. We do not treat sub-events, which are small dips during interstadials, as separate events but instead fit them as part of the interstadials. On the other hand, we do include the interstadials 22 and 13, which follow the stadials 23.1 and 14 (denoted as “quasi-stadials” by Rasmussen et al., 2014). These have some resemblance to the so-called rebound events of, e.g., interstadials 12, 8, and 7. However, they are longer and larger in amplitude. Even though the stadials 23.1 and 14 do not fully reach the values of the stadials before and after, a sawtooth fit whereby these are included in the interstadial is not satisfactory because the resulting gradual linear cooling is not representative of the actual trends. Our choice to consider them as separate events is difficult to justify on the basis of the NGRIP δ18O record alone. Nevertheless, it is unlikely to change the conclusions of our analysis, which are based on statistical robustness tests.
Our analysis uses other datasets that are not derived from Greenland ice cores. These are referred to as external forcings, although not all are truly external to the climate system but rather obtained from independent data sources. As a proxy for global ice volume, we use the LR04 ocean sediment stack (Raymo and Lisiecki, 2005). To represent Antarctic temperatures, we choose the δ18O record of the EDML ice core on the AICC12 timescale (EPICA Community Members, 2010). These data were processed by interpolation to an equidistant 20-year grid and subsequent smoothing with a 600-year Hamming window. Greenhouse gas forcing is represented by a composite CO2 record from different Antarctic ice cores on the AICC12 gas timescale (Bereiter et al., 2015a). Furthermore, we consider changes in insolation due to orbital variations. Firstly, we use incoming solar radiation at 65∘ N integrated over the summer (referred to as 65Nint hereafter), which we define as the annual sum of the radiation on days exceeding an average of 350 W m−2 (Huybers, 2006). Secondly, we use incoming solar radiation at 65∘ N at summer solstice (referred to as 65Nss hereafter) (Laskar et al., 2004a). In addition, we consider the raw orbital parameters of obliquity, eccentricity, and precession index (Laskar et al., 2004a).
2.2 Fitting routine
We aim to fit a continuous piecewise linear waveform to the record. This is not possible by simply cutting the time series into DO cycles and fitting each cycle individually because the points at which the time series is cut need to be defined from the fit and in turn influence the fit. Fitting the whole time series at once to a piecewise linear model with 186 parameters, corresponding to 6 parameters for each of the 31 DO events, will be difficult to achieve without invoking very complicated constraints because of high noise and an abundance of sub-event features. Instead, we propose the following iterative fitting routine that converges to a consistent fit. We start with a guess for the stadial onset and end times, which determine the constant stadial levels. Then we fit a sawtooth shape individually to each event. Thereafter, we update the stadial onset and end times according to the fit and repeat the procedure. When after some iterations the onset and end times do not change significantly anymore, the fit has converged and is consistent.
The initial guess of the stadial onsets and ends is based on the timings reported by Rasmussen et al. (2014). The time series is divided into segments at these times, which are kept fixed throughout an iteration. For each event i, we take a segment consisting of a stadial and interstadial period plus the following stadial period. These segments are fitted individually to a piecewise linear model, as shown in Fig. 1. The model starts with a constant line at the beginning of the stadial. The constant is fixed to the mean level of the stadial , at which the stadial beginnings and ends are determined by the initial guess or the previous iteration. A first break point (parameter b1) of this constant is determined, followed by a linear up-slope (parameter s1). The slope ends at the second break point (parameter b2). After this break point there is a linear down-slope (parameter s2), which ends at a break point (parameter b3). After this break point there is a steeper down-slope until a last break point (parameter b4), which is at the level of the next stadial that is determined from the previous iteration. After all events have been fit, the parameters b4 and b1 of each event update the beginnings and ends of the stadials. The updated stadials yield a new segmentation of the time series and new stadial levels, which are then used as constant segments in the next iteration. The hope is that if the problem is well behaved, the beginnings and ends of the stadials do not change significantly anymore after a certain number of iterations, meaning that a consistent fit of the entire time series is obtained. An algorithm for this routine, along with details of the optimization procedure to fit each event, is given in Appendix A.
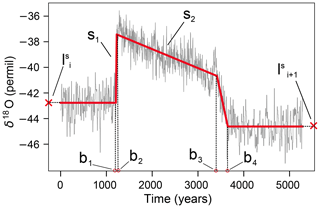
Figure 1Piecewise linear model fit to DO event 20, for which the time series consists of GS-21.1, GI-20, and GS-20. The parameters of the piecewise linear model are the four break points , the up-slope s1, and the down-slope s2. The levels and of GS-21.1 and GS-20 are constant during an iteration of the fitting routine and are updated after each iteration when all break points have been determined.
The fitting procedure outlined above yields a single best fit that we hope to be close to the absolute global minimum of the optimization problem and furthermore as consistent as possible, meaning that the stadial sections that were used for the fit in the last iteration are identical to the stadial sections defined by the resulting fit. Additionally to this best fit we assess the uncertainty in each of the parameters that arises due to noise in the record. We cannot estimate this from the output of our fitting procedure in a straightforward way. Instead, we use bootstrapping to repeatedly generate synthetic data for each transition and optimize the parameters. Like this, we yield a distribution on each parameter. Due to computational demands, we do not combine this with our iterative procedure but rather resample and fit every transition independently. Thus, we neglect the covariance structure of the errors in the parameters of neighboring transitions. However, we still consider it to be a very good estimate of the uncertainty due to the noise in the record. The detailed procedure is given in Appendix C.
2.3 DO event features
From the best-fit parameters of each DO cycle a variety of features follow.
For each rapid warming period, gradual interstadial cooling period, and
rapid cooling period at the end of an interstadial, we consider the duration, rate of change, and
amplitude. Furthermore, several absolute levels are of interest, including the constant stadial
levels, the interstadial levels after the abrupt warming, and the interstadial level before the rapid
cooling. As a level relative to each event, we consider the level before the rapid cooling above the
previous stadial level, which is given by the rapid warming amplitude minus the gradual cooling
amplitude. Finally, the gradual cooling amplitude divided by the rapid warming amplitude measures
the position of the point of rapid cooling within the event amplitude. In total, we consider 15
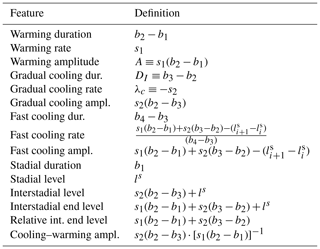
interdependent features, which are listed in Table 1.
2.4 Data analysis
Our aim is to develop an empirical understanding of the evolution of the DO cycles. To this end, we employ several tools to search for relations between different features, as well as between features and external climate factors. Additionally, the distributions of the individual features themselves hold important information, especially when there is no strong external modulation in time. We test the distributions using Anderson–Darling (AD), Cramér–von Mises, and Kolmogorov–Smirnov tests. Since the AD test is typically the most powerful and the other tests yield qualitatively unchanged results in all of our analyses, we only report p values for the AD test.
Because of the large number of possible combinations of features, we first preselect significant and potentially relevant relationships and thereafter investigate in detail whether the results are robust to outliers, among other things. In some cases we also consider relationships of features and forcings that are not significant for the whole dataset but for a large subset. This might highlight the fact that there were qualitatively different periods within the last glacial or that some DO events are of a different nature than most.
We first consider Pearson and Spearman correlation coefficients rp and rs of pairs of features and external climate factors. We preselect combinations with p values p<0.1, which are estimated by permutation tests that assume independent samples. For a given number of data points in a sequence, the true p values should often be higher due to autocorrelation. Along with other potential artifacts, this is investigated individually for the preselected combinations.
Next, in order to find relations between more than two variables, we search for multiple linear regression models to explain selected features of the data. Here, we often use logarithmic quantities because it is otherwise often unlikely to find linear relationships that are not dominated by outliers. Given a feature as a response variable, we consider linear regression models of combinations of two other features or forcings, preselect the models with the largest coefficients of determination, and then further analyze them.
Furthermore, in order to find subsets of events that have distinct properties or relationships that are only valid in part of the data, we perform a clustering analysis on the data using two different algorithms (K-means and agglomerative hierarchical clustering). Given our sample size of 31 events, we search for clusterings with two or three clusters. Clusterings are assessed by considering the mean Silhouette coefficient, which is a distance-based measure for the validity of clusters. With the abovementioned tools, we perform an analysis on the entire set of features and forcings. From the results obtained, we report the selected findings that are most robust and relevant in Sect. 4 of this paper.
The significance of such an analysis must be viewed in light of the multiple comparisons problem. Tests for significant correlations of many pairs of features using, e.g., the Spearman correlation yield a non-negligible number of false positives when using confidence levels that are reasonable for our purposes. We consider features of both the same and neighboring events, yielding and tests, respectively. Furthermore, we test the correlation of all features and forcings, yielding another tests. Assuming these are all independent tests, the expected number of false positives is 45 at 90 %, 22.5 at 95 %, and 4.5 at 99 % confidence. Since we derive 15 features from only six independent parameters for each DO cycle, many pairs of features are related, and thus we expect true positives for correlation tests. For instance, this is true for warming amplitude and interstadial level, as well as relative interstadial level and gradual cooling amplitude. Similarly, due to the constraints on the parameters, the rates and durations of fast and gradual cooling are correlated. These types of correlations are not relevant and thus reduce the number of pairwise correlations to consider. For combinations of amplitude, duration, and rates of a given linear segment we also expect correlation because they are trivially related: duration equals amplitude divided by rate. However, it is interesting to test whether the rates or the amplitudes are more strongly correlated with the durations. We investigate this for the different periods of the DO cycles below.
There are sophisticated methods to control the multiple comparisons problem. These could be helpful to better detect false positives from our analysis, but they depend on being able to properly estimate the significance of individual correlations between features with autocorrelation and assess the statistical dependence of the hypothesis tests due to the dependence of some of the features. For simplicity, we do not consider such an analysis, but we consider individually significant correlations as suggestions to be investigated further.
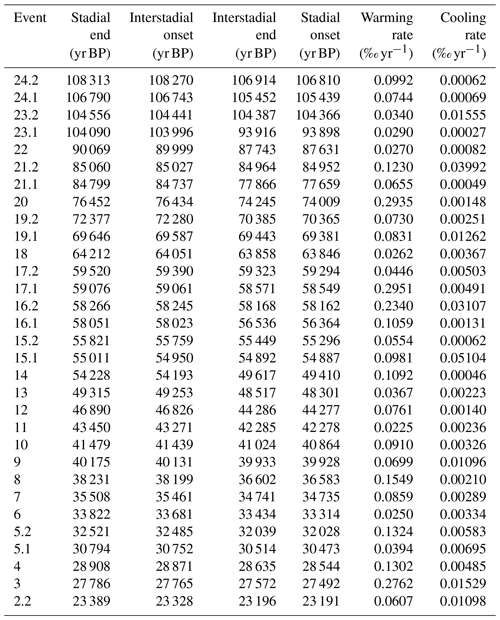
The fitting routine is performed for 40 iterations so that initial fluctuations in the parameters have died out and converged to a consistent fit, as detailed in Appendix B. Figure 2 superimposes the resulting fit onto the high-resolution NGRIP time series. We fit 31 DO events in total, starting with DO 24.2 and ending at DO 2.2, excluding the two outermost events of the last glacial because they are very nonstationary in their stadial parts. Table 2 shows all parameters obtained from the fit. Instead of for each transition, we show the corresponding times of stadial end, interstadial onset, interstadial end, and stadial onset.
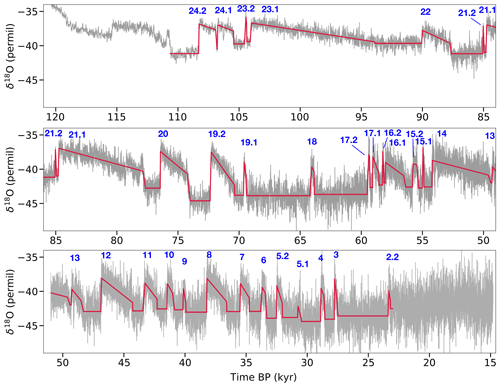
Figure 2 High-resolution NGRIP δ18O time series and the piecewise linear fit obtained by our method. The numbers above the interstadials indicate the names of the DO cycles considered in this study.
3.1 Sawtooth shape of DO events
In our fit, all transitions follow the characteristic sawtooth shape. For a few events, this is because of the constraints we use in the fitting algorithm. Typically, the constraints do not strictly bound the best-fit parameters, but they force the fit into another local minimum that is consistent with the sawtooth shape, which often yields parameters that are still clearly within the constraints. There are, however, four events with parameters close to the bounds. This happens for GI-5.1 and GI-3, which both have ratios of rapid to gradual cooling rates very close to the constraint value of 2.0. Similarly, for GI-15.2 and GI-6 the ratio of gradual to rapid cooling duration is close to 2.0. Detailed pictures of each transition and the corresponding fit are shown in Fig. S2.
The fact that constraints are needed to ensure that each event follows a sawtooth shape can be used to classify which events fall outside this description. To this end, we perform another run of the iterative fitting routine without using constraints 3, 4, 6, and 7 listed in Appendix A. From the resulting fit we then analyze which of the events are not consistent with the sawtooth shape. For this, we use four criteria:
-
the abrupt cooling rate is at least twice as large as the gradual cooling rate;
-
the gradual cooling lasts at least twice as long as the abrupt cooling;
-
there is gradual cooling after the rapid warming, i.e., the gradual cooling rate is negative; and
-
the abrupt cooling amplitude is larger than 0.5 ‰.
Criterion 1 is not met by events 23.1, 19.2, 15.1, 11, 5.1, 3, and 2.2; criterion 2 by events 21.2, 19.2, 17.2, 15.2, 15.1, 11, 10, 9, 8, 6, 5.1, 3, and 2.2; criterion 3 by event 11; and criterion 4 by events 23.1 and 15.1. By demanding that all of these criteria are met, we thus conclude that the following 14 out of 31 events fall outside the sawtooth description: 23.1, 21.2, 19.2, 17.2, 15.2, 15.1, 11, 10, 9, 8, 6, 5.1, 3, and 2.2.
3.2 Uncertainty of fit parameters and features
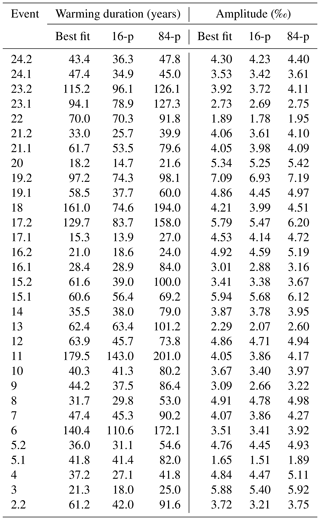
From the best fit, we estimate the uncertainty of each parameter via bootstrapping, as explained in Appendix C. Distributions of the parameters for DO event 20 are shown in Fig. 3. Table 3 lists the durations and amplitudes of the warmings for each event along with a bootstrap confidence interval consisting of the 16th and 84th percentiles, which would correspond to the ±σ range if the distributions were Gaussian. The actual distributions are often skewed so that the best-fit values lie close to the edges of the confidence intervals or even outside the intervals.
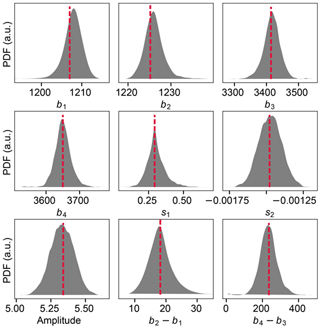
Figure 3 Gaussian kernel density of the model parameters and some derived quantities for the DO event 20 after 5000 iterations of the bootstrap resampling procedure. The parameter values for the best fit, as reported in Sect. 3, are indicated with red dashed lines. The amplitude feature is given by s1(b2−b1).
The uncertainty varies from event to event. In the case of the warming durations, the average bootstrap standard deviation is 20.0 years, with a minimum of 3.4 years for GI-16.2 and a maximum of 57.4 years for GI-18. Shorter warmings typically also have smaller uncertainties. As a comparison, the durations of the rapid coolings at the end of an interstadial have a larger uncertainty of 53.6 years. This is expected because the rapid cooling is typically less well pronounced in the record compared to the rapid warming. The coolings also have a larger spread in the bootstrap standard deviations, with a minimum of 4.6 years for GI-16.2 and a maximum of 209.9 years for GI-23.1. Similarly, the onset times of the rapid warmings have an average bootstrap standard deviation of 11.4 years, whereas the stadial onsets have a corresponding average uncertainty of 31.7 years.
3.3 Comparison of NGRIP and GRIP records
As a complementary approach to assess the uncertainties of the features, we compare them to those derived in the same way from another Greenland ice core. We chose the δ18O record of the GRIP ice core, which is measured at a similar resolution to the NGRIP record and has been transferred to the GICC05 timescale starting at the onset of GI-23-1. We fit the record with 40 iterations of our algorithm using the same constraints and hyperparameters. Again, the algorithm converges to a consistent fit, wherein each of the events is well approximated by a sawtooth shape. We now describe how well the features of NGRIP and GRIP correspond for the 26 mutual events starting at GS-22.
For the gradual cooling rates we find rp=0.64 and rs=0.65. Here, the discrepancy is only due to a handful of short events that show a clear linear cooling slope in one record but are more plateau-like in the other. This happens for the interstadials 18, 16.2, and 5.1, which do not show a slope in GRIP, and 17.2, which does not show a strong slope in NGRIP. Removing these events yields rp=0.97 and rs=0.98. The warming durations yield rp=0.55 and rs=0.63. There are no outliers, but there is a rather large spread, indicating that the warming duration is a less robust feature compared to the cooling rate. With 69 years on average, the GRIP warmings are 8 years shorter than in NGRIP. The average absolute deviation of warming durations in the two cores is 31 years, with a maximum discrepancy of 103 years for GI-10, with 40 years in NGRIP and 143 years in GRIP. Such deviations can arise if there is a slight step in the record before the most rapid warming and the algorithm includes this in the fit.
The warming amplitudes are very well correlated with rp=0.87 and rs=0.83. The average amplitude of 3.87 ‰ in GRIP is 0.45 ‰ lower than in NGRIP. The stadial levels are also well correlated with rp=0.78 and rs=0.66. There is a quite consistent offset between the cores of 1.84 ‰ due to differences in altitude and latitude of the GRIP and NGRIP sites. Exceptions include GS-21.1, which does not follow the offset but is at a similar level in both GRIP and NGRIP, and GS-14, which is difficult to define and thus vulnerable to give different results due to different noise in the cores.
The rapid cooling durations, i.e., b4−b3, show an average absolute deviation between the two cores of 59 years, with rp=0.46 and rs=0.53. This corroborates the fact that this feature is harder to define than the rapid warmings. The break points b3 and b4 are very susceptible to noise and can yield qualitatively different results for different cores. As a result, the abrupt cooling of GI-19.2 lasts 208 (20) years in GRIP (NGRIP), and for GI-12 it lasts 294 (9) years in GRIP (NGRIP). Conversely, the abrupt coolings of GI-19.1, GI-10, and GI-6 last much longer in NGRIP, with 62, 160, and 120 years in NGRIP versus 2, 5, and 2 years in GRIP, respectively. Consequently, we do not report any results concerning the rapid cooling period in this paper.
The stadial and interstadial durations are very well correlated with rs=0.99 and rs=0.97, respectively. The average absolute deviation is 59 years for interstadials and 73 years for stadials, which is small compared to the average durations. The biggest discrepancies between the two cores come from the indeterminacy in the rapid coolings of certain events, as described above.
In summary, the uncertainties obtained by bootstrapping and by comparison with the GRIP ice core are compatible, giving confidence in the estimates of the former method. The average bootstrap standard deviation of rapid warming and cooling durations is 20 and 54 years, respectively. This compares well to the average absolute deviation between GRIP and NGRIP of warming and cooling durations of 31 and 59 years, respectively. The discrepancy of 31 years for warming durations also includes a systematic bias of warmings that are 8 years longer on average in GRIP. Thus, the unbiased uncertainty is likely even closer to the one obtained by bootstrapping. Shorter-timescale features like rapid warming durations are not fully representative for every single event in one core. However, the overall trends are consistent, as seen by significant correlation. Features on a longer timescale, such as most of the cooling slopes and stadial levels, as well as the stadial and interstadial durations, are clearly representative.
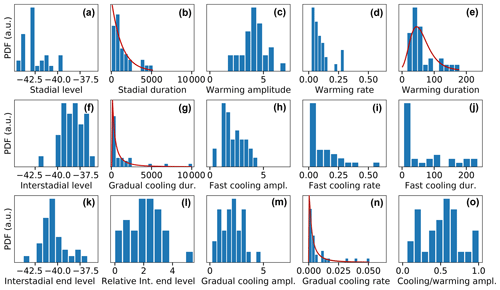
Figure 4 Histograms of our sample of 31 events for all features considered in this study, as defined in Table 1. The red curves in (b) and (e) are fits with the exponential and Gumbel distributions, respectively, whereas those in (g) and (n) are fits with the lognormal distribution.
In Fig. 4 we show histograms of all the DO event features derived from the fit parameters that we consider in this study, as defined in Sect. 2.3. The histograms show that the features have different types of distributions. Whether an event feature should be considered an independent sample from a distribution depends on whether it shows a significant trend over time. If we consider the event-wise sequence of one feature to be an evenly spaced time series we can calculate the autocorrelation and determine by a permutation test whether the value at a given lag is significantly larger than what could be expected in an uncorrelated sample for a given confidence. By considering autocorrelations up to lag 5, we find that the three different levels (stadial, interstadial, and level before rapid cooling) show significant autocorrelation at 95 % confidence until a lag of 3. We also find significant autocorrelation for four other features at only one specific lag value each, which we believe are false positives. When independently testing the hypothesis of significant autocorrelation at 95 % confidence for 15 different time series (features) at 5 lags, there is an expected value of 3.75 false positives. The corresponding data are shown in Fig. S3. As a result, in most cases we can consider the features of each event to be independent samples. This helps to assess the significance of correlations between features with permutation tests. A general overview of the correlations between different features and forcings can be seen in Fig. 5 and is explained further in Appendix D. The most important results of our statistical analysis are presented in the following sections.
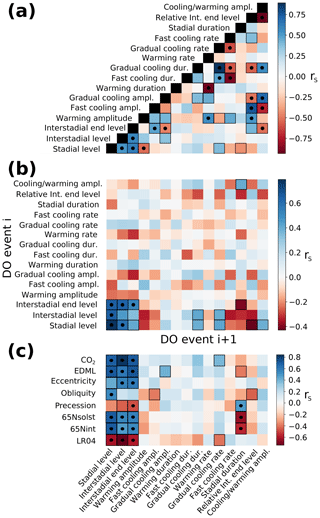
Figure 5 Spearman correlation heat map of (a) pairs of features within the same DO cycle, (b) pairs of features in adjacent DO cycles, and (c) pairs of one feature and one external forcing at the relevant time point of the feature. Correlations that are significant at 95 % (99 %) according to a permutation test are highlighted with a black frame (dot).
4.1 Interstadial periods
4.1.1 Relationship of cooling rates, amplitudes, and durations
We focus on the factors influencing the durations of the interstadial periods . In our fit, these durations are furthermore defined by , where A is the amplitude and λc the rate of the gradual cooling. If for every interstadial the gradual cooling were perfectly linear and the jump to stadial conditions always occurred after the same amplitude of cooling , the duration would be inversely proportional to the cooling rate . Conversely, if the interstadials had a fixed cooling rate and the jump to stadial conditions happened after variable cooling magnitudes, the durations would be proportional to the cooling amplitudes .
We test which of the two scenarios is better supported by the data. This depends on whether the cooling amplitudes or the cooling rates have a larger spread than the other. The coefficient of variation for the amplitudes is CV = 0.51, whereas for the rates we find CV = 1.49. The correlation of durations and cooling rates () is clearly significant given the sample size of 31 events and weak autocorrelation of the sequence of interstadial durations and rates. This confirms and extends the finding by Schulz (2002) to the whole glacial period. On the other hand, for durations and cooling amplitudes we find rs=0.40, which is mainly due to two outliers: the two longest interstadials GI-23.1 and GI-21.1. Removing these reduces the correlation to rs=0.30, which is not significant at 95 % confidence. As a result, there is no relationship between durations and amplitudes that goes beyond outlier events as opposed to durations and cooling rates. Furthermore, the correlation of cooling amplitudes and rates is not significant.
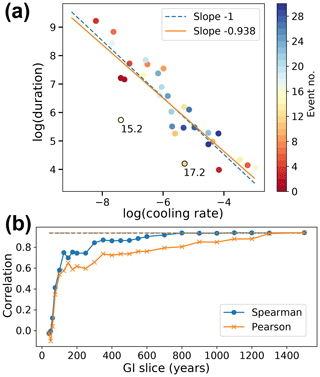
Figure 6 (a) Scatterplot of the logarithms of interstadial durations and cooling rates. The color coding indicates the temporal sequence of the events starting with GI-24.2 as event 0. Two linear fits obtained by ordinary least squares are shown. For one of them we fixed the slope to −1 and varied only the intercept. (b) Correlation coefficients of the logarithms of interstadial duration and the linear slope fitted to a slice of the beginning of the interstadial as a function of the length of that slice. The values of the Spearman (Pearson) correlation coefficients using slopes obtained from the full interstadials are marked with a dashed (dotted) line.
In Fig. 6a we show a scatterplot of log λc and log DI along with a linear regression yielding a slope of −0.94. The 95 % confidence interval of this slope obtained via bootstrapping is [−1.12, −0.75]. Because we do not account for errors in the rates estimated from the data the regressed slope is biased towards 0 due to attenuation and the true slope will be closer to −1. The model is consistent with the data, wherein the spread is caused by the fact that the jump back to stadial conditions happens after varying cooling amplitudes, which have a mean of 2.04 and standard deviation of 1.04.
4.1.2 Distribution of interstadial cooling rates and durations
The relationship between interstadial durations and cooling rates also manifests itself in the respective distributions. As seen in Fig. 4g and n, both features are strongly skewed. Both are consistent with lognormal distributions, with p=0.47 and p=0.89 for durations and rates, respectively. A fit with this distribution is illustrated in the figure. Because the two features are approximately inversely related with , the fact that one is a lognormal random variable implies that the other is, too. If DI is distributed lognormally with parameters μ and σ, then follows a lognormal distribution with parameters and σ. In our data this relation holds: we estimate μ and σ from the data DI and use the observed average amplitude . The data are consistent (p=0.33) with a lognormal distribution, with and σ.
As opposed to other skewed distributions like exponential, Gumbel, and power law, both durations and cooling rates are also consistent with an inverse Gaussian distribution. The observation that the durations and rates and are both well fitted by the inverse Gaussian despite their inverse relation is explained by the similar shape of the reciprocal inverse Gaussian distribution. If a variable is inverse Gaussian X∼IG(x), then the distribution of is reciprocal inverse Gaussian . A moderately sized sample of Y is still likely to be consistent with an inverse Gaussian distribution due to the similarity of the two. The inverse Gaussian could make an appealing model for the interstadials, since it arises as a distribution of first hitting times at a constant level for Brownian motion with a constant drift. However, the proxy time series in interstadials look qualitatively different than what is expected from this model because they are quite linear and yet have strongly varying slopes. In order for the model to produce roughly linear time series, the drift has to be high, which results in very similar slopes of the time series with the resulting distribution of first hitting times converging to a Gaussian. We leave a further discussion on which mechanism could yield lognormal or inverse Gaussian distributions of durations or cooling rates for upcoming studies. Instead, in the following we focus on implications of the approximate linearity of the interstadial time series.
4.1.3 Predictability of interstadial durations
The strong relationship of interstadial durations and cooling rates might have some implications for DO event dynamics. If the durations are correlated more strongly with the cooling rates than with the amplitudes, they can already be approximately predicted as soon as the rate is established, which might happen early in the interstadial. To test this, we take small slices of the beginnings of each interstadial, fit a linear slope s to them, and then calculate how well these slopes correlate with the durations of the full interstadials as we increase the length of the slices. Due to noise in the beginning of the interstadials, for some interstadials a small positive slope is detected. We set these slopes instead to because in our analysis we use the logarithms of slopes and durations. For the relatively short events 15.2 and 17.2, no negative slopes are obtained when fitting the whole interstadial part independently as opposed to the slopes obtained in the fit of the entire time series. We thus have to exclude these two outliers in the following. In Fig. 6b we show how the correlation between the logarithm of the slopes of these slices and the durations log DI evolves as we increase the length of the slices. The correlation of the slopes estimated from the full interstadials and the durations, when excluding events 15.2 and 17.2, is rs=0.94 (rp=0.94) and is indicated by a dashed (dotted) line. We can see that the correlation rapidly increases up to a length of 150 years. Thereafter the correlation stabilizes until another more rapid increase at 350 years. The rapid increase in correlation is partly due to a non-negligible number of events already being at full length (6 events at 150 years and 12 events at 350 years). Still, the slopes of the remaining events also correlate well with the durations. At 350 years, the correlation of the durations with the slopes estimated from the slices is almost as good as with the slopes from the full interstadials. There remain a handful of longer interstadials (23.2, 22, 14, and 11) that do not settle to a clear negative slope after 350 years. For the latter three events, this is due to sub-events that occur shortly after the interstadial onset.
Our interpretation is that the cooling rate is an indicator of a timescale of large-scale climate reorganization, which can already be measured relatively early in the interstadial and which remains approximately constant. Although we can see that there are exceptions, we conclude that for most events the interstadial duration can be predicted a few hundred years after the rapid warming. Some of the unexplained variance of this prediction is due to other factors influencing the interstadial duration that are not diagnosed by the linear cooling rate but, e.g., by the cooling amplitude.
4.1.4 Influence of external forcing
Given the previous result, we investigate whether the variability in the timescale associated with the cooling rate can be explained by other features of the DO cycles or by external forcing. Among correlations of the cooling rates with other features deemed significant by a permutation test, none are relevant, either because they are caused by a few outliers or else directly due to their definition and parameter constraints.
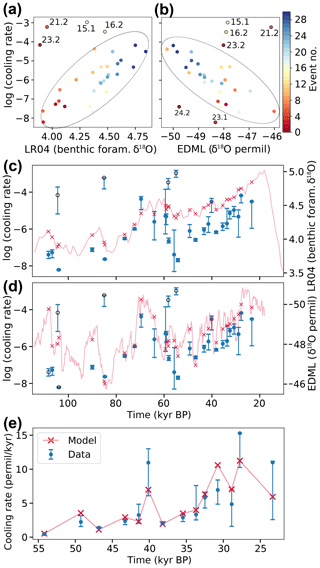
Figure 7 (a–b) Scatterplot of the logarithm of the interstadial cooling rates and (a) LR04 and (b) EMDL at time points corresponding to the interstadial onsets. (c) Time series of the cooling rates (dots) and the LR04 stack (crosses). The error bars on the cooling rates are given by the 16th to 84th percentile obtained by bootstrapping. (d) Time series of the cooling rates (dots) and the EDML stack (crosses). Note the inverted axis for EDML. (e) Time series of the interstadial cooling rates starting at GI-14 and of a linear regression model of the CO2 record fitted to the logarithm of the cooling rates.
Considering external climate factors, we find rs=0.40 and rp=0.35 for the logarithm of the cooling rates with LR04 at the time of the interstadial maximum. This correlation is, however, influenced by a common trend of the two quantities and is not significant anymore at 90 % confidence when removing a linear trend. On the other hand, there is a large subset of events that appears to be linearly related.
As shown in Fig. 7a and c, the furthest outliers from an approximate linear relationship are the interstadials 23.2, 21.2, 16.2, and 15.1. Removing these outliers yields rp=0.79, which clearly goes beyond a common trend with rp=0.63 after linearly detrending. For the younger half of the record starting with GI-14 we find rp=0.84, corresponding to the finding by Schulz (2002), who reports that the interstadial cooling rates starting from GI-14 are forced by global sea level. We note, however, that the correlation after GI-14 is largely due to a common trend, as we find rp=0.37 after linear detrending, which is not significant at 90 % confidence. Nevertheless, as shown above, when discarding a few outliers there is evidence for significant correlation as we include older parts of the record.
A better predictor of the interstadial cooling rates of the more recent DO cycles is given by the CO2 composite record. Whereas for the older half of the glacial there is no significant correlation, when starting at GI-14, we find and after linear detrending. In Fig. 7e we illustrate how well the cooling rates of this period can be predicted from CO2 by linearly regressing CO2 onto the logarithm of the cooling rates and then exponentiating the result.
Additionally, in a subset of the events, there is a linear relationship between the logarithm of the cooling rates and EDML at the interstadial onsets. While the entire dataset is not significantly correlated at 90 % confidence ( and ), removing events 24.2, 23.2, 23.1, 21.2, 16.2, and 15.1 yields an approximately linear relationship, as indicated in Fig. 7b and d. The correlation then becomes and or and after linearly detrending, which is significant at 99 % confidence. Thus, in this subset there is evidence for anticorrelation beyond a simple linear trend. Again, the linear relationship is strongest for the younger half of the record, which starts at GI-14 and does not have outliers. Here, we find and after linearly detrending, which is significant at 99 % confidence.
A corresponding linear relationship between the logarithms of interstadial durations and Antarctic temperature in different ice cores has been noted before by Buizert and Schmittner (2015). In our data we find rp=0.29 and rs=0.27 for these quantities, which is not significant at 90 % confidence. This disagreement comes from the fact that Buizert and Schmittner (2015) view each of the interstadials 24, 23, 21, 17, 16, 15, and 2 as one event, whereas we consider these as two events each, as suggested by the analysis of Rasmussen et al. (2014). Removing the events 24.2, 23.2, 23.1, 21.2, 17.2, 16.2, and 15.1 yields a strong linear relationship of rp=0.91, comparable to the findings by Buizert and Schmittner (2015). It is robust to linear detrending with rp=0.87. Most of these outliers are very short events, and discarding them removes a lot of the variability of the interstadial durations, similar to lumping them together with adjacent longer events.
4.2 Stadial periods
4.2.1 Stadial duration distribution
The stadial periods are defined to start after the rapid cooling and end at the onset of the rapid warming, and their duration is thus b1. Due to this definition GS-24.2 is exceptionally short with 20 years, as the proxy shows rapid warming again right after the rapid cooling without stabilizing. Thus, the durations are highly variable, ranging up to 5169 years for GS-19.1, with an average of 1328 years. The distribution is skewed, as seen in Fig. 4b, where an exponential fit is also given. The data are consistent with an exponential (p=0.79) and a lognormal distribution (p=0.18). Among these two distributions, the exponential is preferred by a relative likelihood test by a factor of 16. This distribution is relevant for climate dynamics, as it arises in the low noise limit of noise-induced escape times from asymptotically stable equilibria in dynamical systems (Day, 1987).
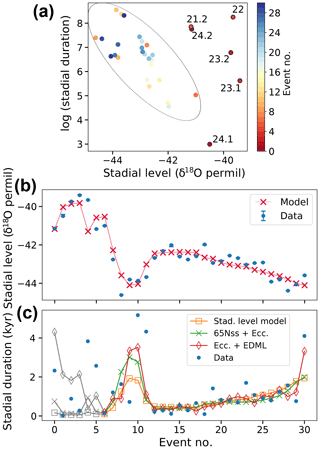
Figure 8 (a) Scatterplot of stadial levels and logarithmic durations. Outliers from an approximate linear relationship are labeled. (b) Event series of observed stadial levels and those modeled by , where X1 is 65Nint and X2 the eccentricity. (c) Models predicting the observed stadial durations (crosses). The first six events, indicated by gray markers, were discarded when fitting the models. The model based on predicted stadial levels from insolation (squares) is given by . The second model (circles) is given by , where X1 is 65Nss and X2 eccentricity. The third model (diamonds) is given by , where X1 is EDML and X2 eccentricity.
4.2.2 Influence of stadial levels and forcing on durations
In the following we discuss whether the stadial duration variability is influenced by other features in the data or external factors. Among external factors, the durations are best correlated with 65Nss (). The only DO feature that is significantly and robustly correlated with the durations is the stadial levels with . In Fig. 8a we plot the stadial levels against the logarithms of the durations. If one discards the first six events of the record, there is a linear anticorrelation of or after linear detrending. This could be either due to common forcing or a direct influence on the durations.
While the stadial levels correlate well with LR04 and EDML due to a common linear trend, there is better correlation with insolation, as seen by rp=0.60 for 65Nss. Removing the outliers GS-24.2 and GS-22 yields rp=0.82, which does not change when linearly detrending. To see whether this forcing explains most of the correlation of durations and levels, we remove a linear fit to 65Nss from each variable and find . Even though the significance of this correlation is unclear due to the autocorrelation of the stadial levels, this could imply that there is more information in the stadial levels about the durations than simply common insolation forcing. On the other hand, insolation components in addition to 65Nss might explain more of the observed variability.
We investigate whether multiple linear regression models with two predictors explain the stadial levels and durations better. A model comprised of 65Nint and eccentricity determines the levels very well (R2=0.86), as shown in Fig. 8b. These modeled levels correlate well with the logarithm of the stadial durations ( when excluding the earliest six events). As model for the durations, we linearly regress the modeled levels onto the log durations and exponentiate. In Fig. 8c the result is compared to two other models that directly regress external forcings on the log durations. None of the models fits the first six events adequately. Thereafter, all three models produce a similar trend. The model based on predicted stadial levels, and a model with direct forcing by 65Nss and eccentricity, shows similar skill with R2=0.29 and R2=0.30, respectively. The third model based on eccentricity and the EDML record is slightly better with R2=0.46, mainly because it fits two of the longest stadials better. Still, all of the models only fit the overall trend, on top of which variability is left unexplained. Unless the correlation is nearly perfect, a linear correlation of the logarithm still leaves a lot of room for scatter in the original scale.
The exponential tail in the variability of the stadial durations is not a result of the modulation by the external forcings we consider. To demonstrate this, we remove the forcing influence by fitting a linear model of one or more forcings to the log durations. Detrended data are obtained by adding the mean of the logarithmic data to the residuals of the fit and then exponentiating. When using 65Nss as forcing, we find p=0.15 for the exponential distribution. With the model of both eccentricity and 65Nss, as introduced above, we find p=0.29. Thus, the distribution of the detrended data is still long-tailed and consistent with an exponential distribution.
4.2.3 Are stadials with Heinrich events special?
Besides DO events, Heinrich events are the other major mode of glacial millennial-scale climate variability. They correspond to massive discharges of ice-rafted debris found in ocean sediment cores (Heinrich, 1988), with large climatic impacts that are well documented in numerous proxy records at various locations. While constraints on their duration and timing need to be improved, we follow Seierstad et al. (2014) for the temporal link of Heinrich events and the GICC05 chronology. This yields the set of Heinrich events H2, H3, H4, H5a, H5, H6, H7a, H7b, and H8, which overlap stadials 3, 5.2, 9, 13, 15.1, 18, 20, 21.1, and 22, respectively. Since some Heinrich events are less established in the community, we also look at the reduced set of H2, H3, H4, H5, and H6.
We test whether these “Heinrich stadials” have significantly different properties than the remaining stadials, such as longer durations, by randomly sampling nine stadials (five for the reduced set) from the entire set without replacement and calculating the mean duration of this subset. This is repeated until we can estimate the probability of trials yielding a higher mean duration than the actual set of Heinrich stadials. If this is less than 5 % (corresponding to p=0.05) we reject the hypothesis that Heinrich stadials have the same mean duration as the remaining stadials at 95 % confidence. This test gives essentially the same results as a one-sided t test.
For the full (reduced) set of Heinrich events we find p=0.028 (p=0.022). It is not obvious whether this should be considered significant in the sense of a hypothesis that Heinrich events prolong stadials. A better statistical test is needed, since if the events were to occur randomly during the course of stadials they would naturally be found preferentially in longer stadials. We leave a resolution of this for upcoming work. Based on the idea that Heinrich stadials are colder than normal, a test on the stadial levels yields p=0.052 (p=0.047). Again, this is probably not significant since Heinrich events mostly occur in the younger glacial with generally lower levels. We can reject the notion that DO events following Heinrich events are “stronger”. A test on the DO warming amplitudes yields p=0.102 (p=0.472), whereas a test on the interstadial durations yields p=0.403 (p=0.583). This might depend on the precise timing of H3, which in our analysis precedes the especially weak GI-5.1.
4.3 Abrupt warming periods
4.3.1 Warming durations
The rapid warming transitions in NGRIP as determined by our method have an average duration of 63.2 years. There is a large spread, with a minimum duration of 15.3 years for GI-17.1 and a maximum of 179.5 years for GI-11, but there is no clear trend, as we find both short and long warmings in early and later parts of the record. The distribution is skewed as seen in Fig. 4e. Five transitions last over 100 years (interstadials 6, 11, 17.2, 18, 23.2). For each of them there is not only a single abrupt warming, but also a systematic departure from stadial to warmer values before, as can be seen in Fig. S1 in the Supplement. Our algorithm includes these early trends in the warming transition. Other methods to define the abrupt warmings might give different results in these cases. Rousseau et al. (2017) define the transition onsets via the derivative, and consequently the transitions into interstadials 6 and 11 are reported as much shorter. Given our definition of abrupt warmings, we can at least argue that the longest warming transitions are not a result of local noise, because in our fit of the GRIP record the same transitions are also among the longest and clearly above average.
In our analysis we cannot identify any DO cycle features, external forcings, or combinations thereof that explain a significant part of the variability in the warming durations. Thus, we aim to infer something about the mechanism of the warming transitions from the distribution of their durations. The lognormal (p=0.63), Gumbel (p=0.053), and inverse Gaussian (p=0.95) distributions cannot be rejected at 95 % confidence by the data. A fit with the Gumbel distribution is illustrated in Fig. 4e. The relative likelihood of the Akaike information criterion shows that the inverse Gaussian distribution is 9.7 times more likely than the Gumbel distribution, and the lognormal distribution is 7.6 times more likely than the Gumbel distribution. We cannot choose between lognormal and inverse Gaussian with any confidence.
4.3.2 A model for the stadial–interstadial transition
In the following we compare the warming durations to what is expected in the framework of noise-induced transitions in multi-stable systems. The DO warmings are much shorter than the time spent in the stadial state. If we consider the stadial–interstadial transition as a noise-induced transition from one metastable state to another, starting at the stadial onset, most of the time is spent in the vicinity of the stadial state. The part of the trajectory that leaves this vicinity for the last time and then moves towards the other state (interstadial) is referred to as the reactive trajectory. Because of the high noise level in the record, an unknown part of which is non-climatic or regional and changes over time, we do not estimate reactive trajectories by defining neighborhoods of two metastable states. Instead, we believe the warming periods obtained by our piecewise linear fit are reasonable estimates. Figure 9a illustrates the reactive trajectory (green) leading up to GI-20. In Fig. 9b the different parts of this stadial–interstadial transition are projected onto an arbitrary potential that features two metastable states. For overdamped motion driven by additive noise in such a potential, it has been proven that the reactive trajectory durations converge to a Gumbel distribution in the zero noise limit (Cérou et al., 2013). Similarly, there is numerical evidence for the Gumbel distribution applying to one-dimensional spatially extended systems for low noise (Rolland et al., 2016). Because in our data we cannot separate the true climatic noise potentially driving the observed large-scale climate transitions from other types of noise, it is hard to say whether a low noise condition is met and a Gumbel distribution should be expected.
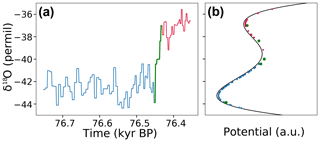
Figure 9 (a) Stadial–interstadial transition leading up to GI-20 (red), including our estimate of the so-called reactive part of the trajectory (green) preceded by 350 years of the stadial GS-21.1. (b) Data points of the same time series projected onto an arbitrary one-dimensional potential function with two minima as a conceptual model for the transition.
With a small numerical experiment we address the case of finite noise levels and small sample sizes. We use stochastic motion in a double-well potential as a generic model for a noise-induced transition from one metastable state to another. It is given by the stochastic differential equation , with the potential and the Wiener process Wt. For zero noise, there are two fixed points at and x=1. We initialize the system at and repeatedly collect reactive trajectories, which start when they last leave and end as they enter x>0.9. Small samples of 31 reactive trajectory durations are indeed typically consistent with a Gumbel distribution for a range of different noise levels, but they can be consistent with other distributions, too.
To show this, we collect p values of AD tests on many small samples. For the Gumbel distribution at a low noise level of σ=0.00045, 96.3 % of the p values are above 0.05. Thus, in this case, very rarely is a sample of 31 reactive trajectory durations rejected by a hypothesis test on the Gumbel distribution. For a higher noise level of σ=0.5, 80.1 % still yield p>0.05. However, the lognormal distribution fits equally well, with 95.4 % (93.6 %) yielding p>0.05 for σ=0.00045 (σ=0.5). The distribution that most reliably fits the data is the inverse Gaussian, with >99.9 % (>99.9 %) yielding p>0.05 for σ=0.00045 (σ=0.5), despite the fact that in the zero noise limit the correct distribution is Gumbel. It has been noted that the inverse Gaussian also fits well for large sample sizes (Cérou et al., 2011). Even a non-skewed distribution can be consistent with the samples, as seen for the Gaussian distribution, with 55.1 % (22.8 %) yielding p>0.05 for σ=0.00045 (σ=0.5). Similar values are obtained for the logistic distribution.
This implies that a small sample of 31 reactive trajectories cannot reliably identify the true distribution and thus a potential mechanism. Still, the data are at least consistent with the expected behavior of noise-induced escape from a metastable state. Other simple mechanisms can be consistent with the data, too. For example, as mentioned above, the inverse Gaussian is the distribution of time elapsed for a Brownian motion with drift to reach a fixed level.
4.3.3 Warming amplitudes
The average amplitude of the warmings is 4.2 ‰, with most events clustering around this value. The most extreme values are 7. ‰ for GI-19.2 and 1.7 ‰ for GI-5.1, which is almost not visually discernible as an event in the δ18O series. The warming amplitudes anticorrelate with the preceding stadial levels. When discarding GI-5.1, this is significant at 99 % confidence with , which is largely due to GI-19.2 being preceded by a very deep stadial, and GS-23.1 and GS-22, which are preceded by very shallow stadials, as they happen early in the glacial. When discarding these events the remaining correlation is still significant at 99 % confidence with rs=0.50. Thus, to some degree, the warming amplitudes are predictable in a statistical sense: when residing in a shallow stadial, the amplitude of the next DO warming will be small, and vice versa for a deep stadial. We also assess whether the variability can be explained by external forcing. Our analysis does not show a relationship between the DO amplitudes and global ice volume (LR04), as has been proposed by McManus et al. (1999) and Schulz et al. (1999). It should be noted, however, that these studies have a quite different notion of DO event amplitudes. Our approach, based on fitting high-resolution data, seems well suited to estimate the actual amplitude of rapid transitions as opposed to low-pass filtering that reduces the amplitude of shorter events. Instead, we find a correlation with 65Nint of and , which is significant at 90 % confidence. However, the correlation is visually not striking. Removing GI-19.2, which occurs close to an insolation minimum, yields a correlation that is not significant at 90 % confidence.
This work presents a statistical analysis of DO event features based on best-fit parameters of a piecewise linear waveform to the NGRIP δ18O record. An assessment of the parameter uncertainties shows that some shorter-timescale features have to be taken with care, such as the rapid warming durations. Here, it is possible that not all individual values are reliable. However, a comparison with a fit to the GRIP record shows that the overall trends and distributions, also of the shorter-timescale features, are robust. Still, different methods or models to define the features might alter the results. As an example, our piecewise linear method yields quite different estimates of the abrupt warming durations compared to Rousseau et al. (2017), wherein abrupt warmings are defined by an estimated derivative of the time series. Our results have an average absolute deviation of 25 years (26 years) compared to their algorithmically (visually) determined warming durations starting at GI-17.1.
Furthermore, the work relies on the classification of Greenland ice core centennial to millennial variability into a set of DO events by Rasmussen et al. (2014). This classification includes short events such as 23.2 and 21.2, which occur early in the glacial and are surrounded by the longest interstadials, as well as 18, 17.2, and 15.2, which are short but do not show a clear gradual cooling. In our analysis, these interstadials frequently show up as outliers. Their presence either showcases the strong irregularity and variability of the processes underlying DO cycles or could indicate that the events are caused by a different trigger and do not represent large-scale reorganizations of the climate system in the same way as longer events. Some of our conclusions might change if all short events were systematically discarded. They do not appear to be local to Greenland, since they are seen in atmospheric methane records (Rhodes et al., 2017) and speleothem records from the Alps (Boch et al., 2011; Moseley et al., 2014) and Asia (Cheng et al., 2016). However, their significance in comparison to longer DO events is an open problem that needs to be evaluated as more precisely dated, high-resolution records from outside Greenland become available.
Our analysis suggests that the mechanisms underlying warming and cooling transitions are likely different due to contrasting statistical properties. The stadial duration distribution closely resembles an exponential, and its large dispersion cannot be explained by external forcing alone (Sect. 4.2.2). This is expected in systems with noise-induced escape from one metastable state to another (Sect. 4.2.1). Furthermore, the distribution of DO warming durations is also consistent with the durations of so-called reactive trajectories in noise-induced transitions (Cérou et al., 2013; Rolland et al., 2016) (Sect. 4.3.2). Thus, the stadial–interstadial transition, i.e., the stadial plus the rapid warming phase, is consistent with a noise-induced escape from a metastable state and thus with spontaneous, unforced climate transitions, such as the ones observed in Drijfhout et al. (2013) and Kleppin et al. (2015). However, evidence for a different scenario might arise with new data or analyses, as in the studies by Rypdal (2016) and Boers (2018), who suggest a bifurcation in a fast climate subsystem before DO warmings, evidenced by increases in high-frequency variance of the ice core record prior to some events. If this is the case, it would mean that the transitions are not purely noise-induced but predictable to some degree and potentially part of a self-sustained oscillation such as in the model experiments by Vettoretti and Peltier (2016) and Klockmann et al. (2018).
The situation is different for the interstadial–stadial transition. Although the interstadial durations are also highly variable, they are characterized by a roughly linear cooling with rates that correlate strongly with the durations. Because this correlation is much stronger than that of the durations and the amplitudes before the rapid DO coolings, the interstadial–stadial transition can be predicted to a good approximation as soon as the rates have stabilized, which happens within the first 150 to 350 years of the interstadial for most DO cycles (Sect. 4.1.3). We interpret this such that after interstadial onset a large-scale reorganization of the climate system takes place on a timescale, which, even though very different from event to event, can be inferred from the cooling rate and stays consistent throughout the interstadial. We suggest that this reorganization is a major driving force of the DO cycle because its timescale predicts with reasonable accuracy when the interstadial–stadial transition takes place, which as a result cannot be purely noise-induced.
External forcing might explain the large variability of this timescale, as proposed by Schulz (2002), who argues that the interstadial cooling rates are controlled by global sea level in the younger half of the last glacial. For the older glacial, this relation is weak due to a number of outliers (Sect. 4.1.4). A physical pathway for such a forcing might be the influences of global ice volume on the strength and stability of the interstadial (strong) mode of the AMOC. However, climate model studies show that enlargement of Northern Hemisphere ice sheets actually enhances the stability of the strong AMOC state (Zhang et al., 2014; Ullman et al., 2014; Muglia and Schmittner, 2015). Intuitively, this would result in longer interstadials, which is in contrast to what the ice core data suggest. This has been addressed by Buizert and Schmittner (2015), wherein Southern Ocean processes are invoked to influence interstadial durations. We find that the correlation of Antarctic temperature and interstadial duration reported in this study is only valid if certain outliers are discarded. Finally, for the younger half of the glacial starting at GI-14, we find that atmospheric CO2 is a much better predictor of the cooling rates. A sensitive dependence of the strong AMOC state on CO2 has been verified in model experiments by Kawamura et al. (2017). However, more experiments with an active carbon cycle are needed to clarify whether CO2 should be considered forcing or a response to the DO cycle. Yet another model showed that changes in CO2 could in fact even be the trigger of DO-type transitions (Zhang et al., 2017).
Thus, the influence of external forcing is different for stadial and interstadial periods, with more evidence for insolation forcing on stadials and ice volume or CO2 on interstadials, which is related to the findings by Lohmann and Ditlevsen (2018). Except for a common forcing envelope of stadial and interstadial levels, there is no strong relationship between features across the different periods of the DO cycle. As a result, our analysis allows for the interpretation of the DO cycle as a manifestation of an excitable system, as proposed by Ganopolski and Rahmstorf (2002) and Timmermann et al. (2003), with a noise-induced transition out of the stadial state to the marginally unstable interstadial state, and a deterministic excursion back to the stadial state. However, the vastly different timescales for this excursion still need an explanation.
We developed a method to fit a continuous piecewise linear waveform to the entire last glacial NGRIP δ18O record that can fit a characteristic sawtooth shape to every DO event. However, we find that for many of the transitions this is ad hoc. Almost half of the events do not show a distinct and significant rapid cooling episode after the more gradual interstadial cooling. An analysis of the DO event features derived from the fit confirms the irregularity and randomness that is evident from visual inspection of the record. There is hardly any evidence for relationships linking the features that describe the stadial, interstadial, and abrupt warming periods, except for a common envelope that governs the stadial and interstadial levels via external forcing. A statistical analysis hints at different mechanisms underlying warming and cooling transitions. This follows from the distributions of the stadial and rapid DO warming durations, on the one hand, and the interstadial durations on the other hand. It is furthermore supported by the different importance of CO2, ice volume, and insolation forcing to explain the stadial and interstadial properties, as well as the fact that the interstadial durations can be predicted to some degree by the linear cooling rates shortly after interstadial onset.
This work is based on the high-resolution NGRIP oxygen isotope record of the entire last glacial period. The data up until 60 kyr BP are available at http://iceandclimate.nbi.ku.dk/data/NGRIP_d18O_and_dust_5cm.xls (last access: 20 September 2019) (NGRIP members, 2015), whereas the older parts of the record are currently in the process of being published by colleagues at Physics of Ice, Climate and Earth at the University of Copenhagen. Until then, the data can be requested from the authors. The insolation dataset 65Nint is publicly available as supporting online material to Huybers (2006) (doi:10.1126/science.1125249) and the orbital forcing parameters from Laskar et al. (2004b); 65Nss insolation is available at http://vo.imcce.fr/insola/earth/online/earth/earth.html (last access: 20 September 2019). The ice volume data from Lisiecki and Raymo (2005) are publicly available at https://doi.pangaea.de/10.1594/PANGAEA.704257 (last access: 20 September 2019). The Antarctic EDML oxygen isotope record is available at https://doi.org/10.1594/PANGAEA.754444 (last access: 20 September 2019) (EPICA Community Members, 2010), whereas the Antarctic composite CO2 record is available at https://www1.ncdc.noaa.gov/pub/data/paleo/icecore/antarctica/antarctica2015co2composite.txt (last access: 20 September 2019) (Bereiter et al., 2015b).

In the following, we detail the optimization procedure to find the best sawtooth-shaped fit for each event, i.e., line 18 of the algorithm above. To determine the six parameters at each transition, we minimize the root mean square deviation of the fit from the time series segment. Due to the high noise level, there are many local minima in this optimization problem. Thus, either a brute-force parameter search on a grid or an advanced algorithm is needed to find a global minimum. We chose an algorithm called basin-hopping, which is described in Olson et al. (2012) and is included in the Scientific Python package scipy.optimize, wherein it can also be customized. The basic idea of the algorithm is the following: given initial coordinates in terms of the parameter vector θ0, one searches for a local minimum of the goal function f(θ), e.g., with a Newton, quasi-Newton, or other method. The argument to this local minimum θn is then randomly perturbed by a kernel to yield new coordinates θ*, which are the starting point of a new local minimization. Next, there is a metropolis accept or reject step: we accept the argument of the local minimization θn+1 as new coordinates if the local minimum is deeper than the previous one , or else with probability , where T is a parameter relating to the typical difference in depth of adjacent local minima. Now we go back to the perturbation step either with old coordinates θn or, if accepted, with new coordinates θn+1 and repeat. The iterative procedure is repeated for a large number of iterations and the result is the argument to the lowest function value found.
Within basin-hopping, one has the freedom of choosing any local minimizer as well as a perturbation kernel. These have to be adapted to our optimization problem. We have several constraints on the parameters that need to be satisfied by the optimization. For instance, we demand that all segments of the fit are present and do not overlap (). Other constraints ensure that the characteristic shape of DO events is fit as well as possible for all events. Among other things, we thus demand the gradual slope to be significantly longer and less steep than the fast cooling transition at the end of an interstadial. An overview of all the constraints we used is given further below. To satisfy them, we chose a multivariate Gaussian perturbation kernel, which is truncated at the respective parameter constraints. The local minimizer choice requires further consideration. Our goal function landscape is very rough and not differentiable. Thus, methods like gradient descent give very poor results in our case. A method that does not depend on derivatives and can handle constraints is called constrained optimization by linear approximation (COBYLA), and we found it to work well in our case.
Two hyperparameters have to be specified in the basin-hopping algorithm: the variance of the perturbation kernel and the parameter T used in the metropolis criterion. These should both be comparable to typical differences in goal function (temperature) and arguments (perturbation width) of neighboring local minima in the minimization problem. We chose these parameters empirically by observing how the goal function changes as we slightly change the fit. Although this varies significantly from transition to transition, we determined single values as a compromise for all transitions. For the kernel variance in the directions of we chose a value of 15, and for s1 and s2 we chose 0.004 and 0.0015, respectively.
The following list contains all constraints used in the optimization problem in order to ensure convergence of the algorithm to a fit within the qualitative limits of the desired characteristic waveform. Specifically, constraints 3 and 4 shall guarantee that there is a distinction between gradual cooling and rapid cooling at the end of an interstadial. With these constraints we can prevent our algorithm from splitting an interstadial in half with two very similar slopes, which can easily happen because there are interstadials that arguably have a rather gradual cooling all the way down to the next stadial with no easily discernable steep cooling at the end. The lower limit of constraint 6 shall help to only fit to the steep part of warming transitions, which might have a slight warming prior to it. The upper limit of constraint 7 is needed in order to force a small negative slope on very short transitions that otherwise could also be viewed as plateaus.
-
No overlap of segments: b2>b1, b3>b2, and b4>b3.
-
Gradual slope cannot go below the following stadial level : .
-
Gradual slope must be twice as long as a steep drop: .
-
The drop at the end of the interstadial must be at least twice as steep as a gradual slope: .
-
The stadial period must not be shorter than 20 years: b1>20, b2>20, , and .
-
Limit the steepness of the up-slope (‰ yr−1): .
-
Limit the steepness of the down-slope (‰ yr−1): .
For the basin-hopping algorithm we use a multivariate Gaussian kernel of fixed variance with , , , , , and .
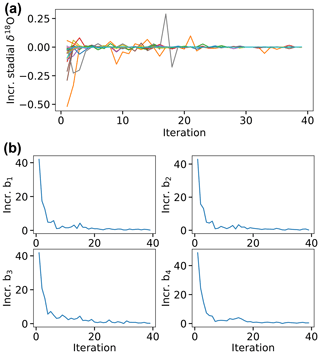
Figure B1 (a) Evolution of the incremental change in all stadial levels compared to the previous iteration for all 40 iterations of the fitting routine. (b) Average over all transitions of the incremental change (absolute value) in the break point parameters b1, b2, b3, and b4.
We repeatedly run our iterative fitting routine and monitor whether the individual parameters converge so that a consistent fit is obtained in the end. Critical for obtaining a consistent fit is that the stadial levels do not change substantially, as explained in the Methods section. In Fig. B1a we show the evolution over 40 iterations of the incremental deviations of the stadial levels compared to the previous iteration. Most stadial levels converge rapidly so that their increments stay below 0.05 ‰. Two short stadials keep fluctuating until around iteration 20 before they converge. Because of the convergence of stadial levels, we consider our fit to be consistent. Furthermore, the best-fit parameters are robust, which can be seen in Fig. B1b. Here, we show the average absolute incremental deviations to the break point parameters at each iteration. After 15 iterations the procedure is stable, with average incremental deviations of roughly 0.4 years for b1 and b2 to 0.5 years for b3 and b4, which result from the stochastic fitting algorithm. Note that these values are already well below the smallest sample spacing of the original unevenly spaced time series.
Because of the nature of the data, care has to be taken when generating synthetic data. The properties of the data change throughout the record and are also quite different between adjacent stadials and interstadials. Stadials have both a larger variance and a larger effective sample spacing in time than the interstadials. For this reason, synthetic data will be created for each stadial and interstadial period individually. The original data are unevenly spaced, which would provide difficulties on its own, while our data are nearest-neighbor interpolated and oversampled to a 1-year resolution. This means that there are typically multiple neighboring points with the same value, making it challenging to find a valid autoregressive or autoregressive moving-average (ARMA) model for the residuals to generate synthetic data. Instead, we use a block bootstrap resampling technique to keep all relevant structure in the data. We chose a simple block bootstrap whereby non-overlapping blocks of fixed length of the time series are randomly ordered because it preserves the correct mean of the individual stadial and interstadial residuals. More involved methods, such as the stationary bootstrap, could be applied, but it likely will not change any of our conclusions.
In the following, we present the procedure for uncertainty estimation. We denote the original data time series of a given transition as {Xt}, the fit obtained by the data as {Yt}, and the residuals to the fit as . We furthermore use the break points obtained in the fit of this transition.
-
Divide the residuals into four segments at the break points: for i=1…4, where b0=0. Denote the length of as ni.
-
For each segment, divide into ni∕l blocks of length l. Append remaining data points to the last block if ni∕l is a non-integer. The block length l is determined by the length of the segment, as explained below.
-
For each segment, randomly sample blocks without replacement and concatenate until all blocks have been used. This yields resampled segments .
-
Concatenate the four resampled segments and add the fit to get synthetic data
-
Fit to a piecewise linear model with the basin-hopping algorithm.
-
Repeat from step 2.
In order to also be able to resample the shortest segments, while also preserving the autocorrelative structure in all but the shortest segments, we choose the following scheme for the block length l: if the segment length ni is larger than 40 years, choose l=20. If choose l=10. If choose l=5. If ni<10 do not resample and simply return the original segment. The scheme has been determined by looking at the residuals of each segment in all transitions and observing that the autocorrelation drops to nonsignificant values for all segments after 10–15 years. It thus seems reasonable to use the same block length rule for all transitions and segments.
In the following, we give an overview of the pairwise correlations between different features and forcings. We show the Spearman correlation coefficients of all tests and their significance in Fig. 5. Considering Spearman correlations with p<0.05, we find 81 positives at 95 % and 50 positives at 99 % confidence, which is clearly more than expected by chance. However, as detailed in the Methods section, many of these are due to construction and will not be discussed here. We will furthermore omit correlations that are not robust due to the presence of outliers.
Among features within the same DO cycle, the three different levels yield a strong correlation with each other. However, the significance is overestimated due to their autocorrelation, and after linear detrending, the correlations are not significant anymore. Thus, the correlation comes mostly from a common trend associated with the evolution of the background climate state during the glacial. Furthermore, we find significant correlations of fast cooling, gradual cooling, and warming amplitudes, and a correlation of interstadial levels and gradual cooling amplitudes. This implies a certain consistency of DO cycles, wherein a large-amplitude warming is typically also followed by a large-amplitude cooling (gradual and/or fast). This is equivalent to the fact that the stadial levels are autocorrelated. In Sect. 4 we furthermore discuss the correlation of the gradual cooling durations with the gradual cooling amplitudes and rates, as well as the correlation of the stadials levels with the stadial durations and warming amplitudes.
For features in adjacent DO cycles, we do not expect any true positives a priori because no features are related by construction. Significant correlations at 99 % confidence are only found for the levels. Due to their autocorrelation, the significance determined by permutation tests are not reliable, however. Detrending shows that the correlations are dominated by a common linear trend due to the slowly changing background climate state. The remaining eight correlations significant at 95 % confidence could either be false positives or a result of common external forcing. This is because seven of the eight correlations involve the levels, which are clearly influenced by forcing, as detailed below.
We furthermore correlate the features with all forcings at the onset times of the respective periods within the DO cycles. The tests clearly indicate more significant correlations than expected by chance. However, due to autocorrelation, the significance is overestimated by permutation tests. In particular, the levels yield significant correlation with most forcings; however, both are autocorrelated. By linearly detrending and discarding outliers where necessary, we find that the interstadial levels are best correlated with LR04, EDML, and CO2, the interstadial end levels with 65Nss and precession, and the stadial levels with LR04, 65Nint, 65Nss, obliquity, and eccentricity. Additional significant correlations we found are discussed in Sect. 4 and include those of gradual cooling rates with the LR04 and CO2 forcings, as well as those of stadial durations and different insolation forcings.
The supplement related to this article is available online at: https://doi.org/10.5194/cp-15-1771-2019-supplement.
JL and PD designed the study, interpreted the results, and wrote the paper. JL performed the statistical analysis.
The authors declare that they have no conflict of interest.
We gratefully acknowledge discussions of this work with Sune O. Rasmussen.
This research has been supported by the Horizon 2020 Framework Programme, H2020 Marie Skłodowska-Curie Actions (grant no. CRITICS (643073)).
This paper was edited by Barbara Stenni and reviewed by two anonymous referees.
Bereiter, B., Eggleston, S., Schmitt, J., Nehrbass-Ahles, C., Stocker, T. F., Fischer, H., Kipfstuhl, S., and Chappellaz, J.: Revision of the EPICA Dome CO2 record from 800 to 600 kyr before present, Geophys. Res. Lett., 42, 542–549, 2015a. a
Bereiter, B., Eggleston, S., Schmitt, J., Nehrbass-Ahles, C., Stocker, T. F., Fischer, H., Kipfstuhl, S., and Chappellaz, J. A.: Antarctic Ice Cores Revised 800 KYr CO2 Data, available at: https://www.ncdc.noaa.gov/paleo-search/study/17975, Version date: 4 February 2015, 2015b.
Boch, R., Cheng, H., Spötl, C., Edwards, R. L., Wang, X., and Häuselmann, Ph.: NALPS: a precisely dated European climate record 120–60 ka, Clim. Past, 7, 1247–1259, https://doi.org/10.5194/cp-7-1247-2011, 2011. a
Boers, N.: Early-warning signals for Dansgaard-Oeschger events in a high-resolution ice core record, Nat. Comm., 9, 2556, https://doi.org/10.1038/s41467-018-04881-7, 2018. a
Buizert, C. and Schmittner, A.: Southern Ocean control of glacial AMOC stability and Dansgaard-Oeschger interstadial duration, Paleoceanography, 30, 1595–1612, 2015. a, b, c, d
Capron, E., Landais, A., Chappellaz, J., Schilt, A., Buiron, D., Dahl-Jensen, D., Johnsen, S. J., Jouzel, J., Lemieux-Dudon, B., Loulergue, L., Leuenberger, M., Masson-Delmotte, V., Meyer, H., Oerter, H., and Stenni, B.: Millennial and sub-millennial scale climatic variations recorded in polar ice cores over the last glacial period, Clim. Past, 6, 345–365, https://doi.org/10.5194/cp-6-345-2010, 2010. a
Cérou, F., Guyader, A., Lelièvre, T., and Pommier, D.: A multiple replica approach to simulate reactive trajectories, J. Chem. Phys., 134, 054108, https://doi.org/10.1063/1.3518708, 2011. a
Cérou, F., Guyader, A., Lelièvre, T., and Malrieu, F.: On the length of one-dimensional reactive paths, ALEA, Lar. Am. J. Probab. Math. Stat., 10, 359–389, 2013. a, b
Cheng, H., Edwards, R. L., Sinha, A., Spötl, C., Yi, L., Chen, S., Kelly, M., Kathayat, G., Wang, X., Li, X., Kong, X., Wang, Y., Ning, Y., and Zhang, H.: The Asian monsoon over the past 640,000 years and ice age terminations, Nature, 534, 640–646, 2016. a
Day, M. V.: Recent progress on the small parameter exit problem, Stochastics, 20, 121–150, 1987. a
Dokken, T. M., Nisancioglu, K. H., Li, C., Battisti, D. S., and Kissel, C.: Dansgaard-Oeschger cycles: Interactions between ocean and sea ice intrinsic to the Nordic seas, Paleoceanography, 28, 491–502, 2013. a
Drijfhout, S., Gleeson, E., Dijkstra, H. A., and Livina, V.: Spontaneous abrupt climate change due to an atmospheric blocking–sea-ice–ocean feedback in an unforced climate model simulation, P. Natl. Acad. Sci. USA, 110, 19713–19718, 2013. a, b
EPICA Community Members: Stable oxygen isotopes of ice core EDML, PANGAEA, https://doi.org/10.1594/PANGAEA.754444, 2010. a
Ganopolski, A. and Rahmstorf, S.: Rapid changes of glacial climate simulated in a coupled climate model, Nature, 409, 153–158, 2001. a
Ganopolski, A. and Rahmstorf, S.: Abrupt Glacial Climate Changes due to Stochastic Resonance, Phys. Rev. Lett., 88, 038501, https://doi.org/10.1103/PhysRevLett.88.038501, 2002. a
Gkinis, V., Simonsen, S. B., Buchardt, S. L., White, J. W. C., and Vinther, B. M.: Water isotope diffusion rates from the NorthGRIP ice core for the last 16,000 years – Glaciological and paleoclimatic implications, Earth Planet. Sc. Lett., 405, 132–141, 2014. a
Heinrich, H.: Origin and Consequences of Cyclic Ice Rafting in the Northeast Atlantic Ocean During the Past 130,000 Years, Quaternary Res., 29, 142–152, 1988. a
Henry, L. G., McManus, J. F., Curry, W. B., Roberts, N. L., Piotrowski, A. M., and Keigwin, L. D.: North Atlantic ocean circulation and abrupt climate change during the last glaciation, Science, 353, 470–474, 2016. a
Huybers, P.: Early Pleistocene Glacial Cycles and the Integrated Summer Insolation Forcing, Science, 313, 508–511, 2006. a
Johnsen, S. J., Clausen, H. B., Dansgaard, W., Gundestrup, N., Hammer, C. U., Andersen, U., Andersen, K. K., Hvidberg, C. S., Dahl-Jensen, D., Steffensen, J. P., Shoji, H., Sveinbjörnsdóttir, Á. E., White, J., Jouzel, J., and Fisher, D.: The δ18O record along the Greenland Ice Core Project deep ice core and the problem of possible Eemian climatic instability, J. Geophys. Res., 102, 26397–26410, 1997. a
Kageyama, M., Merkel, U., Otto-Bliesner, B., Prange, M., Abe-Ouchi, A., Lohmann, G., Ohgaito, R., Roche, D. M., Singarayer, J., Swingedouw, D., and X Zhang: Climatic impacts of fresh water hosing under Last Glacial Maximum conditions: a multi-model study, Clim. Past, 9, 935–953, https://doi.org/10.5194/cp-9-935-2013, 2013. a
Kawamura, K., Abe-Ouchi, A., Motoyama, H., Ageta, Y., Aoki, S., Azuma, N., Fujii, Y., Fujita, K., Fujita, S., Kotaro F., Furukawa, T., Furusaki, A., Goto-Azuma, K., Greve, R., Hirabayashi, M., Hondoh, T., Hori, A., Horikawa, S., Horiuchi, K., Igarashi, M., Iizuka, Y., Kameda, T., Kanda, H., Kohno, M., Kuramoto, T., Matsushi, Y., Miyahara, M., Miyake, T., Miyamoto, A., Nagashima, Y., Nakayama, Y., Nakazawa, T., Nakazawa, F., Nishio, F., Obinata, I., Ohgaito, R., Oka, A., Okuno, J., Okuyama, J., Oyabu, I., Parrenin, F., Pattyn, F., Saito, F., Saito, T., Saito, T., Sakurai, T., Sasa, K., Seddik, H., Shibata, Y., Shinbori, K., Suzuki, K., Suzuki, T., Takahashi, A., Takahashi, K., Takahashi, S., Takata, M., Tanaka, Y., Uemura, R., Watanabe, G., Watanabe, O., Yamasaki, T., Yokoyama, K., Yoshimori, M., and Yoshimoto, T. (Dome Fuji Ice Core Project Members): State dependence of climatic instability over the past 720,000 years from Antarctic ice cores and climate modeling, Sci. Adv., 3, e1600446, https://doi.org/10.1126/sciadv.1600446, 2017. a
Kleppin, H., Jochum, M., Otto-Bliesner, B., Shields, C. A., and Yeager, S.: Stochastic Atmospheric Forcing as a Cause of Greenland Climate Transitions, J. Climate, 28, 7741–7763, 2015. a, b
Klockmann, M., Mikolajewicz, U., and Marotzke, J.: Two AMOC States in Response to Decreasing Greenhouse Gas Concentrations in the Coupled Climate Model MPI-ESM, J. Climate, 31, 7969–7984, 2018. a, b
Laskar, J., Robutel, P., Joutel, F., Gastineau, M., Correia, A. C. M., and Levrard, B.: A long term numerical solution for the insolation quantities of the Earth, Astron. Astrophys., 261–285, 2004a. a, b
Laskar, J., Gastineau, M., and Joutel, F.: A long term numerical solution for the insolation quantities of the Earth, available at: http://vo.imcce.fr/insola/earth/online/earth/earth.html (last access: 20 September 2019), Version date: 17 November 2014, 2004b.
Li, C., Battisti, D. S., and Bitz, C. M.: Can North Atlantic Sea Ice Anomalies Account for Dansgaard–Oeschger Climate Signals?, J. Climate, 23, 5457–5475, 2010. a
Lisiecki, L. E. and Raymo, M. E.: Pliocene-Pleistocene stack of globally distributed benthic stable oxygen isotope records, PANGAEA, https://doi.org/10.1594/PANGAEA.704257, 2005.
Lohmann, J. and Ditlevsen, P. D.: Random and externally controlled occurrences of Dansgaard-Oeschger events, Clim. Past, 14, 609–617, https://doi.org/10.5194/cp-14-609-2018, 2018. a
Lynch-Stieglitz, J.: The Atlantic Meridional Overturning Circulation and Abrupt Climate Change, Annu. Rev. Mar. Sci., 9, 83–104, 2017. a
McManus, J. F., Oppo, D. W., and Cullen, J. L.: A 0.5-Million-Year Record of Millennial-Scale Climate Variability in the North Atlantic, Science, 283, 971–975, 1999. a
Moseley, G. E., Spötl, C., Svensson, A., Cheng, H., Brandstätter, S., and Edwards, R. L.: Multi-speleothem record reveals tightly coupled climate between central Europe and Greenland during Marine Isotope Stage 3, Geology, 42, 1043–1046, 2014. a
Muglia, J. and Schmittner, A.: Glacial Atlantic overturning increased by wind stress in climate models, Geophys. Res. Lett., 42, 9862–9869, 2015. a
NGRIP Members: High-resolution record of Northern Hemisphere climate extending into the last interglacial period, Nature, 431, 147–151, 2004. a
NGRIP members: NGRIP oxygen isotope record in 5 cm resolution, available at: http://iceandclimate.nbi.ku.dk/data/NGRIP_d18O_and_dust_5cm.xls (last access: 20 September 2019), Version date: 25 February 2017, 2014.
Olson, B., Hashmi, I., Molloy, K., and Shehu, A.: Basin Hopping as a General and Versatile Optimization Framework for the Characterization of Biological Macromolecules, Lect. Notes. Artif. Int., 674832, https://doi.org/10.1155/2012/674832, 2012. a
Petersen, S. V., Schrag, D. P., and Clark, P. U.: A new mechanism for Dansgaard-Oeschger cycles, Paleoceanography, 28, 24–30, 2013. a
Rasmussen, S. O., Bigler, M., Blockley, S. P., Blunier, T., Buchardt, S. L., Clausen, H. B., Cvijanovic, I., Dahl-Jensen, D., Johnsen, S. J., Fischer, H., Gkinis, V., Guillevic, M., Hoek, W. Z., Lowe, J., Pedro, J. B., Popp, T., Seierstad, I. K., Steffensen, J. P., Svensson, A. M., Vallelonga, P., Vinther, B. M., Walker, M. J. C., Wheatley, J. J., and Winstrup, M.: A stratigraphic framework for abrupt climatic changes during the Last Glacial period based on three synchronized Greenland ice-core records: refining and extending the INTIMATE event stratigraphy, Quat. Sci. Rev., 106, 14–28, 2014. a, b, c, d, e, f, g, h, i
Raymo, M. E. and Lisiecki, L. E.: A Pliocene-Pleistocene stack of 57 globally distributed benthic δ18O records, Paleoceanography, 20, PA1003, https://doi.org/10.1029/2004PA001071, 2005. a
Rhodes, R. H., Brook, E. J., McConnell, J. R., Blunier, T., Sime, L. C., Faïn, X., and Mulvaney, R.: Atmospheric methane variability: Centennial-scale signals in the Last Glacial Period, Global Biogeochem. Cy., 31, 575–590, 2017. a
Rolland, J., Bouchet, F., and Simonnet, E.: Computing Transition Rates for the 1-D Stochastic Ginzburg–Landau–Allen–Cahn Equation for Finite-Amplitude Noise with a Rare Event Algorithm, J. Stat. Phys., 162, 277–311, 2016. a, b
Rousseau, D.-D., Boers, N., Sima, A., Svensson, A., Bigler, M., Lagroix, F., Taylor, S., and Antoine, P.: (MIS3 & 2) millennial oscillations in Greenland dust and Eurasian aeolian records – A paleosol perspective, Quat. Sci. Rev., 169, 99–113, 2017. a, b, c
Rypdal, M.: Early-Warning Signals for the Onsets of Greenland Interstadials and the Younger Dryas–Preboreal Transition, J. Climate, 29, 4047–4056, 2016. a
Sadatzki, H., Dokken, T. M., Berben, S. M. P., Muschitiello, F., Stein, R., Fahl, K., Menviel, L., Timmermann, A., and Jansen, E.: Sea ice variability in the southern Norwegian Sea during glacial Dansgaard-Oeschger climate cycles, Sci. Adv., 5, eaau6174, https://doi.org/10.1126/sciadv.aau6174, 2019. a
Schulz, M.: The tempo of climate change during Dansgaard-Oeschger interstadials and its potential to affect the manifestation of the 1470-year climate cycle, Geophys. Res. Lett., 29, 1002, https://doi.org/10.1029/2001GL013277, 2002. a, b, c, d
Schulz, M., Berger, W. H., Sarntheim, M., and Grootes, P. M.: Amplitude variations of 1470-year climate oscillations during the last 100,000 years linked to fluctuations of continental ice mass, Geophys. Res. Lett., 26, 3385–3388, 1999. a
Seierstad, I. K., Abbott, P. M., Bigler, M., Blunier, T., Bourne, A. J., Brook, E., Buchardt, S. L., Buizert, C., Clausen, H. B., Cook, E., Dahl-Jensen, D., Davies, S. M., Guillevic, M., Johnsen, S. J., Pedersen, D. S., Popp, T. J., Rasmussen, S. O., Severinghaus, J. P., Svensson, A. B., and Vinther, M.: Consistently dated records from the Greenland GRIP, GISP2 and NGRIP ice cores for the past 104 ka reveal regional millennial-scale δ18O gradients with possible Heinrich event imprint, Quat. Sci. Rev., 106, 29–46, 2014. a
Svensson, A., Andersen, K. K., Bigler, M., Clausen, H. B., Dahl-Jensen, D., Davies, S. M., Johnsen, S. J., Muscheler, R., Rasmussen, S. O., Röthlisberger, R., Steffensen, J. P., Vinther, B. M.: The Greenland Ice Core Chronology 2005, 15–42 ka. Part 2: comparison to other records, Quat. Sci. Rev., 25, 3258–3267, 2006. a
Timmermann, A., Gildor, H., Schulz, M., and Tziperman, E.: Coherent Resonant Millennial-Scale Climate Oscillations Triggered by Massive Meltwater Pulses, J. Climate, 16, 2569–2585, 2003. a, b
Ullman, D. J., LeGrande, A. N., Carlson, A. E., Anslow, F. S., and Licciardi, J. M.: Assessing the impact of Laurentide Ice Sheet topography on glacial climate, Clim. Past, 10, 487–507, https://doi.org/10.5194/cp-10-487-2014, 2014. a
Vettoretti, G. and Peltier, W. R.: Thermohaline instability and the formation of glacial North Atlantic super polynyas at the onset of Dansgaard-Oeschger warming events, Geophys. Res. Lett., 43, 5336–5344, 2016. a, b
Zhang, X., Lohmann, G., Knorr, G., and Purcell, C.: Abrupt glacial climate shifts controlled by ice sheet changes, Nature, 512, 290–294, 2014. a, b
Zhang, X., Knorr, G., Lohmann, G., and Barker, S.: Abrupt North Atlantic circulation changes in response to gradual CO2 forcing in a glacial climate state, Nat. Geosci., 10, 518–523, 2017. a, b
- Abstract
- Introduction
- Methods and materials
- Piecewise linear fit of NGRIP record
- Statistical analysis of DO event features
- Discussion
- Conclusions
- Data availability
- Appendix A: Iterative algorithm to fit piecewise linear model
- Appendix B: Convergence of iterative fitting routine
- Appendix C: Uncertainty estimation of fitting parameters
- Appendix D: Correlation analysis of features and forcings
- Author contributions
- Competing interests
- Acknowledgements
- Financial support
- Review statement
- References
- Supplement
- Abstract
- Introduction
- Methods and materials
- Piecewise linear fit of NGRIP record
- Statistical analysis of DO event features
- Discussion
- Conclusions
- Data availability
- Appendix A: Iterative algorithm to fit piecewise linear model
- Appendix B: Convergence of iterative fitting routine
- Appendix C: Uncertainty estimation of fitting parameters
- Appendix D: Correlation analysis of features and forcings
- Author contributions
- Competing interests
- Acknowledgements
- Financial support
- Review statement
- References
- Supplement