the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
A clumped isotope calibration of coccoliths at well-constrained culture temperatures for marine temperature reconstructions
Ismael Torres-Romero
Madalina Jaggi
Stefano M. Bernasconi
Heather M. Stoll
Numerous recent studies have tested the clumped isotope (Δ47) thermometer on a variety of biogenic carbonates such as foraminifera and bivalves and showed that most follow a common calibration. However, there may be a difference between biogenic-carbonate-based calibrations and the most recent inorganic carbonate calibrations that are assumed to have formed close to isotopic equilibrium. Biogenic calibrations such as those based on foraminifera from seafloor sediments suffer from uncertainties in the determination of the calcification temperatures. Therefore, well-constrained laboratory cultures without temperature uncertainty can help resolve these discrepancies. Although the sample size requirements for a reliable Δ47 measurement have decreased over the years, the availability and preservation of many biogenic carbonates are still limited and/or require substantial time to be extracted from sediments in sufficient amounts. Coccoliths, on the other hand, are abundant and often well-preserved in sediments, and they are a potential interesting target for palaeoceanography. We thus determined the Δ47–temperature relationship for coccoliths due to their relative ease of growth in the laboratory. The carbon and oxygen isotopic compositions of coccolith calcite have limited use in palaeoenvironmental reconstructions due to physiological effects that cause variability in the carbon and oxygen isotopic fractionation during mineralization. However, the relatively limited data available suggest that clumped isotopes may not be significantly influenced by these effects. We cultured three species of coccolithophores under controlled carbonate system conditions with CO2(aq) concentrations between 5 and 45 µM, pH between 7.9 and 8.6 units, and temperatures between 6 and 27 °C.
Our well-constrained results agree with a previous culture study that there are no apparent species- or genus-specific vital effects on the Δ47–temperature relationship in coccolithophores despite significant deviations from equilibrium in the C and O isotopic composition. We find that while varying environmental parameters other than temperature does not have a significant effect on Δ47, changing the parameters yields coccolith Δ47–temperature calibrations that agree within 1.2 ppm. Our coccolith-specific Δ47–temperature calibration with well-constrained temperatures shows a consistent, positive offset of 2–3 °C to the inorganic carbonate calibrations, which point to as yet unknown coccolith-specific disequilibrium effects.
Thus, we suggest the use of our coccolith-specific calibration for further coccolith palaeoceanographic studies and that calibrations derived from laboratory-grown biogenic carbonates are desirable to reinforce the confidence of clumped-isotope-based temperature reconstructions in palaeoceanography.
- Article
(1927 KB) - Full-text XML
-
Supplement
(858 KB) - BibTeX
- EndNote
Clumped isotope thermometry is an increasing commonly used methodology for the reconstruction of palaeotemperatures, palaeohydrology, and diagenetic regimes, as well as use as an isotopic tracer (see Huntington and Petersen, 2023, for a recent review). In a carbonate molecule, bonds between the rare heavy isotopes 13C and 18O can be formed and their excess abundance relative to a stochastic distribution is denominated as “clumping”, which increases with decreasing temperature. To measure this clumping, the carbonate is converted to CO2 by reaction with phosphoric acid, and the excess abundance of 13C18O16O (cardinal mass 47) in the released CO2 relative to a stochastic distribution is measured and reported as Δ47 (Schauble et al., 2006; Eiler, 2007). In early studies, before the introduction of carbonate standardization (Bernasconi et al., 2021), Δ47 in different calibration studies of the same carbonate material had widely variable relationships with temperature. More recent studies (Meinicke et al., 2020; Anderson et al., 2021) have shown that most but not all of these discrepancies were caused by poor interlaboratory comparability caused by the lack of a robust standardization methodology (Bernasconi et al., 2018, 2021).
Based on these recent studies, Δ47 has a consistent relationship with temperature and its temperature dependence is well-established empirically at a large range of temperatures (e.g. Anderson et al., 2021; Fiebig et al., 2021). The Δ47–temperature relationship is independent of the carbon and oxygen isotope composition of the fluid from which carbonates precipitate (Ghosh et al., 2006). Empirical calibrations between temperature and Δ47 have been established for temperatures between 0 and 1100 °C for inorganic carbonates (Kele et al., 2015; Bonifacie et al., 2017; Kelson et al., 2017; Müller et al., 2019; Swart et al., 2019; Jautzy et al., 2020; Anderson et al., 2021). Further empirical studies on biogenic carbonates, such as for foraminifera, coccoliths, gastropods, and bivalves, have found similar relationships between Δ47 and calcification temperature (Katz et al., 2017; Peral et al., 2018; Leutert et al., 2019; Piasecki et al., 2019; de Winter et al., 2022; Huyghe et al., 2022), although specific types of biogenic carbonates such as shallow-water corals (Spooner et al., 2016; Davies et al., 2022), juvenile bivalves (Huyghe et al., 2022), and brachiopods (Bajnai et al., 2018; Davies et al., 2023; Letulle et al., 2023) do not show these relationships. However, there are clear discrepancies between most inorganic calibrations (Swart et al., 2019; Jautzy et al., 2020; Anderson et al., 2021; Fiebig et al., 2021) and an often-used biogenic calibration (Meinicke et al., 2020). One interpretation is that this discrepancy results from uncertainties in the calculation of calcification temperatures for planktonic foraminifera and is resolved with an alternate approach to calcification temperature estimation (Daëron and Gray, 2023). With this study using cultured coccoliths, we generate biogenic carbonate under well-constrained temperature conditions, so there is very little uncertainty in the calcification temperatures.
Other methodological problems can also limit the overall use of clumped isotopes. The relative abundance of Δ47 compared to all isotopologues of CO2 is only ∼ 45 ppm, which requires a sample in the range of 80 to 120 µg with Thermo Fisher Kiel IV devices coupled to Thermo Fisher 253 Plus mass spectrometers (Müller et al., 2017) for a single measurement on 2–10 mg with common acid bath systems (e.g. Ghosh et al., 2006; Kelson et al., 2017; Peral et al., 2018; Fiebig et al., 2021). As the analytical error in clumped isotope measurements is large compared to the natural variability, many replicates are needed to achieve an analytical uncertainty allowing meaningful interpretations in palaeoceanography (Bernasconi et al., 2021; Fernandez et al., 2017; Daëron, 2021). Sample size requirements can be a major limiting factor for biogenic calcite. Both limited abundance and time requirements for picking single species limit the availability of planktonic foraminifera, and the need for sampling precise seasonal increments in slow-growing molluscs can also restrict the mass of carbonate available for analysis (Leutert et al., 2019; de Winter et al., 2022; Huyghe et al., 2022). Coccoliths are a promising alternative as they are often found in greater abundance and have a better preservation potential than foraminifera (Berger, 1973; Subhas et al., 2019). The abundance of coccolith-associated polysaccharides (CAPs) both around and within the coccolith aid in protecting the coccolith calcite from dissolution and overgrowth, and they remain in place for millions of years (Henriksen et al., 2004; Sand et al., 2014; Lee et al., 2016). In part due to these CAPs, coccolithophores have a fine control on the formation of coccolith calcite. Calcite crystals are nucleated in a circular protococcolith ring upon an organic baseplate within the coccolith vesicle, which subsequently matures into a coccolith (Brownlee et al., 2015; Walker et al., 2019). The coccolith is then extruded towards the exterior of the cell, where it adheres to the cell and forms an interlocking system of coccoliths known as a coccosphere (Brownlee et al., 2015; Taylor et al., 2017; Walker et al., 2018). CAPs and other organic compounds are found in abundance in all calcification steps. Intracrystalline CAPs from different species of coccolithophores can be crystal-inhibiting (such as E. huxleyi; Henriksen et al., 2004; Gal et al., 2016; Walker et al., 2019) or promote calcite specifically even in unfavourable conditions (such as G. oceanica; Walker et al., 2019). Extracrystalline CAPs can aid in the adherence of the coccolith to the cell and of the coccoliths to each other, and they maintain the coccosphere structure (Walker et al., 2018). Subsequently, there are few anion substitutions and a lack of lattice defects on the coccolith surface that further aid in better preservation relative to foraminifera (Berman et al., 1993; Stoll et al., 2001; Frøhlich et al., 2015; Walker et al., 2019). Additionally, there are a multitude of specialized pathways that regulate the fluxes of cations such as Ca2+ and dissolved inorganic carbon (DIC) species into various intracellular compartments to allow for controlled calcification and photosynthesis (Brownlee et al., 2015; Gal et al., 2017; Taylor et al., 2017).
Biogenic carbonates often feature carbon and oxygen isotopic compositions that differ from those expected for abiogenic carbonates near equilibrium, offsets informally called “vital effects”, as a result of the complexity of coccolith calcification described above. Such offsets have been described for coccolith calcite (Ziveri et al., 2003; Rickaby et al., 2010; Ziveri et al., 2012; Candelier et al., 2013; Hermoso et al., 2014; Stevenson et al., 2014; Hermoso et al., 2016, Katz et al., 2017) and the contributing processes simulated in models (Langer et al., 2012; Ziveri et al., 2012; Bolton and Stoll, 2013; Holtz et al., 2017; McClelland et al., 2017). The vital effects limit the use of stable isotope signatures of coccolith calcite in palaeoceanography. However, initial studies of clumped isotopes in coccolithophorids found that while multiple coccolithophore species display clear carbon and oxygen vital effects, they follow previous Δ47–temperature calibrations (Drury and John, 2016; Katz et al., 2017), making them potentially useful for palaeoceanography. However, because these studies and calibrations were performed before carbonate standardization (Bernasconi et al., 2021) and have a limited number of replicate analyses, robustness and interpretation of their conclusions need to be verified with new studies. Other aspects such as the dissolved inorganic carbon chemistry in the cultures and growth conditions as possible influences on Δ47 also still need to be examined.
To this end, three species of calcifying coccolithophores were cultured under controlled temperature and carbonate chemistry conditions. A temperature range of 21 °C and CO2(aq) range of 40 µM was covered. Coccolithophores from the Gephyrocapsa genus were cultured between 6 and 27 °C, using the warm-adapted G. oceanica and the cold-adapted G. muellerae. Inter-genus vital effects were tested through comparison with Calcidiscus leptoporus, which features distinct carbon and oxygen isotopic vital effects compared to Gephyrocapsa in previous studies (Ziveri et al., 2003; Hermoso et al., 2014; Katz et al., 2017). Finally, through comparison with a previous coccolith culture (Katz et al., 2017), as well as inorganic (Anderson et al., 2021; Daëron and Vermeesch, 2024), biogenic (Peral et al., 2018; Meinicke et al., 2020; de Winter et al., 2022), and recalculated (Daëron and Gray, 2023) Δ47–temperature calibrations, the potential need for a coccolith-specific calibration is assessed.
2.1 Batch and continuous culture setup
Three monoclonal coccolithophore strains, Gephyrocapsa oceanica (RCC 1303), Gephyrocapsa muellerae (RCC 3370), and Calcidiscus leptoporus (RCC 1130) obtained from the Roscoff Culture Collection, were cultured at ETH Zürich. G. oceanica is an abundant cosmopolitan coccolithophore species that has been found at temperatures between 12–27 °C but favours temperatures above 20 °C (Sett et al., 2014; von Dassow et al., 2021). G. muellerae is from the same genus as G. oceanica, favours colder and less saline conditions, and can grow at 6 °C (von Dassow et al., 2021). C. leptoporus is a large coccolithophore, is especially abundant in low-latitude upwelling settings, is resistant to dissolution and thus a major contributor to coccolith carbonate, and is known to have large isotopic vital effects (Thierstein and Young, 2004; Ziveri et al., 2007; Langer et al., 2012; Hermoso, 2014). Thus, the three strains were cultured to provide a temperature range of 21 °C while also highlighting potential isotopic vital effects. G. oceanica was cultured in a turbidostat or continuous culture setup as seen in Fig. 1a between a CO2(aq) of 5 and 45 µM for at least two temperatures (Table 1). All three strains were grown in at least two temperatures in batch culture setup as seen in Fig. 1b and provide a wide range of temperatures (Table 1).
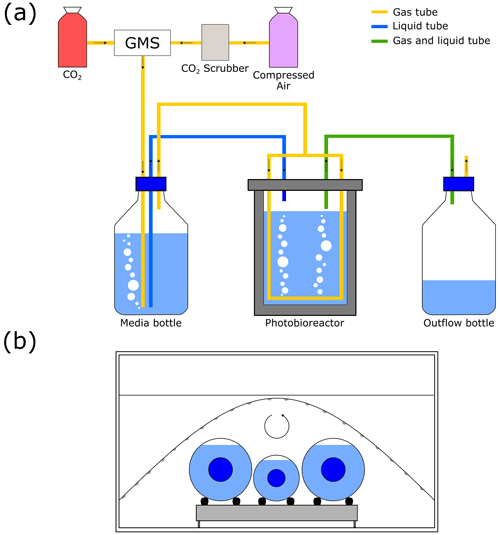
Figure 1Photobioreactor and incubator systems. (a) Photobioreactor with controlled CO2 gas input, adjusted from Zhang et al. (2022). (b) Incubator with a roller containing two 2 L bottles and one 1 L bottle as well as an LED strip for batch cultures.
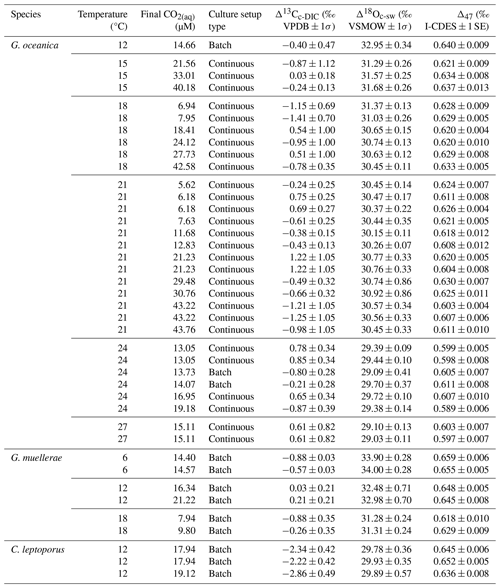
Table 1Overview table for all included data points for Sects. 3, 4.1, and 4.2 including temperature (°C), culture setup type, CO2(aq) (µM), Δ13Cc-DIC (‰; VPDB), Δ18Oc-sw (‰; VSMOW), and Δ47 values (‰; I-CDES). 1 standard deviation (σ) is included for Δ13Cc-DIC and Δ18Oc-sw, which take the evolution of the media over time into account, and 1 standard error (SE) for Δ47.
All cultures were carried out in artificial seawater, following Kester et al. (1967), as the basis of a K/2 medium (Keller et al., 1987). The final pH and DIC were adjusted through addition of HCl and Na2CO3 and covered a range of 40 µM of CO2(aq) values. A Tris buffer was not included for all experiments as this would interfere with the carbonate chemistry control. Prior to inoculation, the K/2 medium was sterilized through a 0.2 µm Millipore Stericup filter.
Before starting the experiments, the strains were maintained at a constant temperature of 18 °C and slowly acclimatized to the experimental temperature for at least four to six generations. Cultures were inoculated at cell densities of ∼ 5000 cells mL−1 for G. oceanica and G. muellerae and ∼ 2000 cells mL−1 for C. leptoporus.
Batch cultures were carried out in 1 or 2 L Nalgene polycarbonate sterile flasks with 50 and 100 mL headspace, respectively, and kept in a lit incubator set to the experimental temperature (±0.1 °C). For the duration of the experiments, the flasks were rotated on a roller set at 10 rpm to reduce settling and allow for uniform light exposure; see Fig. 1b. C. leptoporus did not grow under turbulent conditions and was manually shaken every day (Houdan et al., 2006). The cultures were illuminated by LED lights on a sinusoidal 14 to 10 h light–dark cycle and a maximum luminosity of 120 µmol photons m−2 s−1. Harvesting took place in a semi-continuous manner, where 80 %–90 % of the total volume was harvested and then refreshed when the culture reached a set cell density (100–150 × 103 cells mL−1). In general, we used a higher cell density compared to previous culturing studies due to the larger sample material requirement for clumped isotope measurements. Yet each strain was maintained in their early to mid-exponential phase to prevent a reservoir effect and an enriching of the δ13C of the media (δ13CDIC) relative to the initial conditions (Barry et al., 2012; Hermoso, 2014). Certain batch and continuous cultures had a higher cell density and significant drift in the DIC, pH, or CO2(aq) over the course of the experiment and serve to test the sensitivity of vital effects to a varying carbon system.
Continuous cultures were performed in a 1 L (FMT 150/1000) or 3 L (FMT 150/3000) photobioreactor (PBR) connected to a PP600 peristaltic pump and a GMS 150 gas mixing system (Photon Systems Instruments, Drásov, Czech Republic); see Fig. 1a. For a more detailed description of the experimental setup see Zhang et al. (2022). The strains were illuminated with LEDs on a 16 to 8 h light–dark cycle with a maximum luminosity of 200 µmol photons m−2 s1. The optical density (OD), which is proportional to the cell density, was calibrated to a zero point before inoculation. With continuous OD monitoring and (sub-)daily measurements of the cell density, the OD could be set to a cell density threshold between 100 and 200 × 103 cells mL−1. If the OD exceeded this threshold, the peristaltic pump pumped fresh media into the PBR equivalent to 10 % of the culture volume, and medium from inside the PBR was pushed into the outflow bottle. Ambient air was first scrubbed of CO2 and then passed through a gas mixing system with a set amount of CO2 with a constant composition (δ13C = −14.36 ± 0.06 ‰ VPDB; δ18O = 19.85 ± 0.14 ‰ VSMOW). Thus, the pCO2 was controlled and maintained at a constant level, which was checked at the beginning and end of each experiment. Temperatures were continuously controlled with a pH–temperature probe in the vessel, which kept a constant temperature with < 0.1 °C deviation through Peltier elements at the bottom of the vessel.
Cell density and size were measured using a Z2 Coulter particle counter and size analyser with an aperture size of 100 µm (Beckman Coulter, Inc., Brea, California, United States), which were used to determine growth rates. Cell counts were taken systematically every 24 h with an extra measurement taken before and after harvest.
The net growth rate for batch cultures were calculated as
where Nt is the cell count at time t (in days) and N0 is the initial cell count.
For continuous cultures, the dilution rate, which equates to the volume of the output (Vout) over the volume of the PBR over time t, also needs to be considered:
Cells were harvested by centrifugation at 4000 rpm for 5 min. The pellet containing coccoliths was rinsed with deionized water to remove traces of salts through four cycles of centrifugation and removal of the supernatant. Subsequently, the wet pellet of organic matter and coccoliths was transferred to a 2 mL vial, which was then stored at −20 °C for later analysis.
At the beginning, at each harvest, and at the end of an experiment, 12 mL of water was sampled for pH and cell density measurement. Each aliquot was centrifuged once at 4000 rpm for 5 min, and the supernatant was used for DIC, δ13CDIC, and δ18OSW measurements. Some batch and continuous cultures were kept until higher cell densities were reached. In these cases, pH, DIC, and δ13CDIC were measured more often to track the evolutions from initial conditions as a result of cell growth and cell density increase.
2.2 Sample cleaning
Contaminants from organic matter or sulfur compounds contained within carbonates are known to interfere with the clumped isotopic measurements for carbonates (Eiler and Schauble, 2004; Dennis and Schrag, 2010). In this study we used three methodologies for the removal of possible contaminants from the coccolith pellet. Initially the aliquots were dried in a 60 °C oven for at least 4 h to remove any remaining water that could dilute the cleaning reagents. Then one of three cleaning methodologies was performed.
One method used oxidation of the organic matter through reaction with an 18 % H2O2 solution neutralized with NaOH to pH 8–9 following the protocol of Falster et al. (2018). The second methodology used a solution of 10 % H2O2 neutralized with NH3 to pH 8–9. For both solutions the pellets were reacted overnight at room temperature and then rinsed four to five times with Milli-Q until a neutral pH of 7 was obtained. The third method used is total lipid extraction (TLE), following Matyash et al. (2008). The pellets were first suspended in 1 mL of isopropanol and homogenized through vortexing and sonication until there were no visible clumps. 3 mL of methyl-tert-butyl ether was added and the total solution was again vortexed. 1 mL of DI water was added and the sample was centrifuged at 4000 rpm for 5 min. This method removes the polar and apolar organic compounds from the pellet into the upper 4 mL of the solution. This supernatant is subsequently discarded, while maintaining 1 mL of the aqueous phase with the cleaned coccolith pellet at the bottom. When abundant organic matter was still visible after one cycle of cleaning, the procedure was repeated. After all three cleaning methodologies, the samples were dried at 60 °C for at least 4 h.
In order to confirm the effectiveness of the different cleaning methodologies and their effect on the coccolith carbonate, high-resolution scanning electron images were taken using a JSM-7100F JEOL scanning electron microscope (SEM) at ScopeM, ETH Zürich; see Fig. S1. As harvested from the cultures, all coccoliths exhibited regular morphology with no evidence of coccolith malformation. The cleaning protocol causes slight dissolution, fragmentation, and breakage of some of the coccoliths. Any difference in isotope measurements as a result of cleaning protocols was within the standard deviation or error of each measurement (±0.15 ‰ for δ13C and δ18O; ±0.016 for Δ47).
2.3 Isotope measurements
2.3.1 Coccolith carbon, oxygen, and clumped isotopes
Carbon, oxygen, and clumped isotopes from the cultured coccoliths were measured on two Thermo Fisher Scientific mass spectrometers, a MAT 253 and a 253 Plus, coupled to Kiel IV preparation devices as described in Müller et al. (2017). Aliquots of 110–180 µg of sample and carbonate standards (ETH-1, 2, 3; IAEA C2) were measured with a Kiel device at 70 °C. The samples were reacted for 300 s with three drops of 104 % phosphoric acid, and the released CO2 was immediately frozen in a liquid nitrogen (LN2) trap kept at −190 °C. After the sample was fully reacted, the first LN2 trap was heated to −100 °C, and the CO2 gas was transferred through a 10 mm PorapakQ (50–80 mesh) to a second LN2 trap kept at −190 °C. The PorapakQ tubing was coated with Sulfinert 2000, stuffed with silver wool, and kept at −40 °C to capture and eliminate possible organic contaminants. The second LN2 trap was then heated to room temperature and measured using the long-integration dual-inlet protocol (Hu et al., 2014; Müller et al., 2017). The initial gas intensity of the sample gas was recorded and then immediately measured for 400 s, 40 cycles of 10 s. Subsequently, the reference gas was measured for the same duration starting at the same initial gas intensity. Before measuring, background scans at different beam intensities were carried out to determine the pressure-dependent background on all beams (Bernasconi et al., 2013; Meckler et al., 2014). Using the Easotope software (John and Bowen, 2016) a pressure-sensitive baseline correction was applied, and raw carbon and oxygen values were converted to VPDB using the Brand parameters as suggested by Daëron et al. (2016). Further, the raw vs. accepted Δ47 values for the carbonate standards and an empirical transfer function were used to convert and normalize the sample Δ47 data to the Intercarb carbon dioxide equilibrium scale (I-CDES; Bernasconi et al., 2021).
Each individual reported clumped isotope value consists of at least 10 replicates, with an average of 13 replicates. Long-term accuracy and reproducibility of the Δ47 measurements were evaluated based on monitoring of the IAEA-C2 international carbonate standard, which was treated as an unknown sample (MAT 253: Δ47= 0.6385 ± 0.034, MAT 253 Plus: Δ47= 0.6411 ± 0.026 ‰; 1σ n= 241) and fit within the accepted values (0.6409 ‰ ± 0.003 ‰; Bernasconi et al., 2021). Analytical errors are reported at the 95 % confidence interval (Fernandez et al., 2017) without taking into account the standardization error. However, as the measurements are carried out with a 50:50 standard to sample ratio, the additional uncertainty related to standardization would be small (Bernasconi et al., 2021).
2.3.2 DIC and seawater carbon and oxygen isotopes
DIC and pCO2 were measured on a Picarro G2131-i cavity ring-down spectrometer (Picarro Inc, USA) coupled to an AS-D1 DIC–δ13C analyser (Apollo Scitech, USA). For DIC measurements, 3 mL of centrifuged media was taken and reacted within the AS-D1 analyser with 0.9 mL of a 3 % H2PO4 and 7 % NaCl solution. The absolute DIC concentration was found through quantification of the extracted CO2 concentration as described in Deng et al. (2022). A threshold of ≤ 20 ppm pCO2 for background synthetic air (80 % N2, 20 % O2; PanGas) was first defined. After at least 10 measurements of background air below this threshold, the stable baseline was reached and the sample was injected into the measuring chamber. As the extracted CO2 flowed into the measuring chamber, measurements of pCO2 were taken every 3–5 s until all of the extracted CO2 had passed through the measuring chamber and the stable baseline was reached again. For the absolute DIC concentration, the integrated area of pCO2 between the two baselines is plotted against the total DIC content. The latter is defined as the volume multiplied by the measured DIC. A certified reference material, NOAA batch 186 with a known absolute DIC concentration of 2012 µM, is used for calibration. Through variation of the certified reference material volume, a range of integration areas and total DIC content was obtained and internally defined. Two secondary standards with calibrated DIC concentrations were also used. Each measurement was repeated twice with the same centrifuged media in quick succession to reduce CO2 exchange with the atmosphere, which gave an average DIC and uncertainty for each measured replicate. At least three of these replicates were taken and measured for each experiment.
For δ13CDIC measurements, 1 mL of centrifuged media was acidified with 150 µL of 104 % H2PO4 in a He-flushed vial. Subsequently the δ13CDIC was measured on a Gasbench II coupled to a Delta V Plus mass spectrometer (Thermo Fisher Scientific, USA). Two in-house NaHCO3 standards dissolved in deionized water with δ13CDIC values of −4.66 ‰ and −7.94 ‰ were used.
The oxygen isotopic composition of the seawater (δ18Osw) was measured on a Picarro L2130-i isotope wavelength-scanned cavity ring-down spectrometer following Gupta et al. (2009). The water sample is first passed through a salt catchment trap, vaporized, and injected at a uniform concentration and flow rate into the Picarro spectrometer. This delivers a pulse with a constant concentration profile, during which the δ2H and δ18O are measured. Three in-house standards calibrated to three IAEA and USGS standards (SLAP2, GRESP, and VSMOW2) were run every 20 samples. Another in-house standard is run as an unknown sample. All standards fell within 1 standard deviation of their accepted value. Measurement precision was affected by the residual salt from the seawater. At least two seawater measurements were taken for each experiment. Subsequently an average δ18Osw and uncertainty (mean σ= 0.32 ‰) for each condition were obtained; see Table S1. This uncertainty is used for the uncertainty of the oxygen isotope offset from seawater, δ18Oc – δ18Osw (Δ18Oc-sw) as reported in Table 1, and will be used in subsequent figures (mean σ= 0.29 ‰).
The pH measurements were made using a Mettler Toledo LE410 pH probe (Mettler Toledo, Greifensee, Switzerland) and were calibrated with three NBS standards (pH = 4.00, 7.01, 9.03 at 21 °C), with a standard deviation of ±0.01. All pH measurements are given on the NBS scale. Seawater carbon chemistry was calculated through CO2SYS (Lewis and Wallace, 1998), with input of measured pH and DIC, and using the K1 and K2 constants of Leuker et al. (2000), KHSO4 of Dickson (1990), KHF of Perez and Fraga (1987), and the [B]I value of Lee et al. (2010).
DIC and pH measurements are compared and normalized to the initial measured values to detect potential drift and stability of the carbon chemistry of each culture. These are reported as initial DIC – measured DIC (ΔDIC) and initial pH – measured pH (ΔpH) in Table S1. We report the uncertainty of the fractionation between coccolith calcite and DIC (Δ13Cc-DIC) from both the standard deviation of δ13Cc and the range of all measured δ13CDIC values over the course of the sampled culture to take into account the potential effect of DIC evolution and drift, and this will be used in subsequent figures.
The same medium was used for both batch and continuous cultures and thus the same δ13CDIC would be expected for both. However, through the continuous bubbling and gas exchange in the continuous cultures, there is a potential for different δ13CDIC values than the batch culture setup. Indeed, there is a nonsystematic enrichment of 0 ‰–1 ‰ for the batch culture δ13CDIC. However, the fractionation between coccolith calcite and DIC, i.e. Δ13Cc-DIC, is not affected by these differences.
An often-used index in coccolithophore geochemistry studies (McClelland et al., 2017; Phelps et al., 2021) for the relative usage of carbon supply and demand is the dimensionless τ:
It reflects the degree of carbon utilization by the coccolithophore as measured through growth rate (μ), defined in Eqs. (1) and (2) for batch and continuous culture setup, respectively, the cell radius (r), and cellular carbon density (ρ) against the diffusive CO2 supply into the cell set by (CO2(aq)) and the permeability to CO2 (Pc). We use a Pc of 1.4 × 10−3 µm d−1 (Blanco-Ameijeiras et al., 2020) and ρ of 2 × 10−3 µM (McClelland et al., 2017). It is assumed that there is only a diffusive supply of CO2 into the cell. Our cell size measurements assume a perfect coccosphere for each counted cell, which results in a coccosphere radius that is slightly different than the cell radius. This is taken into account, together with uncertainties in μ and CO2(aq), in the uncertainty of the final τ value.
Pearson correlation coefficients (ρ) are used to determine whether two parameters are linearly correlated. If the ρ value is near 1 or −1, there is a strong correlation and one parameter has an effect on the other. Weak correlations are defined here as ρ≤ ±0.40 and significance is given by a p value < 0.05.
3.1 Carbon chemistry
3.1.1 DIC, pH, and CO2(aq)
The stability of the carbon chemistry was monitored with at least three DIC and pH measurements for each culture. Drift from the initial conditions was less than ±20 % and ±0.20 for ΔDIC and ΔpH, respectively, for 40 culture experiments (Fig. S2 and Table S1). To ensure only well-constrained culture conditions are considered, 15 experiments with ΔDIC≥ 20 % or ΔpH≥ 0.20 are excluded from our main analysis in Figs. 2 through 5 but are evaluated in a subsequent comparison (see Sect. 4.3). The ranges of the well-constrained dataset were 1312–5621 µM for DIC, 7.9–8.6 units for pH, and 5.6–43.8 µM for CO2(aq).
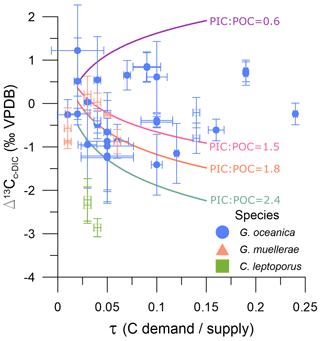
Figure 2Coccolith carbon isotope fractionation relative to external DIC (Δ13Cc-DIC) against the carbon demand vs. supply (τ). Blue circles are G. oceanica, orange triangles are G. muellerae, and green squares are C. leptoporus. Open and filled symbols are batch and continuous cultures, respectively. Error bars are as described in the “Materials and methods” section. Lines represent the model simulations of McClelland et al. (2017) at different PIC:POC ratios; purple: 0.6, pink: 1.5, orange: 1.8, grey: 2.4.
3.1.2 Carbon isotopes
The carbon isotope composition of the DIC (δ13CDIC) varies between −5.10 ‰ and 0.80 ‰, with a similarly large range of −5.52 ‰ and −0.07 ‰ for all species' coccolith carbon isotopes (δ13Cc; Table S1). This is mostly due to the large variability in δ13Cc for G. oceanica, which can be attributed to the range of different experimental conditions. The δ13Cc in G. muellerae varies between −4.68 ‰ and −3.66 ‰, while the δ13Cc in C. leptoporus varies between −5.15 ‰ and −5.04 ‰.
The fractionation Δ13Cc-DIC ranges between −1.41 ‰ and 1.22 ‰ for G. oceanica, −0.88 ‰ and 0.21 ‰ for G. muellerae, and −2.86 ‰ and −2.22 ‰ for C. leptoporus. No significant linear correlations were identified between Gephyrocapsa Δ13Cc-DIC and carbonate system parameters (DIC, pH, CO2(aq)) or culture parameters (cell density and ΔDIC) (Table S2). Gephyrocapsa culture data are also not significantly correlated with τ, the index of carbon demand vs. supply (Fig. 2; ρ= 0.06, p value = 0.74). Including Calcidiscus does not improve the correlation or significance with any parameter apart from ΔDIC.
3.2 Oxygen isotopes
The δ18Osw values are given in Table S1 for all cultures and vary by ∼ 1.6 ‰ across experiments, with no systematic differences between batch and continuous cultures. For a given temperature, C. leptoporus has systematically lower δ18Oc values by ∼ 3 ‰, while G. oceanica and G. muellerae have similar δ18Oc values at the same temperature. The interspecies variations are independent of culture setup and experimental condition.
The oxygen isotope offset from seawater, δ18Oc – δ18Osw (Δ18Oc-sw), varies systematically for all experimental conditions as seen in Fig. 3 and Table 1. Calcidiscus has a systematic offset of ∼ 3 ‰ relative to Gephyrocapsa at the cultured growth temperatures, which agrees with previous culturing studies (Ziveri et al., 2003; Candelier et al., 2013; Stevenson et al., 2014; Hermoso et al., 2016; Katz et al., 2017). For G. oceanica, there is a significant negative correlation between Δ18Oc-sw and temperature (ρ= −0.94, p value < 0.05), which remains when including G. muellerae (ρ= −0.97, p value < 0.05). The Δ18Oc-sw–temperature relationship is consistent between setups and experimental conditions and is not influenced by the variability in δ18Osw values. The available data indicate that the range of Δ18Oc-sw is similar within the Gephyrocapsa genus.
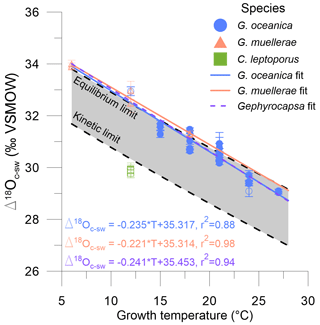
Figure 3The fractionation of oxygen isotopes in coccolith calcite from seawater (Δ18Oc-sw), both in VSMOW, in relation to the growth temperature in degrees Celsius (°C). Blue circles are G. oceanica, orange triangles are G. muellerae, and green squares are C. leptoporus. Open and filled symbols are batch and continuous cultures, respectively. Linear regression fits are calculated for G. oceanica and G. muellerae separately, as well as for the whole Gephyrocapsa genus, with equivalent formulae. Error bars are as described in the “Materials and methods” section, and temperature error bars are smaller than symbols. The equilibrium and kinetic limits are from Watkins et al. (2014) and defined as and , respectively.
3.3 Clumped isotopes
The Δ47 values are shown in Table 1 and Fig. 4 and range from 0.589 ‰–0.640 ‰ for temperatures between 12–27 °C for G. oceanica, 0.618 ‰–0.659 ‰ between 6–18 °C for G. muellerae, and 0.636 ‰–0.652 ‰ at 12 °C for C. leptoporus. There is variation of ∼ 25 ppm at given experimental conditions, in particular at 21 and 24 °C, although all data points fall within the long-term standard deviation of the standards used for correction of 0.020 ‰. There is no resolvable difference between species or genus at given temperatures; differences are within ±0.016 ‰ of each other.
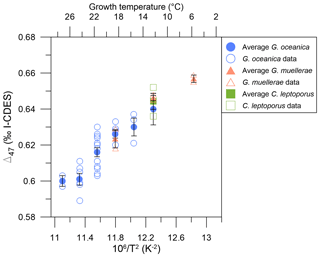
Figure 4Δ47 values from coccolith calcite versus 106/T2 for all data points and averages. Averages are full symbols, while individual data points are empty symbols. Blue circles are G. oceanica, orange triangles are G. muellerae, and green squares are C. leptoporus data. Error bars are as described in the “Materials and methods” section, and temperature error bars are smaller than symbols.
For our culture experiments, in order to evaluate whether processes promoting variable stable isotope effects would systematically affect the Δ47–temperature relationship we manipulated the media carbonate chemistry in ways that produced variable stable isotope vital effects in coccoliths in previous cultures. We also contrasted two coccolith genera that exhibit different ranges of vital effects. Multiple physiological explanations for coccolith vital effects have been proposed (Rickaby et al., 2010; Moolna and Rickaby, 2012; Hermoso et al., 2014, 2016) and simulated previously in cellular models (Ziveri et al., 2012; Bolton and Stoll, 2013; Holtz et al., 2015, 2017; McClelland et al., 2017). In our discussion, in Sect. 4.1 and 4.2 we briefly summarize these mechanisms and quantify the vital effect in each experiment so that in Sect. 4.3 we may compare the vital effect to the Δ47 variations. The focus of this study is the calibration of the temperature dependence of Δ47 in coccolith calcite. Therefore, we will only briefly discuss the causes and mechanisms leading to isotopic disequilibrium in the cultures, focusing in particular on those that could also affect Δ47.
4.1 Oxygen isotope vital effects in coccolith calcite
At a given temperature, equilibrium oxygen isotope fractionation between calcite and water is inferred to be most closely represented by natural carbonates precipitated at extremely slow rates and independent of pH (Coplen, 2007; Daëron et al., 2019). The model of Watkins et al. (2013, 2014) approximates this equilibrium and is shown as the “equilibrium limit” in Fig. 3. This approximation is derived from the assumed equilibrium of Coplen (2007), with potential small growth rate and pH effects present for carbonates not precipitated in equilibrium. Non-equilibrium fractionation effects between DIC and calcite that manifest at faster growth rates in experiments both with and without carbonic anhydrase (CA) include lower Δ18Oc-w and a pH dependence. This effect presumably but not necessarily occurs because calcite forms from both bicarbonate and carbonate ions in proportion to their abundance in solution. At a higher pH the proportion of calcite carbon derived from the carbonate ion increases (McConnaughey, 1989; Clark et al., 1992; Dietzel et al., 1992; Zeebe and Wolf-Gladrow, 2001; Watkins et al., 2014; Devriendt et al., 2017). Here, a pH of 8.3 at the crystallization site and the fastest growth rate is assumed in the model of Watkins et al. (2013, 2014) and Watkins and Devriendt (2022), with which the “kinetic limit” is derived and illustrated in Fig. 3. This gives an approximate 2 ‰ offset and incorporates a large range of experimentally derived and modelled inorganic calcites precipitated in the presence of CA. Additionally, numerous experiments and potentially many natural biogenic and abiogenic systems may precipitate calcite from a solution in which equilibrium between DIC and H2O is not maintained due to a lack of CA or fast calcification rates (Devriendt et al., 2017; Guo, 2020). Rayleigh fractionation of oxygen isotopes in the internal DIC pool occurs as a result, which is transferred to the isotopic composition of the calcite and leads to lower Δ18Oc-w values, thus exacerbating the disequilibrium fractionation potentially present between the DIC and calcite as described above.
Recent studies suggest that in certain systems such as synthetically precipitated calcite, oxygen isotope disequilibrium does not affect Δ47, even for systems with intermediate oxygen isotope fractionations that fall between the kinetic and equilibrium limits, as seen in Fig. 3 (Kelson et al., 2017; Levitt et al., 2018; Jautzy et al., 2020; Fiebig et al., 2021). Models also suggest little to no Δ47 disequilibrium for biogenic carbonates such as foraminifera and bivalves, as the magnitude of potential Δ47 disequilibrium is below the current analytical resolution for Δ47 measurements, although this is pH- and growth-rate-dependent (Defliese and Lohmann, 2015; Watkins and Hunt, 2015; Watkins and Devriendt, 2022). However, this does not hold for corals, brachiopods, and speleothems, where systematic δ18O and Δ47 disequilibria are present, and should be explored further in more biogenic carbonates (Watkins and Hunt, 2015; Guo and Zhou, 2019; Guo, 2020).
Offsets from the equilibrium limit (ΔΔ18Ooff) were calculated to quantify the vital effect in oxygen isotopes. Offsets may potentially arise from pH variability, growth rate, calcification rate, or disequilibrium within the DIC–H2O system. Calcidiscus is significantly different from equilibrium (t test; t(4) = −58.68, p value < 0.05) and falls outside the equilibrium and kinetic limits as seen in Fig. 3. Although for Gephyrocapsa the mean ΔΔ18Ooff value is around zero and there is no significant difference from the abiogenically defined equilibrium (t test; t(72) = −0.47, p value = 0.64), there is a range of ∼ 1.5 ‰ in ΔΔ18Ooff among different experiments. Previously published Gephyrocapsa data have a positive ΔΔ18Ooff of 0 ‰–1 ‰ (Fig. 5; Ziveri et al., 2003; Hermoso et al., 2016).
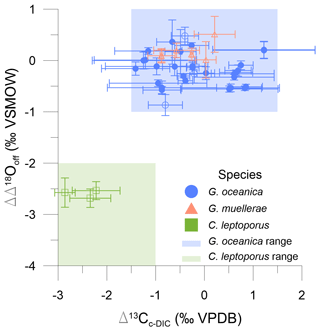
Figure 5The oxygen isotope offset from the equilibrium limit in Watkins et al. (2014) (ΔΔ18Ooff) against the coccolith carbon isotope fractionation relative to external DIC (Δ13Cc-DIC). Blue circles are G. oceanica, orange triangles are G. muellerae, and green squares are C. leptoporus data. Open and filled symbols are batch and continuous cultures, respectively. The Δ13Cc-DIC and ΔΔ18Ooff range of previous G. oceanica and C. leptoporus studies are given as a blue and green background, respectively. Error bars are as described in the “Materials and methods” section.
CA has been suggested as a potential equilibration catalyst for both oxygen isotopes and Δ47 within the DIC–H2O system in calcifying organisms. Even at an elevated pH, the equilibration time is considerably shortened for abiogenic carbonates precipitated in the presence of CA (Uchikawa and Zeebe, 2012; Kelson et al., 2017). A lack or low activity of CA can potentially cause the variable ΔΔ18Ooff seen in our data. While the pH of the intracellular calcification site for coccoliths is not well-constrained, there is experimental evidence for CA in the biomineralization pathway of Emiliania huxleyi (Zhang et al., 2021). Although CA has not been explicitly found in Gephyrocapsa, it is associated with the cytosol or chloroplast or is extracellular in other coccolithophores (Nimer et al., 1994; Elzenga et al., 2000; Herfort et al., 2002; Rost et al., 2003). Furthermore, genes have been found associated with biomineralization and CA expression in E. huxleyi (Quinn et al., 2006; Soto et al., 2006; Richier et al., 2011). Models show a requirement of CA activity in the calcification pathway of coccolithophores, either in the cytosol or coccolith vesicle itself, as a purely uncatalysed exchange would have carbon isotope values that are too enriched in the coccolith calcite (Holtz et al., 2015; McClelland et al., 2017). Thus, it is probable that CA is present in coccolithophores. However, the activity of CA is not well-constrained so it remains uncertain whether it is sufficient to ensure full equilibration of the DIC–H2O system for both oxygen isotopes and Δ47.
For Gephyrocapsa, the 1.5 ‰ range in ΔΔ18Ooff also did not correlate with pH, growth rate, DIC, CO2(aq), or τ (Figs. S4, S5; Table S2). The 1.5 ‰ range in ΔΔ18Ooff may be explained by varying degrees of isotopic equilibration between the DIC pool and intracellular water in different experiments. Nonsystematic disequilibria effects could be present for our continuous culture setup as the equilibration time for oxygen isotopic exchange between our bubbled CO2 gas and the seawater media is of the order of hours (Zeebe and Wolf-Gladrow, 2001; Uchikawa and Zeebe, 2012). In support of this interpretation, there is a difference of ∼ 0.5 ‰ between all continuous and batch culture ΔΔ18Ooff values (t test; t(38) = 1.76, p value = 0.09, Fig. 5, Table S1). Further variability in ΔΔ18Ooff could be a result of variable intracellular pH and/or varying calcification rates as well as the presence and activity of CA. However, these physiological variations do not exhibit systematic relationships with the individual environmental parameters such as growth rate, external pH, or carbonate system. This suggests a potential for complex co-regulation of the physiological factors and/or multiple environmental controls, which are best evaluated by cellular models and beyond the scope of this study.
4.2 Carbon isotope vital effects in coccolith calcite
In this study (Fig. 5), all continuous (and most batch) cultures for G. oceanica fall within the expected range of 0 ± 1.5 ‰ for Δ13Cc-DIC as found in other studies (see Fig. S3; Rickaby et al., 2010; Moolna and Rickaby, 2012; Hermoso, 2014; Katz et al., 2017). There are no comparable culture studies for G. muellerae. The Δ13Cc-DIC values fall within the range of G. oceanica. Both species will be combined in any inter-genera analyses for Sect. 4. C. leptoporus has a Δ13Cc-DIC of −2.0 ± 1.0 ‰, comparable to previous culturing studies (Fig. 5; Ziveri et al., 2003; Hermoso et al., 2014; Katz et al., 2017).
Models of the vital effect in coccolith carbon simulate multiple processes affecting Δ13Cc-DIC (Bolton and Stoll, 2013; Holtz et al., 2017; McClelland et al., 2017). The carbon utilization (or demand) as a function of the supply, termed τ, is an index used to describe changes in cellular carbon uptake (relative significance of diffusive CO2 uptake vs. active HCO uptake) and depletion of the intracellular dissolved carbon pool that impact the carbon isotopic fractionation (Eq. 3, Fig. 2). The cellular calcification (particulate inorganic carbon; PIC) relative to photosynthesis (particulate organic carbon; POC) is described as the PIC:POC ratio. The PIC:POC intensity will modulate the Δ13Cc-DIC response to τ. For moderately to heavily calcified cells with relatively high PIC:POC ratios, models simulate a decrease in Δ13Cc-DIC with increasing τ, for example as might be triggered by decreasing concentrations of CO2(aq) (Eq. 3, Fig. 2). However, lightly calcified cells with PIC:POC of 0.5 exhibit a slight increase in Δ13Cc-DIC with increasing τ, while cells with PIC:POC near 1 have Δ13Cc-DIC nearly insensitive to τ. The G. oceanica in our experiments features a range of PIC:POC ratios from 0.4 to 1.3 (Torres-Romero et al., 2024), which likely contributes to the absence of a single clear trend between Δ13Cc-DIC and τ. We have not determined the PIC:POC in our Calcidiscus, but it is generally characterized by a PIC:POC of 1.2–2.3 (Langer et al., 2006, 2012; Bolton and Stoll, 2013). The lower Δ13Cc-DIC of Calcidiscus correlates with lower ΔΔ18Ooff (Fig. 5), as observed in size fractions from sediments (e.g. Bolton and Stoll, 2013), but the physiological mechanism of this correlation has not yet been quantitatively explored in a coupled model of carbon and oxygen isotope fractionation in coccoliths.
4.3 Calibration of coccolith clumped isotopes and temperature
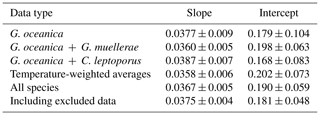
Despite the significant vital effects in carbon and oxygen isotopes, our coccolith Δ47 values show a consistent relationship with temperature (Fig. 6), which is similar to previous calibration studies (see Sect. 4.4, 4.5). In order to calculate a reliable coccolith Δ47–temperature regression, we used a simple least-squares fitting following Williamson (1968) and York et al. (2004), using the Excel spreadsheet by Cantrell (2008). This methodology considers the uncertainties from both the Δ47 and temperature measurements. While the omni-variant generalized least-squares regression would be better suited, as this incorporates the full error covariance (Daëron and Vermeesch, 2024), our data are standardized through reference materials in a moving time window and thus cannot be analysed through this method. As pointed out in a number of studies (Bonifacie et al., 2017; Fernandez et al., 2017; Katz et al., 2017; Kelson et al., 2017; de Winter et al., 2022), the bias from a low number of analytical replicates and the small temperature range can lead to significant differences in calibration slope and intercepts. In order to determine potential species- or genus-dependent effects, an unorthodox approach was initially tested. G. oceanica contains the most diverse and largest range of temperature data points, while C. leptoporus only contains one temperature point and three Δ47 data points. Thus, the other two species' datasets will be successively included and evaluated for significance relative to the G. oceanica dataset. Further, each biological and technical Δ47 sample and uncertainty are taken individually to have an equal contribution of each data point to the final calibration. The initial uncertainty of 0.1 °C for temperature is 0.018 K−2 after conversion to 1/T2. The resulting slopes and intercepts of the Δ47–temperature regressions are seen in Table 2, with corresponding errors. With the successive inclusion of the two other species, there is no significant change or offset in slope or intercept relative to the initial G. oceanica regression. All regression lines fall within 0.0012 ‰ error of each other, which shows that with the available data and at the current analytical precision there is no discernible species- or genus-specific vital effect that affects the Δ47–temperature relationship.
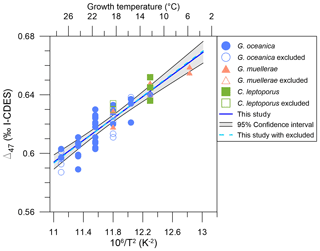
Figure 6Δ47 values compared to temperature (in K) for cultured coccoliths. York regression and its 95 % confidence interval are shown as a blue line and light grey envelope. The species are colour- and symbol-coded following Fig. 2. Blue circles are G. oceanica, orange triangles are G. muellerae, and green triangles are C. leptoporus. Empty symbols are excluded data but are still included for illustration and the coccolith Δ47–temperature calibration.
Table 2Slope and intercepts with 1σ for the Δ47–temperature regression using the Williamson–York bivariate least-squares method.
Secondly, we tested the potential influence of variable carbonate chemistry and the carbon and oxygen vital effects on the Δ47–temperature relationship. To this end, we normalized our Δ47 data against the Meinicke et al. (2020) Δ47–temperature calibration at each temperature to generate residual values (ΔΔ47,off). Pearson correlation tests were then performed for the normalized ΔΔ47,off residual values against the different carbonate chemistry parameters. The resulting Pearson correlation coefficients are shown in Table 3. Apart from a weak, nonsignificant, positive and negative correlation for the batch and continuous culture setup ΔΔ47,off and pH, respectively, as well as a moderate but significant positive correlation between the continuous culture setup ΔΔ47,off and ΔΔ18Ooff, there are no conclusive or significant correlations for all measurements and experimental setups. There is no significant difference in the normalized ΔΔ47,off values between batch and continuous culture setups (t test; t(38) = 0.35, p value = 0.73), further indicating that carbonate chemistry does not have an effect on the measured Δ47 value. The nonsignificant correlation in Δ13Cc-DIC and ΔΔ47,off for all setups shows that the processes responsible for the carbon isotope vital effect do not significantly influence the coccolith Δ47–temperature relationship (Fig. S6). While there is a moderate, significant positive correlation between ΔΔ18Ooff and ΔΔ47,off, it is only present for the continuous culture setup and has an r2 of 0.20. Thus, there is no evidence of an important impact of the oxygen isotope vital effect on coccolith Δ47 values.
Table 3Pearson correlation coefficients (ρ) between ΔΔ47,off and pH, DIC, and CO2(aq) for all measurements, continuous culture, and batch culture setup. An asterisk indicates where the p value is < 0.05.

Thirdly, average Δ47 values were calculated for each species at every growth temperature. These temperature-weighted averages can highlight bias from a low number of measurement replicates at certain growth temperatures, such as at 6 and 27 °C. The resulting Δ47–temperature regression is indistinguishable from regressions using individual Δ47 sample data points (±6.1 ppm; Table 2).
Lastly, if there are no species-specific or carbonate-chemistry-related vital effects in the Δ47–temperature relationship, the data that were initially excluded due to the poorly characterized carbonate system (see Sect. 3.1.1) and poor constraining of the stable carbon and oxygen isotope fractionations (i.e. data points with ΔDIC≥ 20 % or ΔpH≥ 0.20) can also be included. If the Δ47–temperature relationship in coccoliths is purely related to temperature, this will not interfere with the resulting calibration. Indeed, the slope and intercept fall within error of the other regressions, albeit with a slightly higher slope and lower intercept, as seen in Table 2 and Fig. 6.
Based on the above analysis we conclude that all 55 data points can be considered for a coccolith Δ47–temperature calibration (T in K, ±1σ).
4.4 A unified coccolith Δ47–temperature calibration?
The similar culturing study of three coccolithophore species by Katz et al. (2017) also found that species-specific vital effects do not correlate with variations in the Δ47–temperature relationship and found a consistent Δ47–temperature correlation. However, the study was conducted before the introduction of the I-CDES standardization methodology using carbonates and used gas-based standardization; consequently the data could have a systematic difference that cannot be resolved with certainty. Thus, when comparing to other calibration studies we will not include Katz et al. (2017) in the dataset and use Eq. (4) as a coccolith Δ47–temperature calibration, which is only based on our culture data in the I-CDES framework.
4.5 A coccolith- or biogenic-specific calibration?
In Figs. 7 and 8 we compare our data with previous biogenic and inorganic carbonate Δ47–temperature studies, with the method of temperature measurement or estimations in Table 4. The slopes and the intercepts of the equations with a limited number of replicates and a limited range of temperatures have larger uncertainties (Bonifacie et al., 2017; Fernandez et al., 2017; Kelson et al., 2017) and all datasets have significant scatter due to their small variability. If the data are not in I-CDES already, the datasets are converted to I-CDES using the methodology described in Bernasconi et al. (2021).
Table 4Average ΔΔ47,off residuals relative to our dataset comparing our coccolith calibration equations and those from the Peral et al. (2018, 2022), Meinicke et al. (2020, 2021), Daëron and Vermeesch (2024) MIT, Daëron and Gray (2023) original temperatures, and Daëron and Gray (2023) recalculated temperatures. Equivalent temperature offset is based on the equivalent Δ47 value at the average growth temperature (18.71 °C) using Eq. (4). Method of measurement or estimation of temperatures for each study is given.
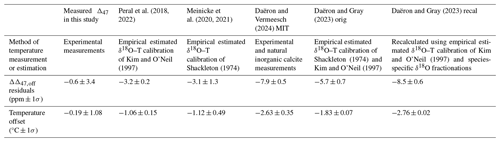
Figure 7Δ47 versus temperature for coccolith calcite and previous biogenic and inorganic calibrations. The York linear fit and 95 % confidence interval for the unified coccolith calcite Δ47–temperature are shown as a blue line with grey shading. Daëron and Gray (2023 orig; dash–dot, dot–dash brown line), Daëron and Gray (2023 recal; dash–dot, dot–dash grey line), and Daëron and Vermeesch (2024 MIT; dashed orange line).
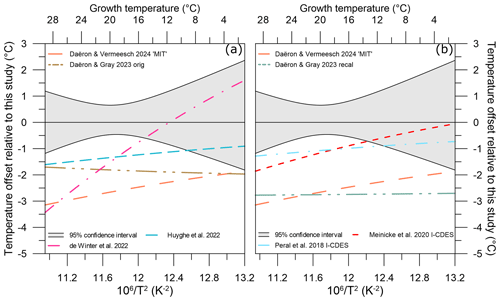
Figure 8Temperature offset of different Δ47–temperature calibrations relative to our study's equivalent temperature. (a) Temperature offsets of two non-foraminifera biogenic carbonate calibration studies: de Winter et al. (2022; dash–dot–dash pink line) and Huyghe et al. (2022; dashed blue line). (b) Temperature offsets of two planktic foraminifera biogenic carbonate calibration studies: Peral et al. (2018; dash–dot–dash light blue line) and Meinicke et al. (2020; dashed red line), using original published temperatures. Other included studies' calibration data are colour-coded following Fig. 7. The 95 % confidence interval for our study is given as light grey shading.
While overall the individual Δ47 values for coccolith calcite fall within the scatter of the previous calibrations, our coccolith Δ47–temperature regression systematically plots above it. To identify and evaluate how this would impact temperature reconstructions, a similar exercise to Sect. 4.3 was performed. At all growth temperatures, a Δ47 value was calculated from each calibration. ΔΔ47,off residuals were then generated through comparison with our study's calibration at each temperature.
All non-coccolith calibrations yield negative residuals (ΔΔ47,off) relative to our coccolith Δ47–temperature calibration. This results in lower calculated Δ47 temperatures compared to our calibration (Fig. 8). Positive offsets were found for aragonite (Calderescu et al., 2021; de Winter et al., 2022) and brachiopods (Bajnai et al., 2018; Davies et al., 2023; Letulle et al., 2023) when compared to the Anderson et al. (2021) inorganic carbonate calibration. However, brachiopods show a complex system of kinetic disequilibrium effects in both Δ47 and Δ48 associated with early-stage CO2 absorption in the DIC, and do not have the CA enzyme. In addition, de Winter et al. (2022) argued that the Δ47–temperature relationship is nonlinear at temperatures > 100 °C and calibrations are substantially biased by data with a large temperature range such as in Anderson et al. (2021) when used at temperatures < 30 °C. The MIT calibration uses only the inorganic carbonates from the Anderson et al. (2021) dataset and indeed yields lower and non-overlapping ΔΔ47,off residuals relative to our calibration (Fig. 8). Using only the data < 30 °C from Anderson et al. (2021) to calculate a temperature regression does yield overlapping ΔΔ47,off residuals relative to our calibration; however, due to the steeper slope of the calibration, the ΔΔ47,off residuals are strongly temperature-dependent. The nonlinearity of the Δ47–temperature relationship is thus most likely not a major cause for the consistent offset of our coccolith calibration (see Table S3).
Both the variability and absolute ΔΔ47,off residuals differ for all compared calibrations. The Daëron and Gray (2023) and MIT calibrations yield ΔΔ47,off residuals that do not overlap with our dataset between 2–28 °C. The original Peral et al. (2018, 2022), Meinicke et al. (2020, 2021), de Winter et al. (2022), and Huyghe et al. (2022) calibrations do yield ΔΔ47,off residuals within the uncertainty of our dataset. Temperature offsets at the average growth temperature of our dataset, 18.7 °C, are between 0 and 4 °C for the different calibrations but vary in magnitude at different temperatures; see Table 4.
The high variability of the temperature offsets over the given temperature range for certain biogenic carbonate studies such as de Winter et al. (2022) suggests that nonuniform disequilibrium effects are present. As such, two conclusions can be derived and discussed: there is a coccolith-specific calibration or the calcification temperatures for previous studies are underestimated. Our well-constrained coccolith cultures allow for the exclusion of effects from environmental variabilities, such as CO2(aq) (here between 5.6 and 43.8 µM), pH (here between 7.9 and 8.6 units), coccolithophore growth rate, and vital effects on Δ47 values as discussed in Sect. 4.3. The processes responsible for vital effects observed in the coccolith carbon and oxygen isotopes do not lead to corresponding variations in the Δ47–temperature relationship, where ΔΔ47,off values are within 0.0012 ‰ despite up to ∼ 3 ‰ variability for carbon and oxygen isotopes for our experimental conditions. This is below our analytical uncertainty for Δ47; thus, while we cannot fully rule out the possibility that vital effects do not affect coccolith ΔΔ47,off residuals, the offset from the inorganic equilibrium calibration must be similar at all temperatures, systematic, and unrelated to vital effects. Indeed, for the available dataset and range in carbonate chemistry no species- or genus-related effects are present, although this must be further examined in future studies with in situ temperatures such as sediment traps or cultures with a wider range of seawater chemistry.
To a certain degree, another potential cause of the offset of our coccolith from previous biogenic carbonate calibrations is also likely the uncertainty related to the determination of calcification temperatures in previous calibrations based on foraminifera collected from core tops. Often indirectly inferred or estimated from other proxies, these uncertainties in the calcification temperatures can result in large variabilities, obscure potential effects related to temperature, and result in differences between calibrations. In particular, there is no directly measured constraint on the calcification temperatures, only inference and empirical relationships from other proxies. Meinicke et al. (2020) compared and discussed three different methods of determining the calcification temperature of the foraminifera used in their study and concluded that using their oxygen isotope composition and the temperature calibration of Shackleton et al. (1974) provides the most robust estimate of the true calcification temperatures. In an extensive study, Daëron and Gray (2023) redetermined the oxygen isotope fractionation in the foraminifera species that were used by Meinicke et al. (2020, 2021) and Peral et al. (2018, 2022) for their clumped isotope calibrations using data from foraminifera from laboratory cultures and plankton tows. They concluded that foraminifera calcification temperatures are best approximated by using the Kim and O'Neil (1997) calibration with species-specific offsets. They tested this concept by comparing the calcification temperatures determined for the Meinicke et al. (2020, 2021) and Peral et al. (2018, 2022) datasets with reconstructed water column temperatures at the sites of the core tops (Fig. 7 in Daëron and Gray, 2023) and concluded that this is a better estimate of calcification temperatures than previously published. The applications of these revised species-specific oxygen isotope fractionation curves result in a nonsystematic 1–2 °C offset toward colder temperatures from the original studies of Peral et al. (2018, 2022) and Meinicke et al. (2020, 2021; Fig. 8), especially at temperatures below 15 °C, and lead to a coincidence between these two foraminifera-based calibrations and the inorganic calibration of Anderson et al. (2021). A close examination of Fig. 7 in Daëron and Grey (2023), however, shows that the majority of their discordant samples (i.e. those that record temperatures outside the measured water column temperatures at the living depth of the specific species) are on the cold part of the calibration; 12 are below 13 °C. Moreover, at least seven of the ones that are considered concordant as the error bars overlap with the measured temperatures have an average that is 1–2 °C below the lowest measured temperature. About 27 of the 37 data points below 15 °C are either colder than the lowest temperature or only overlap with the coldest temperatures of the observed water column temperature range. We suggest that this would impart a cold bias to those samples. Further, the proposed extension of the calcification depths to 500 m would also give a cold bias and is not supported by foraminifera living depths (Schiebel and Hembleben, 2017). Based on these considerations, we suggest that the use of calcification temperatures from oxygen isotopes needs further testing, ideally on laboratory-cultured specimens, and warrants caution and consideration.
The tightly controlled growth temperatures of our coccolithophore cultures eliminate the problem of uncertain calcification temperatures as in the case of foraminifera calibrations (Meinicke et al., 2020; Daëron and Gray, 2023). Indeed, the offsets of our coccolith calibration relative to the inorganic MIT calibration are consistent, with little variability, and suggest a uniform disequilibrium mechanism (ΔΔ47,off = −0.0079 ± 0.0005 ‰). The purely foraminifera-based calibrations, using both the original and recalculated calcification temperatures of Peral et al. (2018, 2022) and Meinicke et al. (2020, 2021), show more variability relative to the inorganic MIT calibration ( 0.0023 ± 0.0012 ‰ and −0.0013 ± 0.0015 ‰, respectively) and suggest variable disequilibrium effects. However, at this stage it is difficult to state whether this is due to general foraminifera or species-specific disequilibria or due to uncertainties related to the calcification temperature. This highlights the importance of and uncertainties related to the calcification temperature and their implications.
Modelling studies for inorganic calcite, grown in the presence of CA and at growth rates and pH ranges relevant for coccolithophores, show offsets for carbon and oxygen and find kinetic disequilibrium effects that are pH- and crystal-growth-rate-dependent (Hill et al., 2014; Watkins and Hunt, 2015; Uchikawa et al., 2021; Watkins and Devriendt, 2022). Between our cultured temperatures of 6–27 °C and in saline conditions, a shift from pH 8 to 8.5 can give an offset of ∼ 3 ‰ for δ18O and ∼ 90 ppm for Δ47 at very fast crystal growth rates (10−5 mol m−2 s−1) and offsets of ∼ 1 ‰ for δ18O and ∼ 1 ppm for Δ47 for 1000 times slower crystal growth rates (10−7 mol m−2 s−1; Fig. 6 in Watkins and Devriendt, 2022). The latter is comparable to estimated coccolith calcification rates of 10−7–10−8 mol m−2 s−1 (Langer et al., 2006, 2012; Sett et al., 2014). Also, the modelled difference of Δ47 between HCO relative to CO at 25 °C, with a difference of ∼ 5 pH units, and saline conditions is ∼ 0.034 ‰ and ∼ 7 ‰ for δ18O (Hill et al., 2014; Watkins and Devriendt, 2022). Thus, the difference due to calcification mechanisms by regulating internal pH and thus the HCO ratio that has been postulated to drive the carbon and oxygen vital effect differences between different coccolithophore and foraminifera species cannot be applied on its own to explain the Δ47 offset from equilibrium (Spero et al., 1997; Rickaby et al., 2010; Ziveri et al., 2012; Devriendt et al., 2017; Holtz et al., 2017). Rather, a crystal growth rate variability between species is likely the cause of the 3 ‰ offset in ΔΔ18Ooff between C. leptoporus and G. oceanica and only ±1.2 ppm difference in Δ47. Perhaps a difference due to species-specific coccolith-associated proteins and CAPs that can influence different calcite saturation states within the coccolith vesicle and lead to more crystal growth rate variability can also have an effect (Gal et al., 2016; Lee et al., 2016; Walker et al., 2019). Other effects may also be at play, such as species-specific metabolic pathways unique to coccolithophores, diffusion of cations or DIC species into the coccolith vesicle, surface speciation, or crystal surface interactions with cations from solution (Hermoso, 2014; Sand et al., 2014; Gal et al., 2017; Taylor et al., 2017). However, while the offset from the equilibrium inorganic calcite is systematic across the three coccolithophore species cultured here, no definitive cause of this observed offset can be definitively determined in this study, and there is more work needed to identify the disequilibrium processes for other coccolithophore species. Future studies with constrained and in situ temperature measurements such as in sediment traps (Clark et al., 2024a) or cultures are recommended to disentangle and validate our findings of this coccolith clumped isotope disequilibrium.
In this study we cultured three species of coccolithophores (Gephyrocapsa oceanica, G. muellerae, and Calcidiscus leptoporus) in continuous and batch culture setups for temperatures between 6 and 27 °C and CO2(aq) between 5 and 45 µM. Vital effects in carbon and oxygen isotopes in coccoliths were observed and their magnitude is consistent with previous culturing studies. We show that for our well-constrained continuous culture setup there are no systematic external environmental influences from pH, DIC, or CO2(aq) on the carbon and oxygen isotopic values for both G. oceanica and G. muellerae. Both species precipitate coccolith calcite close to isotopic equilibrium with the water (Δ13Cc-DIC= ±1.5 ‰; ΔΔ18Ooff= ±1 ‰). C. leptoporus shows pronounced vital effects in both carbon and oxygen isotopes, although no clear physiological conclusions can be drawn on the source of these vital effects. A calcification model would aid in describing the sources of the vital effects.
We establish a coccolith-specific Δ47–temperature calibration and observe a consistent offset from previous inorganic calibrations ( −0.0079 ± 0.0005 ‰), which suggests disequilibrium effects in coccolith Δ47 for all three coccolithophore species. There are, however, no effects on the calibration that are due to differences in environmental parameters or species. Our coccolith Δ47 data indicate that coccolithophores precipitate coccolith calcite in clumped isotope disequilibrium with their environment. Our coccolith Δ47–temperature calibration (Eq. 4), with well-constrained temperatures, also shows offsets from previous biogenic carbonate calibration studies. Thus, we suggest the use of our coccolith Δ47–temperature calibration to reconstruct temperatures from well-screened and/or well-preserved coccolith calcite, regardless of species.
All data presented in this paper are available in the EarthChem database at https://doi.org/10.60520/IEDA/113247 (Clark et al., 2024b).
The supplement related to this article is available online at: https://doi.org/10.5194/cp-20-2081-2024-supplement.
AJC: cell culture, analyses, and writing. ITR: cell culture and analyses. MJ: analyses, SMB: supervision, analyses, funding acquisition, and writing. HMS: supervision, funding acquisition, and writing.
The contact author has declared that none of the authors has any competing interests.
Publisher's note: Copernicus Publications remains neutral with regard to jurisdictional claims made in the text, published maps, institutional affiliations, or any other geographical representation in this paper. While Copernicus Publications makes every effort to include appropriate place names, the final responsibility lies with the authors.
The authors thank Anne-Greet Bittermann of ScopeM for support and assistance in this work. We would like to thank Luc Beaufort and two anonymous reviewers for their constructive comments and editorial support.
This work was supported by ETH core funding (ETH-02 21-1) and an SNF grant (no. 200021_182070).
This paper was edited by Luc Beaufort and reviewed by two anonymous referees.
Anderson, N., Kelson, J., Kele, S., Daëron, M., Bonifacie, M., Horita, J., Mackey, T., John, C., Kluge, T., Petschnig, P., Jost, A., Huntington, K., Bernasconi, S., and Bergmann, K.: A Unified Clumped Isotope Thermometer Calibration (0.5–1,100 °C) Using Carbonate-Based Standardization, Geophys. Res. Lett., 48, e2020GL092069, https://doi.org/10.1029/2020GL092069, 2021.
Bajnai, D., Fiebig, J., Tomašových, A., Milner Garcia, S., Rollion-Bard, C., Raddatz, J., Löffler, N., Primo-Ramos, C., and Brand, U.: Assessing kinetic fractionation in brachiopod calcite using clumped isotopes, Sci. Rep., 8, 533, https://doi.org/10.1038/s41598-017-17353-7, 2018.
Barry, J., Hall-Spencer, J., and Tyrrell, T.: In situ perturbation experiments: natural venting sites, spatial/temporal gradients in ocean pH, manipulative in situ pCO2 perturbations, in: Guide to best practices for ocean acidification research and data reporting, edited by: Riebesell, U., Fabry, V., Hansson, L., and Gattuso, J.-P., Office for Official Publications of the European Communities, Luxembourg, 123–136, https://doi.org/10.2777/66906, 2012.
Berger, W.: Deep-sea carbonates: evidence for a coccolith lysocline, Deep-Sea Res., 20, 917–921, 1973.
Berman, A., Hanson, J., Leiserowitz, L., Koetzle, T., Weiner, S., and Addadi, B.: Biological Control of Crystal Texture: A Widespread Strategy for Adapting Crysta Properties to Function, Science, 259, 776–779, https://doi.org/10.1126/science.259.5096.776, 1993.
Bernasconi, S., Hu, B., Wacker, U., Fiebig, J., Breitenbach, S., and Rutz, T.: Background effects on Faraday collectors in gas-source mass spectrometry and implications for clumped isotope measurements, Rapid Commun. Mass Sp., 27, 603–612, https://doi.org/10.1002/rcm.6490, 2013.
Bernasconi, S., Müller, I., Bergmann, K., Breitenbach, S., Fernandez, A., Hodell, D., Jaggi, M., Meckler, A., Millan, I., and Ziegler, M.: Reducing Uncertainties in Carbonate Clumped Isotope Analysis Through Consistent Carbonate-Based Standardization, Geochem. Geophy. Geosy., 19, 2895–2914, https://doi.org/10.1029/2017GC007385, 2018.
Bernasconi, S., Daëron, M., Bergmann, K., Bonifacie, M., Meckler, A., Affek, H., Anderson, N, Bajnai, D., Barkan, E., Beverly, E., Blamart, D., Burgener, L., Calmels, D., Chaduteau, C., Clog, M., Davidheiser-Kroll, B., Davies, A., Dux, F., Eiler, J., Elliott, B., Fetrow, A., Fiebig, J., Goldberg, S., Hermoso, M., Huntington, K., Hyland, E., Ingalls, M., Jaggi, M., John, C., Jost, A., Katz, S., Kelson, J., Kluge, T., Kocken, I., Laskar, A., Leutert, T., Liang, D., Lucarelli, J., Mackey, T., Mangenot, X., Meinicke, N., Modestou, S., Muller, I., Murray, S., Neary, A., Packard, N., Passey, B., Pelletier, E., Petersen, S., Piasecki, A., Schauer, A., Snell, K.E., Swart, P., Tripati, A., Upadhyay, D., Vennemann, T., Winkelstern, I., Yarian, D., Yoshida, N., Zhang, N., and Ziegler, M.: InterCarb: A Community Effort to Improve Interlaboratory Standardization of the Carbonate Clumped Isotope Thermometer Using Carbonate Standards, Geochem. Geophy. Geosy. 22, e2020GC009588, https://doi.org/10.1029/2020GC009588, 2021.
Blanco-Ameijeiras, S., Stoll, H., Zhang, H., and Hopkinson, B.: Influence of temperature and CO2 on plasma-membrane permeability to CO2 and HCO in the marine haptophytes Emiliania huxleyi and Calcidiscus leptoporus (Prymnesiophyceaea), J. Phycol., 56, 1283–1294, https://doi.org/10.1111/jpy.13017, 2020.
Bolton, C. and Stoll, H.: Late Miocene threshold response of marine algae to carbon dioxide limitation, Nature, 500, 558–562, https://doi.org/10.1038/nature12448, 2013.
Bonifacie, M., Calmels, D., Eiler, J., Horita, J., Chaduteau, C., Vasconcelos, C., Agrinier, P., Katz, A., Passey, B., Ferry, J., and Bourrand, J.: Calibration of the dolomite clumped isotope thermometer from 25 to 350 °C, and implications for a universal calibration for all (Ca, Mg, Fe)CO3 carbonates, Geochim. Cosmochim. Ac., 200, 255–279, https://doi.org/10.1016/j.gca.2016.11.028, 2017.
Brownlee, C., Wheeler, G., and Taylor, A.: Coccolithophore biomineralization: New questions, new answers, Semin. Cell Dev. Biol., 46, 11–16, https://doi.org/10.1016/j.semcdb.2015.10.027, 2015.
Caldarescu, D., Sadatzki, H., Andersson, C., Schafer, P., Fortunato, H., and Meckler, A.: Clumped isotope thermometry in bivalve shells: A tool for reconstructing seasonal upwelling, Geochim. Cosmochim. Ac., 294, 174–191, https://doi.org/10.1016/j.gca.2020.11.019, 2021.
Candelier, Y., Minoletti, F., Probert, I., and Hermoso, M.: Temperature dependence of oxygen isotope fractionation in coccolith calcite: A culture and core top calibration of the genus Calcidiscus, Geochim. Cosmochim. Ac., 100, 264–281, 2013.
Cantrell, C. A.: Technical Note: Review of methods for linear least-squares fitting of data and application to atmospheric chemistry problems, Atmos. Chem. Phys., 8, 5477–5487, https://doi.org/10.5194/acp-8-5477-2008, 2008.
Clark, A., Jaggi, M., Bernasconi, S., and Stoll, H.: Do coccolith clumped isotopes record sea surface temperatures? A sediment trap perspective, EGU General Assembly 2024, Vienna, Austria, 14–19 Apr 2024, EGU24-15587, https://doi.org/10.5194/egusphere-egu24-15587, 2024a.
Clark, A., Torres-Romero, I., Jaggi, M., Bernasconi, S., and Stoll, H.: Coccolith specific clumped isotope calibration data, Version 1.0, Interdisciplinary Earth Data Alliance (IEDA), EarthChem [data set], https://doi.org/10.60520/IEDA/113247, 2024b.
Clark, I., Fontes, J., and Fritz, P.: Stable isotope disequilibria in travertine from high pH waters: Laboratory investigations and field observations from Oman, Geochim. Cosmochim. Ac., 56, 2041–2050, https://doi.org/10.1016/0016-7037(92)90328-G, 1992.
Coplen, T.: Calibration of the calcite-water oxygen-isotope geothermometer at Devils Hole, Nevada, a natural laboratory, Geochim. Cosmochim. Ac., 71, 3948–3957, https://doi.org/10.1016/j.gca.2007.05.028, 2007.
Daëron, M.: Full Propagation of Analytical Uncertainties in Δ47 Measurements, Geochem. Geophy. Geosy., 22, e2020GC009592, https://doi.org/10.1029/2020GC009592, 2021.
Daëron, M. and Gray, W.: Revisiting oxygen-18 and clumped isotopes in planktic and benthic foraminifera, Paleoceanography and Paleoclimatology, 38, 2023–2032, https://doi.org/10.1029/2023PA004660, 2023.
Daëron, M. and Vermeesch, P.: Omnivariant Generalized Least Squares regression: Theory, geochronological applications, and making the case for reconciled Δ47 calibrations, Chem. Geol., 647, 121881, https://doi.org/10.1016/j.chemgeo.2023.121881, 2024.
Daëron, M., Blamart, D., Peral, M., and Affek, H.: Absolute isotopic abundance ratios and the accuracy of Δ47 measurements, Chem. Geol., 442, 83–96, https://doi.org/10.1016/j.chemgeo.2016.08.014, 2016.
Daëron, M., Drysdale, R., Peral, M., Huyghe, D., Blamart, D., Coplen, T., Lartaud, F., and Zanchetta, G.: Most Earth-surface calcites precipitate out of isotopic equilibrium, Nat. Commun., 10, 429, 10.1038/s41467-019-08336-5, 2019.
Davies, A., Guo, W., Bernecker, M., Tagliavento, M., Raddatz, J., Gischler, E., Flögel, S., and Fiebig, J.: Dual clumped isotope thermometry of coral carbonate, Geochim. Cosmochim. Ac., 338, 66–78, https://doi.org/10.1016/j.gca.2022.10.015, 2022.
Davies, A., Brand, U., Tagliavento, M., Bitner, M., Bajnai, D., Staudigel, P., Bernecker, M., and Fiebig, J.: Isotopic disequilibrium in brachiopods disentangled with dual clumped isotope thermometry, Geochim. Cosmochim. Ac., 359, 135–147, https://doi.org/10.1016/j.gca.2023.08.005, 2023.
de Winter, N., Witbaard, R., Kocken, I., Müller, I., Guo, J., Goudsmit, B., and Ziegler, M.: Temperature Dependence of Clumped Isotopes (Δ47) in Aragonite, Geophys. Res. Lett., 49, e2022GL099479, https://doi.org/10.1029/2022GL099479, 2022.
Defliese, W. and Lohmann, K.: Non-linear mixing effects on mass-47 CO2 clumped isotope thermometry: Patterns and implications, Rapid Commun. Mass Sp., 29, 901–909, https://doi.org/10.1002/rcm.7175, 2015.
Deng, X., Li, Q., Su, J., Liu, C., Atekwana, E., and Cai, W.: Performance evaluations and applications of a δ13C-DIC analyzer in seawater and estuarine waters, Sci. Total Environ., 833, 155013, https://doi.org/10.1016/j.scitotenv.2022.155013, 2022.
Dennis, K. and Schrag, D.: Clumped isotope thermometry of carbonatites as an indicator of diagenetic alteration, Geochim. Cosmochim. Ac., 74, 4110–4122, https://doi.org/10.1016/j.gca.2010.04.005, 2010.
Devriendt, L., Watkins, J., and McGregor, H.: Oxygen isotope fractionation in the CaCO3-DIC-H2O system, Geochim. Cosmochim. Ac., 214, 115–142, https://doi.org/10.1016/j.gca.2017.06.022, 2017.
Dickson, A.: Standard potential of the reaction: AgCl(s) + 1/2H2(g) = Ag(s) + HCl(aq), and the standard acidity constant of the ion HSO in synthetic sea water from 273.15 to 318.15 K, J. Chem. Thermodyn., 22, 113–127, https://doi.org/10.1016/0021-9614(90)90074-Z, 1990.
Dietzel, M., Usdowski, E., and Hoefst, J.: Chemical and C- and O-isotope evolution of alkaline drainage waters and the precipitation of calcite, Appl. Geochem., 7, 177–184, https://doi.org/10.1016/0883-2927(92)90035-2, 1992.
Drury, A. and John, C.: Exploring the potential of clumped isotope thermometry on coccolith-rich sediments as a sea surface temperature proxy, Geochem. Geophy. Geosy., 17, 4092–4104, https://doi.org/10.1002/2016GC006459, 2016.
Eiler, J.: “Clumped-isotope” geochemistry-The study of naturally-occurring, multiply-substituted isotopologues, Earth Planet. Sc. Lett., 262, 309–327, https://doi.org/10.1016/j.epsl.2007.08.020, 2007.
Eiler, J., and Schauble, E.: 18O13C16O in Earth's atmosphere, Geochim. Cosmochim. Ac., 68, 4767–4777, https://doi.org/10.1016/j.gca.2004.05.035, 2004.
Elzenga, J., Prins, H., and Stefels, J.: The role of extracellular carbonic anhydrase activity in inorganic carbon utilization of Phaeocystis globosa (Prymnesiophyceae): A comparison with other marine algae using the isotopic disequilibrium technique, Limnol. Oceanogr., 45, 372–380, https://doi.org/10.4319/lo.2000.45.2.0372, 2000.
Falster, G., Delean, S., and Tyler, J.: Hydrogen Peroxide Treatment of Natural Lake Sediment Prior to Carbon and Oxygen Stable Isotope Analysis of Calcium Carbonate, Geochem. Geophy. Geosy., 19, 3583–3595, https://doi.org/10.1029/2018GC007575, 2018.
Fernandez, A., Müller, I., Rodríguez-Sanz, L., van Dijk, J., Looser, N., and Bernasconi, S.: A Reassessment of the Precision of Carbonate Clumped Isotope Measurements: Implications for Calibrations and Paleoclimate Reconstructions, Geochem. Geophy. Geosy., 18, 4375–4386, https://doi.org/10.1002/2017GC007106, 2017.
Fiebig, J., Daëron, M., Bernecker, M., Guo, W., Schneider, G., Boch, R., Bernasconi, S., Jautzy. J., and Dietzel, M.: Calibration of the dual clumped isotope thermometer for carbonates, Geochim. Cosmochim. Ac., 312, 235–256, https://doi.org/10.1016/j.gca.2021.07.012, 2021.
Frølich, S., Sørensen, H., Hakim, S., Marin, F., Stipp, S., and Birkedal, H.: Smaller calcite lattice deformation caused by occluded organic material in coccoliths than in mollusk shell, Cryst. Growth Des., 15, 2761–2767, https://doi.org/10.1021/acs.cgd.5b00118, 2015.
Gal, A., Wirth, R., Kopka, J., Fratzl, P., Faivre, D., and Scheffel, A.: Macromolecular recognition directs calcium ions to coccolith mineralization sites, Science, 353, 590–593, https://doi.org/10.1126/science.aaf7889, 2016.
Gal, A., Sviben, S., Wirth, R., Schreiber, A., Lasalle-Kaiser, B., Faivre, D., and Scheffel, A.: Trace-Element Incorporation into Intracellular Pools Uncovers Calcium-Pathways in a Coccolithophore, Adv. Sci., 4, 1700088, https://doi.org/10.1002/advs.201700088, 2017.
Ghosh, P., Adkins, J., Affek, H., Balta, B., Guo, W., Schauble, E., Schrag, D., and Eiler, J.: 13C–18O bonds in carbonate minerals: A new kind of paleothermometer, Geochim. Cosmochim. Ac., 70, 1439–1456, https://doi.org/10.1016/j.gca.2005.11.014, 2006.
Guo, W.: Kinetic clumped isotope fractionation in the DIC-H2O-CO2 system: Patterns, controls, and implications, Geochim. Cosmochim. Ac., 268, 230–257, https://doi.org/10.1016/j.gca.2019.07.055, 2020.
Guo, W. and Zhou, C.: Patterns and controls of disequilibrium isotope effects in speleothems: Insights from an isotope-enabled diffusion-reaction model and implications for quantitative thermometry, Geochim. Cosmochim. Ac., 267, 196–226, https://doi.org/10.1016/j.gca.2019.07.028, 2019.
Gupta, P., Noone, D., Galewsky, J., Sweeney, C., and Vaughn, B.: Demonstration of high-precision continuous measurements of water vapor isotopologues in laboratory and remote field deployments using wavelength-scanned cavity ring-down spectroscopy (WS-CRDS) technology, Rapid Commun. Mass Sp., 23, 2534–2542, https://doi.org/10.1002/rcm.4100, 2009.
Henriksen, K., Young, J., Brown, P., and Stipp, S.: Coccolith biomineralisation studied with atomic force microscopy, Palaeontology, 47, 725–743, https://doi.org/10.1111/j.0031-0239.2004.00385.x, 2004.
Herfort, L., Thake, B., and Roberts, J.: Acquisition and use of bicarbonate by Emiliania huxleyi, New Phytol., 156, 427–436, https://doi.org/10.1046/j.1469-8137.2002.00523.x, 2002.
Hermoso, M.: Coccolith-derived isotopic proxies in palaeoceanography: Where geologists need biologists, Cryptogamie, Algol, 35, 323–351, https://doi.org/10.7872/crya.v35.iss4.2014.323, 2014.
Hermoso, M., Horner, T., Minoletti, F., and Rickaby, R.: Constraints on the vital effect in coccolithophore and dinoflagellate calcite by oxygen isotopic modification of seawater, Geochim. Cosmochim. Ac., 141, 612–627, https://doi.org/10.1016/j.gca.2014.05.002, 2014.
Hermoso, M., Minoletti, F., Aloisi, G., Bonifacie, M., McClelland, H., Labourdette, N., Renforth, P., Chaduteau, C., and Rickaby, R.: An explanation for the 18O excess in Noelaerhabdaceae coccolith calcite, Geochim. Cosmochim. Ac., 189, 132–142, https://doi.org/10.1016/j.gca.2016.06.016, 2016.
Hill, P., Tripati, A., and Schauble, E.: Theoretical constraints on the effects of pH, salinity, and temperature on clumped isotope signatures of dissolved inorganic carbon species and precipitating carbonate minerals, Geochim. Cosmochim. Ac., 125, 610–652, https://doi.org/10.1016/j.gca.2013.06.018, 2014.
Holtz, L., Wolf-Gladrow, D., and Thoms, S.: Simulating the effects of light intensity and carbonate system composition on particulate organic and inorganic carbon production in Emiliania huxleyi, J. Theor. Biol., 372, 192–204, https://doi.org/10.1016/j.jtbi.2017.01.030, 2015.
Holtz, L., Wolf-Gladrow, D., and Thoms, S.: Stable carbon isotope signals in particulate organic and inorganic carbon of coccolithophores – A numerical model study for Emiliania huxleyi, J. Theor. Biol., 420, 117–127, https://doi.org/10.1016/j.jtbi.2015.02.024, 2017.
Houdan, A., Probert, I., Zatylny, C., Véron, B., and Billard, C.: Ecology of oceanic coccolithophores. I. Nutritional preferences of the two stages in the life cycle of Coccolithus braarudii and Calcidiscus leptoporus, Aquat. Microb. Ecol., 44, 291–301, https://doi.org/10.3354/ame044291, 2006.
Hu, B., Radke, J., Schlüter, H., Heine, F., Zhou, L., and Bernasconi, S.: A modified procedure for gas-source isotope ratio mass spectrometry: The long-integration dual-inlet (LIDI) methodology and implications for clumped isotope measurements, Rapid Commun. Mass Sp., 28, 1413–1425, https://doi.org/10.1002/rcm.6909, 2014.
Huntington, K. and Petersen, S.: Frontiers of Carbonate Clumped Isotope Thermometry, Annu. Rev. Earth Pl. Sc., 51, 611–641, https://doi.org/10.1146/annurev-earth-031621-085949, 2023.
Huyghe, D., Daëron, M., de Rafelis, M., Blamart, D., Sébilo, M., Paulet, Y., and Lartaud, F.: Clumped isotopes in modern marine bivalves, Geochim. Cosmochim. Ac., 316, 41–58, https://doi.org/10.1016/j.gca.2021.09.019, 2022.
Jautzy, J., Savard, M., Dhillon, R., Bernasconi, S., and Smirnoff, A.: Clumped isotope temperature calibration for calcite: Bridging theory and experimentation, Geochem. Perspect. Lett., 14, 36–41, https://doi.org/10.7185/geochemlet.2021, 2020.
John, C. and Bowen, D.: Community software for challenging isotope analysis: First applications of `Easotope' to clumped isotopes, Rapid Commun. Mass Sp., 30, 2285–2300, https://doi.org/10.1002/rcm.7720, 2016.
Katz, A., Bonifacie, M., Hermoso, M., Cartigny, P., and Calmels, D.: Laboratory-grown coccoliths exhibit no vital effect in clumped isotope (Δ47) composition on a range of geologically relevant temperatures, Geochim. Cosmochim. Ac., 208, 335–353, https://doi.org/10.1016/j.gca.2017.02.025, 2017.
Kele, S., Breitenbach, S., Capezzuoli, E., Meckler, A., Ziegler, M., Millan, I., Kluge, T., Deak, J., Hanselmann, K., John, C., Yan, H., Liu, Z., and Bernasconi, S.: Temperature dependence of oxygen- and clumped isotope fractionation in carbonates: A study of travertines and tufas in the 6–95 °C temperature range, Geochim. Cosmochim. Ac., 168, 172–192, https://doi.org/10.1016/j.gca.2015.06.032, 2015.
Keller, M., Seluin, R., Claus, W., and Guillard, R.: Media for the culture of oceanic ultraphytoplankton, J. Phycol., 23, 633–638, https://doi.org/10.1111/j.1529-8817.1987.tb04217.x, 1987.
Kelson, J., Huntington, K., Schauer, A., Saenger, C., and Lechler, A.: Toward a universal carbonate clumped isotope calibration: Diverse synthesis and preparatory methods suggest a single temperature relationship, Geochim. Cosmochim. Ac., 197, 104–131, https://doi.org/10.1016/j.gca.2016.10.010, 2017.
Kester, D., Duedall, I., Connors, D., and Pytkowicz, R.: Preparation of Artificial Seawater, Limnol. Oceanogr., 12, 176–179, https://doi.org/10.4319/lo.1967.12.1.0176, 1967.
Kim, S. and O'Neil, J.: Equilibrium and nonequilibrium oxygen isotope effects in synthetic carbonates, Geochim. Cosmochim. Ac., 61, 3461–3475, https://doi.org/10.1016/S0016-7037(97)00169-5, 1997.
Langer, G., Geisen, M., Baumann, K.-H., Kläs, J., Riebesell, U., Thoms, S., and Young, J. R.: Species-specific responses of calcifying algae to changing seawater carbonate chemistry, Geochem. Geophy. Geosy., 7, Q09006, https://doi.org/10.1029/2005GC001227, 2006.
Langer, G., Oetjen, K., and Brenneis, T.: Calcification of Calcidiscus leptoporus under nitrogen and phosphorus limitation, J. Exp. Mar. Biol. Ecol., 413, 131–137, 10.1016/j.jembe.2011.11.028, 2012.
Lee, K., Kim, T., Byrne, R., Millero, F., Feely, R., and Liu, Y.: The universal ratio of boron to chlorinity for the North Pacific and North Atlantic oceans, Geochim. Cosmochim. Ac., 74, 1801–1811, https://doi.org/10.1038/ncomms13144, 2010.
Lee, R., Mavridou, D., Papadakos, G., McClelland, H., and Rickaby, R.: The uronic acid content of coccolith-associated polysaccharides provides insight into coccolithogenesis and past climate, Nat. Commun., 7, 1801–1811, https://doi.org/10.1016/j.gca.2009.12.027, 2016.
Letulle, T., Gaspard, D., Daëron, M., Arnaud-Godet, F., Vinçon-Laugier, A., Suan, G., and Lécuyer, C.: Multi-proxy assessment of brachiopod shell calcite as a potential archive of seawater temperature and oxygen isotope composition, Biogeosciences, 20, 1381–1403, https://doi.org/10.5194/bg-20-1381-2023, 2023.
Leuker, T., Dickson, A., and Keeling, C.: Ocean pCO2 calculated from dissolved inorganic carbon, alkalinity, and equations for K1 and K2: validation based on laboratory measurements of CO2 in gas and seawater at equilibrium, Mar. Chem., 70, 105–119, https://doi.org/10.1016/S0304-4203(00)00022-0, 2000.
Leutert, T., Sexton, P., Tripati, A., Piasecki, A., Ho, S., and Meckler, A.: Sensitivity of clumped isotope temperatures in fossil benthic and planktic foraminifera to diagenetic alteration, Geochim. Cosmochim. Ac., 257, 354–372, https://doi.org/10.1016/j.gca.2019.05.005, 2019.
Levitt, N., Eiler, J., Romanek, C., Beard, B., Xu, H., and Johnson, C.: Near Equilibrium 13C–18O Bonding During Inorganic Calcite Precipitation Under Chemo-Stat Conditions, Geochem. Geophy. Geosy., 19, 901–920, https://doi.org/10.1002/2017GC007089, 2018.
Lewis, E. and Wallace, D.: Program Developed for CO2 System Calculations, CDIAC, ESS-DIVE repository [data set], https://doi.org/10.15485/1464255, 1998.
Matyash, V., Liebisch, G., Kurzchalia, T., Shevchenko, A., and Schwudke, D.: Lipid extraction by methyl-terf-butyl ether for high-throughput lipidomics, J. Lipid Res., 49, 1137–1146, https://doi.org/10.1194/jlr.D700041-JLR200, 2008.
McClelland, H., Bruggeman, J., Hermoso, M., and Rickaby, R.: The origin of carbon isotope vital effects in coccolith calcite, Nat. Commun., 8, 14511, https://doi.org/10.1038/ncomms14511, 2017.
McConnaughey, T.: 13C and 18O isotopic disequilibrium in biological carbonates: II. in vitro simulation of kinetic isotope effects, Geochim. Cosmochim. Ac., 53, 163–171, https://doi.org/10.1016/0016-7037(89)90283-4, 1989.
Meckler, A., Ziegler, M., Millán, M., Breitenbach, S., and Bernasconi, S.: Long-term performance of the Kiel carbonate device with a new correction scheme for clumped isotope measurements, Rapid Commun. Mass Sp., 28, 1705–1715, https://doi.org/10.1002/rcm.6949, 2014.
Meinicke, N., Ho, S., Hannisdal, B., Nürnberg, D., Tripati, A., Schiebel, R., and Meckler, A.: A robust calibration of the clumped isotopes to temperature relationship for foraminifers, Geochim. Cosmochim. Ac., 270, 160–183, https://doi.org/10.1016/j.gca.2019.11.022, 2020.
Meinicke, N., Reimi, M., Ravelo, A., and Meckler, A.: Coupled and Clumped Isotope Measurements Indicate Lack of Substantial Mixed Layer Cooling in the Western Pacific Warm Pool During the Last ∼ 5 Million Years, Paleoceanography, 36, e2020PA004115, https://doi.org/10.1029/2020PA004115, 2021.
Moolna, A. and Rickaby, R.: Interaction of the coccolithophore Gephyrocapsa oceanica with its carbon environment: Response to a recreated high-CO2 geological past, Geobiology, 10, 72–81, https://doi.org/10.1111/j.1472-4669.2011.00308.x, 2012.
Müller, I., Fernandez, A., Radke, J., van Dijk, J., Bowen, D., Schwieters, J., and Bernasconi, S.: Carbonate clumped isotope analyses with the long-integration dual-inlet (LIDI) workflow: scratching at the lower sample weight boundaries, Rapid Commun. Mass Sp., 31, 1057–1066, https://doi.org/10.1002/rcm.7878, 2017.
Müller, I., Rodriguez-Blanco, J., Storck, J., do Nascimento, G., Bontognali, T., Vasconcelos, C., Benning, L., and Bernasconi, S.: Calibration of the oxygen and clumped isotope thermometers for (proto-)dolomite based on synthetic and natural carbonates, Chem. Geol., 525, 1–17, https://doi.org/10.1016/j.chemgeo.2019.07.014, 2019.
Nimer, N., Guan, Q., and Merrett, M.: Extra- and intra-cellular carbonic anhydrase in relation to culture age in a high-calcifying strain of Emiliania huxleyi Lohmann, New Phytol., 126, 601–607, https://doi.org/10.1111/j.1469-8137.1994.tb02954.x, 1994.
Peral, M., Daëron, M., Blamart, D., Bassinot, F., Dewilde, F., Smialkowski, N., Isguder, G., Bonnin, J., Jorissen, F., Kissel, C., Michel, E., Vazquez Riveiros, N., and Waelbroeck, C.: Updated calibration of the clumped isotope thermometer in planktonic and benthic foraminifera, Geochim. Cosmochim. Ac., 239, 1–16, https://doi.org/10.1016/j.gca.2018.07.016, 2018.
Peral, M., Bassinot, F., Daëron, M., Blamart, D., Bonnin, J., Jorissen, F., Kissel, C., Michel, E., Waelbroeck, C., Rebaubier, H., and Gray, W.: On the combination of the planktonic foraminiferal , clumped (Δ47) and conventional (δ18O) stable isotope paleothermometers in palaeoceanographic studies, Geochim. Cosmochim. Ac., 339, 22–34, https://doi.org/10.1016/j.gca.2022.10.030, 2022.
Perez, F. and Fraga, F.: Association Constant of Fluoride and Hydrogen ions in seawater, Mar. Chem., 21, 168, https://doi.org/10.1016/0304-4203(87)90036-3, 1987.
Phelps, S., Stoll, H., Bolton, C., Beaufort, L., and Polissar, P.: Controls on Alkenone Carbon Isotope Fractionation in the Modern Ocean, Geochem. Geophy. Geosy., 22, e2021GC009658, https://doi.org/10.1029/2021GC009658, 2021.
Piasecki, A., Bernasconi, S., Grauel, A., Hannisdal, B., Ho, S., Leutert, T., Marchitto, T., Meinicke, N., Tisserand, A., and Meckler, N.: Application of Clumped Isotope Thermometry to Benthic Foraminifera, Geochem. Geophy. Geosy., 20, 2082–2090, https://doi.org/10.1029/2018GC007961, 2019.
Quinn, P., Bowers, R., Zhang, X., Wahlund, T., Fanelli, M., Olszova, D., and Read, B.: cDNA microarrays as a tool for identification of biomineralization proteins in the coccolithophorid Emiliania huxleyi (Haptophyta), Appl. Environ. Microb., 72, 5512–5526, https://doi.org/10.1128/AEM.00343-06, 2006.
Richier, S., Fiorini, S., Kerros, M., von Dassow, P., and Gattuso, J.: Response of the calcifying coccolithophore Emiliania huxleyi to low pH/high pCO2: From physiology to molecular level, Mar. Biol., 158, 551–560, https://doi.org/10.1007/s00227-010-1580-8, 2011.
Rickaby, R. E. M., Henderiks, J., and Young, J. N.: Perturbing phytoplankton: response and isotopic fractionation with changing carbonate chemistry in two coccolithophore species, Clim. Past, 6, 771–785, https://doi.org/10.5194/cp-6-771-2010, 2010.
Rost, B., Riebesell, U., Burkhardt, S., and Sültemeyer, D.: Carbon acquisition of bloom-forming marine phytoplankton, Limnol. Oceanogr., 48, 55–67, https://doi.org/10.4319/lo.2003.48.1.0055, 2003.
Sand, K., Pedersen, C., Sjöberg, S., Nielsen, J., Makovicky, E., and Stipp, S.: Biomineralization: Long-term effectiveness of polysaccharides on the growth and dissolution of calcite, Cryst. Growth Des., 14, 5486–5494, https://doi.org/10.1021/cg5006743, 2014.
Shackleton, N.: Attainment of isotopic equilibrium between ocean water and the benthonic foraminifera genus Uvigerina: isotopic changes in the ocean during the last glacial, in: Les Méthodes quantitatives d’étude des variations du climat au cours du Pléistocène, Colloques Internationaux du C.N.R.S., vol. 219, 203–209, 1974.
Schauble, E., Ghosh, P., and Eiler, J.: Preferential formation of 13C–18O bonds in carbonate minerals, estimated using first-principles lattice dynamics, Geochim. Cosmochim. Ac., 70, 2510–2529, https://doi.org/10.1016/j.gca.2006.02.011, 2006.
Schiebel, R., and Hemleben, C.: Planktic foraminifers in the modern ocean, Springer-Verlag Berlin Heidelberg, 366 pp., ISBN 978-3-662-50295-2, 2017.
Sett, S., Bach, L., Schulz, K., Koch-Klavsen, S., Lebrato, M., and Riebesell, U.: Temperature modulates coccolithophorid sensitivity of growth, photosynthesis and calcification to increasing seawater pCO2, PLoS ONE, 9, e88308, https://doi.org/10.1371/journal.pone.0088308, 2014.
Soto, A., Zheng, H., Shoemaker, D., Rodriguez, J., Read, B., and Wahlund, T.: Identification and preliminary characterization of two cDNAs encoding unique carbonic anhydrases from the marine alga Emiliania huxleyi, Appl. Environ. Microb., 72, 5500–5511, https://doi.org/10.1128/AEM.00237-06, 2006.
Spero, H., Bijma, J., Lea, D., andBemis, B.: Effect of seawater carbonate concentration on foraminiferal carbon and oxygen isotopes, Nature, 390, 497–500, https://doi.org/10.1038/37333, 1997.
Spooner, P., Guo, W., Robinson, L., Thiagarajan, N., Hendry, K., Rosenheim, B., and Leng, M.: Clumped isotope composition of cold-water corals: A role for vital effects?, Geochim. Cosmochim. Ac., 179, 123–141, https://doi.org/10.1016/j.gca.2016.01.023, 2016.
Stevenson, E., Hermoso, M., Rickaby, R., Tyler, J., Minoletti, F., Parkinson, I., Mokadem, F., and Burton, K.: Controls on stable strontium isotope fractionation in coccolithophores with implications for the marine Sr cycle, Geochim. Cosmochim. Ac., 128, 225–235, https://doi.org/10.1016/j.gca.2013.11.043, 2014.
Stoll, H., Ruiz Encinar, J., Ignacio Garcia Alonso, J., Rosenthal, Y., Probert, I., and Klaas, C.: A first look at paleotemperature prospects from Mg in coccolith carbonate: Cleaning techniques and culture measurements, Geochem. Geophy. Geosy., 2, 2000GC000144, https://doi.org/10.1029/2000GC000144, 2001.
Subhas, A., McCorkle, D., Quizon, A., McNichol, A., and Long, M.: Selective Preservation of Coccolith Calcite in Ontong-Java Plateau Sediments, Paleoceanography and Paleoclimatology, 34, 2141–2157, https://doi.org/10.1029/2019PA003731, 2019.
Thierstein, H. and Young, J. (Eds.): Coccolithophores, Springer Berlin Heidelberg, https://doi.org/10.1007/978-3-662-06278-4, 2004.
Swart, P., Murray, S., Staudigel, P., and Hodell, D.: Oxygen isotopic exchange between CO2 and phosphoric acid: Implications for the measurement of clumped isotopes in carbonates, Geochem. Geophy. Geosy., 20, 3730–3750, https://doi.org/10.1029/2019GC008209, 2019.
Taylor, A., Brownlee, C., and Wheeler, G.: Coccolithophore Cell Biology: Chalking Up Progress, Annu. Rev. Mar. Sci., 9, 283–310, https://doi.org/10.1146/annurev-marine-122414-034032, 2017.
Torres-Romero, I., Clark, A., Wijker, R., Jaggi, M., Zhang, H., and Stoll, H.: Temperature-dependent carbon isotope fractionation in coccolithophores, Front. Earth Sci., 12, 1331179, https://doi.org/10.3389/feart.2024.1331179, 2024.
Uchikawa, J. and Zeebe, R.: The effect of carbonic anhydrase on the kinetics and equilibrium of the oxygen isotope exchange in the CO2-H2O system: Implications for δ18O vital effects in biogenic carbonates, Geochim. Cosmochim. Ac., 95, 15–34, https://doi.org/10.1016/j.gca.2012.07.022, 2012.
Uchikawa, J., Chen, S., Eiler, J., Adkins, J., and Zeebe, R.: Trajectory and timescale of oxygen and clumped isotope equilibration in the dissolved carbonate system under normal and enzymatically-catalyzed conditions at 25 °C, Geochim. Cosmochim. Ac., 314, 313–333, https://doi.org/10.1016/j.gca.2021.08.014, 2021.
von Dassow, P., Muñoz Farías, P., Pinon, S., Velasco-Senovilla, E., and Anguita-Salinas, S.: Do Differences in Latitudinal Distributions of Species and Organelle Haplotypes Reflect Thermal Reaction Norms Within the Emiliania/Gephyrocapsa Complex?, Front. Mar. Sci., 8, 785763, https://doi.org/10.3389/fmars.2021.785763, 2021.
Walker, C., Heath, S., Salmon, D., Smirnoff, N., Langer, G., Taylor, A., Brownlee, C., andWheeler, G.: An Extracellular Polysaccharide-Rich Organic Layer Contributes to Organization of the Coccosphere in Coccolithophores, Front. Mar. Sci., 5, 00306, https://doi.org/10.3389/fmars.2018.00306, 2018.
Walker, J., Marzec, B., Lee, R., Vodrazkova, K., Day, S., Tang, C., Rickaby, R., and Nudelman, F.: Polymorph Selectivity of Coccolith-Associated Polysaccharides from Gephyrocapsa Oceanica on Calcium Carbonate Formation In Vitro, Adv. Funct. Mater., 29, 1807168, https://doi.org/10.1002/adfm.201807168, 2019.
Watkins, J. and Devriendt, L.: A Combined Model for Kinetic Clumped Isotope Effects in the CaCO3-DIC-H2O System, Geochem. Geophy. Geosy., 23, e2021GC010200, https://doi.org/10.1029/2021GC010200, 2022.
Watkins, J. and Hunt, J.: A process-based model for non-equilibrium clumped isotope effects in carbonates, Earth Planet. Sc. Lett., 432, 152–165, https://doi.org/10.1016/j.epsl.2015.09.042, 2015.
Watkins, J., Nielsen, L., Ryerson, F., and DePaolo, D.: The influence of kinetics on the oxygen isotope composition of calcium carbonate, Earth Planet. Sc. Lett., 375, 349–360, https://doi.org/10.1016/j.epsl.2013.05.054, 2013.
Watkins, J., Hunt, J., Ryerson, F., and DePaolo, D.: The influence of temperature, pH, and growth rate on the δ18O composition of inorganically precipitated calcite, Earth Planet. Sc. Lett., 404, 332–343, https://doi.org/10.1016/j.epsl.2014.07.036, 2014.
Williamson, J.: Least-squares fitting of a straight line, Can. J. Phys., 18, 1845–1847, https://doi.org/10.1139/p68-523, 1968.
York, D., Evensen, N., Martìnez, M., and De Basabe Delgado, J.: Unified equations for the slope, intercept, and standard errors of the best straight line, Am. J. Phys., 72, 367–375, https://doi.org/10.1119/1.1632486, 2004.
Zeebe, R. and Wolf-Gladrow, D.: CO2 in seawater: equilibrium, kinetics, isotopes, Elsevier Oceanography Series, Vol. 65, Gulf Professional Publishing, ISBN 0-444-50579-2, 2001.
Zhang, H., Blanco-Ameijeiras, S., Hopkinson, B., Bernasconi, S., Mejia, L., Liu, C., and Stoll, H.: An isotope label method for empirical detection of carbonic anhydrase in the calcification pathway of the coccolithophore Emiliania huxleyi, Geochim. Cosmochim. Ac., 292, 78–93, https://doi.org/10.1016/j.gca.2020.09.008, 2021.
Zhang, H., Torres-Romero, I., Anjewierden, P., Jaggi, M., and Stoll, H.: The DIC carbon isotope evolutions during CO2 bubbling: Implications for ocean acidification laboratory culture, Front. Mar. Sci., 9, 1045634, https://doi.org/10.3389/fmars.2022.1045634, 2022.
Ziveri, P., Stoll, H., Probert, I., Klaas, C., Geisen, M., Ganssen, G., and Young, J.: Stable isotope “vital effects” in coccolith calcite, Earth Planet Sc. Lett., 210, 137–149, https://doi.org/10.1016/S0012-821X(03)00101-8, 2003.
Ziveri, P., de Bernardi, B., Baumann, K., Stoll, H., and Mortyn, P.: Sinking of coccolith carbonate and potential contribution to organic carbon ballasting in the deep ocean, Deep-Sea Res. Pt. II, 54, 659–675, https://doi.org/10.1016/j.dsr2.2007.01.006, 2007.
Ziveri, P., Thoms, S., Probert, I., Geisen, M., and Langer, G.: A universal carbonate ion effect on stable oxygen isotope ratios in unicellular planktonic calcifying organisms, Biogeosciences, 9, 1025–1032, https://doi.org/10.5194/bg-9-1025-2012, 2012.





