Impact of millennial-scale oceanic variability on the Greenland ice-sheet evolution throughout the last glacial period

Temperature reconstructions from Greenland ice-sheet (GrIS) ice cores indicate the occurrence of more than 20 abrupt warmings during the last glacial period (LGP) known as Dansgaard-Oeschger (D-O) events. Although their ultimate cause is still debated, evidence from both proxy data and modelling studies robustly links these to reorganisations of the Atlantic Meridional Overturning Circulation (AMOC). During the LGP, the GrIS expanded as far as the continental shelf break and was thus more directly exposed to oceanic changes than in the present. Therefore oceanic temperature fluctuations on millennial timescales could have had a non-negligible impact on the GrIS. Here we assess the effect of millennial-scale oceanic variability on the GrIS evolution from the last interglacial to the present day. To do so, we use a three-dimensional hybrid ice-sheet–shelf model forced by subsurface oceanic temperature fluctuations, assumed to increase during D-O stadials and decrease during D-O interstadials. Since in our model the atmospheric forcing follows orbital variations only, the increase in total melting at millennial timescales is a direct result of an increase in basal melting. We show that the GrIS evolution during the LGP could have been strongly influenced by oceanic changes on millennial timescales, leading to oceanically induced ice-volume contributions above 1 m sea level equivalent (SLE). Also, our results suggest that the increased flux of GrIS icebergs as inferred from North Atlantic proxy records could have been triggered, or intensified, by peaks in melting at the base of the ice shelves resulting from increasing subsurface oceanic temperatures during D-O stadials. Several regions across the GrIS could thus have been responsible for ice mass discharge during D-O events, opening the possibility of a non-negligible role of the GrIS in oceanic reorganisations throughout the LGP.

1 Introduction

Ice cores from the Greenland ice sheet (GrIS) indicate that the climate of Greenland experienced multiple abrupt temperature increases during the last glacial period (LGP) known as Dansgaard-Oeschger (D-O) events (Dansgaard et al., 1993). D-Os have waiting times between consecutive events of around 1500 years and, with decreasing probability, 3000 and 4500 years (Alley et al., 2001) and are characterised by an initial abrupt warming of 10–16 ^∘C (interstadial state) followed by a slow cooling which finally ends with an abrupt return to glacial background conditions (stadial state) (Johnsen et al., 1992; Kindler et al., 2014). These millennial-scale climate fluctuations were first observed in Greenland ice cores (Anklin et al., 1993; Grootes et al., 1993), but strong evidence is also found in numerous marine sediments records, especially in the Nordic Seas and North Atlantic (Bond et al., 1993; Rasmussen et al., 1996; Voelker et al., 1998), tropical and subtropical stalagmite proxy archives (Fleitmann et al., 2009; Wang et al., 2001), and in Antarctic ice-sheet (AIS) ice cores (Barbante et al., 2006), suggesting a worldwide imprint of D-O events (Voelker, 2002).

The numerous and extensive evidence from paleo records (e.g. Shackleton et al., 2000; Böhm et al., 2015; Gottschalk et al., 2015; Henry et al., 2016) and from results from a variety of models, ranging from Earth system models of intermediate complexity (EMICs) to comprehensive general circulation models (GCMs) (e.g. Ganopolski and Rahmstorf, 2001; Shaffer et al., 2004; Peltier and Vettoretti, 2014; Vettoretti and Peltier, 2016, 2018) widely attribute the cause of D-O events to reorganisations of the Atlantic Mean Overturning Circulation (AMOC), which are likely modulated by variations in the oceanic convection over the Nordic Seas and North Atlantic (Dokken and Jansen, 1999; Rasmussen and Thomsen, 2004; Dokken et al., 2013; Barker et al., 2015; Hoff et al., 2016; Rasmussen et al., 2016); a recent review on the available evidence was provided by Lynch-Stieglitz (2017). However, the final cause of these AMOC reorganisations is still unclear. Numerous modelling studies have explored the problem. Much work attributes AMOC instability to freshwater discharge from the Northern Hemisphere (NH) ice sheets (Ganopolski and Rahmstorf, 2001; Vellinga and Wood, 2002; Menviel et al., 2014; Bagniewski et al., 2017) directly connected to changes in the strength (Skinner and Elderfield, 2007) and in the location (Sévellec and Fedorov, 2015) of deep convection. Other possible mechanisms link the origin of D-O events to sea-ice cover variability (Li et al., 2005, 2010; Sime et al., 2019) or to linked sea-ice–ice-shelf fluctuations (Boers et al., 2018; Petersen et al., 2013). Still others connect AMOC reorganisations to climatic perturbations in the atmosphere associated with changes in ice-sheet dynamics (Wunsch, 2006; Zhang et al., 2014a), to progressive CO₂ atmospheric variations (Zhang et al., 2017), to changes in atmospheric heat transport (Wang et al., 2015), or to combined changes in wind and atmospheric CO₂ concentrations driven by the Southern Ocean (Banderas et al., 2015). Recently, D-O events have been explained as the result of a non-linear internal salt oscillator in the Atlantic (Peltier and Vettoretti, 2014; Vettoretti and Peltier, 2016, 2018) without the need to invoke any external forcing.

Despite the evidence for millennial-scale climate variability during the LGP in Greenland, the specific role of the GrIS in this framework has not been investigated in depth. Whether the GrIS was an active or a passive player in this oscillatory system is unknown and its evolution between the last interglacial (LIG) and the Last Glacial Maximum (LGM) is still debated (Vasskog et al., 2015). Evidence of ice-rafted debris (IRD) deposition in marine sediment cores suggests that the GrIS could have been a non-negligible source of iceberg discharge during the LGP (Jonkers et al., 2010). Cores drilled in the Irminger Sea (Bond and Lotti, 1995; Van Kreveld et al., 2000), Denmark Strait (Voelker and Haflidason, 2015; Andrews et al., 2017), close to Scoresby Sund (Stein et al., 1996) and in the North Atlantic close to the Reykjanes Ridge (Barker et al., 2015; Hodell et al., 2010; Rasmussen et al., 2016) show evidence of iceberg transport sourced in East Greenland and Northeast Greenland, among other origins; also, sediments in Fram Strait show imprints of iceberg discharge from the northern GrIS (Darby et al., 2002). Still, other work links the IRD deposition found close to the east–southeast marine margin of the GrIS to local ice-sheet instability (Verplanck et al., 2009) and associated sediments found in the Labrador Sea to iceberg discharge coming from Baffin Bay during the Younger Dryas (Andrews et al., 2012). Also, other work based on paleo reconstructions explicitly affirms that ocean temperature increase played a fundamental role in the GrIS retreat in the last deglaciation (Jennings et al., 2017). Recent proxy data collected by morain-derived marine shells suggest that the margin of the Northeast Greenland Ice Stream (NEGIS) region may have fluctuated throughout the LGP by more than 200 km (Larsen et al., 2018). All these examples suggest that the GrIS may have experienced substantial variability during the LGP and beyond.

From a modelling perspective, only a few studies have tackled the response of the GrIS to millennial-scale climate variability throughout the LGP. Charbit et al. (2007) simulated the evolution of NH ice sheets by forcing their ice-sheet model with a glacial–interglacial climate anomaly scaled by a climatic index taken from the GRIP reconstruction, which retained millennial-scale temperature fluctuations. However, their model accounted only for grounded ice; ice shelves were not included and the effect of the ocean was thus not taken into account. Huybrechts (2002) also investigated the response of the GrIS to millennial-scale climate variability during the LGP with an ice-sheet model. However, the GrIS extent was controlled by orbital-only variations in past eustatic sea level, and millennial-scale fluctuations, both in sea level and in the ocean temperature, were omitted. Marshall and Koutnik (2006) assessed the response of the NH ice sheets to climate variability at millennial timescales. They simulated the GrIS evolution using an ice-sheet model that included a calving parameterisation and that was forced by millennial-scale temperature variations. Their results showed very little response of the GrIS to the imposed climate variability, with a weak increase in iceberg flux only during interstadials. However, this study did not explicitly investigate the effect of the millennial-scale variability in the ocean either.

A recent study has demonstrated the important role of oceanic conditions in the evolution of the GrIS throughout the past two glacial cycles (Tabone et al., 2018). This study, however, focused on orbital oceanic variations. Thus, the effect of oceanic millennial-scale variations on the GrIS remains to be explored. Sea surface temperatures (SSTs) inferred from planktonic foraminifera in North Atlantic sediment cores typically vary from 7–8.5 ^∘C during interstadials to 3–3.5 ^∘C during stadials (Rasmussen et al., 2016). Recent SST estimates from a stack of sediment cores of the North Atlantic suggest a broad range of interstadial–stadial temperatures fluctuating between a maximum of 15 ^∘C and a minimum of 0 ^∘C, but typical SST anomalies in each location are lower (2–6 ^∘C) (Jensen et al., 2018). Moreover, oceanic temperatures reconstructed from sediment cores in Denmark Strait (Sessford et al., 2018) and the Nordic Seas (Ezat et al., 2014) suggest stadial–interstadial subsurface temperature anomalies of 3–4 and 2–5 ^∘C, respectively, during the central part of the LGP. Oceanic temperature variations associated with D-O events may thus have an appreciable impact on the GrIS.

Here we use a three-dimensional, thermomechanical, hybrid ice-sheet–shelf model to investigate this issue. Stadial–interstadial temperature variations in the ocean are expressed in the model through a linear parameterisation of the submarine melting rate at the grounding line and below the ice shelves. We characterise the millennial-scale variability in the ocean by performing two large ensembles of simulations: one forced by both orbital and millennial-scale components in the oceanic temperature signal and the other forced solely by orbital frequencies. In both ensembles, the atmospheric forcing only includes orbital changes; thus comparison between the two large ensembles returns the impact of millennial-driven oceanic fluctuations on the GrIS evolution. Moreover, we investigate the impact of the oceanic-induced perturbations at the marine margin on the GrIS interior. This gives further insight into the potential role of the ocean in dynamic reorganisations of the ice sheet and enhanced ice discharge.

The paper is structured as follows: the ice-sheet–shelf model, the forcing methods and the methodology used to study the sensitivity of the GrIS to millennial fluctuations in the submarine melting are described in Sect. 2; in Sect. 3, we first characterise the millennial-scale variability effect in the ocean on the GrIS evolution; then we describe the impact of this oceanic oscillation on the GrIS transient dynamics. We then discuss results and caveats of the model, and this is followed by the conclusions.

2 Tools and methods

2.1 GRISLI-UCM ice-sheet–shelf model

Here we use the three-dimensional, thermo-mechanical, hybrid ice-sheet–shelf model GRISLI-UCM (Alvarez-Solas et al., 2018; Tabone et al., 2018), developed from the GRISLI ice-sheet model (Ritz et al., 2001), which has been substantially modified through diverse parameterisations of ice-sheet boundary conditions (e.g. surface mass balance, basal sliding and basal melt). The model solves deformational-flow-driven grounded areas via the shallow-ice approximation (SIA; Hutter, 1983) and floating shelves predominantly moving under plug flow via the shallow-shelf approximation (SSA; Morland et al., 1987). Transitional areas where these two flow regimes coexist are solved by adding the velocities of the SIA and SSA solutions (Winkelmann et al., 2011). The ice base of SIA-solved areas is supposed to be in a cold phase (below the pressure melting point) and does not admit sliding. By contrast, transitional zones conditionally allow for basal sliding as long as the ice base is temperate (at the pressure melting point) and the effective pressure at the bed is below a critical threshold. Once this condition is satisfied, the basal shear traction is calculated to be proportional to the ice-base velocity and to a coefficient depending on the basal water pressure and the bed roughness. Glacial isostatic adjustment (GIA) of the bedrock related to changes in the ice pressure is calculated through the Elastic Lithosphere Relaxing Asthenosphere model (Le Meur and Huybrechts, 1996). Grounding-line migration is expressed through a flotation condition between the temporally variable sea level prescribed in the model and the ice thickness calculated at the ice–ocean interface. In this study the position of the grounding line is diagnosed at sub-grid-scale precision by interpolating the ice thickness over the grid cell including the grounding line (adapted from Gladstone et al., 2010). The calculation returns the grounded percentage of the grid cell and avoids the simplistic assumption that the grounding line lies on the last grounded coarse-grid point before floating ice.

The total ice mass balance is defined at any time as the difference between the mass balance at the ice surface (accumulation minus ablation), basal melting at the ice base and ice calving. Surface ablation is calculated by the positive degree day (PDD) scheme (Reeh, 1989). This scheme is known to be overly simplistic for both ice-sheet models (Robinson and Goelzer, 2014) and EMICs (Bauer and Ganopolski, 2017) in the paleo context, as it does not incorporate the effect of incoming solar radiation changes. Nevertheless, since here we focus on the sensitivity of the ice sheet to millennial-scale oceanic variations during the LGP, the choice of this scheme should be sufficient for our purposes. Surface precipitation is exponentially proportional to atmospheric temperatures, which vary through an index approach (Banderas et al., 2018; Blasco et al., 2019; Tabone et al., 2018) (Sect. 2.2). Geothermal heat flux exchanged at the base of grounded ice is taken from Shapiro and Ritzwoller (2004). Basal melting at the grounding line and at the ice-shelf base is described in detail in Sect. 2.3. Calving is calculated following a two-rule criterion: the ice front must not exceed a critical thickness (H=200 m) and ice advected from upstream must fail to maintain the ice thickness above that imposed threshold (Peyaud et al., 2007; Colleoni et al., 2014).

The GRISLI-UCM model is applied here to the GrIS domain, with a spatial resolution of 20 km by 20 km. Since the goal of this work is to investigate the sensitivity of the GrIS to past millennial-scale variability in the ocean, we force the ice-sheet model through spatially variable surface atmospheric temperatures and precipitation that reflect orbital variations only. This allows us to study the direct effect of millennial-scale fluctuations on the GrIS evolution due to the ocean only, unperturbed by the millennial-scale atmospheric variability.

2.2 Atmospheric forcing

As in Tabone et al. (2018), the atmospheric temperature forcing applied to the model follows an index-anomaly method in which the present-day temperature $T_{\mathrm{atm}}^{\mathrm{clim}}$ is modified by fluctuations of past temperature anomalies ΔT_atm(t):

$$\begin{array}{}\text{(1)}& T_{\mathrm{atm}}\left(t\right)=T_{\mathrm{atm}}^{\mathrm{clim}}+\mathrm{\Delta }{T}_{\mathrm{atm}}\left(t\right),\end{array}$$

where

$$\begin{array}{}\text{(2)}& \mathrm{\Delta }{T}_{\mathrm{atm}}\left(t\right)=(\mathrm{1}-\mathit{\alpha }(t\left)\right)\mathrm{\Delta }{T}_{\mathrm{atm}}^{\mathrm{orb}}.\end{array}$$

The present-day temperature climatology $T_{\mathrm{atm}}^{\mathrm{clim}}$ is obtained from the regional climate model MAR forced by the ERA-Interim reanalysis (Fettweis et al., 2013) for the period 1981–2010. The resulting atmospheric temperature T_atm(t) is a 2-D field which varies in time according to α(t), which is a spatially uniform climatic index derived from a composite series of various proxy-derived temperature anomalies from the LIG to the present day (Tabone et al., 2018) (Fig. 1a). This temperature anomaly signal is then smoothed to remove the spectral components below the orbital frequencies ($\mathrm{1}/f<\mathrm{18}$ ka) and is normalised between 0 and 1 to build the index α (α=1 at present day (PD) and α=0 at the LGM) (Fig. 1b). Thus, by construction, $\mathrm{\Delta }{T}_{\mathrm{atm}}^{\mathrm{orb}}$ is the glacial–interglacial atmospheric temperature anomaly, which is here taken from glacial minus present-day anomaly snapshots of the EMIC CLIMBER-3α model (Montoya and Levermann, 2008). This orbital forcing method is likewise applied to the precipitation field, which is parameterised through the ratio of glacial and present-day precipitation anomalies $\mathit{\delta }{P}_{\mathrm{ann}}^{\mathrm{orb}}$, as in Tabone et al. (2018):

$$\begin{array}{}\text{(3)}& P_{\mathrm{ann}}\left(t\right)=P_{\mathrm{ann}}^{\mathrm{clim}}\cdot \left(\mathit{\alpha }\left(t\right)+(\mathrm{1}-\mathit{\alpha }(t\left)\right)\cdot \mathit{\delta }{P}_{\mathrm{ann}}^{\mathrm{orb}}\right).\end{array}$$

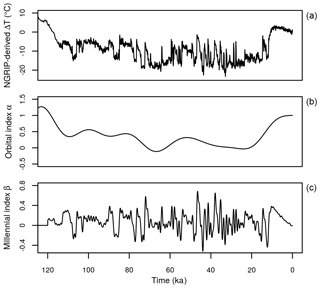
Figure 1 North Greenland Ice Core (NGRIP)-temperature anomaly reconstruction (a) used to construct the orbital-index α(t) (b) and the millennial-index β(t) (c) for the last glacial period. α(t) is built from the NGRIP-derived temperature anomalies (Tabone et al., 2018), filtered to remove the spectral components below the orbital period ($\mathrm{1}/f<\mathrm{18}$ ka) and normalised between 0 and 1. β(t) is derived by subtracting the orbital α(t) index from the NGRIP-derived temperature signal, normalised between 0 and 1 and then filtered below 1 ka to remove sub-millennial periods.

2.3 Oceanic forcing

The methodology used to force the ocean is similar to that of Tabone et al. (2018), except that here we include the millennial-scale variability in the ocean which was omitted in the previous work. This approach is analogous to that of Blasco et al. (2019) for the Antarctic domain. Here, the basal melting rate at the grounding line is parameterised as

$$\begin{array}{}\text{(4)}& B\left(t\right)=\mathit{\kappa }(T_{\mathrm{ocn}}^{\mathrm{clim}}-T_{\mathrm{f}})+\mathit{\kappa }\mathrm{\Delta }{T}_{\mathrm{ocn}}\left(t\right),\end{array}$$

where

$$\begin{array}{}\text{(5)}& \mathrm{\Delta }{T}_{\mathrm{ocn}}\left(t\right)=(\mathrm{1}-\mathit{\alpha }(t\left)\right)\mathrm{\Delta }{T}_{\mathrm{ocn}}^{\mathrm{orb}}+\mathit{\beta }\mathrm{\Delta }{T}_{\mathrm{ocn}}^{\mathrm{mil}}.\end{array}$$

The formulation is adapted from Beckmann and Goosse (2003) and permits the translation of changes in ocean temperature into changes in basal melt through an ocean–ice heat-flux exchange scaling factor κ ($\mathrm{m}{\mathrm{a}}^{-\mathrm{1}}{\mathrm{K}}^{-\mathrm{1}}$). The first term of Eq. (4) is the prescribed basal melting rate for the present day, where T_f is the temperature at the base of the ice shelf, assumed to be at the freezing point; T_ocn is the temperature of the ocean at the present day; and $T_{\mathrm{ocn}}^{\mathrm{clim}}$ is the mean climatological temperature of the ocean. Since the present-day basal melt rate for the whole Greenland domain is largely unconstrained, we assume it to be spatially constant (hereafter referred to as $B_{\mathrm{ref}}=\mathit{\kappa }(T_{\mathrm{ocn}}^{\mathrm{clim}}-T_{\mathrm{f}})$ (m a⁻¹)). The reference basal melt is then perturbed by a time-dependent anomaly, which includes both orbital and millennial variability. β (Fig. 1c) is the millennial index, derived from the same normalised temperature anomaly signal as α. Specifically, it is built by subtracting the orbital α index (Fig. 1b) from the unfiltered multi-proxy temperature signal (Fig. 1a) normalised between 0 and 1 and then filtering to remove periods below 1 ka to eliminate sub-millennial components of the signal. $\mathrm{\Delta }{T}_{\mathrm{ocn}}^{\mathrm{orb}}$ and $\mathrm{\Delta }{T}_{\mathrm{ocn}}^{\mathrm{mil}}$ are the glacial–interglacial and interstadial–stadial oceanic subsurface temperature anomalies (K), respectively. The term $(\mathrm{1}-\mathit{\alpha }(t\left)\right)\cdot \mathrm{\Delta }{T}_{\mathrm{ocn}}^{\mathrm{orb}}$ reflects the subsurface temperature variations resulting from orbital changes. The term $\mathit{\beta }\cdot \mathrm{\Delta }{T}_{\mathrm{ocn}}^{\mathrm{mil}}$ expresses the millennial-scale temperature changes at the subsurface assumed to be in antiphase with respect to the Greenland atmospheric temperature inferred from Greenland ice cores (e.g. Johnsen et al., 2001 and Kindler et al., 2014). Thus, we are assuming that subsurface water temperatures increase during stadials and decrease during interstadials. This is in agreement with the presence of warming subsurface waters during stadial periods as suggested by several records of the North Atlantic and Nordic Seas (Ezat et al., 2014; Jonkers et al., 2010; Rasmussen and Thomsen, 2004; Rasmussen et al., 2016; Sessford et al., 2018; Dokken et al., 2013) and supported by modelling work (Vettoretti and Peltier, 2015; Brady and Otto-Bliesner, 2011; Mignot et al., 2007; Knutti et al., 2004; Marcott et al., 2011). The result is a submarine melting signal that peaks during D-O stadials. This is consistent with the oceanic forcing of ice-sheet models used previously to inspect the effect of subsurface warming during the coldest stadials, i.e. Heinrich events (Alvarez-Solas et al., 2010, 2013; Bassis et al., 2017) or, as done recently, to investigate the origin of D-O events through a conceptual model (Boers et al., 2018).

As in Tabone et al. (2018) and Blasco et al. (2019), basal melt under the ice shelves is 10 % of that near the grounding line, as supported by recent estimates in Greenland (Rignot and Steffen, 2008; Münchow et al., 2014; Wilson et al., 2017). To prevent unconstrained accretion below ice shelves and at the grounding line, negative basal melt rate (freezing) is cut off to 0 m a⁻¹. Changes in global sea level at orbital timescales are prescribed in the model and are used to compute the grounding-line position. The applied sea-level variation time series is taken from Bintanja and Van de Wal (2008). The signal is inferred from a marine benthic oxygen isotope record reconstructed for the last 3 Myr through an ice-sheet model coupled to a simple marine temperature model.

2.4 Perturbed basal melting parameters and LE description

Following the discussion above, we can rewrite the basal melting equation (Eq. 4) as

$$\begin{array}{}\text{(6)}& B\left(t\right)=B_{\mathrm{ref}}+\mathit{\kappa }\left((\mathrm{1}-\mathit{\alpha }(t\left)\right)\mathrm{\Delta }{T}_{\mathrm{ocn}}^{\mathrm{orb}}+\mathit{\beta }\mathrm{\Delta }{T}_{\mathrm{ocn}}^{\mathrm{mil}}\right).\end{array}$$

Written in this form, the basal melting formulation depends on the choice of four parameter values: B_ref, κ, $\mathrm{\Delta }{T}_{\mathrm{ocn}}^{\mathrm{orb}}$ and $\mathrm{\Delta }{T}_{\mathrm{ocn}}^{\mathrm{mil}}$. These variables are here all considered as spatially uniform around Greenland for the sake of simplicity, leading to a spatially homogeneous basal melting rate. To assess the GrIS response to millennial-scale variability in the ocean, we could simply consider varying the value of κ, which is the sensitivity of the oceanic forcing (Tabone et al., 2018). However, by construction of Eq. (6), increasing κ does not necessarily mean increasing the millennial-scale oceanic forcing alone, since this would enhance concurrently both the millennial and the orbital-scale components in the ocean. Therefore, investigating the oceanic millennial-scale variability effect on the past GrIS is not as straightforward as expected. Moreover, none of the four parameters of Eq. (6) is perfectly constrained in reality, and a sensitivity study on the influence of their chosen values on the GrIS evolution would be required.

For these reasons, it is first useful to characterise the impact of millennial-scale variability in the ocean on the GrIS evolution by testing a broad range of values of the key parameters in Eq. (6): $\mathrm{\Delta }{T}_{\mathrm{ocn}}^{\mathrm{mil}}$, set to vary between 0 and 3 K; B_ref, between 0 and 10 m a⁻¹ (chosen as a reasonable climatic mean between Rignot et al., 2010, Rignot et al., 2016, Straneo et al., 2012 and Wilson et al., 2017 for the largest tidewater glaciers around the GrIS and Liu et al., 2015 and Rignot et al., 2013 for Antarctica); and κ, between 0 and 10 $\mathrm{m}{\mathrm{a}}^{-\mathrm{1}}{\mathrm{K}}^{-\mathrm{1}}$ (following Rignot and Jacobs, 2002 for Antarctica). The reduction of the problem to 3 degrees of freedom is supported by estimates of subsurface temperatures at both short (millennial) and long (orbital) timescales that have the same amplitudes. Reconstructed LGM–present-day subsurface anomalies, which at orbital timescales are considered to follow those at the surface, are between 0 and −3 K around Greenland (Annan and Hargreaves, 2013; Margo, 2009). A similar range of values is found for the interstadial–stadial subsurface temperature anomalies (Alvarez-Solas et al., 2018; Brady and Otto-Bliesner, 2011; Vettoretti and Peltier, 2015; Zhang et al., 2014b). Also, in our experimental set-up the α and β indices share the same normalisation. Thus, interstadial–stadial and glacial–interglacial anomalies share the same amplitude of forcing. Also, it should be noted that B_ref depends on κ (Eq. 4); thus any change in κ results in a change in B_ref too. However, B_ref also depends on the water and freezing-point temperatures at the grounding zone ($T_{\mathrm{ocn}}^{\mathrm{clim}}$ and T_f, respectively), which are largely unconstrained, since they mostly depend on the characteristics of the considered grounding line (e.g. on its depth; Beckmann and Goosse, 2003). To take into account the uncertainty of these quantities, here, $T_{\mathrm{ocn}}^{\mathrm{clim}}-T_{\mathrm{f}}$ is treated as an additional degree of freedom that, although not explicitly perturbed in the equation, allows us to change B_ref independently from κ. Of course, decoupling these two variables requires additional attention in considering a range of values for B_ref and κ that allow for realistic $T_{\mathrm{ocn}}^{\mathrm{clim}}-T_{\mathrm{f}}$. The simulations that do not fulfill this requirement will be discarded a posteriori in the analysis.

Table 1 Range of parameter values sampled by the LHS technique for generating the TOT and ORB ensembles.

To test a wide range of combinations between the three key parameters, we perform a large ensemble (LE) of model simulations using the near-random Latin hypercube sampling (LHS) technique (McKay et al., 1979), which allows us to efficiently explore the phase space of the key parameters minimising the LE computational cost with respect to the full-factorial sampling technique. The LHS method has already been used to constrain different ice-sheet model parameters and to assess their influence on the model's behavior (Stone et al., 2010; Applegate et al., 2012; Stone et al., 2013; Robinson et al., 2017). The parameter values are sampled from the specified ranges and, assuming, as discussed, that they are independent of each other, they are randomly combined to generate a total LE of 100 simulations, named TOT simulations. At the same time, we perform another set of identical simulations, except for the fact that the climatic index associated with the millennial-scale variability (β) is set to zero. These are named ORB simulations and are used for direct comparison with the TOT simulations, as discussed in Sect. 3 (see Table 1 for a full list of the phase space of parameters investigated within the two LEs). To initialise the model we use the present-day topography of Greenland from Schaffer et al. (2016). All the simulations of the LE cover the last two glacial cycles, with the first considered as a spin-up and therefore not analysed.

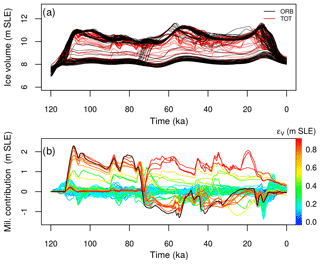
Figure 2 (a) Ice-volume evolutions simulated by ORB (black curves) and TOT (red curves) throughout the LGP (m SLE); (b) TOT-ORB ice-volume anomaly, intended as the oceanic millennial-scale variability contribution to the GrIS ice-volume variation (m SLE; positive values indicate ice gained by TOT with respect to ORB). The colour scale indicates the root mean square deviation (ε) calculated in terms of ice-volume residuals between TOT and ORB simulations (m SLE). Black line in (b) refers to the simulation corresponding to the maximum GrIS response to millennial-scale variability in the ocean.

3 Results

3.1 Characterisation of oceanic millennial-scale variability effect

A first evaluation of the effect of millennial-scale oceanic variability on the whole GrIS can be made by looking at the evolution of its simulated ice volume throughout the LGP (Fig. 2a). Apart from low oceanic forcing configurations for which both ORB (black curves) and TOT (red curves) present small ice-volume deviations from their simulated present-day value, TOT simulations show higher ice-volume fluctuations than ORB ones, especially during Marine Isotope Stage 3 (MIS3, ca. 60–25 ka). A better representation of the impact of millennial-scale variability on the GrIS evolution can be obtained by considering deviations in ice volume from the orbital-only forced reference simulation (ORB) (Fig. 2b). Those anomalies can reach peaks of almost 2 m SLE at certain times during the LGP, with changing rates of more than 1 m SLE in less than 2 kyr. However, isolated peaks in volume anomalies do not necessarily imply a high millennial-scale ice-volume variation over the whole LGP since they may result from sparse melting peaks, and the contribution of the oceanic variability to ice-volume changes needs to be quantified for the entire time series. This can be done by calculating the root mean square deviation (here specified by the greek letter ε) of the ice-volume (V) residuals between TOT and ORB averaged in time for each simulation of the LE (m SLE) as

$$\begin{array}{}\text{(7)}& {\mathit{\epsilon }}_V=\sqrt{{\displaystyle \frac{\mathrm{1}}{N_{\mathrm{t}}-\mathrm{1}}}\sum _{t=\mathrm{1}}^{N_{\mathrm{t}}}{\left(V_{\mathrm{TOT}}\left(t\right)-V_{\mathrm{ORB}}\left(t\right)\right)}^{\mathrm{2}}}.\end{array}$$

N_t is the total number of time steps in each simulation and V_TOT(t)−V_ORB(t) is the ice-volume residual calculated as the difference between the two simulations at each time step. This quantity tells us how much the volume in the TOT simulation, including millennial-scale variability, deviates from that in the background throughout the whole LGP. The larger its value, the larger the impact of oceanic millennial-scale variability on the GrIS.

A second and complementary approach is to calculate the deviation of the ice speed (U) simulated by TOT from its background state ORB. The methodology is similar to that used for the ice volume, except for the fact that now ε is first calculated for each grid point ij as ${\mathit{\epsilon }}_{U,ij}=\sqrt{\frac{\mathrm{1}}{N_{\mathrm{t}}-\mathrm{1}}{\sum }_{t=\mathrm{1}}^{N_{\mathrm{t}}}\left(U_{ij,\mathrm{TOT}}\right(t)-U_{ij,\mathrm{ORB}}(t){)}^{\mathrm{2}}}$ and then averaged for the entire domain:

$$\begin{array}{}\text{(8)}& {\mathit{\epsilon }}_U={\displaystyle \frac{\sqrt{{\sum }_{ij}{\mathit{\epsilon }}_{ij}^{\mathrm{2}}}}{N}},\end{array}$$

where N is the total number of grid points of the GrIS domain.

Ice-volume evolution is a good benchmark for understanding the overall effect of the oceanic variability throughout the time, but U is the direct expression of how the ice dynamics are affected by the forcing. Therefore, we jointly examine the ε calculated for ice volume and velocities. The higher the millennial-scale variability in the ocean is, the more the ice volume and ice velocity in TOT are expected to deviate from the ORB simulation. Specifically, we are interested in understanding which combination of perturbed parameters in the basal melting equation (Eq. 6) leads to the highest millennial variability in terms of both quantities. We find that the effect of a high oceanic millennial-scale variability is fairly well constrained in the parameter phase space, at least per each couple of analysed variables (Fig. 3). Very low oceanic-driven variability is generally associated with low values of κ and ΔT_ocn (weak oceanic forcing). These configurations lead to basal melting evolutions that do not deviate much from the reference-state basal melting throughout the LGP (blue curves of Fig. S1 in the Supplement). Low millennial-scale variability is also found for combinations of low B_ref with high κ (or high $\mathrm{\Delta }{T}_{\mathrm{ocn}}^{\mathrm{mil}}$) and for high κ with high $\mathrm{\Delta }{T}_{\mathrm{ocn}}^{\mathrm{mil}}$. The reason is that these are associated with a basal-melt evolution that rapidly saturates at the cut-off value 0 m a⁻¹ (no melting, since freezing is not allowed) after the LIG and maintains that state throughout the LGP (light blue curves in Fig. S1). It is between these two configurations that the resulting basal melting signal allows for a high millennial-scale variability in the ocean. This is usually ensured by medium–high B_ref and high κ, but also by combinations of high B_ref and relatively low κ (red curves showing a positive volume anomaly during MIS3 in Fig. 2b). In these cases, the high ε is a result of the large ice-volume variation between a GrIS configuration in ORB that is confined inland by a persistent high melting during the whole LGP and a less confined one in TOT as a result of a basal melting that saturates at zero at certain intervals. In any case, the highest millennial variability in the ocean is associated with a signal that contains sufficiently high melting peaks at millennial timescales and that sometimes saturates at 0 m a⁻¹ (red curves in Fig. S1). A similar logic can be followed considering $\mathrm{\Delta }{T}_{\mathrm{ocn}}^{\mathrm{mil}}$ instead of κ. High κ must be associated with low $\mathrm{\Delta }{T}_{\mathrm{ocn}}^{\mathrm{mil}}$ and vice versa to produce high millennial-scale variability in the basal melt, as reflected in Fig. 3 as well.

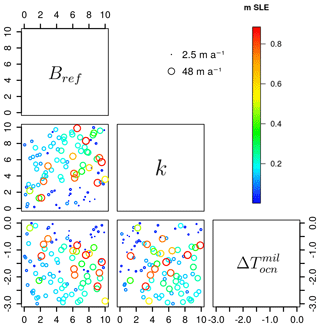
Figure 3 Evaluation of the effect of the oceanic millennial-scale variability for each pair of parameters perturbed in the basal melting equation (Eq. 6). The ranges of ε_V (m SLE, colour scale) from Eq. (7) and ε_U (m a⁻¹, circle size) from Eq. (8) are shown. The simulation with the highest millennial-scale variability is represented by the largest red circle; the simulation with the lowest variability is represented by the smallest blue circle.

3.2 Oceanic millennial-scale variability impact on transient dynamics

The aim of this section is to investigate the effect of oceanic millennial-scale variability on the transient GrIS dynamics and ice-sheet evolution during the LGP. To this end, we choose the simulation from the LE which corresponds to the maximum millennial-scale variability response in terms of both ice volume and velocity and we compare it to its corresponding background simulation. Specifically, we associate the largest millennial-scale variability in the ocean to the maximum value given by the product of the two scores (${\mathit{\epsilon }}_{\mathrm{TOT}}={\mathit{\epsilon }}_V\cdot {\mathit{\epsilon }}_U$). As expected from the characterisation of the millennial variability discussed above, the chosen simulation has medium–high B_ref (7.6 m a⁻¹), high κ (8.3 $\mathrm{m}{\mathrm{a}}^{-\mathrm{1}}{\mathrm{K}}^{-\mathrm{1}}$) and consequently medium $\mathrm{\Delta }{T}_{\mathrm{ocn}}^{\mathrm{mil}}$ (1.2 K) values. This experiment shows a millennial-scale contribution to ice-volume variation of more than 1 m SLE during the highest peaks of melting (black curve of Fig. 2b). From now on, this simulation and its corresponding orbital-only reference simulation are referred to as TOT_max and ORB_max, respectively.

We compare ice thickness, velocity and migration of the grounding-line position simulated by TOT_max with those of ORB_max for the whole LGP (movie in Supplement). Since the millennial-scale variability in the ocean is built to represent temperature variations at the subsurface (Fig. 4a), each submarine melting peak is associated with a stadial interval occurring between two near D-O events, also referred to as Greenland Stadial (GS) (Rasmussen et al., 2014). Here we show the comparison specifically for GS 15 (ca. 55 ka), that is linked to one of the most pronounced basal melting peaks during MIS3 (Fig. 4). Note that when a comparison is made between two GrIS extensions that show a mismatch in ice cover, the resulting velocity difference refers to the ice velocity of the simulation in which the grounding line has not retreated yet. In TOT_max the high melting peak leads to a large ice-thickness decrease, associated with a substantial grounding-line retreat, especially in the Kangerlussuaq and Sermilik fjords (SE Greenland) and the NEGIS region (Fig. 5). The area near Baffin Bay (NW Greenland) is also affected by inland grounding-line migration, but the retreat is limited if compared to the other zones. The outlet glacier at Jakobshavn Isbrae (W Greenland) also strongly responds to the forcing, but the response, compared to the ORB_max simulation, decreases throughout the melting peak. This is related to the large ice thickness simulated by ORB_max in the 20 kyr previous to GS 15, which increases the amount of glacial water produced at the base of the ice stream, eventually enhancing basal sliding and ice discharge when a persistent submarine melting is applied. On the other hand, the inclusion of millennial-scale oceanic variability allows for frequent ice discharge, limiting the basal-water amount and the ice stream basal velocity, leading to discharge ice more promptly at the beginning of the peak. During the slow subsurface cooling after the GS melting peak (at ca. 52 ka), the grounding line is then free to readvance.

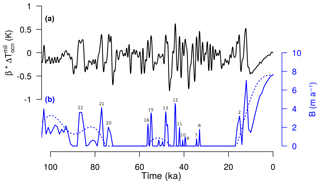
Figure 4 Evolution of (a) millennial-scale subsurface oceanic temperature as defined in Eq. (6) to force the TOT_max simulation and (b) the resulting submarine melting used in both TOT_max (solid line) and ORB_max (dashed line) simulations for the last 100 kyr. Submarine melt peaks are associated with their corresponding Greenland stadials (GSs).

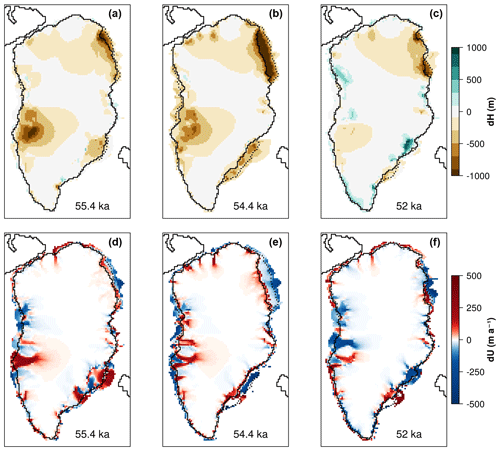
Figure 5 TOT_max − ORB_max ice thickness (m, a, b, c) and velocities (m a⁻¹, d, e, f) during submarine melting rate peak corresponding to GS 15. TOT_max and ORB_max grounding-line positions are shown by solid and dashed lines, respectively.

Simulations show that increased velocities in the NEGIS and Kangerdlugssuaq regions associated with enhanced ice discharge are found also during GS 12 (ca. 43 ka) (movie in Supplement). Appreciable but less pronounced grounding-line variations are likewise observed during GS 13 (ca. 47 ka) and GS 16 (ca. 56 ka), especially in SE Greenland. In GS 16 the weak response to the submarine melting peak is related to a small grounding-line migration in the south. Around GS 13, the pattern is even reversed, since more ice is lost in ORB_max than in TOT_max. This is due to the presence of the persistent melting previous to GS 13 that has already led the SE Greenland to be more retreated and to discharge more ice.

Generally, ORB_max is much more static than TOT_max, showing smaller grounding-line and ice-discharge changes. Evidence from marine records suggest that stadial–interstadial oceanic temperature variations of about 2–5 K at intermediate depths (Ezat et al., 2014; Sessford et al., 2018) likely occurred around Greenland during D-O events. Even larger anomalies are found at the surface (e.g. Jensen et al., 2018; Rasmussen et al., 2016). It is reasonable that such consistent temperature fluctuations were associated with large variations in melting at the base of ice shelves present in Greenland during the last glacial, when grounded ice advanced over the continental shelf. Therefore, a more variable submarine melt configuration such as that of TOT_max is expected to better reflect the oceanic temperature variation found during D-O events. However, there is no certainty as to whether more ice variability associated with this melting fluctuation is actually a better representation of reality than the ORB_max case.

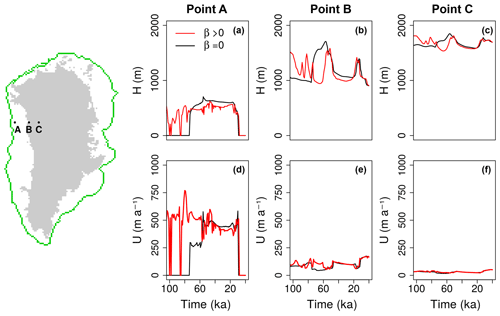
Figure 6 Transient dynamics specified for three locations along Baffin Bay. Ice thickness (a, b, c) and velocity (d, e, f) LGP evolution is shown for the glacial marine margin (point A), present-day marine margin (point B) and far in the interior of the ice sheet (point C). Black curves indicate the dynamics of the ORB_max simulation, red curves represent the dynamics of the TOT_max simulation. The green line on the map on the left-hand side shows the maximum GrIS glacial extent simulated in TOT_max.

The inclusion of millennial-scale variability in the forcing results in ice-thickness variations of hundreds of meters at the marine margin when compared to the corresponding orbital-only case. These ocean-driven fluctuations in ice mass are first exhibited at the ice–ocean front but penetrate through the ice-sheet interior by several tens of kilometers. This is related to the propagation of velocities along fast-flowing ice streams, which, especially around the west GrIS, Sermilik, Kangerlussuaq and NEGIS regions, can penetrate far inland promoting significant ice discharge into the ocean. This effect can be seen by analysing the LGP ice-thickness and velocity evolution for a single grid point of the domain, at three strategic locations: close to the glacial marine margin (A), close to the PD marine margin (B, glacial ice-sheet interior) and far inland in the ice sheet (C). We show the results of this analysis explicitly for the Baffin Bay region (Fig. 6), but another three areas around the Greenland domain have been investigated (Fig. S2 for Jakobshavn Isbrae, Fig. S3 for the NEGIS and Fig. S4 for Kangerlussuaq fjord). Around Baffin Bay the highest differences in transient dynamics between ORB_max and TOT_max are found at the beginning of the LGP. For almost 30 kyr, the margin of ORB_max is constrained close to the continental border, whereas intermittent periods of submarine melt in TOT_max allow the ice edge to rapidly advance and retreat, showing high-velocity fluctuations (600–800 m a⁻¹) (point A). A similar response is found in the proximity of the PD marine margin, about 160 km far from the glacial ice–ocean border (point B), where the effect of the millennial-scale variability in the ocean is found in ice-thickness variations of 500 m. This effect is diffused inland, still reaching differences of 200 m 300 km away from the ocean border (point C), despite minor or no observable difference in velocities. These estimates further corroborate the results found for the Baffin Bay region in the 2-D plots (movie in Supplement). The region including the Jakobshavn Isbrae (Fig. S2) seems to be slightly less affected by the millennial fluctuation in basal melting than the region of Baffin Bay. Still, appreciable ice-thickness variations are found close to the marine margin, especially at the beginning of the glacial period and around 75–50 ka, when the ice shelf repeatedly disappears in the presence of rapid melting peaks. Little evidence of this ice fluctuation is found in the ice interior, however, although slightly increased velocities with respect to ORB_max around 60 ka limit ice growth, culminating in ice ∼700 m lower than that of the ORB_max (point B). The oceanically induced variability rapidly decays further inland (point C). However, it must be noted that this latter location is more than 600 km away from the marine margin; thus this attenuation is expected. Millennial-scale fluctuations in submarine melting also impact the NEGIS glacial evolution (Fig. S3). Intermittent periods of no melting at the beginning of the glacial period allow the ice margin to strongly fluctuate back and forth over the continental shelf (point B). By contrast, persistent basal melting in ORB_max associated with very high velocity (higher than 3000 m a⁻¹) constrains ice expanding offshore (point C). The absence of ice at location A for almost the whole LGP as simulated by TOT_max precludes the buttressing effect that limits ice discharge from the ice-sheet interior, as seen in the ORB_max simulation. By contrast, the presence of millennial-scale fluctuations in the ocean helps to maintain ice advection from the interior toward the ice–ocean margin, favouring ice discharge and limiting the ice increase by 300 m (point B) and 200 m inland (point C). Finally, oceanic temperature variability at millennial timescales strongly affects the region around Kangerlussuaq fjord (Fig. S4), where ice growth and loss clearly induce ice-thickness differences of more than 1000 m up to 300 km away from the ice-shelf edge.

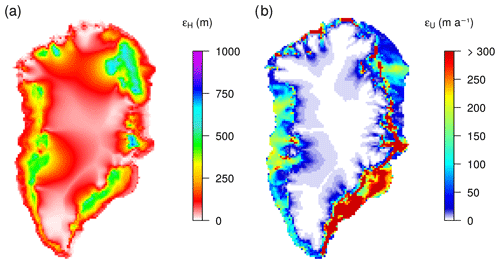
Figure 7 Root mean square deviation ε for ice thickness H (m) and velocity U (m a⁻¹) calculated between TOT_max and ORB_max, following Eq. (8).

The response of the GrIS to millennial-scale variability in the ocean throughout the whole LGP is summarised in Fig. 7 at a large spatial scale. Ice thickness and velocity ε both calculated following Eq. (8) for the whole time period show that regions that exhibit a strong response to the ocean in terms of ice-thickness variations are also subjected to strong changes in velocity. This is highlighted in regions such as Baffin Bay, Jakobshavn Isbrae, Kangerlussuaq and Sermilik fjords, and NEGIS, confirming the results discussed in this section for specific times and locations.

4 Discussion

4.1 Comparison of model results to proxy data

Our simulations show that small ocean temperature variations can result in significant ice-volume fluctuations from the background glacial GrIS configuration. Also, the GrIS may have contributed to IRD discharge during the LGP, as suggested by proxy records (e.g. Andrews et al., 2017; Barker et al., 2015; Bond and Lotti, 1995; Hodell et al., 2010; Jonkers et al., 2010; Rasmussen et al., 2016; Van Kreveld et al., 2000; Voelker and Haflidason, 2015), and it is therefore interesting to outline its possible imprint associated with millennial-scale variability in the ocean.

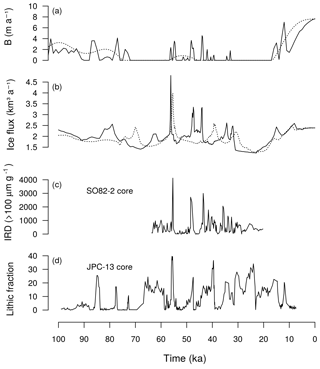
Figure 8 Simulated submarine melt (a) and simulated ice flux averaged over the southeast GrIS region (b) are compared to ice-discharge proxy data taken from the SO82-2 (c) and the JPC-13 (d) sediment cores in the North Atlantic.

We compare our model results to proxy data taken from sediment cores drilled in locations that may have been partly affected by recurrent ice discharge from the GrIS throughout the LGP. The analysed sites are located in the central North Atlantic, one along the eastern side of the Reykjanes Ridge (core JPC-13; Hodell et al., 2010), close to the so-called IRD belt (Ruddiman, 1977), and the other on its western flank, further north in the ocean (core SO82-2; Rasmussen et al., 2016). IRD from both sediment cores are thought to have a possible east GrIS source (Hodell et al., 2010; Van Kreveld et al., 2000). Therefore, we compare those IRD data to the modelled ice flux averaged over the area between Kangerlussuaq and Sermilik Fjords (Fig. 8). A very good agreement is found between the ice flux modelled by TOT_max and the proxy data, especially during MIS 3. It is suprising how well the ice-dicharge events corresponding to GS 16 and GS 13 (and GS 12 for SO82-2) are reproduced by the model when oceanic millennial-scale variability is considered. Some other peaks in ice discharge, such as those linked to GS 6 and GS 7, are also recognizable. These results suggest that high peaks in submarine melting, resulting from strong stadial–interstadial oceanic warming, may have triggered massive iceberg discharge from the east GrIS ice shelf to both locations. Those GrIS-sourced icebergs eventually reached the central North Atlantic, at least during certain stadial phases of D-O cycles. Although these results agree with the evidence that most of the IRDs found close to Reykjanes Ridge have eastern GrIS and Icelandic origins (Van Kreveld et al., 2000), the hypothesis that part of the IRDs, especially those from sediment core JPC-13 (Hodell et al., 2010), have a Laurentide Ice Sheet source cannot be discarded. Also, although evidence supports the presence of an ice shelf in Denmark Strait during certain periods of the LGP (Barker et al., 2015; Van Kreveld et al., 2000; Voelker et al., 1998), this assumption is still debated (Andrews et al., 2017) and a more profound analysis of sediment cores and models is required to confirm this hypothesis.

Another two locations situated in the Labrador Sea (MD95-2024; Weber et al., 2001) and in the northwestern margin of Iceland (PS2644-5; Voelker and Haflidason, 2015) have also been investigated (Figs. S5 and S6). Gamma ray density (g m⁻³) reconstructed from sediment core MD95-2024 (Labrador Sea, Fig. S5) is compared to the simulated ice flux averaged over the Baffin Bay region. All main Heinrich events (HEs) and some of the GS of the LGP can be recognised in the gamma ray density signal (Weber et al., 2001), which follows the IRD data extracted from the same sediment core. A very weak model–data agreement is found. The most important source of IRD found in the Labrador Sea is thought to be the Hudson Bay, which is likely responsible for the majority of iceberg discharge during HEs; thus this could explain the very low correspondence between model and data for this location. Finally, the total lithic fragment (IRD and thepra grains) extracted from sediment core PS2644-5 (NW Iceland, Fig. S6) is compared to the simulated ice flux averaged over the ice-covered Denmark Strait area close to Scoresby Sund. Some correspondence between modelled ice flux from the east GrIS and IRD deposition is found, especially during MIS3. Thus, we cannot rule out that millennial-scale variability in the ocean is partly responsible for enhanced iceberg production from the east–southeast GrIS bringing IRD to the PS2644-5 site by the East Greenland Current (Voelker and Haflidason, 2015).

Despite individual disagreements and with certain nuances, all of these comparisons show that a more responsive GrIS, as obtained when the model is forced with millennial-scale oceanic variability at the subsurface (TOT_max), is in better agreement with proxies compared to the orbital-only simulation (ORB_max). Rapid (millennial-scale) basal melting fluctuations allow for ice-flux increases that match the timing of some of the peaks of the proxy data, meaning that the GrIS could have contributed to the ice discharge at those times. With this analysis, we do not aim to precisely reconstruct the timing and spatial distribution of the iceberg discharge during D-O events. Instead, we aim to explore the implications of considering the oceanic millennial-scale variability on the GrIS ice fluctuation during the LGP. It is remarkable how much the sole presence of millennial-scale variability in the ocean can influence the GrIS evolution and ice discharge during the LGP interstadials, notwithstanding that millennial-scale variability is neglected in the atmosphere. However, tracing the origin of IRD deposition is a complex and open problem that needs a deeper understanding of changes in the ocean column during D-O events, as well as a better knowledge of the oceanic and glaciological processes that ultimately determine the deposition of IRD on the ocean floor due to iceberg discharge.

4.2 Model limitations and caveats in basal melting parameterisation

Some of the GRISLI-UCM model limitations already discussed by Tabone et al. (2018), such as the coarse model resolution (20 km by 20 km), which impedes the correct solution of small and steep fjords, the relatively simple GIA scheme, which takes into account only local changes in the ice load, and the PDD ablation scheme, which does not consider changes in past insolation, are also present in this work.

The simplicity of the submarine melt parameterisation adopted here allows for a direct investigation of the effect of past oceanic temperature fluctuations on the GrIS evolution. However it may disregard complex processes occurring at the ice–ocean interface. Moreover, here we have introduced a cut-off value to prevent freezing at the ice-shelf base and thus limit ice accretion during the glacial period. This assumption is reasonable for the low spatial resolution of the model; however, it ignores an existing process, since freezing is observed at the base of many marine glaciers, even for the present day (at least in Antarctica; Rignot et al., 2013). A parameterisation accounting for variations in salinity (Holland et al., 2008) or the geometry of the ice-shelf cavity (Gladstone et al., 2012) or the slope of the base of the ice shelf (Little et al., 2012) or more complex schemes describing meltwater buoyancy and water convection in the ice-shelf cavity (Jenkins, 2011) could help to describe in detail the processes below the ice shelves and along the grounding line. Recently, a fairly simple parameterisation applied for the AIS resolving ice-shelf cavities and using a boundary-layer theory for the melt has been capable of capturing the effect of ocean circulation below the ice shelves (Reese et al., 2018). With this sensitivity study we do not aim to perfectly reproduce reality but rather to analyse the possible effects of an ocean driven by millennial variability on the ice-sheet evolution in Greenland. The parameterisation used here was explicitly developed for paleoclimatic simulations and fits this purpose well.

The basal melting evolution reproduced in the TOT_max simulation (solid line in Fig. 4b) is strongly related to a specific combination of the perturbed parameters in the basal melting equation (Eq. 6). This combination is reasonably chosen from the range of possible values as it produces the maximum oceanic millennial variability in the LE, but the same analysis could be performed for other basal melting configurations. A different magnitude of the melting peaks during MIS3 (Fig. S1) or a different distribution of the melting peaks (resulting from the use of a different temperature reconstruction to create the α and β indices) may vary the timing of grounding-line advance and retreat or ice growth and loss. This is also true for the orbitally driven basal melting forcing applied to the ORB_max simulation (dashed line in Fig. 4), which shows submarine melting rates higher than 0 m a⁻¹ for only 10 kyr during MIS3 (between 55 and 45 ka). A different melt configuration could vary the timing and spatial distribution of grounding-line migration and ice cover.

Many authors associate D-O events to changes in sea-ice cover over the Nordic Seas (Dokken et al., 2013; Hoff et al., 2016; Jensen et al., 2018; Li et al., 2010; Sime et al., 2019), which were disregarded in our set-up. The use of spatially variable fields could add a further degree of realism to the simulations. Perturbing the model with spatially variable subsurface oceanic temperatures, which may reflect variations in sea-ice cover, instead of a simple temperature time series, would likely affect the simulation of local ice mass variations throughout the last glacial cycle. Both stadial–interstadial and glacial–interglacial temperature anomalies could be taken from existing transient model outputs, for instance. However, a complete map of the observed PD basal melting rates for the whole Greenland domain does not exist yet, in contrast to Antarctica (Rignot et al., 2013), thus limiting the effectiveness of including additional complexity at this time. The fact that the few available model reconstructions of stadial–interstadial oceanic temperatures suggest that subsurface warming increases almost homogeneously across the ocean during the stadials, at least in the Nordic Seas (Zhang et al., 2014b; Alvarez-Solas et al., 2018), supports the choice of ignoring spatial oceanic variations as a first approach. This is also in agreement with large-scale subsurface warming suggested by Rasmussen and Thomsen (2004) and Marcott et al. (2011). Thus, considering a spatial variation in oceanic temperatures (and sea ice) around the GrIS is not considered fundamental for this study, which primarily aims to look at the response of the whole GrIS to D-O events.

Finally, atmospheric precipitation and temperature used to perturb the ice-sheet model vary only at long (orbital) timescales, while shorter (millennial-scale) variations related to the D-O events are not considered here. This simplified experimental design is chosen following previous results demonstrating the important role of the ocean in the GrIS evolution over the last glacial periods at orbital timescales (Tabone et al., 2018). The experiments here allow us to directly investigate how millennial-scale variability in the ocean can impact the evolution of the GrIS. However, we have omitted an important component of the climate system, and to comprehensively understand the effect of millennial-scale fluctuations on Greenland, further experiments should be done by including this variability in air temperature and precipitation.

5 Conclusions

We have assessed the effect of the millennial-scale oceanic variability on the evolution of the GrIS during the LGP. To do so, we used an ice-sheet–shelf model, in which the millennial-scale variability in the ocean was imposed as a fluctuation in the basal melting rate at the grounding line and below the ice shelves, resulting from oceanic temperature anomalies at the subsurface, where warmer (cooler) waters are associated with D-O stadials (interstadials). We first characterised the millennial variability through a sensitivity test for a broad range of values of the perturbed parameters in the submarine melting equation. We showed that the millennial-scale contribution to ice-volume variations during the LGP could have reached peaks of more than 1 m SLE. The southeastern area around Kangerlussuaq fjord, Baffin Bay and the NEGIS regions were found to be very sensitive to millennial-scale variability in the ocean. Ice thicknesses simulated at the marine margin differed by 500–1000 m from those simulated by orbital-only driven oceanic variations. Moreover, imprints of these differences are still found for several tens (hundreds – in certain regions) of kilometers far from the ice–ocean interface due to the velocity-driven upstream propagation of the ice-flow perturbation. Although the aim of this work was far from assessing the true timing and spatial distribution of any GrIS ice discharge that occurred during the D-O events, we showed that considering the millennial-scale variability in the ocean is necessary to reproduce some of the IRD peaks observed in proxy data. Specifically, the basal melting increase during D-O stadials, associated with warmer oceanic waters at the subsurface, could have been responsible for the enhanced release of Greenland icebergs as inferred from North Atlantic sediment cores. Our work thus suggests that millennial-scale-induced changes in ocean circulation and temperature may be important drivers of the GrIS evolution during the LGP, advancing the hypothesis of a potential role of the GrIS in oceanic reorganisations at millennial timescales.